Как найти равенство углов 7 класс

Как доказать, что углы треугольников равны

Как доказать, что углы треугольников равны? Рассмотрим возможные варианты.

Углы треугольников могут быть равны в следующих случаях:

1) Угол — общий (один и тот же угол принадлежит одновременно двум различным треугольникам).

3) Углы при основании равнобедренного треугольника равны.

4) Если дана биссектриса треугольника, то исходный угол разделен ею на два равных угла.

5) Если дана высота треугольника, то она образует два прямых (а значит, равных) угла.

6) Угол, смежный с прямым, есть прямой угол (а значит, они равны между собой).

7) Углы, смежные с равными, равны между собой.

8) Соответствующие углы равных треугольников равны между собой.

9) Если к равным углам прибавить равные углы, то получим равные углы.

10) Если из равных углов вычесть равные углы, то получим равные углы.

11) Внутренние накрест лежащие углы при параллельных прямых и секущей равны между собой.

12) Соответственные углы при параллельных прямых и секущей равны между собой.

13) Углы равны по условию.

14) Углы равны по построению.

15) Углы равны по доказанному.

5 Comments

На вопрос вы так и не ответили. «Как доказать, что углы равны?» а не «В каких случаях углы равны?». Как-то так; информация не полная, а так все отлично.

Равенство углов следует из равенства треугольников. Значит, в большинстве задач, чтобы доказать, что углы равны, нужно доказать равенство треугольников.
Еще можно доказать, что два угла являются углами при основании равнобедренного треугольника, соответственными или внутренними накрест лежащими углами при параллельных прямых и т.д. — об этом сказано выше.

А если в «моём» случае не подходит?

Значит, искать «свой», подходящий вариант.

Спасибо, очень много вариантов! Я уж думала никогда не найду ответ, а тут белая куча ответов! Спасибо!

Признаки равенства треугольников

О чем эта статья:

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

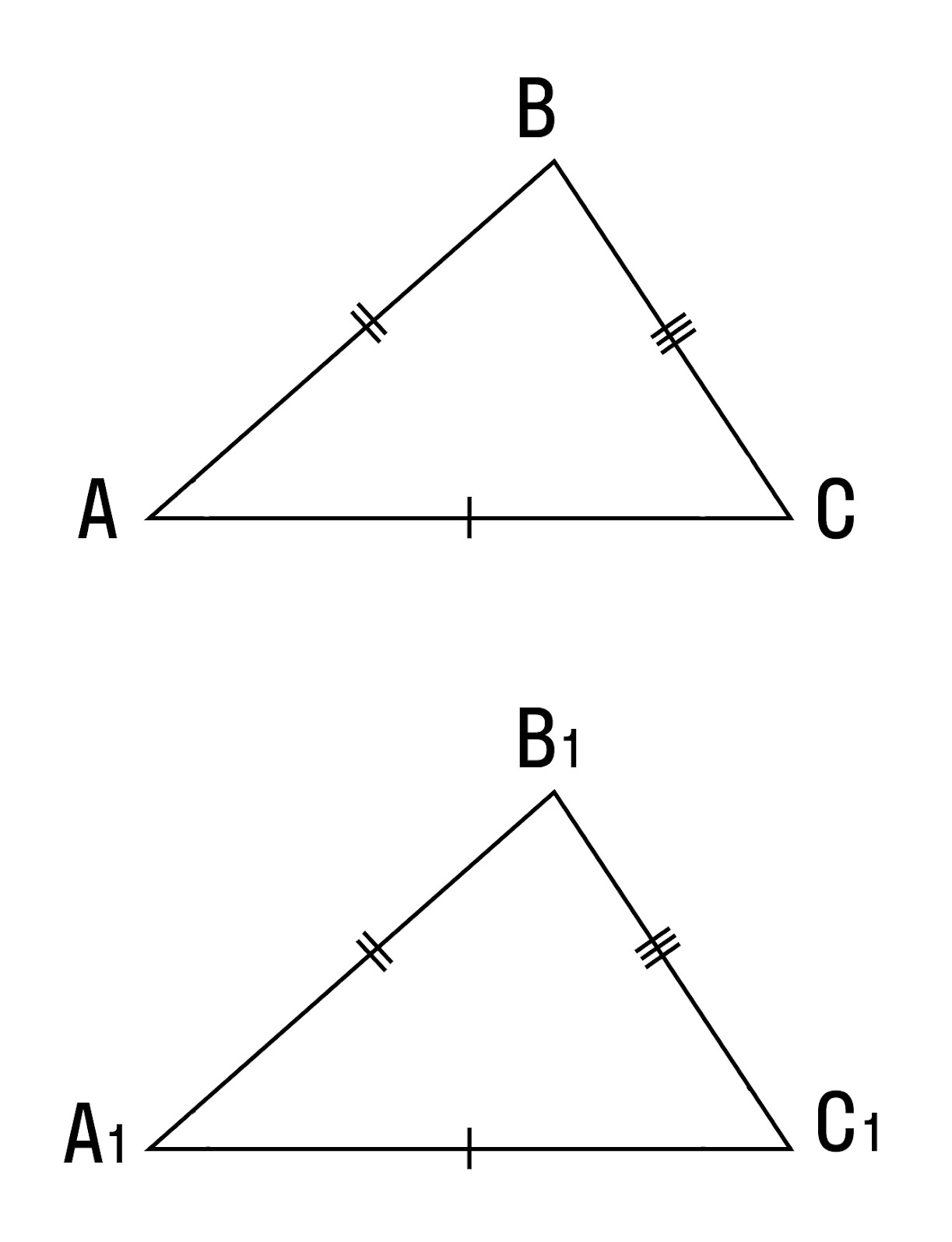
Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

1. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
2. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
3. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
4. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
5. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Как установить и доказать, что треугольники равны

Геометрия как отдельный предмет начинается у школьников в 7 классе. До этого времени они касаются геометрических задач достаточно лёгкой формы и в основном того, что можно рассмотреть на наглядных примерах: площади комнаты, земельного участка, длины и высоты стен в помещениях, периметра плоских предметов и прочее. В нача ле изучения непосредственно геометрии появляются первые сложности, такие, например, как понятие прямой, так как потрогать руками эту прямую нет возможности. Что касается треугольников -это самый простой вид многоугольников, содержащий всего три угла и три стороны.

Тема треугольников одна из основных важных и больших тем школьной программы в геометрии 7−9 классов. Усвоив её хорошо, возможно решать очень сложные задачи. При этом можно изначально рассматривать совершенно другую геометрическую фигуру, а затем разделить её для удобства на подходящие треугольные части.

Как доказать, что треугольники равны

Для работы над доказательством равенства ∆ ABC и ∆A1B1C1 нужно хорошо усвоить признаки равенства фигур и уметь ими пользоваться. Перед изучением признаков необходимо научиться определять равенство сторон и углов простейших многоугольников.

Чтобы доказать, что углы треугольников равны, помогут следующие варианты:

1. ∠ α = ∠ β исходя из построения фигур.
2. Дано в условии задания.
3. При двух параллельных прямых и наличии секущей могут образоваться как внутренние накрест лежащие, так и соответственные ∠ α = ∠ β.
4. Прибавляя (вычитая) к (из) ∠ α = ∠ β равные углы.
5. Всегда сходны вертикальные ∠ α и ∠ β
6. Общий ∠ α, одновременно принадлежащий ∆ MNK и ∆ MNH .
7. Биссектриса делит ∠ α на два равнозначных.
8. Смежный с ∠90° — угол, равный исходному.
9. Смежные равным углам равны.
10. Высота образует два смежных ∠90° .
11. В равнобедренном ∆ MNK при основании ∠ α = ∠ β.
12. В равных ∆ MNK и ∆ SDH соответствующие ∠ α = ∠ β.
13. Доказанное ранее равенство ∆ MNK и ∆ SDH .

Это интересно: Как найти периметр треугольника.

3 признака равенства треугольников

Доказательство равенства ∆ ABC и ∆A1B1C1 очень удобно производить, опираясь на основные признаки тождественности этих простейших многоугольников. Существует три таких признака. Они являются очень важными при решении многих геометрических задач. Стоит рассмотреть каждый.

• I признак. Две стороны и угол между ними ∆ ABC соответственно = двум сторонам и углу ∆ A1B1C1 , следовательно, треугольники равны.
• II признак. Сторона и два прилежащих к ней угла ∆ ABC соответственно = стороне и двум углам ∆ A1B1C1 , => треугольники равны.
• III признак. Если все стороны ∆ ABC соответственно = сторонам ∆ A1B1C1 , то имеющиеся треугольники равны.

Перечисленные выше признаки являются теоремами и доказываются методом наложения одной фигуры на другую, соединения вершин соответственных углов и начала лучей. Доказательства равенства треугольников в 7 классе описаны в очень доступной форме, но сложны в изучении школьниками на практике, так как содержат большое количество элементов, обозначенных заглавными латинскими буквами. Это не совсем привычно для многих учеников на момент начала изучения предмета. Подростки путаются в названиях сторон, лучей, углов.

Доказательство подобия треугольников

Чуть позже появляется ещё одна важная тема «Подобие треугольников». Само определение «подобие» в геометрии означает схожесть формы при различии размеров. Для примера можно взять два квадрата, первый со стороной 4 см, а второй 10 см. Эти виды четырёхугольников будут похожи и, одновременно, иметь отличие, поскольку второй будет больше, причём каждая сторона увеличена в одинаковое количество раз.

В рассмотрении темы подобия также приводятся 3 признака:

• Первый — о двух соответственно равных углах двух рассматриваемых треугольных фигур.
• Второй — об угле и образующих его сторонах ∆ MNK , которые равны соответственным элементам ∆ SDH .
• Третий — указывает на пропорциональность всех соответственных сторон двух нужных фигур.

Как же доказать, что треугольники подобны? Достаточно воспользоваться одним из выше перечисленных признаков и грамотно описать весь процесс доказательства задания. Тема подобия ∆ MNK и ∆ SDH проще воспринимается школьниками исходя из того, что к моменту её изучения ученики уже свободно пользуются обозначениями элементов в геометрических построениях, не путаются в огромном количестве названий и умеют читать чертежи.

Завершая прохождение обширной темы треугольных геометрических фигур, учащиеся уже в совершенстве должны знать, как доказать равенство ∆ MNK = ∆ SDH по двум сторонам, установить равны два треугольника или нет. Учитывая, что многоугольник, имеющий ровно три угла — это одна из важнейших геометрических фигур, к усвоению материала следует подойти серьёзно, уделяя особое внимание даже мелким фактам теории.

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/priznaki-ravenstva-treugolnika

[/spoiler]

Как доказать, что углы треугольников равны? Рассмотрим возможные варианты.

Углы треугольников могут быть равны в следующих случаях:

1) Угол — общий (один и тот же угол принадлежит одновременно двум различным треугольникам).

2) Вертикальные углы равны.

3) Углы при основании равнобедренного треугольника равны.

4) Если дана биссектриса треугольника, то исходный угол разделен ею на два равных угла.

5)  Если дана высота треугольника, то она образует два прямых (а значит, равных) угла.

6) Угол, смежный с прямым, есть прямой угол (а значит, они равны между собой).

7) Углы, смежные с равными, равны между собой.

8) Соответствующие углы равных треугольников равны между собой.

9) Если к равным углам прибавить равные углы, то получим равные углы.

10) Если из равных углов вычесть равные углы, то получим равные углы.

11) Внутренние накрест лежащие углы при параллельных прямых и секущей равны между собой.

12) Соответственные углы при параллельных прямых и секущей равны между собой.

13) Углы равны по условию.

14) Углы равны по построению.

15) Углы равны по доказанному.

Угол. Равенство углов. Измерение углов. Построение углов. Урок №12
Проведем два луча и , которые выходят из одной точки. Получим геометрическую фигуру, которая называется углом. Лучи и называются сторонами угла, точка – вершиной угла. Угол обозначается знаком «» и тремя большими буквами: и (читается: угол АОВ или угол ВОА). При этом буква, обозначающая вершину угла, пишется посередине. Угол можно обозначать и одной буквой – названием его вершины, например .
Два угла называются равными, если их можно наложить друг на друга так, чтобы они совпали.
Два дополнительных друг другу лучи образуют развернутый угол.

Прямым углом называют половину развернутого угла. Величина прямого угла равен 90 °. Величина развернутого угла равна 180 °.
Угол, величина которого меньше прямого угла, называется острым. Угол, величина которого больше прямого угла и меньше развернутого угла называется тупым.
Построение угла заданной величины
Для того, чтобы построить угол в 40 °, надо:
1. Отметить произвольную точку и обозначить её, например, буквой А.
2. Провести луч с началом в точке А и на нем обозначить произвольную точку В. Таким образом получим луч АВ.
3. Наложить транспортир так, чтобы центр его совпал с точкой А, а луч АВ прошел через начало отсчета на шкале.
4. На этой же шкале транспортира найти штрих, который соответствует 40 °. Обозначить на чертеже точку С напротив штриха с отметкой 40 °.
5. Провести луч АС. Построенный угол ВАС и является искомым. .

Полный урок смотрите в следующем видео:

Домашнее задание:

1. Начерти три угла. Измерь их с помощью транспортира.
2. Развернутый угол разделен на два угла так, что один угол больше второго на 20 °. “Найди градусную меру каждого угла.
3. Пользуясь транспортиром, построй углы, равные 60 °, 100 °, 155 °.
4. Развернутый угол разделен на две части так, что один из образованных углов больше другого на 36 °. Найди градусную меру каждого из углов.
5. Развернутый угол разделен на три части так, что первый из образованных углов в 2 раза меньше второго и в 3 раза меньше третьего. Найди градусную меру каждого из углов и построй их.
6. Начерти (в разных положениях): а) три прямых угла; б) три острых угла; в) три тупых угла. С помощью транспортира измерь и запиши их градусные меры.
7. Прямой угол разделен на два угла так, что величина одного угла в 4 раза больше второго угла. Вычисли градусную меру каждого угла.
8. Запиши все углы, изображенные на рисунке:

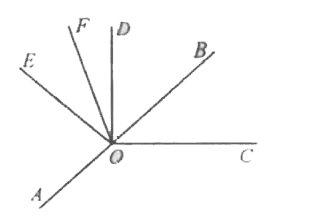
9. Вычисли величину угла :

10. Одна сторона треугольника в 2 раза меньше другой стороны и на 12м меньше третьей стороны. Найди стороны треугольника, если его периметр равен 92м.
11. Сумма длин первой и второй сторон треугольника 50м, сумма длин второго и третьего сторон – 58м. Найди периметр треугольника, если сумма длин первой и третьей сторон 58м.

Угол — это геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла). Плоскость, содержащая обе стороны угла, делится углом на две области.

Содержание:

1. Луч
2. Понятие угла
3. Измерение углов
4. Равенство углов. Биссектриса угла
5. Смежные углы
6. Вертикальные углы

Луч

На рисунке 2.47 изображена прямая , на ней отмечена точка В, которая разделяет прямую на три части:

1)    первая состоит из точек, лежащих левее точки В;

2)    вторая состоит из самой точки В;

3)    третья состоит из точек, лежащих правее точки В.

Объединение первого или третьего множеств с точкой В называется лучом или полупрямой. Таким образом, точка В определила на прямой два луча.

Точка В называется началом каждого из этих лучей или начальной точкой полупрямой.

Луч обозначается латинскими буквами: одной строчной (например, на рис. 2.48) или двумя заглавными, одна из которых обозначает начало луча, а вторая — какую-либо точку на луче (например, луч ВС на рис. 2.49).

Полупрямые прямой , на которые она разбивается точкой В, называются дополнительными.

В повседневной жизни мы часто употребляем понятие направления: направление движения пешехода или автомобиля, направление удара мяча в

футбольном матче, направление полета самолета или ракеты и т. д.

При задании направления используют понятие луча. В геометрии считают, что направление задается лучом, а определить понятие «направление» можно как множество лучей, сонаправлен-ных (одинаково направленных) с данным (рис. 2.50).

1.    Если два луча лежат на одной прямой, то будем считать их одинаково направленными, если один из них содержится в другом, и противоположно направленными, если один из них не содержится в другом.

2.    Если два луча параллельны, но не лежат на одной прямой, то проведем через их начала плоскость, которая разделит пространство на два полупространства. Если лучи лежат в одном из этих полупространств, то они сонаправлены (рис. 2.51). Если же лучи лежат в разных полупространствах, то они противоположно направлены (рис. 2.52).

Понятие угла

На рисунке 2.53 два луча OA и ОВ имеют общее начало. Эти два луча с общим началом всегда лежат в одной плоскости.

При таком расположении лучи разбивают плоскость, которую они образуют, на две части (рис. 2.54). Эти части плоскости вместе с образовавшими их лучами в геометрии называются углами.

Определение. Углом называется фигура, состоящая из двух различных лучей с общим началом и ограниченной ими части плоскости.

На рисунке 2.54 лучи OA и ОВ имеют общее начало — точку О и разбивают плоскость на две части. Исходя из определения угла, получили два различных угла.

Точка, из которой выходят ограничивающие угол лучи, называется вершиной угла, а сами лучи — сторонами угла (рис. 2.55). Лучи OA и ОС на этом рисунке определяют два угла.

Весь угол изобразить на рисунке нельзя, как нельзя на рисунке изобразить весь луч. Каждый угол в действительности продолжается бесконечно. На рисунке 2.56 выделены только части изображенных углов.

Слово «угол» иногда заменяют знаком . Часто при изображении угла чертят только выходящие из вершины начальные участки его сторон, а ту часть, которую хотят указать, обозначают дужкой (рис. 2.57)

Угол обозначается или одной заглавной буквой, поставленной у вершины угла, например: (рис. 2.57), или тремя буквами, из которых одна ставится при вершине угла, а две другие — у каких-нибудь точек сторон, например: (рис. 2.57). Буква, стоящая при вершине угла, всегда записывается между двумя другими буквами. Иногда угол обозначают цифрой, поставленной внутри угла (рис. 2.58).

Для изучения свойств углов используется понятие луча, проходящего между сторонами угла.

Определение. Луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла.

На рисунке 2.59 луч ОВ проходит между сторонами угла АОС, так как он исходит из вершины угла АОС и пересекает отрезок MP. Концы отрезка MP лежат на сторонах угла АОС.

Возьмем луч АС (рис. 2.60) и будем поворачивать его вокруг точки А против часовой стрелки, например, до положения АВ, тогда его последовательные положения «заметут» угол со сторонами АС и АВ.

Продолжая вращать луч в том же направлении, мы будем получать все новые и новые углы. В определенный момент оба луча составят прямую линию (рис. 2.61). Такой угол называется развернутым углом.

Развернутый угол есть часть плоскости, ограниченная прямой, т. е. полуплоскость (рис. 2.62). Сторонами развернутого угла являются две дополнительные полупрямые.

Определение. Развернутым углом называют угол, стороны которого являются дополнительными полупрямыми одной прямой.

Если продолжить вращение луча дальше, чем показано на рисунке 2.62, то будут получаться новые углы (рис. 2.63), пока луч не вернется в свое первоначальное положение (рис. 2.64).

Самый большой возможный угол, полученный в ходе вращения луча, называется полным углом. Полный угол, в сущности, есть вся плоскость (рис. 2.65), а не ее часть, ограниченная двумя лучами.

Измерение углов

Каждый угол характеризуется его величиной, которая называется градусной мерой угла. Измерение углов осуществляется аналогично измерению отрезков — оно основано на сравнении их с углом, принятым за единицу измерения. Обычно за единицу измерения углов принимают градус — угол, равный части развернутого угла. Градус обозначают знаком .

Градусную меру часто называют просто величиной угла. Величина угла, равного  части градуса, называется минутой и обозначается знаком , часть минуты называется секундой и обозначается знаком . Например, угол в 60 градусов 32 минуты 17 секунд записывается так: 60°32’17”.

Так как градус составляет часть развернутого угла, развернутый угол равен 180°.

Определение. Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле, называют градусной мерой угла.

В зависимости от градусной меры углы бывают трех видов: острые, прямые и тупые.

Определение. Угол, равный 90°, называют прямым углом. Прямой угол обозначается буквой d. Угол, меньший 90°, называют острым углом. Угол, больший 90°, называют тупым углом.

Градусные меры угла обозначаются или так же, как сами углы, или буквами греческого алфавита. Например, запись читается: величина (или градусная мера) угла АОВ равна 45 градусам. На рисунке 2.66 величина острого угла записана: , читаем: величина угла меньше 90 градусов. Аналогично записываются и читаются величины прямого и тупого углов (рис. 2.67, 2.68).

Основные свойства измерения углов

Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Например, на рисунке 2.69 луч ОС проходит между сторонами угла АОВ, градусная мера угла АОВ равна сумме градусных мер углов АОС и СОВ, то есть

Для измерения градусных мер углов (величин углов) на уроках геометрии применяется транспортир (рис. 2.70). На рисунке 2.71 показано, как с помощью транспортира можно измерять угол в 30°, 90°, 120°. На рисунке 2.72 показано, как с помощью транспортира можно отложить от полупрямой OA в верхнюю полуплоскость угол с данной градусной мерой 60°.

Пример: 

Между сторонами угла COD, равного 120°, проходит луч OA. Найдите углы СОА и AOD, если их градусные меры относятся как 4:2.

Решение: 

Из условия задачи имеем:

1.    

2.    Луч OA проходит между сторонами угла COD.

3.    

Найдите градусные меры углов СОА и AOD.

4.     (2, свойства измерения углов).

5.    Так как градусные меры углов СОА и AOD относятся как 4:2, то можно считать, что состоит из 6 частей (1, 2, 3, 4).

6.    

Равенство углов. Биссектриса угла

Как и при определении равенства отрезков, рассматриваются два определения равенства углов.

Определение. Углы равны, если равны их градусные меры.

На рисунке 2.73 изображены два угла ABC и DEM, величины которых равны, а значит, по определению, эти углы равны. Равенство углов обозначается так:

Определение. Углы называются равными, если их можно совместить наложением друг на друга.

Развернутые углы при наложении всегда могут быть совмещены. Отсюда следует, что все развернутые углы равны между собой. Полные углы равны между собой.

Пусть есть два угла: (рис. 2.74). Если угол 1 наложить на угол 2 так, чтобы их вершины совпали, одна из сторон угла 1 совместится со стороной угла 2, но при этом угол 1 составит только часть угла 2 (рис. 2.75). В этом случае говорят, что величина угла 1 меньше величины угла 2. Можно сформулировать по-другому: угол 1 меньше угла 2.

Используя понятие равенства углов, можно дать определение одному из важных понятий геометрии — биссектрисе угла.

Определение. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.

На рисунке 2.76 луч ОМ — биссектриса угла АОВ, при этом

Смежные углы

Определение. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.

На рисунке 2.77 являются смежными, так как лучи OA и ОС — дополнительные полупрямые, а луч ОВ — общая сторона этих углов.

Теорема 4.

Сумма смежных углов равна 180°.

Из теоремы 4 вытекают следующие следствия — свойства смежных углов.

Следствие 1. Если два угла равны, то смежные с ними углы равны.

Следствие 2. Угол, смежный с прямым углом, есть прямой угол.

Следствие 3. Угол, смежный с острым, является тупым, а смежный с тупым — острым.

Вертикальные углы

На рисунке 2.78 изображены две пересекающиеся в точке О прямые АВ и CD. При пересечении этих прямых образовалось четыре угла:

Определение. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.

На рисунке 2.78 углы 1 и 3, 2 и 4 вертикальные.

Теорема 5.

Вертикальные углы равны.

Очевидно, что две пересекающиеся прямые образуют смежные и вертикальные углы. Смежные углы дополняют друг друга до 180°. Угловая мера меньшего из них называется углом между прямыми.

Пример:

На рисунке 2.79 угол COD равен 30°. Чему равны углы АОК и DOK?

Решение: 

Из условия задачи имеем:

1.    Прямые СК и AD пересекаются в точке О.

2.    (рис. 2.79)

3.    Найдите углы АОК и DOK.

4.    Углы COD и АОК вертикальные (1, определение вертикальных углов).

5.     (2, свойство вертикальных углов).

6.    Угол DOK смежный с углом COD (1, определение смежных углов).

7.     (6, свойство смежных углов).

Эта лекция взята со страницы полного курса лекций по изучению предмета “Математика”:

• Математика решение заданий и задач

Смотрите также дополнительные лекции по предмету “Математика”: