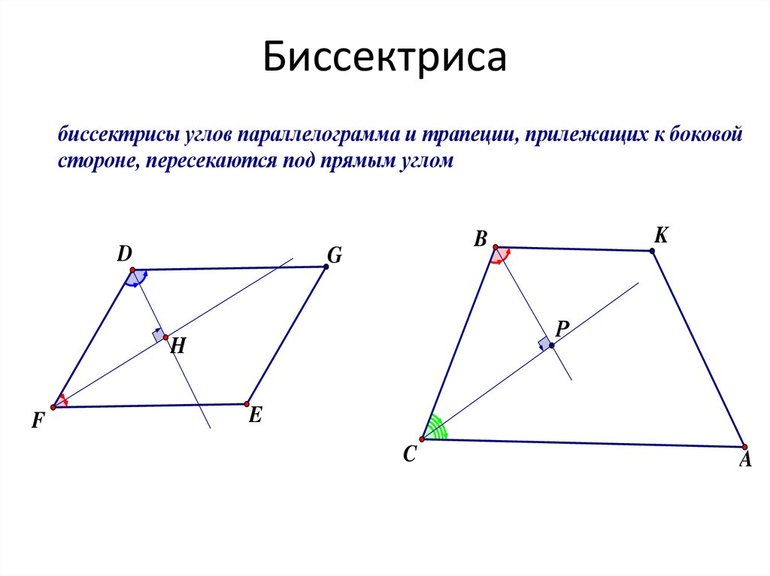
Утверждение.
Биссектриса параллелограмма отсекает от него равнобедренный треугольник.

Дано: ABCD — параллелограмм,
AF — биссектриса ∠BAD,
F ∈ BC.
Доказать: ∆ ABF — равнобедренный.
Доказательство:
1) ∠BAF=∠DAF (так как AF — биссектриса ∠BAD по условию).
2) ∠BFA=∠DAF (как внутренние накрест лежащие углы при BC ∥ AD м секущей AF).

3) Следовательно, ∠BAF=∠BFA.
4) Следовательно, треугольник ABF — равнобедренный с основанием AF (по признаку).
5) Следовательно, AB=BF.
Что и требовалось доказать.
Хотя равенство сторон AB и BF доказывать не просили, доказательство того, что биссектриса параллелограмма отсекает от него равнобедренный треугольник, нужно как раз для обоснования равенства одной стороны и отсеченного отрезка на другой стороне параллелограмма.
Равнобедренный треугольник в параллелограмме
Биссектриса параллелограмма может быть проведена из вершины острого или тупого угла фигуры. Доказательство теоремы о равнобедренности образуемых прямой треугольников в этих случаях имеет аналогичный порядок. Чтобы доказать утверждение, нужно знать признак равнобедренности треугольника:
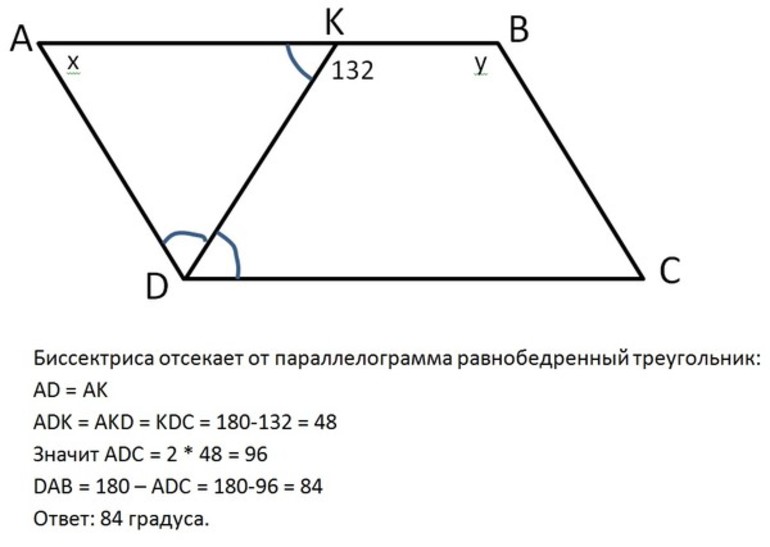
- Согласно условию, проведенная из острого угла А биссектриса AF делит одну из сторон ABCD на 2 отрезка.
- Свойство биссектрисы позволяет утверждать, что углы FAD и BAF равны между собой.
- Определение внутренних накрест лежащих углов, которые образует секущая AF с прямыми ВС и AD, приводит к выводу о равенстве FAD и BFA.
- Поскольку углы BFA и BAF равны, этот признак свидетельствует о равнобедренности треугольника ABF.
- Стороны АВ и BF являются равными и соответствуют отрезку m, который образован при делении ВС биссектрисой.
С помощью аналогичных рассуждений можно доказать, что биссектриса тупого угла параллелограмма делит противоположную сторону на отрезки и отсекает от него равнобедренный треугольник.
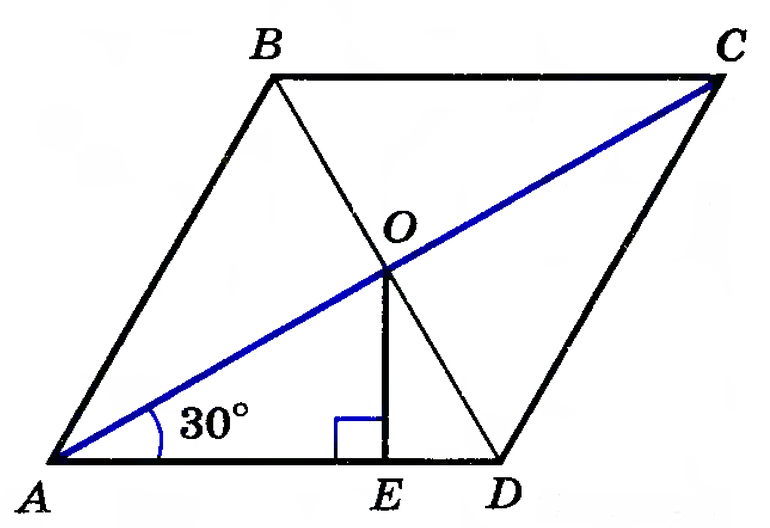
Точка пересечения прямых
Согласно свойству, проведенные из смежных углов параллелограмма биссектрисы пересекаются в точке на противоположной стороне, если она в 2 раза больше меньшей. Доказать это утверждение можно следующим способом:
- В равнобедренном треугольнике АВО сторона АО является биссектрисой четырехугольника АВСD.
- Признак равнобедренности предполагает равенство АВ и ВО.
- Согласно свойству, равенство СО и СD свидетельствует о равнобедренности треугольника СDО.
- Стороны АВ и СD равны как противолежащие, из чего следует равенство ВО и СО.
- Поскольку АВ и ВО равны, то ВО = СО, поэтому АВ равна половине ВС, значит большая сторона фигуры в 2 раза превышает величину меньшей.
Доказательство свойства позволяет предположить, что биссектрисы смежных углов пересекаются внутри либо вне параллелограмма. При этом одна сторона больше или меньше половины другой. Если ее величина больше половины соседней, значит прямые пересекутся внутри фигуры.
Биссектрисы, проведенные через смежные углы, пересекаются с продолжением противоположных сторон параллелограмма в вершинах ромба. В зависимости от величины другой стороны, ромб совпадает с ним либо обладает большим или меньшим периметром. Если частить с построением этой фигуры, то длины сторон параллелограмма будут бесконечными.
Свойства односторонних углов
Параллелограмм АВСД имеет смежные углы при параллельных прямых АВ и СД, обозначенные а1 и а2. Для доказательства теоремы о перпендикулярности биссектрис нужно знать свойства смежных углов, сумма которых равна 180 градусам.
Поскольку биссектрисы можно провести внутри острого или тупого угла параллелограмма, то величину смежного с ним внешнего угла можно сложить, получив 180 градусов. Если обозначить их через АО и ДЕ, то углы ОАВ и ЕДС будут равны половинам а1 и а2 соответственно. Так как а1 + а2 = 180, то (а1 + а2) / 2 = 90, значит АО и ДЕ образуют прямой угол АКД.
Применять свойство биссектрис можно при нахождении периметра фигуры. Должны быть известны данные о соотношениях или длинах отрезков, образованных при пересечении противолежащей стороны биссектрисой. Например, она делит на отрезки ВК и КС сторону параллелограмма ABCD, величины которых известны.
Формула определения периметра будет иметь вид: P=2 (n+n+m). Где ВС=BК+КC=n+m, а АВ=ВК=n по свойству биссектрисы. С учетом признака равнобедренности треугольника можно построить эту прямую, дополнив рисунок фигуры без транспортира с помощью циркуля.
Противолежащие углы и биссектрисы
Согласно свойству параллельных прямых, биссектрисы a и b проходят параллельно друг другу. Они образуют внутри фигуры со сторонами mnkp другой параллелограмм, следовательно, он обладает параллельными противоположными сторонами. Прямые, на которых они лежат, соответствуют сторонам исходной фигуры, поэтому ее биссектрисы a и b являются равными.
Углы, которые образованы отрезками a и m, а также b и k, согласно свойствам биссектрис и параллелограммов, равны. Противолежащие равные по величине углы, образованные отрезками mp и nk, можно разделить пополам. Прямая b, пересекающая отрезки n и p, образует с ними накрест лежащие углы, признак которых состоит в их равенстве. Они равны разделенным пополам противоположным и являются соответственными при параллельных прямых n и p.
Вершины образуемого прямоугольника
Биссектрисы параллелограмма пересекаются в точках, представляющих собой вершины прямоугольника, что можно доказать следующим образом:
- Согласно исходным данным, параллелограмм ABCД имеет внешние углы, через вершины которых В и С проведены прямые, разделяющие их пополам.
- Если К, М, Р и О представляют собой точки пересечения биссектрис, исходящей из вершин фигуры, то они образуют четырехугольник.
- По свойству смежных внутренних углов, образуемых параллельными прямыми и секущей, все стороны четырехугольника КМРО перпендикулярны между собой.
- Если через середину ВС фигуры провести медиану треугольника ВКС в параллелограмме, то эта точка Х разделит ВС на равные отрезки ВХ и СХ.
- Отсюда следует равенство углов ХКС, КСХ и КСТ, где Т — это точка, принадлежащая прямой СД.
- Вывод из доказательства: прямые СД и КХ параллельны.
Аналогичным способом можно доказать параллельность других сторон прямой СД. Следовательно, диагональ КР образованного биссектрисами параллелограмма прямоугольника КМРО содержит точки Х и Т. Доказательство предполагает следующее равенство: КР = КХ + ХТ + ТР = ХС + СД + ТД = ВС + СД, поэтому величина диагонали равна сумме двух смежных сторон параллелограмма.
Ромб и его диагонали
Параллелограмм, имеющий биссектрису, которая совпадает с его диагональю, представляет собой ромб. Чтобы доказать это, нужно провести диагональ AC, соединяющую противоположные вершины ABCD. Способ доказательства теоремы основан на равенстве противолежащих углов параллелограмма.
Согласно свойству биссектрисы, отрезок АС делит пополам углы BCD и BAD. Они имеют одинаковую величину, поскольку противоположные углы равны. Диагональ АС — основание треугольников ACB и ACD. Согласно признаку равнобедренности АВ и АС, а также AD и CD, равны между собой. По свойству равенства противоположных сторон параллелограмма AB = CD и AD = BC.
Фигура ABCD, представляющая собой по условию параллелограмм, имеет равные по величине AB, AD, BC и CD в соответствии с доказательством. Отсюда следует, что параллелограмм ABCD по определению ромб. В нем биссектриса АС — это его диагональ.
Примеры решения задач
Биссектрисы смежных углов параллелограмма пересеклись в точке на его противолежащей стороне. Зная его меньшую сторону, можно найти большую, а также наоборот. Допустим, что длина меньшей стороны фигуры составляет 5 сантиметров.
Обозначив вершины фигуры A, B, C, D, а точку на AD буквой Р, достаточно иметь в виду, что AD=AР+РD=AB+CD. Это доказывает признак равенства накрест лежащих углов СВР и АРВ, а также ВСР и СРD при параллельных прямых. Формула для нахождения большей стороны будет иметь вид: AD=2AB=10, поскольку AB = CD. При необходимости найти меньшую можно по формуле: AD=AB/2.

По условию задачи биссектриса, исходящая из острого угла параллелограмма, разделяет его противоположную сторону на отрезки 73 мм и 54 мм, если считать от вершины тупого угла. Требуется вычислить периметр параллелограмма ABCD. Точка Е делит сторону ВС на отрезки заданной длины, поскольку АЕ — биссектриса угла ВАD. Эта прямая представляет собой секущую для параллельных AD и BC.
Отсекая равнобедренный треугольник АВЕ, биссектриса ВЕ является его основанием, поэтому сторона параллелограмма АВ равна отрезку ВЕ, длина которого по условию 73 мм. В сумме ВЕ и ЕС равны ВС, что составляет 127 мм. Отсюда периметр ABCD соответствует удвоенной сумме его сторон: Р = 2 (73+127) = 400 мм. Чтобы найти большую сторону параллелограмма ABCD при известном периметре 128 мм, можно использовать аналогичное доказательство равнобедренности треугольника.
По условию соотношение отрезков, образуемых точкой пересечения биссектрисы DЕ с противоположной стороной ВС, равно 4:3, если считать от острого угла при вершине А. Из равенства противоположных сторон ABCD и признака равнобедренного треугольника следует AD=BC=АЕ=4х, а ЕВ=3х, поэтому CD=АЕ+ЕВ=4х+3х=7х. Зная периметр ABCD, можно составить уравнение Р=2 (7х+4х)=128. Отсюда 22х=128, а х=32, поэтому большая сторона параллелограмма CD=32*7=224 мм.
Выпускники, которые рассчитывают успешно сдать ЕГЭ, в обязательном порядке должны повторить тему «Свойства биссектрисы параллелограмма». Как показывает статистика, при прохождении аттестационного испытания задачи по данному разделу планиметрии вызывают сложности у большого количества учащихся. При этом задания, в которых необходимо применить свойства биссектрисы угла параллелограмма, встречаются в ЕГЭ ежегодно. Таким образом, справляться с ними должны все учащиеся.
Образовательный портал «Школково» предлагает выстроить процесс подготовки к прохождению аттестационного испытания по-новому. Занимаясь вместе с нашим ресурсом, выпускники смогут определить наиболее сложные для себя темы и ликвидировать пробелы в знаниях.
Чтобы задания ЕГЭ не вызывали трудностей, рекомендуем вначале повторить основные понятия и свойства биссектрисы параллелограмма. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».
Для того чтобы окончательно понять принцип решения задач по данному разделу планиметрии, мы рекомендуем выполнить соответствующие упражнения. Большая подборка заданий различного уровня сложности представлена в разделе «Каталог». Для каждого упражнения на сайте приведен алгоритм решения и дан правильный ответ. Последовательно выполняя их, учащиеся смогут понять, как правильно применять свойства биссектрисы внутреннего угла параллелограмма.
Получать новые знания и оттачивать собственные навыки по данной теме или, например, в решении задач на тему «Прямоугольник» в ЕГЭ учащиеся могут в онлайн-режиме, находясь в Москве или любом другом российском городе. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.
Рассмотрим одну из базовых задач планиметрии — биссектриса угла параллелограмма делит противолежащую сторону на отрезки.
Утверждение.
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
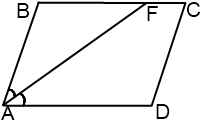
Пусть биссектриса угла A параллелограмма ABCD делит противолежащую сторону на отрезки BF=m, FC=n. Тогда:
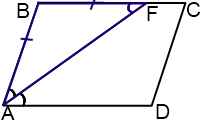 1)∠BAF=∠FAD
1)∠BAF=∠FAD
(так как AF — биссектриса угла A по условию);
2) ∠BFA=∠FAD (как внутренние накрест лежащие при AD ∥ BC и секущей AF);
3) следовательно, ∠BAF=∠BFA;
4) следовательно, треугольник ABF — равнобедренный (по признаку);
5) следовательно, AB=BF=m.
Этот рисунок иллюстрирует случай, когда дана биссектриса острого угла параллелограмма.
Если в задаче сказано, что биссектриса тупого угла параллелограмма делит сторону на отрезки, рассуждения аналогичны.
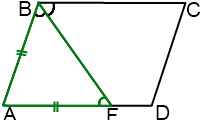
На базе этой задачи существует много других задач. Например: биссектриса угла A параллелограмма ABCD делит противолежащую сторону BC на отрезки BF=m, FC=n. Найти периметр параллелограмма.
После доказательства того, что AB=BF=m, нахождение периметра не вызывает затруднений: P=2(AB+BC)=2(m+m+n).
Содержание:
С четырехугольником вы уже знакомились на уроках математики. Дадим строгое определение этой фигуры.
Определение четырехугольника:
Четырехугольником называется фигура, состоящая из четырех точек (вершин четырехугольника) и четырех отрезков, которые их последовательно соединяют (сторон четырехугольника). При этом никакие три его вершины не лежат на одной прямой и никакие две стороны не пересекаются.
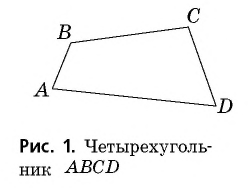
На рисунке 1 изображен четырехугольник с вершинами 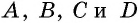
Говорят, что две вершины четырехугольника являются соседними вершинами, если они соединены одной стороной; вершины, которые не являются соседними, называют противолежащими вершинами. Аналогично стороны четырехугольника, имеющие общую вершину, являются соседними сторонами, а стороны, не имеющие общих точек,— противолежащими сторонами. На рисунке 1 стороны 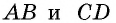 — соседние для стороны
— соседние для стороны 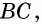 а сторона
а сторона 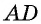 — противолежащая стороне
— противолежащая стороне 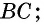 вершины
вершины 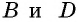 — соседние с вершиной
— соседние с вершиной 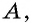 а вершина
а вершина 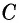 — противолежащая вершине
— противолежащая вершине 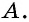
Четырехугольник обозначают, последовательно указывая все его вершины, причем буквы, которые стоят рядом, должны обозначать соседние вершины. Например, четырехугольник на рисунке 1 можно обозначить 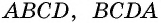 или
или 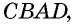 но нельзя обозначать
но нельзя обозначать 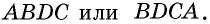
Определение
Диагональю четырехугольника называется отрезок, соединяющий две противолежащие вершины.
В четырехугольнике 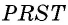 (рис. 2) диагоналями являются отрезки
(рис. 2) диагоналями являются отрезки 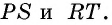 Следует отметить, что любой четырехугольник имеет диагональ, которая делит его на два треугольника.
Следует отметить, что любой четырехугольник имеет диагональ, которая делит его на два треугольника.
Определение
Периметром четырехугольника называется сумма длин всех его сторон. Периметр четырехугольника (как и треугольника) обозначают буквой 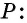
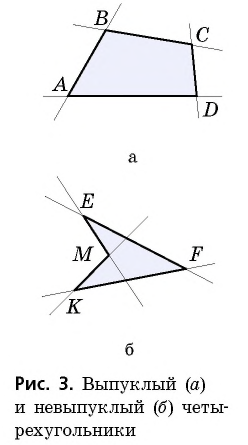
Любой четырехугольник ограничивает конечную часть плоскости, которую называют внутренней областью этого четырехугольника (на рис. 3, а, б она закрашена).
На рисунке 3 изображены два четырехугольника и проведены прямые, на которых лежат стороны этих четырехугольников. В четырехугольнике 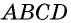 эти прямые не проходят через внутреннюю область — такой четырехугольник является выпуклым (рис. 3, а). В четырехугольнике
эти прямые не проходят через внутреннюю область — такой четырехугольник является выпуклым (рис. 3, а). В четырехугольнике 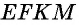 прямые
прямые 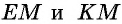 проходят через внутреннюю область — этот четырехугольник является невыпуклым (рис. 3, б).
проходят через внутреннюю область — этот четырехугольник является невыпуклым (рис. 3, б).
Определение
Четырехугольник называется выпуклым, если он лежит по одну сторону от любой прямой, содержащей его сторону.
Действительно, четырехугольник 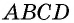 на рисунке 3, а лежит по одну сторону от любой из прямых
на рисунке 3, а лежит по одну сторону от любой из прямых 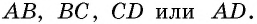 В школьном курсе геометрии мы будем рассматривать только
В школьном курсе геометрии мы будем рассматривать только
выпуклые четырехугольники (другие случаи будут оговорены отдельно).
Определение
Углом (внутренним углом) выпуклого четырехугольника  при вершине
при вершине  называется угол
называется угол 
Угол, смежный с внутренним углом четырехугольника при данной вершине, называют внешним углом четырехугольника при данной вершине.
Углы, вершины которых являются соседними, называют соседними углами, а углы, вершины которых являются противолежащими,— противолежащими углами четырехугольника.
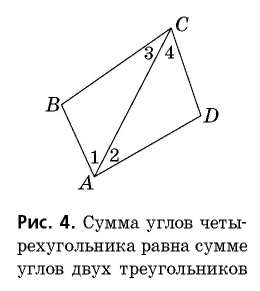
Теорема (о сумме углов четырехугольника)
Сумма углов четырехугольника равна 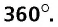
Доказательство:
В данном четырехугольнике 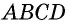 проведем диагональ, которая делит его на два треугольника (рис. 4). Поскольку
проведем диагональ, которая делит его на два треугольника (рис. 4). Поскольку 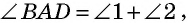
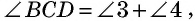 сумма углов четырехугольника
сумма углов четырехугольника 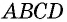 равна сумме всех углов треугольников
равна сумме всех углов треугольников 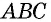 и
и 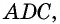 то есть равна
то есть равна 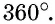 Теорема доказана.
Теорема доказана.
Пример:
Углы четырехугольника 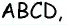 соседние с углом
соседние с углом 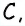 равны, а противолежащий угол в два раза больше угла
равны, а противолежащий угол в два раза больше угла 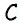 (см. рис. 1). Найдите угол
(см. рис. 1). Найдите угол 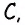 если
если 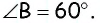
Решение:
Углами, соседними с углом 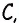 являются углы
являются углы 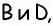 а углом, противолежащим к
а углом, противолежащим к 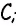 — угол
— угол 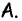 По условию задачи
По условию задачи 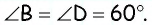 Поскольку сумма углов четырехугольника равна
Поскольку сумма углов четырехугольника равна 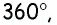 то
то 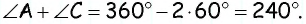 Если градусная мера угла
Если градусная мера угла 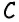 равна
равна 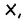 то градусная мера угла
то градусная мера угла 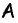 по условию равна
по условию равна 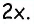 Отсюда имеем:
Отсюда имеем: 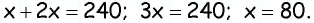 Следовательно,
Следовательно, 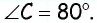
Ответ: 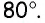
Определение параллелограмма
Определение параллелограмма
Рассмотрим на плоскости две параллельные прямые, пересеченные двумя другими параллельными прямыми (рис. 7).
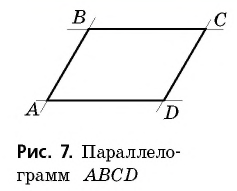
В результате такого пересечения образуется четырехугольник, который имеет специальное название — параллелограмм.
Определение
Параллелограммом называется четырехугольник, противолежащие стороны которого попарно параллельны.
На рисунке 7 изображен параллелограмм 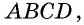 в котором
в котором 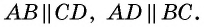
Пример:
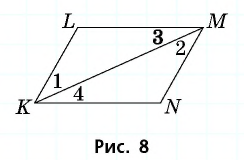
На рисунке 8  Докажите, что четырехугольник
Докажите, что четырехугольник  — параллелограмм.
— параллелограмм.
Решение:
Из равенства треугольников  следует равенство углов:
следует равенство углов: 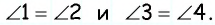 Углы 1 и 2 являются внутренними накрест лежащими при прямых
Углы 1 и 2 являются внутренними накрест лежащими при прямых 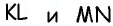 и секущей
и секущей 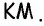 Аналогично углы 3 и 4 являются внутренними накрест лежащими при прямых
Аналогично углы 3 и 4 являются внутренними накрест лежащими при прямых 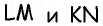 и секущей
и секущей 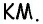 По признаку параллельности прямых имеем:
По признаку параллельности прямых имеем: 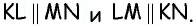 Следовательно, в четырехугольнике
Следовательно, в четырехугольнике  противолежащие стороны попарно параллельны, т.е.
противолежащие стороны попарно параллельны, т.е.  — параллелограмм по определению.
— параллелограмм по определению.
Как и в треугольнике, в параллелограмме можно провести высоты (рис. 9).
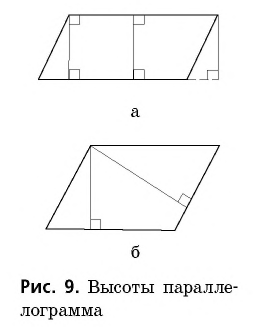
Определение
Высотой параллелограмма называется перпендикуляр, проведенный из точки одной стороны к прямой, которая содержит противолежащую сторону.
Очевидно, что к одной стороне параллелограмма можно провести бесконечно много высот (рис. 9, а),— все они будут равны как расстояния между параллельными прямыми, а из одной вершины параллелограмма можно провести две высоты к разным сторонам (рис. 9, б). Часто, говоря «высота параллелограмма», имеют в виду ее длину.
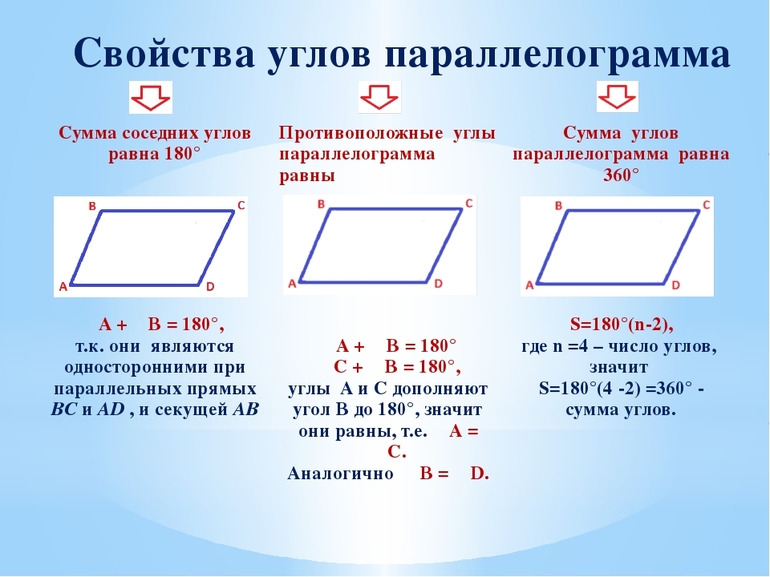
Свойства параллелограмма
Непосредственно из определения параллелограмма следует, что любые два его соседних угла являются внутренними односторонними при параллельных прямых, которые содержат противолежащие стороны. Это означает, что сумма двух соседних углов параллелограмма равна 
Докажем еще несколько важных свойств сторон, углов и диагоналей параллелограмма.
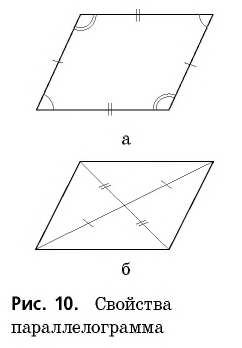
Теорема (свойства параллелограмма)
В параллелограмме:
- противолежащие стороны равны;
- противолежащие углы равны;
- диагонали точкой пересечения делятся пополам.
Свойства 1 и 2 иллюстрирует рисунок 10, а, а свойство 3 — рисунок 10, б.
Доказательство:
Проведем в параллелограмме  диагональ
диагональ  (рис. 11) и рассмотрим треугольники
(рис. 11) и рассмотрим треугольники 
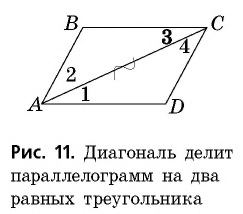
У них сторона 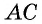 — общая,
— общая, 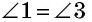 как внутренние накрест лежащие при параллельных прямых
как внутренние накрест лежащие при параллельных прямых 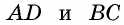 и секущей
и секущей 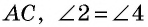 как внутренние накрест лежащие при параллельных прямых
как внутренние накрест лежащие при параллельных прямых 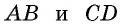 и секущей
и секущей 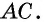 Следовательно,
Следовательно, 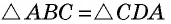 по второму признаку равенства треугольников. Отсюда, в частности, следует, что
по второму признаку равенства треугольников. Отсюда, в частности, следует, что 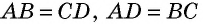 и
и 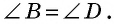 А поскольку
А поскольку 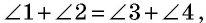 то
то 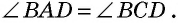 Следовательно, свойства 1 и 2 доказаны.
Следовательно, свойства 1 и 2 доказаны.
Для доказательства свойства 3 проведем в параллелограмме 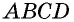 диагонали
диагонали 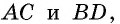 которые пересекаются в точке
которые пересекаются в точке 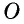 (рис. 12).
(рис. 12).
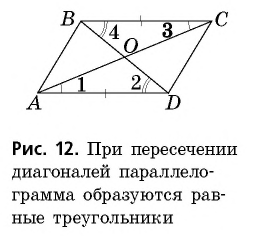
Рассмотрим треугольники 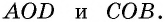 У них
У них 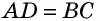 по доказанному,
по доказанному, 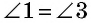 как внутренние накрест лежащие при параллельных прямых
как внутренние накрест лежащие при параллельных прямых 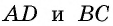 и секущей
и секущей 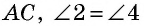 как внутренние накрест лежащие при параллельных прямых
как внутренние накрест лежащие при параллельных прямых 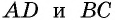 и секущей
и секущей 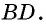 Следовательно,
Следовательно, 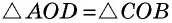 по второму признаку. Отсюда следует, что
по второму признаку. Отсюда следует, что 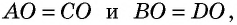 т. е. точка
т. е. точка 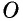 является серединой каждой из диагоналей
является серединой каждой из диагоналей 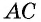 и
и 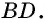 Теорема доказана полностью.
Теорема доказана полностью.
Пример №1
Сумма двух углов параллелограмма равна 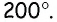 Найдите углы параллелограмма.
Найдите углы параллелограмма.
Решение:
Пусть дан параллелограмм 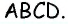 Поскольку сумма двух соседних углов параллелограмма равна
Поскольку сумма двух соседних углов параллелограмма равна  то данные углы могут быть только противолежащими. Пусть
то данные углы могут быть только противолежащими. Пусть 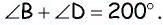 Тогда по свойству углов параллелограмма
Тогда по свойству углов параллелограмма 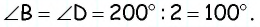 Сумма всех углов параллелограмма равна
Сумма всех углов параллелограмма равна 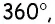 поэтому
поэтому 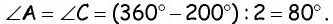
Ответ: 
Пример №2
В параллелограмме  биссектриса угла
биссектриса угла 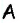 делит сторону
делит сторону  пополам. Найдите периметр параллелограмма, если
пополам. Найдите периметр параллелограмма, если 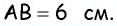
Решение:
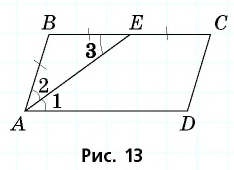
Пусть в параллелограмме  биссектриса угла
биссектриса угла  пересекает сторону
пересекает сторону  в точке
в точке 
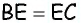 (рис. 13). Заметим, что
(рис. 13). Заметим, что 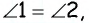 поскольку
поскольку  — биссектриса угла
— биссектриса угла 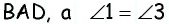 как внутренние накрест лежащие при параллельных прямых
как внутренние накрест лежащие при параллельных прямых 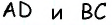 и секущей
и секущей 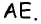 Отсюда
Отсюда 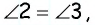 т.е. по признаку равнобедренного треугольника треугольник
т.е. по признаку равнобедренного треугольника треугольник 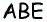 — равнобедренный с основанием
— равнобедренный с основанием 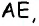 значит,
значит, 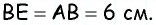 По условию
По условию 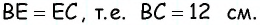 Следовательно, поскольку противолежащие стороны параллелограмма равны, то
Следовательно, поскольку противолежащие стороны параллелограмма равны, то 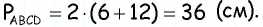
Ответ: 36 см.
Признаки параллелограмма
Теоремы о признаках параллелограмма
Для того чтобы использовать свойства параллелограмма, во многих случаях необходимо сначала убедиться, что данный четырехугольник действительно является параллелограммом. Это можно доказать либо по определению (см. задачу в п. 2.1), либо по признакам — условиям, гарантирующим, что данный четырехугольник — параллелограмм. Докажем признаки параллелограмма, которые чаще всего применяются на практике.
Теорема (признаки параллелограмма)
- Если две противолежащие стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм.
- Если противолежащие стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
- Если диагонали четырехугольника точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Доказательство:
1) Пусть в четырехугольнике 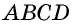
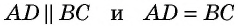 (рис. 15).
(рис. 15).
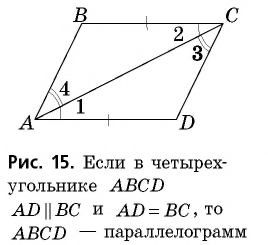
Проведем диагональ 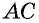 и рассмотрим треугольники
и рассмотрим треугольники 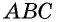 и
и 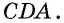 Они имеют общую сторону
Они имеют общую сторону 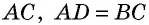 по условию,
по условию, 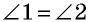 как внутренние накрест лежащие при параллельных прямых
как внутренние накрест лежащие при параллельных прямых 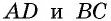 и секущей
и секущей 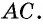 Следовательно,
Следовательно, 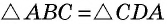 по первому признаку равенства треугольников. Из равенства этих треугольников следует равенство углов 3 и 4. Но эти углы являются внутренними накрест лежащими при прямых
по первому признаку равенства треугольников. Из равенства этих треугольников следует равенство углов 3 и 4. Но эти углы являются внутренними накрест лежащими при прямых 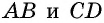 и секущей
и секущей 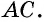 Тогда по признаку параллельности прямых
Тогда по признаку параллельности прямых 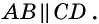 Таким образом, в четырехугольнике
Таким образом, в четырехугольнике 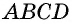 противолежащие стороны попарно параллельны, откуда следует, что
противолежащие стороны попарно параллельны, откуда следует, что 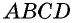 — параллелограмм по определению.
— параллелограмм по определению.
2) Пусть в четырехугольнике 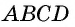
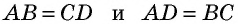 (рис. 16).
(рис. 16).
Снова проведем диагональ  и рассмотрим треугольники
и рассмотрим треугольники  и
и 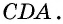 В этом случае они равны по третьему признаку: сторона
В этом случае они равны по третьему признаку: сторона 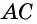 — общая,
— общая, 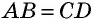 и
и 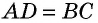 по условию. Из равенства треугольников следует равенство углов 1 и 2, которые являются внутренними накрест лежащими при прямых
по условию. Из равенства треугольников следует равенство углов 1 и 2, которые являются внутренними накрест лежащими при прямых 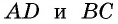 и секущей
и секущей 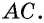 По признаку параллельности прямых
По признаку параллельности прямых 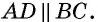 Следовательно, в четырехугольнике
Следовательно, в четырехугольнике 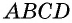 стороны
стороны 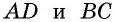 параллельны и равны, и по только что доказанному признаку 1
параллельны и равны, и по только что доказанному признаку 1 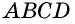 — параллелограмм.
— параллелограмм.
3) Пусть в четырехугольнике 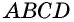 диагонали пересекаются в точке
диагонали пересекаются в точке 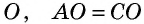 и
и 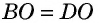 (рис. 17). Рассмотрим треугольники
(рис. 17). Рассмотрим треугольники 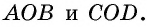 Эти треугольники равны по первому признаку:
Эти треугольники равны по первому признаку: 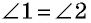 как вертикальные, а
как вертикальные, а 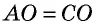 и
и 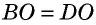 по условию. Следовательно, равны и соответствующие стороны и углы этих треугольников:
по условию. Следовательно, равны и соответствующие стороны и углы этих треугольников: 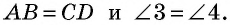 Тогда
Тогда 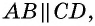 и
и 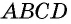 — параллелограмм по признаку 1.
— параллелограмм по признаку 1.
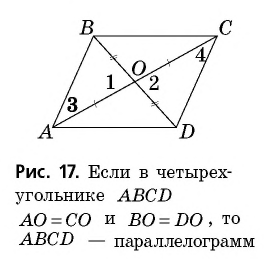
Теорема доказана полностью.
Пример №3
В параллелограмме  точки
точки  — середины сторон
— середины сторон  соответственно (рис. 18). Докажите, что четырехугольник
соответственно (рис. 18). Докажите, что четырехугольник  —параллелограмм.
—параллелограмм.
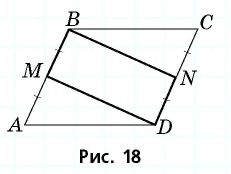
Решение:
Рассмотрим четырехугольник 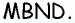 Стороны
Стороны 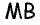 и
и 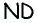 параллельны, т.к. лежат на прямых, содержащих противолежащие стороны параллелограмма
параллельны, т.к. лежат на прямых, содержащих противолежащие стороны параллелограмма 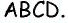 Кроме того,
Кроме того, 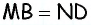 как половины равных сторон
как половины равных сторон 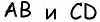 параллелограмма
параллелограмма 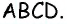 Таким образом, в четырехугольнике
Таким образом, в четырехугольнике 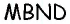 две стороны параллельны и равны. Следовательно, четырехугольник
две стороны параллельны и равны. Следовательно, четырехугольник 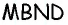 — параллелограмм.
— параллелограмм.
Попробуйте самостоятельно найти другие способы решения этой задачи, основанные на применении других признаков и определения параллелограмма.
Необходимые и достаточные условия
Каждый из признаков параллелограмма указывает на определенную особенность, наличия которой в четырехугольнике достаточно для того, чтобы утверждать, что он является параллелограммом. Вообще в математике признаки иначе называют достаточными условиями. Например, перпендикулярность двух прямых третьей — достаточное условие параллельности данных двух прямых.
В отличие от признаков, свойства параллелограмма указывают на ту особенность, которую обязательно имеет любой параллелограмм. Свойства иначе называют необходимыми условиями. Поясним такое название примером: равенство двух углов необходимо для того, чтобы углы были вертикальными, ведь если этого равенства нет, вертикальными такие углы быть не могут.
В случае верности теоремы «Если 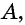 то
то 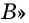 утверждение
утверждение 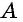 является достаточным условием для утверждения
является достаточным условием для утверждения 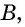 а утверждение
а утверждение 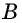 — необходимым условием для утверждения
— необходимым условием для утверждения 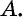 Схематически это можно представить так:
Схематически это можно представить так:

Таким образом, необходимые условия (свойства) параллелограмма следуют из того, что данный четырехугольник — параллелограмм; из достаточных условий (признаков) следует то, что данный четырехугольник — параллелограмм.
Сравнивая свойства и признаки параллелограмма, нетрудно заметить, что одно и то же условие (например, попарное равенство противолежащих сторон) является и свойством, и признаком параллелограмма. В таком случае говорят, что условие является необходимым и достаточным. Необходимое и достаточное условие иначе называют критерием. Например, равенство двух углов треугольника — критерий равнобедренного треугольника.
Немало примеров необходимых и достаточных условий можно найти в других науках и в повседневной жизни. Все мы знаем, что воздух — необходимое условие для жизни человека, но не достаточное (человеку для жизни нужно еще много чего, среди прочего — пища). Выигрыш в лотерею — достаточное условие для материального обогащения человека, но оно не является необходимым — ведь улучшить свое финансовое положение можно и другим способом. Попробуйте самостоятельно найти несколько примеров необходимых и достаточных условий.
Виды параллелограммов
Прямоугольник
Определение
Прямоугольником называется параллелограмм, у которого все углы прямые.
На рисунке 28 изображен прямоугольник 
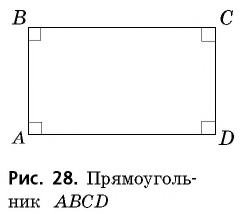
Поскольку прямоугольник является частным случаем параллелограмма, он имеет все свойства параллелограмма: противолежащие стороны прямоугольника параллельны и равны, противолежащие углы равны, диагонали точкой пересечения делятся пополам и т.д. Однако прямоугольник имеет некоторые особые свойства. Докажем одно из них.
Теорема (свойство прямоугольника)
Диагонали прямоугольника равны.
Доказательство:
Пусть дан прямоугольник  с диагоналями
с диагоналями 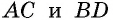 (рис. 29). Треугольники
(рис. 29). Треугольники 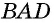 и
и 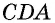 прямоугольные и равны по двум катетам
прямоугольные и равны по двум катетам 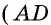 — общий,
— общий, 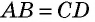 как противолежащие стороны прямоугольника). Отсюда следует равенство гипотенуз этих треугольников, т. е.
как противолежащие стороны прямоугольника). Отсюда следует равенство гипотенуз этих треугольников, т. е. 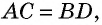 что и требовалось доказать.
что и требовалось доказать.
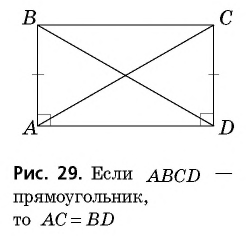
Имеет место и обратное утверждение (признак прямоугольника): если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником. Докажите это утверждение самостоятельно. Таким образом, можно утверждать, что равенство диагоналей параллелограмма — необходимое и достаточное условие (критерий) прямоугольника.
Опорная задача
Если все углы четырехугольника прямые, то этот четырехугольник — прямоугольник. Докажите.
Решение:
Пусть в четырехугольнике 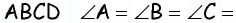
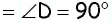 (см. рис. 28). Углы
(см. рис. 28). Углы 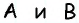 являются внутренними односторонними при прямых
являются внутренними односторонними при прямых 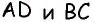 и секущей
и секущей 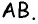 Поскольку сумма этих углов составляет
Поскольку сумма этих углов составляет  то по признаку параллельности прямых
то по признаку параллельности прямых 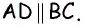 Аналогично доказываем параллельность сторон
Аналогично доказываем параллельность сторон 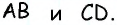 Следовательно, по определению параллелограмма
Следовательно, по определению параллелограмма 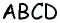 — параллелограмм. А поскольку все углы этого параллелограмма прямые, то
— параллелограмм. А поскольку все углы этого параллелограмма прямые, то 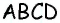 — прямоугольник по определению.
— прямоугольник по определению.
Ромб
Определение
Ромбом называется параллелограмм, у которого все стороны равны.
На рисунке 30 изображен ромб 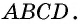
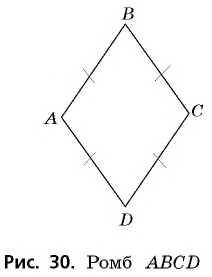
Он обладает всеми свойствами параллелограмма, а также некоторыми дополнительными свойствами, которые мы сейчас докажем.
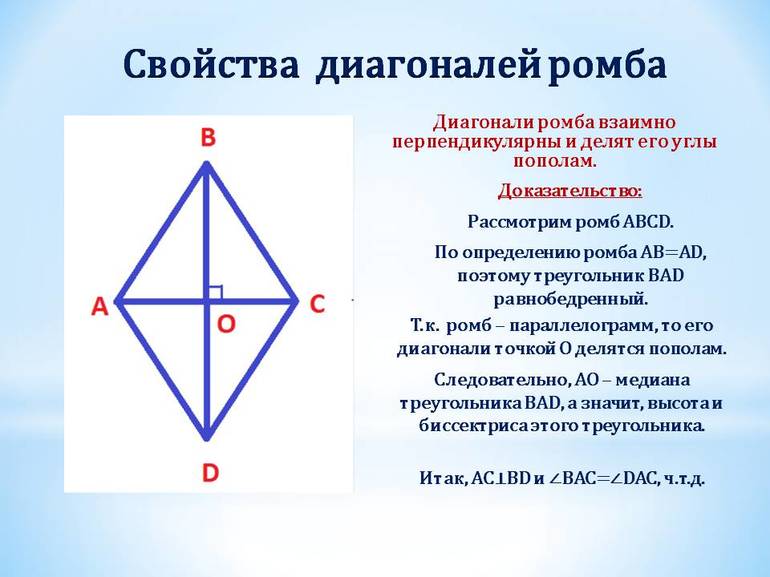
Теорема (свойства ромба)
Диагонали ромба перпендикулярны и делят его углы пополам.
Эти свойства ромба иллюстрируются рисунком 31.
Доказательство:
Пусть диагонали ромба  пересекаются в точке
пересекаются в точке  (рис. 32). Поскольку стороны ромба равны, то треугольник
(рис. 32). Поскольку стороны ромба равны, то треугольник равнобедренный с основанием
равнобедренный с основанием 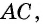 а по свойству диагоналей параллелограмма точка
а по свойству диагоналей параллелограмма точка 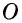 — середина
— середина 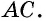 Следовательно, отрезок
Следовательно, отрезок 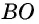 — медиана равнобедренного треугольника, которая одновременно является его высотой и биссектрисой. Это означает, что
— медиана равнобедренного треугольника, которая одновременно является его высотой и биссектрисой. Это означает, что 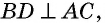 т.е. диагонали ромба перпендикулярны, и
т.е. диагонали ромба перпендикулярны, и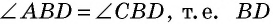 — биссектриса угла
— биссектриса угла 
Аналогично доказываем, что диагонали ромба являются биссектрисами и других его углов. Теорема доказана.
Опорная задача
Если все стороны четырехугольника равны, то этот четырехугольник — ромб. Докажите.
Решение:
Очевидно, что в четырехугольнике, все стороны которого равны, попарно равными являются и противолежащие стороны. Следовательно, по признаку параллелограмма такой четырехугольник — параллелограмм, а по определению ромба параллелограмм, у которого все стороны равны, является ромбом.
Решая задачи, помещенные в конце этого параграфа, вы докажете другие признаки прямоугольника и ромба.
Квадрат
На рисунке 33 изображен еще один вид параллелограмма — квадрат.
Определение
Квадратом называется прямоугольник, у которого все стороны равны.
Иначе можно сказать, что квадрат — это прямоугольник, который является ромбом. Действительно, поскольку квадрат является прямоугольником и ромбом и, конечно же, произвольным параллелограммом, то:
- все стороны квадрата равны, а противолежащие стороны параллельны;
- все углы квадрата прямые;
- диагонали квадрата равны, перпендикулярны, делят углы квадрата пополам и делятся точкой пересечения пополам.
Связь между отдельными видами параллелограммов. Равносильные утверждения
Исходя из определений произвольного параллелограмма и его отдельных видов, мы можем схематически отобразить связь между ними (рис. 34).
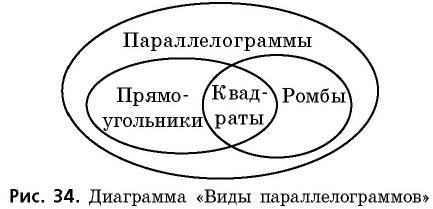
На схеме представлены множества параллелограммов, прямоугольников и ромбов. Такой способ наглядного представления множеств называют диаграммами Эйлера — Венна. Диаграмма Эйлера — Венна для параллелограммов демонстрирует, что множества прямоугольников и ромбов являются частями (подмножествами) множества параллелограммов, а множество квадратов — общей частью (пересечением) множеств прямоугольников и ромбов. Диаграммы Эйлера — Венна часто используют для подтверждения или проверки правильности логических рассуждений.
Подытоживая материал этого параграфа, обратим также внимание на то, что возможно и другое определение квадрата: квадратом называется ромб с прямыми углами. В самом деле, оба приведенных определения описывают одну и ту же фигуру. Такие определения называют равносильными. Вообще два утверждения называются равносильными, если они или оба выполняются, или оба не выполняются. Например, равносильными являются утверждения «В треугольнике две стороны равны» и «В треугольнике два угла равны», ведь оба они верны, если рассматривается равнобедренный треугольник, и оба ложны, если речь идет о разностороннем треугольнике.
Равносильность двух утверждений также означает, что любое из них является необходимым и достаточным условием для другого. В самом деле, рассмотрим равносильные утверждения «Диагонали параллелограмма равны» и «Параллелограмм имеет прямые углы». Из того, что диагонали параллелограмма равны, следует, что он является прямоугольником, т.е. имеет прямые углы, и наоборот: параллелограмм с прямыми углами является прямоугольником, т.е. имеет равные диагонали. На этом примере легко проследить логические шаги перехода от признаков фигуры к ее определению и далее — к свойствам. Такой переход довольно часто приходится выполнять в процессе решения задач.
Трапеция
Как известно, любой параллелограмм имеет две пары параллельных сторон. Рассмотрим теперь четырехугольник, который имеет только одну пару параллельных сторон.
Определение
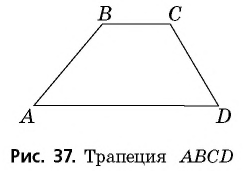
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Параллельные стороны трапеции называют ее основаниями, а непараллельные стороны — боковыми сторонами. На рисунке 37 в трапеции  стороны
стороны  являются основаниями, а
являются основаниями, а 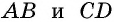 — боковыми сторонами.
— боковыми сторонами.
Углы, прилежащие к одной боковой стороне, являются внутренними односторонними при параллельных прямых, на которых лежат основания трапеции. По теореме о свойстве параллельных прямых из этого следует, что сумма углов трапеции, прилежащих к боковой стороне, равна 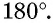 На рисунке 37
На рисунке 37 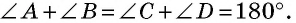
Определение
Высотой трапеции называется перпендикуляр, проведенный из точки одного основания к прямой, содержащей другое основание.
Очевидно, что в трапеции можно провести бесконечно много высот (рис. 38),— все они равны как расстояния между параллельными прямыми.
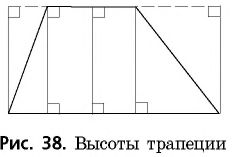
Чаще всего в процессе решения задач высоты проводят из вершин углов при меньшем основании трапеции.
Частные случаи трапеций
Как среди треугольников и параллелограммов, так и среди трапеций выделяются отдельные виды, обладающие дополнительными свойствами.
Определение
Прямоугольной трапецией называется трапеция, в которой одна из боковых сторон перпендикулярна основаниям.
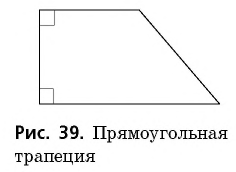
На рисунке 39 изображена прямоугольная трапеция. У нее два прямых угла при меньшей боковой стороне. Эта сторона одновременно является и высотой трапеции.
Определение
Равнобедренной трапецией называется трапеция, в которой боковые стороны равны.
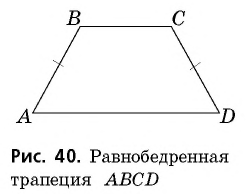
На рисунке 40 изображена равнобедренная трапеция  с боковыми сторонами
с боковыми сторонами 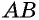 и
и 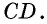 Иногда равнобедренную трапецию также называют равнобокой или равнобочной.
Иногда равнобедренную трапецию также называют равнобокой или равнобочной.
У равнобедренной трапеции так же, как и у равнобедренного треугольника, углы при основании равны. Докажем это в следующей теореме.
Теорема (свойство равнобедренной трапеции)
В равнобедренной трапеции углы при основании равны.
Доказательство:
Пусть 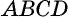 — данная трапеция,
— данная трапеция, 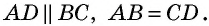
Перед началом доказательства заметим, что этой теоремой утверждается равенство углов при каждом из двух оснований трапеции, т. е. необходимо доказать, что 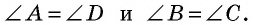
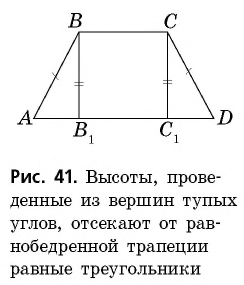
Проведем высоты 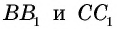 из вершин тупых углов и рассмотрим прямоугольные треугольники
из вершин тупых углов и рассмотрим прямоугольные треугольники 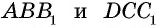 (рис. 41). У них
(рис. 41). У них 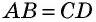 как боковые стороны равнобедренной трапеции,
как боковые стороны равнобедренной трапеции, 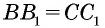 как расстояния между параллельными прямыми
как расстояния между параллельными прямыми 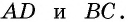 Следовательно,
Следовательно, 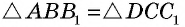 по гипотенузе и катету. Отсюда следует, что
по гипотенузе и катету. Отсюда следует, что 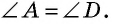 Углы трапеции
Углы трапеции  также равны, поскольку они дополняют равные углы
также равны, поскольку они дополняют равные углы 
Теорема доказана.
Имеет место также обратное утверждение (признак равнобедренной трапеции):
- если в трапеции углы при основании равны, то такая трапеция является равнобедренной.
Докажите этот факт самостоятельно.
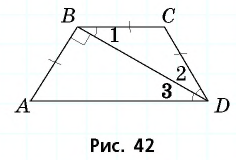
Пример №4
Меньшее основание равнобедренной трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне. Найдите углы трапеции.
Решение:
Пусть дана равнобедренная трапеция 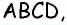 в которой
в которой 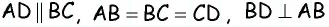 (рис. 42). По условию задачи треугольник
(рис. 42). По условию задачи треугольник 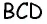 равнобедренный с основанием
равнобедренный с основанием 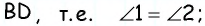 с другой стороны,
с другой стороны, 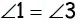 как внутренние накрест лежащие при параллельных прямых
как внутренние накрест лежащие при параллельных прямых  и
и 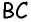 и секущей
и секущей 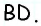 Пусть градусная мера угла 1 равна
Пусть градусная мера угла 1 равна 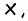 тогда в данной трапеции
тогда в данной трапеции 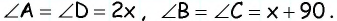 Поскольку сумма углов, прилежащих к боковой стороне, составляет
Поскольку сумма углов, прилежащих к боковой стороне, составляет  имеем:
имеем: 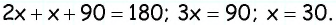 Следовательно,
Следовательно, 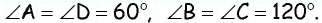
Ответ: 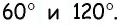
Построение параллелограммов и трапеций
Задачи на построение параллелограммов и трапеций часто решают методом вспомогательного треугольника. Напомним, что для этого необходимо выделить в искомой фигуре треугольник, который можно построить по имеющимся данным. Построив его, получаем две или три вершины искомого четырехугольника, а остальные вершины находим по данным задачи.
Пример №5
Постройте параллелограмм по двум диагоналям и углу между ними.
Решение:
Пусть 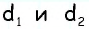 — данные диагонали параллелограмма,
— данные диагонали параллелограмма, 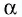 — угол между ними. Анализ
— угол между ними. Анализ
Пусть параллелограмм  построен (рис. 43).
построен (рис. 43).
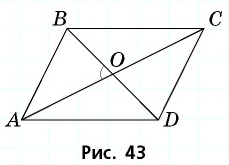
Треугольник 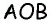 можно построить по двум сторонам и углу между ними
можно построить по двум сторонам и углу между ними 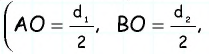
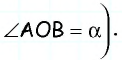
Таким образом, мы получим вершины  искомого параллелограмма.
искомого параллелограмма.
Вершины 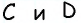 можно получить, «удвоив» отрезки
можно получить, «удвоив» отрезки 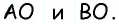
Построение
1. Разделим отрезки 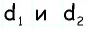 пополам.
пополам.
2. Построим треугольник 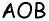 по двум сторонам и углу между ними.
по двум сторонам и углу между ними.
3. На лучах 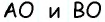 отложим отрезки
отложим отрезки 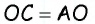 и
и 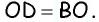
4. Последовательно соединим точки 
Доказательство:
Четырехугольник 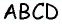 — параллелограмм, поскольку по построению его диагонали
— параллелограмм, поскольку по построению его диагонали 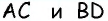 точкой пересечения делятся пополам. В этом параллелограмме
точкой пересечения делятся пополам. В этом параллелограмме 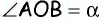 (по построению),
(по построению),
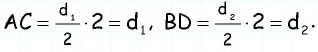
Исследование
Задача имеет единственное решение при любых значениях 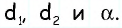
В некоторых случаях для построения вспомогательного треугольника на рисунке-эскизе необходимо провести дополнительные линии.
Пример №6
Постройте трапецию по четырем сторонам.
Решение:
Пусть 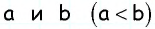 — основания искомой трапеции,
— основания искомой трапеции, 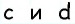 — ее боковые стороны.
— ее боковые стороны.
Анализ
Пусть искомая трапеция 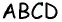 построена (рис. 44).
построена (рис. 44).
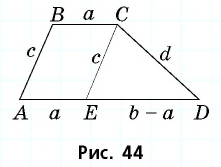
Проведем через вершину  прямую
прямую  параллельную
параллельную  Тогда
Тогда 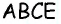 — параллелограмм по определению, следовательно,
— параллелограмм по определению, следовательно,  Кроме того,
Кроме того, 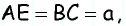 следовательно,
следовательно, 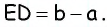 Вспомогательный треугольник
Вспомогательный треугольник 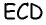 можно построить по трем сторонам. После этого для получения вершин
можно построить по трем сторонам. После этого для получения вершин 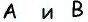 надо отложить на луче
надо отложить на луче  и на луче с началом в точке
и на луче с началом в точке 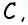 параллельном
параллельном  отрезки длиной
отрезки длиной 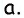
Построение
1. Построим отрезок 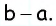
2. Построим треугольник 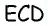 по трем сторонам
по трем сторонам 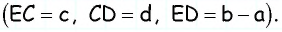
3. Построим луч, проходящий через точку 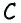 и параллельный
и параллельный  При этом построенный луч и луч
При этом построенный луч и луч  должны лежать по одну сторону от прямой
должны лежать по одну сторону от прямой 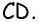
4. На луче  от точки
от точки 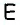 отложим отрезок
отложим отрезок 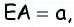 на луче с началом
на луче с началом 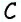 — отрезок
— отрезок 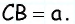
5. Соединим точки 
Доказательство:
По построению 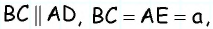 следовательно,
следовательно,  — параллелограмм по признаку. Отсюда
— параллелограмм по признаку. Отсюда  Кроме того,
Кроме того, 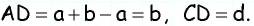 Следовательно,
Следовательно,  — искомая трапеция.
— искомая трапеция.
Исследование
Задача имеет единственное решение, если числа 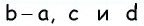 удовлетворяют неравенству треугольника.
удовлетворяют неравенству треугольника.
Теорема Фалеса
Для дальнейшего изучения свойств трапеции докажем важную теорему.
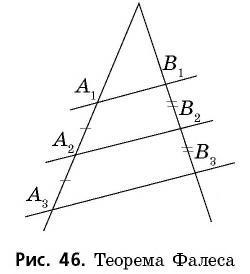
Теорема (Фалеса)
Параллельные прямые, которые пересекают стороны угла и отсекают на одной из них равные отрезки, отсекают равные отрезки и на другой стороне.
Доказательство:
Пусть  — точки пересечения параллельных прямых с одной из сторон данного угла, а
— точки пересечения параллельных прямых с одной из сторон данного угла, а  — соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если
— соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если 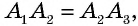 то
то 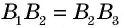 (рис. 46).
(рис. 46).
Проведем через точку  прямую
прямую 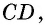 параллельную
параллельную 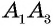 (рис. 47).
(рис. 47).
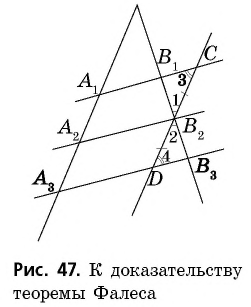
Четырехугольники 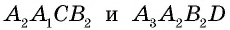 — параллелограммы по определению. Тогда
— параллелограммы по определению. Тогда 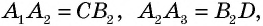 а поскольку
а поскольку 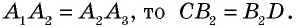
Рассмотрим треугольники 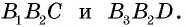 У них
У них 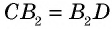 по доказанному,
по доказанному, 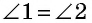 как вертикальные, a
как вертикальные, a 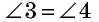 как внутренние накрест лежащие при параллельных прямых
как внутренние накрест лежащие при параллельных прямых  и секущей
и секущей  Следовательно,
Следовательно, 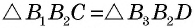 по второму признаку, откуда
по второму признаку, откуда 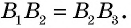
Теорема доказана.
Заметим, что в условии данной теоремы вместо сторон угла можно рассматривать две произвольные прямые, поэтому теорема Фалеса может формулироваться и следующим образом: параллельные прямые, которые пересекают две данные прямые и отсекают на одной из них равные отрезки, отсекают равные отрезки и на другой прямой.
Пример №7
Разделите данный отрезок на  равных частей.
равных частей.
Решение:
Решим задачу для 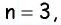 т.е. разделим данный отрезок
т.е. разделим данный отрезок  на три равные части (рис. 48).
на три равные части (рис. 48).
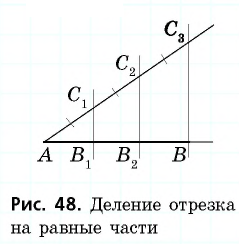
Для этого проведем из точки 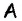 произвольный луч, не дополнительный к лучу
произвольный луч, не дополнительный к лучу 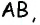 и отложим на нем равные отрезки
и отложим на нем равные отрезки 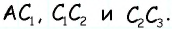 Проведем прямую
Проведем прямую 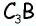 и параллельные ей прямые через точки
и параллельные ей прямые через точки  По теореме Фалеса эти прямые делят отрезок
По теореме Фалеса эти прямые делят отрезок  на три равные части. Аналогично можно разделить произвольный отрезок на любое количество равных частей.
на три равные части. Аналогично можно разделить произвольный отрезок на любое количество равных частей.
Средняя линия треугольника
Теорема Фалеса помогает исследовать еще одну важную линию в треугольнике.
Определение
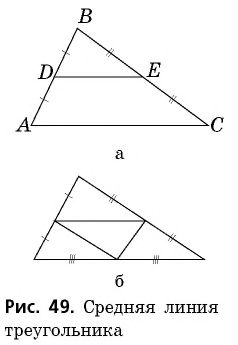
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
На рисунке 49, а отрезок 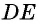 — средняя линия треугольника
— средняя линия треугольника  В любом треугольнике можно провести три средние линии (рис. 49, б).
В любом треугольнике можно провести три средние линии (рис. 49, б).
Теорема (свойство средней линии треугольника)
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Доказательство:
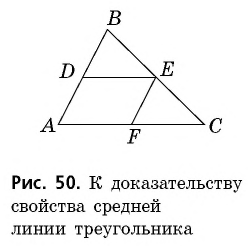
Пусть 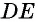 — средняя линия треугольника
— средняя линия треугольника 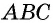 (рис. 50). Докажем сначала, что
(рис. 50). Докажем сначала, что 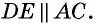 Проведем через точку
Проведем через точку 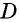 прямую, параллельную
прямую, параллельную 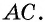 По теореме Фалеса она пересечет отрезок
По теореме Фалеса она пересечет отрезок 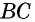 в его середине, т.е. будет содержать отрезок
в его середине, т.е. будет содержать отрезок 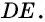 Следовательно,
Следовательно, 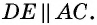
Проведем теперь среднюю линию 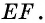 По только что доказанному она будет параллельна стороне
По только что доказанному она будет параллельна стороне 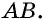 Четырехугольник
Четырехугольник 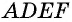 с попарно параллельными сторонами по определению является параллелограммом, откуда
с попарно параллельными сторонами по определению является параллелограммом, откуда 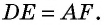 А поскольку точка
А поскольку точка  — середина
— середина  то
то 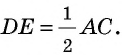
Теорема доказана.
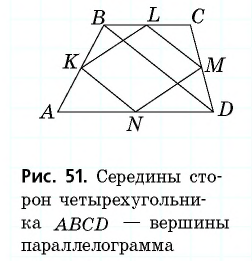
Опорная задача (теорема Вариньона) Середины сторон четырехугольника являются вершинами параллелограмма. Докажите.
Решение:
Пусть точки 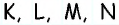 — середины сторон четырехугольника
— середины сторон четырехугольника 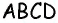 (рис. 51). Проведем диагональ
(рис. 51). Проведем диагональ 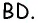 Отрезки
Отрезки 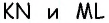 — средние линии треугольников
— средние линии треугольников  соответственно. По свойству средней линии треугольника они параллельны стороне
соответственно. По свойству средней линии треугольника они параллельны стороне  и равны ее половине, т.е. параллельны и равны между собой. Тогда по признаку параллелограмма четырехугольник
и равны ее половине, т.е. параллельны и равны между собой. Тогда по признаку параллелограмма четырехугольник  — параллелограмм.
— параллелограмм.
Средняя линия трапеции
Определение
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.
На рисунке 52 отрезок 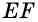 — средняя линия трапеции
— средняя линия трапеции 
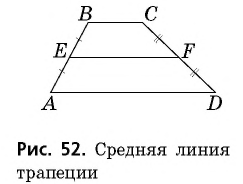
Теорема (свойство средней линии трапеции) Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть 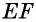 — средняя линия трапеции
— средняя линия трапеции  с основаниями
с основаниями 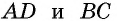 (рис. 53).
(рис. 53).
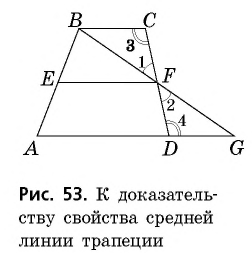
Проведем прямую  и отметим точку
и отметим точку 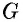 — точку пересечения прямых
— точку пересечения прямых 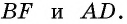 Рассмотрим треугольники
Рассмотрим треугольники 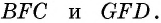 У них
У них 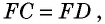 поскольку
поскольку 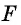 — середина
— середина 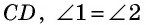 как вертикальные, a
как вертикальные, a 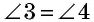 как внутренние накрест лежащие при параллельных прямых
как внутренние накрест лежащие при параллельных прямых 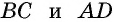 и секущей
и секущей 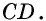 Следовательно,
Следовательно, 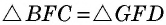 по второму признаку, откуда
по второму признаку, откуда 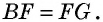 Тогда по определению
Тогда по определению 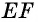 — средняя линия треугольника
— средняя линия треугольника 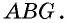 По свойству средней линии треугольника
По свойству средней линии треугольника 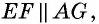 поэтому
поэтому 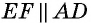 и
и 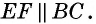 Кроме того, из доказанного равенства треугольников следует, что
Кроме того, из доказанного равенства треугольников следует, что 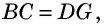 откуда
откуда 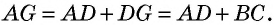 По свойству средней линии треугольника
По свойству средней линии треугольника 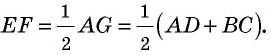
Теорема доказана.
Пример №8
Через точки, делящие боковую сторону трапеции на три равные части, проведены прямые, параллельные основаниям трапеции. Найдите длины отрезков этих прямых, заключенных внутри трапеции, если ее основания равны 2 м и 5 м.
Решение:
Пусть в трапеции  (рис. 54).
(рис. 54).
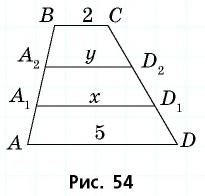
По теореме Фалеса параллельные прямые, которые проходят через точки 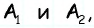 отсекают на боковой стороне
отсекают на боковой стороне 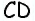 равные отрезки, т.е.
равные отрезки, т.е. 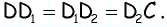 Тогда по определению
Тогда по определению 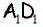 — средняя линия трапеции
— средняя линия трапеции 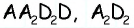 — средняя линия трапеции
— средняя линия трапеции 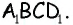 Пусть
Пусть 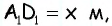
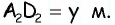 По свойству средней линии трапеции имеем систему:
По свойству средней линии трапеции имеем систему:
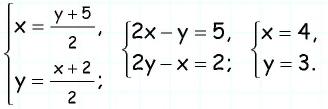
Ответ: 3 м и 4 м.
Вписанные углы
Градусная мера дуги
В седьмом классе изучение свойств треугольников завершалось рассмотрением описанной и вписанной окружностей. Но перед тем как рассмотреть описанную и вписанную окружности для четырехугольника, нам необходимо остановиться на дополнительных свойствах углов.
До сих пор мы изучали только те углы, градусная мера которых не превышала  Расширим понятие угла и введем в рассмотрение вместе с самим углом части, на которые он делит плоскость.
Расширим понятие угла и введем в рассмотрение вместе с самим углом части, на которые он делит плоскость.
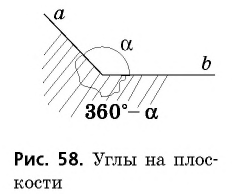
На рисунке 58 угол 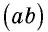 делит плоскость на две части, каждая из которых называется плоским углом. Их градусные меры равны
делит плоскость на две части, каждая из которых называется плоским углом. Их градусные меры равны 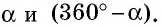
Используем понятие плоского угла для определения центрального угла в окружности.
Определение
Центральным углом в окружности называется плоский угол с вершиной в центре окружности.
На рисунке 59, а, б стороны угла с вершиной в центре окружности 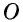 пересекают данную окружность в точках
пересекают данную окружность в точках  При этом образуются две дуги, одна из которых меньше полуокружности (на ней обозначена промежуточная точка
При этом образуются две дуги, одна из которых меньше полуокружности (на ней обозначена промежуточная точка 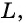 рис. 59, а), а другая — больше полуокружности (на ней обозначена промежуточная точка
рис. 59, а), а другая — больше полуокружности (на ней обозначена промежуточная точка 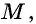 рис. 59, б).
рис. 59, б).
Для того чтобы уточнить, какой из двух плоских углов со сторонами 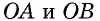 мы рассматриваем как центральный, мы будем указывать дугу окружности, которая соответствует данному центральному углу (т.е. содержится внутри него).
мы рассматриваем как центральный, мы будем указывать дугу окружности, которая соответствует данному центральному углу (т.е. содержится внутри него).
На рисунке 59, а центральному углу 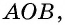 обозначенному дужкой, соответствует дуга
обозначенному дужкой, соответствует дуга 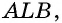 а на рисунке 59, б — дуга
а на рисунке 59, б — дуга 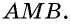 В случае, когда лучи
В случае, когда лучи 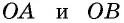 дополнительные, соответствующая дуга
дополнительные, соответствующая дуга 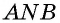 является полуокружностью (рис. 59, в).
является полуокружностью (рис. 59, в).
Определение
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Градусную меру дуги, как и саму дугу, обозначают так: 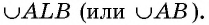 Например, на рисунке 59, в
Например, на рисунке 59, в 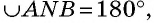 т. е. градусная мера полуокружности составляет
т. е. градусная мера полуокружности составляет 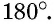 Очевидно, что градусная мера дуги всей окружности составляет
Очевидно, что градусная мера дуги всей окружности составляет 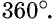
Концы хорды 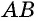 делят окружность на две дуги —
делят окружность на две дуги — 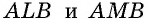 (рис. 59, г). Говорят, что эти дуги стягиваются хордой
(рис. 59, г). Говорят, что эти дуги стягиваются хордой 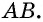
Вписанный угол
Определение
Вписанным углом называется угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
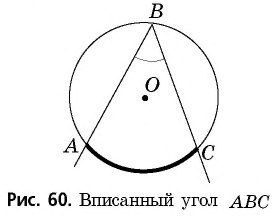
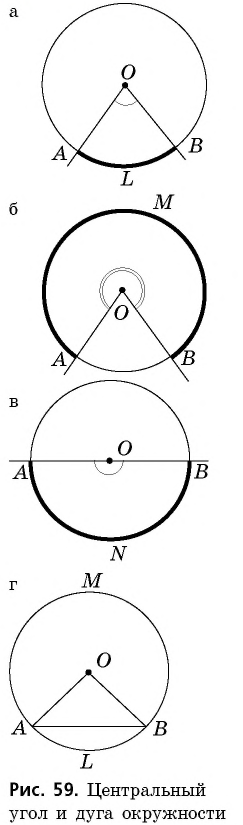
На рисунке 60 изображен вписанный угол  Его вершина
Его вершина  лежит на окружности, а стороны пересекают окружность в точках
лежит на окружности, а стороны пересекают окружность в точках  и
и 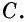 Дуга
Дуга 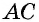 (на рисунке она выделена) лежит внутри этого угла. В таком случае говорят, что вписанный угол
(на рисунке она выделена) лежит внутри этого угла. В таком случае говорят, что вписанный угол 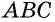 опирается на дугу
опирается на дугу 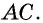
Теорема (о вписанном угле)
Вписанный угол измеряется половиной дуги, на которую он опирается.
Доказательство:
Пусть в окружности с центром 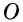 вписанный угол
вписанный угол 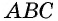 опирается на дугу
опирается на дугу 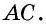 Докажем, что
Докажем, что 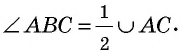 Рассмотрим три случая расположения центра окружности относительно данного вписанного угла (рис. 61).
Рассмотрим три случая расположения центра окружности относительно данного вписанного угла (рис. 61).
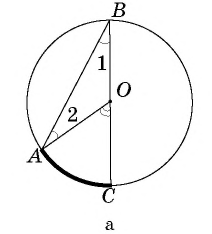
1) Пусть центр окружности лежит на одной из сторон данного угла (рис. 61, а). В этом случае центральный угол  является внешним углом при вершине
является внешним углом при вершине 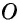 равнобедренного треугольника
равнобедренного треугольника 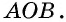 По теореме о внешнем угле треугольника
По теореме о внешнем угле треугольника 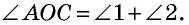 А поскольку углы 1 и 2 равны как углы при основании равнобедренного треугольника, то
А поскольку углы 1 и 2 равны как углы при основании равнобедренного треугольника, то 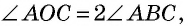
т.е. 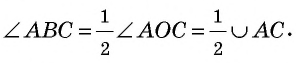
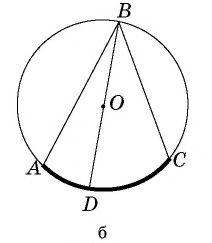
2) Пусть центр окружности лежит внутри угла  (рис. 61, б). Луч
(рис. 61, б). Луч  делит угол
делит угол  на два угла. По только что доказанному
на два угла. По только что доказанному 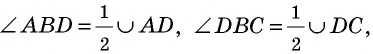 следовательно,
следовательно, 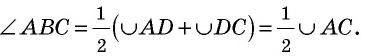
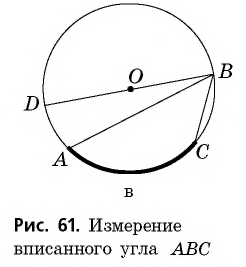
3) Аналогично в случае, когда центр окружности лежит вне вписанного угла (рис. 60, б),
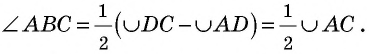
Теорема доказана.
Только что доказанную теорему можно сформулировать иначе.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
Пример №9
Найдите угол  если
если 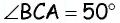 (рис. 62).
(рис. 62).
Решение:
Для того чтобы найти угол  необходимо найти градусную меру дуги
необходимо найти градусную меру дуги  на которую он опирается. Но непосредственно по данным задачи мы можем найти только градусную меру дуги
на которую он опирается. Но непосредственно по данным задачи мы можем найти только градусную меру дуги 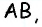 на которую опирается угол
на которую опирается угол  из теоремы о вписанном угле
из теоремы о вписанном угле 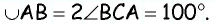 Заметим, что дуги
Заметим, что дуги 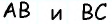 вместе составляют полуокружность, т.е.
вместе составляют полуокружность, т.е. 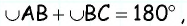 следовательно,
следовательно, 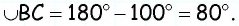 Тогда по теореме о вписанном угле
Тогда по теореме о вписанном угле 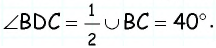
Ответ: 
Следствия теоремы о вписанном угле
По количеству и значимости следствий теорема о вписанном угле является одной из «богатейших» геометрических теорем. Сформулируем наиболее важные из этих следствий.
Следствие 1
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Действительно, по теореме о вписанном угле градусная мера каждого из вписанных углов на рисунке 63 равна половине дуги 
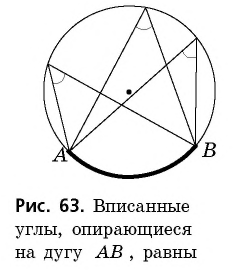
Следствие 2
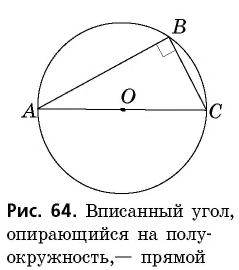
Вписанный угол, опирающийся на полуокружность,— прямой, и наоборот: любой прямой вписанный угол опирается на полуокружность.
Действительно, поскольку градусная мера полуокружности равна 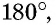 то угол
то угол 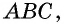 который опирается на полуокружность, равен
который опирается на полуокружность, равен 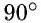 (рис. 64). Обоснование обратного утверждения проведите самостоятельно.
(рис. 64). Обоснование обратного утверждения проведите самостоятельно.
Следствие 3
Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
Первое из приведенных утверждений вытекает из следствия 2. Если в треугольнике  угол
угол  прямой (рис. 65, а), то дуга
прямой (рис. 65, а), то дуга  на которую опирается этот угол, является полуокружностью.
на которую опирается этот угол, является полуокружностью.
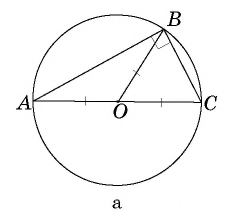
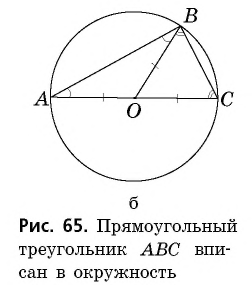
Тогда гипотенуза  — диаметр описанной окружности, т.е. середина гипотенузы — центр окружности. Утверждение о длине медианы следует из равенства радиусов:
— диаметр описанной окружности, т.е. середина гипотенузы — центр окружности. Утверждение о длине медианы следует из равенства радиусов:
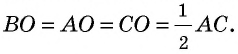
Отметим еще один интересный факт: медиана прямоугольного треугольника, проведенная к гипотенузе, делит данный треугольник на два равнобедренных треугольника с общей боковой стороной. Из этого, в частности, следует, что углы, на которые медиана делит прямой угол, равны острым углам треугольника (рис. 65, б).
В качестве примера применения следствий теоремы о вписанном угле приведем другое решение задачи, которую мы рассмотрели в п. 7.2.
Пример №10
Найдите угол 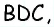 если
если 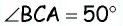 (см. рис. 62).
(см. рис. 62).
Решение:
Проведем хорду  (рис. 66).
(рис. 66).
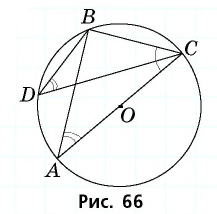
Поскольку вписанный угол  опирается на полуокружность, то по следствию 2
опирается на полуокружность, то по следствию 2 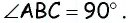 Значит, треугольник
Значит, треугольник 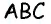 прямоугольный,
прямоугольный, 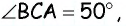 тогда
тогда 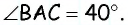 По следствию 1 углы
По следствию 1 углы 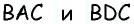 равны, поскольку оба они опираются на дугу
равны, поскольку оба они опираются на дугу  Следовательно,
Следовательно, 
Ответ: 
Вписанные четырехугольники
Определение
Четырехугольник называется вписанным в окружность, если все его вершины лежат на этой окружности.
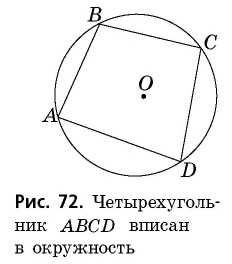
Четырехугольник  на рисунке 72 является вписанным в окружность. Иначе говорят, что окружность описана около четырехугольника.
на рисунке 72 является вписанным в окружность. Иначе говорят, что окружность описана около четырехугольника.
Как известно, около любого треугольника можно описать окружность. Для четырехугольника это можно сделать не всегда. Докажем свойство и признак вписанного четырехугольника.
Теорема (овписанном четырехугольнике)
- Сумма противолежащих углов вписанного четырехугольника равна
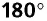 (свойство вписанного четырехугольника).
(свойство вписанного четырехугольника). - Если сумма противолежащих углов четырехугольника равна
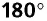 то около него можно описать окружность (признак вписанного четырехугольника).
то около него можно описать окружность (признак вписанного четырехугольника).
Доказательство:
1) Свойство. Пусть четырехугольник 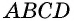 вписан в окружность (рис. 72). По теореме о вписанном угле
вписан в окружность (рис. 72). По теореме о вписанном угле 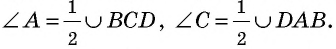
Следовательно, 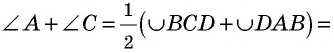
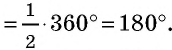
Аналогично доказываем, что 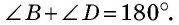
2) Признак. Пусть в четырехугольнике 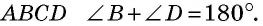 Опишем окружность около треугольника
Опишем окружность около треугольника  и докажем от противного, что вершина
и докажем от противного, что вершина  не может лежать ни внутри этой окружности, ни вне ее. Пусть точка
не может лежать ни внутри этой окружности, ни вне ее. Пусть точка  лежит внутри окружности, а точка
лежит внутри окружности, а точка  — точка пересечения луча
— точка пересечения луча 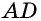 с дугой
с дугой 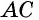 (рис. 73).
(рис. 73).
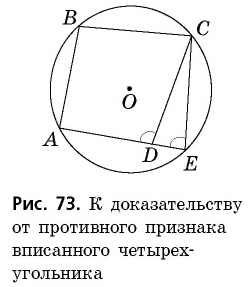
Тогда четырехугольник 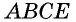 — вписанный. По условию
— вписанный. По условию 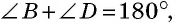 а по только что доказанному свойству вписанного четырехугольника
а по только что доказанному свойству вписанного четырехугольника 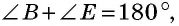 т.е.
т.е. 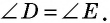 Но угол
Но угол 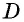 четырехугольника
четырехугольника 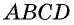 — внешний угол треугольника
— внешний угол треугольника 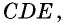 и по теореме о внешнем угле треугольника он должен быть больше угла
и по теореме о внешнем угле треугольника он должен быть больше угла  Следовательно, мы пришли к противоречию, т.е. точка
Следовательно, мы пришли к противоречию, т.е. точка  не может лежать внутри окружности. Аналогично можно доказать, что точка
не может лежать внутри окружности. Аналогично можно доказать, что точка 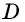 не может лежать вне окружности. Тогда точка
не может лежать вне окружности. Тогда точка 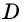 лежит на окружности, т.е. около четырехугольника
лежит на окружности, т.е. около четырехугольника 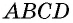 можно описать окружность.
можно описать окружность.
Теорема доказана.
Следствие 1
Около любого прямоугольника можно описать окружность.
Если параллелограмм вписан в окружность, то он является прямоугольником
Прямоугольник, вписанный в окружность, изображен на рисунке 74.
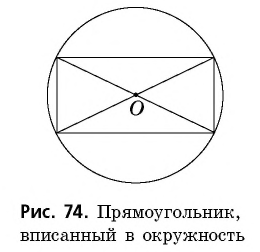
Центр описанной окружности является точкой пересечения диагоналей прямоугольника (см. задачу 255).
Следствие 2
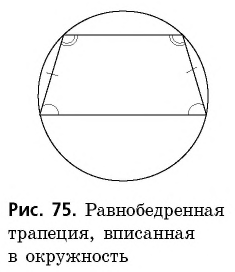
Около равнобедренной трапеции можно описать окружность.
Если трапеция вписана в окружность, то она равнобедренная.
Равнобедренная трапеция, вписанная в окружность, изображена на рисунке 75.
Описанные четырехугольники
Определение
Четырехугольник называется описанным около окружности, если все его стороны касаются этой окружности.
Четырехугольник  на рисунке 76 является описанным около окружности. Иначе говорят, что окружность вписана в четырехугольник.
на рисунке 76 является описанным около окружности. Иначе говорят, что окружность вписана в четырехугольник.
Оказывается, что не в любой четырехугольник можно вписать окружность. Докажем соответствующие свойство и признак.
Теорема (об описанном четырехугольнике)
- В описанном четырехугольнике суммы противолежащих сторон равны (свойство описанного четырехугольника).
- Если в четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность (признак описанного четырехугольника).
Доказательство:
1) Свойство. Пусть стороны четырехугольника  касаются вписанной окружности в точках
касаются вписанной окружности в точках  (рис. 76).
(рис. 76).
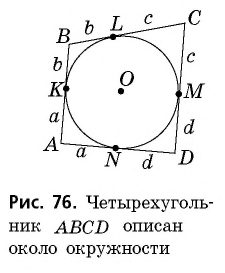
По свойству отрезков касательных 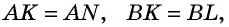
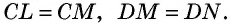 С учетом обозначений на рисунке
С учетом обозначений на рисунке 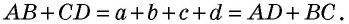
2) Признак. Пусть в четырехугольнике 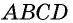 с наименьшей стороной
с наименьшей стороной 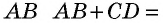
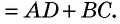 Поскольку по теореме о биссектрисе угла точка
Поскольку по теореме о биссектрисе угла точка 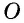 (точка пересечения биссектрис углов
(точка пересечения биссектрис углов 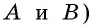 равноудалена от сторон
равноудалена от сторон 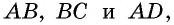 то можно построить окружность с центром
то можно построить окружность с центром 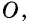 которая касается этих трех сторон (рис. 77, а). Докажем от противного, что эта окружность касается также стороны
которая касается этих трех сторон (рис. 77, а). Докажем от противного, что эта окружность касается также стороны 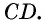
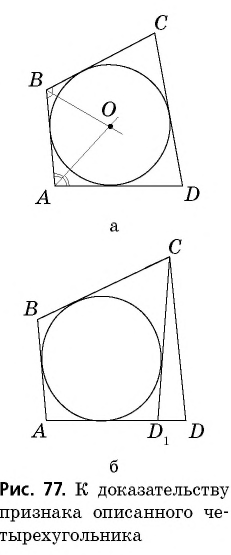
Предположим, что это не так. Тогда прямая  либо не имеет общих точек с окружностью, либо является секущей окружности. Рассмотрим первый случай (рис. 77, б). Проведем через точку
либо не имеет общих точек с окружностью, либо является секущей окружности. Рассмотрим первый случай (рис. 77, б). Проведем через точку  касательную к окружности, которая пересекает сторону
касательную к окружности, которая пересекает сторону  в точке
в точке 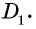 Тогда по свойству описанного четырехугольника
Тогда по свойству описанного четырехугольника 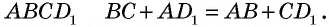 Но по условию
Но по условию 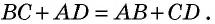 Вычитая из второго равенства первое, имеем:
Вычитая из второго равенства первое, имеем: 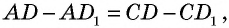 т.е.
т.е. 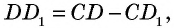 что противоречит неравенству треугольника для треугольника
что противоречит неравенству треугольника для треугольника 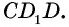
Таким образом, наше предположение неверно. Аналогично можно доказать, что прямая 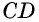 не может быть секущей окружности. Следовательно, окружность касается стороны
не может быть секущей окружности. Следовательно, окружность касается стороны 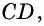 т. е. четырехугольник
т. е. четырехугольник  описанный. Теорема доказана.
описанный. Теорема доказана.
Замечание. Напомним, что в данной теореме рассматриваются только выпуклые четырехугольники.
Следствие
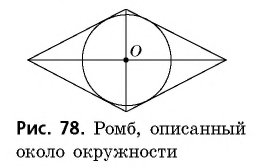
В любой ромб можно вписать окружность. Если в параллелограмм вписана окружность, то он является ромбом
Ромб, описанный около окружности, изображен на рисунке 78. Центр вписанной окружности является точкой пересечения диагоналей ромба (см. задачу 265, а).
Пример №11
В равнобедренную трапецию с боковой стороной 6 см вписана окружность. Найдите среднюю линию трапеции.
Решение:
Пусть  — данная равнобедренная трапеция с основаниями
— данная равнобедренная трапеция с основаниями  По свойству описанного четырехугольника
По свойству описанного четырехугольника 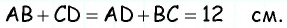 Средняя линия трапеции равна
Средняя линия трапеции равна 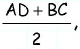 т.е. равна 6 см.
т.е. равна 6 см.
Ответ: 6 см
Геометрические софизмы
Многим из вас, наверное, известна древнегреческая история об Ахиллесе, который никак не может догнать черепаху. История математики знает немало примеров того, как ложные утверждения и ошибочные результаты выдавались за истинные, а их опровержение давало толчок настоящим математическим открытиям. Но даже ошибки и неудачи могут принести пользу математикам. Эти ошибки остались в учебниках и пособиях в виде софизмов — заведомо ложных утверждений, доказательства которых на первый взгляд кажутся правильными, но на самом деле таковыми не являются. Поиск и анализ ошибок, содержащихся в этих доказательствах, часто позволяют определить причины ошибок в решении других задач. Поэтому в процессе изучения геометрии софизмы иногда даже более поучительны и полезны, чем «безошибочные» задачи и доказательства.
Рассмотрим пример геометрического софизма, связанного с четырехугольниками, вписанными в окружность.
Окружность имеет два центра.
Доказательство:
Обозначим на сторонах произвольного угла  точки
точки  и проведем через эти точки перпендикуляры к сторонам
и проведем через эти точки перпендикуляры к сторонам 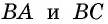 соответственно (рис. 79).
соответственно (рис. 79).
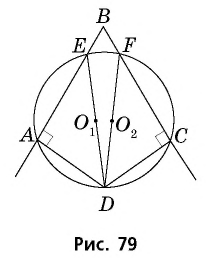
Эти перпендикуляры должны пересекаться (ведь если бы они были параллельны, то параллельными были бы и стороны данного угла — обоснуйте это самостоятельно). Обозначим точку 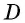 — точку пересечения перпендикуляров.
— точку пересечения перпендикуляров.
Через точки 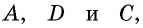 не лежащие на одной прямой, проведем окружность (это можно сделать, поскольку окружность, описанная около треугольника
не лежащие на одной прямой, проведем окружность (это можно сделать, поскольку окружность, описанная около треугольника 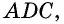 существует и является единственной). Обозначим точки
существует и является единственной). Обозначим точки 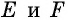 — точки пересечения этой окружности со сторонами угла
— точки пересечения этой окружности со сторонами угла 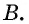 Прямые углы
Прямые углы 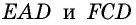 являются вписанными в окружность. Значит, по следствию теоремы о вписанных углах, отрезки
являются вписанными в окружность. Значит, по следствию теоремы о вписанных углах, отрезки 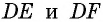 являются диаметрами окружности, которые имеют общий конец
являются диаметрами окружности, которые имеют общий конец 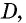 но не совпадают. Тогда их середины
но не совпадают. Тогда их середины 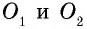 являются двумя разными центрами одной окружности, т.е. окружность имеет два центра.
являются двумя разными центрами одной окружности, т.е. окружность имеет два центра.
Ошибка этого «доказательства» заключается в неправильности построений на рисунке 79. В четырехугольнике 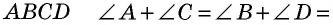
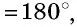 т.е. он вписан в окружность. Это означает, что в ходе построений окружность, проведенная через точки
т.е. он вписан в окружность. Это означает, что в ходе построений окружность, проведенная через точки 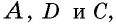 обязательно пройдет через точку
обязательно пройдет через точку 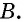 В таком случае отрезки
В таком случае отрезки 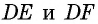 совпадут с отрезком
совпадут с отрезком 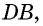 середина которого и является единственным центром построенной окружности.
середина которого и является единственным центром построенной окружности.
Среди задач к этому и следующим параграфам вы найдете и другие примеры геометрических софизмов и сможете самостоятельно потренироваться в их опровержении. Надеемся, что опыт, который вы при этом приобретете, поможет в дальнейшем избежать подобных ошибок при решении задач.
Четырехугольник и окружность в задачах. Метод вспомогательной окружности
При решении задач об окружностях и четырехугольниках иногда следует использовать специальные подходы. Один из них заключается в рассмотрении вписанного треугольника, вершины которого являются вершинами данного вписанного четырехугольника.
Пример №12
Найдите периметр равнобедренной трапеции, диагональ которой перпендикулярна боковой стороне и образует с основанием угол  если радиус окружности, описанной около трапеции, равен 8 см.
если радиус окружности, описанной около трапеции, равен 8 см.
Решение:
Пусть дана вписанная трапеция 
 (рис. 80).
(рис. 80).
Заметим, что окружность, описанная около трапеции, описана также и около прямоугольного треугольника 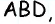 значит, ее центром является середина гипотенузы
значит, ее центром является середина гипотенузы  Тогда
Тогда 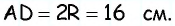 В треугольнике
В треугольнике 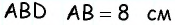 как катет, противолежащий углу
как катет, противолежащий углу 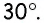 Поскольку в прямоугольном треугольнике
Поскольку в прямоугольном треугольнике 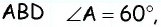 то углы при большем основании трапеции равны
то углы при большем основании трапеции равны 
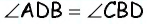 как внутренние накрест лежащие при параллельных прямых
как внутренние накрест лежащие при параллельных прямых 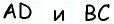 и секущей
и секущей 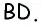 Следовательно, в треугольнике
Следовательно, в треугольнике 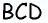 два угла равны, т.е. он является равнобедренным с основанием
два угла равны, т.е. он является равнобедренным с основанием 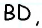 откуда
откуда  Тогда
Тогда 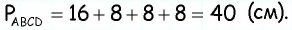
Ответ: 40 см.
Особенно интересным и нестандартным является применение окружности (как описанной, так и вписанной) при решении задач, в условиях которых окружность вообще не упоминается.
Пример №13
Из точки  лежащей на катете
лежащей на катете  прямоугольного треугольника
прямоугольного треугольника  проведен перпендикуляр
проведен перпендикуляр  к гипотенузе
к гипотенузе  (рис. 81). Докажите, что
(рис. 81). Докажите, что 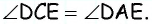
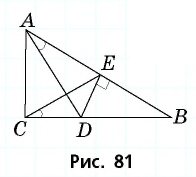
Решение:
В четырехугольнике 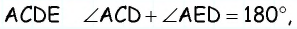 значит, около него можно описать окружность. В этой окружности вписанные углы
значит, около него можно описать окружность. В этой окружности вписанные углы 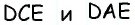 будут опираться на одну и ту же дугу, и по следствию теоремы о вписанном угле
будут опираться на одну и ту же дугу, и по следствию теоремы о вписанном угле 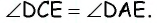
Метод решения задач с помощью дополнительного построения описанной или вписанной окружности называют методом вспомогательной окружности.
Замечательные точки треугольника
Точка пересечения медиан
В седьмом классе в ходе изучения вписанной и описанной окружностей треугольника рассматривались две его замечательные точки — точка пересечения биссектрис (иначе ее называют инцентром треугольника) и точка пересечения серединных перпендикуляров к сторонам.
Рассмотрим еще две замечательные точки треугольника.
Теорема (о точке пересечения медиан треугольника)
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, начиная от вершины треугольника.
Доказательство:
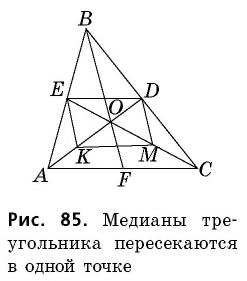
Пусть в треугольнике 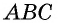 проведены медианы
проведены медианы 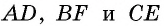 (рис. 85).
(рис. 85).
Докажем, что они пересекаются в некоторой точке 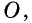 причем
причем 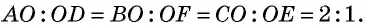
Пусть 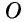 — точка пересечения медиан
— точка пересечения медиан 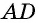 и
и 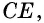 точки
точки 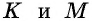 — середины отрезков
— середины отрезков 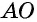 и
и 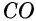 соответственно. Отрезок
соответственно. Отрезок 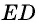 — средняя линия треугольника
— средняя линия треугольника 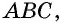 и по свойству средней линии треугольника
и по свойству средней линии треугольника 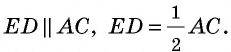 Кроме того,
Кроме того,  — средняя линия треугольника
— средняя линия треугольника  и по тому же свойству
и по тому же свойству 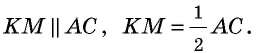 Значит, в четырехугольнике
Значит, в четырехугольнике 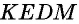 две стороны параллельны и равны. Таким образом,
две стороны параллельны и равны. Таким образом,  – параллелограмм, и его диагонали
– параллелограмм, и его диагонали 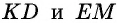 точкой пересечения делятся пополам. Следовательно,
точкой пересечения делятся пополам. Следовательно, 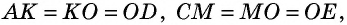 т.е. точка
т.е. точка 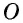 делит медианы
делит медианы 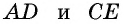 в отношении 2:1.
в отношении 2:1.
Аналогично доказываем, что и третья медиана 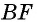 точкой пересечения с каждой из медиан
точкой пересечения с каждой из медиан 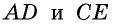 делится в отношении 2 :1. А поскольку такая точка деления для каждой из медиан единственная, то, следовательно, все три медианы пересекаются в одной точке.
делится в отношении 2 :1. А поскольку такая точка деления для каждой из медиан единственная, то, следовательно, все три медианы пересекаются в одной точке.
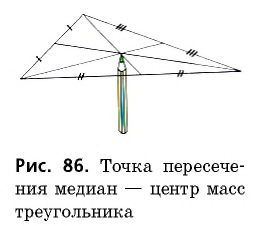
Точку пересечения медиан треугольника иначе называют центроидом или центром масс треугольника. В уместности такого названия вы можете убедиться, проведя эксперимент: вырежьте из картона треугольник произвольной формы, проведите в нем медианы и попробуйте удержать его в равновесии, положив на иглу или острый карандаш в точке пересечения медиан (рис. 86).
Пример №14
Если в треугольнике две медианы равны, то он равнобедренный. Докажите.
Решение:
Пусть в треугольнике  медианы
медианы  равны и пересекаются в точке
равны и пересекаются в точке  (рис. 87).
(рис. 87).
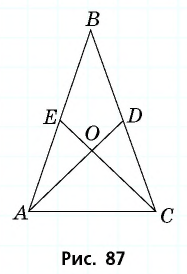
Рассмотрим треугольники  Поскольку точка
Поскольку точка  делит каждую из равных медиан
делит каждую из равных медиан  и
и  в отношении
в отношении 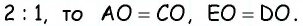 Кроме того,
Кроме того, 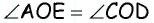 как вертикальные. Значит,
как вертикальные. Значит, 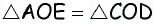 по первому признаку. Отсюда следует, что
по первому признаку. Отсюда следует, что 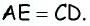
Но по определению медианы эти отрезки — половины сторон  Следовательно,
Следовательно,  т.е. треугольник
т.е. треугольник  равнобедренный.
равнобедренный.
Точка пересечения высот
Теорема (о точке пересечения высот треугольника)
Высоты треугольника (или их продолжения) пересекаются в одной точке.
Доказательство:
Пусть 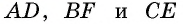 — высоты треугольника
— высоты треугольника 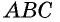 (рис. 88).
(рис. 88).
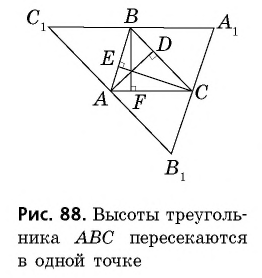
Проведя через вершины треугольника прямые, параллельные противолежащим сторонам, получим треугольник 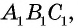 стороны которого перпендикулярны высотам треугольника
стороны которого перпендикулярны высотам треугольника 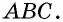 По построению четырехугольники
По построению четырехугольники 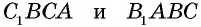 — параллелограммы, откуда
— параллелограммы, откуда 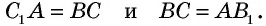 Следовательно, точка
Следовательно, точка 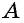 — середина отрезка
— середина отрезка 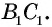 Аналогично доказываем, что
Аналогично доказываем, что 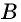 — середина
— середина 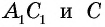 — середина
— середина 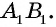
Таким образом, высоты 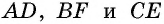 лежат на серединных перпендикулярах к сторонам треугольника
лежат на серединных перпендикулярах к сторонам треугольника  которые пересекаются в одной точке по следствию теоремы об окружности, описанной около треугольника.
которые пересекаются в одной точке по следствию теоремы об окружности, описанной около треугольника.
Точку пересечения высот (или их продолжений) иначе называют ортоцентром треугольника.
Таким образом, замечательными точками треугольника являются:
- точка пересечения биссектрис — центр окружности, вписанной в треугольник;
- точка пересечения серединных перпендикуляров к сторонам — центр окружности, описанной около треугольника;
- точка пересечения медиан — делит каждую из медиан в отношении 2:1, начиная от вершины треугольника;
- точка пересечения высот (или их продолжений).
ИТОГОВЫЙ ОБЗОР ГЛАВЫ I
ЧЕТЫРЕХУГОЛЬНИК

Теорема о сумме углов четырехугольника.
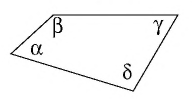
Сумма углов четырехугольника равна 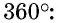
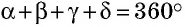
Справочный материал по параллелограмму
Параллелограммом называется четырехугольник, противолежащие стороны которого попарно параллельны
Признаки параллелограмма
Если две противолежащие стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм
Если противолежащие стороны четырехугольника попарно равны, то этот четырехугольник- параллелограм.
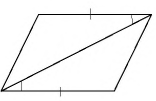

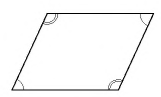
Противолежащие углы параллелограмма равны.
Диагонали параллелограмма точкой пересечения делятся пополам
Если противолежащие углы четырехугольника попарно равны, то этот четырехугольник — параллелограмм
Если диагонали четырехугольника точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм
Виды параллелограммов

Прямоугольником называется параллелограм у которого все углы прямые
Ромбом называется параллелограмм, у которого все стороны равны
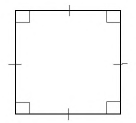
Квадратом называется прямоугольник, у которого все стороны равны
Свойство прямоугольника
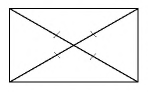
Диагонали прямоугольника равны
Признак прямоугольника
Если все углы четырехугольника равны, то этот четырехугольник является прямоугольником
Свойства ромба
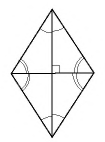
Диагонали ромба перпендикулярны и делят его углы пополам
Признак ромба
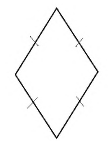
Если все стороны четырехугольника равны, то этот четырехугольник является ромбом
Свойства квадрата
Все стороны квадрата равны, а противолежащие стороны параллельны
Все углы квадрата прямые
Диагонали квадрата равны, перпендикулярны, делят углы квадрата пополам и точкой пересечения делятся пополам
Трапеция
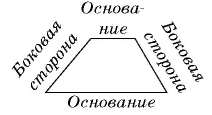
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие непараллельны
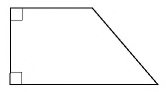
Прямоугольной трапецией называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям
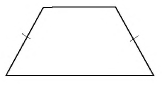
Равнобедренной трапецией называется трапеция, у которой боковые стороны равны.
Свойство равнобедренной
В равнобедренной трапеции углы при основании равны.
Признак равнобедренной
Если в трапеции углы при основании равны, то такая трапеция равнобедренная
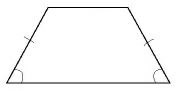
Теорема Фалеса
Параллельные прямые, которые пересекают стороны угла и отсекают на одной из них равные отрезки, отсекают равные отрезки и на другой стороне
Средние линии треугольника и трапеции
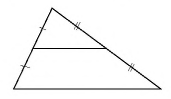
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
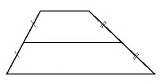
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции
Свойство средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
Свойство средней линии трапеции
Средняя линия трапеции параллельна основаниям и равна их полусумме
Углы в окружности
Центральным углом в окружности называется плоский угол с вершиной в центре окружности
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла
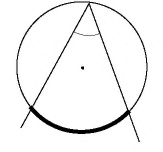
Вписанным углом называется угол, вершина которого лежит на окружности, а стороны пересекают эту окружность
Теорема о вписанном угле Вписанный угол измеряется половиной дуги, на которую он опирается
Следствия теоремы о вписанном угле
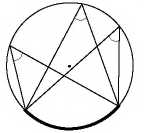
Вписанные углы, опирающиеся на одну и ту же дугу, равны
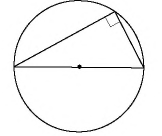
Вписанный угол, опирающийся на полуокружность, прямой, и наоборот: любой прямой вписанный угол опирается на полуокружность
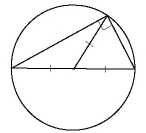
Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы
Вписанные четырехугольники
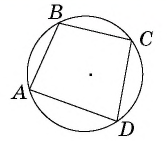
Четырехугольник называется вписанным в окружность, если все его вершины лежат на этой окружности
Признак вписанного четырехугольника
Если сумма противолежащих углов четырехугольника равна 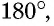 то около него можно описать окружность
то около него можно описать окружность
Около любого прямоугольника можно описать окружность
Около равнобедренной трапеции можно описать окружность
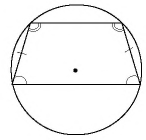
Свойство вписанного четырехугольника
- Сумма противолежащих углов вписанного четырехугольника равна
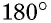
- Если параллелограмм вписан в окружность, то он является прямоугольником
- Если трапеция вписана в окружность, то она равнобедренная
Описанные четырехугольники
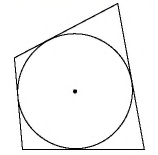
Четырехугольник называется описанным около окружности, если все его стороны касаются этой окружности
Признак описанного четырехугольника
Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность
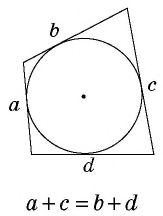
В любой ромб можно вписать окружность
Свойство описанного четырехугольника
- В описанном четырехугольнике суммы противолежащих сторон равны
- Если в параллелограмм вписана окружность, то он является ромбом
Замечательные точки треугольника
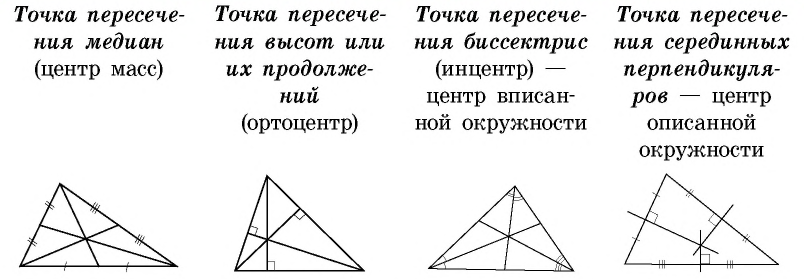
Теорема о точке пересечения медиан треугольника Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, начиная от вершины треугольника
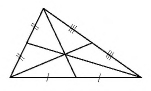
Теорема о точке пересечения высот треугольника Высоты треугольника (или их продолжения) пересекаются в одной точке
Историческая справка
Большая часть теоретических положений, связанных с четырехугольником, была известна еще в Древней Греции. Например, параллелограмм упоминается в работах Евклида под названием «параллельно-линейная площадь». Основные свойства четырехугольников были установлены на практике и только со временем доказаны теоретически.
Одним из творцов идеи геометрического доказательства по праву признан древнегреческий ученый Фалес Милетский (ок. 625-547 гг. до н. э.). Его считали первым среди прославленных «семи мудрецов» Эллады. Механик и астроном, философ и общественный деятель, Фалес значительно обогатил науку своего времени. Именно он познакомил греков с достижениями египтян в геометрии и астрономии. По свидетельству историка Геродота, Фалес предсказал затмение Солнца, которое произошло 28 мая 585 г. до н. э. Он дал первые представления об электричестве и магнетизме. Достижения Фалеса в геометрии не ограничиваются теоремой, названной его именем. Считается, что Фалес открыл теорему о вертикальных углах, доказал равенство углов при основании равнобедренного треугольника, первым описал окружность около прямоугольного треугольника и обосновал, что угол, который опирается на полуокружность, прямой. Фалесу приписывают и доказательство второго признака равенства треугольников, на основании которого он создал дальномер для определения расстояния до кораблей на море.
В молодые годы Фалес побывал в Египте. Согласно легенде, он удивил египетских жрецов, измерив высоту пирамиды Хеопса с помощью подобия треугольников (о подобии треугольников – в следующей главе).
Изучая замечательные точки треугольника, нельзя не вспомнить имена еще нескольких ученых.
Теорему о пересечении высот треугольника доказал в XV в. немецкий математик Региомонтан (1436-1476) – в его честь эту теорему иногда называют задачей Региомонтана.
Выдающийся немецкий ученый Леонард Эйлер (1707-1783), который установил связь между замечательными точками треугольника, является уникальной исторической фигурой. Геометрия и механика, оптика и баллистика, астрономия и теория музыки, математическая физика и судостроение – вот далеко не полный перечень тех областей науки, которые он обогатил своими открытиями. Перу Эйлера принадлежит более 800 научных работ, причем, по статистическим подсчетам, он делал в среднем одно изобретение в неделю! Человек чрезвычайной широты интересов, Эйлер был академиком Берлинской, Петербургской и многих других академий наук, он существенным образом повлиял на развитие мировой науки. Недаром французский математик Пьер Лаплас, рассуждая об ученых своего поколения, утверждал, что Эйлер – «учитель всех нас».
Среди украинских математиков весомый вклад в исследование свойств четырехугольников внес Михаил Васильевич Остроградский (1801-1862). Этот выдающийся ученый, профессор Харьковского университета, получил мировое признание благодаря работам по математической физике, математическому анализу, аналитической механике. Талантливый педагог и методист, Остроградский создал «Учебник по элементарной геометрии», который, в частности, содержал ряд интересных и сложных задач на построение вписанных и описанных четырех. М. В. Остроградский угольников и вычисление их площадей.
- Теорема синусов и теорема косинусов
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников
