Стороны шестиугольника ABCDEK равны. Найди и выпиши названия шести разносторонних треугольников и четырех равнобедренных. Есть ли среди равнобедренных треугольников равносторонние?
reshalka.com
ГДЗ учебник по математике 3 класс Моро. Часть 2. Страница 84. Номер №7
Решение
Получай решения и ответы с помощью нашего бота
Посмотреть калькулятор Вычисления в столбик
Разносторонние треугольники:
BDE, BDM, BKM, BKE, DEM, KEM.
Равнобедренные треугольники:
ABK, BCD, BDK, DEK.
Равносторонний треугольник:
BDK.
Опубликовано 22.08.2017 по предмету Математика от Гость
>> <<
Ответ оставил Гость
Разносторонние: ВЕК, ВDE, BKM, BDM, DME, KME.
Равнобедренные:CBD, BAK, KDE, BDK.
BDK-равносторонний.
Оцени ответ
Подпишись на наш канал в телеграм. Там мы даём ещё больше полезной информации для школьников!

Найти другие ответы
Загрузить картинку
Было бы не плохо начертить шестиугольник. У меня на чертеже вершины располагаются так: вверху А, затем справа В ,С. D,E,F.
В правильном шестиугольнике внутренние углы равны 120 градусам.
Через центр O проводим прямые, соединяя противоположные вершины АD, BE, CF. Диагонали поделили внутренние углы по палам. Мы получили AOB, BOC, COD, DOE, EOF, FOA – равнобедренные и равносторонние треугольники, т.к. все углы равны 60 градусов.
Далее соедините вершины FB AC CE EA и далее легко. Вы получите много разных треугольников.
Тупоугольные треугольники содержат тупой угол. В вашем случае это EAB ABC CDE EFA и туп. углы и тупоугольные треугольники.
Все остальные треугольники разносторонние, т.к. все углы, а значит и стороны разные. Здесь 90,30, 60 градусов. Обозначьте их сами. Так сложно будет их описать.
Стороны шестиугольника ABCDEK равны найти и выпиши 6 разносторонних треугольников и 4 равнобедренных треугольников.
Вы находитесь на странице вопроса Стороны шестиугольника ABCDEK равны найти и выпиши 6 разносторонних треугольников и 4 равнобедренных треугольников? из категории Математика.
Уровень сложности вопроса рассчитан на учащихся 1 – 4 классов. На странице
можно узнать правильный ответ, сверить его со своим вариантом и обсудить
возможные версии с другими пользователями сайта посредством обратной связи.
Если ответ вызывает сомнения или покажется вам неполным, для проверки
найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте
новый вопрос, используя ключевые слова: введите вопрос в поисковую строку,
нажав кнопку в верхней части страницы.
Определение
Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.
Замечание
Т.к. сумма всех углов (n)–угольника равна (180^circ(n-2)), то каждый угол правильного (n)–угольника равен [alpha_n=dfrac{n-2}n cdot 180^circ]
Пример
Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac {4-2}4cdot 180^circ=90^circ);
каждый угол правильного шестиугольника равен (dfrac{6-2}6cdot
180^circ=120^circ).
Теоремы
1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствия
1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.
2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.
Теорема
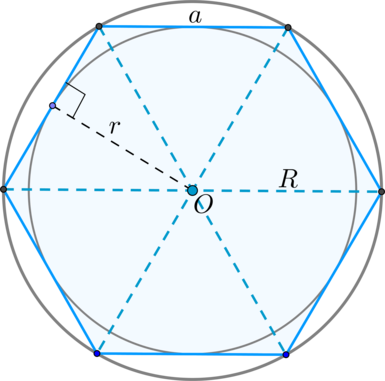
Если (a) – сторона правильного (n)–угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin{aligned}
S&=dfrac n2ar\
a&=2Rcdot sindfrac{180^circ}n\
r&=Rcdot cosdfrac{180^circ}n end{aligned}]
Свойства правильного шестиугольника
1. Сторона равна радиусу описанной окружности: (a=R).
2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.
3. Все углы правильного шестиугольника равны (120^circ).
4. Площадь правильного шестиугольника со стороной (a) равна (dfrac{3sqrt{3}}{2}a^2).
5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.
6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).
Замечание
В общем случае правильный (n)-угольник инвариантен относительно поворота на угол (dfrac{360^circ}{n}).