Кикоин А.К. Когда к телу приложены параллельные силы //Квант. — 1985. — № 2. — С. 23-25.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
Содержание
- 1 Если силы параллельны и направлены в одну сторону
- 2 Если направления параллельных сил противоположны
- 3 Пара сил
Хорошо известно, как найти равнодействующую двух сил, приложенных к материальной точке (рис. 1). На векторах, изображающих эти силы, как на сторонах строят параллелограмм; диагональ со стрелкой на конце, проведенная из точки, к которой приложены силы, и есть вектор равнодействующей.
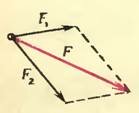
Рис. 1
Когда две силы приложены не к материальной точке, а к телу, но так, как показано на рисунке 2, то равнодействующая определяется таким же образом. Пользуясь тем, что точку приложения силы можно переносить вдоль линии ее действия («Физика 8», § 46), находят точку С, в которой пересекаются линии действия обеих сил.
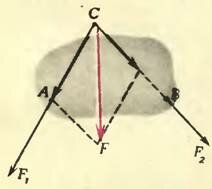
Рис. 2
Полагая, что силы (~vec F_1) и (~vec F_2) приложены именно к этой точке, строят параллелограмм и проводят диагональ. Правда, точка С может оказаться и вне тела, но тогда точку приложения равнодействующей можно выбрать в любом месте на линии ее действия. Действительно, какую бы точку мы не выбрали, равнодействующая сила (~vec F) сообщит телу такое же ускорение или вызовет такой же вращающий момент, как и силы (~vec F_1) и (~vec F_2), вместе взятые.
Если силы параллельны и направлены в одну сторону
Пусть к телу приложены две параллельные сонаправленные силы (рис. 3). Линии действия таких сил нигде не пересекаются, и параллелограмм на них построить нельзя. Тем не менее сложить эти силы и найти их равнодействующую можно.
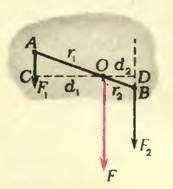
Рис. 3
Нетрудно понять, что равнодействующая направлена параллельно обеим силам и ее модуль равен арифметической сумме модулей складываемых сил. А в какой точке она приложена? Или, другими словами, к какой точке тела надо приложить силу, равную по модулю, но противоположную по направлению равнодействующей, чтобы тело находилось в равновесии?
Чтобы найти точку приложения равнодействующей двух параллельных и одинаково направленных сил, можно воспользоваться правилом моментов («Физика 8», § 48). Проведем прямую, соединяющую точки А и В (см. рис. 3). Где-то на этой прямой должна, очевидно, находиться и точка приложения равнодействующей. Пусть это будет точка О. Допустим, что через эту точку проходит закрепленная ось, перпендикулярная плоскости, содержащей обе складываемые силы (то есть перпендикулярная плоскости рисунка). Если О действительно есть точка приложения равнодействующей, то тело будет находиться в равновесии — равнодействующая уравновешивается силой реакции со стороны оси. С другой стороны, если тело с закрепленной осью находится в равновесии, то алгебраическая сумма моментов сил относительно этой оси должна быть равна нулю. Из рисунка 3 видно, что сила (~vec F_2), будь она единственной, поворачивала бы тело вокруг О по часовой стрелке, то есть ее момент F2d2 положительный, а сила (~vec F_1) если бы она была единственной, поворачивала бы тело против часовой стрелки — ее моменту F1d1 надо приписать отрицательный знак (здесь d1 и d2 — плечи сил (~vec F_1) и (~vec F_2)).
Следовательно,
(~F_2 d_2 – F_1 d_1 = 0), или (~frac{F_1}{F_2} = frac{d_2}{d_1}) .
Из подобия треугольников АОС и BOD находим, что (~frac{d_1}{d_2} = frac{r_1}{r_2}) . Поэтому окончательно получаем
(~frac{F_1}{F_2} = frac{r_2}{r_1}) .
Это значит, что равнодействующая двух параллельных, одинаково направленных сил приложена к точке, делящей отрезок, соединяющий точки приложения складываемых сил, в отношении, обратном отношению модулей сил. Ясно, что эта точка лежит ближе к большей из сил.
Если направления параллельных сил противоположны
Приложенные к телу параллельные силы могут быть направлены и в противоположные стороны (рис. 4). Теперь точка приложения равнодействующей (~vec F) не может находиться где-то между точками приложения сил (~vec F_1) и (~vec F_2). Ведь вокруг любой точки, лежащей между ними, каждая сила поворачивает тело против часовой стрелки, знаки моментов этих сил одинаковы, и их сумма не может быть равна нулю, как это требуется для равновесия.
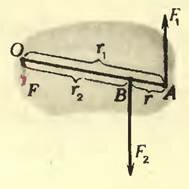
Рис. 4
Легко догадаться, что точка приложения равнодействующей лежит за точкой приложения большей силы, как это и показано на рисунке 4. Модуль же равнодействующей равен модулю разности модулей сил (~vec F_1) и (~vec F_2). В какой же именно точке приложена равнодействующая? На каком расстоянии r2 от точки приложения большей силы? Воспользуемся опять правилом моментов:
(~frac{F_1}{F_2} = frac{r_2}{r_1}), или (~F_2 = F_1 frac{r_1}{r_2}) .
Вычтем из правой и левой частей последнего равенства величину F1:
(~F_2 – F_1 = F_1 frac{r_1}{r_2} – F_1 = F_1 left( frac{r_1}{r_2} – 1 right) = F_1 frac{r_1 – r_2}{r_2}) ,
откуда
(~r_2 = frac{F_1(r_1 – r_2)}{F_2 – F_1} = frac{F_1 r}{F_2 – F_1}) . (*)
Таким образом, точка приложения равнодействующей двух противоположно направленных параллельных сил расположена тем дальше от точки приложения большей из них, чем меньше разность модулей этих сил.
Пара сил
Мы видели, что если к телу приложены параллельные силы, одинаково или противоположно направленные, то всегда можно найти модуль и направление равнодействующей этих сил и определить точку ее приложения. Если к этой точке приложить силу, равную равнодействующей по модулю, но противоположную ей по направлению, то тело будет находиться в равновесии — оно не будет двигаться поступательно и не будет вращаться.
Но, оказывается, есть один случай, когда равнодействующую найти нельзя. Так бывает, если к телу приложены две параллельные, противоположно направленные силы, по модулю равные друг другу. Про такие силы говорят, что они образуют пару сил. Модуль их равнодействующей равен, конечно, нулю, а из формулы (*) видно, что при F2 — F1 =0 расстояние r2 до точки приложения равнодействующей равно бесконечности, то есть что такой точки попросту не существует. И в самом деле, какая же может быть точка приложения равнодействующей, которой нет?
Достаточно, однако, взглянуть на рисунок 5, чтобы понять, что под действием пары сил тело не будет находиться в равновесии — оно будет вращаться. Значит, у пары сил есть некоторый вращающий момент. Но относительно какой оси?
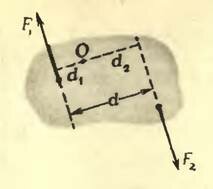
Рис. 5
Нетрудно показать, что суммарный момент сил, составляющих пару, одинаков для любой оси, перпендикулярной плоскости, в которой лежат обе эти силы (перпендикулярной плоскости рисунка). Действительно, возьмем любую точку О и проведем через нее ось вращения. Момент M1 силы (~vec F_1) относительно этой оси равен F1d1, момент M2 силы (~vec F_2) относительно этой же оси равен F2d2. Суммарный момент М обеих сил равен M1 + M2 :
(~M = F_1 d_1 + F_2 d_2) .
Так как F1 = F2 = F, то
(~M = F (d_1 + d_2) = Fd) ,
где d — расстояние между линиями действия сил, составляющих пару, называемое плечом пары сил. Значит, момент пары сил равен произведению модуля одной из сил на плечо пары. Так и говорят — момент пары сил — и не указывают относительно какой оси.
Как же все-таки «ведет» себя тело, к которому приложена пара сил? Чтобы ответить на этот вопрос, вспомним, что центр масс тела (о нем говорится в § 44 «Физики 8») движется так, как будто в нем сосредоточена вся масса тела и к нему приложены все действующие на тело силы (это утверждение называется в физике теоремой о движении центра масс). Но если сумма сил равна нулю, то центр масс не может тронуться с места (если, конечно, он покоился до приложения сил). Когда на тело действует пара сил, сумма сил как раз и равна нулю, и она не может привести в движение центр масс. Тело, однако, вращается. Значит, вращается оно вокруг оси, проходящей через центр масс (ведь все точки на оси вращения находятся в покое). Оси вращения, проходящие через центры масс тел, тем и замечательны, что на них не действуют никакие силы.
Сложение параллельных сил
Найдем
равнодействующую двух действующих на
твердое тело параллельных сил в двух
случаях:
1.
Силы направлены в одну сторону.
Равнодействующая
двух действующих на абсолютно твердое
тело параллельных сил, направленных в
одну сторону, равна по модулю сумме
модулей слагаемых сил, им параллельна
и направлена в туже сторону. Линия
действия равнодействующей проходит
между точками приложения слагаемых сил
на расстояниях от этих точек, обратно
пропорциональных этим силам.
![]()
 ,
,
![]() .
.
(1.15)
2.
Силы направлены
в разные стороны.
Р авнодействующая
авнодействующая
двух действующих на абсолютно твердое
тело параллельных сил, направленных в
разные стороны, равна по модулю разности
модулей слагаемых сил, им параллельна
и направлена в сторону большей силы.
Линия действия равнодействующей проходит
вне отрезка, соединяющего точки приложения
слагаемых сил, на расстояниях от этих
точек, обратно пропорциональных силам.
![]() ,
,
![]() .
.
(1.16)
С
помощью приведенных формул можно решать
задачи и о разложении силы на две ей
параллельные.
Пара сил
Пара
сил – это
система двух равных по модулю, параллельных
и направленных в противоположные стороны
сил.
Плоскость,
проходящая через линии действия сил
пары, называется плоскостью
действия пары.
Расстояние
между линиями действия сил пары называется
плечом пары.
П ара
ара
сил не имеет равнодействующей. Действие
пары на тело сводится к некоторому
вращательному эффекту, численно
характеризуемому моментом пары сил.
Моментом
пары сил
называется величина, равная взятому с
соответствующим знаком произведению
модуля одной из силы пары на ее плечо
![]() .
.
(1.17)
Свойства пары сил
1.
Действие пары сил на тело не изменится,
если у нее произвольным образом изменить
силы и плечо при неизменном моменте
пары.
2.
Не изменяя действия пары сил, ее можно
переносить произвольным образом в
плоскости ее действия.
3. Пару сил можно
повернуть в плоскости ее действия на
любой угол.
4.
Действие нескольких пар сил, приложенных
в одной плоскости, можно заменить одной
парой сил, момент которой равен
алгебраической сумме моментов заданных
пар сил.
Условие равновесия плоской системы сил
Для
равновесия произвольной плоской системы
сил необходимо и достаточно, чтобы
алгебраическая сумма проекций всех сил
на оси координат и алгебраическая сумма
моментов всех сил относительно любой
точки равнялись нулю
![]() .
.
(1.18)
Теорема о параллельном переносе силы
Теорема:
Силу,
приложенную к твердому телу, можно, не
изменяя оказываемого действия, переносить
параллельно ей самой в любую точку тела,
прибавляя при этом пару с моментом,
равным моменту переносимой силы
относительно точки, куда сила переносится.

Приведение плоской системы сил к заданному центру
Пользуясь
теоремой о параллельном переносе,
систему сил, действующую на твердое
тело, можно перенести в одну точку. Эту
точку будем называть центром
приведения.
При
этом сила
![]() ,равная
,равная
геометрической сумме всех сил системы,
называетсяглавным
вектором системы,
а величина
![]() ,
,
равная сумме моментов всех сил системы
относительно центра приведенияO,
называется главным
моментом системы относительно центра
O.
Теорема:
Всякая плоская
система сил, при приведении к произвольному
центру O
заменяется одной силой R,
равной главному вектору системы, и
приложенной в центре приведения, и одной
парой с моментом MO,
равным главному моменту системы
относительно центра O.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Приведение двух параллельных сил к равнодействующей:
Две параллельные силы, направленные в одну сторону, всегда имеют, равнодействующую, направленную в ту же сторону и по модулю равную сумме модулей слагаемых сил. Линия действия равнодействующей делит расстояние между линиями действия слагаемых сил внутренним образом на части, обратно пропорциональные модулям слагаемых сил
Сложение двух параллельных сил, направленных в одну сторону
Если векторы сил параллельны между собой, то линии действия их не пересекаются и их нельзя складывать по правилу сложения сил. Для приведения параллельных сил к равнодействующей существуют другие правила, выводом которых мы теперь займемся.
Пусть на твердое тело (рис. 22, а) действуют две силы: 
Приложим к тому же телу в точках А и В две равные силы  и
и  (рис. 22, б), направленные по прямой AB в противоположные стороны. Силы
(рис. 22, б), направленные по прямой AB в противоположные стороны. Силы  и
и  взаимно уравновешивают друг друга, наличие таких сил эквивалентно их отсутствию, а следовательно, система четырех действующих на данное тело сил (
взаимно уравновешивают друг друга, наличие таких сил эквивалентно их отсутствию, а следовательно, система четырех действующих на данное тело сил ( ,
,  ,
,  и
и  ) эквивалентна двум данным силам
) эквивалентна двум данным силам  и
и  . Сложив затем силы
. Сложив затем силы  и
и  , приложенные к телу в точке А, мы заменим их одной силой
, приложенные к телу в точке А, мы заменим их одной силой 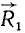 , приложенной к той же точке А. Сложив силы
, приложенной к той же точке А. Сложив силы  и
и  , приложенные к телу в точке В, мы заменим их одной силой
, приложенные к телу в точке В, мы заменим их одной силой 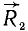 . Силы
. Силы  и
и  эквивалентны системе сил (F1,
эквивалентны системе сил (F1,  ,
, и
и  ), а следовательно, они эквивалентны двум силам (
), а следовательно, они эквивалентны двум силам ( и F2).
и F2).
Перенесем силы 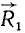 и
и 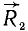 в точку D пересечения их линий действия (рис. 22, в) и там разложим каждую из них на две составляющие, параллельные силам
в точку D пересечения их линий действия (рис. 22, в) и там разложим каждую из них на две составляющие, параллельные силам 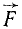 и
и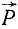 . Мы получим четыре силы (
. Мы получим четыре силы (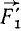 ,
, 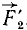 ,
,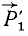 и
и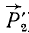 ), приложенные к точке D и эквивалентные системе сил (
), приложенные к точке D и эквивалентные системе сил ( и
и  ), причем
), причем 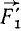 =
=  ,
,  =
=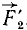 ,
, 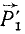 =
= ,
, 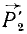 =
=  . Заметим, что силы
. Заметим, что силы 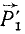 и
и 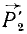 равны между собой по величине и действуют по одной и той же прямой в противоположные стороны, а потому они уравновешивают друг друга, т. е. наличие этих сил эквивалентно их отсутствию, и мы можем отбросить силы
равны между собой по величине и действуют по одной и той же прямой в противоположные стороны, а потому они уравновешивают друг друга, т. е. наличие этих сил эквивалентно их отсутствию, и мы можем отбросить силы  и
и  . Останутся только две силы, приложенные в одной и той же точке D, а именно
. Останутся только две силы, приложенные в одной и той же точке D, а именно  , равная данной силе
, равная данной силе  , и
, и  , равная силе
, равная силе  .
.
Таким образом, систему двух параллельных сил ( ,
,  ), приложенных в разных точках А и В твердого тела, мы заменили эквивалентной системой таких же сил, но приложенных к одной точке D. Очевидно, что равнодействующая этой системы приложена в той же точке D, направлена в ту же сторону, что и слагаемые силы, а по .модулю равна сумме модулей этих сил:
), приложенных в разных точках А и В твердого тела, мы заменили эквивалентной системой таких же сил, но приложенных к одной точке D. Очевидно, что равнодействующая этой системы приложена в той же точке D, направлена в ту же сторону, что и слагаемые силы, а по .модулю равна сумме модулей этих сил:
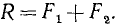 (10)
(10)
Перенесем равнодействующую 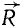 по линии действия в точку С, лежащую на прямой AB (рис. 22, г). Из подобия полученных треугольников ACD и BCD, соответственным силовым треугольникам (см. рис. 22, в), можно написать
по линии действия в точку С, лежащую на прямой AB (рис. 22, г). Из подобия полученных треугольников ACD и BCD, соответственным силовым треугольникам (см. рис. 22, в), можно написать
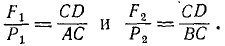
Деля первую пропорцию на вторую и принимая во внимание, что P1=P2, получим
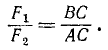 (11)
(11)
Следовательно (рис. 22, д), две параллельные силы  и
и  , направленные в одну сторону, приведены к одной равнодействующей
, направленные в одну сторону, приведены к одной равнодействующей 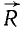 , направленной в ту же сторону и по модулю равной сумме модулей слагаемых сил. Линия действия равнодействующей R лежит между линиями действия слагаемых сил и делит расстояние AB на части, обратно пропорциональные модулям слагаемых сил.
, направленной в ту же сторону и по модулю равной сумме модулей слагаемых сил. Линия действия равнодействующей R лежит между линиями действия слагаемых сил и делит расстояние AB на части, обратно пропорциональные модулям слагаемых сил.
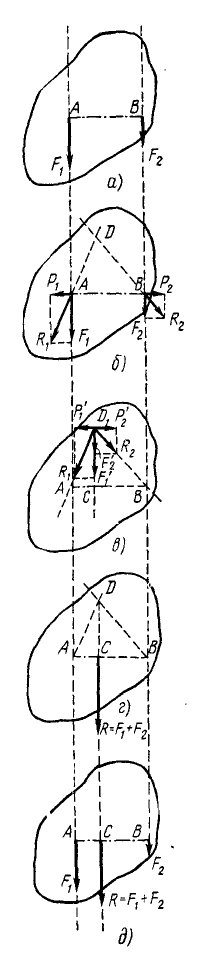
Рис. 22
Две неравные параллельные силы, направленные в противоположные стороны, имеют равнодействующую, направленную в сторону большей силы и по модулю равную разности модулей слагаемых сил. Линия действия равнодействующей делит расстояние между линиями действия слагаемых сил внешним образом на части, обратно пропорциональные модулям слагаемых сил
Сложение параллельных сил, направленных в противоположные стороны
Параллельные силы, направленные в противоположные стороны, могут быть приведены к равнодействующей только в том случае, если модули слагаемых сил не равны между собой.
Пусть на твердое тело (рис. 23, а) действуют две силы:  приложенная к точке А, и
приложенная к точке А, и  , приложенная к точке В. Линии действия этих сил параллельны, но направления противоположны. По величине силы не равны, пусть F1 > F2. Приложим к тому же телу в точках А и В две взаимно уравновешенные силы
, приложенная к точке В. Линии действия этих сил параллельны, но направления противоположны. По величине силы не равны, пусть F1 > F2. Приложим к тому же телу в точках А и В две взаимно уравновешенные силы  и
и  (рис. 23, б).
(рис. 23, б).
Сложив затем силы  и
и  , приложенные к точке А, мы заменим их одной силой
, приложенные к точке А, мы заменим их одной силой 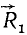 . Сложив
. Сложив  и
и  заменим их силой
заменим их силой 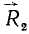 . Перенесем силы
. Перенесем силы 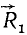 и
и 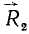 в точку D пересечения их линий действия (рис. 23, в) и там разложим каждую из них на две составляющие, параллельные силам
в точку D пересечения их линий действия (рис. 23, в) и там разложим каждую из них на две составляющие, параллельные силам 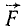 и
и 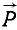 . В точке D мы получим пучок четырех сил (
. В точке D мы получим пучок четырех сил (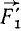 ,
, 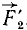 ,
,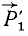 и
и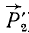 ), эквивалентный системе двух данных параллельных сил (
), эквивалентный системе двух данных параллельных сил ( и
и  ), причем F1 =
), причем F1 = 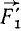 =
=  ,
,  =
=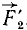 ,
, 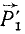 =
= ,
, 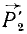 =
=  .Отбросим взаимно уравновешенные силы P’1 и P2. Тогда в точке D останутся лишь две силы
.Отбросим взаимно уравновешенные силы P’1 и P2. Тогда в точке D останутся лишь две силы 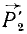 и
и  . Равнодействующая этой системы сил приложена в точке D, направлена в сторону большей силы, а по модулю равна разности модулей слагаемых сил:
. Равнодействующая этой системы сил приложена в точке D, направлена в сторону большей силы, а по модулю равна разности модулей слагаемых сил:
P = F1-F2. (10′)
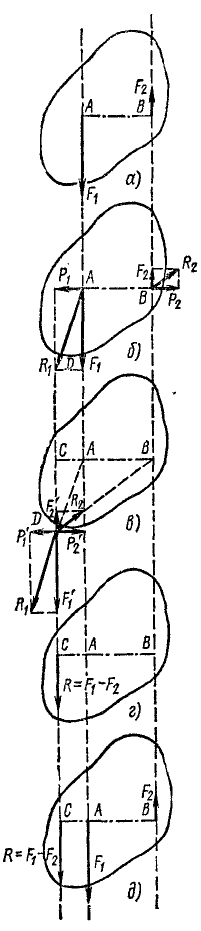
Рис. 23
Перенесем равнодействующую P по линии действия к точке С, лежащей на прямой AB (рис. 23, г). Из подобия треугольников ACD, BCD и соответствующих силовых треугольников можно написать пропорции
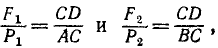
откуда
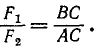 (11)
(11)
Следовательно (рис. 23, д), две неравные параллельные силы F1 и F2, направленные в противоположные стороны, приведены нами к одной равнодействующей R, направленной в сторону большей силы и по модулю равной разности модулей слагаемых сил. Линия действия равнодействующей лежит за линией действия большей силы и делит расстояние между слагаемыми силами на части, обратно пропорциональные модулям сил.
Из равенств (10) или (10/) и (11) можно получить следующие производные пропорции, полезные при решении задач:
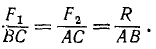 (12)
(12)
Заметим, что теоремы о проекциях равнодействующей пучка сил (см. § 6), конечно, остаются справедливыми и для проекций равнодействующей параллельных сил, так как направляющие косинусы параллельных сил одинаковы.
Данную силу можно разложить на две, ей параллельные, для которых данная сила является равнодействующей.
- Заказать решение задач по теоретической механике
Разложение силы на параллельные составляющие
Задача приведения к равнодействующей двух параллельных сил имеет всегда однозначное решение. Обратная задача — разложение данной силы R на две, ей параллельные, 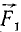 и
и 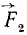 -неопределенная и может иметь сколько угодно решений. Задача становится определенной, если заданы расстояния AC и BC до линии действия этих сил или заданы расстояние (AC, BC или АВ) и модуль одной из сил. Имея заданный величины, можно определить искомые по выведенным формулам:
-неопределенная и может иметь сколько угодно решений. Задача становится определенной, если заданы расстояния AC и BC до линии действия этих сил или заданы расстояние (AC, BC или АВ) и модуль одной из сил. Имея заданный величины, можно определить искомые по выведенным формулам:
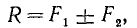 (10, 10/)
(10, 10/)
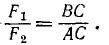 (11)
(11)
Задача №1
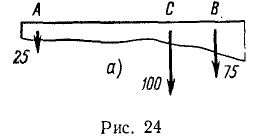
Вес (G=100 кГ) балки приложен в точке С. Как расположить опоры А и В, чтобы давление балки на опору В равнялось 75 кГ?
Решение. Для получения ответа достаточно подставить числовые данные в формулы (10), (10/) и (11). Но задача не имеет однозначного решения. Опору В можно поместить в любой точке балки, причем: 1) если балка давит на опору В сверху вниз (рис. 24), то опора А должна быть расположена по другую сторону от C на расстоянии, определяемом из пропорции: ЛС:ВС = 75:25, т. е. на расстоянии AC=3BC: 2) если же балка давит на опору В снизу вверх, то опора А должна быть расположена между C и В на расстоянии от С, определяемом из пропорции:
AC: BC = 75:175, т. е. на расстоянии 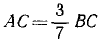 . Чтобы задача стала определенной, надо в условии указать вверх или вниз направлено давление балки на точку В и задать одно из расстояний (АС, BC или АВ).
. Чтобы задача стала определенной, надо в условии указать вверх или вниз направлено давление балки на точку В и задать одно из расстояний (АС, BC или АВ).
Задача №2
Однородный стержень AB весом G = 100 кГ опирается одним концом на гладкий горизонтальный пол, другим — на гладкую плоскость, наклоненную под углом 30° к горизонту. У конца В стержень поддерживается веревкой с грузом P, перекинутой через блок С. Отрезок .веревки BC параллелен наклонной плоскости. Пренебрегая трением на блоке, определить груз P и давления NА и NВ на пол и на наклонную плоскость (рис. 25, а).
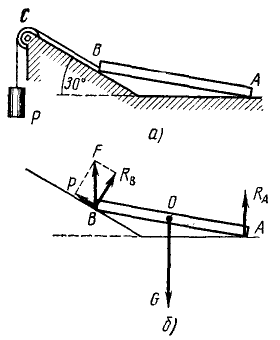
Рис. 25
Решение. Одна из искомых сил действует на пол, другая —на наклонную плоскость, третья приложена к грузу. Но груз поддерживается веревкой, и натяжение веревки равно весу P груза. Блок C меняет направление силы натяжения веревки. Поэтому на точку В стержня действует в направлении BC сила P. На ту же точку В действует реакция Rв, по принципу равенства действия и противодействия равная и противоположная искомому давлению стержня на наклонную плоскость; на точку А действует реакция RА, равная и противоположная давлению N стержня на пол. Таким образом, рассмотрев равновесие стержня А В, мы сможем определить все искомые силы.
На стержень AB действуют следующие силы: 1) вес G, приложенный в середине стержня и направленный вниз; 2) реакция Рд пола в точке А, направленная вертикально (перпендикулярно виртуальным перемещениям); 3) в точке В натяжение P нити, направленное по нити, и реакция RВ наклонной плоскости, перпендикулярная к плоскости. Но если мы сложим эти две силы по правилу параллелограмма и заменим их одной силой F (рис. 25, б), то мы можем рассматривать балку как находящуюся в равновесии под действием трех сил: G, RА, F. Известно, что две из этих сил (G и Ra) вертикальны, следовательно, вертикальна и третья сила F.
Так как вес стержня приложен в его середине, а силы F и RА-по концам, то, следовательно, 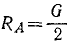 и
и 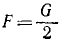 .
.
Из чертежа видно, что 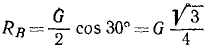 ;
; 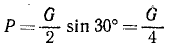 . Искомые давления NA и NВ равны и противоположны реакциям RА и RВ.
. Искомые давления NA и NВ равны и противоположны реакциям RА и RВ.
Ответ. P = 25 κΓ∙, NА = 50κΓ; NВ = 43,3 кГ.
Задача №3
Чтобы поднять лебедкой груз (заводское оборудование) весом G=6T на второй этаж заводского корпуса, не допустив возникновения горизонтальных усилий на стены здания, монтажники перекинули трос от лебедки L к грузу G через два блока, находящихся на одной вертикали, причем блок O1 прикреплен к полу первого этажа (рис. 26, а), а блок O2— к потолочной балке второго этажа. Определить силу, действующую на балку в точке C крепления блока O2, и реакции от действия этой силы на опоры А и В балки, если AB= 12 м, AC = 4м и груз прямолинейно.
Решение. Рассмотрим сначала равновесие блока O2, а затем равновесие балки АВ.
На блок O2 действуют следующие силы (рис. 26, б): 1) сила натяжения ветви троса, на которой висит груз, равная весу груза (6 Т) и направленная по этой ветви вниз; 2) сила натяжения ветви троса, направленная к блоку O1; эта сила тоже равна 6 Т, так как блок не меняет величину силы; 3) реакция в оси. блока O2. Очевидно, что реакция в оси направлена вертикально вверх и равна 12 Т, так как она уравновешивает две направленные вниз силы по 6 T каждая. Следовательно, на балку AB в месте C крепления блока действует сила, равная 12 T и направленная вниз.
При рассмотрении равновесия балки AB мы, кроме этой силы в 12 T, учтем и вызванные ею реакции в точках опоры А и В (рис. 26, в). Реакции в опорах равны и противоположны давлениям, и мы находим их из пропорции (12):
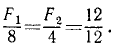
Ответ. Сила, действующая на балку в точке C= 12 Т; F1 =8 Т; F2 = 4T.
- Пара сил в теоретической механике
- Приведение системы сил к данной точке
- Система сил на плоскости
- Естественный и векторный способы определения движения точки
- Теорема моментов количества движения
- Теорема кинетической энергии
- Условие равновесия системы сходящихся сил в геометрической форме
- Условия равновесия системы сходящихся сил в аналитической форме
Параллельными силами называются силы, линии действия которых параллельны. Определим правила сложения и вычитания параллельных сил.
Задача 1. Сложить две параллельные силы, направленные в одну сторону.
Рассмотрим абсолютно твердое тело, на которое действует система двух параллельных сил и
, приложенных к точкам
и
, находящихся на расстоянии
друг от друга. Для определенности будем считать, что силы
и
направлены вертикально вниз.
Определим равнодействующую этих сил и точку ее приложения.
Решение.
Приложим силы и
в соответствующих точках
и
(рис.С.30)

- В соответствие с аксиомой №2, добавим к системе сил
уравновешенную систему сил
, как показано на рисунке.
- Складывая попарно соответствующие силы,
получим силы и
, линии действия которых пересекаются в точке
.
- Поскольку силы
и
являются скользящими векторами (следствие из аксиомы №2), то их можно перенести вдоль линии действия в точку пересечения
.
- Теперь разложим силы
и
, приложенные к точке
на вертикальное и горизонтальное направления. Получим, что
и
.
- Вычтем уравновешенную систему сил
, приложенную к точке
(аксиома №2). Тогда
.
- Силы
и
теперь приложены к точке
, поэтому (в силу аксиомы №3) их можно сложить
.
Сила приложена к точке
. Так как сила
является скользящим вектором (следствие из аксиомы №2), то ее можно перенести вдоль линии действия в точку
, являющейся точкой пересечения прямой
и линией действия силы
.
Примем расстояние от точки до точки
равной
. То есть
, тогда расстояние между точками
и
равно
.
Таким образом, равнодействующая двух параллельных сил
и
равна
, причем ее модуль
. Равнодействующая
приложена в точке
.
- Определим теперь положение точки
.
Из подобия треугольников и
(
) следует справедливость пропорции
или
(С.12)
Из подобия треугольников и
следует справедливость пропорции
или
(С.13)
В равенствах (С.12) и (С.13) правые части равны, следовательно, равны и левые части
или
.
Отсюда следует, что (С.14).
Таким образом, определено положение точки приложения равнодействующей параллельных сил и
.
Частный случай. Если , то
, и
.
Задача 2. Сложить две параллельные силы, направленные в разные стороны.
Рассмотрим абсолютно твердое тело, на которое действует система двух параллельных сил и
, приложенных к точкам
и
, находящихся на расстоянии
друг от друга. Для определенности будем считать, что сила
направлена вертикально вниз, а
направлена вертикально вверх.
Определим равнодействующую этих сил и точку ее приложения.
Решение.
Приложим силы и
в соответствующих точках
и
(рис.С.31)
Проведем построения, аналогичные задаче 1.

- В соответствие с аксиомой №2, добавим к системе сил
уравновешенную систему сил
, как показано на рис.С.31.
- Складывая попарно силы,
получим силы и
, линии действия которых пересекаются в точке
(рис.С.31).
- Поскольку силы
и
являются скользящими векторами (следствие из аксиомы №2), то их можно перенести вдоль линии действия в точку пересечения
.
- Теперь разложим силы
и
, приложенные к точке
на вертикальное и горизонтальное направления. Получим, что
и
.
- Вычтем уравновешенную систему сил
, приложенную к точке
(аксиома №2). Тогда
.
- Силы
и
теперь приложены к точке
, поэтому (в силу аксиомы №3) их можно сложить
.
Сила приложена к точке
. Так как сила
является скользящим вектором (следствие из аксиомы №2), то ее можно перенести вдоль линии действия в точку
, являющейся точкой пересечения прямой
и линией действия силы
.
Примем расстояние от точки до точки
равной
. То есть
, тогда расстояние между точками
и
равно
.
Таким образом, как следует из рисунка, равнодействующая двух параллельных разнонаправленных сил
и
равна
, причем ее модуль
. Равнодействующая
приложена в точке
.
Определим теперь положение точки .
Из
подобия треугольников и
(
) следует справедливость пропорции
или
(С.15)
Из подобия треугольников и
(
) следует справедливость пропорции
или
(С.16)
В равенствах (С.15) и (С.16) правые части равны, следовательно равны и левые части
или
.
Отсюда следует, что (С.17)
Таким образом, определено положение точки приложения равнодействующей параллельных и направленных в разные стороны сил и
.
Содержание:
- Параллельные силы. Добавление двух параллельных сил
- Момент силы относительно центра (точки)
- Момент силы относительно центра как вектор
- Пара сил. Момент пары сил
- Свойства пары сил
- Условия равновесия тела под действием системы пар сил, расположенных в одной плоскости
Из физики известно, что две параллельные силы, направленные в одну сторону, эквивалентны равнодействующей, которая равна сумме этих сил, параллельна им и направлена в ту же сторону; линия действия равнодействующей делит отрезок, соединяющий точки приложения данных сил на части, обратно пропорциональные модулям этих сил.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Параллельные силы. Добавление двух параллельных сил
Если линии действия сил параллельны, то такие силы носят название “параллельные
силы “.
Рассмотрим вопрос о добавлении сил, линии действия которых параллельны. При этом здесь могут быть два случая: когда параллельные силы имеют одинаковое направление и когда параллельные силы противоположно направлены.
1. Рассмотрим случай, когда две параллельные силы имеют одинаковое направление.
Есть тело, к которому приложены две параллельные силы:  — в точке А и
— в точке А и  — в точке В (рис. 1.12). Направление сил
— в точке В (рис. 1.12). Направление сил  и
и  одинаково. Добавить силы — это значит определить их равнодействующую.
одинаково. Добавить силы — это значит определить их равнодействующую.
Сначала соединим точки А и В прямой. Далее приложим в точках А и В уравновешенную систему сил  и
и  . Причем
. Причем  = –
= –  . Векторы сил
. Векторы сил  и
и  размещены на прямой АВ. Вторая аксиома статики позволяет это сделать. В результате в точках A и B полученные по две силы (в точке A —
размещены на прямой АВ. Вторая аксиома статики позволяет это сделать. В результате в точках A и B полученные по две силы (в точке A —  и
и  , а в точке В —
, а в точке В —  и
и  ), которые можно добавить (благодаря третьей аксиоме статики) и в каждой точке получить равнодействующие силы —
), которые можно добавить (благодаря третьей аксиоме статики) и в каждой точке получить равнодействующие силы —  и
и  .
.
Перенесем точки приложения равнодействующих  и
и  вдоль линий их действия в точку пересечения D. Далее разложим каждую равнодействующую на составляющие:
вдоль линий их действия в точку пересечения D. Далее разложим каждую равнодействующую на составляющие:
 разлагается на
разлагается на  и
и  , а
, а  — на
— на  и
и  . По уже известной второй аксиоме статики приложенные в точке D силы
. По уже известной второй аксиоме статики приложенные в точке D силы  и
и  является уравновешенной системой сил, которую можно отбросить. Остаются приложенные в точке D две силы
является уравновешенной системой сил, которую можно отбросить. Остаются приложенные в точке D две силы  и
и  , направление которых совпадает. Добавим их и получим равнодействующую
, направление которых совпадает. Добавим их и получим равнодействующую  , модуль которой будет равняться
, модуль которой будет равняться
R = P1 + P2 .

Перенесем вектор равнодействующей силы  с точки D в точку С, которая расположена на прямой АВ. Рассмотрим треугольники, которые есть на рис.1.12. Обозначим буквами концы векторов сил
с точки D в точку С, которая расположена на прямой АВ. Рассмотрим треугольники, которые есть на рис.1.12. Обозначим буквами концы векторов сил  – L,
– L,  – M,
– M,  – K,
– K,  – N. Как видно из рис. 1.12, ∆ADC подобный ∆AKL и ∆BCD подобный ∆BMN. Для подобных треугольников можем составить такие две пропорции
– N. Как видно из рис. 1.12, ∆ADC подобный ∆AKL и ∆BCD подобный ∆BMN. Для подобных треугольников можем составить такие две пропорции  =
=  и
и  =
=  . Приравняем их, поскольку в них есть общий член DC,
. Приравняем их, поскольку в них есть общий член DC,
получим
DC =  =
=  .
.
Покажем обозначены буквами (AL, BM, KL, MN) в этом выражении силы (P1, P2, P3, P4). Будем иметь:

Если сократить множители P3 и P4 (P3 = P4) и перегруппировать, то получим следующее соотношение

Таким образом, на основании полученных выражений, окончательно можно сформулировать следующую теорему.
Равнодействующая двух параллельных сил, направленных в одну сторону, является суммой этих сил, параллельная этим силам и направлена в ту же сторону, точка ее
приложения делит внутренним образом отрезок, соединяющий силы, на части, обратно пропорциональные силам.
2. Далее рассмотрим случай, когда есть две параллельные силы, но направление
которых противоположно. Как в этом случае определить их равнодействующую?
Представим, что к произвольному телу в точках А и В приложены две параллельные силы  и
и  , которые имеют противоположное направление (рис. 1.13). Считаем, что модули сил
, которые имеют противоположное направление (рис. 1.13). Считаем, что модули сил  и
и  не одинаковы. Далее будет понятно, почему так принимается. Как и в предыдущем случае, соединим точки А и В прямой, присоединим в точках А и В уравновешенную систему сил
не одинаковы. Далее будет понятно, почему так принимается. Как и в предыдущем случае, соединим точки А и В прямой, присоединим в точках А и В уравновешенную систему сил  = –
= –  , векторы которой расположены на прямой АВ и имеют противоположное направление. Добавим силы, приложенные в точках А и В, и получим две равнодействующие
, векторы которой расположены на прямой АВ и имеют противоположное направление. Добавим силы, приложенные в точках А и В, и получим две равнодействующие  и
и  . Как видим, эти равнодействующие имеют направление разное, но они не параллельные и линии их действия пересекаются, в данном случае впереди тела в точке D. Как и в предыдущем случае, перенесем равнодействующую
. Как видим, эти равнодействующие имеют направление разное, но они не параллельные и линии их действия пересекаются, в данном случае впереди тела в точке D. Как и в предыдущем случае, перенесем равнодействующую  и
и  по линиях их действия в точку D и разложим каждую на составляющие. уравновешенную систему сил
по линиях их действия в точку D и разложим каждую на составляющие. уравновешенную систему сил  и
и  отвергаем и окончательно имеем в точке D две силы
отвергаем и окончательно имеем в точке D две силы  и
и  , которые лежат на одной прямой и имеют противоположное направление. Эти силы можно геометрически добавить, получив их равнодействующую. В данном случае это будет разница сил, модуль которой равен
, которые лежат на одной прямой и имеют противоположное направление. Эти силы можно геометрически добавить, получив их равнодействующую. В данном случае это будет разница сил, модуль которой равен
R = P1 – P2 .
Направление этой равнодействующей — в сторону большей силы, то есть, в сторону силы P1.
Перенесем равнодействующую R с точки D вдоль линии ее действия в точку C, которая
расположена на прямой AB. В данном случае точка C размещена за пределами отрезке AB, то есть за точкой A, где была приложена большая сила P1.
Найдем место расположения точки C. Как и в предыдущем случае, рассмотрим треугольники. Обозначим буквами концы векторов сил:
 – L,
– L,  – M,
– M,  – K,
– K,  – N. Как видно из рис. 1.13, ∆BCD является подобным ∆DMN, а ∆ACD — подобный ∆DLK. Для подобных треугольников составим такие две пропорции
– N. Как видно из рис. 1.13, ∆BCD является подобным ∆DMN, а ∆ACD — подобный ∆DLK. Для подобных треугольников составим такие две пропорции



Поскольку каждая пропорция содержит множитель CD, то приравняем их,  Покажем, как и в предыдущем случае, силы, которые в этом выражении обозначены буквами. Будем иметь
Покажем, как и в предыдущем случае, силы, которые в этом выражении обозначены буквами. Будем иметь  Сократим дальше данное равенство на P4, P3 (P3 = P4), получим такое соотношение
Сократим дальше данное равенство на P4, P3 (P3 = P4), получим такое соотношение

Таким образом, на основании полученных выражений, окончательно можно записать так.
Равнодействующая двух параллельных сил, направленных в противоположные стороны, равна разности этих сил и направлена в сторону большей силы; точка приложения равнодействующей силы делит внешним образом расстояние между точками приложения заданных сил на отрезки, обратно пропорциональные этим силам.
Момент силы относительно центра (точки)
Алгебраическая величина момента:
Вращательный эффект силы характеризуется ее моментом относительно центра (точки), а также и относительно оси (последний будет далее).
Рассмотрим произвольное тело (рис. 1.14), которое может поворачиваться вокруг точки О (точнее вокруг оси, перпендикулярной плоскости рисунка и проходит через точку О). Приложим в других точках тела A, B, C векторы сил  ,
, ,
, и определим сначала, смогут ли они поворачивать тело вокруг точки О.
и определим сначала, смогут ли они поворачивать тело вокруг точки О.
Как видно из рисунка, сила  , которая приложена в точке A, может вернуть тело вокруг точки О против хода часовой стрелки. Сила
, которая приложена в точке A, может вернуть тело вокруг точки О против хода часовой стрелки. Сила  — за ходом стрелки часов. Однако сила
— за ходом стрелки часов. Однако сила  не может вращать тело вокруг точки О, поскольку линия действия силы
не может вращать тело вокруг точки О, поскольку линия действия силы  пересекает данную точку. Таким образом силы
пересекает данную точку. Таким образом силы  и
и  создают вращательный эффект (момент) относительно точки О, а сила
создают вращательный эффект (момент) относительно точки О, а сила  — нет.
— нет.

Моментом силы относительно центра (точки) называется взят из соответствующим знаком произведение силы на плечо. Плечо силы относительно центра — это кратчайшее расстояние (перпендикуляр) между данным центром и линией действия силы.
Момент считается положительным, если сила пытается вернуть тело относительно данной точки против часовой стрелки и отрицательным, если – по часовой стрелке.
Момент силы  относительно точки O обозначается как mo (
относительно точки O обозначается как mo ( ).
).
Покажем на рис. 1.14 плечи сил, которые создают моменты относительно точки О, и определим алгебраические величины моментов этих сил

Таким образом, момент силы характеризуется тремя параметрами: модулем, плоскостью действия и направлением поворота.
Момент силы относительно центра как вектор
Рассмотрим силу  , вектор которой произвольно расположен в пространстве (рис. 1.15). Определим момент силы
, вектор которой произвольно расположен в пространстве (рис. 1.15). Определим момент силы  относительно произвольной точки O, для чего опустим из точки О до вектора силы
относительно произвольной точки O, для чего опустим из точки О до вектора силы  перпендикуляр, это будет плечо h. Тогда алгебраическая величина момента силы
перпендикуляр, это будет плечо h. Тогда алгебраическая величина момента силы  относительно точки О будет равна
относительно точки О будет равна
mo (Р) = Ph.
Обозначим буквами А и В конце вектора силы  и соединим их с точкой О. Основой треугольника АОВ является вектор силы
и соединим их с точкой О. Основой треугольника АОВ является вектор силы  , а вершина размещена в точке О. Плечо h является высотой треугольника АОВ. В этот момент силы
, а вершина размещена в точке О. Плечо h является высотой треугольника АОВ. В этот момент силы  относительно точки О является двойной площадью треугольника АОВ, то есть
относительно точки О является двойной площадью треугольника АОВ, то есть
mo ( ) = 2S ∆AOB.
) = 2S ∆AOB.
Далее проведем через точку О пространственную декартову систему координат Охyz с ортами  ,
, ,
, . Считаем, что расстояние OA является радиус- вектором
. Считаем, что расстояние OA является радиус- вектором  точки A приложения вектора силы
точки A приложения вектора силы  .
.
Поскольку момент силы  относительно точки O, как мы определили, является двойной площадью треугольника, то построим параллелограмм ОАВD. Фактически вектор силы
относительно точки O, как мы определили, является двойной площадью треугольника, то построим параллелограмм ОАВD. Фактически вектор силы  мы перенесли параллельно самому себе в точку O. Теперь можно видеть, что в точке O приложены два вектора
мы перенесли параллельно самому себе в точку O. Теперь можно видеть, что в точке O приложены два вектора  и
и  , на которых и построено параллелограмм. А это, как известно, является векторное произведение двух векторов
, на которых и построено параллелограмм. А это, как известно, является векторное произведение двух векторов  x
x  . Таким образом, момент силы относительно точки
. Таким образом, момент силы относительно точки  o (
o ( ) o является результирующим вектором произведения двух векторов
) o является результирующим вектором произведения двух векторов  и
и  , то есть
, то есть  o (
o ( ) =
) =  x
x  .
.

Окончательно сформулируем определение.
Момент силы относительно центра O, как результирующий вектор произведения  x
x  , проходит через точку O перпендикулярно площади треугольника ОАВ, и направлен в ту сторону, из которого можно видеть вращения тела под действием силы
, проходит через точку O перпендикулярно площади треугольника ОАВ, и направлен в ту сторону, из которого можно видеть вращения тела под действием силы  относительно точки O против часовой стрелки. По модулю он равен двойной площади треугольника, который образует вектор силы
относительно точки O против часовой стрелки. По модулю он равен двойной площади треугольника, который образует вектор силы  и точка O.
и точка O.
Таким образом, момент силы относительно точки как вектор полностью определяет вращательное эффект силы, которая приложена к телу: линия его действия определяет плоскость вращения, его направление определяет направление вращения, а длина в определенном масштабе определяет модуль момента.
Определим аналитически значение момента силы относительно точки.
В принятой системе координат векторы  и
и  можно выразить через соответствующие проекции на оси. А именно:
можно выразить через соответствующие проекции на оси. А именно:

где x, y, z — проекции радиус — вектора  на оси координат; Px, Py, Pz — проекции вектора силы
на оси координат; Px, Py, Pz — проекции вектора силы  на соответствующие оси;
на соответствующие оси;  ,
, ,
, — соответствующие орты осей координат.
— соответствующие орты осей координат.
Поскольку
 o (
o ( ) =
) =  x
x  ,
,
то, как известно из векторной алгебры, векторное произведение можно записать в виде определителя третьего порядка через проекции векторов на оси координат и орты, а именно

Раскрыв данный определитель по элементам первой строки, получим

Коэффициенты при единичных векторах в выражении являются проекциями момента силы относительно точки как вектор на оси координат x, y, z. А именно

Пара сил. Момент пары сил
Пара сил — это совокупность двух равных по величине, параллельных и противоположно направленных сил.
Рассмотрим произвольное тело (рис. 1.16), к которому в точках A и B приложенные силы  ,
, . Причем
. Причем  =
=  и
и  //
// , то есть к телу приложена пара сил.
, то есть к телу приложена пара сил.
Плоскость, в которой расположены силы пары, называется плоскости действия пары.
Пара сил не имеет равнодействующей силы, поэтому она не может уравновеситься
одной силой, и характеризуется моментом, вызывающим вращения тела под действием сил пары в плоскости действия пары.
Моментом пары называется взято с соответствующим знаком произведение одной из сил пары на плечо пары. Плечо пары — это расстояние (по перпендикуляру) между линиями действия сил, которые составляют пару.
Момент пары считается положительным, если он пытается вращать тело против часовой стрелки и, наоборот, — отрицательным, если пытается вращать тело по часовой стрелке.
Момент пары по модулю сказывается m(  ,
, ). Определим момент пары сил, которая изображена на рис. 1.16.
). Определим момент пары сил, которая изображена на рис. 1.16.
m(  ,
, ) = P1h.
) = P1h.

Момент пары сил можно представить вектором. Этот вектор перпендикулярен плоскости действия пары и направлен в ту сторону, с которой видим вращения тела под действием пара против часовой стрелки (правило буравчика). Момент  (
(  ,
, ) как вектор показан на рис. 1.16. Однако момент пары сил как вектор не имеет фиксированной точки приложения, поскольку он является свободным вектором.
) как вектор показан на рис. 1.16. Однако момент пары сил как вектор не имеет фиксированной точки приложения, поскольку он является свободным вектором.
Свойства пары сил
К телу могут быть приложены несколько пар сил. Две пары сил будут эквивалентными, если при прочих равных условиях их воздействие на тело одинакова. Поскольку пара сил характеризуется моментом пары, то пары сил, лежащие в одной плоскости будут эквивалентны, если они имеют одинаковые моменты (одинаковые по величине и направлению).
Из этих положений вытекают основные свойства (условия эквивалентности) пар сил:
— не меняя действия пары сил на тело, пару сил можно поворачивать и переносить, как угодно, в плоскости ее действия;
— действие пара на тело не меняется, если составляющие силы и плечо пары менять, но так, чтобы момент пары и плоскость действия оставались неизменными;
— когда на тело действует система пар сил, то пары и моменты пар можно добавлять. Если все пары данной системы пар расположены в одной плоскости, то момент результирующей пары равен алгебраической сумме моментов составляющих пар

Условия равновесия тела под действием системы пар сил, расположенных в одной плоскости
Если на тело действует система пар сил с моментами m1, m2, …, mn и момент
результирующей пары M, как уже известно, будет равняться алгебраической сумме
моментов составляющих пар, то для равновесия тела необходимо и достаточно, чтобы
момент результирующей пары равен нулю. В таком случае и алгебраическая сумма моментов составляющих пар тоже должна равняться нулю. аналитически это будет выглядеть так

Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
