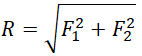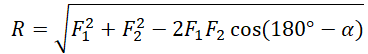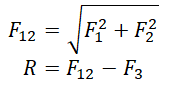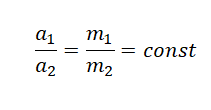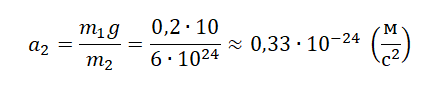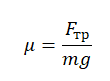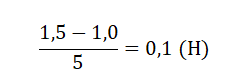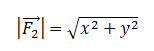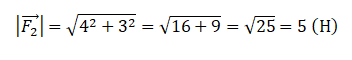Формула равнодействующей всех сил в физике
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline{F}$ – это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
[overline{F}=moverline{a} left(1right),]
где $m$ – масса тела, на которое действует сила $overline{F}$; $overline{a}$ – ускорение, которое сила $overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.
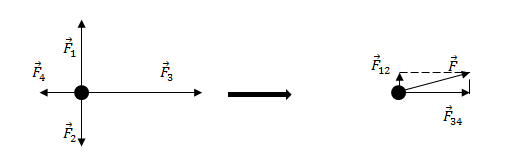
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(2right).]
Формула (2) – это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
[sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(3right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Пример 1
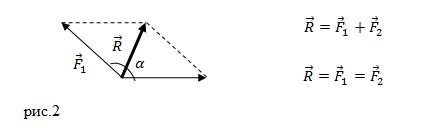
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60{}^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
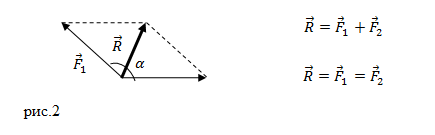
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline{F}$ можно найти, используя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{20}^2+{10}^2+2cdot 20cdot 10{cos (60{}^circ ) }}approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
Пример 2
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
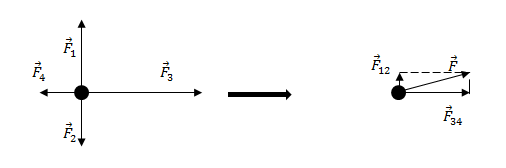
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
[overline{F}={overline{F}}_1+{overline{F}}_2+{overline{F}}_3+{overline{F}}_4left(2.1right).]
Найдем равнодействующую сил ${overline{F}}_1$ и ${overline{F}}_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
[F_{12}=F_1-F_2=17-11=6 left(Hright).]
Так как $F_1>F_2$, то сила ${overline{F}}_{12}$ направлена в туже сторону, что и сила ${overline{F}}_1$.
Найдем равнодействующую сил ${overline{F}}_3$ и ${overline{F}}_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
[F_{34}=F_3-F_4=18-10=8 left(Нright).]
Направление силы ${overline{F}}_{34}$ совпадает с направлением вектора ${overline{F}}_3$, так как ${overline{F}}_3>{overline{F}}_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
[overline{F}={overline{F}}_{12}+{overline{F}}_{34}left(2.2right).]
Силы ${overline{F}}_{12}$ и ${overline{F}}_{34}$ взаимно перпендикулярны. Найдем длину вектора $overline{F}$ по теореме Пифагора:
[F=sqrt{F^2_{12}+F^2_{34}}=sqrt{6^2+8^2}=10 left(Нright).]
Ответ. $F$=10 Н
Читать дальше: формула равнодействующей силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Три закона Ньютона
Динамика — раздел механики, изучающий причины движения тел и способы определения их ускорения. В нем движение тел описывается с учетом их взаимодействия.
Большой вклад в развитие динамики внес английский ученый Исаак Ньютон. Он первым смог выделить законы движения, которым подчиняются все макроскопические тела. Эти законы называют законами Ньютона, законами механики, законами динамики или законами движения тел.
Внимание! Законы Ньютона нельзя применять к произвольным телам. Они применимы только к точке, обладающей массой — к материальной точке.
Основное утверждение механики
Для описания движения тела можно взять любую систему отсчета. Обычно для этого используется система отсчета, связанная с Землей. Если какое-то тело меняет свою скорость, рядом с ним всегда можно обнаружить другое тело, которое на него действует. Так, если поднять камень и отпустить, он не останется висеть в воздухе, а упадет вниз. Следовательно, на него что-то подействовало. В данном случае сама Земля притянула камень к себе. Отсюда следует основное утверждение механики:
Основное утверждение механики
Изменение скорости (ускорение) тела всегда вызывается воздействием на него других тел.
Согласно утверждению, если на тело не действуют никакие силы, его ускорение будет нулевым, и оно будет либо покоиться, либо двигаться равномерно и прямолинейно (с постоянной скоростью).
Но в нашем мире мы не всегда это наблюдаем. И этому есть объяснение. Если тело покоится, оно действительно не меняет свою скорость. Так, мяч лежит на траве до тех пор, пока его не пнут. После того, как его пнут, он начинает катиться, но затем останавливается. Пока мяч катится, к нему больше не прикасаются. Казалось бы, согласно основному утверждению механики, мяч должен катиться вечно. Но этого не происходит, потому что на мяч действует сила трения, возникающая между его поверхностью и травой.
Основное утверждение механики можно проиллюстрировать в открытом космосе в месте, где сила притяжения космических тел пренебрежимо мала. Если в космосе придать телу скорость и отпустить, оно будет двигаться с такой скоростью по прямой линии до тех пор, пока на него не подействуют другие силы. Ярким примером служат межгалактические звезды, или звезды-изгои. Гравитационно они не связаны ни с одной из галактик, а потому движутся с постоянной скоростью. Так, звезда HE 0437-5439 удаляется от нашей галактики с постоянной скоростью 723 км/с.
Свободное тело — тело, на которое не действуют другие тела. Свободное тело либо покоится, либо движется прямолинейно и равномерно.
Первый закон Ньютона
Исаак Ньютон, изучая движение тел, заметил, что относительно одних систем отсчета свободные тела сохраняют свою скорость, а относительно других — нет. Он разделил их на две большие группы: инерциальные системы отсчета и неинерциальные. В этом кроется первый закон динамики.
Первый закон Ньютона
Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действие компенсировано.
Примером инерциальной системы отсчета служит система отсчета, связанная с Землей (геоцентрическая). Другой пример — гелиоцентрическая система отсчета (связанная с Солнцем).
Неинерциальная система отсчета — система отсчета, в которой тела могут менять свою скорость при отсутствии на них действия других тел.
Примером неинерциальной системы отсчета служит автобус. Когда он движется равномерно и прямолинейно, стоящие внутри пассажиры находятся относительно него в состоянии покоя. Но когда автобус останавливается, пассажиры падают вперед, т. е. меняют свою скорость, хотя на них не действуют другие тела.
Второй закон Ньютона
В примере с автобусом видно, что пассажиры стараются сохранить свою скорость относительно Земли — инерциальной системы отсчета. Такое явление называется инерцией.
Инерция — явление, при котором тело сохраняет состояние покоя или равномерного прямолинейного движения.
Инертность — физическое свойство, заключающееся в том, что любое тело оказывает сопротивление изменению его скорости (как по модулю, так и по направлению).
Не все тела одинаково инертны. Вы можете взять мячик и придать ему большое ускорение. Но вы не можете придать такое же ускорение гире, хотя она обладает похожим размером. Но мячик и гиря различаются между собой массой.
Масса — скалярная физическая величина, являющаяся мерой инертности тела. Чем больше масса, тем больше инертность тела.
Масса обозначается буквой m. Единица измерения массы — кг. Прибор для измерения массы — весы.
Чтобы придать одинаковую скорость двум телам с разной инертностью, к телу с большей инертностью придется приложить больше силы. Попробуйте сдвинуть с места стол, а затем — шкаф. Сдвинуть с места стол будет проще.
Если же приложить две одинаковые силы к телам с разной инертностью, будет видно, что тело с меньшей инертностью получает большее ускорение. Если приставить к пружине теннисный шарик, а затем сжать ее и резко отпустить, шарик улетит далеко. Если вместо теннисного шарика взять железный, он лишь откатится на некоторое расстояние.
Описанные выше примеры показывают, что между силой, прикладываемой к телу, и ускорением, которое оно получает в результате прикладывания этой силы, и массой этого тела есть взаимосвязь. Она раскрывается во втором законе Ньютона.
Второй закон Ньютона
Сила, действующая на тело, равна произведению массы этого тела на ускорение, которое сообщает эта сила.
F = ma
где F — сила, которую прикладывают к телу, a — ускорение, которое сообщает эта сила, m — масса тела
Сила — количественная мера действия тел друг на друга, в результате которого тела получают ускорения.
Сила — векторная физическая величина. Обозначается F. Единица измерения — Н (Ньютон). Прибор для измерения силы — динамометр.
Пример №1. Определить, с какой силой действует Земля на яблоко, если, упав с ветки, оно получило ускорение 9,8 м/с2. Масса яблока равна 200 г.
Сначала переведем массу яблока в кг. 200 г = 0,2 кг. Теперь найдем силу, действующую на яблоко со стороны Земли, по второму закону Ньютона:
F = ma = 0,2 ∙ 9,8 = 1,96 (Н)
Равнодействующая сила
Иногда на тело действуют несколько сил. Тогда при описании его движения вводится понятие равнодействующей силы.
Определение
Равнодействующая сила — векторная сумма всех сил, действующих на тело одновременно.
R = F1 + F2 + F3 + …
В этом случае второй закон Ньютона формулируется так:
Второй закон Ньютона через равнодействующие силы
Если на тело действует несколько сил, то их равнодействующая R будет равна произведению массы на ускорение этого тела.
ma = R = F1 + F2 + F3 + …
Правила сложения сил и их проекций
|
Сложение двух сил, направленных вдоль одной прямой в одну сторону |
|
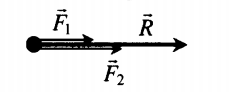 |
Если F1↑↑F2, то:
R = F1 + F2 Равнодействующая сила сонаправлена с обеими силами. |
|
Сложение двух сил, направленных вдоль одной прямой во взаимно противоположных направлениях |
|
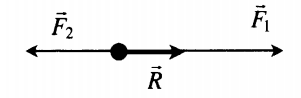 |
Если F1↑↓F2, то:
R = |F1 – F2| Равнодействующая сила направлена в сторону направления большей по модулю силы. |
|
Сложение двух сил, перпендикулярных друг к другу |
|
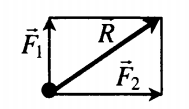 |
Если F1 перпендикулярна F2, то равнодействующая сила вычисляется по теореме Пифагора:
|
|
Сложение двух сил, расположенных под углом α друг к другу |
|
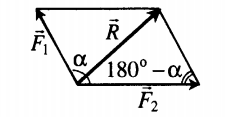 |
Если F1 и F2 расположены под углом α друг к другу, равнодействующая сила вычисляется по теореме косинусов:
|
|
Сложение трех сил |
|
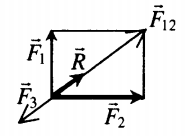 |
Способ сложения определяется правилами сложения векторов. В данном случае:
|
|
Сложение проекций сил |
|
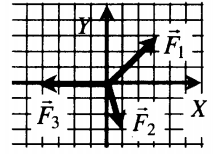 |
Проекция на ось ОХ:
F1x + F2x – F3x = 0 Проекция на ось OY: F1y – F2y = 0 |
Третий закон Ньютона
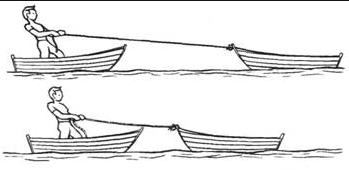
Когда одно тело действует на другое, начинается взаимодействие этих тел. Это значит, если тело А действует на тело В и сообщает ему ускорение, то и тело В действует на тело А, тоже придавая ему ускорение. К примеру, если сжать пружину руками, то руки будут чувствовать сопротивление, оказываемое силой упругости пружины. Если же, находясь в лодке, начать тянуть за веревку вторую лодку, то обе лодки будут двигаться навстречу друг другу. То есть, вы, находясь в своей лодке, тоже будете двигаться навстречу второй лодке.
Иногда на тело действует сразу несколько сил, но тело продолжает покоиться. В этом случае говорят, что силы друг друга компенсируют, то есть их равнодействующая равна нулю.
Две силы независимо от их природы считаются равными по модулю и противоположно направленными, если их одновременное действие на тело не меняет его скорости.
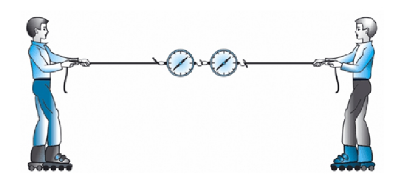
Примером такого явления служит ситуация, когда при перетягивании каната его никто не может перетянуть в свою сторону. Если взять два каната и присоединить между ними два динамометра, а затем начать игру в перетягивание, выяснится, что показания динамометра всегда будут одинаковыми. Это значит, что независимо от масс и придаваемых ускорений два взаимодействующих тела оказывают друг на друга равные по модулю силы. В этом заключается смысл третьего закона Ньютона.
Третий закон Ньютона
Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны.
FA = –FB
Используя второй закон Ньютона, третий закон механики можно переписать иначе:
m1a1 = –m2a2
Отсюда следует:
Отношение модулей ускорений a1 и a2 взаимодействующих друг с другом тел определяется обратным отношением их масс и совершенно не зависит от характера действующих между ними сил.
Пример №2. Определить ускорение, с которым движется Земля к падающему на нее яблоку. Масса яблока равна 0,2 кг. Ускорение свободного падения принять равной за 10 м/с2. Массу Земли принять равно 6∙1024 кг.
Согласно третьему закону Ньютона модули сил, с которыми взаимодействуют Земли и яблоко, равны. Поэтому:
F1 = F2
Отсюда:
m1a1 = m2a2
Пусть тело 1 будет яблоко, а тело 2 — Земля. Тогда a1 будет равно g. Отсюда ускорение, с которым движется Земля к падающему на нее яблоку, равна:
Задание EF17993
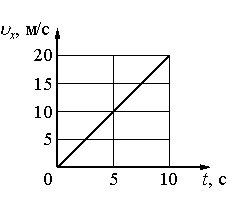
а) 2Н
б) 8 Н
в) 10 Н
г) 20 Н
Алгоритм решения
1.Записать исходные данные.
2.Проанализировать задачу.
3.Записать второй закон Ньютона.
4.Определить ускорение по графику проекции скорости от времени.
5.Подставить найденное ускорение в формулу второго закона Ньютона и произвести вычисления.
Решение
Запишем исходные данные:
Так как графиком скорости является прямая, непараллельная ось времени, тело движется с постоянным ускорением. Если ускорение постоянно, равнодействующая сил тоже будет постоянной в любой момент времени. Поэтому нам достаточно использовать координаты любой, более удобной для их определения точки. К примеру, в точке, соответствующей моменту времени 10 с.
Запишем второй закон Ньютона:
F = ma
Ускорение тела определяется как отношение изменения скорости ко времени, в течение которого эта скорость менялась. Согласно графику, за 10 секунд скорость изменилась на 20 м/с. Следовательно, ускорение равно:
a = 20/10 = 2 (м/с2)
Теперь можем вычислить равнодействующую сил:
F = ma = 5∙2 = 10 (Н)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18915
Необходимо собрать экспериментальную установку, с помощью которой можно определить коэффициент трения скольжения стали по дереву. Для этого школьник взял стальной брусок с крючком. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?
а) деревянная рейка
б) динамометр
в) мензурка
г) пластмассовая рейка
д) линейка
Алгоритм решения
1.Проанализировать задачу. Выяснить, какие предметы необходимы для проведения опыта.
2.Вывести формулу для коэффициента трения.
3.Определить, какую величину нужно измерить, чтобы рассчитать коэффициент трения, и какой прибор для этого нужен.
Решение
Для определения коэффициента трения стали по дереву, нужен не только стальной груз, но и деревянная поверхность. То есть, понадобится деревянная рейка.
Сила трения определяется формулой:
Отсюда коэффициент трения равен:
Ускорение свободного падения известно. Массу можно измерить на весах, но весов в вариантах ответа нет. Силу трения можно измерить динамометром. Следовательно, для опыта нужны только динамометр и деревянная рейка. Рейка из пластика не понадобится, так как цели расчета коэффициента трения стали по пластику нет. Мензурка используется для определения объема жидкости. В данном опыте она тоже не нужна.
Ответ: аб
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17589
Система отсчёта, связанная с Землёй, считается инерциальной. В этом случае систему отсчёта, связанную с самолётом, можно считать инерциальной, если самолёт движется:
а) равномерно и прямолинейно, набирая высоту
б) с постоянным ускорением по горизонтали
в) равномерно, выполняя поворот
г) по взлетной полосе при взлете
Алгоритм решения
- Сформулировать первый закон Ньютона об инерциальных системах отсчета.
- На основании закона сделать вывод, при каких условиях система отсчета, связанная с самолетом, может считаться инерциальной.
- Проанализировать все 4 ситуации, приведенные в вариантах ответа.
- Выбрать тот вариант, который описывает ситуацию, не противоречащую условию, выведенному в шаге 2.
Решение
Первый закон Ньютона формулируется так:
«Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действие компенсировано».
Чтобы система отсчета, связанная с самолетом, была инерциальной, она должна быть неподвижной или двигаться относительно Земли — инерциальной системы отсчета — равномерно и прямолинейно.
Когда самолет движется равномерно и прямолинейно, набирая высоту, самолет движется с собственным ускорением, которое компенсируется ускорением свободного падения. И это единственный верный ответ, так как:
- Самолет, двигаясь с постоянным ускорением по горизонтали, движется неравномерно, что противоречит условию.
- Самолет, двигаясь равномерно во время поворота, движется непрямолинейно (с центростремительным ускорением).
- Самолет, двигаясь по взлетной полосе при взлете, движется прямолинейно, но неравномерно, так как он разгоняется из состояния покоя.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22791

Ответ: ( ± ) Н.
Внимание! Записывать ответ следует последовательностью цифр без запятых.
Алгоритм решения
1.Записать исходные данные.
2.Определить цену деления шкалы.
3.Записать значение измерения с учетом погрешности.
Решение
Из условий задачи известно, что погрешность равна цене деления шкалы. Цена деления шкалы определяется отношением разности двух ближайших числовых обозначений на шкале и количеству делений между ними. Возьмем ближайшие значения 1,0 и 1,5. Между ними 5 делений. Следовательно, цена деления шкалы динамометра равна:
Так как погрешность равна цене деления, она также равна 0,1 Н.
Стрелка динамометра показывает 1,1 Н. Следовательно, вес груза равен: 1,1±0,1. Но по условию задачи ответ нужно записать без запятых и прочих знаков. Следовательно, верный ответ: 1101.
Ответ: 1101
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17484
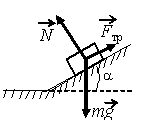
а) N cosα
б) N
в) N sinα
г) mg + Fтр
Алгоритм решения
- Запись второго закона Ньютона в векторном виде.
- Вывод формулы равнодействующей силы трения и силы тяжести.
- Нахождение модуля равнодействующей силы трения и силы тяжести.
Решение
Записываем второй закон Ньютона в векторном виде с учетом того, сто скорость тела не меняется (ускорение равно 0):
N + mg + Fтр = 0
Отсюда равнодействующая силы трения и силы тяжести равна:
mg + Fтр = –N
Следовательно, равнодействующая силы трения и силы тяжести направлена противоположно силе реакции опоры, но равна ей по модулю. Отсюда:
|mg + Fтр| = N
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18548
Алгоритм решения
- Изобразить на рисунке второй вектор с учетом правил сложения векторов.
- Записать геометрическую формулу для расчета модуля вектора по его проекциям.
- Выбрать систему координат и построить проекции второй силы на оси ОХ и ОУ.
- По рисунку определить проекции второй силы на оси.
- Используя полученные данные, применить формулу для расчета вектора по его проекциям.
Решение
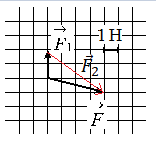
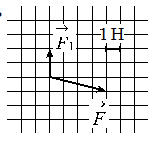
Построим вектор второй силы. Его начало должно совпадать с концом вектора первой силы, а его конец — с концов равнодействующей этих сил. Этот вывод следует из сложения векторов правилом треугольника.
Модуль вектора равен корню из суммы квадратов его проекций на оси ОХ и ОУ:
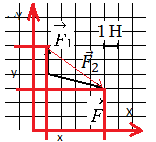
Выберем систему координат и построим проекции второй силы на оси ОХ и ОУ:
Согласно рисунку, проекция второй силы на ось ОХ равна: x = 4 (Н). Ее проекция на ось ОУ равна: y = 3 (Н).
Подставим известные данные в формулу и вычислим модуль вектора второй силы:
Ответ: 5
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 16.5k
Ранее мы уже познакомились с понятием силы и знаем, что она имеет две характеристики: направление и численное значение. В жизни обычно на тело действуют сразу несколько сил.
Например, если рассмотреть ситуацию, когда спускается парашютист, то можно заметить, что на него действуют сразу две силы: и сила тяжести, и сила сопротивления воздуха.
На груз, подвешенный на пружине, тоже действуют две силы — сила тяжести и сила упругости пружины.
В каждом таком случае мы можем заменить несколько сил, действующих на тело, одной. И она будет равноценна по своему действию всем этим силам.
На данном уроке мы узнаем, как называется такая сила и как ее найти.
Равнодействующая сил
Дадим определение. Какую силу называют равнодействующей нескольких сил?
Равнодействующая сил — это сила, которая производит на тело такое же действие, как несколько одновременно действующих сил.
Так же, как и любая сила, равнодействующая является векторной величиной. Она обозначается буквой $vec R$, а ее числовое значение — буквой $R$. Равнодействующая сила измеряется в ньютонах ($Н$).
Сложение сил, действующих на тело по одной прямой
Если силы направлены в одну сторону
Проведем эксперимент: возьмем два груза (рисунок 1, а), масса которых равна $102 space г$ и $204 space г$, и подвесим их к пружине. Наши грузы имеют вес $1 space Н$ и $2 space Н$ и воздействуют на пружину, из-за чего она растягивается на определенную длину. Сделаем отметку, на какое расстояние вытянулась пружина.
А теперь снимем два груза и подберем один груз, который растянет пружину на такую же длину. Вес этого груза окажется равен $3 space Н$ (рисунок 1, б).
Из опыта можно сделать вывод, что:
- Равнодействующая сил, направленных по одной прямой в одну сторону, направлена в ту же сторону, что и действующие на тело силы;
- Модуль равнодействующей сил равен сумме модулей составляющих сил.
Изобразим графически эти силы на рисунке 2.
Чему равна равнодействующая двух сил, направленных по одной прямой в одну сторону?
Силы, которые мы будем складывать, обозначены буквами $F_1$ и $F_2$. Тогда для всех действующих сил будет иметь место равенство:
$R = F_1 + F_2$.
Если силы направлены в противоположные стороны
Рассмотрим еще один опыт, представленный на рисунке 3.
Поставим гирю на динамометр со столиком (рисунок 3, а). Рассматриваемым телом в данном случае будет сам столик. Гиря весит $5 space Н$, т.е. действует на столик с силой в $5 space Н$, причем эта сила направлена вертикально вниз.
Теперь привяжем к столику нить и потянем вертикально вверх с силой, равной $2 space Н$ (рисунок 3, б). Динамометр покажет силу $3 space Н$. Эта сила и будет равнодействующей двух сил: $5 space Н$ и $3 space Н$.
- Если две силы направлены по одной прямой в противоположные стороны, то их равнодействующая будет направлена в сторону той силы, которая больше по модулю.
- Модуль равнодействующий сил в таком случае равен разности модулей составляющих сил
Изобразить силы можно следующим образом (рисунок 4):
Чему равна равнодействующая двух сил, направленных по одной прямой в противоположные стороны?
Равнодействующая сил равна:
$R = F_2 space − space F_1$.
Как будет двигаться тело под действием двух равных противоположно направленных сил?
Если силы, действующие на тело, будут равны, то мы получим, что равнодействующая сил равна нулю, то есть $R = 0$. Другими словами, в этом случае тело будет покоиться или двигаться прямолинейно и равномерно.
Как мы уже говорили, когда тело растянет пружину и остановится, это значит, что сила тяжести и сила упругости уравновесили друг друга. В этом случае тело будет находиться в состоянии покоя, например, как на рисунке 1.
Упражнения
Упражнение №1
Человек, масса которого $70 space кг$, держит на плечах ящик массой $20 space кг$. С какой силой человек давит на землю?
Дано:
$m_1 = 70 space кг$
$m_2 = 20 space кг$
$g = 9.8 frac{Н}{кг}$
$P$ — ?
Показать решение и ответ
Скрыть
Решение:
Без ящика на плечах человек давит на землю с весом $P_1$, а ящик (если его поставить на землю) — с весом $P_2$.
Вес направлен вертикально вниз. В данной задаче мы применим понятие равнодействующей сил к их общему весу $P$:
$R = P = P_1 + P_2$
Человек с ящиком на плечах стоит на месте. Значит его вес будет равен силе тяжести, действующей на него:
$P_1 = F_{тяж1} = gm_1$.
Вес ящика тоже будет равен силе тяжести, действующей на него:
$P_2 = F_{тяж2} = gm_2$.
Тогда общий вес, с которым человек давит на землю с ящиком на плечах, будет равен:
$P = gm_1 + gm_2 = g cdot (m_1 + m_2)$,
$P = 9.8 frac {Н}{кг} cdot (70 space кг + 20 space кг) = 9.8 frac {Н}{кг} cdot 90 space кг = 882 space Н$.
Ответ: $P = 882 space Н$.
Упражнение №2
Отец посадил сына себе на плечи. Масса отца составляет $90 space кг$, сына — $35 space кг$. С какой силой отец теперь будет давить на землю?
Дано:
$m_о = 90 space кг$
$m_с = 35 space кг$
$g = 9.8 frac{Н}{кг}$
$P$ — ?
Показать решение и ответ
Скрыть
Решение:
В одиночку отец давит на землю с весом $P_о$, сын — с весом $P_с$.
Вес направлен вертикально вниз. В данной задаче мы применим понятие равнодействующей сил к их общему весу $P$:
$R = P = P_о + P_c$
Отец с сыном не двигаются, значит:
$P_о = gm_о$ и $P_с = gm_с$.
Тогда общий вес, с которым отец давит на землю держа сына на плечах, будет равен:
$P = gm_о + gm_с = g cdot (m_о + m_с)$,
$P = 9.8 frac {Н}{кг} cdot (90 space кг + 35 space кг) = 9.8 frac {Н}{кг} cdot 125 space кг = 1 225 space Н$.
Ответ: $P = 1 225 space Н$.
Упражнение №3
В игре по перетягиванию каната участвуют четыре человека. Два из них тянут канат в одну сторону с силами $330 space Н$ и $380 space Н$, два — в противоположную сторону с силами $300 space Н$ и $400 space Н$. В каком направлении будет двигаться канат и чему равна равнодействующая этих сил? Сделайте чертеж.
Дано:
$F_1 = 330 space Н$
$F_2 = 380 space Н$
$F_3 = 300 space Н$
$F_4 = 400 space Н$
$R — ?$
Показать решение и ответ
Пусть первые два участника тянут канат вправо с силами $F_1$ и $F_2$, другие два — влево с силами $F_3$ и $F_4$.
Скрыть
Решение:
Сначала найдем чему равна равнодействующая сил первых двух участников. Они тянут канат в одну сторону, значит:
$R_1 = F_1 + F_2 = 330 space Н + 380 space Н = 710 space Н$.
Теперь найдем равнодействующую сил для левой стороны участников:
$R_2 = F_3 + F_4 = 300 space Н + 400 space Н = 700 space Н$.
Теперь мы можем найти равнодействующую сил для всех участников:
$R = R_1 space − space R_2 = 710 space Н space − space 700 space Н = 10 space Н$.
Графически силы изображены на рисунке 5. Так как силы участников направлены в противоположные стороны, равнодействующая сил будет направлена в ту сторону, где у участников большая сила, то есть вправо.
Ответ: канат будет двигаться в сторону первых двух участников, $R = 10 space Н$.
Упражнение №4
Человек спускается на парашюте, двигаясь равномерно. Сила тяжести парашютиста вместе с парашютом $700 space Н$. Чему равна сила сопротивления воздуха?
Дано:
$F_{тяж} = 700 space Н$
$upsilon = const$
$F_с — ?$
Показать решение и ответ
Скрыть
Решение:
Сила тяжести, действующая на парашютиста и парашют, направлена вертикально вниз, а сила сопротивления воздуха — противоположно его движению, то есть вертикально вверх.
В задаче сказано, что парашютист двигается равномерно ($upsilon = const$). Значит равнодействующая сил, действующая на него и парашют, равна нулю:
$R = 0$.
Тогда мы можем сказать, что силы, действующие на парашютиста и парашют, по модулю равны друг другу:
$F_с = F_{тяж} = 700 space Н$.
Ответ: $F_с = 700 space Н$.
Как находить равнодействующую векторов
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline $) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline $ — это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline $) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
Формула (2) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
$overline =0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60<>^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline $ можно найти, используя теорему косинусов:
Вычислим модуль равнодействующей силы:
[F=sqrt ^2+ ^2+2cdot 20cdot 10 ^circ ) >>approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
Найдем равнодействующую сил $ >_1$ и $ >_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
Так как $F_1>F_2$, то сила $ >_ $ направлена в туже сторону, что и сила $ >_1$.
Найдем равнодействующую сил $ >_3$ и $ >_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
Направление силы $ >_ $ совпадает с направлением вектора $ >_3$, так как $ >_3> >_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
Силы $ >_ $ и $ >_ $ взаимно перпендикулярны. Найдем длину вектора $overline $ по теореме Пифагора:
Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
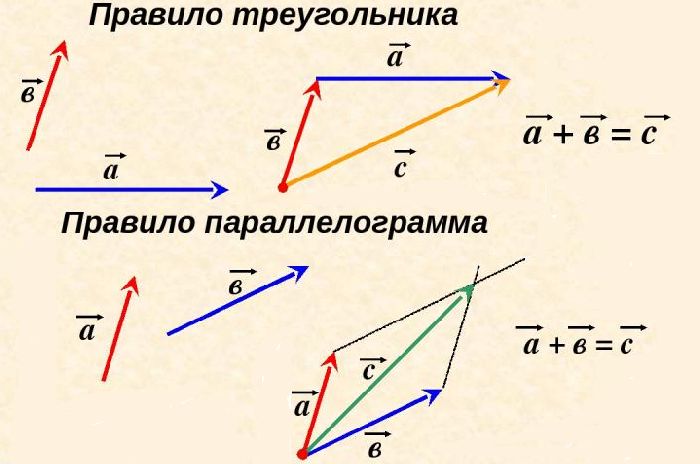
Правило параллелограмма и правило многоугольника
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .
Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .
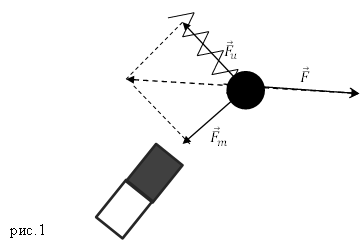
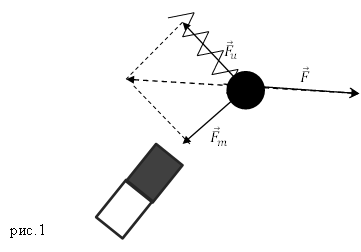
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
I. Механика
Тестирование онлайн
Определение
Это векторная сумма всех сил, действующих на тело.
Велосипедист наклоняется в сторону поворота. Сила тяжести и сила реакции опоры со стороны земли дают равнодействующую силу, сообщающую центростремительное ускорение, необходимое для движения по окружности
Взаимосвязь со вторым законом Ньютона
Вспомним закон Ньютона:
Равнодействующая сила может быть равна нулю в том случае, когда одна сила компенсируется другой, такой же силой, но противоположной по направлению. В этом случае тело находится в покое или движется равномерно.
|
Сила Архимеда уравновешивается силой тяжести, тело равномерно перемещается в жидкости вниз. |
Сила тяжести уравновешивается силой упругости. Книга покоится Если равнодействующая сила НЕ равна нулю, то тело движется равноускоренно. Собственно именно эта сила является причиной неравномерного движения. Направление равнодействующей силы всегда совпадает по направлению с вектором ускорения. Когда требуется изобразить силы, действующие на тело, при этом тело движется равноускоренно, значит в направлении ускорения действующая сила длиннее противоположной. Если тело движется равномерно или покоится длина векторов сил одинаковая.
|
Равнодействующая сила

4.7
Средняя оценка: 4.7
Всего получено оценок: 166.
Обновлено 31 Октября, 2021
4.7
Средняя оценка: 4.7
Всего получено оценок: 166.
Обновлено 31 Октября, 2021
Законы Ньютона – математическая абстракция. В реальности причиной движения или покоя тел, а также их деформации, выступают сразу несколько сил. Поэтому важным дополнениям к законам механики будет введение понятия равнодействующей силы и его применение.
О причинах изменений
Классическая механика разделена на два раздела – кинематику, при помощи уравнений описывающую траекторию движения тел, и динамику, которая разбирается с причинами изменения положения объектов или самих объектов.
Причиной изменений выступает некоторая сила, которая есть мера действия на тело других тел или силовых полей (например, электромагнитное поле или гравитация). К примеру, сила упругости вызывает деформацию тела, сила тяжести – падение тел на Землю.
Сила – это векторная величина, то есть, ее действие – направленное. Модуль силы в общем случае пропорционален некоему коэффициенту (для деформации пружины – это ее жесткость), а также параметрам действия (масса, заряд).
Например, в случае кулоновской силы – это величина обоих зарядов, взятых по модулю, квадрат расстояние между зарядами и коэффициент k, в системе СИ определяемый выражением: $k = {1 over 4 pi epsilon}$, где $epsilon$ – диэлектрическая постоянная.
Сложение сил
В случае, когда на тело действует n сил, говорят о равнодействующей силе, а формула второго закона Ньютона принимает вид:
$mvec a = sumlimits_{i=1}^n vec F_i$
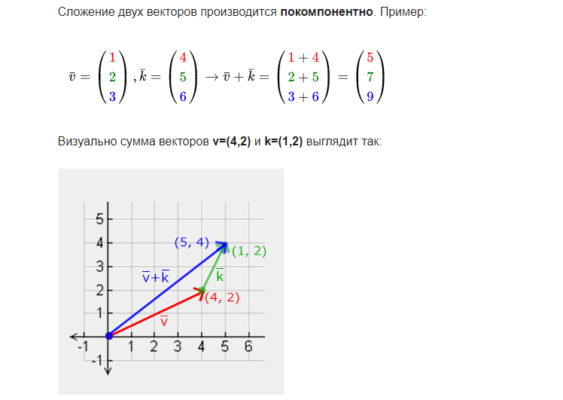
Поскольку F – векторная величина, сумма сил называется геометрической (или векторной). Такое сложение выполняется по правилу треугольника или параллелограмма, либо по компонентам. Поясним каждый метод на примере. Для этого запишем формулу равнодействующей силы в общем виде:
$F = sumlimits_{i=1}^n vec F_i$
А силу $F_i$ представим в виде:
$F = (F_{xi}, F_{yi}, F_{zi})$
Тогда суммой двух сил будет новый вектор $F_{ab} = (F_{xb} + F_{xa}, F_{yb} + F_{ya}, F_{zb} + F_{za})$.
Абсолютное значение равнодействующей можно рассчитать так:
$F = sqrt{(F_{xb} + F_{xa})^2 + (F_{yb} + F_{ya})^2 + (F_{zb} + F_{za})^2}$
Теперь дадим строгое определение: равнодействующая сила есть векторная сумма всех сил, оказывающих влияние на тело.
Разберем правила треугольника и параллелограмма. Графически это выглядит так:
Внешне они кажутся различными, но когда доходит до вычислений, сводятся к нахождению третьей стороны треугольника (или, что тоже самое, диагонали параллелограмма) по теореме косинусов.
Если сил больше двух, иногда удобней пользоваться правилом многоугольника. По своей сути – это всё тот же треугольник, только повторенный на одном рисунке некоторое количество раз. В случае, если по итогу контур получился замкнутым, общее действие сил равно нулю и тело покоится.
Задачи
- На ящик, размещенный в центре декартовой прямоугольной системы координат, действуют две силы: $F_1 = (5, 0)$ и $F_2 = (3, 3)$. Рассчитать равнодействующую двумя методами: по правилу треугольника и при помощи покомпонентного сложения векторов.
Решение
Равнодействующей силой будет векторная сумма $F_1$ и $F_2$.
Поэтому запишем:
$vec F = vec F_1 + vec F_2 = (5+3, 0+3) = (8, 3)$
Абсолютное значение равнодействующей силы:
$F = sqrt{8^2 + 3^2} = sqrt{64 + 9} = 8,5 Н$
Теперь получим тоже значение при помощи правила треугольника. Для этого сначала найдем абсолютные значения $F_1$ и $F_2$, а также угол между ними.
$F_1 = sqrt{5^2 + 0^2} = 5 Н$
$F_2 = sqrt{3^2 + 3^2} = 4,2 Н$
Угол между ними – 45˚, так как первая сила параллельна оси Оx, а вторая делит первую координатную плоскость пополам, то есть является биссектрисой прямоугольного угла.
Теперь, разместив вектора по правилу треугольника, рассчитаем по теореме косинусов равнодействующую:
$F = sqrt{F_1^2 + F_2^2 – 2F_1F_2 cos135} = sqrt{F_1^2 + F_2^2 + 2F_1F_2 sin45} = sqrt{25 + 18 + 2 cdot 5 cdot 4,2 cdot sin45} = 8,5 Н$
- На машину действуют три силы: $F_1 = (-5, 0)$, $F_2 = (-2, 0)$, $F_1 = (7,0)$. Какова их равнодействующая?
Решение
Достаточно сложить иксовые компоненты векторов:
$F = -5 – 2 + 7 = 0$
Что мы узнали?
В ходе урока было введено понятие равнодействующей сил и рассмотрены различные методы ее расчета, а также введена запись второго закона Ньютона для общего случая, когда количество сил неограниченно.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 166.
А какая ваша оценка?