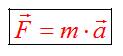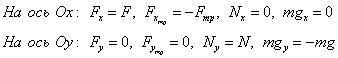Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Скорость автомобиля массой 1000 кг, движущегося вдоль оси Ox, изменяется со временем в соответствии с графиком (см. рис.). Систему отсчета считать инерциальной. Чему равна равнодействующая всех сил, действующих на автомобиль? (Ответ дайте в ньютонах.)
2
На тело, находящееся на горизонтальной плоскости, действуют три горизонтальные силы (см. рис., вид сверху). Каков модуль равнодействующей этих сил, если
(Ответ дайте в ньютонах и округлите до десятых.)
3
Две силы 3 H и 4 H приложены к одной точке тела, угол между векторами сил равен 90°. Чему равен модуль равнодействующей сил? (Ответ дайте в ньютонах.)
4
Под действием одной силы F1 тело движется с ускорением 4 м/с2. Под действием другой силы F2, направленной противоположно силе F1, ускорение тела равно 3 м/с2. С каким ускорением тело будет двигаться при одновременном действии сил F1 и F2? Ответ дайте в метрах на секунду в квадрате.
5
Тело подвешено на двух нитях и находится в равновесии. Угол между нитями равен 90°, а силы натяжения нитей равны 3 H и 4 H. Чему равна сила тяжести, действующая на тело? (Ответ дайте в ньютонах.)
Пройти тестирование по этим заданиям
Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Правило параллелограмма и правило многоугольника
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
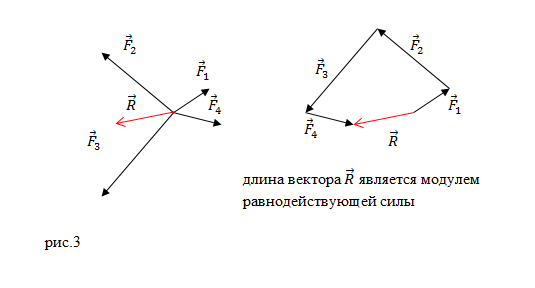
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Пример 1
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную – F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β – F 3 cos γ = F x = 4 – 3 3 2 ≈ – 0 , 6 Н .
Точно также для проекций на ось O Y : – F 2 sin β + F 3 sin γ = F y = 3 – 2 3 2 ≈ – 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 – 2 3 4 – 3 3 ≈ 0 , 4 .
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
Как найти равнодействующую трех векторов
Скорость автомобиля массой 1000 кг, движущегося вдоль оси Ox, изменяется со временем в соответствии с графиком (см. рисунок). Систему отсчета считать инерциальной. Чему равна равнодействующая всех сил, действующих на автомобиль? (Ответ дайте в ньютонах.)
Согласно второму закону Ньютона, равнодействующая всех сил, действующих на тело, связана с ускорением и массой тела соотношением Из графика определим ускорение, которое остается постоянным на протяжении всего интервала времени:
Таким образом, равнодействующая всех сил равна
а если бы ускорение было отрицательно, то и равнодействующая была бы отрицательной?
Скорость, сила, ускорение — все это векторные величины. Правильно говорить не про их знак, а про знак проекции этих векторов на некоторую ось. Если проекция скорости уменьшается, то ускорение направлено против оси, а значит, так же направлена и равнодействующая. Следовательно, проекции этих величин отрицательны. По графику модуля скорости о знаке проекций судить нельзя. Действительно, имея только график, приведенный в условии, мы не можем сказать, ускоряется тело вдоль оси или против. Проекция ускорения может быть тут как положительной, так и отрицательной.
“Систему отсчета считать инерциальной.” Возможно ошибаюсь, ребят, но, вроде, в ИСО равнодействующая всех сил равна нулю.
ИСО — это система отсчета, в которой тело, на которое не действует никаких внешних сил, двигается равномерно и прямолинейно или покоится.
Равнодействующая сил, конечно, же может и отличаться от нуля, это, согласно второму закону Ньютона, приведет к появлению ускорения.
т.е. в инерциальной системе отсчёта нет силы трения?
и ещё: вы говорите, что тело в ИСО движется равномерно, а в условии задачи дано равноускоренное движение. так бывает?
Я не так говорю, не вырывайте слова и контекста. Я даю определение ИСО: это система отсчета, в которой тело, НА КОТОРОЕ НЕ ДЕЙСТВУЮТ ВНЕШНИЕ СИЛЫ, двигается равномерно и прямолинейно, либо покоится. А вот если СИЛЫ ДЕЙСТВУЮТ, то это приводит к появлению ускорения, о чем нам и говорит второй закон Ньютона.
Наличие силы трения определяется свойством поверхностей, а не выбором системы отсчета. И в данной задаче, она, конечно, присутствует и направлена по скорости движения автомобиля, иначе бы он просто не мог бы разгоняться. Но чему она равна, мы найти из данного графика не можем, так как есть и другие силы, например, сила сопротивления воздуха. Что мы может тут определить, так это равнодействующую всех сил. Именно ей определяется ускорение.
Пыталась найти ускорение как тангенс угла наклона касательной, то есть производную от v по t. Тут угол – 45 град, тангенс = 1, ускорение, стало быть, так же 1 м/с^2.
Подскажите пожалуйста, где в моих рассуждениях ошибка?
Ошибка в том, что тангенс надо считать, учитывая масштаб графика по осям. То есть Вы должны определить катеты прямоугольного треугольника, используя числа на осях, а потом поделить один катет на другой.
Кстати, простое доказательство, почему Ваше решение не верно. Сожмем картинку с графиком по вертикали в два раза. Угол на рисунке изменится, а ускорение, конечно, же останется прежним.
а почему считают ускорение до 8с. а не до 18, если найдем ускорение по всей длине то получается 10-0/18=1,8 и получается другой ответ!
Делить нужно на 20. Масштаб по горизонтальной оси: в одной клеточке 4 с
На тело, находящееся на горизонтальной плоскости, действуют три горизонтальные силы (см. рисунок, вид сверху). Каков модуль равнодействующей этих сил, если (Ответ дайте в ньютонах и округлите до десятых.)
На рисунке обозначена равнодействующая векторов и
Поскольку модуль вектора силы равен 1 Н, заключаем, что масштаб рисунка такой, что сторона одного квадрата сетки соответствует модулю силы 1 Н. Таким образом, модуль равнодействующей равен по теореме Пифагора
А как определили эту равнодействующую трёх сил, я понять не могу?!
Чтобы найти равнодействующую, необходимо сложить вектора всех сил (например, по правилу треугольника или параллелограмма складываем вектора по два).
Если сложить вектор и вектор , получится вектор, направленный вверх длиной в одну клеточку. Теперь осталось прибавить к нему вектор . В результате и получается то, что показано красной стрелкой.
векторы F1 и F3 никак нельзя сложить правилом треугольника! дак как эту задачц решить тут решения совсем непонятные!
Когда Вы складываете параллельные вектора, у Вас просто получается “вырожденный треугольник”. Правила все те же, к концу первого вектора прикладываем начало второго. Сумма векторов — это вектор, который начинается в начале первого и заканчивается в конце второго. То есть в данном случае у Вас получится вектор, направленный вверх и длиной в одну клеточку.
Две силы 3 H и 4 H приложены к одной точке тела, угол между векторами сил равен 90°. Чему равен модуль равнодействующей сил? (Ответ дайте в ньютонах.)
Силы и их равнодействующая указаны на рисунке. По теореме Пифагора, модуль равнодействующей сил равен
Под действием одной силы F1 тело движется с ускорением 4 м/с 2 . Под действием другой силы F2, направленной противоположно силе F1, ускорение тела равно 3 м/с 2 . С каким ускорением тело будет двигаться при одновременном действии сил F1 и F2? Ответ дайте в метрах на секунду в квадрате.
Согласно второму закону Ньютона, ускорение тела пропорционально равнодействующей всех сил, действующих на него: Силы и по условию, направлены противоположно, поэтому при их одновременном действии тело будет двигаться с ускорением
Тело подвешено на двух нитях и находится в равновесии. Угол между нитями равен 90°, а силы натяжения нитей равны 3 H и 4 H. Чему равна сила тяжести, действующая на тело? (Ответ дайте в ньютонах.)
Всего на тело действует три силы: сила тяжести и силы натяжения двух нитей. Поскольку тело находится в равновесии, равнодействующая всех трех сил должна равняться нулю, а значит, модуль силы тяжести равен
в условии написано,что нужно найти вес тела.
а в решении модуль силы тяжести.
Как вес может измеряться в Ньютонах.
В условии ошибка(
Вы путаете понятия массы и веса. Весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Как следует из определения, эта сила приложена даже не к телу, а к опоре. Невесомость — это состояние, когда у тела пропадает не масса, а вес, то есть тело перестает давить на другие тела.
Согласен, в решении была допущена некоторая вольность в определениях, сейчас она поправлена.
Понятие “вес тела” введен в учебную физику крайне неудачно. Если в бытовом понятии вес обозначает массу то в школьной физике, как вы правильно заметили весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Заметим, что речь идет об одной опоре и об одной нити. Если опор или нитей несколько несколько, понятие веса исчезает.
Привожу пример. Пусть в жидкости на нити подвешено тело. Оно растягивает нить и давит на жидкость с силой равной минус сила Архимеда. Почему же, говоря о весе тела в жидкости, мы не складываем эти силы, как Вы делаете в своем решении?
Я зарегистрировался на Вашем сайте, но не заметил, что же изменилось в нашем общении. Прошу извинить мою тупость, но я, будучи человеком старым, недостаточно свободно ориентируюсь на сайте.
Действительно, понятие веса тела весьма расплывчато, когда тело имеет несколько опор. Обычно вес в этом случае определяют как сумму взаимодействий со всеми опорами. При этом воздействие на газообразные и жидкие среды, как правило, исключается. Это как раз подпадает под описанный Вами пример, с подвешенным в воде грузиком.
Здесь сразу вспоминается детская задачка: “Что весит больше: килограмм пуха или килограмм свинца?” Если решать эту задачу по-честному, то нужно несомненно учитывать силу Архимеда. А под весом скорее всего мы будем понимать то, что нам будут показывать весы, то есть силу, с которой пух и свинец давят, скажем, на чашку весов. То есть здесь сила взаимодействие с воздухом как бы из понятия веса исключается.
С другой стороны, если считать, что мы откачали весь воздух и кладем на весы тело, к которому привязана веревочка. То сила тяжести будет уравновешиваться суммой силы реакции опоры и силой натяжения нити. Если мы понимаем вес как силу действия на опоры, препятствующие падению, то вес тут будет равен этой сумме силы растяжения нити и силы давления на чашку весов, то есть совпадать по величине с силой тяжести. Опять возникает вопрос: чем нитка лучше или хуже силы Архимеда?
В целом тут можно договориться до того, что понятие веса имеет смысл только в пустом пространстве, где есть только одна опора и тело. Как тут быть, это вопрос терминологии, которая, к сожалению, у каждого здесь своя, поскольку не столь уж это и важный вопрос 🙂 И если силой Архимеда в воздухе во всех обычных случаях можно пренебречь, а значит, на величину веса она особо повлиять не может, то для тела в жидкости это уже критично.
Если уж быть совсем честным, то разделение сил на виды весьма условно. Представим себе ящик, который тащат по горизонтальной поверхности. Обычно говорят, что на ящик действуют две силы со стороны поверхности: сила реакции опоры, направленная вертикально, и сила трения, направленная горизонтально. Но ведь это две силы, действующие между одними и теми же телами, почему же мы просто не рисуем одну силу, являющуюся их векторной суммой (так, кстати, иногда и делается). Тут, это, наверное, вопрос удобства 🙂
Так что я немного в замешательстве, что делать с данной конкретной задачей. Проще всего, наверное, переформулировать ее и задавать вопрос про величину силы тяжести.
Не переживайте, все в порядке. При регистрации Вы должны были указать e-mail. Если теперь зайти на сайт под своим аккаунтом, то при попытке оставить комментарий в окне “Ваш e-mail” должен сразу появляться тот самый адрес. После этого система будет автоматически подписывать Ваши сообщения.
Формула модуля равнодействующей силы
На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.
Формула равнодействующей всех сил
Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
Формула (1) – это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.
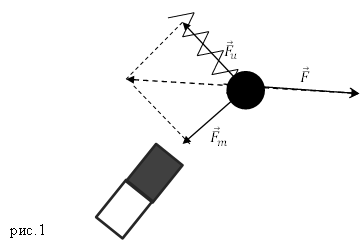
Складывают векторы, используя правило треугольника (рис.1)
правило параллелограмма (рис.2).
или многоугольника (рис.3):
Второй закон Ньютона и формула модуля равнодействующей
Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:
$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач с решением
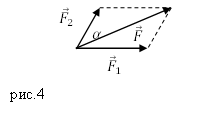
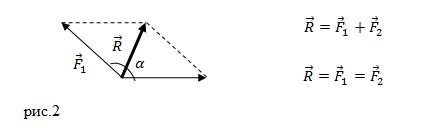
Задание. К материальной точке приложены силы, направленные под углом $alpha =60<>^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?
Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline$ найдем, применяя теорему косинусов:
Вычислим модуль равнодействующей силы:
[F=sqrt<<40>^2+<20>^2+2cdot 40cdot 20<cos (60<>^circ ) >>approx 52,92 left(Нright).]
Ответ. $F=52,92$ Н
Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A<cos (omega t)(м) >$, где $s$ – путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?
Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:
Следовательно, модуль силы можно найти как:
Ускорение точки будем искать, используя связь между ним и перемещением точки:
Первая производная от $s$ по времени равна:
Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:
Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:
[spoiler title=”источники:”]
http://phys-ege.sdamgia.ru/test?theme=206
http://www.webmath.ru/poleznoe/fizika/fizika_134_formula_modulja_ravnodejstvujushhej_sily.php
[/spoiler]
I. Механика
Тестирование онлайн
Определение
Это векторная сумма всех сил, действующих на тело.
Велосипедист наклоняется в сторону поворота. Сила тяжести и сила реакции опоры со стороны земли дают равнодействующую силу, сообщающую центростремительное ускорение, необходимое для движения по окружности
Взаимосвязь со вторым законом Ньютона
Вспомним закон Ньютона:
Равнодействующая сила может быть равна нулю в том случае, когда одна сила компенсируется другой, такой же силой, но противоположной по направлению. В этом случае тело находится в покое или движется равномерно.

Сила Архимеда уравновешивается силой тяжести, тело равномерно перемещается в жидкости вниз. |

Сила тяжести уравновешивается силой упругости. Книга покоится |
Если равнодействующая сила НЕ равна нулю, то тело движется равноускоренно. Собственно именно эта сила является причиной неравномерного движения. Направление равнодействующей силы всегда совпадает по направлению с вектором ускорения.
Когда требуется изобразить силы, действующие на тело, при этом тело движется равноускоренно, значит в направлении ускорения действующая сила длиннее противоположной. Если тело движется равномерно или покоится длина векторов сил одинаковая.

Сила реакции опоры (сила, направленная вверх) длиннее силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вверх |

Сила реакции опоры (сила, направленная вверх) короче силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вниз. Вектор силы тяжести, направленный вниз, длиннее. |
Нахождение равнодействующей силы
Для того, чтобы найти равнодействующую силу, необходимо: во-первых, верно обозначить все силы, действующие на тело; затем изобразить координатные оси, выбрать их направления; на третьем шаге необходимо определить проекции векторов на оси; записать уравнения.
Кратко: 1) обозначить силы; 2) выбрать оси, их направления; 3) найти проекции сил на оси; 4) записать уравнения.
Как записать уравнения? Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю. Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.
Примеры
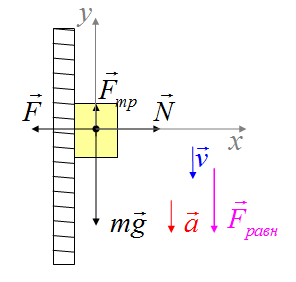
На движущееся равномерно по горизонтальной поверхности тело, действуют сила тяжести, сила реакции опоры, сила трения и сила, под действием которой тело движется.
Обозначим силы, выберем координатные оси
Найдем проекции
Записываем уравнения
Тело, которое прижимают к вертикальной стенке, равноускоренно движется вниз. На тело действуют сила тяжести, сила трения, реакция опоры и сила, с которой прижимают тело. Вектор ускорения направлен вертикально вниз. Равнодействующая сила направлена вертикально вниз.
Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.
Главное запомнить
1) Если тело покоится или движется равномерно, то равнодействующая сила равна нулю и ускорение равно нулю;
2) Если тело движется равноускоренно, значит равнодействующая сила не нулевая;
3) Направление вектора равнодействующей силы всегда совпадает с направлением ускорения;
4) Уметь записывать уравнения проекций действующих на тело сил
Системы и блоки*
Формула равнодействующей всех сил в физике
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline{F}$ – это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
[overline{F}=moverline{a} left(1right),]
где $m$ – масса тела, на которое действует сила $overline{F}$; $overline{a}$ – ускорение, которое сила $overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(2right).]
Формула (2) – это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
[sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(3right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Пример 1
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60{}^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline{F}$ можно найти, используя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{20}^2+{10}^2+2cdot 20cdot 10{cos (60{}^circ ) }}approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
Пример 2
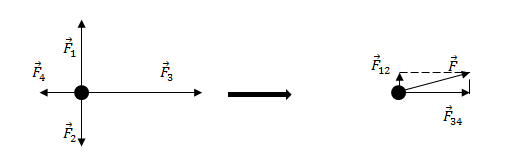
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
[overline{F}={overline{F}}_1+{overline{F}}_2+{overline{F}}_3+{overline{F}}_4left(2.1right).]
Найдем равнодействующую сил ${overline{F}}_1$ и ${overline{F}}_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
[F_{12}=F_1-F_2=17-11=6 left(Hright).]
Так как $F_1>F_2$, то сила ${overline{F}}_{12}$ направлена в туже сторону, что и сила ${overline{F}}_1$.
Найдем равнодействующую сил ${overline{F}}_3$ и ${overline{F}}_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
[F_{34}=F_3-F_4=18-10=8 left(Нright).]
Направление силы ${overline{F}}_{34}$ совпадает с направлением вектора ${overline{F}}_3$, так как ${overline{F}}_3>{overline{F}}_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
[overline{F}={overline{F}}_{12}+{overline{F}}_{34}left(2.2right).]
Силы ${overline{F}}_{12}$ и ${overline{F}}_{34}$ взаимно перпендикулярны. Найдем длину вектора $overline{F}$ по теореме Пифагора:
[F=sqrt{F^2_{12}+F^2_{34}}=sqrt{6^2+8^2}=10 left(Нright).]
Ответ. $F$=10 Н
Читать дальше: формула равнодействующей силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
По графику скорости тела (см.
Рисунок) определите модуль и направление равнодействующей силы , действующих на автомобиль массой 1, 5т.

Вы открыли страницу вопроса По графику скорости тела (см?. Он относится к категории
Физика. Уровень сложности вопроса – для учащихся 1 – 4 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Физика,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.