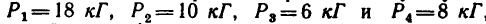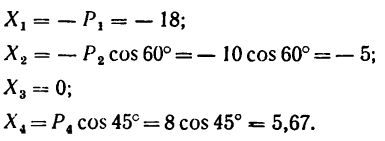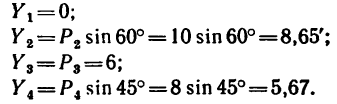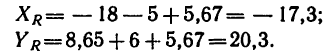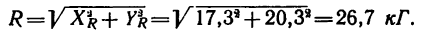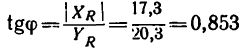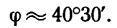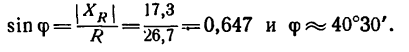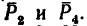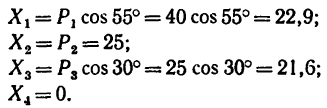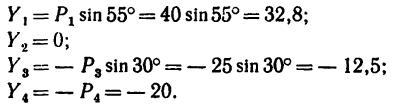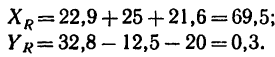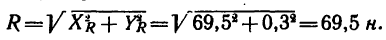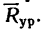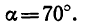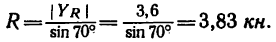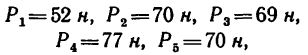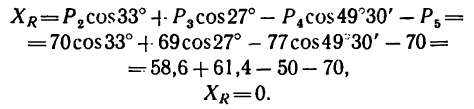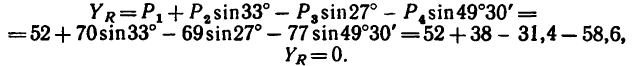поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,926 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Определение равнодействующей сходящихся сил:
Для сложения любого числа сходящихся сил применяется правило многоугольника. Используя это правило, задачу можно решить либо графическим методом либо методом проекций.
Задачи, решены методом проекций. Графическим методом рекомендуется решить эти задачи самостоятельно.
Задача №1
Определить равнодействующую четырех сил:
Решение — методом проекций.
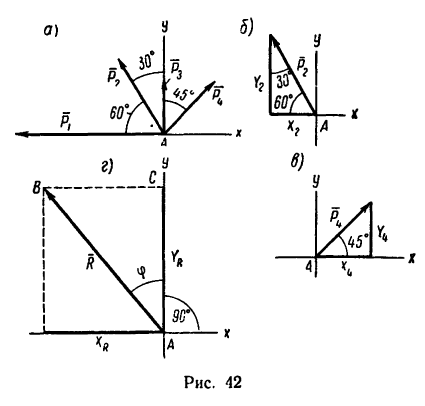
1. Изображаем на рисунке четыре данные силы и выбираем расположение осей проекций. В данном случае удобно начало осей поместить в точке А, а оси совместить с силами 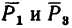
2. Находим проекции данных сил на ось х:
3. Находим проекции данных сил на ось у:
Если трудно определить знак и числовое значение проекции, то необходимо помнить, что проектируемую силу и две проекции на взаимно перпендикулярные оси всегда можно представить в виде прямоугольного треугольника. В тех случаях, когда еще нет достаточных навыков, силы и ее проекции можно изобразить отдельно, как показано на рис. 42,6 для силы 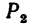
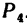
Для сил 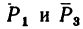
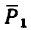
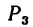
4. Находим проекции искомой равнодействующей 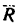
Проекция на ось х получается отрицательной, а на ось у положительной. Значит вектор 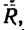
5. Находим модуль равнодействующей (т. е. заканчиваем решение задачи первым путем, см. п. 7 в § 4-1):
6. Находим угол ф, определяющий направление R относительно оси у (см. рис. 42, а):
и, следовательно,
Для определения угла 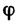

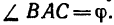
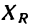
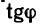
Угол 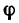
Для определения угла 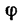
Таким образом, равнодействующая четырех заданных сил равна 26,7 кГ направлена под углом 40°30′ к положительному направлению оси у и под углом 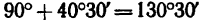
Задача №2
К концу В веревки АВ прикреплено кольцо, на которое действуют четыре силы: 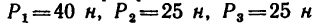
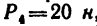
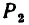
Решение — методом проекций.
1. Веревка будет натянута равнодействующей четырех заданных сил. Следовательно, определив модуль равнодействующей, получим усилие, возникшее в веревке, а определив направление равнодействующей, найдем положение натянутой веревки.
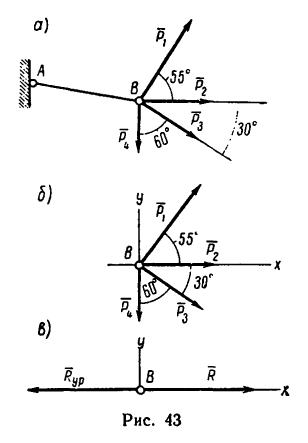
2. Изобразим точку В с действующими на нее силами на отдельном рисунке (рис. 43, 6) и совместим оси проекций с силами
3. Найдем проекции заданных сил на ось х:
4. Найдем проекции заданных сил на ось у:
5. Найдем проекции равнодействующей R на оси х и у:
6. Найдем модуль равнодействующей:
Как видно, в данном случае проекция равнодействующей на ось у очень мала по сравнению с проекцией на ось х. Поэтому равнодействующая практически численно равна проекции на ось х. Следовательно, можно принять, что вектор равнодействующей направлен вдоль оси х вправо (проекция на ось х положительна), т. е. горизонтально.
Таким образом, четыре заданные силы натягивают веревку равнодействующей силой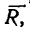
Другой конец веревки (точка А, рис. 43,а) закреплен, поэтому на кольцо В со стороны веревки действует еще одна сила, численно равная равнодействующей, но направленная в противоположную сторону. Эта сила называется уравновешивающей системы четырех сил.
На рис. 43, в показаны равнодействующая 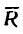
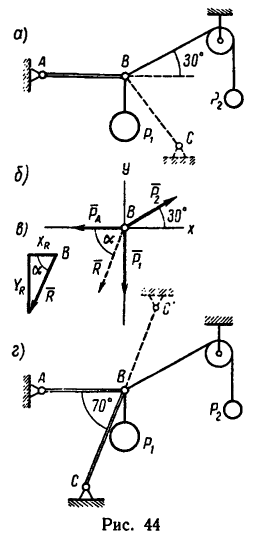
Задача №3
На конце В горизонтального стержня АВ необходимо прикрепить две нити с грузами 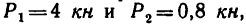
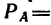
Соединения стержней между собой и с опорами шарнирные.
Решение — методом проекций.
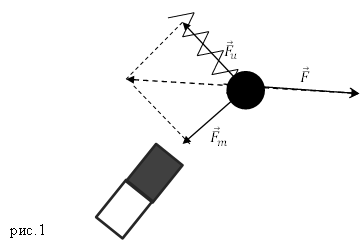
1. На точку В действуют три силы: 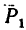
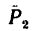
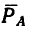
2. Оси проекций совместим с силами 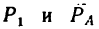
3. Обе проекции получаются отрицательными. Значит равнодействующая расположится так, как показано штриховым 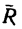
4. Определим значение угла а из треугольника, образуемого 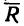
Этому значению соответствует угол
5. Стержень ВС необходимо установить под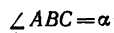
Описанное положение стержня показано на рис. 44, г.
Если же установить стержень, как показано на рисунке штриховой линией ВС, то стержень будет испытывать растяжение, равное той же силе R = 3,83 кн.
Задача №4
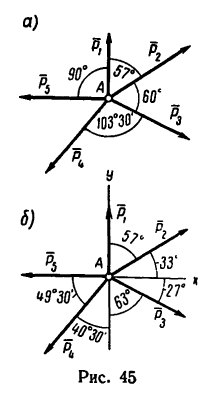
Определить равнодействующую пяти сил:
действующих на точку А, как показано на рис. 45,а.
Решение — методом проекций.
1. Так как силы 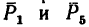
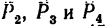
2. Найдем проекцию равнодействующей на ось х:
* Здесь 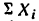
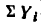
3. Найдем проекцию равнодействующей на ось у:
4. Обе проекции искомой равнодействующей равны нулю, значит и сама равнодействующая также равна нулю.
Таким образом, данная система сил уравновешена. Иными словами, любую из пяти заданных сил можно рассматривать как уравновешивающую четыре остальных.
- Равновесие сходящихся сил
- Равновесие трех непараллельных сил
- Сочлененные системы
- Равновесие пространственной системы сходящихся сил
- Потенциальная энергия
- Обобщенные координаты системы
- Сложение двух сил
- Разложение силы на две составляющие
Формула равнодействующей всех сил в физике
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline{F}$ – это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
[overline{F}=moverline{a} left(1right),]
где $m$ – масса тела, на которое действует сила $overline{F}$; $overline{a}$ – ускорение, которое сила $overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(2right).]
Формула (2) – это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
[sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(3right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Пример 1
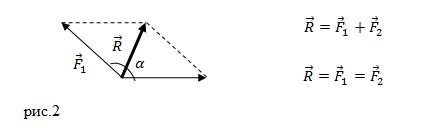
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60{}^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline{F}$ можно найти, используя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{20}^2+{10}^2+2cdot 20cdot 10{cos (60{}^circ ) }}approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
Пример 2
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
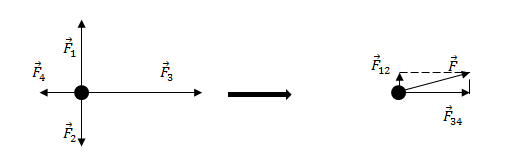
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
[overline{F}={overline{F}}_1+{overline{F}}_2+{overline{F}}_3+{overline{F}}_4left(2.1right).]
Найдем равнодействующую сил ${overline{F}}_1$ и ${overline{F}}_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
[F_{12}=F_1-F_2=17-11=6 left(Hright).]
Так как $F_1>F_2$, то сила ${overline{F}}_{12}$ направлена в туже сторону, что и сила ${overline{F}}_1$.
Найдем равнодействующую сил ${overline{F}}_3$ и ${overline{F}}_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
[F_{34}=F_3-F_4=18-10=8 left(Нright).]
Направление силы ${overline{F}}_{34}$ совпадает с направлением вектора ${overline{F}}_3$, так как ${overline{F}}_3>{overline{F}}_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
[overline{F}={overline{F}}_{12}+{overline{F}}_{34}left(2.2right).]
Силы ${overline{F}}_{12}$ и ${overline{F}}_{34}$ взаимно перпендикулярны. Найдем длину вектора $overline{F}$ по теореме Пифагора:
[F=sqrt{F^2_{12}+F^2_{34}}=sqrt{6^2+8^2}=10 left(Нright).]
Ответ. $F$=10 Н
Читать дальше: формула равнодействующей силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Профи
(536),
на голосовании
5 лет назад
Голосование за лучший ответ
Наталия Бельская
Оракул
(57436)
5 лет назад
1 способ:
Из конца силы F1 проводишь прямую, параллельную силе F2 и равную по длине силе F2. Прямая, соединяющая Начало силы F1 и КОНЕЦ силы F2 и есть равнодействующая (R(1,2)) сил F1 и F2.
Из конца равнодействующей (R(1,2)) проводишь прямую, параллельную силе F3 и равную по длине силе F3. Прямая, соединяющая Начало равнодействующей R(1;2) и КОНЕЦ силы F3 и есть равнодействующая сил F1, F2 и F3 (R (1;2;3)
Из конца равнодействующей (R(1,2,3)) проводишь прямую, параллельную силе F34 и равную по длине силе F4. Прямая, соединяющая Начало равнодействующей R(1;2;3) и КОНЕЦ силы F4 и есть равнодействующая сил F1, F2, F3 и F4(R (1;2;3;4)
II способ:
Сила F1. Силу F2 переносишь в том же направлении (параллельно самой себе) и размера для построения параллелограмма (его стороны F1 и F2). Большая диагональ и есть равнодействующая R(1;2).
Равнодействующая R(1;2). Силу F3 переносишь в том же направлении и размера для построения параллелограмма (его стороны R(1;2) и F3). Большая диагональ и есть равнодействующая R(1;2;3).
Равнодействующая R(1;2;3). Силу F4 переносишь в том же направлении и размера для построения параллелограмма (его стороны R(1;2;3) и F4). Большая диагональ и есть равнодействующая R(1;2;3;4).
Найдите равнодействующую четырех сил если известно что F1 = 150 H и F2 = 770 направлены в одну сторону а F3 = 880 H, и F4 = 1200 H?
– по той же прямой но в противоположную сторону.
На этой странице сайта, в категории Физика размещен ответ на вопрос
Найдите равнодействующую четырех сил если известно что F1 = 150 H и F2 = 770 направлены в одну сторону а F3 = 880 H, и F4 = 1200 H?. По уровню сложности вопрос рассчитан на учащихся
5 – 9 классов. Чтобы получить дополнительную информацию по
интересующей теме, воспользуйтесь автоматическим поиском в этой же категории,
чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы
расположена кнопка, с помощью которой можно сформулировать новый вопрос,
который наиболее полно отвечает критериям поиска. Удобный интерфейс
позволяет обсудить интересующую тему с посетителями в комментариях.