Четвертая аксиома служит основой для сложения сил.
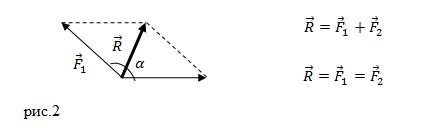
Равнодействующая двух сил, приложенных к одной точке, приложена в этой точке и изображается по величине и направлению диагональю параллелограмма, построенного на данных силах.
Так, равнодействующей двух сил Р и Q, приложенных в точке А (рис. а), будет сила R, представляющая диагональ параллелограмма ACDB, построенного на векторах заданных сил.

Определение равнодействующей двух сил по правилу параллелограмма называется векторным, или геометрическим, сложением и выражается векторным равенством
R = P + Q.
При графическом определении равнодействующей двух сил вместо правила параллелограмма можно пользоваться правилом треугольника. Из произвольной точки А (рис. б) проводим, сохраняя масштаб и заданное направление, вектор первой составляющей силы Р, из его конца проводим вектор, параллельный и равный второй составляющей силе Q. Замыкающая сторона AD треугольника и будет искомой равнодействующей R. Ее можно также представить как диагональ параллелограмма ABDC, построенного на заданных силах.
Модуль равнодействующей двух сил можно определить из Δ ACD:

Поэтому
![]()
или

На основании четвертой аксиомы одну силу R можно заменять двумя составляющими силами Р и Q. Такую замену часто производят при решении задач статики.
Формула равнодействующей всех сил в физике
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline{F}$ – это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
[overline{F}=moverline{a} left(1right),]
где $m$ – масса тела, на которое действует сила $overline{F}$; $overline{a}$ – ускорение, которое сила $overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(2right).]
Формула (2) – это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
[sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(3right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Пример 1
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60{}^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline{F}$ можно найти, используя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{20}^2+{10}^2+2cdot 20cdot 10{cos (60{}^circ ) }}approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
Пример 2
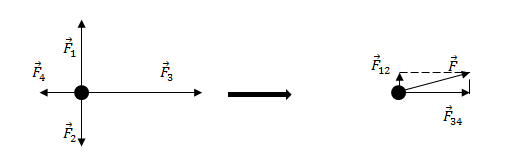
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
[overline{F}={overline{F}}_1+{overline{F}}_2+{overline{F}}_3+{overline{F}}_4left(2.1right).]
Найдем равнодействующую сил ${overline{F}}_1$ и ${overline{F}}_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
[F_{12}=F_1-F_2=17-11=6 left(Hright).]
Так как $F_1>F_2$, то сила ${overline{F}}_{12}$ направлена в туже сторону, что и сила ${overline{F}}_1$.
Найдем равнодействующую сил ${overline{F}}_3$ и ${overline{F}}_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
[F_{34}=F_3-F_4=18-10=8 left(Нright).]
Направление силы ${overline{F}}_{34}$ совпадает с направлением вектора ${overline{F}}_3$, так как ${overline{F}}_3>{overline{F}}_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
[overline{F}={overline{F}}_{12}+{overline{F}}_{34}left(2.2right).]
Силы ${overline{F}}_{12}$ и ${overline{F}}_{34}$ взаимно перпендикулярны. Найдем длину вектора $overline{F}$ по теореме Пифагора:
[F=sqrt{F^2_{12}+F^2_{34}}=sqrt{6^2+8^2}=10 left(Нright).]
Ответ. $F$=10 Н
Читать дальше: формула равнодействующей силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Геометрический
способ сложения сил. Равнодействующая
сходящихся сил. Разложение сил. Проекция
силы на ось и на плоскость. Аналитический
способ задания сил. Аналитический способ
сложения сил. Равновесие системы
сходящихся сил. Статически определимые
и неопределимые системы. Момент силы
относительно центра (или точки). Теорема
Вариньона о моменте равнодействующей.
Сложение и разложение параллельных
сил, расположенных в одной плоскости
[1, с. 18–34; 2, с. 21–20; 3, с. 4–27; 4, с. 11–21].
Решение
многих задач механики связано с известной
из векторной алгебры операцией сложения
векторов и, в частности, сил. Существует
два способа сложения сил: геометрический
и
аналитический.
2.1. Геометрический способ сложения сил.
Равнодействующая
сходящихся сил
И
зучение
статики начнём с рассмотрения
геометрического способа сложения сил.
Величина, равная
геометрической сумме сил какой-нибудь
системы, называется главным
вектором
этой системы сил.
Сложение
двух сил.
Геометрическая сумма
![]()
двух сил
![]()
и
![]()
находится или по правилу параллелограмма
(рис. 2.1а),
или построением силового треугольника
(рис. 2.1б),
изображающего одну из половин этого
параллелограмма. Для построения силового
треугольника надо от произвольной точки
А1
отложить вектор, изображающий одну силу
из сил, а от его конца – вектор, изображающий
вторую силу. Соединяя начало первого
вектора с концом второго, получим вектор,
изображающий силу
![]()
.
Модуль
R
определяется как сторона А1С1
треугольника А1В1С1
из равенства
![]()
,
где
α
– угол между силами.
Следовательно,
![]()
.
(2.1)
Углы
β
и γ, которые сила
образует со слагаемыми силами
и
![]()
,
находятся по теореме синусов. Учитывая,
что
![]()
,
получим
![]()
.
(2.2)
С
ложение
трёх сил, не лежащих в одной плоскости
(рис. 2.2).
Геометрическая
сумма
трёх сил
,
и
![]()
,
не лежащих в одной плоскости, изображается
диагональю параллелепипеда, построенного
на этих силах (правило параллелепипеда).
В справедливости этого убеждаемся,
применяя последовательно правило
параллелограмма.
С
ложение
системы сил
(рис. 2.3).
Геометрическая сумма (главный
вектор) любой
системы сил (рис.
2.3а) определяется
или последовательным
сложением сил системы по правилу
параллелограмма,
или построением
силового
многоугольника (рис.
2.3б). Второй
способ является более простым и удобным.
Для нахождения суммы сил
,
,
…![]()
этим способом откладываем от произвольной
точки О
последовательно векторы, изображающие
в выбранном масштабе слагаемые силы.
Соединяя начало первого вектора с концом
последнего, получаем вектор
![]()
,
изображающий геометрическую сумму или
главный вектор слагаемых сил:
![]()
или
![]()
.
(2.3)
От
порядка, в котором будут откладываться
векторы сил, модуль и направление
не зависит. Легко видеть, что проделанное
построение представляет собой результат
последовательного применения правила
силового треугольника.
Фигура,
построенная на рис.
2.3б, называется
силовым
(в общем случае векторным) многоугольником.
Таким
образом, геометрическая
сумма или главный вектор нескольких
сил изображается замыкающей стороной
силового многоугольника, построенного
из этих сил (правило силового
многоугольника).
При
построении векторного многоугольника
следует помнить, что у всех слагаемых
векторов стрелки должны быть направлены
в одну сторону (по обводу многоугольника),
а у вектора
– в сторону противоположную.
Равнодействующая
сходящихся сил.
Сходящимися
называются
силы, линии действия которых пересекаются
в одной точке (см.
рис.
2.3 а).
Последовательно
применяя аксиому параллелограмма сил,
приходим к выводу, что система сходящихся
сил имеет равнодействующую, равную
геометрической сумме (главному вектору)
этих сил и приложенную в точке их
пересечения.
Следовательно,
если силы
![]()
,
,
…![]()
,
сходятся в одной точке, то сила, равная
главному вектору
,
найденному построением силового
многоугольника, и приложенная в точке
А, будет равнодействующей этой системы
сил.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сложение сил


4.7
Средняя оценка: 4.7
Всего получено оценок: 121.
4.7
Средняя оценка: 4.7
Всего получено оценок: 121.
Если на тело действует несколько сил, то для определения результата их действия необходимо учитывать их все. Это возможно с помощью правил сложения сил. Познакомимся с этими правилами поближе.
Равнодействующая сила
Ситуации, когда на тело действует только одна сила, в Природе сравнительно редки. Практически всегда на любое тело действует сила тяжести, а кроме того, присутствуют силы трения.
Поэтому встает задача определения результата совместного действия всех сил, действующих на тело. Сколько бы таких сил не было – тело либо останется в покое, либо начнет совершать движение. Причем, это всегда будет происходить так, как будто на тело действует только одна сила. Сколько бы сил не действовало на тело, всегда можно подобрать одну такую силу, результат действия которой будет равен действую всех сил, приложенных к телу.
Сила, которая производит то же действие, как и несколько других сил, называется равнодействующей.

Равнодействующая сила используется при решении задач. Заменив силы, действующие на тело, равнодействующей, дальше для определения результата считают, что на тело действует только она.
Правила сложения сил
Действие по нахождению равнодействующей нескольких сил называется сложением сил. Для сложения сил существует переместительный и сочетательный законы. Поэтому, если на тело действует более двух сил, сперва складывают две из них, потом к результату прибавляют третью, потом четвертую – и так до последней силы.
Само сложение пары сил отличается от простого арифметического сложения.
В первую очередь, надо убедиться, что силы приложены к одной точке. Силы, приложенные к разным точкам складывать нельзя.
Во-вторых, необходимо учесть, что сила – величина векторная, а значит, для сложения двух сил необходимо пользоваться не обычным арифметическим сложением, а сложением по векторным правилам. Для сложения сил необходимо найти их проекции на оси системы координат, сложить эти проекции, а потом по проекциям найти результирующую силу.
В простейшем случае, когда координатная ось одна – модули проекций равны модулям самих сил, и их знак совпадает с их направлением. В результате, равнодействующая сил, направленных в одну сторону, направлена в ту же сторону, а ее модуль равен сумме модулей сил. Если силы направлены в разные стороны, равнодействующая их будет направлена в сторону большей по модулю силы, а ее модуль будет равен разности модулей большей и меньшей силы.
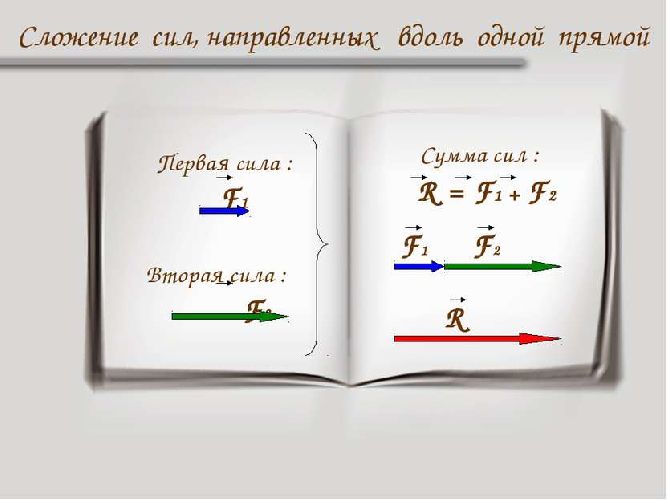
Если координатных осей две или три – необходимо определять проекции на все оси, складывать или вычитать их, в зависимости от направления, а затем, по полученным суммам определять модуль и направление равнодействующей.
Для двух координатных осей при сложении сил нередко удобно использовать правила параллелограмма или треугольника – это приводит к нахождению равнодействующей быстрее.
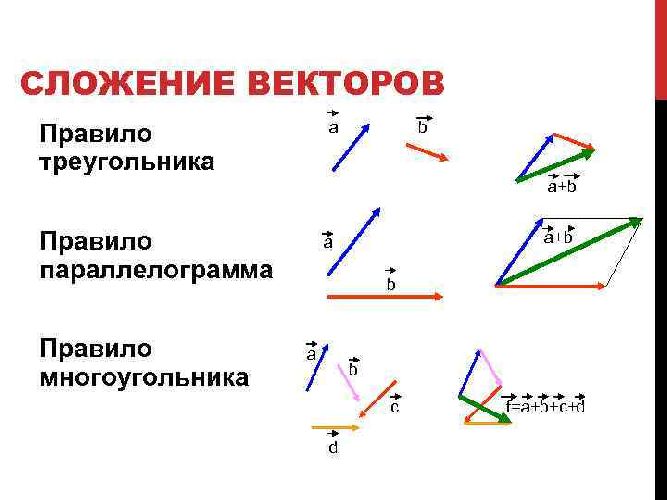

Что мы узнали?
Сила, производящая такой же результат, как несколько других, называется равнодействующей. Для ее нахождения необходимо убедиться, что исходные силы приложены к одной точке, а потом сложить их по правилам сложения векторов.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 121.
А какая ваша оценка?
Статика изучает условия равновесия материальной точки и абсолютного твердого тела.
Абсолютно твердое тело — тело, размеры и форму которого можно считать неизменными.
Под условиями равновесия понимают условия, при которых тело при наличии внешнего воздействия может находиться в покое относительно инерциальной системы отсчета; двигаться поступательно, равномерно и прямолинейно; равномерно вращаться относительно оси, проходящей через центр масс.
Сила. Сложение сил
Основные физические величины, используемые в статике, — сила и момент силы. Сила как величина векторная характеризуется модулем, направлением в пространстве и точкой приложения.
Результат действия силы на материальную точку зависит только от ее модуля и направления. Твердое же тело имеет определенные размеры. Поэтому одинаковые по модулю и направлению силы вызывают различные движения твердого тела в зависимости от точки приложения.
Точку приложения силы можно переносить только вдоль прямой, вдоль которой эта сила действует. Об этом необходимо всегда помнить при осуществлении различных операций над силами.
Сила (~vec R), которая производит на тело такое же действие, как и несколько одновременно действующих на него сил, называется равнодействующей. Она равна геометрической сумме этих сил[~vec R = sum^n_{i=1} vec F_i].
Сложить силы — это значит найти их равнодействующую.
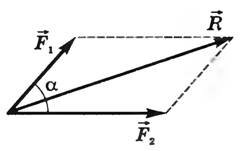
Рис. 1
Если к телу приложено две силы в одной точке, то равнодействующую находят по правилу параллелограмма (рис. 1). Модуль равнодействующей двух сил можно определить по теореме косинусов
(~R = sqrt{F^2_1 + F^2_2 + 2F_1F_2 cos alpha})
или при α = 90°— по теореме Пифагора.
Если непараллельные силы приложены в разных точках тела, то для нахождения их равнодействующей эти силы (~vec F_1) и (~vec F_2) переносят в точку О пересечения прямых, вдоль которых они действуют (рис. 2), а затем производят их векторное сложение по правилу параллелограмма. Точкой приложения равнодействующей силы может быть любая точка прямой, вдоль которой она действует.
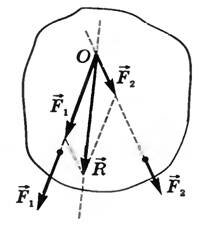
Рис. 2
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 82-83.
