Сила реакции опоры (сила, направленная вверх) короче силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вниз. Вектор силы тяжести, направленный вниз, длиннее.
Нахождение равнодействующей силы
Для того, чтобы найти равнодействующую силу, необходимо: во-первых, верно обозначить все силы, действующие на тело; затем изобразить координатные оси, выбрать их направления; на третьем шаге необходимо определить проекции векторов на оси; записать уравнения. Кратко: 1) обозначить силы; 2) выбрать оси, их направления; 3) найти проекции сил на оси; 4) записать уравнения.
Как записать уравнения? Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю. Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.
Примеры
На движущееся равномерно по горизонтальной поверхности тело, действуют сила тяжести, сила реакции опоры, сила трения и сила, под действием которой тело движется.
Обозначим силы, выберем координатные оси
Тело, которое прижимают к вертикальной стенке, равноускоренно движется вниз. На тело действуют сила тяжести, сила трения, реакция опоры и сила, с которой прижимают тело. Вектор ускорения направлен вертикально вниз. Равнодействующая сила направлена вертикально вниз.
Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.
Главное запомнить
1) Если тело покоится или движется равномерно, то равнодействующая сила равна нулю и ускорение равно нулю;
2) Если тело движется равноускоренно, значит равнодействующая сила не нулевая;
3) Направление вектора равнодействующей силы всегда совпадает с направлением ускорения;
4) Уметь записывать уравнения проекций действующих на тело сил
Системы и блоки*
Блок – механическое устройство, колесо, вращающееся вокруг своей оси. Блоки могут быть подвижными и неподвижными.
Неподвижный блок используется лишь для изменения направления силы.
Тела, связанные нерастяжимой нитью, имеют одинаковые по величине ускорения.
Подвижный блок предназначен для изменения величины прилагаемых усилий. Если концы веревки, обхватывающей блок, составляют с горизонтом равные между собой углы, то для подъёма груза потребуется сила вдвое меньше, чем вес груза. Действующая на груз сила относится к его весу, как радиус блока к хорде дуги, обхваченной канатом.
Ускорение тела А в два раза меньше ускорения тела В.
Фактически, любой блок представляет собой рычаг, в случае неподвижного блока — равноплечий, в случае подвижного — с соотношением плеч 1 к 2. Как и для всякого другого рычага, для блока справедливо правило: во сколько раз выигрываем в усилии, во столько же раз проигрываем в расстоянии
Также используется система, состоящая из комбинации нескольких подвижных и неподвижных блоков. Такая система называется полиспаст.
Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
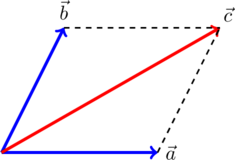
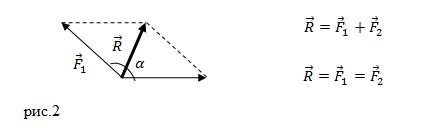
Правило параллелограмма и правило многоугольника
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
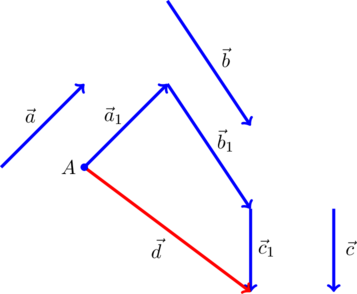
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Пример 1
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную – F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β – F 3 cos γ = F x = 4 – 3 3 2 ≈ – 0 , 6 Н .
Точно также для проекций на ось O Y : – F 2 sin β + F 3 sin γ = F y = 3 – 2 3 2 ≈ – 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 – 2 3 4 – 3 3 ≈ 0 , 4 .
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
[spoiler title=”источники:”]
http://fizmat.by/kursy/dinamika/ravnodejstv
http://zaochnik.com/spravochnik/fizika/elementy-statiki/zakony-slozhenija-sil-v-mehanike/
[/spoiler]
Модуль равнодействующей силы
Четверг, 24 декабря, 2015
В данной статье рассказано о том, как найти модуль равнодействующей сил, действующих на тело. Репетитор по математике и физике объяснит вам, как найти суммарный вектор равнодействующей сил по правилу параллелограмма, треугольника и многоугольника. Материал разобран на примере решения задачи из ЕГЭ по физике.
Как найти модуль равнодействующей силы
Сила, которая оказывает на материальную точку такое же действие, как и несколько других сил, называется равнодействующей этих сил. Для нахождения вектора равнодействующей силы необходимо геометрически (векторно) сложить все силы, которые действуют на материальную точку.
Напомним, что сложить векторы геометрически можно с помощью одного из трех правил: правила параллелограмма, правила треугольника или правила многоугольника. Разберём каждое из этих правил в отдельности.
1. Правило параллелограмма. На рисунке по правилу параллелограмма складываются векторы и
. Суммарный вектор есть вектор
:
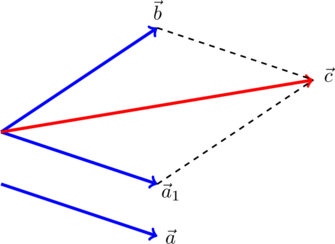
Если векторы и
не отложены от одной точки, нужно заменить один из векторов равным и отложить его от начала второго вектора, после чего воспользоваться правилом параллелограмма. Например, на рисунке вектор
заменен на равный ему вектор
, и
:
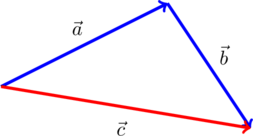
2. Правило треугольника. На рисунке по правилу треугольника складываются векторы и
. В сумме получается вектор
:
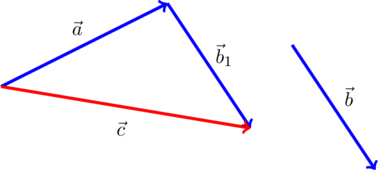
Если вектор отложен не от конца вектора
, нужно заменить его равным и отложенным от конца вектора
, после чего воспользоваться правилом треугольника. Например, на рисунке вектор
заменен равным ему вектором
, и
:
3. Правило многоугольника. Для того, чтобы сложить несколько векторов по правилу параллелограмма, необходимо от произвольной точки отложить вектор, равный первому складываемому вектору, от его конца отложить вектор, равный второму складываемому вектору, и так далее. Суммарным будет вектор, проведенный из точки
в конец последнего отложенного вектора. На рисунке
:
Задача на нахождение модуля равнодействующей силы
Разберем задачу на нахождение равнодействующей сил на конкретном примере из демонстрационного варианта ЕГЭ по физике 2016 года.
Для нахождения вектора равнодействующей сил найдём геометрическую (векторную) сумму всех изображенных сил, используя правило многоугольника. Упрощенно говоря (не вполне корректно с математической точки зрения), каждый последующий вектор нужно отложить от конца предыдущего. Тогда суммарный вектор будет исходить из точки, из который отложен первоначальный вектор, и приходить в точку, где заканчивается последний вектор:
Требуется найти модуль равнодействующей сил, то есть длину получившегося вектора. Для этого рассмотрим вспомогательный прямоугольный треугольник :
Требуется найти гипотенузу этого треугольника. «По клеточкам» находим длину катетов:
Н,
Н. Тогда по теореме Пифагора для этого треугольника получаем:
Н. То есть искомый модуль равнодействующей сил равен
Н.
Итак, сегодня мы разобрали, как находить модуль равнодействующей силы. Задачи на нахождение модуля равнодействующей силы встречаются в вариантах ЕГЭ по физике. Для решения этих задач необходимо знать определение равнодействующей сил, а также уметь складывать векторы по правилу параллелограмма, треугольника или многоугольника. Стоит немного потренироваться, и вы научитесь решать эти задачи легко и быстро. Удачи вам в подготовке к ЕГЭ по физике!
Репетитор по физике на Юго-Западной
Сергей Валерьевич
Формула равнодействующей всех сил в физике
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline{F}$ – это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
[overline{F}=moverline{a} left(1right),]
где $m$ – масса тела, на которое действует сила $overline{F}$; $overline{a}$ – ускорение, которое сила $overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(2right).]
Формула (2) – это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
[sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(3right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Пример 1
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60{}^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline{F}$ можно найти, используя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{20}^2+{10}^2+2cdot 20cdot 10{cos (60{}^circ ) }}approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
Пример 2
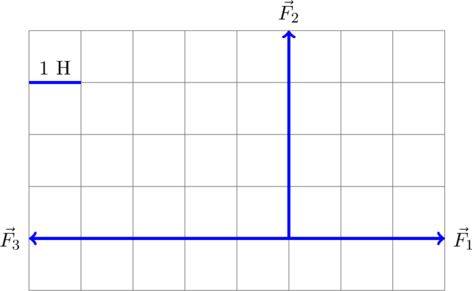
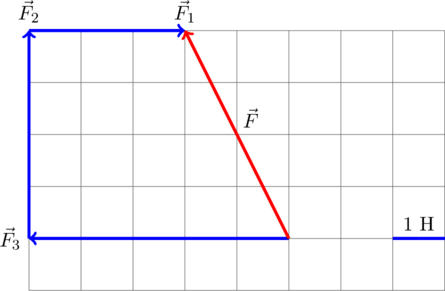
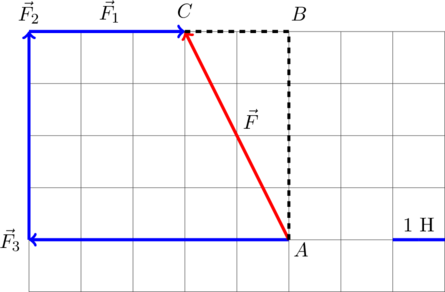
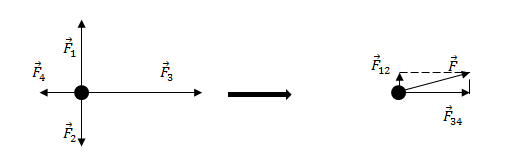
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
[overline{F}={overline{F}}_1+{overline{F}}_2+{overline{F}}_3+{overline{F}}_4left(2.1right).]
Найдем равнодействующую сил ${overline{F}}_1$ и ${overline{F}}_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
[F_{12}=F_1-F_2=17-11=6 left(Hright).]
Так как $F_1>F_2$, то сила ${overline{F}}_{12}$ направлена в туже сторону, что и сила ${overline{F}}_1$.
Найдем равнодействующую сил ${overline{F}}_3$ и ${overline{F}}_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
[F_{34}=F_3-F_4=18-10=8 left(Нright).]
Направление силы ${overline{F}}_{34}$ совпадает с направлением вектора ${overline{F}}_3$, так как ${overline{F}}_3>{overline{F}}_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
[overline{F}={overline{F}}_{12}+{overline{F}}_{34}left(2.2right).]
Силы ${overline{F}}_{12}$ и ${overline{F}}_{34}$ взаимно перпендикулярны. Найдем длину вектора $overline{F}$ по теореме Пифагора:
[F=sqrt{F^2_{12}+F^2_{34}}=sqrt{6^2+8^2}=10 left(Нright).]
Ответ. $F$=10 Н
Читать дальше: формула равнодействующей силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Загрузить PDF
Загрузить PDF
Равнодействующая сила – это векторная сумма всех сил, которая действует на тело.[1]
Если равнодействующая сила равна нулю, то тело находится в покое. Неуравновешенная сила, или равнодействующая сила, значение которой больше или меньше нуля, приводит к ускорению тела.[2]
Суммировать все силы для поиска равнодействующей достаточно просто, но для этого сначала нужно рассчитать или измерить их величину. Как только вы изобразите простую схему действующих сил и убедитесь, что все силы имеют правильный вектор, вычисление равнодействующей силы покажется вам плевым делом.
-
1
Начертите диаграмму свободного тела. Диаграмма свободного тела – это схематичный набросок тела с обозначением векторов всех сил, которые на него действуют. Прочитайте задачу и набросайте схему рассматриваемого тела, обозначив каждую силу, действующую на это тело, стрелками.[3]
- Пример: Вычислить равнодействующую силу тела весом 20 Н, которое лежит на столе и которое толкают вправо под действием силы 5 Н, но при этом остается неподвижным из-за действующей на нее силы трения, равной 5 Н.
-
2
Обозначьте положительные и отрицательные направления сил. Как правило, вверх и вправо направлены силы с положительным значением, а вниз и влево – с отрицательным. Имейте в виду, что в одном направлении могут действовать сразу несколько сил. Силы, действующие в противоположном направлении, должны иметь отрицательные значения (одна положительная, одна отрицательная).[4]
- Если вам нужно представить несколько схем действующих сил, убедитесь, чтобы вектора сил были перенесены правильно.
- Согласно направлению векторов на схеме, пометьте силы знаком «+» или «-».
- Пример: Сила тяжести направлена вниз, делая ее отрицательной. Сила нормальной реакции направлена вверх, что делает ее положительной. Сила, с которой прижимают тело, направлена вправо, что делает ее положительной, тогда как сила трения действует в обратном направлении, то есть, влево (отрицательная).
-
3
Обозначьте все силы. Обозначьте все силы, которые действуют на тело. Если тело лежит на горизонтальной поверхности, на него действует сила тяжести (Fтяж), направленная вниз, а также равная ей сила нормальной реакции, направленная в противоположную сторону (Fн). Помимо этих двух сил отметьте также и другие силы, указанные в задаче. Величину сил запишите в ньютонах рядом с их обозначением.[5]
- Для обозначения силы обычно используется символ F и первые буквы силы в нижнем индексе. Сила трения, к примеру, обозначается так: Fтр.
- Сила тяжести: Fтяж = -20 Н
- Сила нормальной реакции: Fн = +20 Н
- Сила трения: Fтр = -5 Н
- Сила, с которой прижимают тело: Fт = +5 Н
-
4
Сложите все значения. Теперь, когда мы определили вектора и величину всех действующих сил, осталось лишь сложить их вместе. Запишите уравнение для результирующей силы (Fрез), где Fрез будет равна сумме действующих на тело сил.[6]
- Пример: Fрез = Fтяж + Fн + Fтр + Fт = -20 + 20 -5 + 5 = 0 Н. Так как равнодействующая сила равна 0, тело находится в состоянии покоя.
Реклама
-
1
Изобразите схему действующих сил. Когда действие силы на тело происходит под углом, для определения ее величины необходимо найти горизонтальную (Fx) и вертикальную (Fy) проекции этой силы. Для этого мы будем использовать тригонометрию и угол наклона (обозначается символом θ «тета»). Угол наклона θ измеряется против часовой стрелки, начиная от положительной оси х.[7]
- Нарисуйте диаграмму действующих сил, включая угол наклона.
- Укажите вектор направления действия сил, а также их величину.
- Пример: Тело с силой нормальной реакции, равной 10 Н, движется вверх и вправо с силой 25 Н под углом в 45°. Также на тело действует сила трения, равная 10 Н.
- Перечень всех сил: Fтяж = -10 Н, Fн = + 10 Н, Fт = 25 Н, Fтр = -10 Н.
-
2
Вычислите Fx и Fy, используя основные тригонометрические соотношения. Представив наклонную силу (F) в качестве гипотенузы прямоугольного треугольника, а Fx и Fy – в качестве сторон этого треугольника, можно вычислить их по отдельности.[8]
- Напоминаем, что косинус (θ) = прилежащая сторона/гипотенуза. Fx = соз θ * F = cos(45°) * 25 = 17,68 Н.
- Напоминаем, что синус (θ) = противолежащая сторона/гипотенуза. Fy = sin θ * F = sin(45°) * 25 = 17,68 Н.
- Обратите внимание, что под углом на объект одновременно может действовать несколько сил, поэтому вам придется найти проекции Fx и Fy для каждой такой силы. Суммируйте все значения Fx, чтобы получить результирующую силу в горизонтальном направлении, и все значения Fy, чтобы получить результирующую силу в вертикальном направлении.
-
3
Перерисуйте схему действующих сил. Определив все горизонтальные и вертикальные проекции силы, действующие под углом, можете нарисовать новую схему действующих сил, указав также и эти силы. Сотрите неизвестную силу, а вместо нее укажите векторы всех горизонтальных и вертикальных величин.
- К примеру, вместо одной силы, направленной под углом, на схеме теперь будут представлены одна вертикальная сила, направленная вверх, величиной 17,68 Н, и одна горизонтальная сила, вектор которой направлен вправо, а величина равна 17,68 Н.
-
4
Сложите все силы, действующие по координатам х и у. После того как нарисуете новую схему действующих сил, вычислите результирующую силу (Fрез), сложив отдельно все горизонтальные силы и все вертикальные силы. Не забудьте следить за правильным направлением векторов.
- Пример: Горизонтальные вектора всех сил вдоль оси х: Fрезx = 17,68 – 10 = 7,68 Н.
- Вертикальные вектора всех сил вдоль оси у: Fрезy = 17,68 + 10 – 10 = 17,68 Н.
-
5
Вычислите вектор равнодействующей силы. На данном этапе у вас есть две силы: одна действует вдоль оси х, другая – вдоль оси у. Величина вектора силы является гипотенузой треугольника, образованного этими двумя проекциями. Для вычисления гипотенузы достаточно лишь задействовать теорему Пифагора: Fрез = √ (Fрезx2 + Fрезy2).[9]
- Пример: Fрезx = 7,68 Н, а Fрезy = 17,68 Н
- Подставим значения в уравнение и получим: Fрез = √ (Fрезx2 + Fрезy2) = √ (7,682 + 17,682)
- Решение: Fрез = √ (7,682 + 17,682) = √(58,98 + 35,36) = √94,34 = 9,71 Н.
- Сила, действующая под углом и вправо равна 9,71 Н.
Реклама
Об этой статье
Эту страницу просматривали 124 854 раза.
Была ли эта статья полезной?
В задачах динамики учитывают силы, действующие на тело. Векторы сил могут действовать в различных направлениях. Большинство школьных задач можно решить, располагая векторы сил в одной плоскости. Поэтому, в статье будем рассматривать векторы, лежащие в одной плоскости — компланарные векторы.
Что такое равнодействующая
Равнодействующий вектор – это вектор, который мы получаем, когда складываем несколько векторов сил.
Результат сложения может дать:
- вектор, имеющий длину,
- или вектор, не имеющий длины.
Примечание: Когда у вектора отсутствует длина, говорят, что вектор равен нулю. На рисунке нулевой вектор можно изобразить одной точкой. Длины у точки нет – т. е. длина нулевая, а направление может быть любым.
Длина вектора содержит сумму квадратов всех его проекций на оси.
В частности, для вектора ускорения (vec{a}), лежащего на плоскости xOy, длина вычисляется так
[ large left| vec{a} right| = sqrt{ a_{x}^{2} + a_{y}^{2}} ]
Где ( a_{x} ) и ( a_{y} ) — это проекции вектора (ссылка) ( vec{a} ) на оси Ox и Oy.
Когда вектор равен нулю, равна нулю каждая его проекция на осях.
Длина вектора отлична от нуля, когда хотя бы одна его проекция ненулевая.
Прочитайте подробнее о параметрах векторов.
Левая часть силового уравнения
В левой части силового уравнения записываем силы, действующие на тело.
Когда векторы сил направлены вдоль параллельных прямых, проводим на рисунке одну ось. Если векторы сил не параллельные, проводим две оси на плоскости. Раскладываем векторы на проекции по осям. Для каждой оси составляем отдельное уравнение. Количество уравнений совпадает с количеством осей.
Если сила сонаправлена с осью, то она войдет в левую часть уравнения со знаком «+», а если она направлена против оси — то со знаком «минус».
Правая часть силового уравнения
В правой части уравнения записываем равнодействующую. В задаче может присутствовать несколько осей, вдоль каждой оси направляем отдельную проекцию равнодействующей.
Примечание: Тело может вдоль одной оси двигаться с ускорением, а вдоль другой оси двигаться без ускорения, или, вообще, покоиться. Например, тело может двигаться по вертикали под действием силы тяжести, а по горизонтали при этом не смещаться.
Когда проекция равнодействующей вдоль какой-либо оси не равна нулю, тело по оси будет двигаться с ускорением. Это следует из второго закона Ньютона.
Тогда в правой части уравнения запишем:
- (ma), если ускорение направлено туда же, куда направлена ось;
- (- ma), если ускорение направлено противоположно оси;
А когда проекция равнодействующей на ось нулевая, ускорение вдоль оси отсутствует. Тогда вдоль этой оси тело движется с неизменной скоростью, или же, вдоль этой оси движение отсутствует. Это следует из первого закона Ньютона.
В правой части уравнения запишем ноль (0 = ускорения нет).
Векторы сил параллельны
В случае, когда векторы направлены вдоль одной прямой, достаточно выбрать и провести единственную ось.
Выясним, как выглядит силовое уравнение для задачи, в которой векторы сил направлены вдоль единственной оси. Например, парашютист спускается вертикально вниз (рис. 1) на парашюте под действием силы тяжести.
Рис. 1. Парашютист спускается на парашюте, векторы сил направлены вдоль единственной оси
Проведем на рисунке ось, направим ее вверх.
Примечание: Мы можем направить ось вниз, если захотим. При таком направлении оси знаки проекций векторов изменятся на противоположные, но на конечный ответ это никак не повлияет.
Составим левую часть уравнения. В левой части мы запишем силы, действующие на парашютиста:
[large F_{text{сопр}} — m cdot g ]
Сила ( F_{text{сопр}}) направлена по оси, поэтому войдет в уравнение со знаком «+». А сила ( m cdot g ) вошла в уравнение со знаком «минус», так как направлена против оси.
В правую часть уравнения поместим равнодействующую.
Размеры парашюта рассчитаны так, что парашютист опускается вниз с постоянной (неизменной, т. е. одной и той же) скоростью. Значит, скорость есть, она не меняется, ускорения нет.
Математики запишут, что ускорение есть, но оно – нулевое (vec{a}=0).
То есть, вдоль вертикальной оси тело движется без ускорения, значит, силы компенсировались. По первому закону Ньютона, равнодействующая равна нулю и, в правой части уравнения запишем ноль.
Примечания:
- На рисунке 1 скорость обозначена красным вектором, направленным вниз и обозначенным, как (vec{v_{0}}). Обычно математики дописывают нижний индекс к величине, которая не должна меняться. Так как у вектора скорости этот индекс есть, скорость считаем неизменной.
- На рисунке векторы скоростей и ускорений нужно рисовать отдельно от векторов сил! Решая задачу, мы будем складывать векторы (ссылка), имеющие одинаковую размерность. Силы измеряют в Ньютонах, поэтому их можно складывать. А ускорения и скорости измеряют в других единицах, с Ньютонами их сложить не получится. Именно поэтому, чтобы не запутаться, ускорения и скорости рисуем на небольшом расстоянии от тела, отдельно от векторов сил.
Итоговое силовое уравнение имеет вид:
[large F_{text{сопр}} — m cdot g = 0 ]
Зная массу парашютиста, можно вычислить силу сопротивления воздуха. А зная эту силу, можно рассчитать и размеры парашюта.
Векторы сил не параллельны
Когда векторы направлены вдоль разных прямых, будем проводить две взаимно перпендикулярные оси на плоскости.
Разберем задачу равнозамедленного движения тела по горизонтальной шероховатой поверхности (рис. 2).
Рис. 2. Равнозамедленное движения тела по горизонтальной шероховатой поверхности
Поверхность шероховатая, это намек на то, что есть сила трения. А если в условии напишут, что поверхность гладкая, значит, силы трения нет.
Движение равнозамедленное (ссылка), значит, скорость тела уменьшается и есть вектор ускорения, который направлен против вектора скорости.
Нарисуем взаимно перпендикулярные оси. Ось Ox проведем горизонтально, а ось Oy – вертикально. Рассмотрим оси и проекции векторов на них по очереди.
Горизонтальная ось. Пусть движение тела происходит в положительном направлении оси Ox. Сила трения всегда направлена против движения, поэтому направим ее влево. Скорость тела направлена вправо и будет уменьшаться, значит, ускорение, так же, направим влево. Вектор ускорения рисуем отдельно от векторов сил.
Наличие ускорения говорит о том, что вдоль оси Ox равнодействующая имеет не нулевую проекцию. Ускорение направлено против оси, запишем (- ma) в правой части уравнения.
Так выглядит уравнение для горизонтальной оси
[large -F_{text{трен}} = -m cdot a_{x} ]
Вертикальная ось. Вниз направлена сила тяжести, а вверх – сила реакции опоры. Так как поверхность горизонтальная и тело не движется ни вверх, ни вниз, то движения вдоль оси Oy нет. Значит, сила тяжести и реакция опоры компенсировались и нет ускорения вдоль оси Oy. В правой части уравнения для вертикальной оси запишем ноль.
Для вертикальной оси уравнение выглядит так:
[large N — m cdot g = 0 ]
Система, пригодная для решения задачи, состоит из двух уравнений
[ large boxed{ begin{cases} -F_{text{трен}} = -m cdot a_{x} \ N — m cdot g = 0 end{cases} } ]
Куда направить оси
Разберем равнозамедленное движение тела вверх по наклонной шероховатой плоскости (рис. 3).
Силы, действующие на тело в этой задаче, не параллельные, направлены вдоль разных прямых. Поэтому для составления уравнений нужно использовать две взаимно перпендикулярные оси. Попробуем для начала провести ось Oy вертикально, а ось Ox горизонтально.
Рис. 3. Большая часть векторов не лежит на осях, такие векторы придется раскладывать на проекции, чтобы составить силовые уравнения
Из рисунка 3 видно, вдоль оси направлен только один вектор (mg). Остальные векторы сил не параллельны ни одной из осей. Такие векторы придется раскладывать на проекции, это усложнит конечную систему уравнений.
Если выберем оси так, как показано на рисунке 3, на проекции нужно будет разложить три вектора.
Попробуем теперь провести оси так, чтобы как можно большее количество векторов оказались параллельными осям (рис. 4). Из рисунка видно, что только один вектор (mg) окажется ненаправленным вдоль какой-либо оси. Остальные векторы сил параллельны осям.
Рис. 4. Большая часть векторов лежит на осях, раскладывать на проекции нужно только один вектор, силовые уравнения будут иметь простой вид
При таком выборе осей раскладывать на проекции придется только один вектор. Это позволит быстрее решить задачу и решать более простые уравнения.
Примечание: Если мы выбререм оси так, как это представлено на рисунке 3, получим более сложные уравнения. Но решив их, мы получим точно такой же ответ, как и в случае выбора осей на рисунке 4.
Выводы:
- Выбор осей на конечный результат не влияет! А влияет только на сложность полученных уравнений.
- Оси проводим так, чтобы как можно больше векторов оказались направленными вдоль осей.
Движение по наклонной плоскости
Составим систему уравнений для решения такой задачи:
Велосипедист подъезжает с начальной скоростью к подъему, посыпанному песком и, едет в гору на велосипеде по инерции, не крутя педали. Масса велосипедиста с велосипедом, начальная скорость его, коэффициент сопротивления поверхности и угол наклона известны.
Нужно составить систему силовых уравнений, чтобы найти ускорение велосипедиста. А после, зная начальную скорость и ускорение, найти путь, который велосипедист сможет проехать по инерции в горку.
Выражение для ускорения
Составим рисунок, на котором изобразим силы, действующие на велосипедиста (рис. 5)
Рис. 5. Велосипедист едет в гору по инерции, отмечены силы, действующие на велосипедиста, видно, что при таком выборе осей необходимо разложить вектор mg на проекции
Мы провели оси так, чтобы пришлось разложить на проекции только один вектор и система силовых уравнений оказалась достаточно простой.
Пользуясь осями координат, составляем теперь уравнения в проекциях.
Уравнение для проекций векторов на ось Ox:
[ large — F_{text{трен}} – m cdot g_{x} = — m cdot a ]
Уравнение для проекций векторов на ось Oy:
[ large N – m cdot g_{y} = 0 ]
Разложим теперь силу тяжести — вектор (mg) на проекции. Чтобы проделать это разложение, нужно отметить угол (alpha ) межу вектором (mg) и одной из осей. В нашем случае, это угол между вектором (mg) и осью Oy.
[ large begin{cases} m cdot g_{y} = mg cdot cos left(alpha right) \ m cdot g_{x} = mg cdot sin left(alpha right) end{cases} ]
Подставив разложение вектора (mg) в уравнения для осей, получим такую систему уравнений
[ large begin{cases} — F_{text{трен}} – mg cdot sin left(alpha right) = — m cdot a \ N – mg cdot cos left(alpha right) = 0 end{cases} ]
Дополним эту систему выражением для силы трения.
[ large F_{text{трен}} = mu cdot N ]
Запишем эти уравнения в систему и выразим из нее уравнение для ускорения.
[ large begin{cases} N = mg cdot cos left(alpha right) \ F_{text{трен}} = mu cdot mg cdot cos left(alpha right) \ mu cdot mg cdot cos left(alpha right) + mg cdot sin left(alpha right) = m cdot a end{cases} ]
Поделим нижнее уравнение системы на массу велосипедиста и запишем окончательно уравнение для ускорения:
[ large mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a ]
Выражение для пройденного пути
Запишем выражения для связи скоростей и пройденного пути. Велосипедист движется по инерции в гору и его скорость уменьшается из-за силы тяжести и силы сопротивления поверхности, посыпанной песком. Когда скорость велосипедиста обратится в ноль, он, проехав часть пути в гору, остановится. Используем систему двух уравнений, она описывает путь при учете уменьшения скорости до нуля:
[ large begin{cases} 0 = v_{0} — a cdot t \ S = v_{0} cdot t — a cdot frac{t^2}{2} end{cases} ]
Получим теперь уравнение для пути, в котором будут присутствовать только начальная скорость и ускорение и, будет отсутствовать время.
[ large begin{cases} t = frac{v_{0}}{a} \ S = v_{0} cdot frac{v_{0}}{a} — a cdot frac{1}{2} cdot frac{v_{0}}{a} cdot frac{v_{0}}{a} end{cases} ]
Упрощенная система для решения задачи теперь включает всего два уравнения
[ large begin{cases} mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a \ S = v_{0} cdot frac{v_{0}}{a} — frac{v_{0}}{2} cdot frac{v_{0}}{a} end{cases} ]
Подставив в эту систему известные значения начальной (v_{0}) скорости велосипедиста, коэффициент (mu) сопротивления поверхности и угол (alpha) наклона плоскости, сможем посчитать путь, пройденный велосипедистом до его полной остановки.