Нахождение силы тяжести тела тоже связано со сложением параллельных сил. А именно, на каждый элемент тела действует сила тяжести, направленная к земле. Их равнодействующая даёт силу тяжести тела
Точка приложения силы тяжести есть центр тяжести тела. Для однородного тела центр тяжести лежит в его геометрическом центре.
Если же тело неоднородно, например состоит из двух грузов, насаженных на невесомый стержень (силой тяжести стержня можно пренебречь), то его центр тяжести (точка О) делит расстояние между грузами в отношении обратном их массам:
Если тело подвесить на нити в точке О, то сила тяжести уравновесится натяжением нити, то есть тело будет находиться в состоянии равновесия. Другой пример равновесия тела. Когда тело лежит на поверхности стола, то сила тяжести, действующая на него со стороны земли, уравновешивается силой нормальной реакции опоры (силой упругости со стороны стола).
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Задачи 8 – 9 к занятию 25.
Следующая запись: Занятие 27. Статика. Виды равновесий.
Ссылки на другие занятия найдёте в Занятии 1.
Система
параллельных сил и её центр. Сила тяжести.
Центр тяжести тела. [1, с. 86–94; 2, с. 78–87;
3, с. 179–198; 4, с. 29–30].
6.1. Центр параллельных сил
П
онятие
о центре параллельных сил возникает
при решении некоторых задач механики
и, в частности, при определении центров
тяжести тел.
Рассмотрим
систему параллельных и одинаково
направленных сил
,
,…,
,
приложенных к твёрдому телу в точках
А1,
А2,…,
Аn
(рис. 6.1). Очевидно,
что эта система имеет равнодействующую
,
направленную так же, как слагаемые силы,
причём по модулю
.
(6.1)
Если
теперь каждую из сил системы поворачивать
около её точки приложения в одну и ту
же сторону и на один и тот же угол, то
будем получать новые системы одинаково
направленных сил с теми же модулями и
точками приложения, но с другим общим
направлением.
Равнодействующая
каждой из таких систем параллельных
сил, очевидно, будет иметь тот же модуль
R,
но всякий раз другую линию действия.
Можно
показать, что при всех таких поворотах
линия действия равнодействующей всегда
проходит через одну и ту же точку С.
Точка
С,
через которую проходит линия действия
равнодействующей системы параллельных
сил при любых поворотах этих сил около
их точек приложения в одну и ту же сторону
и на один и тот же угол, называется
центром параллельных сил.
Положение
точки С
по отношению к телу является неизменным
и от выбора системы координат не зависит.
Её координаты определяют по формулам:
.
(6.2)
где
,
,
– координаты точек приложения сил
.
Следует
отметить, что формула (6.2) будет справедлива
и для параллельных сил, направленных в
разные стороны, если считать силы
величинами алгебраическими(для одного
направления со знаком плюс, а для другого
– минус) и если при этом
.
6.2. Центр тяжести твёрдого тела
На
любое тело, находящееся вблизи земной
поверхности, действует сила притяжения,
направленная к центру Земли. Эту силу
называют силой
тяжести.
Линии действия сил тяжести всех частиц
тела практически пересекаются в одной
точке – центре Земли. Однако так как
линейные размеры любого тела значительно
меньше радиуса Земли, то можно считать,
что силы тяжести частиц тела параллельны.
Равнодействующая
системы параллельных сил тяжести
отдельных частиц тела будет эквивалентна
силе тяжести всего тела.
Равнодействующую
сил тяжести частиц G1,
G2,…,Gn
данного тела обозначим G.
Модуль этой силы равен весу тела и
определяется по формуле:
.
(6.3)
Эта
равнодействующая будет при любых
положениях тела проходить через одну
и ту же неизменно связанную с телом
точку С,
являющуюся центром параллельных сил
тяжести Gk.
Эта точка
называется центром тяжести тела.
Координаты
центра тяжести определяются по формулам:
,
(6.4)
где
,
,
– координаты точек приложения сил
тяжести
частиц тела.
Следует
отметить, что центр тяжести – это точка
геометрическая: она может лежать и вне
пределов данного тела (например, для
кольца).
Равнодействующая
системы
параллельных сил равна их сумме и
проходит всегда через одну точку,
называемую центром параллельных сил.
Силу
притяжения любого тела, находящегося
вблизи земной поверхности, направленную
к центру Земли, называют силой тяжести.
Центром тяжести тела является центр
параллельных сил тяжести отдельных
частей тела.
Задачи
для самостоятельного решения
З
адача
№ 6.1. Определить
в см
координату хc
центра
тяжести прямолинейного однородного
стержня АВ,
если
заданы координаты точек А
и В:
хА
=
10
см;
хВ
=
40
см.
(Ответ:
хc
=
25см).
Задача
№ 6.2.
(Рис.
6.2). Кронштейн
ABD
состоит
из однородных стержней АВ
и
BD
с
одинаковым линейным весом. Какова должна
быть длина в см
стержня АВ,
чтобы
координата хc
центра
тяжести кронштейна равнялась нулю, если
BD
= 20
см.
(Ответ:
хc
=
28,3
см).
Задача
№ 6.3.
Определить
в см
координату хc
центра тяжести однородной
пластины,
которая имеет вид прямоугольного
треугольника ABD
если
известны координаты вершин хА
= хВ
= 3 см;
хD
= 9
см.
(Ответ:
хc
=
5 см).
Задача
№ 6.4.
(Рис.
6.3).
Определить
координату yc
центра тяжести площади фигуры ABCDEG,
стороны
которой параллельны координатным осям.
Размеры на рисунке заданы в м.
(Ответ:
yc
=
1,19 м)
Вопросы для
самопроверки
1.
Что называют центром параллельных сил?
2.
Равнодействующая и центр системы
параллельных сил.
3. Приведите
формулы для определения координат
центра параллельных сил.
4.
Сила
тяжести. Определение координат центра
тяжести твёрдого тела.
КИНЕМАТИКА
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сила обозначается буквой F
Сила измеряется в Ньютонах [Н]
Равнодействующая сила это сила, которой можно заменить
действие нескольких сил.
Если силы сонаправлены, то равнодействующая равна
их сумме R = F1 + F2
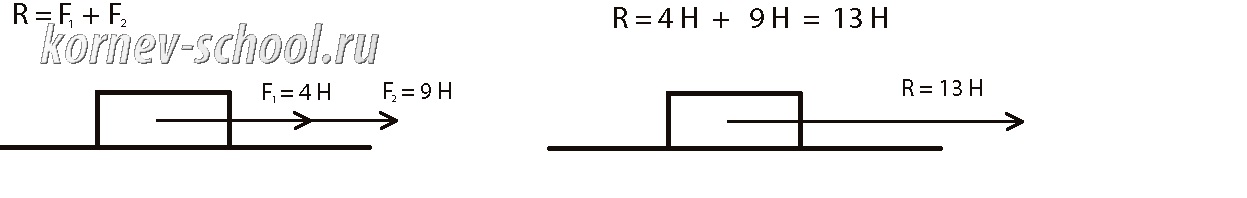
На рисунке две силы 4Н и 9Н заменены одной силой 13Н
Если силы разнонаправлены, то равнодействующая равна разности этих сил R = F1 – F2
Равнодействующая направлена в сторону большей силы
Сила тяжести
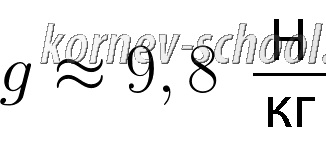
g это ускорение свободного падения, в расчетах будем округлять до 10
1. На тело действуют вправо две силы: F1 = 3Н и F2 = 8Н.
Сделать рисунок с расстановкой сил, определить
равнодействующую силу.
Показать решение
2. На тело действует вправо сила F1 = 7Н и влево сила F2 = 3Н .
Сделать рисунок с расстановкой сил, определить
равнодействующую силу.
Показать решение
3. На автомобиль действует сила тяги F1 = 700Н и сила
сопротивления воздуха F2 = 700Н .
Сделать рисунок с расстановкой сил, определить
равнодействующую силу.
Показать решение
4. На тело вдоль одной прямой действуют три силы: F1 = 7Н ,
F2 = 3Н и F3 =10Н.
Чему может быть равна равнодействующая сила ?
Сделать рисунки с расстановкой сил для всех вариантов,
определить
равнодействующие силы.
Показать решение
Сила тяжести
Сила тяжести — равнодействующая сил притяжения к Земле, она распределена по всему объему тела. Силы притяжения, приложенные к частицам твердого тела, образуют систему сил, линии действия которых сходятся в центре Земли (рис. 8.1). Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.
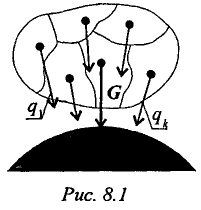
Точка приложения силы тяжести
Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:
Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси.
Изображаем тело, составленное из некоторых частей, в пространственной системе координат (рис. 8.2).
Тело состоит из частей, силы тяжести которых qk приложены в центрах тяжести (ЦТ) этих частей.
Пусть равнодействующая (сила тяжести всего тела) приложена в неизвестном пока центре 
.
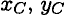и 
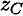— координаты центра тяжест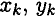и .
и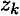 
— координаты центров тяжести частей тела.
Из теоремы Вариньона следует:
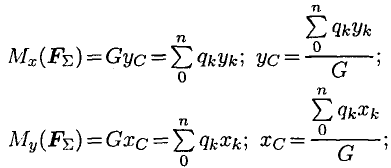
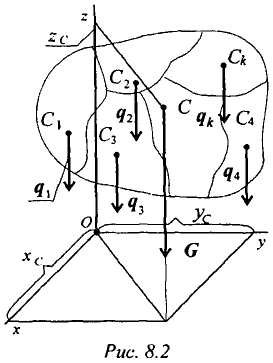
аналогично для оси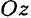 
:
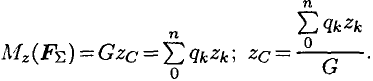
В однородном теле сила тяжести пропорциональна объему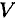 
:
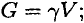
где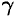 
— вес единицы объема.
Следовательно, в формулах для однородных тел:
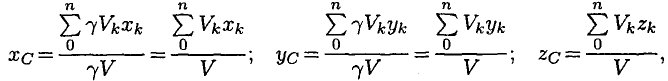
где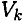 
— объем элемента тела; — объем всего тела.
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Примеры решения задач технической механике
Возможно эти страницы вам будут полезны:
Изучая равновесие сил или определяя равнодействующую сил, мы не рассматривали пока случай, когда силы, действующие на тело, параллельны. Теперь, найдя условия равновесия тела, закрепленного на оси, мы можем рассмотреть и этот случай.
Рассмотрим силы, действующие на рычаг, нагруженный грузами, уравновешивающими друг друга, и подвешенный к неподвижной стойке при помощи динамометра (рис. 122). Можно считать, что ось вращения рычага проходит через точку его подвеса. На рычаг действуют вес
и вес
подвешенных к нему грузов и сила натяжения пружины динамометра
. Будем полагать, что масса самого рычага — настолько мала по сравнению с массами грузов, что ею можно пренебречь. Тогда можно считать, что рычаг находится в равновесии под действием сил
и
. Сила
есть уравновешивающая сила для параллельных сил
и
. Так как при равновесии пружина динамометра располагается вертикально, то сила
параллельна
и
.
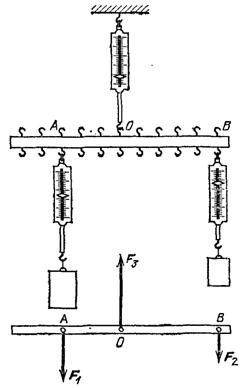
Рис. 122. Исследование равновесия тела при действии трех параллельных сил
Далее, сила
равна по модулю сумме модулей сил
и
. Поскольку мы пренебрегли массой рычага, то
. Расстояния от точки подвеса рычага (его оси вращения
) до точек приложения сил
и
найдем из условия равновесия рычага:
, или
. (80.1)
Это означает, что точка приложения уравновешивающей силы делит расстояние между точками приложения сил в отношении, обратном отношению сил. Следовательно, незакрепленное тело находится в равновесии под действием трех параллельных сил в том случае, когда третья сила, направленная в сторону, противоположную первым двум, по модулю равна сумме их модулей и приложена к точке, делящей расстояние между точками их приложения в отношении, обратном отношению первых двух сил.
Значит, равнодействующая двух параллельных одинаково направленных сил равна сумме этих сил, направлена в ту же сторону и приложена в точке, делящей расстояние между точками приложения сил в отношении, обратном отношению сил.
Легко найти закон сложения и для двух параллельных сил, направленных в противоположные стороны. Любую из трех сил
, действующих на тело, находящееся в равновесии, можно рассматривать как уравновешивающую две другие силы; значит, сила
является уравновешивающей для противоположно направленных параллельных сил
и
. Отсюда, как и раньше, заключаем, что сила, равная и направленная противоположно силе
, является равнодействующей сил
и
. Но
, кроме того, из пропорции (80.1) следует производная пропорция:
, или
.
Таким образом, равнодействующая двух параллельных противоположно направленных сил равна по модулю разности модулей этих сил, направлена в сторону большей силы и приложена в точке, делящей расстояние между точками приложения сил в отношении, обратном отношению сил.
Рис. 123. Точка приложения равнодействующей сил тяжести есть центр тяжести
Если на тело действует несколько параллельных сил, то для нахождения общей равнодействующей надо сначала найти равнодействующую каких-либо двух из этих сил, затем полученную равнодействующую сложить с третьей силой и т. д. В частности, силы тяжести действуют на каждый элемент тела и все эти силы параллельны. Поэтому для нахождения равнодействующей этих сил, т. е. силы тяжести, действующей на все тело, надо последовательно сложить целый ряд параллельных сил. Равнодействующая этих сил равна их сумме, т. е. представляет полную силу притяжения, которую испытывает все тело со стороны Земли, и приложена к определенной точке тела. Точку приложения этой равнодействующей сил тяжести называют центром тяжести тела (рис. 123). Таким образом, действие притяжения Земли на твердое тело таково, как если бы точка приложения силы тяжести лежала в центре тяжести тела. Мы будем пользоваться этим в дальнейшем, заменяя действие сил тяжести, приложенных к отдельным частям твердого тела, действием одной силы, приложенной в его центре тяжести и равной силе тяжести, действующей на все тело. Часто приходится решать задачу, обратную сложению параллельных сил: разложить заданную силу на параллельные ей составляющие силы. Такова, например, задача о распределении сил на опоры балки с грузом или на плечи людей, несущих на шесте груз (рис. 124). Искомые силы
и
, определяются из условия, что их равнодействующая равна весу груза
, и должна быть приложена там, где висит груз. Поэтому
.
Рис. 124. Разложение силы на две параллельные составляющие
