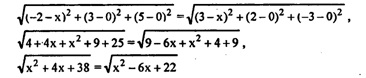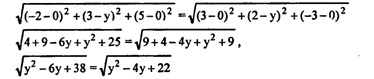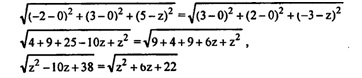Как найти равноудаленную точку 6 класс

Биссектрисы углов A и D трапеции

Расстояние от точки до прямой измеряется длиной перпендикуляра, опущенного из данной точки на прямую. Таким образом, чтобы доказать, что точка M равноудалена от прямых AB, AD и CD , требуется доказать равенство перпендикуляров, проведённых из точки M к прямым, содержащим стороны трапеции AB, AD и CD.

Дано : ABCD — трапеция, AD∥BC, AM — биссектриса ∠BAD, DM — биссектриса ∠DAB, AM∩DM=M, M∈BC,

1) Рассмотрим треугольники AMK и AMF. ∠AKM=90º, ∠AFM=90º (по условию).

∠MAK=∠MAF (так как AM — биссектриса ∠BAD по условию).

Гипотенуза AM — общая.

Из равенства треугольников следует равенство соответствующих сторон: MK=MF.

2) Аналогично, из равенства треугольников DMK и DME следует MK=ME.

3) Значит, MF=MK=ME.

Что и требовалось доказать .

Если точка пересечения биссектрис углов при основании трапеции принадлежит другому основанию, то эта точка равноудалена от трёх сторон трапеции.

Для доказательства можно непосредственно воспользоваться свойством биссектрисы угла.

Так как любая точка биссектрисы угла равноудалена от его сторон, то для угла BAD MF=MK, для угла ADC MK=ME, откуда следует, что все три отрезка равны: MF=MK=ME.

Геометрическое место точек. Теорема о геометрическом месте точек, равноудалённых от двух данных точек, в геометрической и аналитической формах

Определение. Геометрическое место точек – фигура, которая состоит из всех точек на плоскости, обладающих определённым свойством.

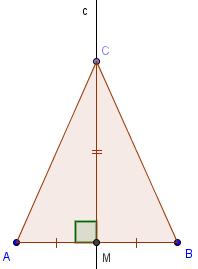
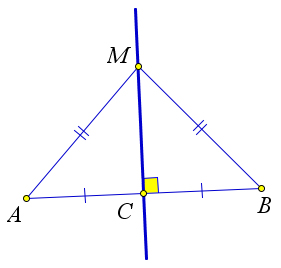
Теорема. Геометрическое место точек, равноудалённых от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки, то есть прямая, перпендикулярная этому отрезку и проходящая через его середину.

1)

Пусть точка C равноудалена от A и B. Отметим точку M – середину отрезка AB. Треугольники ACM и BCM равны по трём сторонам. Углы AMC и BMC равны и дают в сумме развёрнутый угол. Значит, они оба равны 90°.

Мы доказали, что все точки, равноудалённые от двух данных точек, лежат на серединном перпендикуляре.

2) Пусть точка C лежит на серединном перпендикуляре к AB. Треугольники AMC и BMC равны двум катетам, значит, AC=BC.

Мы доказали, что все точки серединного перпендикуляра к отрезку равноудалены от его концов.

Таким образом, геометрическое место точек, равноудалённых от двух данных точек, и серединный перпендикуляр к отрезку, соединяющему эти точки, совпадают.

Четыре замечательные точки треугольника

Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в таком случае называется описанным.

Определение

Окружность называется описанной около многоугольника, если она проходит через все его вершины. Многоугольник в таком случае называется вписанным в данную окружность.

Определение

Точка пересечения медиан треугольника называется центроидом или центром масс.

Замечение

Медианы треугольника пересекаются в одной точке по теореме.

Теорема о биссектрисе, как ГМТ

Биссектриса неразвернутого угла – это геометрическое место точек, равноудаленных от его сторон.

Доказательство

Рассмотрим угол $angle A$.

Докажем, что любая точка, принадлежащая биссектрисе равноудалена от сторон этого угла.

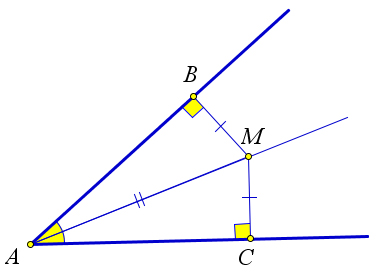
Возьмём произвольную точку $M$ на биссектрисе угла $A$ и опустим из неё перпендикуляры $MB$ и $MC$ на стороны данного угла.

Треугольники $AMB$ и $AMC$ равны по гипотенузе и острому углу, поэтому $MB=MC$, и следовательно, точка $M$ равноудалена от сторон угла.

Обратно: докажем, что если точка равноудалена от сторон угла, то она лежит на биссектрисе.

Возьмём произвольную точку $M$, из которой опущены перпендикуляры $MB$ и $MC$ на стороны угла и при этом $MB=MC$.

Докажем, что точка $M$ принадлежит биссектрисе.

Треугольники $AMB$ и $AMC$ равны по гипотенузе и катету, следовательно, $angle BAM=angle CAM$, то есть $AM$ – биссектриса угла $angle A$.

Теорема

Биссектрисы треугольника пересекаются в одной точке.

Доказательство

Первый способ.

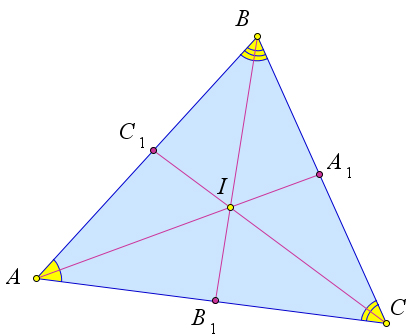
Рассмотрим треугольник $ABC$ в котором проведены биссектрисы $AA_1$, $BB_1$ и $CC_1$.

Перемножая эти равенства, получим: $dfraccdotdfraccdotdfrac=dfraccdot dfraccdotdfrac=1$, а это по теореме Чевы означает, что биссектрисы $AA_1, BB_1$ и $CC_1$ пересекаются в одной точке.

Второй способ.

Рассмотрим треугольник $ABC$ в котором проведены биссектрисы $AA_1$, $BB_1$ и $CC_1$.

Докажем, что все биссектрисы пересекаются в одной точке.

Пусть биссектрисы $AA_1$ и $BB_1$ пересекаются в точке $I$.

Тогда по теореме $rho(I;AB)=rho(I;AC)$, так как $Iin AA_1$, и $rho(I;BA)=rho(I;BC)$, так как $Iin BB_1$.

Тогда $rho(I;CA)=rho(I;CB)$, что означает, что $Iin CC_1$, то есть все три биссектрисы пересекаются в одной точке.

Следствие

В любой треугольник можно вписать окружность, центром которой будет являться точка пересечения его биссектрис. Такая окружность единственна.

Доказательство

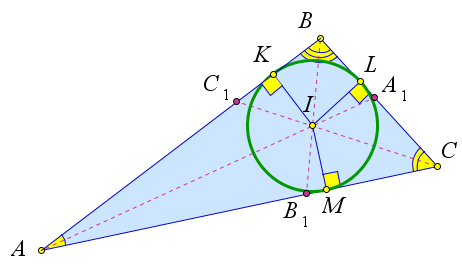
Рассмотрим произвольный треугольник $ABC$ и обозначим буквой $I$ точку пересечения его биссектрис.

Проведем из этой точки перпендикуляры $IK, IL$ и $IM$ к сторонам $AB, BC$ и $CA$ соответственно.

Так как точка $I$ равноудалена от сторон треугольника, то $IK=IL=IM$.

Поэтому окружность с центром $I$ радиуса $IK$ проходит через точки $K, L$ и $M$.

Стороны треугольника $ABC$ касаются этой окружности в точках $K, L, M$ так как они перпендикулярны к радиусам $IK, IL$ и $IM$.

Значит окружность с центром $I$ радиуса $IK$ является вписанной в треугольник $ABC$.

Докажем, что такая окружность единственна.

В самом деле, допустим, что в треугольник можно вписать две окружности.

Тогда центр каждой окружности равноудалён от сторон треугольника и, значит совпадает с точкой $I$ пересечения биссектрис треугольника, а радиус равен расстоянию от точки $I$ до сторон треугольника.

Следовательно, эти окружности совпадают.

Следствие

Если все биссектрисы выпуклого многоугольника пересекаются в одной точке, то в него можно вписать окружность, центром которой будет точка пересечения биссектрис.

Доказательство

Если все биссектрисы пересекаются в одной точке, то эта точка будет равноудалена от всех её сторон, то есть перпендикуляры к сторонам многоугольника будут равны, а окружность с центром в этой точке и с радиусом, равным расстоянию от точки пересечения биссектрис до стороны, будет касаться всех сторон.

Теорема о серединном перпендикуляре, как ГМТ

Серединный перпендикуляр к отрезку – это геометрическое место точек, равноудаленных от концов отрезка.

Доказательство

Рассмотрим отрезок $AB$.

Середину отрезка обозначим $C$.

Докажем, что любая точка, принадлежащая серединному перпендикуляру, равноудалена от сторон.

Действительно, возьмём произвольную точку $M$ на серединном перпендикуляре.

Если $M=C$, то очевидно, что $MA=MB$.

Если $Mneq C$, то треугольники $AMC$ и $BMC$ равны по двум катетам, следовательно $AM=MB$.

Обратно, докажем, что любая точка равноудалённая от сторон, принадлежит серединному перпендикуляру.

Возьмём произвольную точку $M$, для которой $MA=MB$.

Если $M=C$, то очевидно, $M$ принадлежит серединному перпендикуляру.

Если $M C$, то треугольник $AMB$ – равнобедренный, и, следовательно, медиана $MC$ является высотой, то есть $MC$ – серединный перпендикуляр.

Следствие

Все серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство

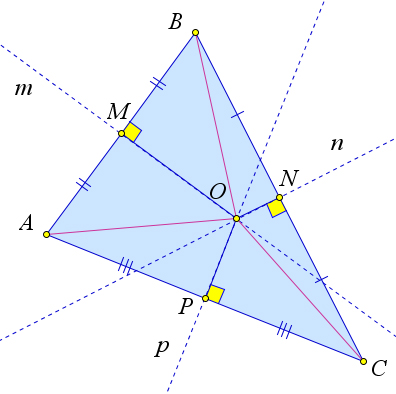
Рассмотрим произвольный треугольник $ABC$, в котором точки $M, N$ и $P$ являются серединами сторон $AB, BC$ и $CA$.

Обозначим серединные перпендикуляры к сторонам $AB, BC, AC$ как $m, n, p$.

Докажем, что эти серединные перпендикуляры пересекаются в одной точке.

Если предположить, что $mparallel n$, то получится, что $nperp BA$, так как $mperp BA$.

Но тогда получится, что через точку $B$ проходят две различные прямые $BA$ и $BC$, перпендикулярные прямой $n$, что невозможно, следовательно, прямые $m$ и $n$ пересекаются.

Пусть они пересекаются в точке $O$.

Тогда по теореме $OA=OB$, так как точка $Oin m$, и $OB=OC$, так как $Oin n$.

Тогда $OA=OC$, и, следовательно, $Oin p$.

Следствие

Около любого треугольника можно описать окружность, центром которой будет точка пересечения серединных перпендикуляров к его сторонам. Такая окружность единственна.

Доказательство

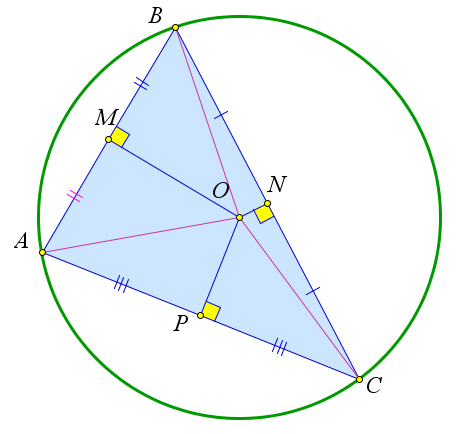
Рассмотрим треугольник $ABC$, в котором серединные перпендикуляры к сторонам пересекаются в точке $O$.

Тогда точка $O$ равноудалена от всех вершин треугольника, то есть $OA=OB=OC$.

Тогда окружность с центром в точке $O$ и радиусом $OA$ будет описанной около данного треугольника.

Докажем, что такая окружность единственна.

Предположим, что в треугольник можно вписать две окружности.

Тогда, центры этих окружностей равноудалены от вершин треугольника.

Но такая точка только одна – это точка пересечения серединных перпендикуляров.

Кроме того их радиусы равны $OA$, следовательно эти окружности совпадают.

Следствие

Если все серединные перпендикуляры к сторонам выпуклого многоугольника пересекаются в одной точке, то около него можно описать окружность, центром которой будет точка пересечения серединных перпендикуляров.

Доказательство

Если все серединные перпендикуляры к сторонам выпуклого многоугольника пересекаются в одной точке, то эта точка равноудалена от всех его вершин, и, следовательно, окружность с центром в этой точке и с радиусом, равным расстоянию от этой точки до какой-либо из его вершин, будет описанной около этого многоугольника.

Теорема

Высоты треугольника (или их продолжения) пересекаются в одной точке.

Доказательство

Рассмотрим произвольный треугольник $ABC$, в котором проведены высоты $AA_1, BB_1, CC_1$.

Докажем, что все высоты пересекаются в одной точке.

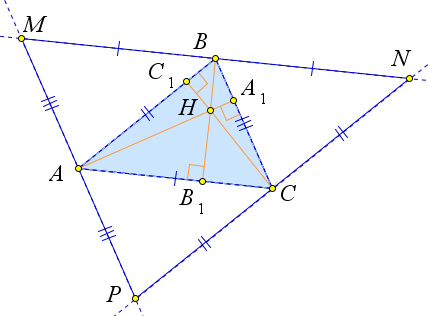
Проведем через точку $B$ прямую, параллельную $AC$, через точку $C$ – прямую, параллельную $AB$, а через точку $A$ – прямую, параллельную $BC$.

Эти прямые, пересекаясь, образуют треугольник $MNP$.

Четырёхугольник $AMBC$ является параллелограммом ($MBparallel AC$, $MAparallel BC$).

Аналогично, $ABNC$ – параллелограмм.

Тогда $MB=AC=BN$, как противоположные стороны параллелограмма.

Следовательно, $B$ – середина $MN$, а $BB_1$ – серединный перпендикуляр к отрезку $MN$.

Аналогично, $AA_1$ – серединный перпендикуляр к отрезку $MP$, $CC_1$ – серединный перпендикуляр к отрезку $PN$.

Получается, что $AA_1, BB_1$ и $CC_1$ пересекаются в одной точке, как серединные перпендикуляры треугольника $MNP$.

Следствие

Если через вершины треугольника провести прямые, параллельные противоположным сторонам, то пересекаясь, они образуют треугольник подобный исходному с коэффициентом $2$. При этом вершины исходного треугольника являются серединами сторон образовавшегося треугольника.

Следствие

Серединные перпендикуляры треугольника являются высотами серединного треугольника. Следовательно, ортоцентр серединного треугольника является центром окружности, описанной около исходного треугольника.

Доказательство

Утверждение полностью следует из доказательства теоремы.

Определение

Точка пересечения высот треугольника называется ортоцентром треугольника.