Как найти равновесие курно дуополия

Дуаполия
Курно – модель олигополии с однородным
товаром, одинаковыми затратами, когда
выпуск конкурента считается заданным
в течении заданного периода.

А

Р

Р

q₁
q₂

MR₁
MR₂

MC=0
Пmax,
если MR=MC
, q₁–
прибыль выпуска максимизирующей.

1. q₁=1/2
   Q,
   т.к. MR=MC.
   Если первая компания не имеет конкурентов,
   то ее прибыль максимизирующий выпуск
   соответствует условию MR=MC
   (1) Вторая компания следует тому же
   условию ( 1 ) занимает половину оставшегося
   рынка, т.е. q2=
   ½ (1-1/2)=1/4 рынка

2. q1=
   ½ (1-1/4) =3/8 Q
   , q2=
   ½ (1- 3/8) =5/16 Q

в
последствии доля 1ой компании убывает,
а 2й наростает пока не установится
равновесие, т.е. отказ от изменения
выпуска.

Равновесие
Курно – такая организация рынка, когда
прибыль максимизируется при заданном
Q
конкурента.

В
числовой версии Курно такой Q
соответсвует 1/3 части рынка

Шаги	q1	q2
1 шаг	1/2	½(1-1/2) = ¼
2 шаг	1/2(1-1/4)=1/2-1/8=3/8	½(1-3/8)=5/16=1/4+1/16
3 шаг	½(1-5/16)=1/2-5/32=11/32	½(1-11/32)=1/2-11/64=21/64=1/4+1/16+1/64
4 шаг	½-1/8-1/32-1/128=1/3	¼+1/16+1/64+1/256=1/3

Аналитическая
версия дуополии Курно

P=a-b*Q?
где а- Рmax,
b=
ΔР/ΔQ,
Q=
q1+q2
МС=С

dq1/dq2=0.
dq2/dq1=0(выпуск
конкурента считается заданным), МС=МR
(прибыль максимизируется)=>П=мах

П1=
aq1-bq1²-bq1q2-cq1
–прибыль 1ой компании

П2=
aq2-
bq2²
–bq2q1-cq2
-прибыль 2ой компании

q1
= (a-c)/2b – 1/2q2 (1)

q2
= (f-c)2b -1/2q1 (2)

формулы
1 и 2 – функции реакции каждой из фирм
на выпуск конкурента при условии его
занятости

П

q1

R1(q2)

R2
(q1)

остроим кривые реагирования дуополии
Курно

С

a-c
a-c
a-c
q2

3b
2b b

a-c/b

a-c/2b

a-c/3b

C-
равновесие Курно. Прибыль максимизирует
выпуски конкурентов курно соответствуют

равенству
при V
q1*.
q2*=a-c/3b.
Это следует из решения системы 1,2.

Отрегулировать
стратегию можно следуя неявному
соглашению о фиксации выпуска

на
уровне ¼ части рынка. Если n=1,
qi=a-c/4b,
Q*=2qi,
P=a+c/2,
т.к.

P=
a-b*Q=a-b*(a-c)/2=a/2+c/2

n>2
, qi=a-c/2b*1/n+1 , где
n->∞

Q=a-c/2b*n/n+1
P=(a+n*c)
/n+1

Устойчивость
м.Курно, При заданном выпуске со стороны
конкурента

равновесие
К. явл. Устойчивым, т.е. устанавлив. При
долях рынка 1/3

34
Модель
асимметричной дуополии, предложенная
Г. фон Штакельбергом в 1934 г., представляет
развитие моделей количественной дуополии
Курно и Чемберлина. Асимметрия дуополии
Штакельберга заключается в том, что
дуополисты могут придерживаться разных
типов поведения — стремиться быть
лидером (англ. leader) или оставаться
последователем (англ. follower). Последователь
Штакельберга придерживается предположений
Курно, он следует своей кривой реагирования
и принимает решения о прибылемаксимизирующем
выпуске, полагая выпуск соперника
заданным. Лидер Штакельберга, напротив,
не столь наивен, как обыкновенный
дуополист Курно. Он настолько изощрен
в понимании рыночной ситуации, что не
только знает кривую

реагирования
соперника, но и инкорпорирует ее в свою
функцию прибыли, так что последняя
принимает вид

А
затем он максимизирует свою прибыль,
действуя подобно монополисту.

Ясно,
что в случае дуополии возможны четыре
комбинации двух типов поведения.

Дуополист
1 — лидер, дуополист 2 — последователь.

Дуополист
2 — лидер, дуополист 1 — последователь.

Оба
дуополиста ведут себя как последователи.

Оба
дуополиста ведут себя как лидеры.

В
случаях 1 и 2 поведение дуополистов
совместимо, один ведет себя как лидер,
другой — как последователь. Здесь не
возникает конфликта и исход их
взаимодействия стабилен. Случай 3 по
сути представляет ситуацию дуополии
Курно, оба дуополиста руководствуются
своими кривыми реагирования, и исход
их взаимодействия стабилен. Нередко
поэтому говорят, что модель Курно — это
частный случай модели Штакельберга.

А
вот в последнем случае, когда оба
дуополиста стремятся стать лидерами,
каждый из них предполагает, что соперник
будет вести себя в соответствии со своей
кривой реагирования, т. е. как монополист
Курно, тогда как на деле ни один из них
не придерживается такого типа поведения.
Исходом подобного взаимодействия
становится неравновесие Штакельберга,
ведущее к развязыванию ценовой войны.
Она будет продолжаться до тех пор, пока
один из дуополистов не откажется от
своих притязаний на лидерство либо
дуополисты вступят в сговор. Сам
Штакельберг считал именно случай 4
наиболее обычным исходом дуополии.
Рассмотрим возможные исходы подробнее.

Последователь
Штакельберга, как уже было сказано,
придерживается своей функции реагирования
вида (11.11), (11.11*) или (11.12), (11.12*), а затем
при определенном количественном решении
соперника, представляющегося последователю
лидером, приспосабливает свой выпуск
к прибылемаксимизи-рующему уровню.
Лидер понимает, что его соперник ведет
себя как последователь, и при данной
его функции реагирования определяет
свой прибылемаксимизирующий выпуск.
Поэтому в случае 4 каждый дуополист
определяет максимум своей прибыли
исходя из предположения, что он является
лидером, а соперник — последователем.
Если в результате прибыль лидера окажется
выше прибыли последователя, дуополист
выберет положение лидера, независимо
от того, что решит соперник. В противном
случае он выберет положение последователя.

Исходя
из аналитической версии модели Курно
(раздел 11.2.1.1.2), представим функцию
прибыли лидера (11.43) для дуополиста 1,
подставив в уравнение его прибыли (11.9)
функцию реагирования дуополиста 2
(11.12*). Тогда (11-9) примет вид

Это
и есть оптимальный выпуск лидера
Штакельберга. Он обеспечивает максимум
его прибыли, поскольку условие второго
порядка также выполняется (Ъ > О по
предположению). В силу симметричности
ситуации, возникающей в случае 4,
прибыле-максимизирующий выпуск дуополиста
2, тоже претендующего на роль лидера,
также составит

Твой мобильный телохранитель

Гитары Hohner!

НЭП об управлении:

(Верхний
индекс I в (11.46) и (11.46*) означает
прибылемакси-мизирующий выпуск лидера).

Определим
теперь прибылемаксимизирующий выпуск
последователя Штакельберга, подставив
(11.46*) в (11.12) и соответственно (11.46) в
(11.12*):

(Верхний
индекс f в (11.47) и (11.47*) означает
прибылемаксимизирующий выпуск
последователя).

Таким
образом, прибылемаксимизирующий выпуск
последователя, q[ , вдвое ниже
прибылемаксимизирующего выпуска лидера,
q (i = 1, 2). Сравнив (11.46), (11.46*), (11.47) и (11.47*) с
(11.17), заметим, что прибылемаксимизирующий
выпуск лидера Штакельберга тот же, что
и у дуополиста Курно, а последователя
вдвое меньше, чем у последнего.

В
случаях 1 и 2, когда один дуополист,
неважно какой именно, ведет себя как
лидер, а другой как последователь, их
общий выпуск будет равен сумме либо
(11.46) и (11.47*), либо (11.46*) и (11.47), т. е.

Подставив
(11.48) в функцию рыночного спроса (11.6),
найдем равновесную цену олигополии
Штакельберга в ситуациях 1,2. Она будет
равна

(11.48)
и (11.49) — параметры равновесия Штакельберга.

Для
того чтобы от равновесия перейти к
неравновесию Штакельберга (от случаев
1 и 2 к случаю 4), определим сначала прибыли
лидера и последователя. Это, между
прочим, поможет нам понять стремление
олигополистов Штакельберга именно к
неравновесию. Подставим сначала значение
q из (11.46) в (11.45). Прибыль лидера, если им
окажется дуопо-лист 1, составит

Симметрично
прибыль дуополиста 2, если тот окажется
лидером, будет

в
(11.9) и (11.9*). Если им окажется дуопо-лист
1, то

Симметрично
прибыль дуополиста 2, если он окажется
последователем, будет

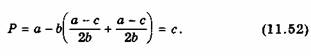
Оба
лидеры

Q1=q2
=a-c/2b

P=a-bq=a-2∙a-c/2b=c
следовательно невыгодно

Если
оба последователи,то каждый следует
своей кривой реагирования.В этом случае
как и в моделе Курно оба займут 2 часть
рынка.На практике компании чаще мотивируют
ценой,чем выпуском,т. е ценовая конкуренция
чаще нежеле количественная

35.
35.Модель
описывает поведение фирм на олигополистическом
рынке,
конкурирующих за счет изменения уровня
цен на свою продукцию. Парадоксальный
вывод модели – фирмы будут назначать
цену, равную предельным
издержкам,
как и фирмы в условиях совершенной
конкуренции–
назван парадоксом
Бертрана.

В
модели приняты следующие предположения:

• На
  рынке имеется по меньшей мере две фирмы,
  производящие однородный продукт;

• Фирмы
  ведут себя некооперативно;

• Предельные
  издержки (MC)
  фирм одинаковы и постоянны;

• Функция
  спроса линейна;

• Фирмы
  конкурируют, устанавливая цену на свою
  продукцию, и выбирают ее независимо и
  одновременно;

• После
  выбора цены фирмы производят объем
  товара, равный величине спроса на их
  продукцию;

• Если
  цены различны, потребители предъявляют
  спрос на более дешевый товар;

• Если
  цены одинаковы, приобретаются товары
  всех фирм в равных долях.

• Модель
  статична (рассматривается принятие
  решения в единичный момент времени).

Предположение
о ценовой конкуренции означает, что
фирмы могут легко изменять объем выпуска
продукции, однако изменить цену после
выбора очень трудно или невозможно.

Равновесие
в классической модели Бертрана

• MC =
  предельные издержки

• p₁ =
  цена фирмы 1

• p₂ =
  цена фирмы 2

• p^M =
  монопольная цена

Оптимальная
цена фирмы 1 зависит от ее ожиданий
относительно цены, назначаемой фирмой
2. Назначение своей цены немного ниже
цены конкурента позволяет получить
весь спрос потребителей D и
максимизирует прибыль. Если фирма 1
ожидает, что фирма 2 будет устанавливать
цену, не превышающую предельных
издержек MC,
то ее наилучшим
ответом является
установление цены, равной предельным
издержкам.

На
диаграмме 1 показана функция наилучших
ответов фирмы 1 p₁’’(p₂).
Она показывает, что при p₂ < MC фирма
1 устанавливает p₁=MC.
При p₂ в
интервале между MC и
монопольной ценой p^M фирма
1 назначает цену немного меньше p₂.
Наконец, если p₂ выше p^M,
фирма 1 назначает монопольную цену
p₁=p^M.

36.Из
современных моделей в экономическом
анализе использется модель «ломаной
кривой спроса». Она была предложена П.
Суизи для объяснения ценовой жесткости
в поведении олигополистов. Данная модель
может быть отнесена к классу моделей
некооперированной ценовой олигополии.

Г
рафически
модель
ломаной кривой спроса
представлена на рис. 6. Наклон кривой
спроса олигополиста определяется
реакцией на его действия других
олигополистов. Он в своих действиях
исходит из наименее благоприятного для
него варианта реакции соперников. В
случае повышения им цены хотя бы некоторые
из его соперников последуют его примеру,
а в случае снижения они сохранят свои
цены на прежнем уровне. Следовательно,
при повышении цены спрос сократиться
существенно, т.к. часть покупателей
переключиться на более дешевые услуги
конкурентов, а в случае понижения цены
рынок олигополиста возрастет незначительно,
поскольку конкуренты сделают то же
самое и сохранят свои рыночные доли.
Как следствие линия спроса на его
продукцию в окрестностях точки А
имеет разный
наклон,
а именно на участке AD
он круче, чем на участке dA.
Значит, в точке А
кривая спроса имеет излом. Подчеркнем,
что речь идет не о действительной, или,
как нередко говорят, объективно данной,
а о субъективной оценке этой кривой
самим олигополистом, или, иначе,
воображаемой им кривой спроса.

37.В
монополистической конкуренции органически
представлены две разные стороны. Одна
из них состоит в том, что фирма создает
легальную монополию, которая с помощью
патентов, торговых и фирменных знаков
защищается от конкурентов. Этому же
способствует дифференциация товаров
– придание им таких индивидуальных
свойств (по качеству, форме, окраске,
упаковке, условиям продажи), которые
делают рынок сбыта монополистическим.
Другая сторона заключается в том, что
на рынке, где продаются однородные
товары, имеется много разных конкурентов,
которые в целях привлечения покупателей
вынуждены прибегать к дифференциации
товаров и услуг.

Монополистическая
конкуренция базируется на
так называемой дифференциации
продукта.
Эта
дифференциация означает, что какие – то
виды продуктов и услуг разделяются на
их подвиды, производством и реализацией
которых занимаются разные компании. В
большинстве своем дифференциация
продукции была порождена максимизирующими
прибыль продавцами, которые реагировали
на различные вкусы потребителей и
стремления к разнообразию.

Прежде
всего, конечно, дифференциация идет по
качеству. Одни и те же потребности можно
удовлетворить продуктами, имеющими
одну потребительную стоимость, но разный
уровень качества. Продукты могут
различаться по надежности, функциональным
свойствам, используемым материалам,
дизайну и пр. Существенное значение
может иметь вид и качество обслуживания
покупателей.Все это влияет на намерения
покупателя и заставляет его выбирать
тот, а не иной товар.

Однако
имеет место и т.н. искусственная
дифференциация: одни и те же товары
могут продаваться в различной упаковке
и различной фасовке, на них могут стоять
разные торговые марки и торговые знаки.
Большое значение для потребителя может
играть в выборе товара близость
расположения магазина, где его можно
купить, поэтому размещение торговых
точек – это тоже условие дифференциации
покупаемого товара.

38.

В течение весьма длительного времени
все действующие на определенный момент
контракты фирмы будут выполнены,
оборудование придет в негодность или
устареет, так что потребуется его замена
и т.д. Это означает, что “по истечении
долгосрочного периода фирма полностью
освобождается от политики, имущества
и обязательств, которыми она связана в
данный момент. Продолжительность
долгосрочного периода, следовательно,
такова, что фирма имеет возможность
пересмотреть все стороны своей политики.
Если, например, фирма установила, что
спрос на ее продукцию возрос, то может
пройти десять лет, прежде чем она позволит
себе осуществить перестройку предприятия
и замену оборудования”1. Таким образом,
долгосрочный период – это такой
промежуток времени, в течение которого
фирма может изменить все факторы
производства, используемые для
изготовления продукта.

Кроме
того, долгосрочный период характеризуется
также изменением числа функционирующих
в отрасли фирм, поскольку в течение
этого вре мени преодолеваются барьеры
для входа и выхода из отрасли. Фирмы с
высокими издержками производства не
смогут продавать свою продукцию по
равновесным ценам и поэтому будут
вынуждены уйти из отрасли. Напротив,
преуспевающие фирмы будут расширять
выпуск, привлекая тем самым производителей
из других отраслей.

В отличие от
долгосрочного в течение краткосрочного
периода фирма имеет минимальную свободу
маневрирования. Она не в состоянии даже
увеличить выпуск продукции в соответствии
с возросшим потребительским спросом.
Для этого фирма должна увеличить закупки
сырья, ввести сверхурочные работы или
нанять дополнительных работников. Даже
после этого пройдет какое-то время,
прежде чем фирма начнет выпускать
дополнительную продукцию. Следовательно,
в течение краткосрочного периода
увеличение спроса может быть удовлетворено
лишь за счет запасов готовой
продукции.

Краткосрочный период
– это отрезок времени, в течение которого
фирма не может изменить общие размеры
основного капитала: сооружений, количества
машин и оборудования, используемых в
производстве. Это период фиксированных
производственных мощностей.

Предполагается
также, что возможности свободного
доступа новых фирм в отрасль в краткосрочный
период весьма ограничены, вследствие
чего число фирм на отраслевом рынке
остается постоянным.

39.Монополистическая
конкуренция базируется на
так называемой дифференциации
товара.Эта
дифференциация означает, что какие – то
виды продуктов и услуг разделяются на
их подвиды, производством и реализацией
которых занимаются разные компании. В
большинстве своем дифференциация
продукции была порождена максимизирующими
прибыль продавцами, которые реагировали
на различные вкусы потребителей и
стремления к разнообразию.

40.На
рынках факторов производства также
действуют законы спроса и предложения.
Однако специфика самих объектов
куп­ли-продажи обуславливает и
некоторые особенности, как спроса и
предложения экономических ресурсов,
так и формирования их равновесной цены.
Во-первых, в отличие от товарных рынков,
на которых покупатель, приобретая товар,
вступает в его полное владение, на рынках
факторов производства покупатель
приобретает только услуги, которые этот
фактор может оказать. Иными словами,
приобретение такого фактора производства,
как рабочая сила, вовсе не означает, что
ее покупатель становится владельцем
работника, обладающего данными знаниями
и умениями. В отношении таких факторов
производства как капитал и земля,
возможно их приобретение как в полную
собствен­ность, так и только услуг
названных факторов. Во-вторых,
спе­цифической чертой спроса на
экономические ресурсы является то, что
он имеет производный, вторичный характер,
т. е. опреде­ляется спросом на готовую
продукцию, производимую с помо­щью
данного ресурса. Как правило, чем выше
спрос на продукт, тем выше спрос и на
ресурсы, необходимые для его выпуска.
В-третьих, спрос на факторы производства
предъявляют лишь предприниматели, т.
е. люди, способные наладить производство
необходимых обществу благ. В-четвертых,
особенность спроса на экономические
ресурсы состоит в том, что спрос на
ресурсы является взаимозависимым. В
производственном процессе раз­личные
ресурсы взаимодействуют друг с другом.
Они взаимоза­меняют или взаимодополняют
друг друга, иногда конкурируют.
Производительность одного фактора
производства зависит от эффективности
другого. Взаимозависимость ресурсов
означает также, что в большинстве случаев
невозможно сказать, сколько продукта
было произведено каким-либо из
производственных ресурсов отдельно от
других. В-пятых, специфика предложения
на этих рынках обусловлена редкостью
экономических ресурсов и производных
от них факторов производства. Если бы
не суще­ствовало проблемы ограниченности
ресурсов, то не существова­ло бы
проблемы выбора и все потребности
общества были бы удовлетворены. Однако
ресурсы редки, и степень редкости во
многом определяет предложение и стоимость
факторов произ­водства на рынке.

Производство
— сфера, где осуществляется соединение
экономических ресурсов для выпуска
необходимых потребителям товаров и
услуг. Произ­водство есть сфера затрат,
создания “отрицательной полезности”.
Смысл экономического прогресса состоит
не в росте производства любых вещей, а
в увеличении количества полезных благ,
ценностей, т. е. всего того, что люди
ценят. Полезность же благ проявляется
только при обмене. Производительность
обмена состоит в том, что люди отчуждают
менее ценные для себя блага, получая за
них более ценные. Обмен также обеспечивает
по­вышение эффективности использования
ресурсов, так как ориентирует производителей
на выпуск тех благ и в том количестве,
в котором нуждает­ся общество.

Экономические
ресурсы, используемые для выпуска благ,
называются фак­торами производства.
К ним относятся: труд, природные ресурсы
(земля), капитал, предпринимательство.
Каждый из факторов создает в процессе
производства свой вид дохода, который
получает его владелец.

На рынке ресурсов
фирма закупает необходимые ей факторы
производст­ва и комбинирует их
определенным образом с целью получения
наиболь­шей отдачи от вложенных
средств. Чем большее количество
какого-либо ресурса использует фирма
(при по­стоянном количестве других
ресурсов), тем меньший доход он приносит.
В этом проявляется принцип (закон)
убывающей производительности пе­ременного
ресурса. Количество каждого используемого
фактора зависит от его производитель­ности
и цены. Предприниматель стремится
изменять количество исполь­зуемых
факторов до тех пор, пока не получит на
каждую последнюю де­нежную единицу,
затраченную на приобретение факторов,
равное по стои­мости количество
конечного продукта. Фирма достигнет
состояния равно­весия, если факторы
производства будут комбинироваться в
соответствии со следующим правилом:

Предельный
продукт труда (MRP_L)

= Предельный
продукт капитала (MRP_K)

Цена
труда (P_L)
Цена
капитала (Р_к)

Следовательно,
фирма должна стараться увеличивать
закупки того фак­тора, цена которого
падает, и сокращать закупки фактора,
который доро­жает.

Предельные
издержки ресурса — это издержки
приобретения каждой до­полнительной
единицы фактора производства. На
совершенно конкурент­ном рынке
факторов производства цена ресурса
постоянна, поэтому гра­фик предельных
издержек ресурса (MRC)
для
отдельной фирмы имеет форму прямой,
параллельной оси абсцисс; кривая
рыночного предложения ресурса имеет
положительный наклон, так как является
кривой издержек упущенных возможностей.
Равновесие на конкурентном рынке
факторов производства достигается
путем уравнивания спроса и предложения.
Это означает, что максимизация прибыли
фирмой достигается при расширении
использования ресурса до тех пор, пока
его предельная производитель­ность
(MRP)
не
уравняется с предельными издержками
(MRC),
т.
е. с це­ной ресурса.

41.
Труд
как экономическая деятельность
(физические и умственные усилия людей
в процессе производства) подразумевает
баланс между полезно­стью
(производительностью) и убытками
(издержками). Полезность труда заключается
в его способности трансформировать
вещи так, чтобы можно было увеличить
степень удовлетворения потребностей.
Убытки труда состоят в отказе от
альтернативного использования времени,
в упущенной выгоде , что счи­тается
издержками.

Каждый
работник решает для себя проблему
предложения труда
на основе потребительского выбора между
досугом и потреблением то­варов и
услуг. Человек
может решить работать больше, меньше
или столько же часов в неделю в ответ
на экзогенное изменение ставки заработной
платы в зависимости от своих предпочтений,
которые могут определяться составом
семьи, культурными традициями, наконец,
индивидуальными особенностями характера.
Более высокая зарплата стимулирует
людей больше тру­диться, замещая досуг
работой (эффект замещения). Однако рост
дохо­дов может привести и к вытеснению
труда свободным временем (эффект дохода).

Сокращение
предложения труда при увеличении
заработной платы происходит из-за
действия эффекта дохода (противоположного
эффекту замещения). Во-первых, человек
располагает лишь 24 часами в сутки, пять
или шесть, из которых ему к тому же просто
необходимо отдыхать; во-вторых, когда
работник достигает определенного уровня
благосостояния, меняется его отношение
к свободному времени, увеличить количество
которое в данном случае можно лишь при
сокращении дополнительной работы.
Данная зависимость предложения рабочей
силы от уровня заработной платы в форме
проявления в определенный момент эффекта
дохода характеризует индивидуальное
предложение труда отдельных лиц или
групп лиц.

На рынке действуют две фирмы. Функция издержек для фирмы 1:

ТС(q₁) = 2 × q_1,

_{и для фирмы 2:}

ТС(q₂) = q₂²

Обратная функция рыночного спроса описывается уравнением:

P(Q) = 250 – 4 × Q,

где

Q = q₁ + q₂.

а) Определите объёмы выпуска фирм в равновесии Курно, максимизирующие их прибыли. Какой в этом случае будет рыночная цена? Какую прибыль получит каждая фирма?

б) Определите параметры рыночного равновесия по Штакельбергу. Какую прибыль получит каждая фирма?

в) Какая установится цена в соответствии с картельным соглашением?

Решение:

а) Подставим общий выпуск двух фирм

Q = q₁ + q₂

в формулу отраслевого спроса, получим:

P(Q) = 250 – 4 × (q₁ + q₂)

Распишем прибыли олигополистов:

П₁ = TR₁ – TC₁ = P × q₁ – 2 × q₁ = (250 – 4 × (q₁ + q₂)) × q₁ – 2 × q₁ =

= 250 × q₁ – 4 × q₁2 – 4 × q₁ × q₂ – 2 × q₁ =

=248 × q₁ – 4 × q₁² – 4 × q₁ × q₂

П₂ = TR₂ – TC₂ = P × q₂ – q₂² = (250 – 4 × (q₁ + q₂)) × q₂ – q₂² =

 = 250 × q₂ – 4 × q₂² – 4 × q₁ × q₂ – q₂² =

 =250 × q₂ – 5 × q₂² – 4 × q₁ × q₂

Каждая фирма стремится к максимуму прибыли.

Найдём максимум функций прибыли. Для этого приравняем к нулю первые производные полученных функций и найдём оптимальный объём выпуска:

П₁‘ = 248 – 8 × q₁ – 4 × q₂ = 0

П₂‘ = 250 – 10 × q₂ – 4 × q₁= 0

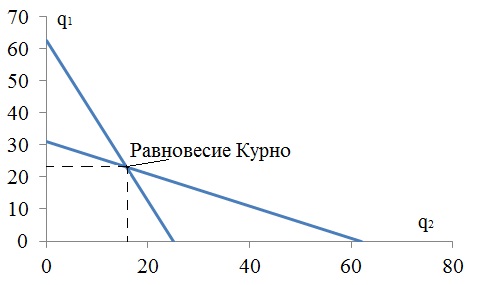
Уравнение реакции для 1 фирмы: q₁ = 31 – 0,5 × q₂ 

Уравнение реакции для 2 фирмы: q₂ = 25 – 0,4 × q₁

Точка пересечения этих линий определяет рыночное равновесие для монополистов.

Решив систему из двух уравнений реакции дуополистов, получим равновесные значения выпуска для первой и второй фирмы.

q*₁ = 23,125

q*₂ = 15,75

Подставив равновесные значения q*₁ и q*₂ в функцию отраслевого спроса

P(Q) = 250 – 4 × (q₁ + q₂),

найдём цену равновесия.

Р = 250 – 4 × 23,125 – 4 × 15,75 = 94,5

Рассчитаем прибыль каждой фирмы в отдельности:

П₁ = 94,5 × 23,125 – 2 × 23,125 = 2139,06

П₂ = 94,5 × 15,75 – 15,75² = 1240,31

б) Пусть фирма 1 выступает в роли лидера, а фирма 2 – в роли последователя.

Тогда прибыль первой фирмы с учётом уравнения реакции фирмы 2 будет равна:

П₁ = 248 × q₁ – 4 × q₁² – 4 × q₁ × (25 – 0,4 × q₁) = 148 × q₁ – 2,4 × q₁²

Она достигает максимума при

П₁‘ = 0

148 – 4,8 × q₁ = 0

q₁ = 30,83

При этом выпуск второй фирмы станет равным:

q₂ = 25 – 0,4 × 30,83 = 12,668,

Р = 250 – 4 × 30,83 – 4 × 12,67 = 76,

П₁ = 76 × 30,83 – 2 × 30,83 = 2281,42,

П₂ = 76 × 12,67 – 12,672 = 802,39.

Таким образом, в результате пассивного поведения фирмы 2 её прибыль снизилась, а фирмы 1 возросла.

В случае лидерства фирмы 2 её прибыль будет равна:

П₂ = 250 × q₂ – 5 × q₂² – 4 × (31 – 0,5 × q₂ ) × q₂ = 126 × q₂ – 3 × q₂²

Определим производную этой функции и приравняем её к нулю.

П₂‘ = 0

126 – 6 × q₂ = 0

q₂ = 21

q₁ = 31 – 0,5 × 21 = 20,5

Р = 250 – 4 × 20,5 – 4 × 21 = 84

П₁ = 84 × 20,5 – 2 × 20,5 = 1681

П₂ = 84 × 21 – 21² = 1323.

Таким образом, в результате пассивного поведения фирмы 1 её прибыль снизилась, а фирмы 2 возросла.

в) Если обе фирмы объединятся в картель, то их общая прибыль будет определяться по формуле:
Пk = TRk – TCk = (250 – 4 × q₁ – 4 × q₂) × (q₁ + q₂) – 2 × q₁ – q₂² =

= 248 × q₁ – 4 × q₁2 – 8 × q₁ × q₂ + 250 × q₂ – 5 × q₂²

Рассчитаем частные производные прибыли по аргументу q₁  и по аргументу q₂:

П_q1‘ = 248 – 8 × q₁ – 8 × q₂ = 0,

П_q2‘ = – 8 × q₁ + 250 – 10 × q₂ = 0.

Решим эту систему уравнений. Вычтем из второго уравнения первое и получим:

2 – 2 × q₂ = 0.

q₂ = 1,

q₁ = 30,

Q = 31,

P = 250 – 4 × 31 = 126,

Прибыль картеля при этом:

Пk =  (250 – 4 × 30 – 4 × 1) × 31 – 2 × 30 – 1² = 3 845

DOI: https://doi.org/10.23670/IRJ.2020.97.7.098

РЕШЕНИЕ ДУОПОЛИИ КУРНО ДЛЯ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО ПАРАМЕТРА ВРЕМЕНИ

Научная статья

Дорофеева Ю.А.*

ORCID: 0000-0002-9327-6705, Петрозаводский государственный университет, Петрозаводск, Россия

* Корреспондирующий автор (julana2008[at]yandex.ru)

Аннотация

Модель дуополии предполагает действие на рынке только двух фирм, при этом каждая из них принимает цену и объем производства конкурента неизменными, и только после этого принимает собственное решение о следующем шаге на рынке. Каждый из двух игроков допускает, что его конкурент всегда будет удерживать свой выпуск стабильным. В классической постановке дуополии Курно определяется равновесие по цене, то есть оптимальную цену для обеих фирм-конкурентов, при которой они получат максимальную прибыль. В данной постановке, в отличие от классической модели, будет рассмотрена задача поиска оптимального решения для времени продаж.

Ключевые слова: теория игр, конкуренция, дуополия, равновесие Нэша, олигополия, рынок, некооперированная игра, модель Курно, объем производства, цена, модель Бертрана.

SOLUTION OF COURNOT DUOPOLY EQUILIBRUM TO DETERMINE THE BEST TIME PARAMETER

Research article

Dorofeeva Yu.A.*

ORCID: 0000-0002-9327-6705, Petrozavodsk State University, Petrozavodsk, Russia

* Corresponding author (julana2008[at]yandex.ru)

Abstract

The duopoly model assumes that only two companies operate in the market. Each of them takes the price and volume of the competitor’s production as something permanent and makes its own decision about the next step at the market based on this information. Each of the two players assumes that the competitor will always keep the release at the same level. In the classical formulation of the Cournot duopoly, equilibrium is determined by price, that is, the best price for both competing companies that allows them to receive the maximum profit. This formulation considers the search for the best solution for the sales time in contrast to the classical model.

Keywords: game theory, competition, duopoly, Nash equilibrium, oligopoly, market, uncooperated game, Cournot model, production volume, price, Bertrand model.

Введение

Дуополия – частный случай олигополии, это та ситуация, при которой на рынке существует всего две компании, выпускающие подобную продукцию. Важно, что фирмы не связаны монополистической договорённостью о цене, рынках сбыта и квотах. Дуополия Курно – это модель равновесия в некооперированной олигополии, при условии, что такие параметры, как цена на свою продукцию и объём своего производства изменяются редко [3]. На рынке действуют только две фирмы, каждая из них отслеживает цену и объем производства конкурента, и только после анализа этих данных принимает собственное решение. Надо отметить, что в силу «стационарности» цены и объёмов производства данную модель можно применить к стабильным компаниям. В отличие от классических статистических прогнозов, дуополии интересны тем, что в этих постановка учитывается конфликт интересов. Прибыль, получаемая фирмой, зависит еще и от решений конкурента, который, в свою очередь, заинтересован максимизировать свою прибыль.

В классических постановках дуополии Курно решается задача поиска оптимальной цены продажи, иногда объема продаж. Интерес представляет вопрос об оптимальном времени продаж, не используя методы статистического прогнозирования.

Постановка задачи

Рассмотрим две фирмы, производящие похожую по цене и качеству сувенирную продукцию, действующих на территории г. Петрозаводска, Республики Карелия. Обе фирмы собираются предложить свою схожую продукцию покупателям, планируя определенный выпуск товара, и находятся в ожидании старта продаж. Допустим, что каждая из них считает, что стоимость единицы товара конкурента и соответствующий объем его продукции неизменными. Затем принимает решение относительно своего объема производства, его затрат, качества материалов с учетом того, что конкурент всегда будет удерживать свой выпуск стабильным. Задача состоит в поиске оптимального момента времени для получения наилучшей прибыли обеими компаниями, учитывая конкуренцию.

В качестве дополнительного исследования требуется найти оптимальную цену при реализации единицы товара сувениров для каждого из конкурентов с помощью дуополии Бертрана.

Реализация решения

Для решения этой задачи нам необходимо проанализировать данные компаний 1 и 2 по следующим финансовым показателям: доходы компаний, их прибыль, расходы, средняя стоимость продукта, рыночный спрос.

Посчитав и проанализировав издержки двух фирм, по финансовым данным был проведен подсчет объема продаж. По имеющемуся дискретному набору значений финансовых показателей издержек за 4 квартала 2019 года с применением метода интерполяции полиномом Лагранжа с помощью программы Wolfram Mathematica, была

получена зависимость издержек от времени. Издержки каждой компании за четыре квартала 2018 и 2019 годов рассчитываются следующим способом:

С = операционные расходы компании за один квартал + другие расходы + налоги.

В результате, зависящие от времени 1 издержки 1 и 2 компаний:

С (г) = 1,72?2 – 9,9г + 31,3, С2 (г) = -2,222 + 15,79г + 20,47

Для всей линейки сувенирной продукции каждой из фирм определена средняя рыночная стоимость товаров: для компании 1 средняя стоимость р = 105,9 руб., для компании 2-р2 = 95 руб.

Прибыль и компании 1 и прибыль Ц72 компании 2 в зависимости от соответствующих объемов выпускаемой продукции 4 (г), ^ (г), в соответствии с [2], [3] вычисляются по формулам:

^(4(0, ^(0) = (р – 4(0 – ?2(0) • – С(г) • 4(0,

П2 (Ч1(t), 42 (г)) = (Р2 – 4100 – 42 (г)) • 42 (г) – С2 (г) • 42 (0-

Каждая фирма стремится к наибольшей прибыли. В данном случае это и будет равновесие по Нэшу, определенное по времени. Для того чтобы найти максимум функции, найдем частные производные по переменным 4 и 4, и приравнивая их к нулю, найдем оптимальную величину времени:

дП

—1 = 105,9 – 42 (г) – 24 (г) -1,722 + 9,9? – 31,3

д41 дП

2 = 95 – 4 (г) – 24 (г) + 2,222 – 15,79г – 20,47

д42

‘дПх

д41

дП

д42

= 0 = 0

Решая систему:

124 (г) = 105,9 – 4 (г) -1,722 + 9,9г – 31,3 [24 (г) = 95 – 4 (г) + 2,22/2 -15,79/ – 20,47

В результате получены выражения:

4 (г) = -1,89г2+11,86г+24,89 4 (г) = 2,05г2 – 13,83г+24,82

Данные функции изображены на рис.1.

Найдём точки пересечения графиков функций 4 (г) и 4 (г) , которые определяют равновесие Нэша для конкурентов: 4(г) = 4(г); ^ = -0.0027,^ = 6.52.

На рис. 1 выделена точка равновесия, соответствующая оптимальной величине времени продаж.

Рис. 1 – График динамики прибыли конкурирующих фирм по времени

В данной модели равновесие Нэша будет сильным, в связи с тем, что отклонение от него грозит минимизацией прибыли, а значит и банкротством.

Дополнительное исследование: определение оптимальной цены продаж с помощью дуополии Бертрана

В качестве дополнения к прогнозу по времени, с помощью дуополии Бертрана найдем оптимальную цену для продажи обеими фирмами с учетом конкуренции.

Данная модель описывает поведение фирм, конкурирующих только за счет изменения уровня цен на свою продукцию. Парадокс модели Бертрана— конкуренты будут назначать цену, равную предельным издержкам, как и фирмы в условиях совершенной конкуренции.

Согласно [2], [8] аналогичным образом, как и в определении оптимального времени продаж, составим уравнение выигрышей и найдем равновесие Нэша.

Введем следующие обозначения:

– с – это себестоимость товара

– с, С – цена на товар

– к -коэффициент взаимозаменяемости товаров

– 4 -начальный спрос на товар.

Выигрыши игроков будут определяться соотношениями:

Н1 (С, С2 ) = (4 – С1 + кс2 )(С -Н2 (С, С2 ) = (4 – С2 + кС1 )(С2 – С)-

Важно отметить, что в данной конфликтной постановке игра задана полностью. И решение данной задачи существует в единственной точке [3, c.8], в отличие от дуополии Курно, которую и требуется определить. В данном сценарии сувенирные товары, выпускаемые конкурентами идентичны, поэтому коэффициент взаимозаменяемости примем равным за 1.

Используя вышеперечисленные финансовые показатели, были построены графики издержек, а также с помощью программы Wolfram Mathematica и с применением метода интерполяции полиномом Лагранжа были получены функции выигрышей для компании 1 и 2.

дН

-1 = -22.8с2 – 8.45^ + 3066.95,

дс1

дН

-^ = -12.4c – 0.84c +1294.24.

2 1

С 2

Решая полученную систему уравнений, получим с — 99.95; с2 — 97.66. Графическое решение представлено на рис.2

о

200-

180 –

N. 160-

ч

__ 120-

100-

80Г ‘ I ‘ -■- 1-1-1

с-

Рис.2 – Равновесие Нэша в дуополии Бертрана для двух конкурирующих фирм

Таким образом, первой фирме выгоднее будет снизить стоимость от 105 руб. 90 коп. до 99 руб. 95 коп., а второй, наоборот, повысить цену с 95 руб до 97 руб.66 коп. Данная точка является равновесием Нэша для обеих фирм, и им не выгодно отклонятся от этих конкурентных цен на свою сувенирную продукцию.

В этом случае, если конкурентная цена устанавливается равной предельным издержкам, то ни одна из компаний не получит прибыли. С другой стороны, если одна из фирм устанавливает цену, соответствующую предельным издержкам, а вторая фирма поднимает свою цену выше себестоимости единицы продукции, то прибыли просто не будет, так как все покупатели обратятся к первой фирме, устанавливающей ту же цену ниже. Равновесия не будет в сценарии с фирмами, устанавливающими различные цены.

Таким образом, равновесие в модели Бертрана существует, в случае, когда обе фирмы устанавливают именно конкурентную цену. Важно отметить, что равновесие Нэша в этой модели является слабым. Конкуренты не будут в проигрыше, если отклонятся от конкурентной цены. Эта ситуация экономически «безопасна». В данном равновесии каждая фирма может заработать не более, чем нулевая прибыль, но при условии, что конкурент установит свою цену и будет удовлетворять все потребности потребителей по этой цене.

Важно отметить, самой выигрышной стратегией в этом случае будет кооперация обоих конкурентов, тогда они смогут установить монопольную цену. На практике это может быть невозможно, поэтому применение данной модели будет зависеть от способности договориться.

Основные результаты

В соответствии со значениями издержек конкурирующих фирм 1 и 2, выпускающих одинаковую линейку сувенирных товаров, с помощью интерполяции были получены функции издержек обеих компаний, зависящие от параметра 1. Была решена задача на нахождение максимума прибыли для каждой компании. В результате решения была получена точка пересечения графиков прибыли, ее координаты (-0.0027 ; 6.52). Взяв положительное значение ^

несложно определить ординату, координаты (6.52;28.79) – это положение, при котором стратегия обоих конкурентов «попадает» в состояние равновесия по Нэшу, то есть она является оптимальной по времени для продажи товара каждой из фирм.

На рис.1 по оси абсцисс обозначены месяцы 2020 года, точка t * — 6.52 соответствует концу июня, началу июля. Именно это время будет оптимальным для продажи продукции в условиях конкуренции и дуополии.

Данный результат вполне объясним тем, что именно это время является туристическим сезоном, и сувенирная продукция достаточно востребована.

Значит, два крупных конкурента, производящих линейку однородной сувенирной продукции получат максимальную прибыль в этот период времени, не смотря на тот факт, что каждая из них захочет максимизировать прибыль.

Модель Бертрана позволила рассчитать конкурентную цену для продажи сувенирной продукции в обозначенный период времени. Равновесие Нэша в данной модели – это цены, которые обеспечат максимальную прибыль обеим фирмам, с — 99.95; с — 97.66.

Заключение

На примере конкуренции двух крупных производителей однородной продукции сувениров на рынке был получен достаточно простой результат, объясняющий «удобное» время продаж. Данный сценарий интересен тем, что постановка дуополии Курно позволяет найти равновесие не по цене или объему выпускаемой продукции, а по параметру времени. Без использования статистических методов прогнозирования и учитывая конфликт, именно дуополии позволяют построить достаточно точный прогноз.

Можно сделать важный вывод о том, что в данной постановке под равновесием в дуополии Курно понимается такой период времени в сочетании с объемом продаж для каждого из фирм-конкурентов, при котором ни у одной из них отсутствует мотивация изменять свои стратегии. Прибыль каждой фирмы максимальна в этой точке, при условии, что конкурент будет продавать в этот же момент времени. Иначе: в точке равновесия дуополии Курно ожидаемый конкурентами сезон продаж запланированного объема продукции любой из фирм совпадает с фактическим, являясь оптимальным. Наличие равновесия в таком сценарии модели Курно говорит о том, что олигополия, как часть и вид рынка допускает устойчивость по времени.

Математическая теория игр позволяет, используя относительно несложный математический аппарат, получить простой и ясный для понимания результат для дуополистов. Одним из важных событий для достижения равновесия является предсказуемость стратегий фирмы-конкурента. Однако именно это может усложнить практическую реализацию данной модели, так как в условиях «экономических соревнований» оценить будущие стратегии соперника может быть проблематично.

Для данного сценария с помощью модели Бертрана получены конкурентные цены, выгодные с точки зрения получения максимальной прибыли.

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Важно подчеркнуть, что данные результаты были получены без статистического аппарата.

Конфликт интересов Conflict of Interest

Не указан. None declared.

Список литературы / References

1. Беллман Р. Динамическое программирование. – М.: Изд-во иностр. Лит., 2009. – 400 с.

2. Мазалов В.В Переговоры. Математическая теория./В.В. Мазалов, А.Э. Менчер, Ю.С. Токарева. – Спб.:Лань,

2012. – 304 с.

3. Мазалов В.В. Математическая теория игр и приложения. Спб.: Лань, 2016. – 448 с.

4. Петросян, Л.А. Теория игр: учеб. пособие для ун-тов / Л.А. Петросян, Н.А. Зенкевич, Е.А. Семина. – М.: Высшая школа, Книжный дом «Университет», 1998. – 304 с.

5. Райзберг Б.А. Современный экономический словарь / Б.А. Райзберг, Л.Ш. Лозовский, Е.Б. Стародубцева. – 6-е изд., перераб. и доп. – М. «ИНФРА-М», 2011

6. Самарский А.А. Теория разностных схем.- М.: Наука, 2009. – 616 с.

7. Экономика: учебник / Под ред. А.И. Архипова, А.К. Большакова. 3-е изд., перераб. и доп. – Москва: Проспект,

2013. – 848 с.

8. Экономическая теория: учебник / Под ред. А.И. Архипова, С.С. Ильина. – М.: ТК Велби, Изд-во Проспект, 2008.

– 608 с.

Список литературы на английском языке / References in English

1. Bellman R. Dinamicheskoe programmirovanie [Dynamic programming]. – Moscow: Izd-vo Inostr. Lit., 2009. – 400 p.

2. Mazalov V.V. Peregovory. Matematicheskaja teorija [Negotiations. The mathematical theory] /V. V. Mazalov, A. E. Mencher, J. S. Tokareva. Saint Petersburg: LAN, 2012. 304 p.

3. Mazalov V. V. Matematicheskaja teorija igr i prilozhenija [Mathematical theory of games and applications]. Saint Petersburg: LAN, 2016. – 448 p.

4. Petrosyan, L. A. Teorija igr: ucheb. posobie dlja un-tov [Game Theory: textbook. manual for Universities] / L. A. Petrosyan, N. A. Zenkevich, E. A. Semina. – M.: Higher school, book house “University”, 1998. – 304 p.

5. Raizberg B. A. Sovremennyj jekonomicheskij slovar’ [Modern economic dictionary] / B.A. Rajzberg, L.Sh. Lozovskij, E.B. Starodubceva. – 6th ed., reprint. and additional-M. “INFRA-M”, 2011

6. Samarsky A. A. Teorija raznostnyh shem [Theory of difference schemes]. – Moscow: Nauka, 2009. – 616 p.

7. Jekonomika: uchebnik [Economy: textbook]. ed by A. I. Arkhipov and A. K. Bolshakov. 3rd ed., reprint. and additional

– Moscow: Prospect, 2013. – 848 p.

8. Jekonomicheskaja teorija: uchebnik [Economic theory: textbook] /ed by A. I. Arkhipov, S. S. Ilyin, Moscow: TC velby, Prospekt publishing House, 2008, 608 p.