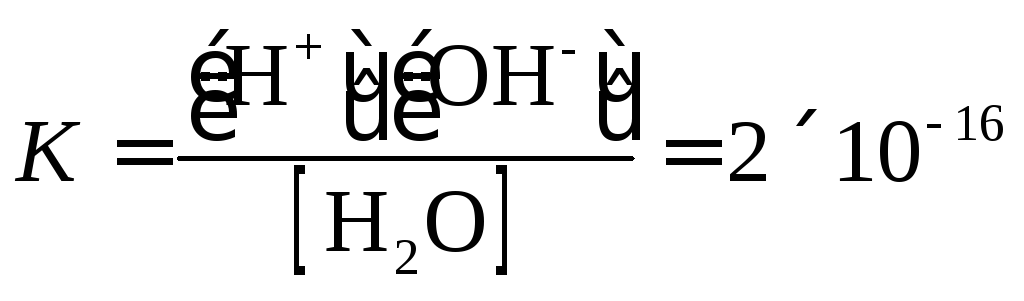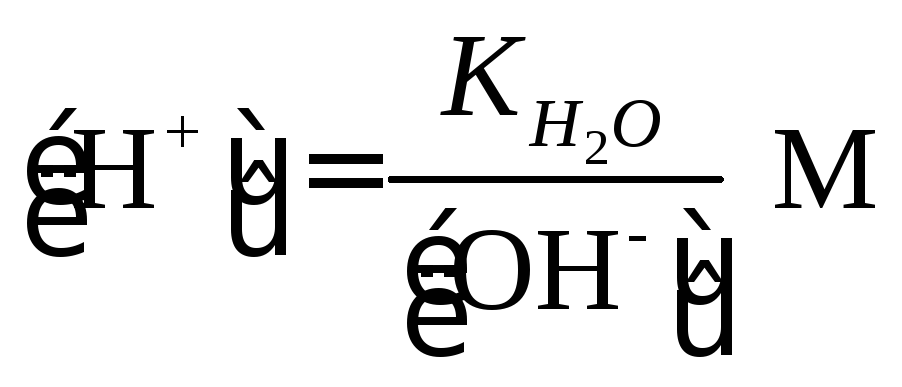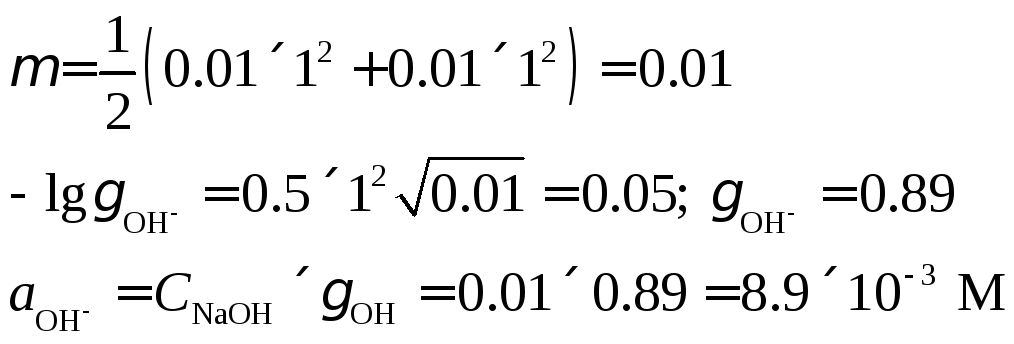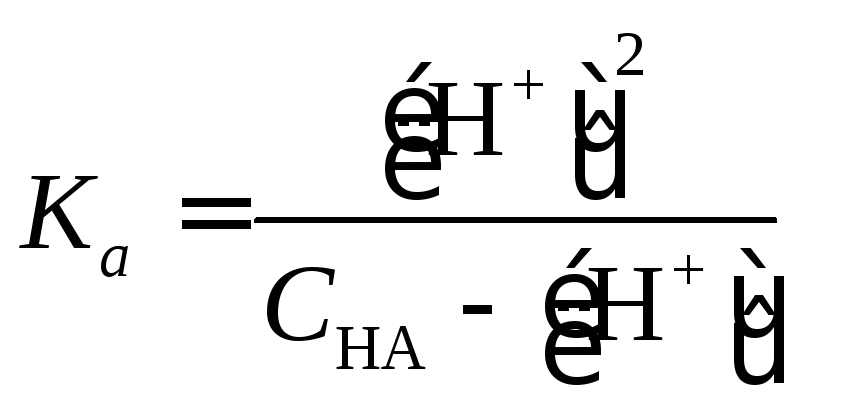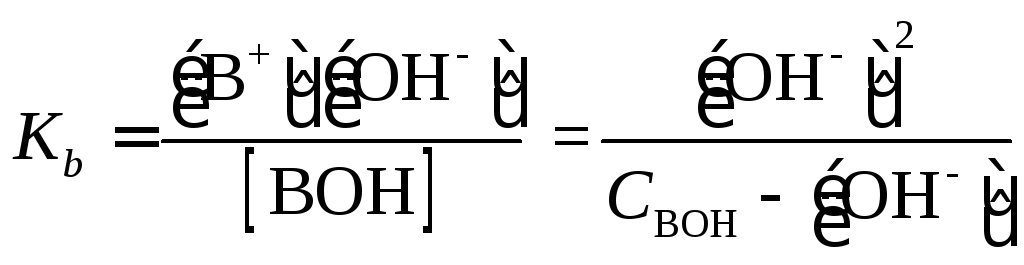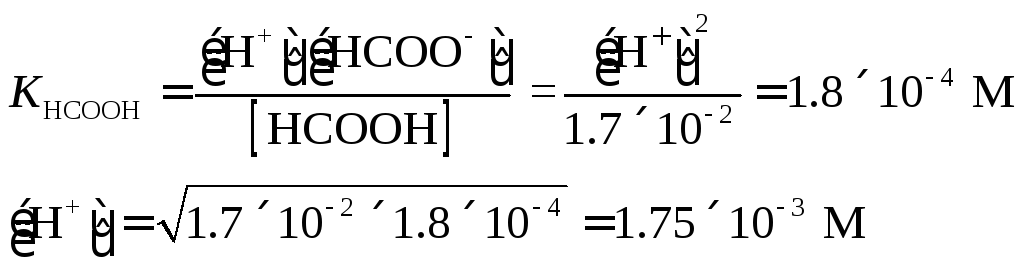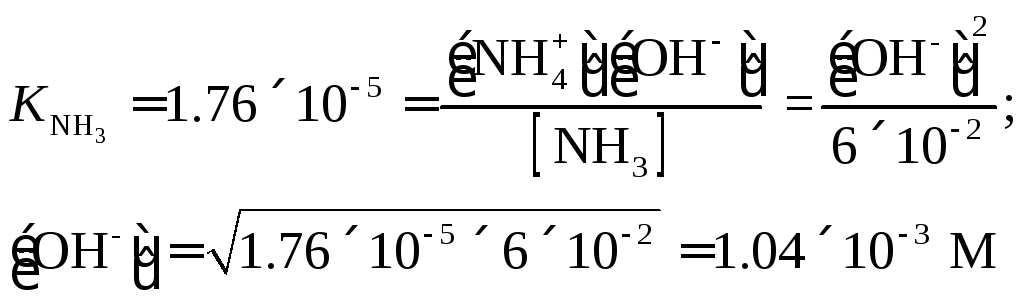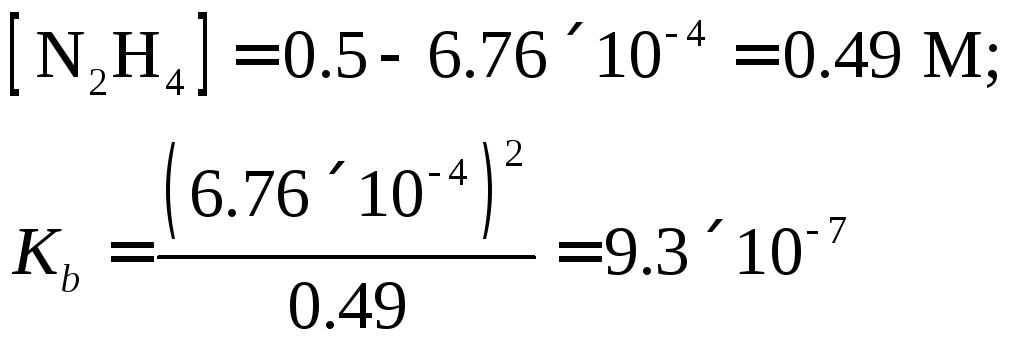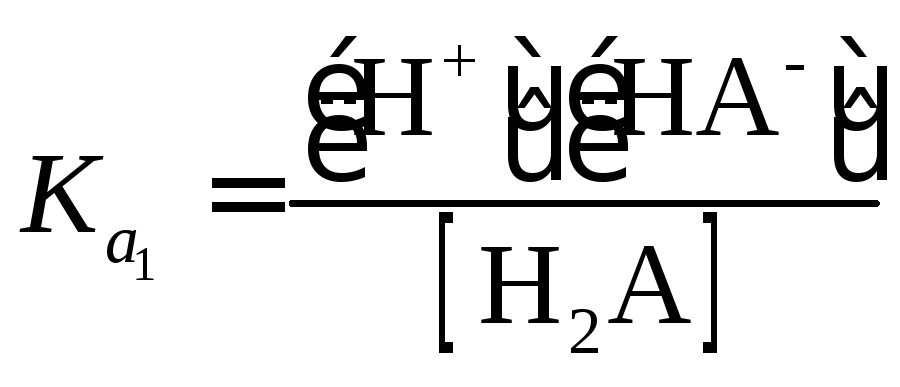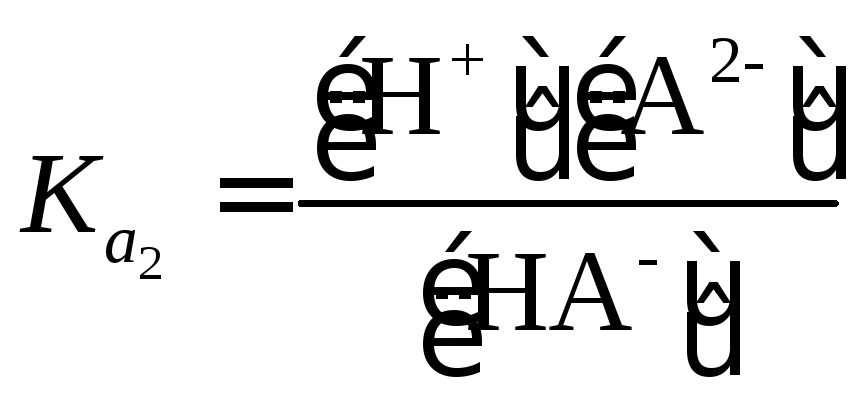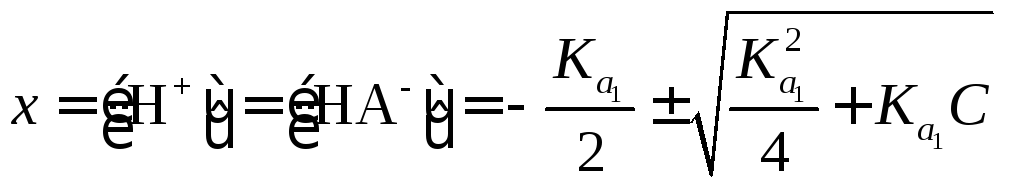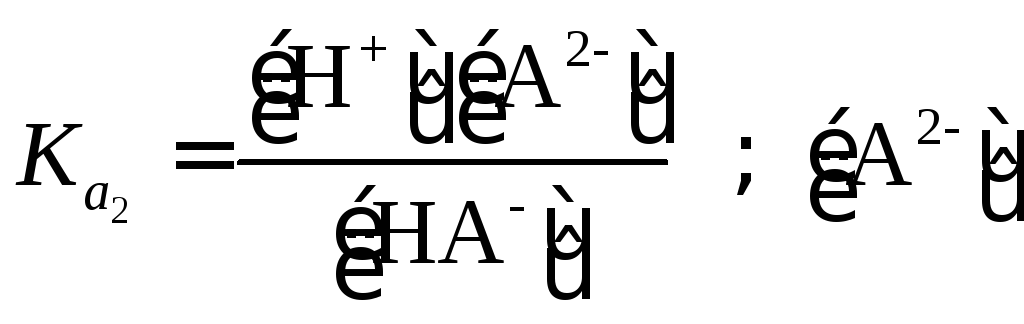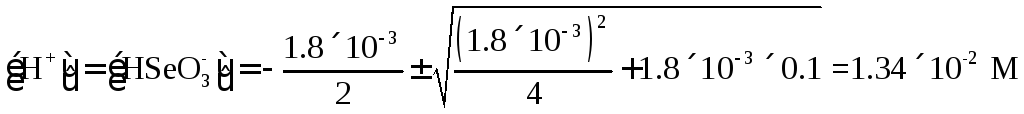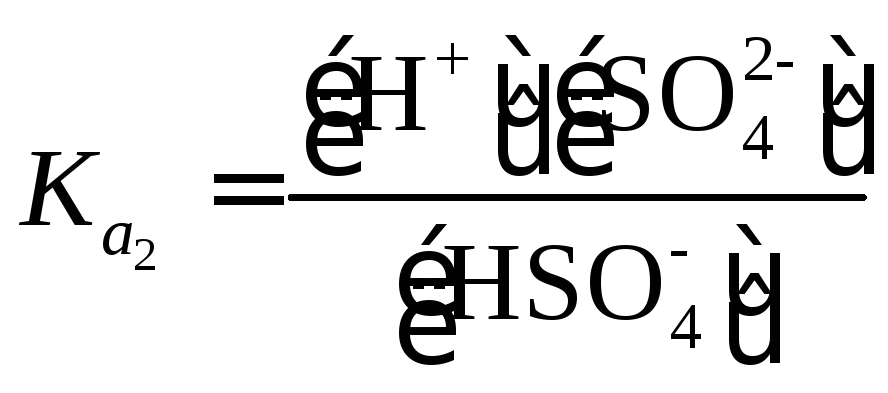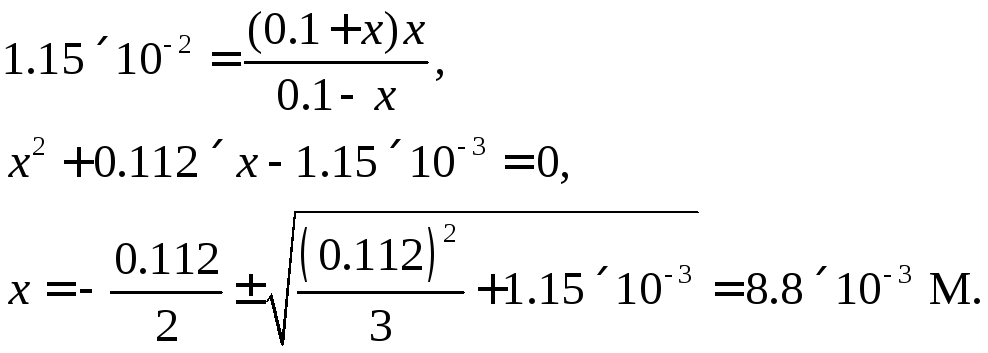Как найти равновесную концентрацию кислоты

1.1. Равновесия в водных растворах кислот и оснований

Согласно
протолитической теории к кислотам
относятся химические соединения,
способные в растворах отдавать протоны,
а к основаниям – вещества, способные
присоединять протоны. Для того чтобы
кислота могла отдать протон, необходимо
присутствие основания, принимающего
этот протон. Отдавая протон, кислота
образует сопряженное с ней основание,
а основание, принимая протон, образует
сопряженную с ним кислоту.

В водных растворах
кислот имеет место следующее равновесие:

(1.1)

В воде, которая
является кислотой и основанием
одновременно, устанавливается равновесие

(1.2)

в сокращенном виде

(1.3)

Константа равновесия
этой реакции при температуре 25° С равна

(1.4)

В
водных растворах масса воды в большинстве
случаев очень велика по сравнению с
массой растворенного вещества, количество
ее в 1 л раствора можно считать постоянным.
Тогда выражение для константы равновесия
запишется следующим образом:

К
[Н₂О]
= [Н⁺]
[ОН^–] (1.5)

Из
уравнения (1.5) следует, что ионное
произведение является величиной
постоянной при постоянной температуре.
Эту константу называют ионным произведением
воды, которое при температуре 25° С равно

(1.6)

В
чистой воде [H⁺]
= [OH^–]
= 1×10^-7
M
. При избытке [OH^–]

(1.7)

При
избытке [Н⁺]

(1.8)

Концентрацию
водородных ионов обычно используют для
характеристики среды. В большинстве
расчетов, относящихся к кислотно-основному
равновесию, концентрации (и другие
величины) удобно выражать в виде
отрицательных логарифмов этих величин,
обозначаемых знаком “р”. Тогда

-lg[H+] = pH	(1.9)
-lg[OH-] = pOH	(1.10)

Ионное произведение
воды тоже можно выразить в логарифмическом
виде

рН + рОН = = 14

(1.11)

Пример
1.
Вычислить рН раствора, концентрация
водородных ионов в котором равна 0.02 М.

Решение.

рН =
– lg[Н⁺]
= -lg(2×10^-2)
= 1.70

Решая
обратную задачу, по известному значению
рН легко найти концентрации водородных
и гидроксид-ионов.

Пример
2.
Вычислить [Н⁺]
и [ОН^–]
раствора, рН которого равен 10.33.

Решение.

[Н⁺]
= 1×10^-10.33
=
4.7×10^-11
М.

рОН =
14 – 10.33 = 3.67.

[ОН^–]
= 1×10^-3.67
= 2.1×10^-4
М.

Сильные
кислоты (НХ) и сильные основания (МОН) в
водных растворах практически полностью
диссоциированы.

HX = H+ + X–	(1.12)
MOH = M+ + OH–	(1.13)

Концентрации
Н⁺
и ОН^–
в этих растворах в первом приближении
можно считать равными общей концентрации
С_А
кислоты (НХ) и соответственно основания
(МОН). Следовательно,

pH = -lgCHX	(1.14)
pOH = -lgCMOH	(1.15)

Эти
выражения являются приближенными. В
более строгих расчетах концентрацию
электролитов следует заменять активностью
ионов. Между концентрацией иона и
активностью его существует следующая
зависимость:

aA = γA×CA

(1.16)

где
γ_A
–
коэффициент
активности. Коэффициент активности
зависит от ионной силы раствора (μ)

(1.17)

где

–
концентрации ионов – катионов и анионов
(М),
–
заряды ионов.

Если

,
коэффициент активности в водных
растворах рассчитывается по формуле

(1.18)

При

расчет
проводится по более сложному уравнению

(1.19)

Для
сильных электролитов только в очень
разбавленных растворах (~ 0.0001 М) γ_A
= 1 и а_А
= С_А.
Коэффициент активности можно не учитывать
также для недиссоциированных молекул.

Для
простоты расчетов в дальнейшем во всех
случаях, кроме оговоренных, вместо
активностей используются концентрации.

Пример
3.
Вычислить рН 0.0018%-ного раствора
хлороводородной кислоты.

Решение.
Найдем концентрацию НС1, выраженную в
М, учитывая, что молекулярная масса НС1
36.46:

рН = –
lg(4.94×10^-4)
= 3.31.

Пример
4. В
250 мл раствора содержится 0.1 г гидроксида
натрия. Вычислить рН раствора.

Решение.
Найдем концентрацию NaOH,
выраженную в моль/л. Молекулярная масса
NaOH
40.

Ионная
сила 0.01 М раствора гидроксида натрия
равна:

pOH
= -lg(8.9×10^-3)
= 2.05

pH
= 14-2.05 = 11.95

Пример
5.
К 3 л воды прибавлен 1 г HNO₃
(ρ
= l.4).
Вычислить рН раствора.

Решение.
По таблицам находим, что в 100 г азотной
кислоты (ρ
= 1.4) содержится 65.3 г HNO₃.
Тогда концентрация HNO₃
в М будет равна

pH
= -lg(3.4×10^-3)
= 2.47

В
случае слабых кислот константа равновесия
реакции {1.2) может быть выражена следующим
уравнением:

(1.20)

где
К_а
–
константа диссоциации кислоты НА.

Если
общую концентрацию кислоты обозначить
С_НА,
а равновесную [НА], то

[НА] = СНА – [Н+].

(1.21)

Из
уравнения (1.2) следует, что [Н⁺]
= [А^–].
Тогда выражение константы диссоциации
слабой кислоты можно записать следующим
образом:

(1.22)

Отсюда
легко найти концентрацию [Н⁺]

(1.23)

Если
кислота диссоциирована в незначительной
степени (),
то приближенно можно считать, что.

	(1.24)
	(1.25)

Слабое
основание, как и слабая кислота, в водных
растворах диссоциирует неполностью

(1.26)

как и для слабой
кислоты,

[BOH] = СBOH – [OН–].

(1.27)

Поскольку
[В⁺]
= [ОН^–],
уравнение для константы диссоциации
слабого основания будет иметь вид

(1.28)

и

(1.29)

Когда
[OH^–]
<< С_вон
(10²
[ОН^–]
< С_вон),
можно принять

	(1.30)
	(1.31)
	(1.32)

Пример
6. Вычислить
рН 0.017 М раствора муравьиной кислоты.

Решение.

C_HCOOH
= 0. = 1.7×10^-2
М

рН = -lg(1.7×10^-3
) = 2.76.

Пример
7. Вычислить
рН 0.06 М раствора аммиака.

Решение.

=
0.06
= 6×10^-2
М

рOН
= -lg(1.04×10^-3
) = 2.98; pH
= 14 – pOH
= 11.02.

Диссоциация
слабых электролитов количественно
характеризуется также степенью
электролитической диссоциации (α).
Степень диссоциации представляет собой
отношение концентрации вещества,
распавшегося на ионы, к общей его
концентрации в растворе. Между константой
диссоциации электролита К_А
и
α существует следующая зависимость:

(1.33)

где С
– молярная концентрация слабого~электролита.
Если α мала (α < 5%), применимо приближенное
уравнение ,
откуда

(1.33)

Пример
8.
Вычислить степень диссоциации муравьиной
кислоты в 1.5%-ном растворе.

Решение.
Находим молярную концентрацию НСООН
(М. м. = 46)

Формиат-ион
и ион водорода образуются только в
результате диссоциации муравьиной
кислоты, следовательно, их концентрации
равны

[H⁺]
= [HCOО^–]
=
х
M,

[НСООН]
= (3.26×10^-1–
х)
М,
отсюда

Если
концентрация диссоциированной части
мала по сравнению с общей концентрацией
кислоты, то в знаменателе ею, как
алгебраическим слагаемым, можно
пренебречь. Тогда

Пример
9. При
какой концентрации бензойная кислота
диссоциирована на 10%?

Решение.
Если неизвестную общую концентрацию
обозначить
,
то концентрация каждого из ионов будет
равна

[Н⁺]
= [С₆Н₅СОО^–]
=
,

а
концентрация недиссоциированной части
будет составлять

[С₆Н₅СООН]
=С(1
– 1×10^-1)
= 9×10^-1
С
М ,

отсюда

или

Пример
10. Уксусная
кислота в 3%-ном растворе диссоциирована
на 0.59 %. Вычислить приближенное значение
константы диссоциации.

Решение.
Находим молярную концентрацию СН₃СООН
(М. м. = 60.05).

Пример
11. 0.5
М раствор гидразина имеет рН = 10.83.
Вычислить константу диссоциации
гидразина.

Решение.

рОН =
14-10.83 = 3.17; [ОН^–]
= 1×10^-3.17
= 6.76×10^-4
М,

Многоосновные
кислоты (H₂SO₄,
H₂SO₃,
H₂CO₃,
Н₂С₂О₄,
Н₃РО₄
и др.) в водных растворах диссоциируют
ступенчато

	(1.35)
	(1.36)
	(1.37)
	(1.38)

Константы
диссоциации по первой ступени всегда
больше, чем по второй ступени:
.
Если
во
много раз больше()
то
концентрация ионов водорода определяется
главным образом диссоциацией кислоты
по первой ступени.

Обозначим
через х
концентрацию
диссоциированной части кислоты. Тогда,
при начальной концентрации кислоты С
равновесные
концентрации будут равны

[Н₂А]
= С-
х
М;

[Н⁺]
= х
М;

[HA-]
= х
М.

Подставив
эти значения в уравнение (1.36), получим:

(1.39)

отсюда

(1.40)

Если
мала,
то приближенно можно считать, что

(1.41)

Поскольку
[Н⁺]~[НА^–],
то из уравнения (1.38) находим

(1.42)

Пример
12. Вычислить
концентрацию ионов водорода и анионов
в 0.1 М растворе селенистой кислоты (К₁
=l.8×10^-3,
К₂
= 3.2×10^-9).

Решение.
Вычисляем концентрацию Н⁺и
НSeО₃^–
по уравнению (1 40)

Концентрация
SeO₃^2-
равна
(3.2×10^-9
M).

Особо
следует рассмотреть равновесия в
растворе серной кислоты. По первой
ступени H₂SO₄
диссоциирует полностью. По второй
ступени константа диссоциации равна
1.15×10^-2.

(1.43)

Пример
13. Найти
концентрации H⁺,
HSO₄^–
и SO₄^2-
в 0.1 М растворе H₂SO₄.

Решение.
Диссоциация H₂SO₄
может быть представлена следующими
уравнениями:

Обозначим
концентрацию SO₄^2-
через х.
Общая
концентрация Н⁺
может быть выражена как сумма начальной
концентрации H₂SO₄
(в соответствии с диссоциацией по первой
ступени) и концентрации SO₄^2-,
образующихся по второй ступени

[Н⁺]
= 0.1 + х

Очевидно,
что концентрация HSO₄^–
будет равна разности между начальной
концентрацией H₂SO₄
и концентрацией SO₄^2-

[HSO₄^–]
= 0.l
– х

Подставляя эти
данные в уравнение (1.43), получим

Следовательно,

[SO₄^2-]
= 8.8×10^-3
M

[Н⁺]
= 0.109 М,

[HSO₄^–]
= 0.091 М.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как вычислить равновесную концентрацию

В ходе химической реакции устанавливается равновесие, когда скорость прямой реакции (в ходе которой исходные вещества превращаются в продукты) становится равной скорости обратной реакции (когда продукты превращаются в исходные вещества). Концентрации всех этих веществ тогда называются равновесными.

Инструкция

В первую очередь вспомните, что такое константа равновесия. Это – величина, характеризующая отношение концентраций (или парциальных давлений) продуктов реакции к концентрациям исходных веществ. Например, если реакция протекает по схеме: А + В = С + D, то Кр = [C][D]/[A][B].

Если же схема протекания реакции такая: 2А + В = 2С, то Кр вычисляется по такой формуле:[C]^2/[B][A]^2. То есть индексы превращаются в показатель степени, в которую нужно возвести концентрацию того или иного компонента.

Рассмотрите пример. Предположим, протекает та самая первая реакция: А + B = C + D. Требуется определить равновесные концентрации всех компонентов, если известно, что начальные концентрации исходных веществ А и В были равны 2 моль/литр, а константа равновесия может быть принята за 1.

Снова запишите формулу константы равновесия для этого конкретного случая: Кр = [C][D]/[A][B]. Учитывая, что Кр = 1, получите: [C][D] = [A][B].

Начальные концентрации веществ А и В вам известны (заданы по условиям задачи). Начальные концентрации продуктов реакции С и D были равны 0, а потом увеличились до неких равновесных значений. Обозначьте равновесную концентрацию вещества С за х, тогда равновесная концентрация вещества А (из которого образовалось С) будет равна (2-х).

Поскольку схема реакции свидетельствует, что из 1 моля вещества А образуется 1 моль вещества С, а из 1 моля вещества В – 1 моль вещества D, то, соответственно, равновесная концентрация D также будет = х, а равновесная концентрация В = (2-х).

Подставив эти величины в формулу, получите: (2-х) (2-х) = х^2. Решив это уравнение, получите: 4х = 4, то есть, х = 1.

Следовательно, равновесные концентрации продуктов реакции C и D равны 1 моль/литр. Но поскольку равновесные концентрации исходных веществ А и В вычисляются по формуле (2-х), то и они также будут равны 1 моль/литр. Задача решена.

Источники:

• Обратимые и необратимые процессы

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Задание 23 в ЕГЭ по химии 2022 года – принципиально новое, вот, что написано в спецификации экзамена:

Давайте разберем, необходимую для решения задания теорию:

Обратимые реакции – это реакции, в которых при одних и тех же условиях реагенты превращаются в продукты и продукты в реагенты (в записи реакции это отражают двумя противоположно направленными стрелочками), например:

В реактор мы помещаем азот N₂ и водород H₂ (идет только прямая реакция), как только в системе появляется аммиак NH₃ – он начинает разлагаться (начинается обратная реакция).

И в какой-то момент система приходит к состоянию равновесия: сколько аммиака образовалось в прямой реакции, столько и разложилось в обратной. Значит, несмотря на то, что прямая и обратная реакции непрерывно идут – концентрации веществ остаются постоянными (равновесные концентрации).

Расчёт равновесных концентраций:

Как мы уже разобрали, понятие равновесие завязано на понятии скорости реакции, поэтому и расчет равновесных концентраций будет идти через расчет скоростей прямой и обратной реакции.

Решим задание из демо-версии:

Фраза “реактор постоянного объема” дана для вашей уверенности, что концентрация будет изменяться только в процессе химических реакций, давление и объем системы – постоянные величины, следовательно мы может оперировать концентрацией так же, как количеством вещества. И решается это задание, как стандартная расчетная задача по уравнению реакции:

Вся информация о начальной и конечной концентрации вещества известна для продукта реакции – SO₃:

Начальная концентрация C1 = 0 моль/л

Равновесная концентрация С2 = 0,4 моль/л

Ответ: 25

Реши еще одно задание самостоятельно – ответы пиши в комментарии:

23.1

В реактор постоянного объема поместили некоторое количество водорода и йода. В результате протекания обратимой реакции

H₂ + I₂ = 2 HI

В реакционной системе установилось химическое равновесие.

Используя данные, приведенные в таблице, определите равновесные концентрации H₂ (Х) и HI (Y)

Выберите из списка номера правильных ответов.

1) 0,025 моль/л

2) 0,05 моль/л

3) 0,1 моль/л

4) 0,15 моль/л

5) 0,2 моль/л

6) 0,3 моль/л



Большинство химических реакций, протекающих в разбавленных растворах слабых электролитов, основаны на равновесных процессах с участием ионов. Правильный расчет физико-химических равновесий позволяет контролировать и управлять химическими реакциями, а также создавать необходимые условия для оптимального протекания технологических процессов, качественных и количественных аналитических определений.

В данной статье приведены основы математического расчета различных химических равновесий, условий и полноты протекания реакций и определения равновесных концентраций веществ в реагирующих системах.

Ключевые слова: химическое равновесие, равновесная концентрация, константа ионизации, слабая кислота, слабое основание, ступенчатая диссоциация, материальный баланс, фосфорная кислота, гидрат аммиака, константа автопротолиза, ионное произведение воды, гидролиз солей, константа гидролиза, произведение растворимости солей

Keywords. Chemical equilibrium, equilibrium concentration, ionization constant, weak acid, weak base, stepwise dissociation, material balance, phosphoric acid, ammonium hydroxide, autoprotolysis constant, ionic product of water, hydrolysis of salts, hydrolysis constant, solubility product of salts.

Рассмотрение вопросов о расчете химических равновесий начнем с конкретных примеров.

Задача 1. Вычислить концентрацию продуктов ступенчатой диссоциации ортофосфорной кислоты в 0,1 М водном растворе. Рассчитать степень диссоциации кислоты в этом растворе.

Решение. Вразбавленных водных растворах ортофосфорная кислота ведет себя как сильная кислота, однако только один из протонов отщепляется легко, и константа ионизации по первой ступени достаточно высокая. Вторая и третья константы ионизации последовательно снижаются на пять порядков.

Запишем уравнения ступенчатой диссоциации ортофосфорной кислоты:

(I ступень) H₃PO₄ + H₂O H₃O⁺ + H₂PO₄^–, ;

(II ступень) H₂PO₄^– + H₂O H₃O⁺ + HPO₄^2–, ;

(III ступень) HPO₄^2– + H₂O H₃O⁺ + PO₄^3–, .

Здесь и далее pK = — lgK_равн — логарифмический показатель констант равновесия, а все расчеты проводятся для стандартных состояний веществ и t=25°C.

С учетом всех трех стадий ступенчатой диссоциации фосфорной кислоты можно составить уравнение материального баланса. Одним из условий материального баланса является неизменность содержания определенного вида атомов (или групп атомов) в процессе химического превращения веществ в изолированной системе. Например, водород в рассматриваемой системе находится в виде гидратированных ионов H₃O⁺ и входит в состав ионов H₂PO₄^–, HPO₄^2–, а также электронейтральных молекул H₃PO₄. Математическая запись этого условия выглядит следующим образом:

.

Баланс по числу атомов фосфора можно представить в следующем виде:

.

Каждое химическое равновесие характеризуется своей константой равновесия. Для рассматриваемых случаев — это ступенчатые константы ионизации:

;

;

.

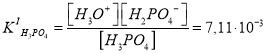
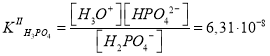
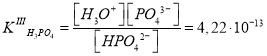
Поскольку значения и различаются приблизительно в 10⁵ раз, концентрацию протонов можно вычислить с учетом диссоциации H₃PO₄ только по первой ступени. Данное допущение не вызывает больших погрешностей расчетов, если многоосновной кислоты превышает примерно в 10³ раз и более.

Предположим, что в процессе диссоциации фосфорной кислоты по первой ступени образуется равное количество ионов H⁺ и H₂PO₄^–, а их равновесную концентрацию обозначим x моль/л. Тогда равновесная концентрация фосфорной кислоты составит (0,1 — x), моль/л:

H₃PO₄ + H₂O H₃O⁺ + H₂PO₄^–

(0,1 – x) xx

Подставим равновесные концентрации этих ионов в выражение для константы равновесия :

,

или .

Решая квадратное уравнение, получаем:

моль/л.

В том случае, если кислота очень слабая, то [H⁺]<0_HA и C⁰_HA — [H⁺] ≈ C⁰_HA. Равновесную концентрацию протонов в таких растворах вычисляют по следующей формуле:

.

Данное допущение оправдано для кислот с pK≥4 (при условии, что C⁰_HA˃˃K_HA). Концентрация иона H₂PO₄^– практически определяется диссоциацией фосфорной кислоты по I ступени: [H₂PO₄^–] = [H₃O⁺] = 2,33·10^–2 моль/л.

Значения и различаются в 10⁵ раз, поэтому концентрацию иона HPO₄^2– определим с учетом диссоциации кислоты по II ступени:

моль/л.

Концентрация аниона, образующегося в результате диссоциации слабой кислоты H₂A по II ступени, численно равна , т. е. [A^2–] =·(H₂A).

Зная равновесные концентрации ионов H₃O⁺ и HPO₄^2–, вычислим концентрацию иона PO₄^3–:

(или 1,14·10^–18моль/л).

По равновесным концентрациям продуктов диссоциации фосфорной кислоты найдем степень диссоциации (α) по всем трем ступеням:

или 23,3 %;

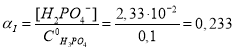
или 2,7·10^–4 %;

или 1,8·10^–9 %.

В растворах, где [H₃O⁺]<0_HA, степень диссоциации (α) можно определить по следующему уравнению:

.

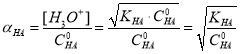
Математическими расчетами были определены области преобладания частиц в водном растворе ортофосфорной кислоты в зависимости от pH среды: H₃PO₄: 0 ≤ pH ≤ 2,12; H₂PO₄^–: 2,12 ≤ pH ≤ 7,21; HPO₄^2–: 7,21 ≤ pH ≤ 12; PO₄^3–: 12 ≤ pH ≤ 14.

Задача 2. Определите, какие продукты будут образовываться при взаимодействии ортофосфорной кислоты и гидрата аммиака в разбавленном водном растворе.

Решение. Для ответа на вопрос рассчитаем константу равновесия следующей реакции в предположении того, что гидрат аммиака (NH₃·H₂O) как основание отщепляет от фосфорной кислоты сразу три протона:

H₃PO₄ + 3 NH₃·H₂O 3 NH₄⁺ + PO₄^3– + 3 H₂O.

С учетом закона действующих масс константу равновесия можно записать в следующем виде:

;

или .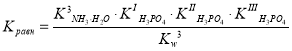

К данному выражению мы пришли с учетом следующих допущений:

а) в водном растворе происходит диссоциация гидрата аммиака:

3 NH₃·H₂O 3 NH₄⁺ + 3 OH^–.

Запишем выражение для константы равновесия данной реакции:

;

выражение носит название константы диссоциации (ионизации) основания NH₃·H₂O.

б) В водном растворе происходит ионизация молекул фосфорной кислоты:

H₃PO₄ + 3 H₂O 3 H₃O⁺ + PO₄^3–.

Запишем выражение для константы равновесия данной реакции с учетом выражений для констант диссоциации фосфорной кислоты по трем ступеням:

.

После преобразований получаем следующее равенство:

,

.

в) Вода (H₂O) — слабый электролит и в незначительной степени подвергается ионизации. Этот процесс называется автопротолизом. Схематично его можно представить так:

H₂O + H₂O H₃O⁺ + OH^–.

Константу равновесия автопротолиза представим в следующем виде:

.

Посредствам измерения электропроводности абсолютно чистой воды было показано, что концентрации ионов H₃O⁺ и OH^– составляют 10^–7 моль/л, а концентрация молекул H₂O составляет 1000/18 = 55,56 моль/л. Отсюда была вычислена константа автопротолиза воды:

.

Диссоциация воды весьма незначительна, поэтому ее концентрацию считают практически неизменной, и выражение для константы диссоциации воды можно представить в следующем виде:

.

Иными словами, произведение концентрации ионов, образующихся в процессе диссоциации воды — есть величина постоянная при данной температуре (25°C), и данная константа называется ионным произведением воды K_w.

С учетом приведенных выше уточнений (а — в) рассчитаем константу равновесия реакции:

.

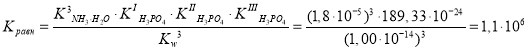
Величина Kравн служит характеристикой необратимости реакции в данных условиях. Так, если значение Kравн очень велико, то это означает, что при равновесии, концентрации продуктов реакции намного превышают концентрации исходных веществ, и реакция прошла почти до конца, — слева направо.

Предположим, что гидрат аммиака отщепляет от фосфорной кислоты один протон. Рассчитаем константу равновесия данной реакции с учетом представленных выше допущений.

H₃PO₄ + NH₃·H₂O H₂PO₄^– + NH₄⁺ + H₂O.

,

.

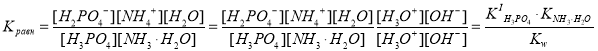
Расчет показал, что химическое равновесие существенно смещено вправо, и реакция в стандартных условиях идет до конца, поскольку значение константы равновесия этой реакции также достаточно велико (K_равн˃˃1).

Пусть на следующей стадии процесса происходит отщепление второго протона. Рассчитаем вероятность этого процесса и сравним с рассмотренными случаями.

H₂PO₄^– + NH₃·H₂O HPO₄^2– + NH₄⁺ + H₂O.

,

.

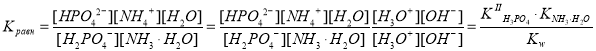
Расчет показывает, что данная стадия также термодинамически вероятна, поскольку значение константы равновесия положительное, и равновесие существенно смещено вправо, однако величина константы равновесия на пять порядков ниже. Это свидетельствует о меньшей вероятности протекания данного процесса по сравнению с предыдущей реакцией.

Наконец, если предположить отщепление третьего протона на следующей стадии, то реакцию можно представить в следующем виде:

HPO₄^2– + NH₃·H₂O PO₄^3– + NH₄⁺ + H₂O.

,

.

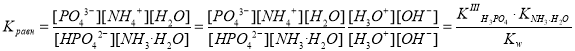
Величина константы равновесия данной реакции свидетельствует о ее неполном прохождении. Равновесие существенно смещено влево.

Таким образом, взаимодействие фосфорной кислоты с гидратом аммиака в основном протекает по схемам:

1) H₃PO₄ + NH₃·H₂O NH₄H₂PO₄ + H₂O,

2) NH₄H₂PO₄ + NH₃·H₂O (NH₄)₂HPO₄ + H₂O;

или H₃PO₄ + 2 NH₃·H₂O 2 (NH₄)₂HPO₄ + 2 H₂O.

Задача 3. Рассчитайте концентрации ионов H₂PO₄^– и PO₄^3– в растворе, в котором общая концентрация фосфат-ионов C⁰_n составляет 0,5 моль/л, а pH раствора равен 5.

Решение. Зная pH раствора, находим концентрацию протонов: [H₃O⁺]=10^–5 моль/л.

Для любого слабого электролита состава AH_n с учетом уравнения материального баланса (например, по числу атомов A) и выражений констант равновесия (пусть n=2 и диссоциация AH_n идет по двум ступеням), после несложных математических преобразований можно записать следующее выражение для концентрации :

.

Если – доля недиссоциированных молекул, то с учетом выражения для , получим:

.

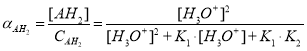
Доли продуктов диссоциации не зависят от общей концентрации электролита, а зависят от концентрации ионов H₃O⁺ и — через константы диссоциации — от природы электролита. Поэтому, если известен pH раствора, то легко можно рассчитать концентрации продуктов диссоциации.

Для любого слабого электролита состава AB₂ можно написать общее выражение знаменателя в формуле для расчета долей продуктов диссоциации (α):

[B]ⁿ + K₁· [B]^n-1 + K₁·K₂· [B]^n-2 + … + K₁·K₂…K_n-1· [B] + K₁·K₂…K_n.

Например, долю ионов AB_n-2 можно определить по следующей формуле:

.

Если из выражений констант ступенчатой диссоциации фосфорной кислоты выразить концентрации соответствующих ионов (H₂PO₄^–, HPO₄^2–, PO₄^3–) и подставить в выражение материального баланса по атомам фосфора, то можно получить следующее уравнение для истинной концентрации фосфорной кислоты :

, , ;

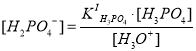
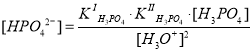
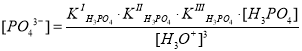
Если перед нами встала задача определения мольной доли, например, фосфорной кислоты, оставшейся в недиссоциированном (молекулярном) состоянии, нам необходимо найти отношение концентрации частиц [H₃PO₄] к суммарной концентрации всех частиц :

.

Вернемся к нашему примеру. Зная значения констант диссоциации фосфорной кислоты аналогичным образом определим долю ионов, образующихся по первой ступени (H₂PO₄^–):

;

;

.

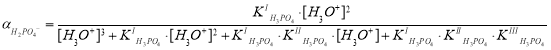
Тогда концентрацию ионов H₂PO₄^– определим следующим образом:

[H₂PO₄^–] = · C⁰_n = 0,99·0,5 = 0,495 моль/л.

Доля ионов, образующихся по второй ступени, определяется по выведенной выше формуле и после подстановки соответствующих значений составит . Концентрацию ионов PO₄^3– определим аналогично:

[PO₄^3–] = · C⁰_n = 3,3·10^–10·0,5 = 16,5·10^–11 моль/л.

Задача 4. Определить pH 0,1 М водных растворов ортогидрофосфата и ортофосфата натрия с учетом процесса гидролиза солей. Возможно ли растворение цинка в данных растворах?

Решение. а)Соль Na₂HPO₄ в водном растворе диссоциирована практически полностью:

Na₂HPO₄ → 2 Na⁺ + HPO₄^2–.

Гидрофосфат-ион (HPO₄^2–) подвергается гидролизу по первой ступени в соответствии со следующей схемой:

HPO₄^2– + H₂O H₂PO₄^– + OH^–,

далее дигидрофосфат-ион подвергается гидролизу по второй ступени:

H₂PO₄^– + H₂O H₃PO₄ + OH^–.

Запишем выражения для констант гидролиза и определим их значения:

,

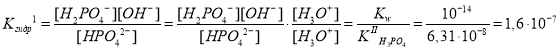
где , так как H₂PO₄^– + H₂O HPO₄^2– + H₃O⁺, а , так как H₂O + H₂O H₃O⁺ + OH^–.

.

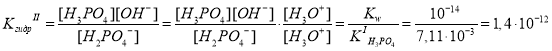
В данных расчетах, как и в предыдущих мы использовали следующий прием: умножили числитель и знаменатель дроби на концентрацию ионов H₃O⁺, тем самым пришли к выражениям для константы ионизации и константы автопротолиза.

K^I_гидр превышает K^II_гидр практически в 10⁵ раз, поэтому гидролизом по второй ступени можно пренебречь.

Гидрофосфат-ион (HPO₄^2–) диссоциирует в водном растворе по следующей схеме:

HPO₄^2– + H₂O H₃O⁺ + PO₄^3–.

Для данного процесса запишем выражение для константы равновесия:

.

Протоны, появляющиеся в результате диссоциации гидрофосфат-ионов, реагируют с OH^–-ионами, образующимися при гидролизе HPO₄^2–-иона. Учитывая, что [H₃O⁺] = [PO₄^3–] и [OH^–] = [H₂PO₄^–], равновесная концентрация протонов в растворе Na₂HPO₄ определяется разностью [H₃O⁺]= = [PO₄^3–] — [H₂PO₄^–] или [OH^–] = [H₂PO₄^–] — [PO₄^3–].

Выразим концентрацию ионов H₂PO₄^– и PO₄^3– через константы равновесий реакций гидролиза и диссоциации иона H₂PO₄^–:

,

.

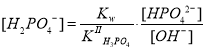
Из ионного произведения воды следует, что , поэтому после подстановки соотношение примет следующий вид:

.

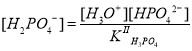
Теперь, зная концентрации фосфат- и дигидрофосфат-ионов, определим равновесную концентрацию протонов:

.

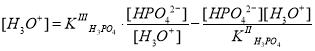
Далее, после преобразований получаем следующее уравнение:

,

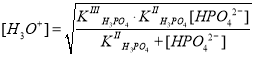
где ; она намного меньше концентрации ионов HPO₄^2– и практически равна начальной концентрации соли Na₂HPO₄, т. е. 0,1 моль/л. Поэтому сумма упрощается: , и уравнение примет следующий вид:

.

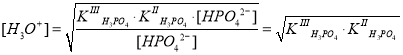
В итоге, величину pH можно определить следующим образом:

.

По данной формуле рассчитаем величину pH в 0,1 М растворе Na₂HPO₄:

.

Аналогично можно показать, что в растворе соли NaH₂PO₄ pH вычисляется по формуле:

.

б) Рассчитаем pH 0,1 М раствора Na₃PO₄. Здесь приведем упрощенный расчет. В данном случае также после диссоциации соли протекает протолиз аниона:

Na₃PO₄ 3 Na⁺ + PO₄^3–,

PO₄^3– + H₂O HPO₄^2– + OH^–.

Запишем выражение для константы равновесия:

,

откуда ,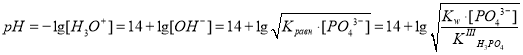

.

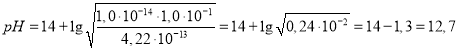
Высокие значения pH среды в данных растворах (0,1 М Na₂HPO₄ pH=9,8; 0,1 М Na₃PO₄ pH=12,7) свидетельствуют о сильнощелочной среде. В задаче стоял вопрос о растворимости цинка в этих растворах. Основываясь на знании химических свойств цинка, в частности, его способности взаимодействовать с растворами щелочей, можно предложить следующие реакции для процессов растворения цинка в растворах Na₂HPO₄ и Na₃PO₄:

2 Na₂HPO₄ + Zn + 4 H₂O = Na₂ [Zn(OH)₄] + 2 NaH₂PO₄ + H₂↑,

2 Na₃PO₄ + Zn + 4 H₂O = Na₂ [Zn(OH)₄] + 2 Na₂HPO₄ + H₂↑.

Задача 5. Вычислить без учета гидролиза и с учетом гидролиза произведение растворимости фосфата серебра , если растворимость этой соли в воде при комнатной температуре равна 4,68·10^–6 моль/л. Вычислить pH насыщенного раствора Ag₃PO₄.

Решение. Внасыщенном растворе Ag₃PO₄ существует равновесие:

Ag₃PO₄ (крист.) 3 Ag⁺ + PO₄^3–

3·4,68·10^–6 моль/л 4,68·10^–6 моль/л.

а) Если растворимость соли составляет 4,68·10^–6 моль/л, то в соответствии с уравнением процесса, но без учета гидролиза получим следующее: [PO₄^3–] = 4,68·10^–6 моль/л, а [Ag⁺] = 3· [PO₄^3–] = 3·4,68·10^–6 моль/л.

По этим данным вычислим :

.

Справочная величина составляет: .

б) Вычислим с учетом процесса гидролиза фосфата серебра.

Образующийся при растворении в воде Ag₃PO₄ ион PO₄^3– подвергается гидролизу:

PO₄^3– + H₂O HPO₄^{2 —} + OH^–

Пусть подверглось гидролизу x моль/л иона PO₄^3–, а образовалось в результате гидролиза по (4,68·10^–6 — x) моль/л ионов HPO₄^{2 –} и OH^–, соответственно.

Запишем выражение для константы гидролиза:

.

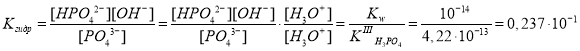
Гидролиз иона PO₄^3– по первой ступени при концентрации 4,68·10^–6 моль/л протекает практически полностью, поэтому за наименьшую равновесную концентрацию x принимаем равновесную концентрацию ионов PO₄^3–, т. е. [PO₄^3–] = x, [HPO₄^2–] = [OH^–] = 4,68·10^–6 — x, моль/л.

Подставим равновесные концентрации в выражение для константы гидролиза:

.

Допустим, что 4,68·10^–6 — x ≈ 4,68·10^–6. Тогда 2,37·10^–2 · x = (4,68·10^–6)² и x = 9,24·10^–10 моль/л. Эта величина достаточно мала и в приближенных расчетах ей можно пренебречь.

Следовательно, [OH^–] ≈ 4,68·10^–6 моль/л и pH = 14 + lg 4,68·10^–6 = 8,67.

Гидролиз Ag₃PO₄ по катиону протекает незначительно. Константа гидролиза Ag⁺ очень мала (). При [Ag⁺] = 3·4,68·10^–6 = 1,4·10^–5 моль/л и [OH^–] = 4,68·10^–6 моль/л концентрация AgOH составит: [AgOH] = β_AgOH [Ag⁺] [OH^–] = 2·10²·1,4·10^–5·4,68·10^–6 = 1,31·10^–8 моль/л, т. е. всего около 0,1 % от начальной концентрации ионов Ag⁺. Здесь β — общая константа устойчивости AgOH, которая определяет следующее равновесие:

Ag⁺ + OH^– AgOH,

.

Следовательно, поправка к pH, учитывающая гидролиз соли по катиону в насыщенном растворе Ag₃PO₄, невелика.

Рассчитаем значение произведения растворимости соли с учетом гидролиза:

.

Данное значение существенно отличается от величины, найденной без учета гидролиза соли.

На простых примерах мы убедились, что расчет химических равновесий с применением простейших алгебраических алгоритмов и приемов, позволяет предсказать принципиальную возможность (вероятность) протекания химической реакции, а также сделать вывод о влиянии тех или иных факторов на смещение химического равновесия с целью достижения необходимого положительного эффекта процесса. На основании значений констант химического равновесия конкурентно протекающих реакций можно сделать вывод о преобладающем значении той или иной реакции в общем массиве термодинамически вероятных процессов.

Литература:

1. Гольбрайх З. Е., Маслов Е. И. Сборник задач и упражнений по химии: Учебное пособие для хим.-технол. спец. вузов. — М.: Высш. шк., 1997.
2. Михайлов В. А. Химическое равновесие: учебное пособие / В. А. Михайлов, О. В. Сорокина, Е. В. Савинкина, М. Н. Давыдова; Под ред. А. Ю. Цевадзе. — М.: БИНОМ. Лаборатория знаний, 2011.
3. Сборник вопросов и задач по аналитической химии. Учебное пособие для вузов / В. П. Васильев, В. Е. Калинина, Л. А. Кочергина и др. Под ред. В. П. Васильева. — М.: Высш. шк., 1976.