Как найти равновесную концентрацию в растворе

Задание 23 в ЕГЭ по химии 2022 года – принципиально новое, вот, что написано в спецификации экзамена:

Давайте разберем, необходимую для решения задания теорию:

Обратимые реакции – это реакции, в которых при одних и тех же условиях реагенты превращаются в продукты и продукты в реагенты (в записи реакции это отражают двумя противоположно направленными стрелочками), например:

В реактор мы помещаем азот N₂ и водород H₂ (идет только прямая реакция), как только в системе появляется аммиак NH₃ – он начинает разлагаться (начинается обратная реакция).

И в какой-то момент система приходит к состоянию равновесия: сколько аммиака образовалось в прямой реакции, столько и разложилось в обратной. Значит, несмотря на то, что прямая и обратная реакции непрерывно идут – концентрации веществ остаются постоянными (равновесные концентрации).

Расчёт равновесных концентраций:

Как мы уже разобрали, понятие равновесие завязано на понятии скорости реакции, поэтому и расчет равновесных концентраций будет идти через расчет скоростей прямой и обратной реакции.

Решим задание из демо-версии:

Фраза “реактор постоянного объема” дана для вашей уверенности, что концентрация будет изменяться только в процессе химических реакций, давление и объем системы – постоянные величины, следовательно мы может оперировать концентрацией так же, как количеством вещества. И решается это задание, как стандартная расчетная задача по уравнению реакции:

Вся информация о начальной и конечной концентрации вещества известна для продукта реакции – SO₃:

Начальная концентрация C1 = 0 моль/л

Равновесная концентрация С2 = 0,4 моль/л

Ответ: 25

Реши еще одно задание самостоятельно – ответы пиши в комментарии:

23.1

В реактор постоянного объема поместили некоторое количество водорода и йода. В результате протекания обратимой реакции

H₂ + I₂ = 2 HI

В реакционной системе установилось химическое равновесие.

Используя данные, приведенные в таблице, определите равновесные концентрации H₂ (Х) и HI (Y)

Выберите из списка номера правильных ответов.

1) 0,025 моль/л

2) 0,05 моль/л

3) 0,1 моль/л

4) 0,15 моль/л

5) 0,2 моль/л

6) 0,3 моль/л

Как вычислить равновесную концентрацию

В ходе химической реакции устанавливается равновесие, когда скорость прямой реакции (в ходе которой исходные вещества превращаются в продукты) становится равной скорости обратной реакции (когда продукты превращаются в исходные вещества). Концентрации всех этих веществ тогда называются равновесными.

Инструкция

В первую очередь вспомните, что такое константа равновесия. Это – величина, характеризующая отношение концентраций (или парциальных давлений) продуктов реакции к концентрациям исходных веществ. Например, если реакция протекает по схеме: А + В = С + D, то Кр = [C][D]/[A][B].

Если же схема протекания реакции такая: 2А + В = 2С, то Кр вычисляется по такой формуле:[C]^2/[B][A]^2. То есть индексы превращаются в показатель степени, в которую нужно возвести концентрацию того или иного компонента.

Рассмотрите пример. Предположим, протекает та самая первая реакция: А + B = C + D. Требуется определить равновесные концентрации всех компонентов, если известно, что начальные концентрации исходных веществ А и В были равны 2 моль/литр, а константа равновесия может быть принята за 1.

Снова запишите формулу константы равновесия для этого конкретного случая: Кр = [C][D]/[A][B]. Учитывая, что Кр = 1, получите: [C][D] = [A][B].

Начальные концентрации веществ А и В вам известны (заданы по условиям задачи). Начальные концентрации продуктов реакции С и D были равны 0, а потом увеличились до неких равновесных значений. Обозначьте равновесную концентрацию вещества С за х, тогда равновесная концентрация вещества А (из которого образовалось С) будет равна (2-х).

Поскольку схема реакции свидетельствует, что из 1 моля вещества А образуется 1 моль вещества С, а из 1 моля вещества В – 1 моль вещества D, то, соответственно, равновесная концентрация D также будет = х, а равновесная концентрация В = (2-х).

Подставив эти величины в формулу, получите: (2-х) (2-х) = х^2. Решив это уравнение, получите: 4х = 4, то есть, х = 1.

Следовательно, равновесные концентрации продуктов реакции C и D равны 1 моль/литр. Но поскольку равновесные концентрации исходных веществ А и В вычисляются по формуле (2-х), то и они также будут равны 1 моль/литр. Задача решена.

Источники:

• Обратимые и необратимые процессы

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Зная
величины констант равновесия и используя
стехиометрические соотношения реакции
(закон сохранения массы), рассчитывают
равновесный состав продуктов по
следующей схеме.

1. Пишут
   уравнение реакции.

2.
Пишут под формулами уравнения начальные
концентрации исходных веществ (в
моль/л). Если начальные концентрации
продуктов реакции не оговариваются в
условии задачи, они обычно принимаются
равными нулю.

3.
Принимают, что в ходе реакции до состояния
равновесия прореагировало x
моль/л какого-либо вещества. Обычно за
x
принимают изменение концентрации того
реагента, стехиометрический коэффициент
при котором в уравнении реакции
наименьший, чтобы избежать дробных
коэффициентов при неизвестном x.
Например, прореагировало x
моль/л вещества А.

4.
По уравнению реакции определяют изменение
концентраций других веществ.

5.
Определяют равновесные концентрации
веществ. При протекании реакции в прямом
направлении до состояния равновесия
происходит уменьшение концентраций
исходных веществ и увеличение концентраций
продуктов реакции.

А
+ b
В 
c
С + D

начальное

состояние
А₀

В₀
С₀
0

число молей

по уравнению
1 b
c
1

изменение

концентраций
x
b
x
c
x
x

равновесное

состояние
А₀
–
x
В₀
–
bx
С₀
+ c
x
x

6.
Пишут выражение закона действующих
масс. Подставляют в него найденные
значения равновесных концентраций.

,

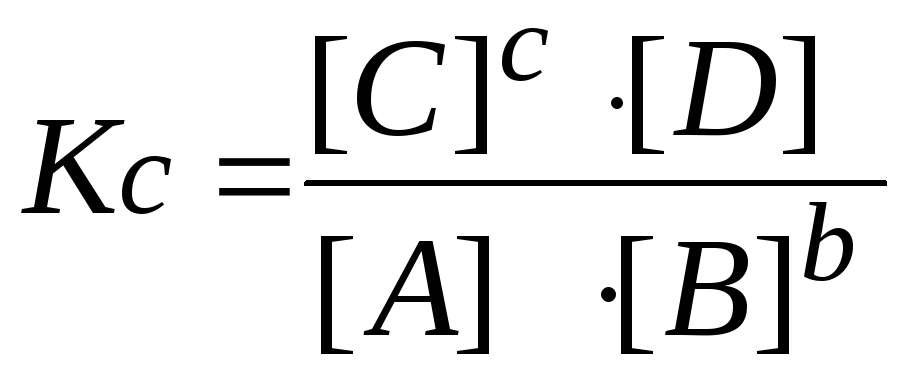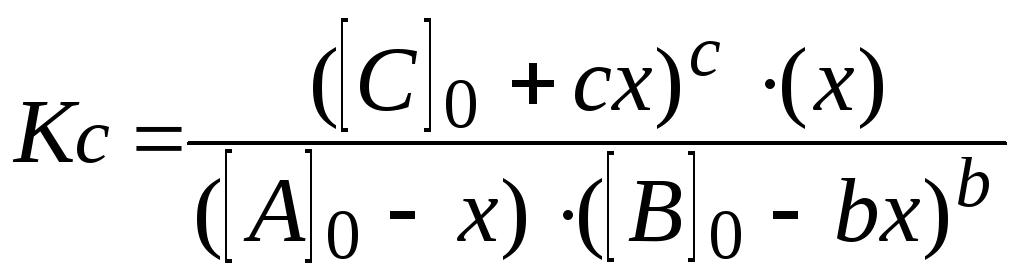
7.
Решают уравнение. При этом учитывают,
что отрицательный корень не имеет
физического смысла, и убыль концентрации
исходного вещества не может быть больше
величины самой концентрации (начальная
концентрация исходного вещества не
может быть меньше его остаточной
равновесной концентрации).

1. Находят
   равновесные концентрации.

А
= А₀–
x;
B
= B₀
–
b
x;

C
= С₀
+
cx;
D
=
x.

4. Смещение химического равновесия. Принцип Ле Шателье

Истинное
химическое равновесие является
динамическим и подвижным: изменение
внешних условий (температуры, давления,
концентраций реагирующих веществ) ведет
к смещению равновесия в сторону прямой
или обратной реакции.

Характер
влияния внешних факторов на равновесные
системы выражает принцип Ле Шателье.

Если
на систему, находящуюся в состоянии
равновесия, оказать внешнее воздействие,
то смещение равновесия происходит в
сторону той реакции (прямой или обратной),
которая ослабляет эффект внешнего
воздействия.

4.1. Изменение концентраций

Равновесное
состояние в системе

H₂
(г)
+ I₂
(г)


2 HI
(г)

характеризуется
(для одной и той же температуры) константой
равновесия:

.

Если,
например, в систему добавить водород,
т.е. увеличить его концентрацию, то
скорость прямой реакции увеличится (в
соответствии с законом действующих
масс):

_пр
= k_пр
[H₂]
[I₂],

_пр

_обр,

равновесие
сместится вправо. Концентрация
йодоводорода будет увеличиваться, а
концентрация водорода и йода будет
уменьшаться. Процесс будет протекать
до тех пор, пока не установится новое
равновесие. Новые равновесные концентрации
всех компонентов будут другими, но
соотношение между ними, определяемое
константой равновесия, останется
постоянным.

Если
в систему ввести дополнительное
количество йодоводорода, то скорость
обратной реакции увеличится:

_обр
=
k_обр
[HI]
²
,
_обр

_пр
,

равновесие
сместится влево.

В
соответствии с принципом Ле Шателье:

–
при увеличении концентрации какого-либо
из веществ, участвующих в равновесии,
равновесие смещается в сторону расхода
этого вещества;

–
при уменьшении концентрации какого-либо
из веществ равновесие смещается в
сторону образования этого вещества.

Удаление
из системы продуктов (или продукта)
реакции ведет к смещению равновесия
в сторону прямой реакции, а уменьшение
концентрации
исходных (или исходного) веществ,
приводит к сдвигу равновесия в направлении
обратной реакции.

Соседние файлы в папке Кинетика_лекции

• #
• #
• #
• #

Вычислить равновесные концентрации

Реакция протекает по уравнению A + B = 2C. Вычислите равновесные концентрации реагирующих веществ, если исходные концентрации веществ А и В соответственно равны 0,5 и 0,7 моль/л, а константа равновесия реакции 50.

Решение задачи

К моменту равновесия концентрации веществ А и В понизятся, а концентрация вещества С увеличится. На каждый моль веществ А и В образуется 2 моль вещества С; поэтому, если понижение концентрации веществ  А и В обозначить через х моль, то увеличение концентрации вещества С будет равно 2х моль. Вычислить равновесные концентрации.

Равновесные концентрации реагирующих веществ будут:

[А] = 0,5 –х (моль/л);

[В] = 0,7 – х (моль/л);

[С] = 2х (моль/л).

 

Где:

K – константа химического равновесия;

[С], [А], [В] – равновесные концентрации соответственно азота, водорода, аммиака, моль/л.

Получаем:

К = 4 х² /(0,5 — х) (0,7-х) = 50

46 х² – 60х + 17,5 = 0.

Решая это уравнение, получаем:

х₁ = 0,86;

х₂ = 0,44.

По условию задачи справедливо значение х₂. Вычислить равновесные концентрации. Отсюда равновесные концентрации реагирующих веществ равны:

[А] = 0,5 –0,44 = 0,06 (моль/л);

[В] = 0,7 – 0,44 = 0,26 (моль/л);

[С] = 2 ⋅ 0,44 = 0,88 (моль/л).

Ответ:

равновесная концентрация вещества А равна 0,06 моль/л;

равновесная концентрация вещества В равна 0,26 моль/л;

равновесная концентрация вещества С равна 0,88 моль/л.

Ni

H₃C-C=N
N=C-CH₃

O
– H …O

Комплексные соединения
применяются в анализе для обнаружения
ионов, «маскировки», растворения и
образования осадков, для количественного
определения веществ (методы
комплексонометрического титрования,
спектрофотометрические методы и др.).
Для грамотного использования реакций
комплексообразования химик-аналитик
должен уметь количественно охарактеризовать
все процессы, которые протекают в
исследуемой равновесной системе.

1.
Расчет равновесных концентраций

в
растворах комплексных солей

Расчет равновесных
концентраций в растворах комплексных
соединений проводится на основании
закона действующих масс. Для реакции:

[ML_n]^m+⇆[ML_n-1]^(m-1)+
+ L^–

Если же рассматривать процесс
диссоциации комплексного иона полностью
до простых частиц или ионов, тогда
необходимо использовать суммарную
константу диссоциации (нестойкости
комплексного иона), которая равна
произведению ступенчатых констант:

[ML_n]^m+⇆M^(m–n)+
+ nL^–

,
где

Пример 1.
Рассчитать равновесные концентрации
ионов в растворе [Ag(NH₃)₂]NO₃,
концентрация которого 0,1 моль/л.

Решение:

[Ag(NH₃)₂]NO₃→
[Ag(NH₃)₂]⁺
+ NO₃^–

[Ag(NH₃)₂]⁺
⇆
[Ag(NH₃)]⁺
+ NH₃

[Ag(NH₃)]⁺
⇆
Ag⁺
+ NH₃

Ag(NH₃)₂]⁺
⇆
Ag⁺
+ 2NH₃

0,1

0,1-x x
2x

Ответ:
[Ag⁺]=1,2^.10^-3
моль/л, [NH₃]=2,4^.10^-3
моль/л.

Если в растворе, содержащем
комплексный ион, присутствует избыток
координируемых частиц, то при расчете
равновесных концентраций необходимо
учитывать, что в растворе будет
доминировать та или иная форма комплексного
иона. Расчет равновесий в данном случае
удобно проводить на основании
распределительных диаграмм, которые
получают путем расчета мольных долей
каждой формы частиц, как функции
равновесной концентрации лигандов.

Если аналитическая
концентрация иона металла равна с,
а концентрация лигандов L,
то уравнение материального баланса
имеет вид:

[M]+[ML]+[ML₂]+…+[ML_n]=c

Концентрацию каждой формы частиц
можно выразить через константу
устойчивости данной формы частицы:

и т.д.

Подставляя в уравнение материального
баланса равновесные концентрации каждой
из форм комплексных частиц, получим:

Далее
рассчитывают мольные доли каждой
частицы, находящейся в растворе:

………….

Пример 2.
Рассчитать концентрации всех частиц в
растворе, содержащем 0,1 моль/л HCl
и 1^.10^-5
моль/л Hg²⁺.

Решение:

В растворе могут находиться
следующие частицы: Hg²⁺,
HgCl⁺,
HgCl₂,
HgCl₃^–,
HgCl₄^2-.
Согласно уравнению материального
баланса:

[Hg²⁺]+[HgCl⁺]+[HgCl₂]+[HgCl₃^–]+[HgCl₄^2-]=1^.10^-5
моль/л.

Выразим равновесные концентрации
комплексных частиц через ступенчатые
константы устойчивости и равновесную
концентрацию незакомплексованных ионов
ртути:

Подставляя полученные значения
равновесных концентраций в уравнения
для расчета мольных долей каждой частицы,
и учитывая, что концентрация лигандов
в растворе во много раз превышает
концентрацию иона комплексообразователя,
так что ее изменением можно пренебречь
и считать постоянной величиной, получаем:

,

откуда
равновесные концентрации всех частиц,
находящихся в растворе будут равны:

;

;
;

;

.

2.
Применение комплексообразования для
обнаружения ионов

При открытии ионов путем
образования окрашенных комплексов
рассчитывают концентрацию лиганда, при
которой образуется достаточное количество
окрашенной формы комплексного иона.
Изменение окраски становится заметным,
когда 1/10 часть всех простых ионов
связывается в комплекс. Окраска простых
ионов будет практически не видна, когда
9/10 всех ионов свяжется в комплекс.

Пример.
Какую концентрацию NaCN
нужно создать в растворе, чтобы открыть
Cu⁺
в виде [Cu(CN)₄]^3-.
Начальная концентрация ионов Cu⁺
в растворе 0,05 моль/л, β_1,2,3,4=1,99^.10³⁰.

Решение:

Для того чтобы окраска
простых ионов была не видна, необходимо,
чтобы 9/10 присутствующих в растворе
ионов Cu⁺
(0,9*0,05) связалось в комплекс. Для этого,
согласно уравнению химической реакции
необходимо в 4 раза больше цианид –
ионов:

0,9*0,05*4=0,18
моль.

Так как комплекс в водном растворе
частично диссоциирует, концентрация
цианидов должна быть выше. Эту избыточную
концентрацию можно рассчитать из закона
действующих масс:

Cu⁺
+ 4CN^–⇄[Cu(CN)₄]^3-

С₀
0,05

[
] 0,05^.0,1
x 0,05^.0,9

Ответ:
начальная концентрация ионов CN^–,
которую нужно создать в растворе будет
равна 4,8^.10^-8+0,18
моль/л.

В данном примере избыточная
концентрация цианид-ионов невелика
благодаря достаточно высокой константе
устойчивости комплекса, однако, если
комплекс менее устойчив, то ее необходимо
обязательно учитывать.

3.
Применение комплексообразования для
«маскировки» ионов

При проведении качественного
или количественного анализа с целью
повышения селективности определения
необходимо устранять мешающее влияние
тех частиц, которые дают сходный эффект
с определяемым компонентом. Одним из
способов устранения мешающего влияния
ионов является связывание их в хорошо
устойчивые комплексы.

Пример.
Вычислить концентрацию аммиака,
достаточную для маскировки ионов Ag⁺
в растворе AgNO₃
(С=0,1 моль/л) при осаждении ионов Pb²⁺
в виде PbCl₂
действием KCl
(C=0,1
моль/л). Объем раствора 1 литр, избыток
осадителя – 2 моль/л.

Решение:

Избыточная концентрация
осадителя задана 2 моль/л. Рассчитаем,
какой должна быть концентрация ионов
Ag⁺,
чтобы осадок AgCl
не образовывался:

.

Найдем концентрацию NH₃,
необходимую для того, чтобы остаточная
концентрация ионов Ag⁺
не превышала 8,9^.10^-11:

Ag(NH₃)₂
⇄
Ag⁺
+ 2NH₃
K_н=5,8^.10^-8

С
0,1

[
] 0,1-8,9^.10^-11
8,9^.10^-11
x

x=[NH₃]=8,1
моль/л

Чтобы 0,1 моль Ag⁺
связать в комплекс, необходимо 2^.0,1=0,2
моль NH₃,
поэтому начальная концентрация аммиака,
которую нужно создать в растворе, должна
быть не меньше 0,2+8,1=8,3 моль/л.

4. Растворение
осадков

Растворимость осадка можно
существенно увеличить путем введения
веществ, образующих растворимые комплексы
с анионом или катионом осадка. Данный
процесс многостадиен и может быть
представлен схематично в виде двух
реакций:

MA

M
+ A      ПР_МА
         

M
+ nL
ML_n
K_у

MA
+ nL
ML_n
+ A        K=ПР_МА^.K_у

При
использовании для расчета суммарного
уравнения не учитывается ступенчатое
образование комплекса, что приводит к
несколько завышенному количеству
требуемого растворителя.

Пример
1. Найти растворимость
AgBr в 0,1 М растворе NH₃.

Решение:

AgBr
Ag⁺
+ Br^–
ПР=5,2^.10^-13

Ag⁺
+ NH₃

AgNH₃⁺
K₁=2,0^.10³

AgNH₃
+ NH₃

Ag(NH₃)₂
K₂=6,9^.10³

AgBr
+ 2NH₃

Ag(NH₃)₂⁺
+ Br^–
       K=ПР^.K₁^.K₂=7,2^.10^-6

С₀
0,1

[ ] 0,1-2x               
x             
x

Ответ:
растворимость AgBr в 1 л 0,1 М NH₃
составляет 2,7^.10^-4
моль, или

2,7^.10^-4.188^.10^-3=50,8
мг

Пример
2. Какую концентрацию
CN^– нужно
создать в растворе, чтобы в 100 мл его
растворился 1 г Cd(OH)₂?

Решение:

Cd(OH)₂
Cd²⁺
+ 2OH^–
ПР=2,2^.10^-14

Cd²⁺
+ 4CN^–
[Cd(CN)₄]^2-
K=1,3^.10¹⁷

Cd(OH)₂
+ 4CN^–
[Cd(CN)₄]^2-
+ 2OH^–
K=
ПР^. K=2,87^.10³

С₀
x

[ ] x-4^.0,0685
    
0,0685          
0,0685^.2

Ответ:
в 100 мл концентрация цианид ионов должна
быть в 10 раз выше, т.е. 0,26 моль/л.

Глава
4. РЕАКЦИИ
ОКИСЛЕНИЯ-ВОССТАНОВЛЕНИЯ

Реакции окисления-восстановления
используют в аналитической химии для
обнаружения ионов, их разделения,
растворения металлов, сплавов,
малорастворимых соединений, для
количественного определения веществ.
Расчет равновесий в реакциях
окисления-восстановления позволяет
выбрать нужный реактив и условия его
применения в анализе. Методы расчета
основаны на знании величин стандартных
окислительно-восстановительных
потенциалов, знании констант равновесия
реакций окисления-восстановления.

1.
Окислительно-восстановительный потенциал

Для
обратимой окислительно-восстановительной
полуреакции процесс превращения
окисленной формы элемента в восстановленную
может быть представлен в виде:

Ox
+ ze

Red ,

где
символом Ох обозначены элементарные
объекты-окислители (атомы, молекулы,
ионы), которые присоединяют электроны
и восстанавливаются, а символом Red

объекты-восстановители, которые отдают
электроны и окисляются. Как видно,
окислители и восстановители взаимосвязаны.
Они образуют пары элементарных объектов
(частиц), называемыми
окислительно-восстановительными парами
(редоксипарами).
При этом объект Ох именуется окисленной,
а объект Red
– восстановленной формами таких пар.
Превращение Ox + ze

Red называют
окислительно-восстановительным переходом
(редоксипереходом) или полуреакцией.
Любую окислительно-восстановительную
реакцию можно представить как сумму
двух полуреакций. Например, редоксиреакция

S₂O₃^2
+ I₂

S₄O₆^2
+ 2I^

является
сочетанием двух полуреакций

2S₂O₃^2

2
S₄O₆^2

I₂
+ 2
2I^

В каждой полуреакции
принимает участие окислительно-восстановительная
пара, содержащая окисленную и
восстановленную формы одного и того же
элемента. Количественно
окислительно-восстановительные свойства
каждой редоксипары характеризуются
величиной окислительно-восстановительного
потенциала (Е).
Чем больше Е,
тем больше сила окислителя и меньше 
восстановителя.

Окислительно-восстановительный
потенциал полуреакции (редоксипотенциал),
измеренный в стандартных условиях
(р=1атм, Т=25⁰С,
a_Ox=a_Red=)
относительно стандартного водородного
электрода, потенциал которого условно
принят равным нулю, называется стандартным
потенциалом и обозначается символом
.
Значения

представлены в справочной литературе
(см. приложение 3). Стандартные потенциалы
окислительно-восстановительных пар,
рассчитанные с учетом влияния на них
ионной силы и рН среды, а также побочных
взаимодействий компонентов пар с
посторонними (или вспомогательными)
частицами в растворе, называют формальными
(реальными) потенциалами и выражают
уравнением Нернста:

,

где
R

газовая постоянная, равная 8,314 Дж/мольК;

F

постоянная Фарадея, равная 96490 Кл/моль.

Часто постоянные величины
объединяют в одну константу, а натуральный
логарифм заменяют десятичным. Значение
величины 2,303 RT/F
при стандартной
стандартной температуре 25 С
равно 0,059. Поэтому уравнение Нернста
обычно записывают так:

.

Если в редоксипереходе
участвуют ионы водорода или гидроксила,
то потенциал Е
будет зависеть и от их концентрации в
растворе:

,

где
q
– стехиометрический коэффициент при
ионе водорода в уравнении реакции.

Пример.
Вычислить редоксипотенциал
пары H₃AsO₄/HAsO₂
при рН 3 и с(H₃AsO₄)
= с(H₃AsO₂)=1
М.

Решение:
Запишем полуреакцию для редоксипары
H₃AsO₄/HAsO₂
:

H₃AsO₄
+ 2+
2H⁺

HAsO₂
+ 2H₂O

По условию задачи рН=3,
следовательно; [H⁺]=10^-3М.

В.

Ответ: 0,4
В.

2.
Направление окислительно-восстановительных
реакций

Значения стандартных
потенциалов позволяют оценить направление
реакции. Реакция окисления-восстановления
протекает в заданном направлении в том
случае, когда разность между стандартными
потенциалами редоксипар будет величиной
положительной, т.е.

E=E
⁰₁
–E⁰
₂>0.

Чем больше разница E⁰₁–E⁰₂,
тем больше вероятность
протекания данной реакции.

Пример 2.
Определите, в каком
направлении пойдет реакция между Fe³⁺и
иодид-ионом?

Решение:
Запишем соответствующие
полуреакции и найдем в таблицах значения
стандартных потенциалов:

Fe³⁺
+ е

Fe²⁺


В;

I₂
+ 2е


2I^–

В.

Найдем разность потенциалов:

E=E
⁰₁
–E⁰
₂=0,77В-0,54В=0,23В.

Вывод:
положительная разность потенциалов
указывает на протекание реакции в
направлении окисления йодид-иона железом
(III).

2Fe³⁺+
2I^–

Fe²⁺
+ I₂

3.
Константа равновесия

окислительно-восстановительной
реакции

О возможности протекания реакций
окисления-восстановления можно судить
по величине константы равновесия,
которая связана со стандартными
потенциалами редоксипар уравнением:

lg
K
=
,

где
E⁰_Ох
и E⁰_Red
–
стандартный потенциал пары, выступающей
в данной реакции в качестве окислителя
(E⁰_Ох)
и в качестве восстановителя(E⁰_Red);

n
– число электронов, участвующих в реакции.

Реакция может протекать в прямом
направлении, если К>1.Чем больше
численное значение К, тем полнее протекает
реакция.

Пример.
Рассчитайте константу
равновесия реакции:

MnO₄^–+5Fe²⁺+8H⁺


Mn²⁺
+5Fe³⁺+
4H₂O.

Решение:
Находим стандартные
окислительно-восстановительные
потенциалы и записываем уравнения
полуреакций:

MnO₄^–+5+8H⁺


Mn²⁺
+
4H₂O

В

Fe²⁺–

Fe³⁺

В

Число электронов,
участвующих в реакции, равно 5. Находим
величину К:

lg
K
=
=62,7

К≈10^63.

Вывод:
численное значение константы К>>1,
значит реакция прошла практически
полностью в прямом направлении.

4. Расчет
растворимости металлов в кислотах

Восстановительная
способность металлов определяется
величинами окислительно-восстановительных
потенциалов. Если металл стоит в ряду
напряжений до водорода (Е⁰<0),
то при растворении в кислотах он способен
восстанавливать водород. Если металл
стоит в ряду напряжения после водорода
(E⁰>0),
то такой металл не способен растворяться
в кислотах неокислителях. Заметное
растворение электроположительных
металлов возможно только в
кислотах-окислителях и только за счет
центрального атома кислотного остатка.
При растворении металлов в
кислотах-окислителях водород из растворов
не выделяется, процесс растворения
сопровождается выделением продуктов
восстановления кислоты (концентрированной
серной или азотной). В зависимости от
природы металла и концентрации
кисоты-окислителя в качестве продуктов
восстановления при использовании в
качестве растворителя азотной кислоты
могут выделяться NO,
NO₂,
NH₄⁺,
а при использовании концентрированной
серной кислоты – SO₂,
H₂S,
S.

4.1.
Растворение металлов в сильных кислотах

Растворение металлов в
сильных кислотах-неокислителях
сопровождается процессом восстановления
водорода. Если количество водорода,
образующегося в результате
окислительно-восстановительного
процесса, больше его растворимости в
воде (8^.10^-4
моль/л при 25С),
то газообразный водород выделяется из
раствора.

Пример 1.
Вычислить растворимость металлической
меди в 1 М растворе соляной кислоты.
Будет ли выделяться газообразный
водород?

Решение:

Cu
– 2e

Cu²⁺
K=2,0^.10^-12

2H⁺
+ 2e

H₂
K=1

______________

Cu
+ 2H⁺

Cu²⁺
+ H₂

1

1-2x
x
x

Так как константа равновесия
суммарного процесса меньше 1, за
неизвестные величины обозначаем
равновесные концентрации частиц, стоящих
в правой части уравнения.

s=[Cu²⁺]=[H₂]=5,6^.10^-6
моль/л

5,6^.10^-6
< 8^.10^-4

Вывод: водород выделяться
не будет.

Пример 2.
Вычислить растворимость металлического
кадмия в 1 М растворе соляной кислоты.
Будет ли выделяться газообразный
водород?

Решение:

Cd
– 2e

Cd²⁺
K=2,57^.10¹³

2H⁺
+ 2e

H₂
K=1

______________

Cd
+ 2H⁺

Cd²⁺
+ H₂

1

2x

Так как суммарная константа
равновесия процесса намного больше 1,
за неизвестную величину удобно обозначить
равновесную концентрацию непрореагировавшей
кислоты.

x=4,93^.10^-8,
следовательно растворимость
моль/л.

Так как
растворимость газообразного водорода
меньше количества, образующегося в
данном процессе, расчет растворимости
необходимо повторить, подставив вместо
величины равновесной концентрации
водорода, его молярную растворимость.

Cd
+ 2H⁺

Cd²⁺
+ H₂

1

2x

8^.10^-4

[H⁺]=1,97^.10^-9,
а [Cd²⁺]=0,05
моль/л.

Для растворения электроположительных
металлов в качестве растворителя
используют кислоты-окислители (азотную
или концентрированную серную).

Пример 3.
Рассчитать растворимость металлической
меди в 6 М растворе азотной кислоты.

Решение:

3
Cu
– 2e

Cu²⁺
K=3,16^.10^-12

2
NO₃^–
+ 4H⁺
+ 3e

NO + 2H₂O
K=1^.10⁴⁸

_____________________________

3Cu
+ 2NO₃^–
+ 8H⁺

3Cu²⁺
+ 2NO + 4H₂O

1. 6

8x

x=2,1^.10^-9.

Так как [NO]=

=1,5
больше растворимости NO
в воде (2,1^.10^-3),
то расчет следует повторить, подставляя
в качестве равновесной концентрации
NO,
его молярную растворимость.

Таким образом, растворимость
металлической меди в 6 М азотной кислоте
составляет ~2,25 моль/л.