Как найти равны ли углы или нет

Как доказать, что углы треугольников равны? Рассмотрим возможные варианты.

Углы треугольников могут быть равны в следующих случаях:

1) Угол — общий (один и тот же угол принадлежит одновременно двум различным треугольникам).

2) Вертикальные углы равны.

3) Углы при основании равнобедренного треугольника равны.

4) Если дана биссектриса треугольника, то исходный угол разделен ею на два равных угла.

5)  Если дана высота треугольника, то она образует два прямых (а значит, равных) угла.

6) Угол, смежный с прямым, есть прямой угол (а значит, они равны между собой).

7) Углы, смежные с равными, равны между собой.

8) Соответствующие углы равных треугольников равны между собой.

9) Если к равным углам прибавить равные углы, то получим равные углы.

10) Если из равных углов вычесть равные углы, то получим равные углы.

11) Внутренние накрест лежащие углы при параллельных прямых и секущей равны между собой.

12) Соответственные углы при параллельных прямых и секущей равны между собой.

13) Углы равны по условию.

14) Углы равны по построению.

15) Углы равны по доказанному.

Угол

Определение угла

Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.

Лучи называются сторонами угла, а их общее начало − вершиной угла.

Обозначение угла

На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают ( small ∠mn ) или ( small ∠O. ) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: ( small ∠AOB ) или ( small ∠BOA. )

Развернутый угол. Внутренняя и внешняя область угла

Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.

Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).

Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.

Фигуру, состоящую из угла и его внутренней области также называют углом.

На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.

Типы углов

В зависимости от величин, углы бывают следующих типов (Рис.5):

• Нулевой угол (0°). Стороны угла совпадают. Его внутренняя область пустое множество.
• Острый угол (больше 0° и меньше 90°)
• Прямой угол (90°). Стороны прямого угла перпендикулярны друг другу.
• Тупой угол (больше 90° и меньше 180°).
• Развернутый угол (180°).
• Невыпуклый угол (от 0° до 180° включительно).
• Выпуклый угол (больше 180° и меньше 360°).
• Польный угол (360°).

Сравнение углов

Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.

На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: ( small ∠2 lt angle 1. )

Градусная мера угла

Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является ( small frac {1}{180} ) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).

Для угла AOB, градусная мера которого равна 120° говорят “угол AOB равен 120° ” и пишут: ( small ∠AOB=120 °. ) Очевидно, что градусная мера развернутого угла равна 180°. ( small frac {1}{60} ) часть градуса называется минутой и обозначается так: ” ‘ “. ( small frac {1}{60} ) часть минуты называется секундой и обозначается так: ” ” “. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: ( small angle AOB=56°6’43”. )

Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.

Как доказать, что углы треугольников равны

Как доказать, что углы треугольников равны? Рассмотрим возможные варианты.

Углы треугольников могут быть равны в следующих случаях:

1) Угол — общий (один и тот же угол принадлежит одновременно двум различным треугольникам).

3) Углы при основании равнобедренного треугольника равны.

4) Если дана биссектриса треугольника, то исходный угол разделен ею на два равных угла.

5) Если дана высота треугольника, то она образует два прямых (а значит, равных) угла.

6) Угол, смежный с прямым, есть прямой угол (а значит, они равны между собой).

7) Углы, смежные с равными, равны между собой.

8) Соответствующие углы равных треугольников равны между собой.

9) Если к равным углам прибавить равные углы, то получим равные углы.

10) Если из равных углов вычесть равные углы, то получим равные углы.

11) Внутренние накрест лежащие углы при параллельных прямых и секущей равны между собой.

12) Соответственные углы при параллельных прямых и секущей равны между собой.

13) Углы равны по условию.

14) Углы равны по построению.

15) Углы равны по доказанному.

5 Comments

На вопрос вы так и не ответили. «Как доказать, что углы равны?» а не «В каких случаях углы равны?». Как-то так; информация не полная, а так все отлично.

Равенство углов следует из равенства треугольников. Значит, в большинстве задач, чтобы доказать, что углы равны, нужно доказать равенство треугольников.
Еще можно доказать, что два угла являются углами при основании равнобедренного треугольника, соответственными или внутренними накрест лежащими углами при параллельных прямых и т.д. — об этом сказано выше.

А если в «моём» случае не подходит?

Значит, искать «свой», подходящий вариант.

Спасибо, очень много вариантов! Я уж думала никогда не найду ответ, а тут белая куча ответов! Спасибо!

Признаки равенства треугольников

О чем эта статья:

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

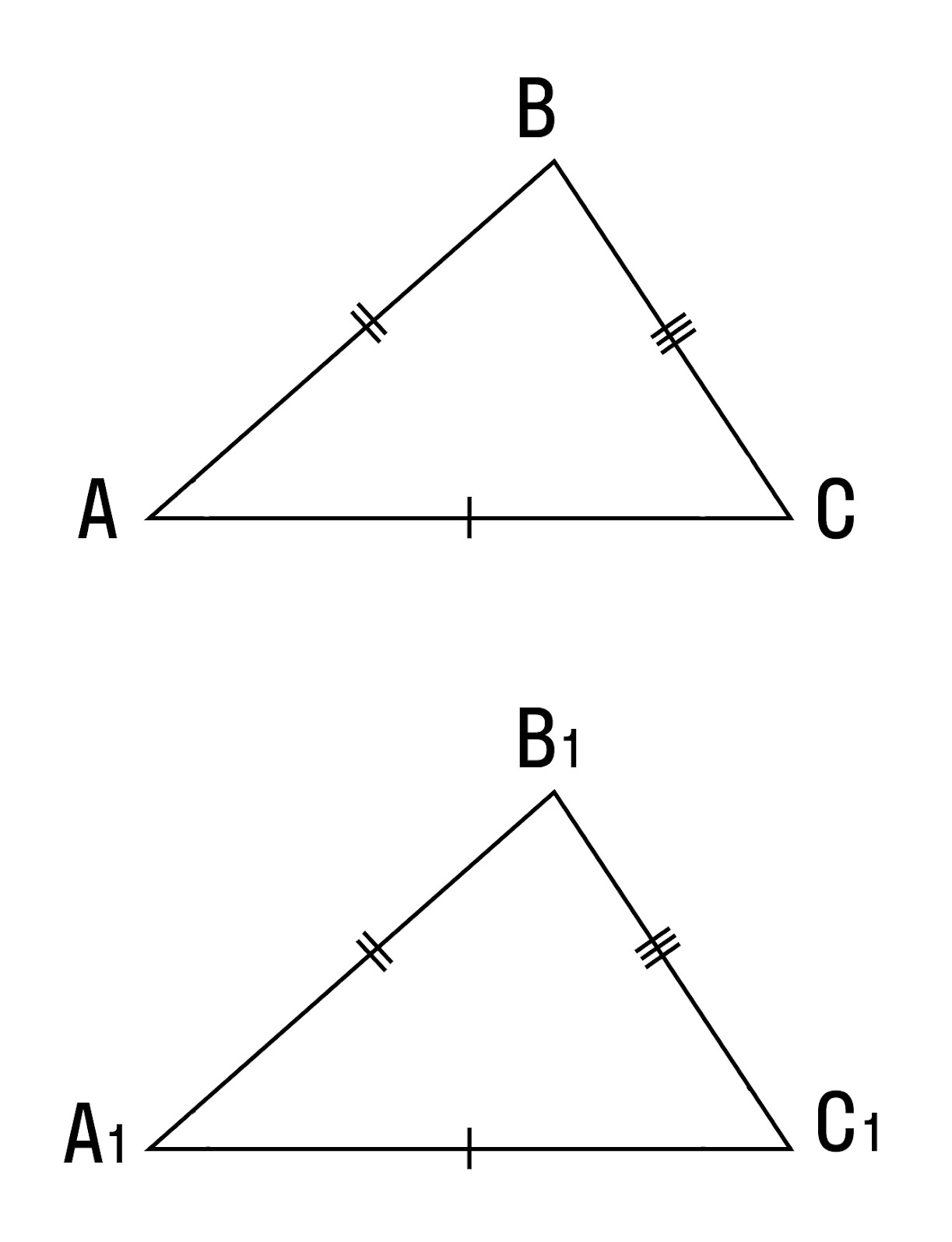
Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

1. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
2. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
3. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
4. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
5. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Как установить и доказать, что треугольники равны

Геометрия как отдельный предмет начинается у школьников в 7 классе. До этого времени они касаются геометрических задач достаточно лёгкой формы и в основном того, что можно рассмотреть на наглядных примерах: площади комнаты, земельного участка, длины и высоты стен в помещениях, периметра плоских предметов и прочее. В нача ле изучения непосредственно геометрии появляются первые сложности, такие, например, как понятие прямой, так как потрогать руками эту прямую нет возможности. Что касается треугольников -это самый простой вид многоугольников, содержащий всего три угла и три стороны.

Тема треугольников одна из основных важных и больших тем школьной программы в геометрии 7−9 классов. Усвоив её хорошо, возможно решать очень сложные задачи. При этом можно изначально рассматривать совершенно другую геометрическую фигуру, а затем разделить её для удобства на подходящие треугольные части.

Как доказать, что треугольники равны

Для работы над доказательством равенства ∆ ABC и ∆A1B1C1 нужно хорошо усвоить признаки равенства фигур и уметь ими пользоваться. Перед изучением признаков необходимо научиться определять равенство сторон и углов простейших многоугольников.

Чтобы доказать, что углы треугольников равны, помогут следующие варианты:

1. ∠ α = ∠ β исходя из построения фигур.
2. Дано в условии задания.
3. При двух параллельных прямых и наличии секущей могут образоваться как внутренние накрест лежащие, так и соответственные ∠ α = ∠ β.
4. Прибавляя (вычитая) к (из) ∠ α = ∠ β равные углы.
5. Всегда сходны вертикальные ∠ α и ∠ β
6. Общий ∠ α, одновременно принадлежащий ∆ MNK и ∆ MNH .
7. Биссектриса делит ∠ α на два равнозначных.
8. Смежный с ∠90° — угол, равный исходному.
9. Смежные равным углам равны.
10. Высота образует два смежных ∠90° .
11. В равнобедренном ∆ MNK при основании ∠ α = ∠ β.
12. В равных ∆ MNK и ∆ SDH соответствующие ∠ α = ∠ β.
13. Доказанное ранее равенство ∆ MNK и ∆ SDH .

Это интересно: Как найти периметр треугольника.

3 признака равенства треугольников

Доказательство равенства ∆ ABC и ∆A1B1C1 очень удобно производить, опираясь на основные признаки тождественности этих простейших многоугольников. Существует три таких признака. Они являются очень важными при решении многих геометрических задач. Стоит рассмотреть каждый.

• I признак. Две стороны и угол между ними ∆ ABC соответственно = двум сторонам и углу ∆ A1B1C1 , следовательно, треугольники равны.
• II признак. Сторона и два прилежащих к ней угла ∆ ABC соответственно = стороне и двум углам ∆ A1B1C1 , => треугольники равны.
• III признак. Если все стороны ∆ ABC соответственно = сторонам ∆ A1B1C1 , то имеющиеся треугольники равны.

Перечисленные выше признаки являются теоремами и доказываются методом наложения одной фигуры на другую, соединения вершин соответственных углов и начала лучей. Доказательства равенства треугольников в 7 классе описаны в очень доступной форме, но сложны в изучении школьниками на практике, так как содержат большое количество элементов, обозначенных заглавными латинскими буквами. Это не совсем привычно для многих учеников на момент начала изучения предмета. Подростки путаются в названиях сторон, лучей, углов.

Доказательство подобия треугольников

Чуть позже появляется ещё одна важная тема «Подобие треугольников». Само определение «подобие» в геометрии означает схожесть формы при различии размеров. Для примера можно взять два квадрата, первый со стороной 4 см, а второй 10 см. Эти виды четырёхугольников будут похожи и, одновременно, иметь отличие, поскольку второй будет больше, причём каждая сторона увеличена в одинаковое количество раз.

В рассмотрении темы подобия также приводятся 3 признака:

• Первый — о двух соответственно равных углах двух рассматриваемых треугольных фигур.
• Второй — об угле и образующих его сторонах ∆ MNK , которые равны соответственным элементам ∆ SDH .
• Третий — указывает на пропорциональность всех соответственных сторон двух нужных фигур.

Как же доказать, что треугольники подобны? Достаточно воспользоваться одним из выше перечисленных признаков и грамотно описать весь процесс доказательства задания. Тема подобия ∆ MNK и ∆ SDH проще воспринимается школьниками исходя из того, что к моменту её изучения ученики уже свободно пользуются обозначениями элементов в геометрических построениях, не путаются в огромном количестве названий и умеют читать чертежи.

Завершая прохождение обширной темы треугольных геометрических фигур, учащиеся уже в совершенстве должны знать, как доказать равенство ∆ MNK = ∆ SDH по двум сторонам, установить равны два треугольника или нет. Учитывая, что многоугольник, имеющий ровно три угла — это одна из важнейших геометрических фигур, к усвоению материала следует подойти серьёзно, уделяя особое внимание даже мелким фактам теории.

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/priznaki-ravenstva-treugolnika

[/spoiler]

Какие углы называются вертикальными: определение и свойства

Содержание:

• Вертикальные углы — что это такое в геометрии, определение
• Свойства вертикальных углов
• Равны или нет, доказательство теоремы
• Примеры решения задач
  • Задача 1
  • Задача 2

Вертикальные углы — что это такое в геометрии, определение

Определение

Вертикальные углы – пара углов с общей вершиной, которые образованы при пересечении двух прямых таким образом, что стороны одного из них являются продолжением сторон другого. Иными словами – они противоположны.

Свойства вертикальных углов

1. Когда две прямые пересекаются, то образуется две пары вертикальных углов.
2. Синусы, косинусы и тангенсы их равны.
3. В сумме два вертикальных угла создают полный угол. Его градус равняется 360^circ.

Равны или нет, доказательство теоремы

Особенность вертикальных углов в том, что они абсолютно идентичны.

Убедимся в справедливости этого свойства. Докажем его: на чертеже 1 и 2, 2 и 3, 3 и 4, 4 и 1 являются смежными, 1 и 3, 2 и 4 – вертикальные.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

По свойству смежных углов, в сумме они дают (180^circ). Используем этот признак и получаем:

(angle1+angle2=180^circ и angle2+angle3=180^circ)

Отсюда выведем, что:

(angle1=180^circ-angle2, angle3=180^circ-angle2)

Уравнение доказало равенство углов 1 и 3.

Примеры решения задач

Задача 1

Дано

(angle1=45^circ)

Найти: значения (angle2, angle3, angle4)

Решение

(angle1) и (angle3) вертикальные. Значит (angle1=angle3=45^circ.)

(angle1) и (angle4) смежные. По правилу о смежных углах:

(angle1+angle4=180^circ)

(angle4=180^circ-angle1=180^circ-45^circ=135^circ)

Так как (angle4) и (angle2) вертикальные, то (angle4=angle2=135^circ.)

Ответ: величина (angle3=45^circ,) величина (angle2) и (angle4=135^circ.)

Задача 2

Дано

Две прямые пересеклись и сформировали четыре угла. Сумма двух из них составляет (140^circ.)

Найти: значения всех углов, образовавшихся при пересечении прямых.

Решение

Поскольку по условию пара углов образует (140^circ), это дает право сделать вывод – они вертикальные, так как смежные в сумме должны достигать (180^circ).

Так как вертикальные углы равны, то значение каждого из них соответствует:

(140/2=70=70^circ)

Оставшиеся углы – смежные к вертикальным и вертикальные по отношению друг к другу. Для того, чтобы их вычислить, выполним следующее действие:

(180-70=110=110^circ)

Ответ: (70^circ), (110^circ), (70^circ), (110^circ).

Текст с ошибкой:

Расскажите, что не так