
Равные дроби видеоурок
Равные дроби

Основное свойство дроби. Математика 5 класс.

6 класс, 8 урок, Основное свойство дроби
Добавить комментарий
Новые уроки
- Видеоурок красивое соло на гитаре
- Упражнения для упругих ягодиц в домашних условиях для девушек видео уроки
- Лунный маникюр шеллаком видео уроки для начинающих
- Видеоурок зарапин
- Укладка плитки видеоурок
Архивы
- Декабрь 2018
- Ноябрь 2018
- Октябрь 2018
- Сентябрь 2018
- Август 2018
- Июль 2018
- Июнь 2018
- Май 2018
- Апрель 2018
- Март 2018
- Февраль 2018
- Январь 2018
Copyright © 2023 Бесплатные видео уроки онлайн
- Подробности
- Категория: Математика 5-6 классы
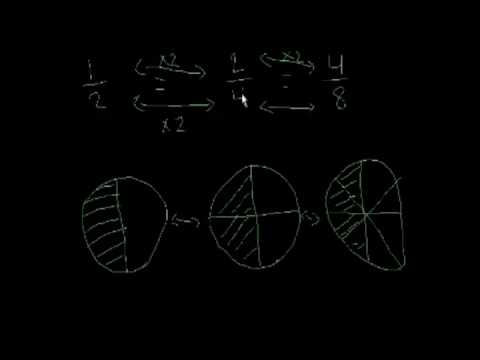
Равенство дробей
Для любой дроби можно указать сколько угодно ей равных дробей.
Например, или
Это можно объяснить так: если отрезок разделить пополам, а половину также пополам, то ясно, что половина отрезка равна двум его четвертям, т. е. Также можно показать, что половина равна трем шестым и т. д. (рис. 4.4).
Можно еще сказать, что дроби и
определяют одно и то же число; записанное в разных формах. Дроби
и
так же определяют одно и то же число, записанное в разных формах, и т. д.
Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится дробь, равная данной, т. е. выполняется равенство
Это свойство называют основным, свойством дроби. С его помощью можно получать дроби, равные данной дроби.
Например,
Равенство (1) можно записать и в обратном порядке:
В таком виде левая часть равенства есть дробь числитель и знаменатель которой имеют общий множитель n.
Если n > 1, то говорят, что можно дробь сократить на n и получить дробь
. Говорят еще, что можно разделить числитель и знаменатель на общий множитель n.
Поэтому основное свойство дробей можно сформулировать по-другому:
Если числитель и знаменатель дроби имеют общий множитель, отличный от 1, то дробь можно сократить на этот множитель. При этом получится дробь, равная данной.
Пример. Сократить дроби
Решение.
Если р—натуральное число, то справедливо равенство
Действительно,
Дробь называется несократимой, если ее числитель и знаменатель не имеют общих простых делителей.
Например, дроби несократимые дроби, так как числа 1 и 2, 3 и 4, б и 7, 11 и 8 не имеют общих простых делителей.
Для каждой дроби существует единственная равная ей несократимая дробь.
Например,
Левые части равенств—данные дроби, а правые равные им несократимые дроби.
Чтобы получить несократимую дробь, равную данной дроби, надо сократить данную дробь на наибольший общий делитель ее числителя и знаменателя. Часто наибольший общий делитель числителя и знаменателя указать трудно. В этом случае сокращение дроби выполняют постепенно.
Пример. Сократить дробь
Решение.
Содержание:
- § 1 Сравнение обыкновенных дробей с помощью координатного луча
- § 2 Сравнение дробей с одинаковыми знаменателями
§ 1 Сравнение обыкновенных дробей с помощью координатного луча
В этом уроке Вы научитесь сравнивать обыкновенные дроби с помощью координатного луча, а также познакомитесь с правилом сравнения дробей с одинаковыми знаменателями.
Для начала, вспомним, что такое обыкновенная дробь.
![]()
Причем, число а называем числителем дроби, а число b – знаменателем дроби. Знаменатель показывает, на сколько частей разделили, а числитель показывает, сколько таких частей взято.
Теперь давайте рассмотрим задачу:
Разобьем прямоугольник на 4 равные части. Две такие части вместе составляют половину прямоугольника.
![]()
![]()
Между прочим, если изобразить две равные дроби на координатном луче, то они будут соответствовать одной и той же точке.
![]()
![]()
![]()
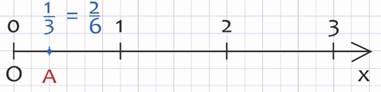
Так как единичный отрезок составляет 6 клеток, значит одна третья его часть – это 2 клетки, т.е. попадаем опять в точку А.
![]()
Таким образом, можно сделать вывод, что:
Равные дроби обозначают одно и то же дробное число.
§ 2 Сравнение дробей с одинаковыми знаменателями
Дробные числа, как и целые, тоже можно сравнивать, складывать, вычитать, умножать и делить. Сегодня мы поговорим о сравнении обыкновенных дробей.
Рассмотрим следующую задачу:
Большой и вкусный торт разрезали на 5 кусков и два куска положили на тарелку, чтобы съесть. Как вы считаете, где больше торта на тарелке или осталось на подносе?
![]()
![]()
Таким образом, получили правило для сравнения дробей с одинаковыми знаменателями:
Из двух дробей с одинаковыми знаменателями меньше та, у которой меньше числитель, и больше та, у которой больше числитель.
![]()
А теперь давайте посмотрим, как располагаются дроби на координатном луче. Например, начертим координатный луч с единичным отрезком 12 клеток.
![]()
![]()
Обратите внимание, которая дробь оказалась правее?
![]()
Таким образом, точка с координатой в виде обыкновенной дроби на координатном луче, имеющая меньшую координату, лежит слева от точки, имеющей большую координату.
Итак, на этом уроке Вы познакомились с правилом сравнения дробей с одинаковыми знаменателями: меньше та дробь, у которой меньше числитель, и больше та, у которой больше числитель, кроме того, узнали, что точка на координатном луче, соответствующая большей дроби, лежит правее
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. – М: 2013.
- Дидактические материалы по математике 5 класс. Автор – Попов М.А. – 2013 год
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор – Минаева С.С. – 2014 год
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010 год
- Контрольные и самостоятельные работы по математике 5 класс. Авторы – Попов М.А. – 2012 год
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009
На этом уроке мы продолжим изучение дробей. Научимся
сравнивать дроби. А также применим знания на конкретных примерах.
Мы с вами уже умеем сравнивать натуральные числа, а
теперь давайте разберёмся, как сравнивают дробные числа.
Задача
Аня и Таня заказали в пиццерии по пицце. Аня
попросила, чтобы её пиццу разрезали на 4
равные части, а Таня – на 8 равных частей.
Аня съела 2 кусочка своей пиццы, а Таня 4 кусочка своей пиццы. Кто из девочек съел больше
пиццы?
Решение
На координатном луче равные дроби соответствуют
одной и той же точке.
Две равные дроби
обозначают одно и то же дробное число.
По чертежу видно, что точки со значениями и
это
одна и та же точка.
С дробными числами можно выполнять те же операции,
что и с натуральными числами. Т.е. дробные числа можно сравнивать, складывать,
вычитать, умножать и делить.
Задание
Сравнить дроби и
.
Запомните правило: из двух дробей с
одинаковыми знаменателями больше та, числитель которой больше и соответственно
меньше та, числитель которой меньше.
Задания
Сравните дроби и
.
Расставьте дроби в порядке возрастания: ,
,
,
и
.
Дробные числа можно сравнивать и при помощи
координатного луча. Как и в случае с натуральными числами, меньше будет
точка, которая имеет меньшую координату и находится левее всех точек, а точка с
большей координатой расположена правее всех остальных точек.
Задание
Отметьте на координатном луче точки с координатами ,
,
,
и
и
укажите, какая из точек будет больше всех, а какая меньше всех.
Решение:
Итоги
Итак, сегодня на уроке мы продолжили изучать дроби,
научились их сравнивать, а также применили свои знания на практике.
