Диагонали ромба вектор ac a
Диагонали ромба вектор ac a
Вопрос по геометрии:
Диагонали ромба AC=a;BD=b.Точка K принадлежит BD и BK:KD=1:3
найдите величину вектора AK
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Решение в скане.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
В ромбе АВСД диагонали АС = а ВД = б разложить по этим двум веторам векторы АВ ВС СД ДА?
Математика | 10 — 11 классы
В ромбе АВСД диагонали АС = а ВД = б разложить по этим двум веторам векторы АВ ВС СД ДА.
Rombus, в буквальном переводе : «бубен»)— этопараллелограмм, у которого все стороны равны.
Ромб спрямыми угламиназываетсяквадратом.
Ав = дс = — ва = — са (1) аналогично другие две стороны
А + В = ад + вс + ав + ва
в силу (1) получаем А + В = 2 * ад
А — В аналогично.
Постройте ромб по диагонали и противоположному углу?
Постройте ромб по диагонали и противоположному углу.
Дан ромб АВСД ?
От вершины С отложили вектор СЕ , равный вектору АВ .
Найдите модуль вектора СЕ , если модуль АС = 8 см , модуль ДВ = 6см.
Составить уравнение диагонали ромба?
Составить уравнение диагонали ромба.
1. Диагонали ромба ABCD пересекаются в точке М?
1. Диагонали ромба ABCD пересекаются в точке М.
1) Выразите вектор AM через векторы AB и BC 2) Найдите вектор BC если диагонали ромба равны 12 и 16.
3) Найдите вектор AC , если A(3 ; 1), C ( — 1 ; 4) 2.
Даны точки A (3 ; 1) , B ( — 1 ; 4), C (2 ; — 3) D ( — 2 ; — 4) 1) Найдите координаты и длины векторов AC и BD 2) Найдите координаты и длину вектора m = 3AC — 4BD.
Как найти периметр ромба если даны диагонали?
Как найти периметр ромба если даны диагонали.
Проведи диагонали у ромба?
Проведи диагонали у ромба.
Диагонали ромба равны 14 и 48 см?
Диагонали ромба равны 14 и 48 см.
Найдите периметр ромба.
Диагонали ромба пропорциональны числам 2 и 3 ?
Диагонали ромба пропорциональны числам 2 и 3 .
Найти диагонали , если площадь ромба 12 см в квадрате.
Периметр ромба равен 100 а разность длина его диагонали равна 10 найдите длину меньшей диагонали этого ромба?
Периметр ромба равен 100 а разность длина его диагонали равна 10 найдите длину меньшей диагонали этого ромба.
Начертить ромб авсд о точка пересечения его диагоналей постройте фигуру в которую перейдет данный ромб при параллельном переносе на вектор во?
Начертить ромб авсд о точка пересечения его диагоналей постройте фигуру в которую перейдет данный ромб при параллельном переносе на вектор во.
На этой странице вы найдете ответ на вопрос В ромбе АВСД диагонали АС = а ВД = б разложить по этим двум веторам векторы АВ ВС СД ДА?. Вопрос соответствует категории Математика и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.
Диагонали ромба ABCD пересекаются в точке М. 1) Выразите вектор AM через векторы АВ и ВС.
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,929
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
На рисунке изображен ромб ABCD, где АВ = 4, ∠BAD = 60°. а) Началом каких ненулевых векторов служит точка В?
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,279
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,949
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Векторы. Действия с векторами. Задание 4 (2015)
Векторы. Действия с векторами. В этой статье мы поговорим о том, что такое вектор, как находить его длину, и как умножать вектор на число, а также как находить сумму, разность и скалярное произведение двух векторов.
Как обычно, немного самой необходимой теории.
Вектор – это направленный отрезок, то есть такой отрезок, у которого есть начало и конец:
Здесь точка А – начало вектора, а точка В – его конец.
У вектора есть два параметра: его длина и направление.
Длина вектора – это длина отрезка, соединяющего начало и конец вектора. Длина вектора обозначается
Два вектора называются равными , если они имеют одинаковую длину и сонаправлены.
Два вектора называются сонаправленными , если они лежат на параллельных прямых и направлены в одну сторону: вектора и сонаправлены:
Два вектора называются противоположно направленными, если они лежат на параллельных прямых и направлены в противоположные стороны: вектора и , а также и направлены в противоположные стороны:
Вектора, лежащие на параллельных прямых называются коллинеарными : вектора , и – коллинеарны.
Произведением вектора на число называется вектор, сонаправленный вектору , если 0″ title=”k>0″/>, и направленный в противоположную сторону, если , и длина которого равна длине вектора , умноженной на :
=k:
Чтобы сложить два вектора и , нужно начало вектора соединить с концом вектора . Вектор суммы соединяет начало вектора с концом вектора :
Это правило сложения векторов называется правилом треугольника .
Чтобы сложить два вектора по правилу параллелограмма , нужно отложить вектора от одной точки и достроить до параллелограмма. Вектор суммы соединяет точку начала векторов с противоположным углом параллелограмма:
Разность двух векторов определяется через сумму: разностью векторов и называется такой вектор , который в сумме с вектором даст вектор :
:
Отсюда вытекает правило нахождения разности двух векторов : чтобы из вектора вычесть вектор , нужно отложить эти вектора от одной точки. Вектор разности соединяет конец вектора с концом вектора ( то есть конец вычитаемого с концом уменьшаемого):
Чтобы найти угол между вектором и вектором , нужно отложить эти вектора от одной точки. Угол, образованный лучами, на которых лежат вектора, называется углом между векторами:
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
Предлагаю вам решить задачи из Открытого банка заданий для подготовки к ЕГЭ по математике , а затем сверить све решение с ВИДЕОУРОКАМИ:
1 . Задание 4 (№ 27709)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов и .
2 . Задание 4 (№ 27710)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).
3 . Задание 4 (№ 27711)
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину суммы векторов и .
4 . Задание 4 (№ 27712)
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину разности векторов и . (чертеж из предыдущей задачи).
5 . Задание 4 (№ 27713)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора .
6 . Задание 4 (№ 27714)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора + .
7 .Задание 4 (№ 27715)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора – .(чертеж из предыдущей задачи).
8 .Задание 4 (№ 27716)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора – .
9 . Задание 4 (№ 27717)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора + .
10 . Задание 4 (№ 27718)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора – .(чертеж из предыдущей задачи).
11 .Задание 4 (№ 27719)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите скалярное произведение векторов и .(чертеж из предыдущей задачи).
12 . Задание 4 (№ 27720)
Стороны правильного треугольника ABC равны Найдите длину вектора +.
13 . Задание 4 (№ 27721)
Стороны правильного треугольника ABC равны 3. Найдите длину вектора -.(чертеж из предыдущей задачи).
14 . Задание 4 (№ 27722)
Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).
[spoiler title=”источники:”]
http://www.soloby.ru/703280/%D1%80%D0%B8%D1%81%D1%83%D0%BD%D0%BA%D0%B5-%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD-%D0%BD%D0%B0%D1%87%D0%B0%D0%BB%D0%BE%D0%BC-%D0%BD%D0%B5%D0%BD%D1%83%D0%BB%D0%B5%D0%B2%D1%8B%D1%85-%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%BE%D0%B2-%D1%81%D0%BB%D1%83%D0%B6%D0%B8%D1%82-%D1%82%D0%BE%D1%87%D0%BA%D0%B0
http://ege-ok.ru/2012/05/25/vektoryi-deystviya-s-vektorami
[/spoiler]
Вопрос от Kostya
896 дней назад
ABCD-ромб. Будут ли равны вектора:
АВ и DC, BC и DA, AB и AD?
Ответ от Оксана
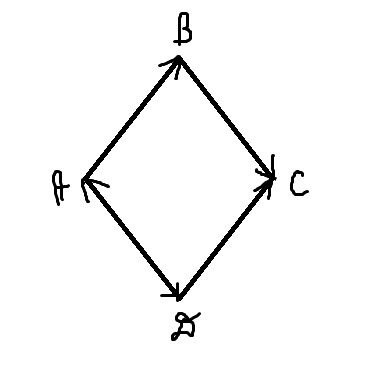
Определение:
Векторы называются равными, если они лежат на одной или параллельных прямых; их направления совпадают и длины равны.
АВ и DС – равны, т.к. лежат на параллельных прямых, равны по модулю (у ромба все стороны равны), направлены в одну сторону.
ВС и DA – не равны, т.к. направлены в разные стороны.
АВ и AD – не равны, т.к. направлены в разные стороны.
Ответ 108 градусов если я все правильно помню
13) а) необходимо из точки О построить перпендикуляр к прямой а и продолжить его от точки О на такое же расстояние как и до прямой а, получим точкуК, через нее проводим прямую, перпендикулярную отрезку ОК, получаем прямую, симметричную прямой а относительно точки О.
б) во втором случае мы просто строим перпендикуляр на прямую а из точки О и проводим прямую перпендикулярную полученному отрезку через точку О.
14) Из точки М проводим перпендикуляр к стороне треугольника и перпендикулярно ему проводим прямую через точку М, и так три раза к каждой стороне. Если необходимо – сторону треугольника продолжаем. Смотри на рисунке: прямая а параллельна стороне АВ, прямая в параллельна стороне АС и прямая с параллельна стороне СВ.
Боковая поверхность состоит из трёх равных равнобедренных треугольника.
Найдем площадь треугольника и умножим на 3.
В равнобедренном треугольнике опустим высоту.
Высота является и медианой и биссектрисой. медиана делит противоположную сторону пополам. Рассмотрим прямоугольный треугольник. Гипотенуза равна 4, катет равен 6/2=3, найдем другой катет по теореме Пифагора: х=Sqrt(16-9)=sqrt(7)/ Это и есть высота. Найдем площадь s=1/2*6*sqrt(7)
s=3*sqrt(7)
sбок.пов.=3*3*sqrt(7)
sбок.пов.=9*sqrt(7)
1)найдём второй катет 1го треугольника x^2=75^2-21^2. ===72
2)P=72+21+75=168
3)P2=1682. +168= ….
щас погоди минут 10
Смотри во вложении.
Материал
урока.
На
прошлых занятиях мы ввели понятие вектора в пространстве.
Отрезок,
для которого указано, какой из его концов является началом, а какой — концом,
называется вектором. Любая точка пространства также является вектором, нулевым
вектором.
Мы
выяснили, что длина ненулевого вектора равна длине
отрезка AB. А длина нулевого
вектора равна 0.
Так
же дали определение коллинеарным векторам. Это векторы, которые лежат на
одной прямой или на параллельных прямых.
Если
коллинеарные векторы имеют одинаковое направление, то они являются сонаправленными.
Если же их направления противоположны, то векторы называют противоположно
направленными.
На
этом уроке мы будем говорить о равных векторах. Определение равных векторов в
пространстве звучит так же, как и определение равных векторов на плоскости.
Равными
называют сонаправленные векторы, длины которых равны.
Ну,
а противоположно направленные векторы, длины которых равны, называют противоположными.
Рассмотрим
пример.
На рисунке изображён куб ABCDA1B1C1D1.
Среди векторов, показанных на рисунке, найдём пары равных и противоположных
векторов.
Перед
нами куб, и стоит вспомнить, что это за фигура. Это многогранник, все грани
которого являются квадратами. Значит, все рёбра куба равны между собой.
Векторы
и
коллинеарны.
Ведь понятно, что ребра AA1
и DD1
параллельны, как противоположные стороны квадрата. Аналогично, параллельны
рёбра DD1
и CC1.
А значит, параллельны рёбра АА1 и CC1.
Так же по рисунку понятно, что данные векторы сонаправлены, а их длины по
условию равны. Тогда векторы и
равны.
Векторы
и
равны по длине,
но противоположно направлены. Значит, эти векторы являются противоположными.
Векторы
и
равны
по длине и сонаправлены, а значит, равны.
Векторы
и
равны
по длине и противоположно направлены, а значит, противоположны.
Также
противоположно направленными и равными по длине будут векторы и
. Они являются
противоположными.
Так
мы с вами выписали две пары равных векторов и три пары противоположных
векторов.
Задача.
правильный
тетраэдр.
,
,
и
середины рёбер
,
,
и
.
1.
Среди изображённых векторов указать пары равных векторов.
2.
Установить вид четырёхугольника .
Решение.
Равными
являются сонаправленные векторы, длины которых равны.
А
для того чтобы векторы были сонаправлены, они должны быть коллинеарны. То есть
должны лежать на параллельных прямых или на одной прямой.
Никакие
рёбра тетраэдра не являются параллельными. Поэтому на рёбрах будем искать
векторы, лежащие на одной прямой. Такими являются векторы и
, а также
и
. Точки P
и М являются серединами соответствующих рёбер. Значит, равны длины векторов и
, а также
и
.
Но
векторы и
противоположно
направлены, а вот векторы и
— сонаправлены.
Так
мы нашли одну пару равных векторов, и
.
Далее
рассмотрим треугольник ABD.
Точки М и N — середины сторон AB
и AD. Значит, МN
— средняя линия. И она параллельна стороне BD,
а также равна её половине.
В
треугольнике CBD отрезок PQ
является средней линией. Он параллелен стороне BD
и равен её половине.
Так
мы получаем, что отрезки МN
и PQ параллельны и равны. Значит, векторы
и
коллинеарны и,
очевидно, сонаправлены. И так как равны их длины, то можно сказать, что эти
векторы равны.
Аналогично,
в треугольнике ADC отрезок NP
является средней линией. Он параллелен стороне AC
и равен её половине.
В
треугольнике ABC отрезок MQ
также
является средней линией. Он параллелен стороне AC
и равен её половине.
Отсюда
получаем, что отрезки NP
и MQ параллельны и равны. А значит,
можем сделать вывод о равенстве векторов и
.
Так
мы с вами нашли три пары равных векторов.
Теперь
осталось определить вид четырёхугольника MNPQ.
Нами
уже установлено, что противоположные стороны этого четырёхугольника параллельны
и равны. А это говорит о том, что данный четырёхугольник является
параллелограммом.
Но
так как все рёбра данного тетраэдра равны, то равны и длины средних линий,
рассматриваемых ранее треугольников.
Получаем,
что MNPQ — параллелограм, все
стороны которого равны между собой. А значит, данный четырёхугольник является
ромбом.
Ответ.
1) ,
,
; 2)
ромб.
Далее
вспомним, что от любой точки плоскости можно отложить вектор равный данному,
и притом только один.
Это
утверждение верно и для любой точки пространства.
Действительно,
если рассмотреть некоторый вектор и
произвольную точку пространства М. Через точки начала и конца данного вектора,
а также через точку М можно провести плоскость.
В
полученной плоскости отложим от точки М вектор равный вектору
. Очевидно, он
искомый. А из построений понятно, что он будет единственным. Ведь первая
аксиома стереометрии говорит, что через 3 точки пространства можно провести
только 1 плоскость.
Говорят
«вектор отложен от
точки М».
Выполним
задание.
В
параллелепипеде ABCDA1B1C1D1
точки K и М — середины сторон A1D1
и B1C1
соответственно. Стоит напомнить, что все грани параллелепипеда являются
параллелограммами, а их противоположные стороны равны. Значит, равны и их
половины.
Итак,
нам нужно назвать векторы, которые получатся, если от данной точки отложить
вектор, равный данному.
Первым
нам нужно назвать вектор, который получится, если от точки C
отложить вектор, равный вектору .
Нам
известно, что от точки пространства можно отложить только один вектор, равный
данному.
Вектор
отложен от
точки C и он равен вектору . Значит, вектор
искомый.
Далее
назовём вектор, который получится, если от точки D
отложить вектор, равный вектору .
Вектор
отложен от
точки D и равен вектору . Значит, он и
является искомым.
Так,
если от точки А1 отложить вектор, равный вектору , то мы получим
вектор .
Если
же от точки C1
отложить вектор, равный вектору , то мы получим
вектор .
И,
отложив от точки М вектор, равный вектору , мы получим
вектор .
Подведём
итоги урока.
На
этом уроке мы выяснили, что, так же как и на плоскости, в пространстве равными
называют сонаправленные векторы, длины которых равны.
Если
же векторы противоположно направлены и их длины равны, то такие векторы
называют противоположными.
Так
же мы отметили, что от любой точки пространства можно отложить вектор, равный
данному вектору, и притом только один.
Всем
этим знаниям мы нашли применение при решении задач.
juthongldede639
Вопрос по математике:
Abcd-ромб. какие векторы равны
1) Ab и dc
2) Cb и Ad
3) Ab и dc, cb и ad
4) все векторы равны

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
dearnola333
3й вариант ответа
(т.к. они парралельные сонаправленные и равны по модулям т.к. это стороны ромба)
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.











