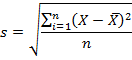Загрузить PDF
Загрузить PDF
Вычислив среднеквадратическое отклонение, вы найдете разброс значений в выборке данных.[1]
Но сначала вам придется вычислить некоторые величины: среднее значение и дисперсию выборки. Дисперсия – мера разброса данных вокруг среднего значения.[2]
Среднеквадратическое отклонение равно квадратному корню из дисперсии выборки. Эта статья расскажет вам, как найти среднее значение, дисперсию и среднеквадратическое отклонение.
-
1
Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.[3]
- Определите количество чисел в наборе данных.
- Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
- Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
- Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.
-
2
Для вычисления среднего значения понадобятся все числа данного набора данных.[4]
- Среднее значение – это усредненное значение всех чисел в наборе данных.
- Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
-
3
Сложите все числа вашего набора данных.[5]
- В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
- Сложите числа еще раз, чтобы проверить ответ.
-
4
Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.[6]
- В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
- В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
- 48/6 = 8
- Среднее значение данной выборки равно 8.
Реклама
-
1
Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.[7]
- Эта величина даст вам представление о том, как разбросаны данные выборки.
- Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
- Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
- Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.
-
2
Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.[8]
- В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
- 10 – 8 = 2; 8 – 8 = 0, 10 – 2 = 8, 8 – 8 = 0, 8 – 8 = 0, и 4 – 8 = -4.
- Проделайте вычитания еще раз, чтобы проверить каждый ответ. Это очень важно, так как полученные значения понадобятся при вычислениях других величин.
-
3
Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.[9]
- При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
- Возведите эти значения в квадрат: 22, 02, 22, 02, 02, и (-4)2 = 4, 0, 4, 0, 0, и 16.
- Проверьте ответы, прежде чем приступить к следующему шагу.
-
4
Сложите квадраты значений, то есть найдите сумму квадратов.[10]
- В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
- Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- Сумма квадратов равна 24.
-
5
Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке. Таким образом, вы получите дисперсию.[11]
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
- n-1 = 5.
- В нашем примере сумма квадратов равна 24.
- 24/5 = 4,8
- Дисперсия данной выборки равна 4,8.
Реклама
-
1
Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.[12]
- Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
- Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
- В нашем примере дисперсия равна 4,8.
-
2
Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.[13]
- Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
- В нашем примере дисперсия равна 4,8.
- √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
- 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).
-
3
Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.[14]
- Обязательно записывайте вычисления.
- Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
- Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.
Реклама
Об этой статье
Эту страницу просматривали 64 646 раз.
Была ли эта статья полезной?
Как найти дисперсию?
Полезная страница? Сохрани или расскажи друзьям
Дисперсия – это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая – значения сравнительно близки друг к другу, если большая – далеки друг от друга (см. примеры нахождения дисперсии ниже).
Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии – среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.
Еще одно формальное определение дисперсии звучит так: “Дисперсия – это второй центральный момент случайной величины” (напомним, что первый начальный момент – это как раз математическое ожидание).
Нужна помощь? Решаем теорию вероятностей на отлично
Формула дисперсии случайной величины
Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$
Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Пример нахождения дисперсии
Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.
Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$
Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором – дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 – (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 – (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором – на 10 единиц от среднего 0.
Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).
Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.
Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.
Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.
Другие задачи с решениями по ТВ
Подробно решим ваши задачи на вычисление дисперсии
Вычисление дисперсии онлайн
Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.
Видео. Полезные ссылки
Видеоролики: что такое дисперсия и как найти дисперсию
Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Спасибо за ваши закладки и рекомендации
Полезные ссылки
Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.
Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по ТВ. Для закрепления материала – еще примеры решений задач по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Разброс (иногда
эту величину называют размахом)
выборки
обозначается буквой R.
Это самый
простой показатель, который можно
получить для выборки — разность между
максимальной и минимальной величинами
данного конкретного вариационного
ряда, т.е.
R
= X
– X
тaх
тiт
Понятно, что чем
сильнее варьирует измеряемый признак,
тем больше величина R,
и наоборот.
Однако может
случиться так, что у двух выборочных
рядов и средние, и размах совпадают,
однако характер варьирования этих рядов
будет различный. Например, даны две
выборки:
X
= 10 15 20 25
30 35 40 45 50
= 30 R
= 40
Y
= 10 28 28 30
30 30 32 32 50
= 30 R
= 40
При равенстве
средних и разбросов для этих двух
выборочных рядов характер их варьирования
различен. Для того чтобы более четко
представлять характер варьирования
выборок, следует обратиться к их
распределениям.
4.5. Дисперсия
Рассмотрим еще
одну очень важную числовую характеристику
выборки, называемую дисперсией.
Дисперсия
представляет собой наиболее часто
использующуюся меру рассеяния случайной
величины (переменной). Дисперсия
это среднее
арифметическое квадратов отклонений
значений переменной от её среднего
значения.
49
(4.4)
где
п — объем
выборки
i—
индекс суммирования
– среднее,
вычисляемое по формуле (4.1).
Вычислим дисперсию
следующего ряда
2 4 6 8 10
(4.5)
Прежде всего найдем
среднее ряда (4.5). Оно равно X
= 6.
Рассмотрим величины:
(Xj
— X)
для каждого
элемента ряда. Иными словами, из каждого
элемента ряда 4.5 вычтем величину среднего
этого ряда. Полученные величины
характеризуют то, насколько каждый
элемент отклоняется от средней величины
в данном ряду. Обозначим полученную
совокупность разностей как множество
Т. Тогда
Г есть:
T
= (2 – 6 = -4; 4 – 6 = -2; 6 – 6 = 0; 8 – 6 = 2; 10 – 6 = 4).
Так образуется
новый ряд чисел. Его особенность в том,
что при сложении этих чисел обязательно
получится ноль. Проверим: (-4) + (-2) + 0 +
2 + 4 = 0.
Отметим, что сумма
такого ряда ∑(Xi
—
)
всегда будет
равна нулю.
Для того чтобы
избавиться от нуля, каждое значение
разности (Xi
—
)
возводят в
квадрат, все их суммируют и затем делят
на число элементов, т.е. применяют формулу
4.4. В нашем примере получится следующее:
=
(-4)
(-4)+(-2)-(-2)+ = 16 + 4 + 0 + 4 + 16 = 40
Это и есть искомая
дисперсия.
Общий алгоритм
вычисления дисперсии для одной выборки
следующий:
50
1. Вычисляется
среднее по выборке.
2. Для каждого
элемента выборки вычисляется его
отклонение от
средней, т.е.
получается множество Т.
3. Каждый элемент
множества T
возводят в квадрат.
4. Находится сумма
этих квадратов.
5. Эта сумма, как
и в случае вычисления среднего, делится
на общее количество членов ряда — я. В
ряде случаев, особенно когда величина
выбоки мала, деление осуществляется не
на величину п,
а на величину
п — 1.
Величина, получающаяся
после пятого шага, и есть искомая
дисперсия.
Расчет дисперсии
для таблицы чисел осуществляется по
формуле 4.6:
(4.6)
где ху
— значения
всех переменых, полученных в эксперименте,
или все элементы таблицы;
индексу меняется
от 1 до p,
где р число
столбцов в таблице, а индекс i
меняется
от 1 до п, где
п — число
испытуемых или число строк в таблице.
—общая средняя
всех элементов таблицы, вычисленная по
формуле 4.3;
N — общее
число всех элементов в таблице
(анализируемой совокупности
экспериментальных данных) и в общем
случае N = р
-п.
Дисперсию для
генеральной совокупности принято
обозначать как σ2,
а дисперсию выборки как
,
причем индекс
х обозначает,
что дисперсия характеризует варьирование
числовых значений признака вокруг их
средней арифметической.
Преимущество
дисперсии перед размахом в том, что
дисперсию можно представить как
сумму ряда чисел (согласно ее оп-
51
ределению), т.е.
разложить на составные компоненты,
позволяя тем самым более подробно
охарактеризовать исходную выборку.
Важная характеристика дисперсии
заключается также и в том, что с её
помощью можно сравнивать выборки,
различные по объему.
Однако сама
дисперсия, как характеристика отклонения
от среднего, часто неудобна для
интерпретации. Так, например, предположим,
что в эксперименте измерялся рост в
сантиметрах, тогда размерность
дисперсии будет являться характеристикой
площади, а не линейного размера (поскольку
при подсчете дисперсии сантиметр
возводится в квадрат).
Для того чтобы
приблизить размерность дисперсии к
размерности измеряемого признака
применяют операцию извлечения квадратного
корня из дисперсии. Полученную величину
называют стандартным
отклонением.
Из суммы квадратов,
деленных на число членов ряда извлекается
квадратный корень.
(4.7)
Другими словами,
стандартное отклонение выборки Sx
представляет
собой корень квадратный, извлеченный
из дисперсии
выборки
. Стандартное отклонение для генеральной
совокупности обозначают также
символом а. Подчеркнем еще раз, что
размерность стандартного отклонения
и размерность исходного ряда совпадают.
В нашем примере
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 января 2023 года; проверки требуют 2 правки.
У этого термина существуют и другие значения, см. Дисперсия.
Диспе́рсия случа́йной величины́ — мера разброса значений случайной величины относительно её математического ожидания. Обозначается ![D[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa482bb7dcd759ae8e7e38fa47bea024feb50892)



Квадратный корень из дисперсии, равный 
Из неравенства Чебышёва следует, что вероятность того, что значения случайной величины отстоят от математического ожидания этой случайной величины более чем на 

Определение[править | править код]
Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания.
Пусть 
где символ 
Замечания[править | править код]
где 




Доказательство 2-й формулы
где 
- Для получения несмещённой оценки дисперсии случайной величины значение
необходимо умножить на
. Несмещённая оценка имеет вид:
Свойства[править | править код]
Условная дисперсия[править | править код]
Наряду с условным математическим ожиданием ![{displaystyle mathbb {E} [X|Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a84d6dab33ae8233f10a39a5b8d346c223b5298)
![{displaystyle D[X|Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fd009ffa0ed890e534a5870b243ff4c8f901a75)
Условной дисперсией случайной величины 

.
Её свойства:
- откуда, в частности, следует, что дисперсия условного математического ожидания
всегда меньше или равна дисперсии исходной случайной величины
.
Пример[править | править код]
Пусть случайная величина 
![{displaystyle displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f3c46b95603c311eaa541789bf49b6666d7f48f)
Тогда математическое ожидание квадрата случайной величины равно
,
и математическое ожидание случайной величины равно
Дисперсия случайной величины равна
См. также[править | править код]
- Среднеквадратическое отклонение
- Моменты случайной величины
- Ковариация
- Выборочная дисперсия
- Независимость (теория вероятностей)
- Скедастичность
- Абсолютное отклонение
- Дельта-метод
Примечания[править | править код]
- ↑ Колмогоров А. Н. Глава IV. Математические ожидания; §3. Неравенство Чебышева // Основные понятия теории вероятностей. — 2-е изд. — М.: Наука, 1974. — С. 63—65. — 120 с.
- ↑ Боровков А. А. Глава 4. Числовые характеристики случайных величин; §5. Дисперсия // Теория вероятностей. — 5-е изд. — М.: Либроком, 2009. — С. 93—94. — 656 с.
Литература[править | править код]
- Гурский Д., Турбина Е. Mathcad для студентов и школьников. Популярный самоучитель. — СПб.: Питер, 2005. — С. 340. — ISBN 5469005259.
- Орлов А. И. Дисперсия случайной величины // Математика случая: Вероятность и статистика — основные факты. — М.: МЗ-Пресс, 2004.
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
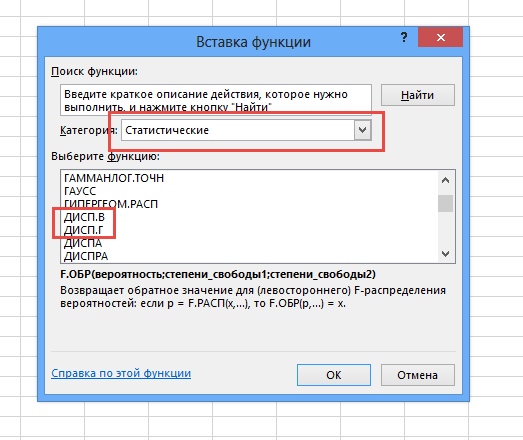
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
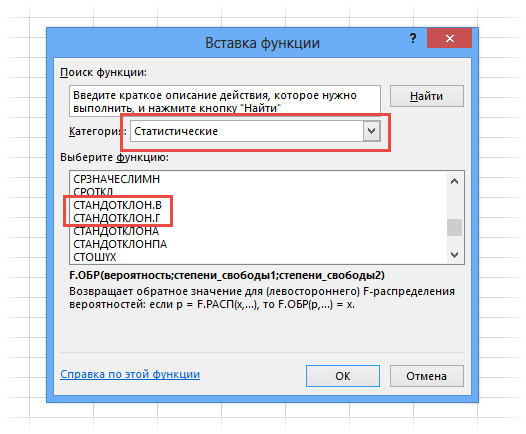
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
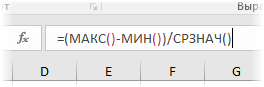
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях:












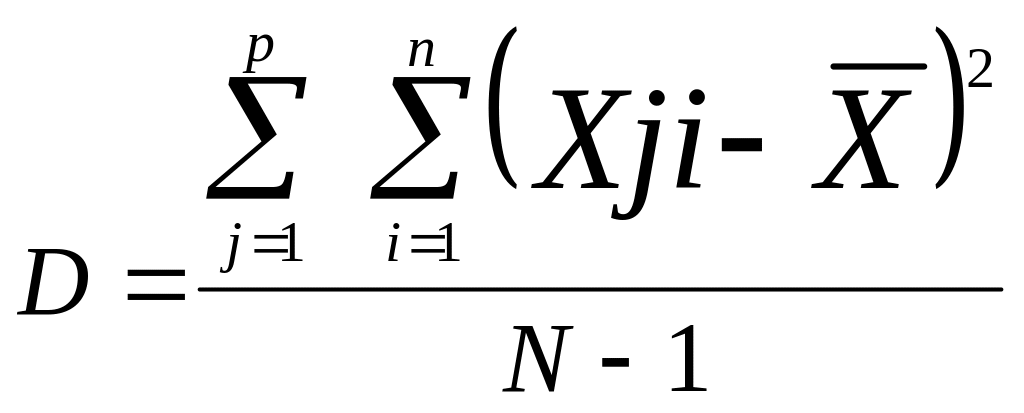

![{displaystyle D[X]=mathbb {E} left[{big (}X-mathbb {E} [X]{big )}^{2}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af0036187b87a8c738238bce5853e1d4b0df5d4b)



![{displaystyle D[X|Y]=mathbb {E} [(X-mathbb {E} [X|Y])^{2}|Y]=mathbb {E} [X^{2}|Y]-mathbb {E} [X|Y]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d07e6493949314f0a9dfb7f20d8c774ead57a94b)
![f_{X}(x)=left{{begin{matrix}1,&xin [0,1]\0,&xnot in [0,1].end{matrix}}right.](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfe7c0979d6e6a936e73de86914b564f78c5db16)
![{displaystyle mathbb {E} left[X^{2}right]=int limits _{0}^{1}!x^{2},dx=left.{frac {x^{3}}{3}}rightvert _{0}^{1}={frac {1}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea35960967b1f07bcc96c2bfd553485ac7704cfd)
![{displaystyle mathbb {E} left[Xright]=int limits _{0}^{1}!x,dx=left.{frac {x^{2}}{2}}rightvert _{0}^{1}={frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cce35565ca3d3e3abeb7d343a40f75e5eb63bda)
![{displaystyle D[X]=mathbb {E} left[X^{2}right]-(mathbb {E} [X])^{2}={frac {1}{3}}-left({frac {1}{2}}right)^{2}={frac {1}{12}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcb8ee8e63837c48b7072b105e89af17b343d862)