Как найти разделенную разность

Как найти разделенную разность

Разделённая ра́зность — обобщение понятия производной для дискретного набора точек.

Определение[править | править код]

Пусть функция f задана на (связном) множестве X, и фиксированы попарно различные точки {displaystyle x_{0},;ldots ,;x_{n}in X.}

Тогда
разделённой разностью нулевого порядка функции f в точке x_{j} называют значение {displaystyle f(x_{j}),} а разделённую разность порядка k для системы точек {displaystyle (x_{j},;x_{j+1},;ldots ,;x_{j+k})} определяют через разделённые разности порядка (k-1) по формуле

{displaystyle f(x_{j};;x_{j+1};;ldots ;;x_{j+k-1};;x_{j+k})={frac {f(x_{j+1};;ldots ;;x_{j+k-1};;x_{j+k})-f(x_{j};;x_{j+1};;ldots ;;x_{j+k-1})}{x_{j+k}-x_{j}}},}

в частности,

{displaystyle f(x_{0};;x_{1})={frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}},}
{displaystyle f(x_{0};;x_{1};;x_{2})={frac {f(x_{1};;x_{2})-f(x_{0};;x_{1})}{x_{2}-x_{0}}}={dfrac {{dfrac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}-{dfrac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}}{x_{2}-x_{0}}},}
{displaystyle f(x_{0};;x_{1};;ldots ;;x_{n-1};;x_{n})={frac {f(x_{1};;ldots ;;x_{n-1};;x_{n})-f(x_{0};;x_{1};;ldots ;;x_{n-1})}{x_{n}-x_{0}}}.}

Свойства[править | править код]

Для разделённой разности верна формула

{displaystyle f(x_{0};;x_{1};;ldots ;;x_{n})=sum _{j=0}^{n}{dfrac {f(x_{j})}{prod limits _{i=0 atop ineq j}^{n}(x_{j}-x_{i})}},}

в частности,

{displaystyle f(x_{0};;x_{1})={frac {f(x_{1})}{x_{1}-x_{0}}}+{frac {f(x_{0})}{x_{0}-x_{1}}},}
{displaystyle f(x_{0};;x_{1};;x_{2})={frac {f(x_{2})}{(x_{2}-x_{1})(x_{2}-x_{0})}}+{frac {f(x_{1})}{(x_{1}-x_{2})(x_{1}-x_{0})}}+{frac {f(x_{0})}{(x_{0}-x_{2})(x_{0}-x_{1})}}.}

Разделённая разность является симметрической функцией своих аргументов, то есть при любой их перестановке её значение не меняется, в частности,

{displaystyle f(x_{0};;x_{1})=f(x_{1};;x_{0}),}
{displaystyle f(x_{0};;x_{1};;x_{2})=f(x_{1};;x_{0};;x_{2})=f(x_{2};;x_{1};;x_{0}),}
{displaystyle f(x_{0};;x_{1};;ldots ;;x_{n-1};;x_{n})=f(x_{n};;x_{n-1};;ldots ;;x_{1};;x_{0}).}

При фиксированной системе точек {displaystyle (x_{0},;ldots ,;x_{n})} разделённая разность является линейным функционалом, то есть для функций f и g и скаляров a и b:

{displaystyle (acdot f+bcdot g)(x_{0};;ldots ;;x_{n})=acdot f(x_{0};;ldots ;;x_{n})+bcdot g(x_{0};;ldots ;;x_{n}).}

Применение[править | править код]

С помощью разделённых разностей функции f для узлов {displaystyle (x_{0},;ldots ,;x_{n})} можно записать как интерполяционный многочлен Ньютона «вперёд»:

{displaystyle {begin{array}{rcl}L_{n}(x)&=&f(x_{0})+f(x_{0};;x_{1})cdot (x-x_{0})+f(x_{0};;x_{1};;x_{2})cdot (x-x_{0})cdot (x-x_{1})+ldots +f(x_{0};;ldots ;;x_{n})cdot prod _{k=0}^{n-1}(x-x_{k})=\&=&f(x_{0})+(x-x_{0})cdot left(f(x_{0};;x_{1})+(x-x_{1})cdot left(f(x_{0};;x_{1};;x_{2})+ldots +(x-x_{n-1})cdot f(x_{0};;ldots ;;x_{n})ldots right)right),end{array}}}

так и интерполяционный многочлен Ньютона «назад»:

{displaystyle {begin{array}{rcl}L_{n}(x)&=&f(x_{n})+f(x_{n};;x_{n-1})cdot (x-x_{n})+f(x_{n};;x_{n-1};;x_{n-2})cdot (x-x_{n})cdot (x-x_{n-1})+ldots +f(x_{n};;ldots ;;x_{0})cdot prod _{k=1}^{n}(x-x_{k})=\&=&f(x_{n})+(x-x_{n})cdot left(f(x_{n};;x_{n-1})+(x-x_{n-1})cdot left(f(x_{n};;x_{n-1};;x_{n-2})+ldots +(x-x_{1})cdot f(x_{n};;ldots ;;x_{0})ldots right)right).end{array}}}

Преимущества:

С использованием

{displaystyle left{{begin{array}{rcl}omega _{j}(x)&=&(x-x_{0})cdot ldots cdot (x-x_{j-1})=prod limits _{k=0}^{j-1}(x-x_{k})=omega _{j-1}(x)cdot (x-x_{j-1}),;j>0,\omega _{0}(x)&=&1end{array}}right.}

первую из формул можно записать в виде

{displaystyle L_{n}(x)=sum _{j=0}^{n}f(x_{0};;ldots ;;x_{j})cdot omega _{j}(x).}

С помощью многочлена Ньютона можно также получить следующее представление разделённых разностей в виде отношения определителей:

{displaystyle f(x_{0};ldots ;x_{n})={frac {left|{begin{array}{ccccc}1&x_{0}&ldots &x_{0}^{n-1}&f(x_{0})\vdots &vdots &ddots &vdots &vdots \1&x_{n}&ldots &x_{n}^{n-1}&f(x_{n})end{array}}right|}{left|{begin{array}{ccccc}1&x_{0}&ldots &x_{0}^{n-1}&x_{0}^{n}\vdots &vdots &ddots &vdots &vdots \1&x_{n}&ldots &x_{n}^{n-1}&x_{n}^{n}end{array}}right|}}.}

История[править | править код]

Ньютон использовал в своей общей формуле интерполяции (см. выше) разделённые разности, но термин, по-видимому, был введён О. де Морганом в 1848 году[1].

Пример[править | править код]

Пример для функции {displaystyle f(x)=2x^{3}-2x^{2}+3x-1}

На приведённом изображении рассмотрен пример вычисления разделённых разностей для

{displaystyle {begin{array}{rcl}f(x)&=&2x^{3}-2x^{2}+3x-1,\x_{i}&=&i,;i=0,ldots ,n,\n&=&5.end{array}}}

См. также[править | править код]

  • Конечные разности
  • Численное дифференцирование

Ссылки[править | править код]

  • Интерполирование Эрмита с использованием разделенных разностей.

Литература[править | править код]

  • Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. — 3-е изд., доп. и перераб. — М.: БИНОМ. Лаборатория знаний, 2004. — 636 с., илл. — ISBN 5-94774-175-X.
  • Корн Г. (Granino A. Korn, Ph.D.), Корн Т. (Theresa M. Korn, M.S.) Справочник по математике (для научных работников и инженеров) (англ. Mathematical handbook for scientist and engineers, 1968). — М.: Наука, 1973. — 832 с., илл.

Примечания[править | править код]

  1. ↑ Конечные разности. Архивная копия от 12 августа 2010 на Wayback Machine в энциклопедии Кругосвет
Источник

Рассмотрим случай,
когда значение функции заданы в
неравноотстающих узлах. При этом вместо
конечных разностей рассматриваются
разделенные разности, являющиеся в
некотором смысле аналогом понятия
производной и определяющиеся следующим
образом.

Пусть функция y
= f(x)
задана своими значениями
,

,
,…,
,
… в узлахпроизвольной сетки.

Разделенные
разности нулевого порядка
совпадают со значениями функции в точках.Разделенными
разностями первого порядка
называются отношения

Разделенными
разностями второго порядка
называются отношения

В общем случае
разделенная
разность k-го
порядка
определяется через разделенную
разность(k-1)-го
порядка по формуле

. (4.36)

Приведем некоторые
свойства разделенных разностей

1. Разделенные
разности всех порядков являются линейной
комбинацией значений
,
а именно справедлива следующая формула:

. (4.37)

2. Разделенная
разность есть симметрическая функция
своих аргументов, т.е. не меняется при
любой их перестановке.

3. Разделенная
разность удовлетворяет равенству

, (4.38)

4. Если узлы
принадлежат отрезкуи функцияf(x)
имеет на
непрерывную производнуюk-го
порядка, то существует такая точка
,
что

. (4.39)

Из этого свойства
вытекает простое следствие. Пусть

есть многочлен
k-й
степени. Тогда, очевидно,
,
и соотношение (4.39) дает для разделенной
разности значение

Итак, у всякого
многочлена k-й
степени разделенные разности k
– го порядка равны постоянной величине
– коэффициенту при старшей степени
многочлена. Разделенные разности высших
порядков (больше k),
очевидно, равны нулю.

4.3.8 Интерполяционный многочлен Ньютона для произвольной сетки узлов

Используя форму
Лагранжа, представим интерполяционный
многочлен в следующем виде:

Здесь
;;
(k
= 1,2,…n)
– интерполяционные многочлены в форме
Лагранжа, построенные по узлам
.

Рассмотрим разности

Таким образом,
используя формулу (3.37), получим

(4.40)

а интерполяционный
многочлен принимает форму

(4.41)

Эта форма называется
интерполяционным
многочленом Ньютона с раздельными
разностями.

Выражение для
погрешности имеет тот же вид, что и в
случае многочлена Лагранжа [см.формулу(4.9)].

Отметим, что в
формуле (4.41) интерполяционного многочлена
на узлы накладывается единственное
условие – их несовпадение. Поэтому
нумерацию узлов можно произвести в
произвольном порядке. Например, индексом
«0» часто обозначают последующий узел
таблицы, за
принимают предпоследний узел и обозначают
егои т.д. В этом случае многочлен (4.41)
принимает форму

(4.42)

и ее называют
многочленом
Ньютона для интерполирования назад.

Сравнение форм
Лагранжа и Ньютона
интерполяционного многочлена позволяет
рекомендовать использование представления
в форме Лагранжа, во-первых, в теоретических
исследованиях, например при изучении
вопроса о сходимости
к;
во-вторых, при интерполировании нескольких
функций на одной и той же сетке узлов,
поскольку в этом случае можно один раз
вычислить множители Лагранжа
и использовать
их для интерполяции всех функций.

Представление в
форме Ньютона оказывается более удобным
в практических расчетах. Действительно,
число используемых узлов и степень
интерполяционного многочлена часто
заранее не известно, а при переходе от
n
узлов к (n+1)-му
узлу в форме Ньютона добавляется лишь
один член, имеющий смысл поправки к уже
вычисленному значению. В то же время в
форме Лагранжа добавление еще одного
слагаемого сопровождается полным
пересчетом полученного ранее результата.
Кроме того, в вычислительной практике
интерполяция обычно осуществляется на
не большом отрезке длиной h<1.
При этом слагаемые формы Ньютона имеет
порядок
,…, т.е. расположены в порядке убывания,
что оказывается полезным при определении
точности результата интерполирования.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Рассмотрим значенияФункцииВ точках

… Выделим всевозможные пары соседних значений:… ив каждом случае вычтем пре

Дыдущее значение из последующего, получим разности:

Эти разности называют конечными разностями первого порядка или просто первыми разностями. Обозначения первых разностей:

(31.4)

Разностями второго порядка или вторыми разностями называют разности первых разностей  _  Обозначают вторые разности через

(31.5)

. Разности третьего порядка (или третьи разности) определяются и обозначаются следующим образом:

Аналогично определяются последующее разности. Разности (и + 1)-го порядка получаются из разностей и-го порядка по формулам

(31.6)

Таблица разностей различных порядков строится согласно схеме (табл. 31.1).

Таблица 31.1

Каждое число из этой таблицы (начиная с третьего столбца) является разностью двух смежных чисел столбца слева (из нижнего числа вычитается верхнее; разность записывается в следующем столбце между этими числами). Третий столбец содержит первые разности, четвертый – вторые и т. д.

Для контроля вычислений при составлении таблицы разностей пользуются следующим утверждением: сумма чисел в каждом столбце разностей равна разности крайних чисел предыдущего столбца.

Разделенные разности первого порядка определяются формулами

(31.7)

Разделенные разности второго порядка получаются из разделенных разностей первого порядка по формулам

(31.8)

Аналогично определяются разделенные разности третьего порядка:

(31.9)

Разделенные разностиГо порядка получаются из разностей-го порядка по формулам

(31.10)

В случае равноотстоящих узлов с шагомРазделенные разно

Сти различных порядков имеют вид:

(31.11)

(31.12)

Пр имер 31.3. Составить таблицу разностей различных порядков при следующих значенияхИ

По формулам (31.4) находим первые разности:

В

Соответствии с формулами (31.5) получаем разности второго порядка:

Аналогично находим разности третьего порядка: ,.И разность

Четвертого порядка

Полученные разности можно представить в виде табл. 31.2.

Таблица 31.2

Замечание. Последние две строки служат для контроля вычислений: в строкеЧисла равны суммам всех чисел, расположенным в соответствующем столбце, в строке– разности последнего и первого числа соответствующего столбца. Совпадение этих чиселВ таблице – по диа

Гонали) означает, что вычисления таблицы верны.

< Предыдущая   Следующая >
Источник

Интерполяция по Ньютону

Дана табличная функция:

i xi yi
0 x0 y0
1 x1 y1
2 x2 y2
 …  … …
n xn yn

или

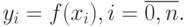y_i = f(x_i), i=overline{0,n}. (
11.1)

Точки с координатами (xi, yi) называются узловыми точками или узлами.

Количество узлов в табличной функции равно

Необходимо найти значение этой функции в промежуточной точке, например, x=D, причем D in[x_0,x_n].

Для решения задачи строим интерполяционный многочлен.

Интерполяционный многочлен по формуле Ньютона имеет вид:

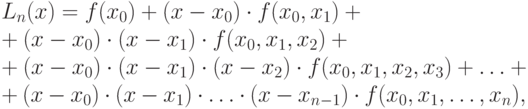L_n(x) = f(x_0) + (x - x_0) cdot f(x_0,x_1) +\ + (x - x_0) cdot(x - x_1) cdot f(x_0,x_1,x_2) +\ + (x - x_0) cdot(x - x_1) cdot(x - x_2) cdot f(x_0,x_1,x_2,x_3) + ldots +\ + (x - x_0) cdot(x - x_1) cdot ldots cdot (x - x_{n-1}) cdot f(x_0,x_1, ldots,x_n), (
11.7)

где

n – степень многочлена,

f(x_0), f(x_0,x_1), f(x_0,x_1,x_2), f(x_0,x_1,ldots, x_n) – разделенные разности 0-го, 1-го, 2-го,:., n-го порядка, соответственно.

Разделенные разности

Значения f(x0), f(x1), : , f(xn), т.е. значения табличной функции в узлах, называются разделенными разностями нулевого порядка (k=0).

Отношение f(x_0,x_1) = frac{f(x_1)-f(x_0)}{x_1 - x_0} называется разделенной разностью первого порядка (k=1) на участке [x0, x1] и равно разности разделенных разностей нулевого порядка на концах участка [x0, x1], разделенной на длину этого участка.

Для произвольного участка [xi, xi+1] разделенная разность первого порядка (k=1) равна

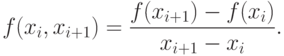
f(x_i,x_{i+1}) = frac{f(x_{i+1})-f(x_i)}{x_{i+1} - x_i}.

Отношение 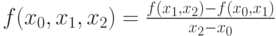f(x_0,x_1,x_2) = frac{f(x_1,x_2)-f(x_0,x_1)}{x_2 - x_0} называется разделенной разностью второго порядка (k=2) на участке [x0, x2] и равно разности разделенных разностей первого порядка, разделенной на длину участка [x0, x2].

Для произвольного участка [xi, xi+2] разделенная разность второго порядка (k=2) равна

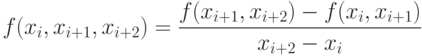
f(x_i,x_{i+1},x_{i+2}) = frac{f(x_{i+1},x_{i+2}) - f(x_i,x_{i+1})}{x_{i+2} - x_i}

Таким образом, разделенная разность k -го порядка на участке [xi, xi+k] может быть определена через разделенные разности (k-1) -го порядка по рекуррентной формуле:

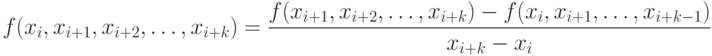f(x_i,x_{i+1},x_{i+2}, ldots,x_{i+k}) = frac{ f(x_{i+1},x_{i+2}, ldots,x_{i+k}) - f(x_i,x_{i+1}, ldots,x_{i+k-1})}{x_{i+k} - x_i} (
11.8)

где

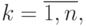
k=overline{1,n},

i=overline{0,n-k},

n – степень многочлена.

Максимальное значение k равно n. Тогда i =0 и разделенная разность n -го порядка на участке [x0,xn] равна f(x_0,x_i, ldots,x_n) = frac{ f(x_1,x_2, ldots,x_n) - f(x_0,x_1, ldots,x_n-1)}{x_n - x_0}, т.е. равна разности разделенных разностей (n-1) -го порядка, разделенной на длину участка [x0,xn].

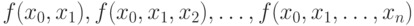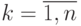Разделенные разности f(x_0,x_1), f(x_0,x_1,x_2), ldots, f(x_0,x_1,ldots, x_n) являются вполне определенными числами, поэтому выражение (11.7) действительно является алгебраическим многочленом n -й степени. При этом в многочлене (11.7) все разделенные разности определены для участков [x0, x0+k], k=overline{1,n}.

Лемма: алгебраический многочлен (11.7), построенный по формулам Ньютона, действительно является интерполяционным многочленом, т.е. значение многочлена в узловых точках равно значению табличной функции

L_n(x_i) = f(x-i) = y_i; i=0,1, ldots n.

Докажем это. Пусть х=х0, тогда многочлен (11.7) равен

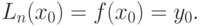
L_n(x_0) = f(x_0) = y_0.

Пусть х=х1, тогда многочлен (11.7) равен

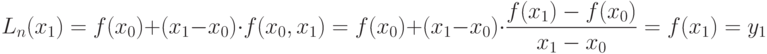
L_n(x_1) = f(x_0) + (x_1 - x_0) cdot f(x_0,x_1) = f(x_0) + (x_1 - x_0) cdot frac{f(x_1) - f(x_0)}{x_1 - x_0} = f(x_1) = y_1

Пусть х=х2, тогда многочлен (11.7) равен

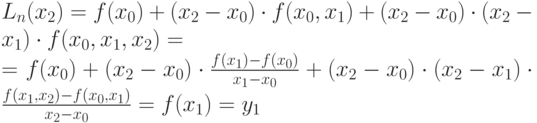
L_n(x_2) = f(x_0) + (x_2 - x_0) cdot f(x_0,x_1) + (x_2 - x_0) cdot (x_2 - x_1) cdot f(x_0,x_1,x_2) =\= f(x_0) + (x_2 - x_0) cdot frac{f(x_1) - f(x_0)}{x_1 - x_0}+ (x_2 - x_0) cdot (x_2 - x_1) cdot frac{f(x_1,x_2) - f(x_0,x_1)}{x_2 - x_0}= f(x_1) = y_1

Заметим, что решение задачи интерполяции по Ньютону имеет некоторые преимущества по сравнению с решением задачи интерполяции по Лагранжу. Каждое слагаемое интерполяционного многочлена Лагранжа зависит от всех значений табличной функции yi, i=0,1,:n. Поэтому при изменении количества узловых точек N и степени многочлена n (n=N-1) интерполяционный многочлен Лагранжа требуется строить заново. В многочлене Ньютона при изменении количества узловых точек N и степени многочлена n требуется только добавить или отбросить соответствующее число стандартных слагаемых в формуле Ньютона (11.7). Это удобно на практике и ускоряет процесс вычислений.

Источник

Макеты страниц

1. Таблица разделенных разностей.

Пусть функция задана на таблице значений аргумента с произвольным (не обязательно постоянным) шагом, причем точки таблицы занумерованы в произвольном (не обязательно возрастающем) порядке. Величины

принято называть разделенными разностями первою порядка функции Разделенные разности второю порядка определяются формулой

Аналогично определяются разделенные разности третьего и более высоких порядков. Общее определение разделенной разности порядка таково:

Таблицу разделенных разностей обычно располагают следующим образом:

Таблица 11.6 (см. скан)

2. Свойства разделенных разностей.

Разделенные разности обладают рядом замечательных свойств. Перечислим без доказательства некоторые из них.

1°. Разделенная разность является симметричной функцией своих аргументов ее значение не меняется при любой их перестановке).

2°. Пусть функция имеет на отрезке содержащем точки производную порядка k. Тогда справедливо равенство

где некоторая точка, расположенная на интервале

3°. В случае, когда таблица значений аргумента имеет постоянный шаг разделенная и конечная разности связаны равенством

Пример 11.7. Приведем таблицу (табл. 11.7) разделенных разностей для функции, заданной табл. 11.1. Вычисления произведены на -разрядной десятичной ЭВМ.

Таблица 11.7 (см. скан)

Перенумеруем теперь узлы, положив Тогда таблица разделенных разностей примет следующий вид:

Таблица 11.8 (см. скан)

В табл. 11.8 подчеркнуты разделенные разности, которые совпадают (как и должно быть в силу свойства 1°) с точностью до вычислительной погрешности с соответствующими разделенными разностями из табл. 11.7 (они также подчеркнуты).

Источник

Добавить комментарий