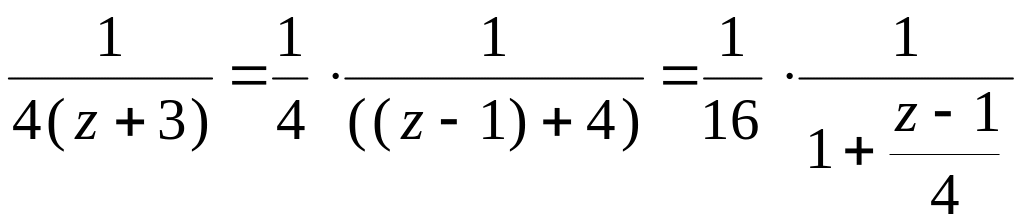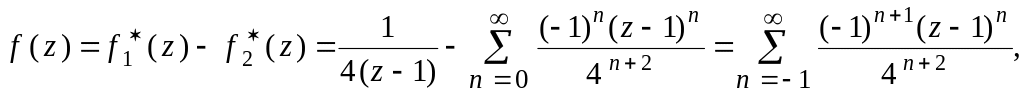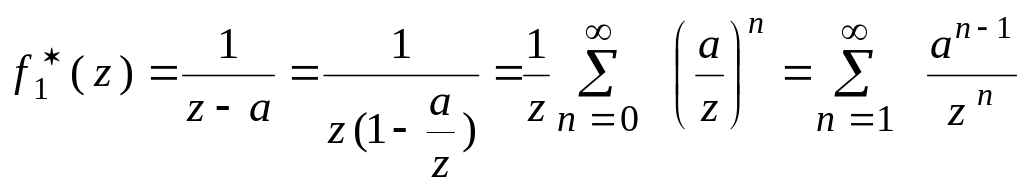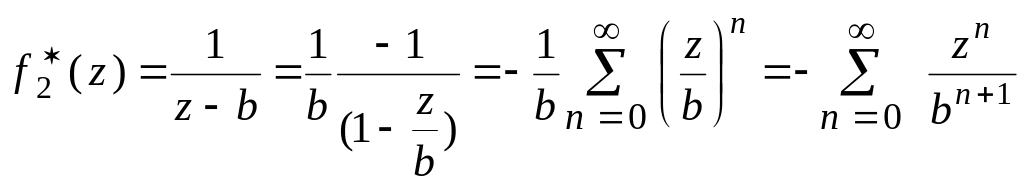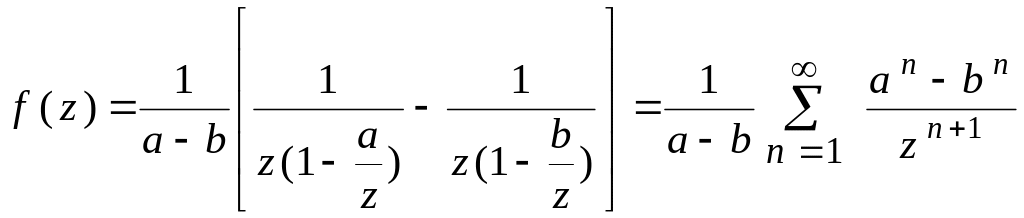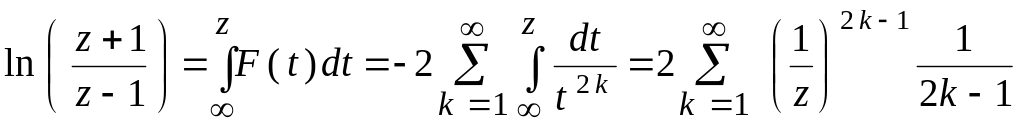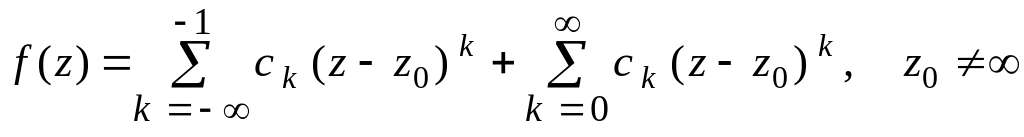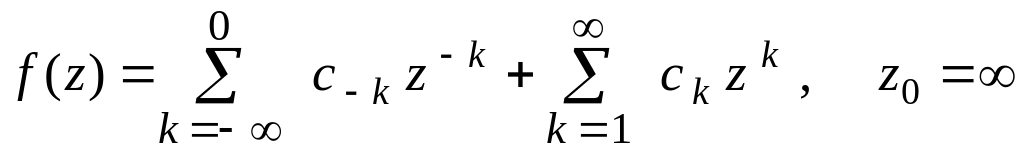Как найти разложение в ряд лорана - Сайт, где вы сможете решить свои вопросы

Ряд Лорана и разложение функций по целым степеням

Ранее рассматривалась задача разложения функции в степенной ряд $sum_{n=0}^{infty} c_n(z-z_0)^n$ , при этом функция предполагалась аналитической в точке z_0 , а ряд сходящимся в круге |z-z_0|<R,~ 0<Rleqslantinfty .

Другим частным случаем функциональных рядов, наряду со степенными, является ряд $sum_{n=-infty}^{infty} c_n(z-z_0)^n$ ряд по целым степеням разности (z-z_0) . Такой ряд сходится в кольце r<|z-z_0|<R,~ r geqslant0,~ Rleqslantinfty и его сумма — функция аналитическая внутри этого кольца.

Можно рассматривать задачу разложения функции, аналитической в кольце r<|z-z_0|<R . Имеет место теорема, аналогичная теореме 3.3.

Теорема Лорана о разложении функции в ряд по целым степеням

Теорема 3.5 (Лорана). Функция f(z) , аналитическая в кольце, представляется в этом кольце сходящимся рядом по целым степеням, т.е. имеет место равенство

$f(z)=sum_{n=-infty}^{infty} c_n(z-z_0)^n.$

(3.24)

Коэффициенты ряда вычисляются по формуле

$c_n= frac{1}{2pi i} ointlimits_{gamma} frac{f(z)}{(z-z_0)^{n+1}},dz,quad n=0,pm1,pm2,ldots,$

(3.25)

где gamma — произвольный контур, принадлежащий кольцу и охватывающий точку z_0 ; в частности, gamma — окружность |z-z_0|=rho,~ r<rho<R .

Имеют место следующие определения.

1. Ряд $sum_{n=-infty}^{infty} c_n(z-z_0)^n$ коэффициенты которого вычисляются по формуле (3.25), называется рядом Лорана функции f(z) .

Заметим, что формула (3.16) получается из формулы (3.25) при ngeqslant0 , но для коэффициентов ряда Лорана не имеет места формула вида (3.17), так как функция в точке z_0 может быть не определена.

2. Совокупность членов ряда с неотрицательными степенями — $sum_{n=0}^{infty} c_n(z-z_0)^n$ называется правильной частью ряда Лорана; члены с отрицательными степенями образуют главную часть ряда Лорана: $sum_{n=-infty}^{-1} c_n(z-z_0)^n$ или $sum_{n=1}^{infty} frac{c_{-n}}{(z-z_0)^n}$ .

3. При r=0 получаем частный случай кольца — вырожденное кольцо 0<|z-z_0|<R . Это — круг с выколотым центром. Точка z_0 — особая точка функции, и разложение в этом случае называется разложением функции в окрестности особой точки.

4. При R=infty область |z-z_0|>r есть внешность круга. В частном случае при z_0=0 — внешность круга |z|>r . Разложение в этом случае называется разложением в окрестности бесконечно удаленной точки и имеет вид

$f(z)= sum_{n=-infty}^{infty}c_nz^n= sum_{n=0}^{infty} c_nz^n+ sum_{n=-infty}^{-1}c_nz^n,$

(3.26)

или, что то же,

$f(z)= sum_{n=0}^{infty} c_nz^n+ sum_{n=1}^{infty} frac{c_{-n}}{z^n},.$

(3.27)

Здесь совокупность неотрицательных степеней $sum_{n=0}^{infty}c_nz^n$ образует главную часть ряда Лорана в окрестности бесконечно удаленной точки; совокупность отрицательных $sum_{n=-infty}^{-1}c_nz^n$ — правильную часть ряда Лорана в окрестности бесконечно удаленной точки.

Пример 3.30. Исследовать возможность разложения функции $f(z)= sqrt{frac{z}{(z+1)(z-2)}}$ в ряды Тейлора и Лорана.

Решение

Функцию $f(z)= sqrt{frac{z}{(z+1)(z-2)}}$ нельзя разложить в ряд по степеням ни в окрестности точки z_0=0 (ряд Тейлора), ни в окрестности точки z_0=infty (ряд Лорана), так как эти точки являются точками ветвления функции и в их окрестностях невозможно выделение однозначных ветвей.

Невозможны также разложения этой функции в ряды по степеням (z+1) и (z-2) , поскольку точки z=-1 и z=2 — также точки ветвления. Разложения по степеням (z-z_0) , где z_0ne0,~z_0ne-1,~ z_0ne2 , возможны.

Функция же $f(z)= frac{z}{(z+1)(z-2)}$ раскладывается по степеням и в ряд Тейлора в круге |z|<1 и в ряд Лорана в области |z|>2 (окрестность бесконечно удаленной точки), а также в кольце 1<|z|<2 . Возможны разложения и по степеням (z+1) и (z-2) в кольцевых областях, а также в окрестностях особых точек z=-1,~ z=2 .

Так как ряды по целым степеням обладают свойствами степенных рядов (см. утверждение 3.2), то, учитывая теорию и практику решения задачи разложения функции в степенной ряд (см. утверждения 3.3 и 3.4), можно сформулировать следующее утверждение.

Утверждение 3.6

1. Функция, аналитическая в кольце r<|z-z_0|<R,~ rgeqslant0,~ Rleqslantinfty , разлагается в этом кольце в ряд Лорана (3.24), коэффициенты которого вычисляются по формуле (3.25).

2. Для коэффициентов ряда имеет место формула оценки коэффициентов — неравенство Коши:

$|c_n|leqslant frac{M}{rho^n},quad n=0,pm1,pm2,ldots$

(3.28)

где $M=max_{zingamma}|f(z)|,~rho$ — радиус окружности (частный случай контура gamma ), по которой производится интегрирование в (3.25).

3. На границах кольца сходимости ряда Лорана есть хотя бы по одной особой точке функции f(z) — его суммы.

4. Частными случаями рядов Лорана являются разложения функции в окрестности особой точки z_0~(r=0) и окрестности бесконечно удаленной точки (z_0=0,~ R=infty) .

5. Разложение в ряд Лорана сводится к разложению в ряд Тейлора, используются основные разложения и действия над рядами.

6. При разложении рациональных дробей, как и в случае рядов Тейлора, выдерется целая часть неправильной дроби, а правильная записывается в виде суммы элементарных дробей, для разложения которых используется формула суммы членов бесконечно убывающей геометрической прогрессии. При этом элементарные дроби преобразуются следующим образом:

– для получения правильной части, т.е. ряда, сходящегося в круге |z-z_0|<R , разложение элементарной дроби записывается в виде

$frac{1}{a-(z-z_0)}= frac{frac{1}{a}}{1-frac{z-z_0}{a}}= sum_{n=0}^{infty} frac{(z-z_0)^n}{a^{n+2}}= sum_{n=0}^{infty} c_n(z-z_0)^n,quad |z-z_0|<|a|,quad ane0;$

– для получения главной части, т.е. ряда, сходящегося вне круга |z-z_0|>r , изложение элементарной дроби записывается в виде

$frac{1}{a-(z-z_0)}= frac{-frac{1}{z-z_0}}{1-frac{a}{z-z_0}}= -sum_{n=0}^{infty} frac{a^n}{(z-z_0)^{n+1}}= sum_{n=1}^{infty} frac{c_n}{(z-z_0)^n},,quad left|frac{a}{z-z_0}right|<1~ Leftrightarrow~ |z-z_0|>|a|.$

Примеры разложения функций в ряд Лорана

Пример 3.31. Разложить функцию $f(z)=frac{z+2}{z^2-2z-3}$ в ряд Лорана по степеням .

Решение

Функция является аналитической всюду, кроме точек z_1=-1 и z_2=3 , в частности: в круге |z|<1 , в кольце 1<|z|<3 и в окрестности бесконечно удаленной точки |z|>3 (рис. 3.4).

В круге |z|<1 функция раскладывается в ряд Тейлора (см. пример 3.21). Получим разложения в двух других областях.

Рассмотрим разложение в кольце. Дробь правильная, ее разложение на элементарные дроби получено в примере (3.21):

$f(z)= frac{z+2}{z^2-2z-3}= frac{z+2}{(z+1)(z-3)}= -frac{1}{4}cdot frac{1}{z+1}+ frac{5}{4}cdot frac{1}{z-3},.$

Чтобы получить разложение в кольце, первое слагаемое раскладываем в области |z|>1 , т.е. записываем главную часть ряда, второе — в круге |z|<3 — правильная часть. Получаем разложения:

$begin{gathered}frac{1}{z+1}= frac{1 slash z}{1+1 slash z}= frac{1 slash z}{1-(-1 slash z)}= sum_{n=0}^{infty} frac{(-1)^n}{z^{n+1}}= sum_{n=1}^{infty} frac{(-1)^{n-1}}{z^n},quad left|-frac{1}{z}right|= frac{1}{|z|}<1~ Leftrightarrow~ |z|>1;\[2pt] frac{1}{z-3}= frac{-1 slash 3}{1-z slash 3}= -sum_{n=0}^{infty} frac{z^n}{3^{n+1}},quad |z|<3. end{gathered}$

Записываем окончательный результат:

$frac{z+2}{z^2-2z-3}= sum_{n=1}^{infty} frac{(-1)^n}{4cdot z^n}-sum_{n=0}^{infty} frac{5cdot z^n}{4cdot 3^{n+1}},quad 1<|z|<3.$

Здесь первое слагаемое — главная часть, а второе — правильная часть ряда Лорана в кольце 1<|z|<3 .

Чтобы получить разложение в области |z|>3 — окрестности бесконечно удаленной точки, нужно и второе слагаемое разложить по отрицательным степеням:

$frac{1}{z-3}= frac{1}{z}cdot frac{1}{1-frac{3}{z}}= sum_{n=0}^{infty} frac{3^n}{z^{n+1}},~~ left|frac{3}{z}right|<1$ или $frac{1}{z-3}= sum_{n=1}^{infty} frac{3^{n-1}}{z^n},~~ |z|>3.$ .

В результате получаем разложение в окрестности бесконечно удаленной точки:

$frac{z+2}{z^2-2z-3}= sum_{n=1}^{infty} frac{(-1)^n}{4z^n}+ frac{5}{4} sum_{n=1}^{infty} frac{3^{n-1}}{z^n}= sum_{n=1}^{infty} frac{(-1)^n+5cdot3^{n-1}}{4}cdot frac{1}{z^n},,quad |z|>3.$

Заметим, что главная часть ряда отсутствует, так как в разложении присутствуют только члены с отрицательными степенями.

Круг и кольцо на комплексной плоскости

Пример 3.32. Разложить функцию $f(z)=frac{z+2}{z^2-2z-3}$ в ряд Лорана: а) по степеням (z-2) ; б) по степеням (z-1) .

Решение

а) Особыми точками функции являются точки z_1=-1 и z_2=3 , причем вторая — ближайшая к центру разложения, т.е. к z_0=2 (рис. 3.5,а); расстояние между z_0=2 и z_2=3 равно единице, поэтому в круге |z-2|<1 функция раскладывается в ряд Тейлора. Расстояние от z_0=2 до другой особой точки z_1=-1 равно трем, и в кольце 1<|z-2|<3 данная функция является аналитической и раскладывается в ряд Лорана. Аналитической она является и в области |z-2|>3 и раскладывается в ней также в ряд Лорана по степеням (z-2) . Оба разложения получаем, как в предыдущем примере, причем замену z-2=t можно сделать в исходной дроби, а можно не вводить обозначения (см. пример 3.21). Запишем разложения в каждой из двух областей, учитывая представление функции в виде суммы элементарных дробей (см. примеры 3.21 и 3.31):

$f(z)= frac{z+2}{z^2-2z-3}= frac{z+2}{(z+1)(z-3)}= -frac{1}{4}cdot frac{1}{z+1}+ frac{5}{4}cdot frac{1}{z-3},.$

Разложение в кольце 1<|z-2|<3,colon

$begin{aligned}frac{1}{z+1}&= frac{1}{z-2+3}= frac{1}{3! left(1+frac{z-2}{3}right)}= frac{1}{3! left(1-left(-frac{z-2}{3}right)right)}= sum_{n=0}^{infty} frac{(-1)^n(z-2)^n}{3^{n+1}},quad |z-2|<3;\[2pt] frac{1}{z-3}&= frac{1}{z-2-1}= frac{1}{z-2}cdot frac{1}{1-frac{1}{z-2}}= sum_{n=0}^{infty} frac{1}{(z-2)^{n+1}}= sum_{n=1}^{infty} frac{1}{(z-2)^n},,quad |z-2|>1.end{aligned}$

Получаем ответ: $frac{z+2}{z^2-2z-3}= sum_{n=0}^{infty} frac{(-1)^{n+1}}{4cdot3^{n+1}}(z-2)^n+ sum_{n=1}^{infty} frac{5}{4(z-2)^n},~1<|z-2|<3$ .

Разложение в области |z-2|>3,colon

$begin{aligned}frac{1}{z+1}&= frac{1}{z-2+3}= frac{1}{z-2}cdot frac{1}{1+ frac{3}{z-2}}= frac{1}{z-2}cdot frac{1}{1-left(-frac{3}{z-2}right)}= sum_{n=0}^{infty} frac{(-1)^n3^n}{(z-2)^{n+1}}= sum_{n=0}^{infty} frac{(-1)^{n-1}3^{n-1}}{(z-2)^n},~~ |z-2|>3;\[2pt] frac{1}{z-3}&= sum_{n=1}^{infty} frac{1}{(z-2)^n},quad |z-2|>1. end{aligned}$

Получаем ответ: $frac{z+2}{z^2-2z-3}= sum_{n=1}^{infty}! left(frac{(-1)^n3^{n-1}}{4}+ frac{5}{4}right)!cdot frac{1}{(z-2)^n},,~ |z-2|>3.$ .

б) Задача решается так же, как и в предыдущем пункте. Различие заключается в том, что в данном случае обе особые точки расположены на одном расстоянии от центра — точки z_0=1 . Поэтому разложения по степеням (z-1) могут быть получены в круге |z-1|<2 и в вырожденном кольце — в области |z-1|>2 (рис. 3.5,б). Разложение в круге | |z-1|<2 — ряд Тейлора — получено в примере 3.21. Запишем разложение в области |z-1|>2colon

$begin{aligned}frac{1}{z+2}&= frac{1}{z-1}cdot frac{1}{1+frac{1}{z-1}}= frac{1}{z-1}cdot frac{1}{1-left(-frac{1}{z-1}right)}= sum_{n=0}^{infty} frac{(-1)^n}{(z-1)^{n+1}}= sum_{n=1}^{infty} frac{(-1)^{n-1}}{(z-1)^n},,quad |z-1|>1;\[2pt] frac{1}{z-3}&= frac{1}{z-1-2}= frac{1}{z-1}cdot frac{1}{1-frac{2}{z-1}}= sum_{n=0}^{infty} frac{2^n}{(z-1)^{n+1}}= sum_{n=1}^{infty} frac{2^{n-1}}{(z-1)^n},,quad |z-1|>2. end{aligned}$

Получаем ответ: $frac{z+2}{z^2-2z-3}= sum_{n=1}^{infty}! left(frac{(-1)^n}{4}+ 5cdot2^{n-3}right)! frac{1}{(z-1)^n},,quad |z-1|>2.$ .

Пример 3.33. Записать разложения функции $f(z)=frac{z+2}{z^2-2z-3}$ в окрестностях особых точек.

Решение

Особыми точками дроби являются z_1=infty,~ z_2=-1,~ z_3=3 . Решим задачу для каждой особой точки z_0 .

Разложение в окрестности бесконечно удаленной точки (z_0=infty) получено в примере 3.31:

$frac{z+2}{z^2-2z-3}= sum_{n=1}^{infty} frac{(-1)^n+5cdot3^{n-1}}{4}cdot frac{1}{z^n},,quad |z|>3.$

Заметим, что в разложении отсутствует главная часть — совокупность членов с положительными степенями .

Запишем разложение в окрестности точки z_0=-1 . Расстояние до другой особой точки z=3 равно четырем, поэтому окрестность точки z_0=-1 — проколотая окрестность, которая записывается в виде 0<|z+1|<4 (рис. 3.6).

Пересечение окружностей на комплексной плоскости

В разложении $frac{z+2}{z^2-2z-3}= -frac{1}{4}cdot frac{1}{z+1}+ frac{5}{4}cdot frac{1}{z-3}$ исходной дроби на элементарные первое слагаемое записано по степеням (z+1) (уже разложено). Это разложение содержит только главную часть, состоящую из одного члена: здесь все c_k=0 , кроме $c_{-1}=-frac{1}{4}$ , и разложение имеет место в области |z+1|>0 . Второе слагаемое раскладываем в окрестности z_0=-1 и, так как для него эта точка не является особой, получим ряд Тейлора в круге |z+1|<4 . Для исходной дроби это будет правильная часть ряда Лорана:

$frac{1}{z-3}= frac{1}{z+1-4}= frac{-1}{4! left(1-frac{z+1}{4}right)}= -sum_{n=0}^{infty} frac{(z+1)^n}{4^{n+1}},,quad left|frac{z+1}{4}right|<1~ Leftrightarrow~ |z+1|<4.$

Получаем ответ: $frac{z+2}{z^2-2z-3}= frac{-1}{4}cdot frac{1}{z+1}-sum_{n=0}^{infty} frac{5(z+1)^{n}}{4^{n+2}},~ 0<|z+1|<4$ .

Для точки z_0=3 задача решается аналогично (рис. 3.6):

$frac{z+2}{z^2-2z-3}= frac{5}{4}cdot frac{1}{z-3}-frac{1}{4}cdot frac{1}{(z-3)+4}= frac{5}{4}cdot frac{1}{z-3}-frac{1}{4} sum_{n=0}^{infty} frac{(-1)^n(z-3)^n}{4^{n+1}},.$

Получаем ответ: $frac{z+2}{z^2-2z-3}= frac{5}{4}cdot frac{1}{z-3}+ sum_{n=0}^{infty} frac{(-1)^{n+1}}{4^{n+2}}(z-3)^n,~ 0<|z-3|<4$ — разложение функции в окрестности особой точки z_0=3 . Заметим, что в полученных разложениях в окрестности каждой особой точки главная часть содержит только одно слагаемое.

Пример 3.34. Исследовать разложения функции $f(z)=frac{z+2}{(z+1)^2(z-3)}$ по степеням (z-z_0) . Записать разложения в окрестностях особых точек.

Решение

Функция может быть разложена в ряд Тейлора по степеням (z-z_0) . окрестности любой конечной точки z_0ne-1,~z_0ne3 ; окрестностью будет круг |z-z_0|<r , где $r=minbigl{|z_0+1|,|z_0-3|bigr}$ — наименьшее из расстояний от точки z_0 до особых точек (рис. 3.7,а).

В ряд Лорана по степеням (z-z_0) функция может быть разложена в кольце r<|z-z_0|<R , где $r=minbigl{|z_0+1|,|z_0-3|bigr},$ $R=maxbigl{|z_0+1|,|z_0-3|bigr}$ и $operatorname{Re}z_0ne1$ , а также во внешности круга, т.е. в области |z-z_0|>R (рис. 3.7,а). Если $operatorname{Re}z_0=1$ , то разложение будет иметь место только в вырожденном кольце вида , так как в этом случае точка го одинаково удалена от обеих особых точек и r=R (рис. 3.7,б).

Расстояния от точек до особых точек на комплексной плоскости

Особенностью примера является наличие в знаменателе множителя (z+1)^2 , поэтому в разложении дроби на элементарные присутствует дробь $frac{1}{(z+1)^2}$ , а именно имеет место равенство

$frac{z+2}{(z+1)^2(z-3)}= frac{-5}{16}cdot frac{1}{z+1}+ frac{-1}{4}cdot frac{1}{(z+1)^2}+ frac{5}{16}cdot frac{1}{z-3},.$

Для разложения дроби $frac{1}{(z+1)^2}$ по степеням (z-z_0),~z_0ne-2 используется правило дифференцирования рядов (см. пример 3.22).

Запишем разложение функции в окрестности z_0 — особой точки.

В случае z_0=-1 в разложении дроби на элементарные две первые дроби представляют собой слагаемые требуемого вида (уже разложены): $frac{1}{z+1}=(z+1)^{-1},~ frac{1}{(z+ 1)^2}=(z+1)^{-2}$ . Эти разложения справедливы во всей плоскости с выколотой точкой z_0=-1 , т.е. в области |z+1|>0 .

От третьего слагаемого получаем правильную часть ряда Лорана:

$frac{1}{z-3}=-sum_{n=0}^{infty} frac{(z+1)^n}{4^{n+1}},,quad |z+1|<4.$

Окончательный ответ: $frac{z+2}{(z+1)^2(z-3)}= frac{-5}{16}cdot frac{1}{z+1}+ frac{-1}{4}cdot frac{1}{(z+1)^2}-sum_{n=0}^{infty} frac{5(z+1)^n}{4^{n+3}},~0<|z+1|<4$ .

В главной части разложения присутствуют два члена, при этом $c_{-1}=-frac{5}{16},~ c_{-2}=-frac{1}{4}$ .

В случае разложения в окрестности z_0=3 главная часть разложения содержит одно слагаемое $frac{5}{16}frac{1}{z-3}$ ; правильная получается от разложения дробей $frac{1}{z+1}$ и $frac{1}{(z+1)^2}$ по степеням (z-3) .

Найдем эти разложения:

$begin{gathered}frac{1}{z+1}= frac{1}{(z-3)+4}= sum_{n=0}^{infty} frac{(-1)^n}{4^{n+1}}(z-3)^n,quad |z-3|<4;\[2pt] frac{1}{(z+1)^2}=-left(frac{1}{z+1}right)'=-sum_{n=0}^{infty}! left(frac{(-1)^n}{4^{n+1}}(z-3)^nright)'= sum_{n=1}^{infty} frac{(-1)^{n+1}n}{4^{n+1}}(z-3)^{n-1}= sum_{n=0}^{infty} frac{(-1)^n(n+1)}{4^{n+2}}(z-3)^n,quad |z-3|<4.end{gathered}$

Записываем ответ: $frac{z+2}{(z+1)^2(z-3)}= frac{5}{16}cdot frac{1}{z-3}+ sum_{n=0}^{infty} frac{(-1)^{n+1}(n+6)}{4^{n+3}}(z-3)^n,quad 0<|z-3|<4.$

Пример 3.35. Разложить функцию $z^3e^{frac{1}{z}}$ в окрестностях точек z_0=0 и z_0=infty .

Решение

Оба разложения — разложения по степеням и получаются из основного разложения, а именно

$z^3e^{frac{1}{z}}= z^3! left(1+frac{1}{z}+ frac{1}{2!z^2}+ ldots+ frac{1}{n!z^n}+ ldotsright)!,$

или

$z^3e^{frac{1}{z}}=z^3+z^2+frac{1}{2!}z+frac{1}{3!}+frac{1}{4!z}+ ldots+ frac{1}{n!z^{n-3}}+ldots,quad |z|>0.$

Различие разложений заключается в записи правильной и главной частей. Так, в случае точки z_0=0 правильная часть содержит конечное число слагаемых — четыре и ответ записывается в виде

$z^3e^{frac{1}{z}}= z^3+z^2+frac{1}{2}z+frac{1}{6}+ sum_{n=-infty}^{-1} frac{z^n}{(3-n)!},quad |z|>0.$

В случае z_0=infty конечное число слагаемых образует главную часть и ответ записывается в виде

$z^3e^{frac{1}{z}}= z^3+z^2+frac{1}{2}z+ sum_{n=-infty}^{0} frac{z^n}{(3-n)!},quad |z|>0.$

Пример 3.36. Разложить по степеням функции: а) $frac{1-cos z}{z^2}$ ; б) $frac{sin z}{z}$ . С помощью полученных разложений найти $limlimits_{zto0}f(z)$ .

Решение

Применяем основные разложения для cos z и sin z и записываем ряды для заданных функций:

а)

$begin{aligned}frac{1-cos z}{z^2}&= frac{1}{z^2}! left(1-sum_{n=0}^{infty} frac{(-1)^n z^{2n}}{(2n)!} right)= frac{1}{z^2}! left(1-1-sum_{n=1}^{infty} frac{(-1)^n z^{2n}}{(2n)!} right)= frac{1}{z^2} sum_{n=1}^{infty} frac{(-1)^{n+1}z^{2n}}{(2n)!}=\ &= sum_{n=1}^{infty} frac{(-1)^{n+1}z^{2n-2}}{(2n)!}= sum_{n=0}^{infty} frac{(-1)^nz^{2n}}{(2n+2)!},,quad |z|>0.end{aligned}$

Таким образом, получаем результат: $frac{1-cos z}{z^2}= frac{1}{2}-frac{z^2}{4!}+ frac{z^4}{6!}-ldots$ .

Справа записан степенной ряд, сходящийся всюду, его сумма при zne0 равна $frac{1-cos z}{z^2}$ , а при z=0 , очевидно, равна $frac{1}{2}$ .

Получаем $limlimits_{zto0} frac{1-cos z}{z^2} = frac{1}{2}$ или $2limlimits_{} frac{1-cos z}{z^2}=1$ . Результат можно записать в виде асимптотической формулы:

$1-cos zsim frac{1}{2},z^2,quad zto0.$

б) $frac{sin z}{z}= frac{1}{z} sum_{n=1}^{infty} frac{(-1)^{n+1}z^{2n-1}}{(2n-1)!}= sum_{n=0}^{infty} frac{z^{2n}(-1)^n}{(2n+1)!},~~|z|>0$ .

Получен результат: $frac{sin z}{z}=1-frac{z^2}{3!}+ldots$ . Отсюда $limlimits_{zto0}frac{sin z}{z}=1$ . Результат, как и в случае “а”, можно записать в виде асимптотической формулы: sin zsim z,~zto0 .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Ряд Лорана комплексной функции — представление этой функции в виде степенного ряда, в котором присутствуют слагаемые с отрицательными степенями. Назван в честь французского математика П. А. Лорана.

Определение[править | править код]

Ряд Лорана в конечной точке ${displaystyle z_{0}in mathbb {C} }$ — функциональный ряд по целым степеням ${displaystyle (z-z_{0})}$ над полем комплексных чисел:

${displaystyle sum _{n=-infty }^{+infty }c_{n}(z-z_{0})^{n},quad }$

где переменная ${displaystyle zin {mathbb {C} }setminus {z_{0}}}$

, а коэффициенты ${displaystyle c_{n}in mathbb {C} }$

для

Этот ряд является суммой двух степенных рядов:

${displaystyle sum _{n=0}^{+infty }c_{n}(z-z_{0})^{n}}$ — часть по неотрицательным степеням ${displaystyle (z-z_{0})}$ ,
${displaystyle sum _{n=-infty }^{-1}{c_{n}}{(z-z_{0})^{n}}}$ — часть по отрицательным степеням ${displaystyle (z-z_{0})}$ .

Ряд Лорана сходится тогда и только тогда, когда сходятся обе (как по отрицательным, так и по положительным степеням) его части.

Если ${displaystyle A_{z_{0}}subseteq ({mathbb {C} }setminus {z_{0}})}$ — область сходимости ряда Лорана такая, что ${displaystyle z_{0}in partial {A_{z_{0}}}}$ , то для ${displaystyle A_{z_{0}}}$

ряд ${displaystyle sum _{n=0}^{+infty }c_{n}(z-z_{0})^{n}}$

называется правильной частью,

ряд ${displaystyle sum _{n=-infty }^{-1}{c_{n}}{(z-z_{0})^{n}}}$

называется главной частью.

Ряд Лорана в бесконечно удалённой точке ${displaystyle z_{0}=infty in {overline {mathbb {C} }}}$ — функциональный ряд по целым степеням над полем комплексных чисел:

${displaystyle sum _{n=-infty }^{+infty }c_{n}z^{n},quad }$

где переменная

{displaystyle zin mathbb {C} setminus {0}}

, а коэффициенты ${displaystyle c_{n}in mathbb {C} }$

для

По внешнему виду ряд для ${displaystyle z_{0}=infty }$ совпадает с рядом для ${displaystyle z_{0}=0}$ , однако, с формальной точки зрения получен с помощью замены ${displaystyle zleftrightarrow {frac {1}{zeta }}}$ для ${displaystyle zeta _{0}=0}$ .

Если ${displaystyle A_{infty }subseteq ({mathbb {C} }setminus {0})}$ — область сходимости ряда Лорана такая, что ${displaystyle infty in partial {A_{infty }}}$ , то для ${displaystyle A_{infty }}$

ряд ${displaystyle sum _{n=-infty }^{0}c_{n}z^{n}}$

называется правильной частью,

ряд ${displaystyle sum _{n=+1}^{+infty }{c_{n}}{z^{n}}}$

называется главной частью.

Свойства[править | править код]

часть по отрицательным степеням ${displaystyle (z-z_{0})}$

сходится во внешности ${displaystyle Delta _{r}={overline {mathbb {C} }}setminus {overline {D}}_{r}={zin {overline {mathbb {C} }}:|z-z_{0}|>r}}$

круга ${displaystyle D_{r}}$

радиуса ${displaystyle r={varlimsup limits _{nrightarrow +infty }},|c_{-n}|^{1/n}in [0;+infty ]}$

Поэтому, если

, то внутренность

области сходимости ряда Лорана непуста и представляет собой круговое кольцо

${displaystyle A={zin mathbb {C} mid 0leq r<|z-z_{0}|<Rleq +infty }=Delta _{r}cap D_{R}}$

а в точках граничной окружности ${displaystyle C_{r}(z_{0})={zin mathbb {C} :|z-z_{0}|=r}}$

— только от ${displaystyle sum _{n=-infty }^{-n_{s}}{c_{n}}{(z-z_{0})^{n}}}$

для произвольного ${displaystyle n_{s}in mathbb {N} }$

Таким образом, как и для степенных рядов поведение ряда Лорана в граничной точках кольца

может быть разнообразным.

${displaystyle sum _{n=-infty }^{+infty }c_{n}(z-z_{0})^{n}=sum _{k=0}^{+infty }t_{k}(zeta _{0})(z-zeta _{0})^{k},quad }$

где ${displaystyle zin D_{rho }(zeta _{0})}$

, а ${displaystyle t_{k}(zeta _{0})={frac {f^{(k)}(zeta _{0})}{k!}}}$

для

т.е. ${displaystyle zeta _{0}}$

является для f(z)

правильной точкой. Таким образом, сумма ряда Лорана в

есть аналитическая функция f(z)

Ряд ${displaystyle sum _{n=-infty ,nneq -1}^{+infty }c_{n}(z-z_{0})^{n},}$

, представляющий в двусвязной области

функцию ${displaystyle f(z)-{frac {c_{-1}}{z-z_{0}}},}$

, для любого компактного

и любой спрямляемой ориентированной кривой

можно интегрировать по gamma

почленно, при этом результат интегрирования зависит только от начальной и конечной точек gamma

и не зависит от формы кривой gamma

${displaystyle c_{n}={frac {1}{2pi i}}int limits _{gamma }{frac {f(z),dz}{(z-z_{0})^{n+1}}}={frac {1}{2pi i}}int limits _{|z-z_{0}|=rho }{frac {f(z),dz}{(z-z_{0})^{n+1}}}}$

где

— любая спрямляемая кривая, лежащая в компактном

и один раз обходящая против часовой стрелки точку $z_{{0}}$

. В частности, в качестве gamma

можно взять любую окружность ${displaystyle C_{rho }={z_{0}+rho e^{it}mid tin [0;2pi ]}}$

радиуса

с центром в $z_{{0}}$

, расположенную внутри кольца сходимости и ориентированную положительно (параметр

должен возрастать).

Теорема Лорана[править | править код]

Применение рядов Лорана основано главным образом на следующей теореме Лорана:

Любая функция f(z)

, являющаяся однозначной и аналитической в кольце ${displaystyle A={zin mathbb {C} mid 0leq r<|z-z_{0}|<Rleq +infty }}$

, представима в

сходящимся рядом Лорана по степеням ${displaystyle (z-z_{0})}$

Представление однозначной аналитической функции f(z) в виде ряда Лорана служит основным инструментом исследования её поведения в окрестности ${displaystyle A_{z_{0}}}$ изолированной особой точки:

1) если точка ${displaystyle z_{0}neq infty }$ , то существует радиус ${displaystyle R_{z_{0}}in (0;+infty ]}$ такой, что
в проколотой окрестности

${displaystyle A_{z_{0}}={zin mathbb {C} mid 0<|z-z_{0}|<R_{z_{0}}}quad }$

функция f(z) представима (сходящимся) рядом Лорана;

2) если точка ${displaystyle z_{0}=infty }$ , то существует радиус ${displaystyle r_{infty }in [0;+infty )}$ такой, что
в проколотой окрестности

${displaystyle A_{infty }={zin mathbb {C} mid r_{infty }<|z|<infty }}$

функция f(z) представима (сходящимся) рядом Лорана.

Тип изолированной особой точки $z_{{0}}$ определяется главной частью ряда Лорана в проколотой окрестности ${displaystyle A_{z_{0}}}$ :

Устранимая особая точка — главная часть ряда Лорана равна 0.
Полюс — главная часть содержит конечное число ненулевых членов.
Существенно особая точка — главная часть содержит бесконечное число ненулевых членов.

Литература[править | править код]

Евграфов М. А. Аналитические функции. — 2-е изд., перераб. и дополн. — М.: Наука, 1968. — 472 с.
Маркушевич А. И. Теория аналитических функций. Том 1: Начала теории. — Изд. 2-е. — М.: Наука, 1967. — 486 с.
Привалов И. И. Введение в теорию функций комплексного переменного. — 13-е. — М.: Наука, 1984. — 432 с.
Титчмарш Е. Теория функций: Пер. с англ. — 2-е изд., перераб. — М.: Наука, 1980. — 464 с.
Шабат Б. В. Введение в комплексный анализ. — М.: Наука, 1969. — 577 с.

Источник

Если
функция

однозначна и аналитична в кольце

,
то она разлагается в нем в ряд
Лорана

где

При
r
= 0 и R
< 
кольцо вырождается в круг с выколотым
центром. Ряды

называются соответственно правильной
и главной частями ряда Лорана.

Определение
12.
Внешность круга

называется окрестностью бесконечно
удаленной точки.

Если

однозначна и аналитична в окрестности
бесконечно удаленной точки (за исключением
может быть только точки z
= ),
то она разлагается в ее окрестности в
ряд

называемый
рядом
Лорана функции f
в окрестности точки

z
= .

Определение
13.
Ряды

называются
соответственно правильной
и главной частями ряда Лорана в окрестности
бесконечно удаленной точки.

Часто
нецелесообразно использовать
непосредственную формулу для подсчета
коэффициентов ряда Лорана, поэтому, как
и в случае ряда Тейлора, прибегают к
некоторым искусственным приемам.

Примеры

38. Разложить
функцию

в ряд Лорана в окрестности точки

:

1)

;
2)

.

Решение:
1) используя метод неопределенных
коэффициентов, разложим рациональную
дробь

на сумму простых дробей

Получаем

Функция

аналитична в круге

,
(особые точки

,
z = 
в круг не попадают) и поэтому ее можно
разложить в ряд Тейлора в окрестности

.
Для этого представим

в виде

Учитывая что

имеем

Функция

аналитична
в кольце

и уже записана рядом Лорана по степеням
(z – 1). Окончательно
получаем

где

.

39.
Разложить функцию

в ряд Лорана: a) в кольце

;
b) в окрестности
бесконечно удаленной точки.

Решение:
а) с помощью метода неопределенных
коэффициентов

можно представить в виде

Функция

аналитична во внешности круга

,
поэтому

Для функции

Окончательно

Решение:
b) окрестностью
бесконечно удаленной точки будет кольцо

,
поэтому из условия

имеем

Получаем

40. Разложить
функцию в ряд Лорана в окрестности точки

:

1)

;
2)

Решение: 1)
запишем дробь

в виде

Тогда

Воспользовавшись
стандартными формулами (22) и (23) для

и

,
получаем

где

.

Решение:
2) представим дробь

в виде

и воспользуемся стандартным разложением
(21):

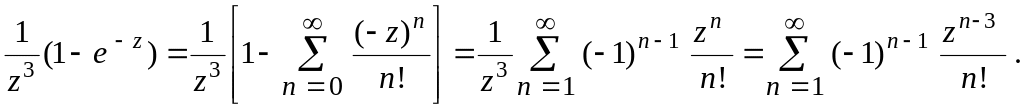
Так
как особые точки функции: z
= 0 и z = ,
то мы получили разложение в кольце

.

Разложить
функцию

в ряд Лорана в области

.

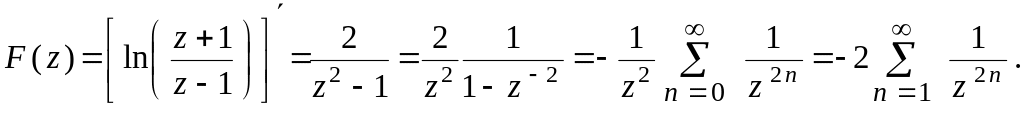
Этот
ряд равномерно сходится на любой гладкой
кривой, соединяющей точку z
c .
Интегрируя почленно, находим

5.4. Классификация изолированных особых точек однозначного характера аналитической функции

Определение
14. Точка

называется изолированной особой точкой
однозначного характера функции

,
если в некоторой окрестности этой точки

однозначная функция

аналитична, а в самой точке

не определена или не аналитична.

Бесконечно
удаленная точка называется изолированной
особой точкой однозначного характера
функции

,
если в кольце

однозначная функция

аналитична.

Точки
ветвления многозначной функции называются
особыми точками
многозначного характера. В дальнейшем
будем рассматривать только изолированные
особые точки однозначного характера.

Классификация
изолированных особых точек может быть
проведена двумя эквивалентными способами:

по виду
лорановского разложения функции в
окрестности особой точки

;

по
характеру поведения функции в окрестности
этой точки.

Определение
15. Точка

называется устранимой особой точкой
функции

если:

1) в
разложении в ряд Лорана функции

в окрестности

отсутствует главная часть ряда, т.е.