Как найти разложение вектора по данному базису

Вектор в произвольном линейном пространстве — это некоторый элемент этого пространства.

Числа $λ, μ$ и $ν$ называются координатами рассматриваемого вектора относительно некоторого базиса $a, b$ и $c$.

В контексте плоскости базисом будет два независимых вектора, лежащих в этой плоскости, а не три, как в объёмном мире.

Любой вектор $d$ имеет лишь единственное разложение по базису векторов, то есть его координаты задаются однозначно через используемый базис.

Декартова система координат является примером аффиной системы координат, причём базисные вектора в ней принято обозначать не буквами $a, b$ и $c$, а $i, j$ и $k$, представляющими собой направленные ортогональные между собой отрезки, причём длина каждого равна единице.

Для декартовой системы координат формула разложения выглядит так:

$d = X cdot vec{i} + Y cdot vec{j} + Z cdot vec{k}$

Здесь $X, Y$ и $Z$ — координаты вектора, а $ i, j$ и $k$ — базис.

Через базис декартовой системы координат выражается скалярное произведение векторов, заданных в этом пространстве. Для этого их координаты записываются через специальную матрицу.

«Разложение вектора по базису векторов: формулировка с примерами решения» 👇

В статье о n-мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n-мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n-векторов. Размерность его соответственно равна n. Возьмем систему из n-единичных векторов:

e(1)=(1, 0,…,0)e(2)=(0, 1,…,0)e(n)=(0, 0,…,1)

Используем эти векторы в качестве составляющих матрицы A: она будет являться единичной с размерностью n на n. Ранг этой матрицы равен n. Следовательно, векторная система e(1), e(2),…, e(n) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n, то размерность пространства n-мерных векторов равна n, а единичные векторы e(1), e(2),…, e(n) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n-мерных векторов, в которой число векторов меньше n, не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e(2), e(1),…, e(n). Она также будет являться базисом n-мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n. Система e(2), e(1),…, e(n) линейно независима и является базисом n-мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n-мерного векторного пространства.

Рассмотрим применение данной теории на конкретных примерах.

Разложение вектора по базису

Примем, что произвольные векторы e(1), e(2),…, e(n) являются базисом векторного n-мерного пространства. Добавим к ним некий n-мерный вектор x→: полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n-мерного векторного пространства единственным образом раскладывается по базису.

Доказанная теория делает понятным выражение «задан n-мерный вектор x=(x1, x2,…, xn)»: рассматривается вектор x→ n-мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n-мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n-мерного векторного пространства задана система из n линейно независимых векторов

e(1)=(e1(1), e2(1),…, en(1))e(2)=(e1(2), e2(2),…, en(2))⋮e(n)=(e1(n), e2(n),…, en(n))

а также задан вектор x=(x1, x2,…, xn).

Векторы e1(1), e2(2),…, en(n) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x→ в базисе e1(1), e2(2),…, en(n), обозначаемые как x~1, x~2,…, x~n.

Вектор x→ будет представлен следующим образом:

x=x~1·e(1)+x~2·e(2)+…+x~n·e(n)

Запишем это выражение в координатной форме:

(x1, x2,…, xn)=x~1·(e(1)1, e(1)2,…, e(1)n)+x~2·(e(2)1, e(2)2,…, e(2)n)+…++x~n·(e(n)1, e(n)2,…, e(n)n)==(x~1e1(1)+x~2e1(2)+…+x~ne1(n), x~1e2(1)+x~2e2(2)++…+x~ne2(n), …, x~1en(1)+x~2en(2)+…+x~nen(n))

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x~1, x~2,…, x~n:

x1=x~1e11+x~2e12+…+x~ne1nx2=x~1e21+x~2e22+…+x~ne2n⋮xn=x~1en1+x~2en2+…+x~nenn

Матрица этой системы будет иметь следующий вид:

e1(1)e1(2)⋯e1(n)e2(1)e2(2)⋯e2(n)⋮⋮⋮⋮en(1)en(2)⋯en(n)

Пусть это будет матрица A, и ее столбцы – векторы линейно независимой системы векторов e1(1), e2(2),…, en(n). Ранг матрицы – n, и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x~1, x~2,…, x~n вектора x→ в базисе e1(1), e2(2),…, en(n).

Применим рассмотренную теорию на конкретном примере.

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c(1)=(c1(1), c2(1),…, cn(1))c(2)=(c1(2), c2(2),…, cn(2))⋮c(n)=(c1(n), e2(n),…, cn(n))

И

e(1)=(e1(1), e2(1),…, en(1))e(2)=(e1(2), e2(2),…, en(2))⋮e(n)=(e1(n), e2(n),…, en(n))

Указанные системы являются также базисами заданного пространства.

Пусть c~1(1), c~2(1),…, c~n(1) – координаты вектора c(1) в базисе e(1), e(2),…, e(3), тогда связь координат будет задаваться системой линейных уравнений:

с1(1)=c~1(1)e1(1)+c~2(1)e1(2)+…+c~n(1)e1(n)с2(1)=c~1(1)e2(1)+c~2(1)e2(2)+…+c~n(1)e2(n)⋮                                                           сn(1)=c~1(1)en(1)+c~2(1)en(2)+…+c~n(1)en(n)

В виде матрицы систему можно отобразить так:

(c1(1), c2(1),…, cn(1))=(c~1(1), c~2(1),…, c~n(1))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)

Сделаем по аналогии такую же запись для вектора c(2):

(c1(2), c2(2),…, cn(2))=(c~1(2), c~2(2),…, c~n(2))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)

И, далее действуя по тому же принципу, получаем:

(c1(n), c2(n),…, cn(n))=(c~1(n), c~2(n),…, c~n(n))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)

Матричные равенства объединим в одно выражение:

c1(1)c2(1)⋯cn(1)c1(2)c2(2)⋯cn(2)⋮⋮⋮⋮c1(n)c2(n)⋯cn(n)=c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)·e1(1)e2(1)⋯en(1)e1(2)e2(2)⋯en(2)⋮⋮⋮⋮e1(n)e2(n)⋯en(n)

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e(1), e(2),…, e(3) через базис c(1), c(2),…, c(n):

e1(1)e2(1)⋯en(1)e1(2)e2(2)⋯en(2)⋮⋮⋮⋮e1(n)e2(n)⋯en(n)=e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)·c1(1)c2(1)⋯cn(1)c1(2)c2(2)⋯cn(2)⋮⋮⋮⋮c1(n)c2(n)⋯cn(n)

Дадим следующие определения:

Из этих равенств очевидно, что

c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)·e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)=10⋯001⋯0⋮⋮⋮⋮00⋯1e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)·c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)=10⋯001⋯0⋮⋮⋮⋮00⋯1 

т.е. матрицы перехода взаимообратны.

Рассмотрим теорию на конкретном примере.

§ 22.Разложение вектора по базису

22.1. Компланарные векторы

Определение. Ненулевые векторы , , называются компланарными, если изображающие их направленные отрезки лежат в одной плоскости или параллельны одной и той же плоскости (рис. 180, а).

Понятие компланарности определяется для произвольной совокупности векторов. Так, любой вектор компланарен некоторой плоскости. Два любых вектора также компланарны некоторой плоскости. Но три любых вектора считаются компланарными некоторой плоскости, если направленные отрезки, изображающие эти векторы, будучи отложенными от одной точки, лежат в одной плоскости. Аналогично определяется компланарность для четырёх, пяти и т. д. произвольной совокупности векторов.

На рисунке 180, б векторы , , компланарны, так как отрезок B1D1 параллелен плоскости ABD, но тройка векторов , и  не является компланарной, так как отрезок AA1 не параллелен плоскости ABD, в которой расположены отрезки AB и AD. Некомпланарны и тройки векторов , , и , , . (Почему?)

Укажите тройки компланарных и некомпланарных векторов, изображённых на рисунке 180, б, в.

Замечание. Если среди трёх векторов хотя бы два коллинеарны, то эти три вектора компланарны.

В самом деле, пусть среди трёх векторов  = ,  = ,  =  коллинеарны векторы и , т. е.  = x. Проведём плоскость α, параллельную непараллельным прямым AB и CD (рис. 181). Тогда MN ‖ α (почему?). От произвольной точки O плоскости α отложим направленные отрезки  = ,  = ,  = .

Эти отрезки лежат в плоскости α (почему?). Следовательно, векторы , и  компланарны. Три вектора, среди которых имеется нулевой вектор, считаются также компланарными.

22.2. Разложение вектора на плоскости

Пусть на плоскости α даны неколлинеарные векторы и ;  — произвольный вектор этой плоскости.

Если вектор коллинеарен с одним из векторов и , то или  = x• + 0• ( ‖ ), или  = 0• + y• ( ‖ ).

Заметим, что  = 0• + 0•.

Пусть теперь вектор  =  не коллинеарен ни с одним из векторов и  (рис. 182). Через точку С проведём прямые a1 ‖ a и b1 ‖ b, при этом получим точки A1 = a ∩ b1 и B1 = b ∩ a1. Тогда по правилу параллелограмма пишем:

 = +  =   x + y = x + y или

 = x + y .(1)

Равенство  = x + y называется разложением вектора по двум неколлинеарным векторам и ; числа x и y называются коэффициентами разложения.

Покажем, что числа x и y в разложении (1) однозначно определены. Действительно, предположим, что существуют другие числа x1 и y1 такие, что, по крайней мере, или x1 ≠ x, или y1 ≠ y и при этом верно равенство

 = x1 + y1.(2)

Из равенств (1) и (2) получаем x + y = x1 + y1 или (x1 – x)  + (y1 – y)  = 0, откуда следует, что либо векторы и  коллинеарны (что противоречит условию), либо y1 = y и x1 = x. Таким образом, нами доказана теорема.

Теорема 34. Если на плоскости дана упорядоченная пара (; ) неколлинеарных векторов, то для любого вектора этой плоскости существует единственная упорядоченная пара чисел (x; y) такая, что выполняется векторное равенство

 = x + y.

Из равенства (1) следует, что любой вектор , компланарный с неколлинеарными векторами и , является линейной комбинацией векторов и . Поэтому пару векторов и  называют базисом на плоскости, а также базисом на множестве всех векторов пространства, компланарных с векторами и .

Определение. Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов и . Векторы и называются базисными векторами.

Базис из векторов и  обозначают (; ). При этом равенство  = x + y называется разложением вектора по базису (; ) (или разложением вектора по базисным векторам и ), а числа x и y — координатами вектора в базисе (; ).

Если вектор компланарен с неколлинеарными векторами и , то выполняется равенство  = x + y.

Справедливо и обратное утверждение: если для векторов , и  выполняется равенство  = x + y, то векторы , и  компланарны.

(Докажите его самостоятельно.)

Таким образом: три вектора , и  (где и  неколлинеарные векторы) пространства компланарны, если существуют числа x и y такие, что выполняется равенство

 = x + y.

Признак компланарности трёх векторов можно сформулировать следующим образом.

Теорема 35 (признак компланарности трёх векторов). Три вектора , и  пространства компланарны тогда и только тогда, когда существуют такие числа x, y, z, из которых хотя бы одно отлично от нуля, что выполняется равенство

x + y + z = .

Докажите это утверждение самостоятельно.

Напомним одно важное векторное равенство на плоскости. Пусть точка O не лежит на прямой AB. Тогда точка M лежит на прямой AB тогда и только тогда, когда  = x• + y• при x + y = 1 (рис. 183).

22.3. Разложение вектора по трём некомпланарным векторам

Определение. Три вектора называются некомпланарными, если изображающие их направленные отрезки не лежат в одной плоскости и не параллельны одной плоскости.

Теорема 36. Если дана упорядоченная тройка (; ; ) некомпланарных векторов, то для любого вектора пространства существует единственная упорядоченная тройка чисел (x; y; z), удовлетворяющая равенству

 = x + y + z.

Доказательство. Пусть даны три некомпланарных вектора , , и произвольный вектор .

Если вектор компланарен с любыми двумя из данных трёх векторов , , , то теорема верна (например, если компланарен с векторами и , то  = 0• + y• + z•) (рис. 184).

Пусть теперь никакие три из векторов , , , не компланарны.

От произвольной точки O отложим векторы  = ,  = ,  =  и  = . Так как направленные отрезки , и  не компланарны, то плоскости AOB, AOC и BOC различны (рис. 185).

Проведём через точку D прямую, параллельную OC (D1 — точка пересечения этой прямой с плоскостью AOB). Тогда по правилу треугольника

 =  =  + .(1)

Векторы , и  компланарны. Следовательно,  = x + y. Так как  = , а вектор коллинеарен вектору  = , т. е. = z, то

 =  = x + y + z.

Таким образом, для произвольного вектора пространства выполняется равенство

 = x + y + z,(2)

где , ,  — данные некомпланарные векторы. Равенство (2) называется разложением вектора по трём некомпланарным векторам , и ; числа x, y, z называются коэффициентами разложения.

Докажем, что коэффициенты x, y и z в разложении (2) однозначно определены. Предположим, что существует другая тройка чисел (x1; y1; z1), для которой верно равенство

 = x1 + y1 + z1.(3)

Вычитая (3) из (2), получаем

(x – x1)  + (y – y1)  + (z – z1)  = .

Из этого равенства на основании теоремы 35 следует, что либо векторы , и  компланарны (что противоречит условию), либо z = z1, x = x1 и y = y1. Следовательно, тройки чисел (x; y; z) и (x1; y1; z1) равны. Теорема доказана. ▼

Из равенства  = x + y + z следует, что любой вектор пространства является линейной комбинацией тройки некомпланарных векторов , и . Поэтому говорят, что эта тройка образует базис векторов в пространстве.

Определение. Базисом векторов в пространстве называется любая упорядоченная тройка некомпланарных векторов. Векторы, образующие базис, называются базисными векторами.

Базис из векторов , и  обозначают (; ; ). Равенство  = x + y + z называется разложением вектора по базису (; ; ) или разложением вектора по базисным векторам , и ; числа x, y, z называются координатами вектора в базисе (; ; ).

Из теоремы 36 следует, что любой вектор пространства можно единственным образом разложить в данном базисе.

ЗадаЧа. В тетраэдре PABC точка M — центроид (точка пересечения медиан, центр тяжести) треугольника PBC, точка H — середина ребра PC, точка E взята на ребре AP так, что AE : EP = 2 : 1. Разложить вектор по базису (; ; ), если  = ,  = ,  =  (рис. 186).

Решение. По правилу ломаной

 =  + + .

Находим: AE : EP = 2 : 1.

 =   =  ( – ) =  ( – );

 = – = – ;

M — центроид треугольника PBC.

 =   = • ( + ) =  ( + ).

Тогда

 =  ( – ) – +  ( + ) = –   +   –  .

Ответ: –   +   –  .

Попробуйте доказать самостоятельно важный стереометрический факт. Пусть даны треугольник ABC и любая точка O, не лежащая в плоскости этого треугольника. В таком случае: точка M тогда и только тогда будет лежать в плоскости ABC, когда выполняется векторное равенство  = x• + y• + z• при условии, что x + y + z = 1 (рис. 187).

ЗадаЧа 6.044. ABCDA1B1C1D1 — куб. Доказать, что центроид M треугольника ACD1 принадлежит диагонали B1D и делит её в отношении 1 : 2, считая от вершины D.

Решение. Для решения задачи достаточно убедиться, что векторы и  (рис. 188) коллинеарны (почему?).

Введём базис  = ,  = ,  =  и найдём разложение векторов и  по этому базису.

По правилу параллелепипеда имеем

 =  + +  =  + + .(1)

Так как точка M — центроид треугольника ACD1, то

 =  ( + + ) =  ( + + ).(2)

Из (1) и (2) следует, что  =  , поэтому векторы и  коллинеарны и сонаправлены. Это означает, что точка M принадлежит диагонали DB1 и DM : DB1 = 1 : 3, откуда DM : MB1 = 1 : 2, что и требовалось доказать.

В данной публикации мы рассмотрим, каким образом можно разложить вектор по двум базисным векторам, а также разберем пример решения задачи по этой теме.

Принцип разложения вектора

Для того, чтобы разложить вектор b по базисным векторам a₁, …, a_n, требуется определить такие коэффициенты x₁, …, x_n, при которых линейная комбинация векторов a₁, …, a_n равняется вектору b, то есть:

x₁a₁ + … + x_na_n = b

где x₁, …, x_n – координаты вектора b в базисе a₁, …, a_n

Пример задачи

Разложим вектор b = {16; 1} по двум базисным векторам m = {2; 1} и n = {1; -3}.

Решение:

1. Векторное уравнение выглядит так:

xm + yn = b

2. Представим его в виде системы линейных уравнений:

3. Теперь нужно решить систему. Из второго уравнения получаем:
x = 1 + 3y.

Подставляем полученное выражение в первое уравнение:
2 · (1 + 3y) + y = 16
2 + 6y + y = 16
7y = 14
y = 2

Следовательно, x = 1 + 3y = 1 + 2 · 2 = 7.

Ответ: b = 7m + 2n.

Пусть

– единичные векторы осей координат, т.е.


и каждый из них одинаково направлен с
координатными осями.
Тройка векторов

называется
координатным
базисом.

Теорема.
Любой вектор пространства можно разложить
по базису
,
т.е. представить
в виде
,
где

– некоторые числа (буквы:

– «мю»,

– «ню»).

Это разложение
единственное.

 Доказательство.
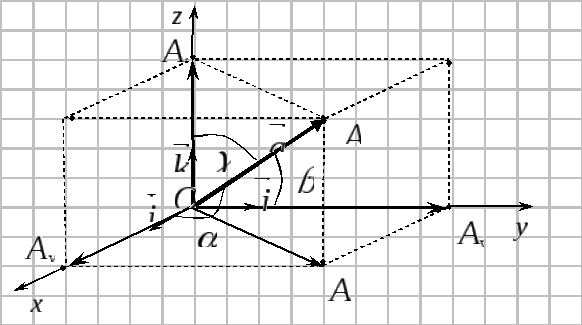
Приложим вектор

к началу координат, обозначим его конец

.
Проведем
через точку

плоскости,
перпендикулярные осям координат. Пусть

,

,

– точки
пересечения этих плоскостей с осями
координат.

Существует
единственная тройка чисел
,
,

таких, что

.

Формула

называется
разложением вектора по координатному
базису.

Числа
,
,

– называются
координатами
вектора

,
т.е. координаты
вектора есть его проекции на соответствующие
координатные оси. В символическом виде
записывают
.

Например, если,
то его
координаты
.

Зная координаты
вектора
,
длину его можно найти по формуле

Если известны
координаты точек

и
,
то координаты вектора равны:
.

Пусть углы вектора

с осями
,
,

соответственно равны
,
,
.
Числа
,
,

называются
направляющими косинусами вектора
.

;
;

;

– основное
свойство направляющих косинусов вектора.

7.4. Действия над векторами, заданными координатами

Пусть векторы

и

заданы своими координатами.

При сложении
(вычитании) векторов их одноименные
координаты складываются (вычитаются),
т.е.

При умножении
вектора на число

координаты его умножаются на это число,
т.е.
.

Если вектор

коллинеарен вектору
,
то можно записать
,
где

– некоторое число, т.е.
,
,
.
Отсюда,
,
,

или

– условие коллинеарности векторов.

7.5. Деление отрезка в данном отношении

,

,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,

Пусть даны координаты
точек

и
;
и отношение
.
Требуется найти координаты точки
.

Из равенства
векторов следует равенство соответствующих
координат:

.

Аналогично,

;

.

В частном случае:


– середина
отрезка, т.е.
.

Пример.
Дан треугольник
,
где
,

,
.

Н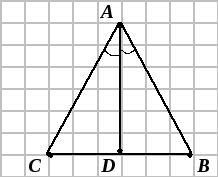айти
координаты точки
–
пересечения
биссектрисы угла

со стороной
.


,
,

,

.

.

;

;

Ответ:
.


§ 8. Скалярное
произведение векторов

8.1. Определение
скалярного произведения

Определение.
Скалярным произведением вектора

на вектор

называется число
(скаляр),
равное произведению длин этих векторов
на косинус угла между ними.

Обозначается:

или
.

Н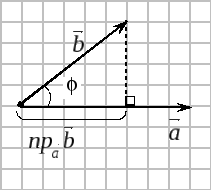айдем
проекцию вектора

на вектор

.

Из геометрии
известно
.

Умножим и разделим
левую часть на
:

,
аналогично находим
.

8.2. Свойства
скалярного произведения

1.


Доказательство.

. 

2.

.

3.

.

4.

.

Определение:
Число, равное

,
называется скалярным
квадратом
вектора
.

5.
Скалярный квадрат вектора равен
квадрату его длины
.

 Доказательство.

.

6.
Скалярное произведение базисных
векторов:

,

.

8.3. Вычисление
скалярного произведения векторов через
координаты

Теорема. Если

,

,
то
.

 Доказательство.
Запишем векторы

и

в виде разложения по базису, т.е.

и

.

Тогда

По свойству
скалярного произведения базисных
векторов
:

	.

Таким образом,
.


8.4. Приложения
скалярного произведения векторов

1. Установление
   перпендикулярности ненулевых векторов:

.

Если , то

– условие перпендикулярности векторов.

2. Вычисление
проекции вектора на вектор:

и

.

3. Определение угла между векторами:

,
т.е.
.

4. Работа постоянной
силы.

Е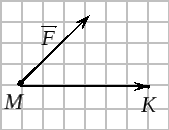сли
точка перемещается прямолинейно из
положения

в положение

под действием силы
,
то работа по перемещению равна:

.

Пример 1.
К точке

приложены три силы
.

Вычислить
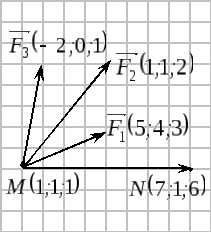
работу по перемещению точки

в точку
.



– равнодействующая
трех сил.

.

.


Пример 2.
Дано:
,

,

,
.

Найти угол между
векторами

и
.

 Так как

или
.

,

,

Таким образом,
.


Пример 3.
Найти длину вектора
,
если
,
,.





Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #