Составим систему линейных уравнений, используя векторы из условия задачи:
$$ begin{cases} 10= 2alpha + 3 beta + 5 gamma \ 3=3 alpha + 7 beta + 4 gamma \ 3 = 1 alpha + 2 beta + 2 gamma end{cases} $$
Запишем систему в привычном виде:
$$ begin{cases} 2alpha + 3 beta + 5 gamma = 10 \ 3 alpha + 7 beta + 4 gamma = 3 \ alpha + 2 beta + 2 gamma = 3 end{cases} $$
Решив систему уравнений любым методом, найдем неизвестные $ alpha, beta, gamma $. К примеру, возьмём метод Крамера.
Найдем главный определитель:
$$ Delta = begin{vmatrix} 2 & 3 & 5 \ 3 & 7 & 4 \ 1 & 2 & 2 end{vmatrix} = $$
$$ = 2 cdot 7 cdot 2 + 3 cdot 4 cdot 1 + 3 cdot 2 cdot 5 – 5 cdot 7 cdot 1 – 4 cdot 2 cdot 2 – 3 cdot 3 cdot 2 = $$
$$ = 28 + 12 + 30 – 35 – 16 – 18 = 1 $$
Так как $ Delta = 1 $ не равно нулю, то СЛАУ имеет единственное решение.
Вычислим дополнительные определители составленные из столбцов главного путём поочередной замены одного из столбцов на свободные члены системы:
$$ Delta_1 = begin{vmatrix} 10 & 3 & 5 \ 3 & 7 & 4 \ 3 & 2 & 2 end{vmatrix} = $$
$$ = 10 cdot 7 cdot 2 + 3 cdot 4 cdot 3 + 3 cdot 2 cdot 5 – 5 cdot 7 cdot 3 – 4 cdot 2 cdot 10 – 3 cdot 3 cdot 2 = $$
$$ = 140 + 36 + 30 – 105 – 80 – 18 = 3 $$
$$ Delta_2 = begin{vmatrix} 2 & 10 & 5 \ 3 & 3 & 4 \ 1 & 3 & 2 end{vmatrix} = $$
$$ = 2 cdot 3 cdot 2 + 10 cdot 4 cdot 1 + 3 cdot 3 cdot 5 – 5 cdot 3 cdot 1 – 4 cdot 3 cdot 2 – 10 cdot 3 cdot 2 = $$
$$ = 12 + 40 + 45 – 15 – 24 – 60 = -2 $$
$$ Delta_3 = begin{vmatrix} 2 & 3 & 10 \ 3 & 7 & 3 \ 1 & 2 & 3 end{vmatrix} = $$
$$ = 2 cdot 7 cdot 3 + 3 cdot 3 cdot 1 + 3 cdot 2 cdot 10 – 10 cdot 7 cdot 1 – 3 cdot 2 cdot 2 – 3 cdot 3 cdot 3 = $$
$$ = 42 + 9 + 60 – 70 – 12 – 27 = 2 $$
Теперь вычислим коэффициенты $ alpha, beta, gamma $:
$$ alpha = frac{Delta_1}{Delta} = frac{3}{1} = 3 $$
$$ beta = frac{Delta_2}{Delta} = frac{-2}{1} = -2 $$
$$ gamma = frac{Delta_3}{Delta} = frac{2}{1} = 2 $$
Зная постоянные $ alpha, beta, gamma $, запишем разложение вектора $ overline{x} $ по векторам $ overline{p}, overline{q}, overline{r} $:
$$ overline{x} = 3overline{p} – 2overline{q} + 2overline{r} $$
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
В данной публикации мы рассмотрим, каким образом можно разложить вектор по двум базисным векторам, а также разберем пример решения задачи по этой теме.
- Принцип разложения вектора
- Пример задачи
Принцип разложения вектора
Для того, чтобы разложить вектор b по базисным векторам a1, …, an, требуется определить такие коэффициенты x1, …, xn, при которых линейная комбинация векторов a1, …, an равняется вектору b, то есть:
x1a1 + … + xnan = b
где x1, …, xn – координаты вектора b в базисе a1, …, an
Пример задачи
Разложим вектор b = {16; 1} по двум базисным векторам m = {2; 1} и n = {1; -3}.
Решение:
1. Векторное уравнение выглядит так:
xm + yn = b
2. Представим его в виде системы линейных уравнений:
![]()
3. Теперь нужно решить систему. Из второго уравнения получаем:
x = 1 + 3y.
Подставляем полученное выражение в первое уравнение:
2 · (1 + 3y) + y = 16
2 + 6y + y = 16
7y = 14
y = 2
Следовательно, x = 1 + 3y = 1 + 2 · 2 = 7.
Ответ: b = 7m + 2n.
Чтобы разложить, вектор b по базисным векторам a1, …, an, необходимо найти коэффициенты x1, …, xn, при которых линейная комбинация векторов a1, …, an равна вектору b:
x1a1 + … + xnan = b,
при этом коэффициенты x1, …, xn, называются координатами вектора b в базисе a1, …, an.
Пример задачи на разложение вектора по базисным векторам
Пример 1. Разложить вектор b = {8; 1} по базисным векторам p = {1; 2} и q = {3; 1}.
Решение: Составим векторное уравнение:
xp + yq = b,
которое можно записать в виде системы линейных уравнений
| 1x + 3y = 8 | |
| 2x + 1y = 1 |
из первого уравнения выражаем x
| x = 8 – 3y | |
| 2x + y = 1 |
Подставим x во второе уравнение
| x = 8 – 3y | |
| 2(8 – 3y) + y = 1 |
| x = 8 – 3y | |
| 16 – 6y + y = 1 |
| x = 8 – 3y | |
| 5y = 15 |
| x = 8 – 3y | |
| y = 3 |
| x = 8 – 3·3 | |
| y = 3 |
| x = -1 | |
| y = 3 |
Ответ: b = –p + 3q.
На чтение 6 мин. Просмотров 1.3k.
Вы узнаете в этой статье что значит разложить вектор по двум неколлинеарным векторам.
Представление вектора vec{c} в виде vec{c}=x vec{a}+y vec{b}, где векторы vec{a} и vec{b} являются неколлинеарными векторами, называется разложением вектора по двум неколлинеарным векторам.
Теорема (о разложении вектора по двум неколлинеарным векторам)
Теорема. Любой вектор с можно единственным образом представить в виде vec{c}=x vec{a}+y vec{b}, где vec{a} и vec{b} — неколлинеарные векторы, х и у — числа.
Коллинеарные вектора vec{m} и vec{n} — это такие вектора, где один из векторов параллелен другому и связан с ним соотношением
vec{m}=kvec{n}
Доказательство:
Пусть даны векторы vec{c}=overrightarrow{AB}, vec{a} и vec{b}. Проведем через точки A и B прямые, параллельные векторам vec{a} и vec{b}, и обозначим точку C их пересечения. Тогда overrightarrow{AB}=overrightarrow{AC}+overrightarrow{CB}.
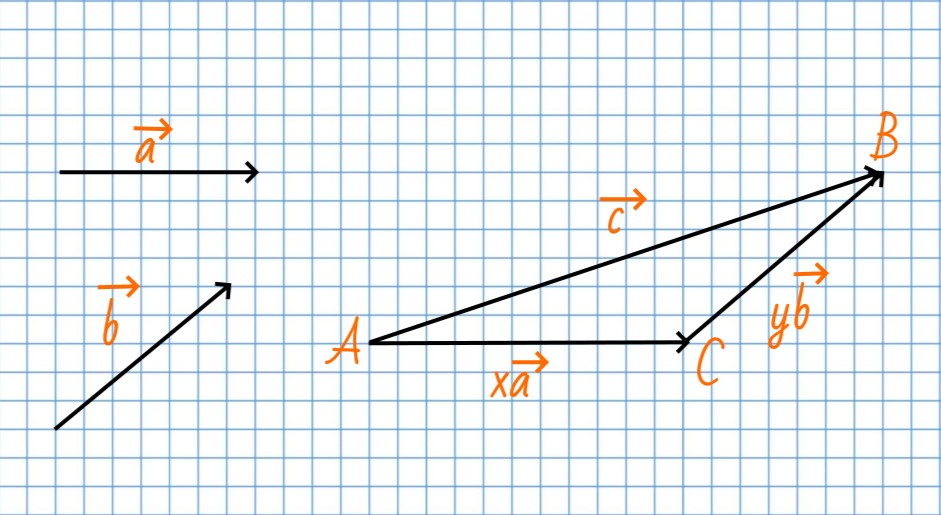
Так как векторы vec{a} и overrightarrow{AC} коллинеарные, то существует такое число х, что overrightarrow{AC} =хvec{a}. Векторы vec{b} и overrightarrow{CB} тоже коллинеарные, следовательно, существует такое число у, что overrightarrow{CB} =yvec{b}.
Таким образом, vec{c}=x vec{a}+y vec{b}.
Докажем единственность такого представления вектора с способом от противного. Допустим, что имеется другое разложение вектора, например, такое:
vec{c}=n vec{a}+m vec{b}, тогда два разложения вектора vec{c} можно приравнять:
n vec{a}+m vec{b}=x vec{a}+y vec{b} (если равны левые части равенств, то равны и правые).
Перенесем все в левую часть равенства:
n vec{a}+m vec{b}-x vec{a}-y vec{b}=0
(n-x)vec{a}+(m-y) vec{b}=0
displaystyle vec{a}=frac{y-m}{n-x} vec{b}
То есть векторы vec{a} и vec{b} получаются коллинеарными. А у нас условие — векторы vec{a} и vec{b} — неколлинеарные вектора.
Таким образом, возможно только единственно возможное представление вектора vec{c} в виде vec{c}=x vec{a}+y vec{b}, где векторы vec{a} и vec{b} являются неколлинеарными векторами.
Теорема доказана.
Если вектор vec{c} коллинеарен какому-либо из векторов vec{a} и vec{b}, то либо число x, либо число y равно нулю.
Базис векторов и разложение вектора по базису
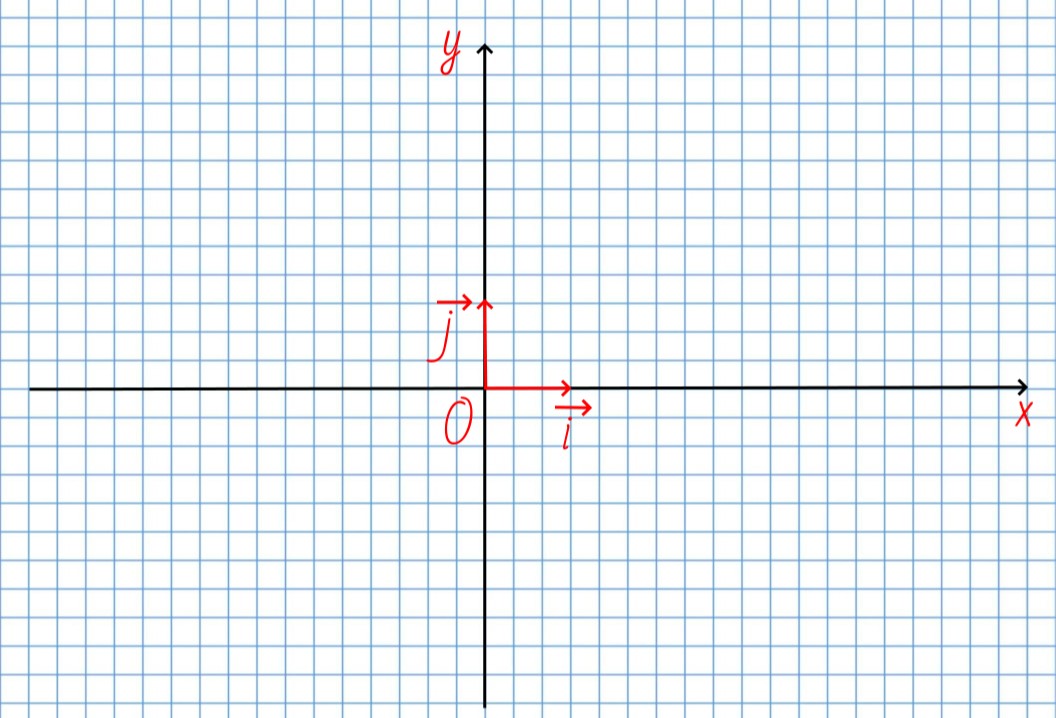
В декартовой системе координат Oxy вектор с координатами (x, y) можно разложить по единичным векторам vec{e_1}(1;0) и vec{e_2}(0;1).
Тогда, например, вектор vec{c}(3; -1) можно представить в виде разложения:
vec{c}=x vec{e_1}+y vec{e_2}=3 vec{e_1}-1 vec{e_2}
Действительно:
begin{cases} 3=3 cdot 1+(-1)cdot 0, \ — 1=3 cdot 0+(-1)cdot 1. end{cases}
Система векторов, по которым можно разложить вектор с коэффициентами разложения равными его координатам, называется базисом вектора. Вектора базиса всегда не коллинеарные. Координаты вектора будут верны только в отношении данного базиса.
Однако, это не отменяет тот факт, что вектор можно разложить и по другим векторам, то есть по новому базису. Тогда говорят о переходе к новому базису векторов.
Обычно в декартовой системе координат базисные векторы на плоскости обозначают так: vec{i}(1;0) и vec{j}(0;1).
В пространственной декартовой системе координат базис векторов будет: vec{i}(1; 0; 0), vec{j}(0;1; 0), vec{k}(0;0;1)
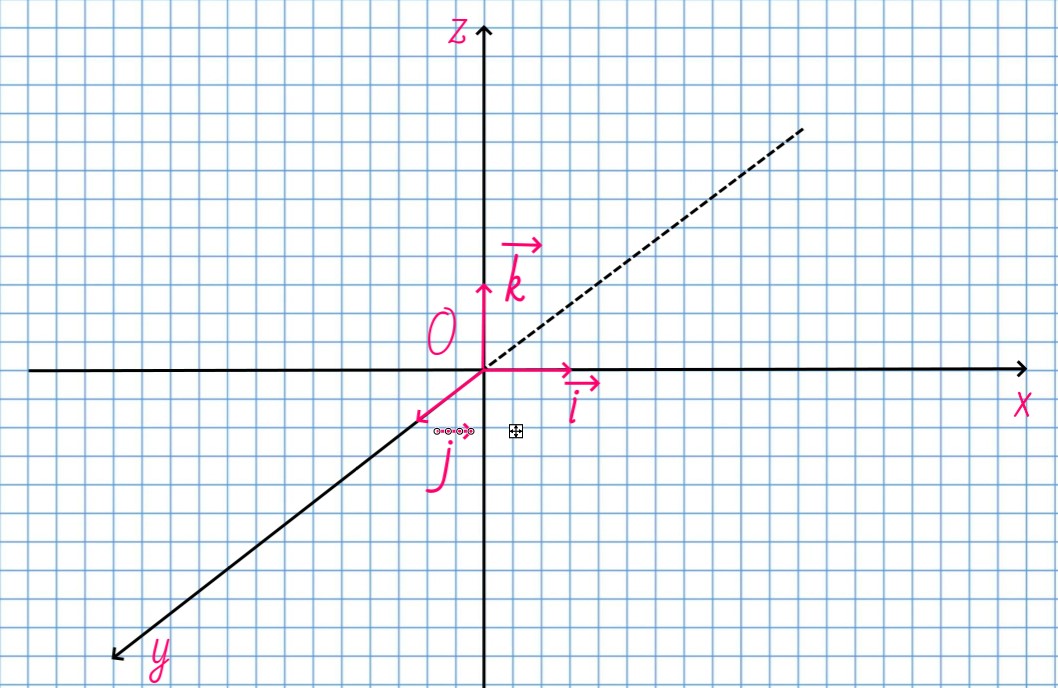
В то же время на любых векторах можно построить свою систему отсчета, тогда данные вектора будут считаться базисом этой системы и в этой системе можно найти координаты любого вектора. То есть любой вектор можно разложить по базису, конечно, если при этом базисные вектора не являются коллинеарными.
Примеры разложения вектора
Пример 1. Разложить вектор vec{c}(0; 1) по двум векторам vec{a}(3; 6) и vec{b}(4; 9).
Решение:
Для разложения вектора vec{c} запишем:
vec{c}=x vec{a}+y vec{b}
Нам нужно найти коэффициенты разложения x и y, для этого разложим каждую координату вектора vec{c}:
- Для абсциссы: 0=x cdot 3+y cdot 4
- Для ординаты: 1=x cdot 6+y cdot 9
Получаем систему из двух уравнений с двумя неизвестными, которую решаем:
begin{cases} 3x+4y=0, \ 6x+9y=1. end{cases}
Решая, получаем: displaystyle x=frac{-4}{3} и y=1
И разложение вектора vec{c} будет иметь вид: displaystyle vec{c}=-frac{4}{3} vec{a}+vec{b}
Пример 2. Найти координаты вектора vec{a} в базисе, если известно разложение вектора по базису vec{e_1} и vec{e_2}:
vec{a}=7 vec{e_1}+5 vec{e_2}
Решение: Координаты вектора в базисе векторов vec{e_1} и vec{e_2} будут равны коэффициентам разложения, то есть vec{a}(7; 5)
Ответ: vec{a}(7; 5)
Пример 3. Разложить вектор vec{b}(1; 2) по базису vec{e_1}(2; 3) и vec{e_2}(2; 5).
Решение:
Запишем разложение вектора по базису:
vec{b}=b_1 vec{e_1}+b_2 vec{e_2}
Получим систему уравнений:
begin{cases} 1=2b_1+4b_2, \ 2=2b_1+5b_2. end{cases}
От второго уравнения системы отнимем первое, получим:
begin{cases} 1=b_2, \ 2=2b_1+5b_2. end{cases}
Тогда:
begin{cases} b_2=1, \ b_1=-1,5. end{cases}
И разложение вектора будет иметь вид: vec{b}=-1,5 vec{e_1}+vec{e_2}
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Вектор в произвольном линейном пространстве — это некоторый элемент этого пространства.
Замечание 1
Базисом трёхмерного пространства называют некоторые линейно независимые вектора $a, b$ и $c$, если любой вектор $d$ может быть выражен в виде линейной комбинации этих векторов, то есть существуют некоторые вещественные коэффициенты $λ, μ$ и $ν$, причём такие, что будет соблюдаться условие $d= λ cdot a + μcdot b + ν cdot c left( 1 right)$.
Числа $λ, μ$ и $ν$ называются координатами рассматриваемого вектора относительно некоторого базиса $a, b$ и $c$.
В контексте плоскости базисом будет два независимых вектора, лежащих в этой плоскости, а не три, как в объёмном мире.
Любой вектор $d$ имеет лишь единственное разложение по базису векторов, то есть его координаты задаются однозначно через используемый базис.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Определение 1
Аффинными координатами некоторой точки $M$ в пространстве называются координаты точки относительно базиса пространства $a, b$ и $c$ и некоторой точки $O$, которую принимают за начало координат.
Декартова система координат является примером аффиной системы координат, причём базисные вектора в ней принято обозначать не буквами $a, b$ и $c$, а $i, j$ и $k$, представляющими собой направленные ортогональные между собой отрезки, причём длина каждого равна единице.
Для декартовой системы координат формула разложения выглядит так:
$d = X cdot vec{i} + Y cdot vec{j} + Z cdot vec{k}$
Здесь $X, Y$ и $Z$ — координаты вектора, а $ i, j$ и $k$ — базис.
Через базис декартовой системы координат выражается скалярное произведение векторов, заданных в этом пространстве. Для этого их координаты записываются через специальную матрицу.
Пример 1
Докажите, что вектора, $a_1…a_4$, перечисленные ниже, являются базисом пространства $mathbb{R^4}$.
$a_1 = (1; 2; -1: -2)$;
$a_2 = (2; 3 0; -1)$;
$a_3 = (1; 2; 1; 4)$;
$a_4 = (1; 3; -1; 0)$
Решение:
Размерность данного пространства равна 4, а это значит, что для проверки того, являются ли эти вектора базисом, нужно доказать их линейную независимость, то есть доказать, что ранг матрицы, составленной из координат этих векторов как из строчек, равен количеству строк.
Составленная матрица имеет вид:
$A = begin{pmatrix} 1 & 2 & -1 & -2 \ 2 & 3 & 0 & -1 \ 1 & 2 & 1 & 4 \ 1 & 3 & -1 & 0 \ end{pmatrix}$
Преобразуем её к треугольной, для краткости описания выполняемых операций строчки будем записывать (n), здесь $n$ — номер строчки.
1) (4) – (1); (3) – (1); (2) – (1) $cdot 2$:
$begin{pmatrix} 1 & 2 & -1 & -2 \ 0 & -1 & 2 & 3 \ 0 & 0 & 2 & 6 \ 0 & 1 & 0 & 2 \ end{pmatrix}$
2) (4) + (2):
$begin{pmatrix} 1 & 2 & -1 & -2 \ 0 & -1 & 2 & 3 \ 0 & 0 & 2 & 6 \ 0 & 0 & 2 & 5 \ end{pmatrix}$
3) (4) – (3):
$begin{pmatrix} 1 & 2 & -1 & -2 \ 0 & -1 & 2 & 3 \ 0 & 0 & 2 & 6 \ 0 & 0 & 0 & -1 \ end{pmatrix}$
Приведённая матрица имеет ранг 4, а значит данные вектора образуют базис этого пространства.
«Разложение вектора по базису векторов: формулировка с примерами решения» 👇
Пример 2
Пусть вектор $vec{k}$ можно разложить с использованием базиса $vec{a}$ и $vec{b}$ по формуле
$vec{k}= 5cdot vec{a} – 3 cdot vec{b}$. Каковы его координаты в соответствии с этим базисом?
Решение:
$vec{a}$ и $vec{b}$ — единичные вектора данного двумерного пространства, а это значит, что коэффициенты при них в заданном равенстве и являются координатами в этом базисе:
$vec{k} = (5; – 3)_{{a; b}}$.
Пример 3
Дан базис из трёх векторов $(1; 1; 3), ( -3; 4; 9), (2; -2; 4)$ и вектор $vec{k}=(8; -9; 6)$. Разложите данный вектор по заданному базису.
Решение:
Воспользуемся формулировкой разложения $(1)$:
$k_1 cdot (1; 1; 3) + k_2 cdot ( -3; 4; 9) + k_3 cdot (2; -2; 4) = (8; -9; 6)$;
Для того чтобы узнать координаты в данном базисе, составим расширенную матрицу, действия со строчками будем записывать как в предыдущем примере:
$begin{array}{ccc|c} 1 & -3 & 2 & 8 \ -1 & 4 & -2 & -9 \ 3 & 9 & 4 & 6 \ end{array}$
1) (2) – (1); (3) – (1) $cdot 3$:
$begin{array}{ccc|c} 1 & -3 & 2 & 8 \ 0 & 1 & 0 & -1 \ 0 & 18 & -2 & -18 \ end{array}$;
2) (1) + (2) $cdot 3$; (3) – (2) $cdot 18$:
$begin{array}{ccc|c} 1 & 0 & 2 & 5 \ 0 & 1 & 0 & -1 \ 0 & 0 & -2 & 0 \ end{array}$;
3) (3) : (-2):
$begin{array}{ccc|c} 1 & 0 & 2 & 5 \ 0 & 1 & 0 & -1 \ 0 & 0 & 1 & 0 \ end{array}$;
4) (1) – (3) $cdot 2$:
$begin{array}{ccc|c} 1 & 0 & 0 & 5 \ 0 & 1 & 0 & -1 \ 0 & 0 & 1 & 0 \ end{array}$;
Координатами вектора $vec{k}$ в заданном базисе будут $(5; – 1; 0)$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

