Амплитуда
Обсудим количественные характеристики колебаний. Начнем с самой очевидной характеристики – амплитуды. Амплитуда обозначается большой буквой А и измеряется в метрах.
Определение
Амплитудой называют максимальное смещение от положения равновесия.
Часто амплитуду путают с размахом колебаний. Размах – это когда тело совершает колебание из одной крайней точки в другую. А амплитуда – это максимальное смещение, т. е. расстояние от точки равновесия, от линии равновесия до крайней точки, в которую оно попало. Помимо амплитуды, существует еще одна характеристика – смещение. Это текущее отклонение от положения равновесия.
А – амплитуда – ![]()
х – смещение – ![]()

Рис. 1. Амплитуда
Посмотрим, как отличаются амплитуда и смещение на примере. Математический маятник находится в состоянии равновесия. Линия расположения маятника в начальный момент времени – линия равновесия. Если отвести маятник в сторону – это и будет его максимальное смещение (амплитуда). В любой другой момент времени расстояние не будет амплитудой, а будет просто смещением.

Рис. 2. Отличие амплитуды и смещения
Период
Следующая характеристика, к которой мы переходим, называется период колебаний.
Определение
Периодом колебаний называется промежуток времени, в течение которого совершается одно полное колебание.
Обратите внимание, что величина «период» обозначается большой буквой ![]() , определяется она следующим образом:
, определяется она следующим образом: ![]() ,
, ![]() .
.

Рис. 3. Период
Стоит добавить, что чем больше мы берем число колебаний за большее время, тем точнее мы определим период колебаний.
Частота
Следующая величина – это частота.
Определение
Число колебаний, совершенных за единицу времени, называют частотой колебаний.

Рис. 4. Частота
Обозначается частота греческой буквой ![]() , которая читается как «ню». Частота – это отношение числа колебаний ко времени, за которое эти колебания произошли:
, которая читается как «ню». Частота – это отношение числа колебаний ко времени, за которое эти колебания произошли: ![]() .
.
Единицы измерения частоты ![]() . Эту единицу называют «герц» в честь немецкого физика Генриха Герца. Обратите внимание, что период и частота связаны через число колебаний и время, в течение которых это колебание совершается. Для каждой колебательной системы частота и период есть величины постоянные. Связь между этими величинами довольно проста:
. Эту единицу называют «герц» в честь немецкого физика Генриха Герца. Обратите внимание, что период и частота связаны через число колебаний и время, в течение которых это колебание совершается. Для каждой колебательной системы частота и период есть величины постоянные. Связь между этими величинами довольно проста: ![]() .
.
Кроме понятия «частота колебаний» нередко пользуются понятием «циклическая частота колебаний», то есть количество колебаний за ![]() секунд. Обозначается она буквой
секунд. Обозначается она буквой ![]() и измеряется в радианах за секунду
и измеряется в радианах за секунду ![]() .
.
Графики свободных незатухающих колебаний
Мы уже знаем решение главной задачи механики для свободных колебаний – закон синуса или косинуса. Также мы знаем, что графики являются мощнейшим инструментом исследования физических процессов. Поговорим о том, как будут выглядеть графики синусоиды и косинусоиды в применении к гармоническим колебаниям.
Для начала определимся с особыми точками во время колебаний. Это необходимо для того, чтобы правильно выбрать масштаб построения. Рассмотрим математический маятник. Первый вопрос, который возникает: какую функцию использовать – синус или косинус? Если колебание начинается с верхней точки – максимального отклонения, законом движения будет закон косинуса. Если же начать движение с точки равновесия – законом движения будет закон синуса.
Если законом движения будет закон косинуса, то через четверть периода маятник будет находиться в положении равновесия, еще через четверть – в крайней точке, еще через четверть – опять в положении равновесия, и еще через одну четверть вернется в начальное положение.
Если маятник колеблется по закону синуса, то через четверть периода он будет находиться в крайней точке, еще через четверть – в положении равновесия. Потом опять в крайней точке, но с другой стороны, и через еще четверть периода вернется в положение равновесия.
Итак, масштабом времени будет не произвольные значение 5 с, 10 с и т. д., а доли периода. Мы будем строить график по четвертям долей периода.
Что же сказать о координате ![]() ? Дальше, чем положение равновесия, маятник не двигается. График будет ограничен значением амплитуды.
? Дальше, чем положение равновесия, маятник не двигается. График будет ограничен значением амплитуды.
Перейдем к построению. ![]() меняется либо по закону синуса, либо по закону косинуса. Ось ординат –
меняется либо по закону синуса, либо по закону косинуса. Ось ординат – ![]() , ось абсцисс –
, ось абсцисс – ![]() . Масштаб времени равен четвертям периода:
. Масштаб времени равен четвертям периода: ![]() График будет лежать в пределах от
График будет лежать в пределах от ![]() до
до ![]() .
.

Рис. 5. Графики зависимости ![]()
График для колебания по закону синуса выходит из нуля и обозначен темно-синим цветом (рис. 5). График для колебания по закону косинуса выходит из положения максимального отклонения и обозначен голубым цветом на рисунке. Графики выглядят абсолютно идентично, но сдвинуты по фазе относительно друг друга на четверть периода или ![]() радиан.
радиан.
Аналогичный вид будут иметь графики зависимости ![]() и
и ![]() , ведь они тоже меняются по гармоническому закону.
, ведь они тоже меняются по гармоническому закону.
Особенности колебаний математического маятника
Математический маятник – это материальная точка массой ![]() , подвешенная на длинной нерастяжимой невесомой нити длиной
, подвешенная на длинной нерастяжимой невесомой нити длиной ![]() .
.
Обратите внимание на формулу периода колебаний математического маятника: ![]() , где
, где ![]() – длина маятника,
– длина маятника, ![]() – ускорение свободного падения.
– ускорение свободного падения.
Чем больше длина маятника, тем больше период его колебаний (рис. 6). Чем длиннее нить, тем дольше маятник раскачивается.

Рис. 6. Зависимость периода колебаний от длины маятника
Чем больше ускорение свободного падения, тем меньше период колебаний (рис. 7). Чем больше ускорение свободного падения, тем сильнее небесное тело притягивает грузик и тем быстрее он стремится вернуться в положение равновесия.

Рис. 7. Зависимость периода колебаний от ускорения свободного падения
Обратите внимание, что период колебаний не зависит от массы груза и амплитуды колебаний (рис. 8).

Рис. 8. Период колебаний не зависит от амплитуды колебаний
Первым на этот факт обратил внимание Галилео Галилей. На основании этого факта предложен механизм маятниковых часов.
Следует отметить, что точность формулы ![]() максимальна лишь для малых, сравнительно небольших отклонений. Например, для отклонения
максимальна лишь для малых, сравнительно небольших отклонений. Например, для отклонения ![]() погрешность формулы составляет
погрешность формулы составляет ![]() . Для более крупных отклонений точность формулы не столь велика.
. Для более крупных отклонений точность формулы не столь велика.
Рассмотрим качественные задачи, которые описывают математический маятник.
Задача. Как изменится ход маятниковых часов, если их: 1) перевезти из Москвы на Северный полюс; 2) перевезти из Москвы на экватор; 3) поднять высоко в гору; 4) вынести из нагретого помещения на мороз.
Для того чтобы правильно ответить на вопрос задачи, необходимо понять, что имеется в виду под «ходом маятниковых часов». Маятниковые часы основаны на математическом маятнике. Если период колебаний часов будет меньше, чем нам нужно, часы начнут спешить. Если же период колебаний станет больше, чем необходимо, часы будут отставать. Задача сводится к ответу на вопрос: что произойдет с периодом колебаний математического маятника в результате всех перечисленных в задаче действий?
Рассмотрим первую ситуацию. Математический маятник переносится из Москвы на Северный полюс. Вспоминаем, что Земля имеет форму геоида, то есть сплюснутого у полюсов шара (рис. 9). Это значит, что на полюсе величина ускорения свободного падения несколько больше, чем в Москве. А раз ускорение свободного падения больше, то период колебаний станет несколько меньше и маятниковые часы начнут спешить. Здесь мы пренебрегаем тем, что на Северном полюсе холоднее.

Рис. 9. Ускорение свободного падения больше на полюсах Земли
Рассмотрим вторую ситуацию. Переносим часы из Москвы на экватор, предполагая, что температура не меняется. Ускорение свободного падения на экваторе несколько меньше, чем в Москве. Это значит, что период колебаний математического маятника увеличится и часы начнут отставать.
В третьем случае часы поднимают высоко в гору, тем самым увеличивая расстояние до центра Земли (рис. 10). Это значит, что ускорение свободного падения на вершине горы меньше. Период колебаний увеличивается, часы будут отставать.

Рис. 10 Ускорение свободного падения больше на вершине горы
Рассмотрим последний случай. Часы выносят из теплой комнаты на мороз. При понижении температуры линейные размеры тел уменьшаются. Это значит, что длина маятника немного сократится. Раз длина стала меньше, то период колебаний также уменьшился. Часы будут спешить.
Мы рассмотрели самые типичные ситуации, которые позволяют разобраться с тем, как работает формула периода колебаний математического маятника.
Фаза колебаний
В заключение рассмотрим еще одну характеристику колебаний – фазу. О том, что такое фаза, более подробно мы будем говорить в старших классах. Сегодня мы должны рассмотреть, с чем можно эту характеристику сравнить, сопоставить и как ее для себя определить. Удобнее всего фазу колебаний сопоставить со скоростью движения маятника.

Рис. 11. Маятники колеблются синфазно (с одинаковыми фазами)
На рисунке 11 представлены два одинаковых маятника. Первый маятник отклонили влево на определенный угол, второй тоже отклонили влево на определенный угол, такой же, как и первый. Оба маятника будут совершать абсолютно одинаковые колебания. В этом случае можно сказать, что маятники совершают колебания с одинаковой фазой, поскольку скорости маятника имеют одно направление и равные модули.

Рис. 12. Маятники совершают колебания в противофазе
На рисунке 12 два таких же маятника, но один отклонен влево, а другой – вправо. У них тоже одинаковые по модулю скорости, но направление противоположное. В этом случае говорят, что маятники совершают колебания в противофазе.
Во всех других случаях, как правило, упоминают о разности фаз.

Рис. 13. Разница фаз
Фазу колебаний в произвольный момент времени можно рассчитать по формуле ![]() , то есть как произведение циклической частоты на время, прошедшее с начала колебаний. Измеряется фаза в радианах.
, то есть как произведение циклической частоты на время, прошедшее с начала колебаний. Измеряется фаза в радианах.
Особенности колебаний пружинного маятника
Формула колебаний пружинного маятника: ![]() . Таким образом, период колебаний пружинного маятника зависит от массы груза и жесткости пружины.
. Таким образом, период колебаний пружинного маятника зависит от массы груза и жесткости пружины.
Чем больше масса груза, тем больше его инертность. То есть маятник будет медленнее разгоняться, период его колебаний будет больше (рис. 14).

Рис. 14. Зависимость периода колебаний от массы
Чем больше жесткость пружины, тем быстрее она стремится вернуться в положение равновесия. Период пружинного маятника будет меньше.

Рис. 15. Зависимость периода колебаний от жесткости пружины
Рассмотрим применение формулы ![]() на примере задачи.
на примере задачи.
Задача. На рисунке представлен график зависимости координаты от времени для пружинного маятника. Найдите массу грузика, если жесткость пружины равна ![]() .
.

Рис. 16. График зависимости координаты от времени для пружинного маятника
Решение:
Массу грузика можно определить из формулы периода колебаний пружинного маятника:
![]()
![]()
Период колебаний ![]() находим, используя график зависимости координаты от времени. Период – это время одного полного колебания. Одно полное колебание совершается за
находим, используя график зависимости координаты от времени. Период – это время одного полного колебания. Одно полное колебание совершается за ![]() (рис. 17).
(рис. 17).

Рис. 17. Период колебаний
Если подставить теперь все необходимые значения в формулу для вычисления массы, получим:
![]()
Ответ: масса грузика составляет приблизительно 10 г.
Так же, как и в случае с математическим маятником, для пружинного маятника период колебаний не зависит от его амплитуды. Естественно, что это справедливо только для небольших отклонений от положения равновесия, когда деформация пружины является упругой. Этот факт был положен в основу устройства пружинных часов (рис. 18).

Рис. 18. Пружинные часы
Заключение
Конечно, кроме колебаний и тех характеристик, о которых мы говорили, существуют и другие не менее важные характеристики колебательного движения. Но о них мы поговорим в старшей школе.
Список литературы
- Кикоин А. К. О законе колебательного движения // Квант. – 1983. – № 9. – С. 30-31.
- Кикоин И. К., Кикоин А. К. Физика: учеб. для 9 кл. сред. шк. – М.: Просвещение, 1992. – 191 с.
- Черноуцан А. И. Гармонические колебания – обычные и удивительные // Квант. – 1991. – № 9. – С. 36-38.
- Перышкин А. В., Гутник Е. М. Физика. 9 кл.: учебник для общеобразоват. учреждений / А. В. Перышкин, Е. М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «abitura.com» (Источник)
- Интернет-портал «phys-portal.ru» (Источник)
- Интернет-портал «fizmat.by» (Источник)
Домашнее задание
- Что такое математический и пружинный маятники? Какая разница между ними?
- Что такое гармоническое колебание, период колебания?
- Груз массой 200 г колеблется на пружине с жесткостью 200 Н/м. Найдите полную механическую энергию колебаний и наибольшую скорость движения груза, если амплитуда колебаний 10 см (трением пренебречь).

Синусоидальное колебание напряжения с постоянной амплитудой.
Амплиту́да (лат. amplitudo — значительность, обширность, величие, обозначается заглавной буквой А) — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины.
В общем случае гармоническое колебание математически записывается в виде:
или
,
где 

— амплитуда колебания, то есть максимальное за период отклонение колеблющейся величины от среднего за период значения, размерность
совпадает с размерностью
в общем случае амплитуда зависит от времени, например, при затухающем собственном колебании осциллятора;
(радиан/с, градус/с) — круговая (угловая) частота, показывающая, на сколько радиан (градусов) изменяется фаза колебания за 1 с;
(радиан, градус) — начальная фаза колебания.
Амплитуда в разных разделах физики
- амплитуда для механического колебания тела (вибрация), для волн на струне или пружине — это расстояние и записывается в единицах длины;
- амплитуда звуковых волн и аудиосигналов обычно относится к амплитуде давления воздуха в волне, но иногда описывается как амплитуда смещения относительно равновесия (воздуха или диафрагмы говорящего). Её логарифм обычно измеряется в децибелах (дБ);
- для электромагнитного излучения амплитуда соответствует величине напряженности электрического и магнитного поля.
Форма изменения амплитуды называется огибающей.
Формальное определение в радиотехнике[править | править код]
Амплитуда — наибольшее значение, которое принимает какая-либо величина, изменяющаяся по гармоническому закону[1].
Формальное определение предполагает применение термина «амплитуда» только для гармонической функции; «амплитуда» — модуль коэффициента перед гармонической функцией. В связи с этим термин «амплитуда» следует отличать от терминов, применимых к произвольным функциям:
- Максимальное значение сигнала — наибольшее мгновенное значение сигнала на протяжении заданного интервала времени[1][2];
- Минимальное значение сигнала — наименьшее мгновенное значение сигнала на протяжении заданного интервала времени[1][2];
- Размах сигнала — разность между максимальным и минимальным значениями сигнала на протяжении заданного интервала времени[1][2].
См. также[править | править код]
- Волна
- Длина волны
- Резонанс
- Фаза колебаний
- Комплексная амплитуда
- Период колебаний
- Амплитудная модуляция
- Амплитуда сейсмической волны
- Механическая волна
- Частота колебаний
Примечания[править | править код]
- ↑ 1 2 3 4 ОСТ 45.159-2000. Отраслевая система обеспечения единства измерений. Термины и определения
- ↑ 1 2 3 ГОСТ 16465-70. Сигналы радиотехнические измерительные. Термины и определения
Ссылки[править | править код]
- Амплитуда, в астрономии // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Амплитуда, в теории функций // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.

Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):

Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):

Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.

Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Рассмотрим величины, с помощью которых можно охарактеризовать колебания.

Рис. (1). Движение пустых качелей и качелей с мальчиком
Сравним колебания двух качелей на рисунке (1) — пустых качелей и качелей с мальчиком. Качели с мальчиком колеблются с большим размахом, то есть их крайние положения находятся дальше от положения равновесия, чем у пустых качелей.
Амплитудой колебаний (A) называется максимальное отклонение колеблющегося тела от положения равновесия.
([A]=1~м)
Полным колебанием называют движение, за которое тело возвращается в исходную точку (из которой началось колебание).
За одно полное колебание тело дважды максимально отклоняется от положения равновесия, поэтому один полный путь одного полного колебания равен четырём амплитудам: (s=4A).
Период колебаний — это промежуток времени, за который тело совершает одно полное колебание.
([T]=1~с)
Пример:
ударим по столу двумя линейками — металлической и деревянной (рис. (2)) Линейки после этого начнут колебаться, но за один и тот же промежуток времени металлическая линейка (B) сделает больше колебаний, чем деревянная (A).

Рис. (2). Колебания металлической (B) и деревянной (A) линеек
Число колебаний в единицу времени называется частотой колебаний.
Обрати внимание!
Обозначается частота греческой буквой
ν
(«ню»). За единицу частоты принято одно колебание в секунду. Эта единица в честь немецкого учёного Генриха Герца названа герцем (Гц).
Период колебания (T) и частота колебаний
ν
связаны следующей зависимостью:
Свободные колебания в отсутствие трения и сопротивления воздуха называются собственными колебаниями, а их частота — собственной частотой колебательной системы.
Для описания закономерностей колебательной системы необходимо учитывать зависимость параметров колебания от параметров системы. Например, период колебаний и их частота зависят от массы груза и жёсткости пружины для физического маятника.

Рис. (3). Движение пустых качелей и качелей с мальчиком
Рассмотрим колебания двух одинаковых пустых качелей на рисунке (3). В один и тот же момент времени красные качели из положения равновесия начинают движение вперед, а зелёные качели из положения равновесия движутся назад. Движение качелей таково, что их амплитуды и периоды колебаний одинаковы. А если одинаковы периоды, то и частота колебаний совпадает. Однако, направлений движения качелей противоположно. О таких движениях говорят, что они движутся в противофазах.
Красные пустые качели и качели с мальчиком тоже колеблются с одинаковыми частотами. Направление скоростей этих качелей тоже совпадает. Это означает, что колебания происходят в одинаковых фазах, т.е. совпадают по фазе.
Фаза — физическая величина. Её используют для описания колебания тела.
Исходя из выше сказанного следует, что характеристиками колебательного движения являются:
- амплитуда,
- частота (можно использовать период),
- фаза.
Источники:
Рис. 1, 3. Движение пустых качелей и качелей с мальчиком.
Рис. 2. Колебания металлической и деревянной линеек.
Параметры вибрационного процесса
- Виброперемещение, S – это расстояние между крайними точками перемещения колеблющегося элемента вдоль оси измерения. Виброперемещение измеряется в линейных единицах: в микронах – мкм; в миллиметрах – мм, при больших значениях виброперемещения, например, грохотов (1 мм = 1000 мкм). Параметром, дополняющим виброперемещение является частота вращения. Например, допустимое значение виброперемещения 20 мкм при частоте вращения 1500 об/мин и 10 мкм при частоте вращения 3000 об/мин.
Виброперемещение измеряется при возникновении низкочастотной вибрации, верхняя граница частотного спектра не более 200 Гц. Эти измерения актуальны в строительной виброакустике, при проведении балансировки роторов, при исследовании машин с малыми зазорами между узлами и деталями, при исследовании упругих деформаций и прогнозе усталостных разрушений. - Виброскорость, v – производная виброперемещения по времени. Этот параметр характеризует мощность колебательного (вибрационного) процесса, направленного на разрушение деталей и характеризует энергетическое воздействие на узлы объекта контроля (энергия колебания E = m × V2 / 2). Виброскорость – это скорость перемещения контролируемой точки оборудования. Виброскорость одновременно учитывает перемещение контролируемой точки и частоту колебаний, вызвавших вибрацию. Виброскорость измеряется в миллиметрах на секунду, мм/с.
Виброскорость измеряют в частотном диапазоне 10…1000 Гц. По уровню виброскорости определяют техническое состояние машин, их узлов и деталей. - Виброускорение, а – производная виброскорости по времени. Параметр характеризует силу инерции, которая воздействует на объект при вибрации:
F = m × a, где F – сила инерции; m – масса объекта; а – виброускорение.
Виброускорение – это ускорение перемещения контролируемой точки оборудования или это скорость изменения скорости. Виброускорение характеризует силовое динамическое взаимодействие элементов агрегата. Виброускорение измеряется в метрах на секунду в квадрате, м/с2, иногда используется единица ускорения свободного падания – g, 1 g = 9,8 м/с2.
Виброускорение измеряется при наличии вибрации в широкой полосе частот, от 50 до 10000 Гц и более. Эти измерения актуальны при виброакустической диагностике для оценки силы ударов и раннего обнаружения повреждений в подшипниках качения и зубчатых передачах.
Примечание: существует редко используемый параметр вибрации – резкость – третья производная перемещения по времени, размерность – км/с3. - Частота, f – характеристика периодического процесса, равная количеству повторений в единицу времени, обратно пропорциональна периоду колебаний:
f = 1/T, где Т – период, время полного цикла колебаний (с).
Единицей измерения частоты в Международной системе единиц (СИ) является герц (русское обозначение – Гц; международное – Hz), названный в честь немецкого физика Генриха Герца. Одно колебание в секунду соответствует 1 Гц.
При частоте вращения 3000 об/мин, частота колебаний составляет:
f = n / 60 = 3000 / 60 = 50 Гц.
Частота колебаний позволяет идентифицировать источник колебаний.
Гармонические колебания в разных точках машины, совпадающие по частоте, называются синхронными. Синхронные колебания отличаются друг от друга амплитудой и фазой. - Фаза колебаний, φ – определяет положение характерной точки колебаний (максимального, минимального значения или перехода от отрицательного к положительному значению) относительно зафиксированного положения метки. Измеряется в градусах. Используется при балансировке, обследовании металлоконструкций, диагностировании механизмов.
Колебания в двух точках, совпадающие по фазе, называют синфазными, а отличающиеся на 1800 – противофазными. Сдвиг фаз синхронных гармонических колебаний – это разность фаз двух синхронных гармонических колебаний гармонических колебаний в заданный момент времени. Этот параметр часто используют при анализе вибрации.
Для гармонического колебательного процесса существует ряд особенностей, которые характеризуют связь между перемещением, скоростью и ускорением:
- перемещение, скорость и ускорение – гармонические функции одной частоты;
- связь между амплитудами перемещения, скоростью и ускорением – линейная, и определяется с помощью соотношений:
v = 2 π × f× S = a × 103 / (2 π × f),
S = v / (2 π × f )= a × 103 / (2 π × f)2,
а = (2 π × f)2 × S × 10-3 = 2 π × f × v × 10-3,
формулы приведены для следующей размерности: S – мкм, v – мм/с; а – м/с2; - между фазами перемещения, скорости и ускорения существует сдвиг на 900, то есть скорость по фазе опережает перемещение на четверть периода, а ускорение опережает перемещение на полпериода – 1800 (рисунок 70).
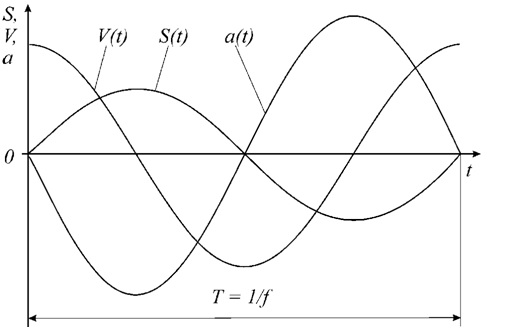
Рисунок 70 – Сдвиг фаз между параметрами гармонических колебаний
Пример
Для роторного механизма, имеющего частоту вращения 3000 об/мин (50 Гц) зафиксировано значение виброперемещения – 20 мкм. Определить соответствующие значения виброскорости и виброускорения.
v = 2 π × f × S = 6,28 × 50 × 20 = 6,28 мм/с;
а = 2π × f × v = 6,28 × 50 × 6,28 = 1,97 м/с2.
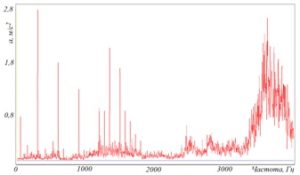
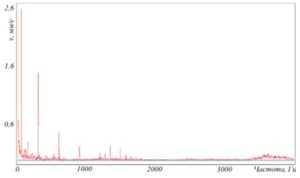
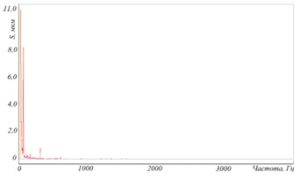
Исходя из данных соотношений, можно сделать вывод о том, что зависимости между перемещением, скоростью, ускорением и частотой будут различными. На графике перемещения будет преобладать низкочастотная область, а на графике ускорения ‑ высокочастотная при ослаблении низкочастотной (рисунок 71).
|
Виброускорение |
Виброскорость |
Виброперемещение |
Рисунок 71 – Спектрограммы параметров вибрации, зафиксированных в одной точке
Числовые значения уровней ускорения, скорости и перемещения в логарифмических координатах (при пороговых значениях по ISO 1683) равны только в одной точке – при частоте 159 Гц (рисунок 72). На эту частоту настраиваются калибраторы вибрации. В этой точке значение виброперемещения составляют 10 мкм, значения виброскорости – 10 мм/с, а значения виброускорения – 10 м/с2.
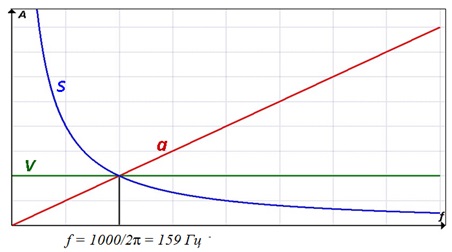
Рисунок 72 – Точка вибрационного контроля
Основные характеристики колебательных процессов
- Размах колебаний – разность между наибольшим и наименьшим значениями колеблющейся величины в рассматриваемом интервале времени (рисунок 73). Для гармонических колебаний размах колебаний равен удвоенной пиковой амплитуде, так как временная реализация в этом случае симметрична.
Размах колебаний является необходимым в тех случаях, когда смещение механических колебаний детали машины является критическим с точки зрения максимально допустимых механических напряжений и зазоров. Используется в основном при измерении виброперемещения.

Рисунок 73 – Характеристики колебательных процессов
- Пиковое значение – определяется как наибольшее отклонение колеблющейся величины от среднего положения хПИК = IхМАХI.
Используется как составляющая при измерении виброускорения. Пиковое значение эффективно при оценке кратковременных механических ударов и так далее. Однако пиковое значение отображает только максимальное значение исследуемых колебаний, а не их временное развитие. - Среднеарифметическое мгновенных значений вибрации – среднее значение измеренных данных, характеризует общую интенсивность вибрации:
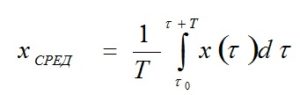 где τ – текущее значение временной координаты, Т – период измерения.
где τ – текущее значение временной координаты, Т – период измерения.
Среднее значение отображает временное развитие исследуемых колебаний, но его практическое применение ограничено ввиду того, что оно не имеет непосредственной связи ни с какой физической величиной этих колебаний. - Среднее квадратичное значение (СКЗ) – квадратный корень из среднего арифметического или среднего интегрального значения квадрата колеблющейся величины в рассматриваемом периоде времени:
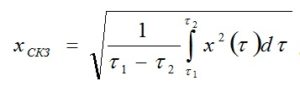 Для получения правильного значения, интервал усреднения должен быть не меньше одного периода колебания. Используется при измерении виброскорости. Пересчёт значений виброускорения, виброскорости и виброперемещения, определённых в результате анализа спектра, как функции угловой частоты ω, в среднее квадратическое значение виброскорости проводится по следующим формулам:
Для получения правильного значения, интервал усреднения должен быть не меньше одного периода колебания. Используется при измерении виброскорости. Пересчёт значений виброускорения, виброскорости и виброперемещения, определённых в результате анализа спектра, как функции угловой частоты ω, в среднее квадратическое значение виброскорости проводится по следующим формулам:
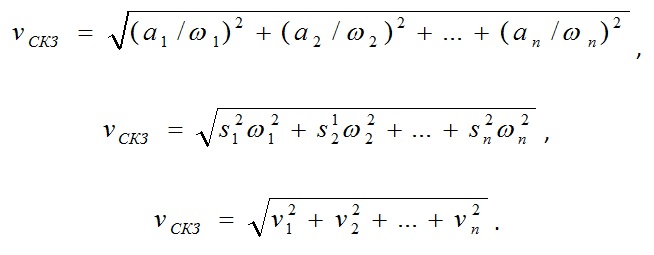 Возможно определение среднего квадратического значения виброскорости по максимальному и минимальному значению виброскорости в спектре:
Возможно определение среднего квадратического значения виброскорости по максимальному и минимальному значению виброскорости в спектре:
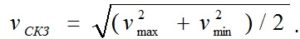 Среднеквадратическое значение учитывает временное развитие исследуемых колебаний и непосредственно отображает значение, связанное с энергией сигнала и, следовательно, разрушающей способностью этих колебаний.
Среднеквадратическое значение учитывает временное развитие исследуемых колебаний и непосредственно отображает значение, связанное с энергией сигнала и, следовательно, разрушающей способностью этих колебаний. - Коэффициент амплитуды или пик-фактор – отношение пикового (xПИК) к среднеквадратичному (xСКЗ) значению: KПФ = xПИК / xСКЗ.
Пик-фактор характеризует развитие повреждения. Значения пик-фактора в начальном периоде работы механизма составляют 3…4. При зарождении повреждений значения пик-фактора увеличиваются до 10…15. Увеличение степени повреждений снижает значения пик-фактора до 3…4 (рисунок 74).
Для гармонических колебаний: KПФ = 1,41; xПИК = А; xСРЕД = 0,637А; xСКЗ = 0,707А.

Рисунок 74 – Изменения значения пик-фактора
- Эксцесс – отношение момента четвёртого порядка к квадрату момента второго порядка. Эксцесс определяет степень отклонения параметра от нормального распределения: b = m4 / (m2)2, где m4 – момент четвёртого порядка; m2 – момент второго порядка.
При определении статистических моментов используются значения:
– среднее арифметическое – сумма относительных отклонений;
– дисперсия – сумма квадратов относительных отклонений;
– асимметрия – сумма кубов относительных отклонений;
– островершинность – сумма четвёртой степени относительных отклонений.
Значения эксцесса используется для определения развития различных неисправностей элементов машин, так как отклонение от нормального распределения является однозначным признаком появления неисправности.
Относительные единицы вибрации – 20-ти кратные десятичные логарифмы отношения измеренного значения параметра вибрации (vИЗМ) к некоторому начальному уровню (vНАЧ) и измеряются в децибелах (дБ). Для виброскорости:
Lv = 20 lg (vИЗМ / vНАЧ).
Для виброускорения:
Lа = 20 lg (аИЗМ / аНАЧ).
Увеличение уровня на 6 дБ соответствует удвоению амплитуды, независимо от исходного значения. Изменение уровня на 20 дБ означает рост амплитуды в десять раз. Для временных реализаций вибрации всегда используются линейные единицы измерения амплитуды: мгновенное значение сигнала может быть и отрицательным, и поэтому его невозможно логарифмировать.
При использовании логарифмических характеристик необходимо указывать стандартный пороговый уровень, принятый при обработке значений вибрации. По Правилам Российского Морского Регистра Судоходства и ГОСТ 12.1.034-81, пороговый уровень принят: vНАЧ = 5·10-5 мм/с; аНАЧ = 3·10-4 м/с2. По ГОСТ 30296-95: vНАЧ = 5·10-8 м/с; аНАЧ = 1·10-6 м/с2. По ISO 1683: vНАЧ = 1·10-6 мм/с; аНАЧ = 1·10-6 м/с2; SНАЧ = 1·10-6 мкм.
Обычно, аналоговый вибрационный временной сигнал преобразуется в цифровой вид и используется для спектрального анализа в частотной области. Сложность формы временного сигнала, его интерпретация сильно затруднена, поэтому часто временная форма сигнала игнорируется. В то же время информацию, которую может дать временная форма, недоступна при рассмотрении спектра вибрации.
Например, случайный процесс (непрерывный шум) и переходный процесс, связанный с какими-то нерегулярными событиями, имеют схожие спектры, которые, тем не менее, соответствуют сигналам совершенной разной природы, что отчетливо видно по их временным реализациям. Во временной области легко различим стук деталей, приводящий к асимметрии формы сигнала, который может быть следствием ослабления механических соединений.
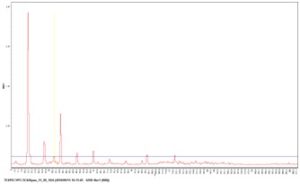
Обследование вибрационного состояния редуктора РМ-400 механизма передвижения мостового крана проведено при работе оборудования в режиме холостого хода при частоте вращения двигателя 720 об/мин. При работе редуктора наблюдаются глухие стуки. Значения общего уровня виброскорости – 3,0 мм/с, виброускорения – 1,8 м/с2. В спектрограмме виброскорости подшипника тихоходного вала редуктора (рисунок 75а) зубцовая частота второй передачи представлена составляющей на частоте 31,5 Гц, с амплитудой 0,2 мм/с. Запись временного сигнала виброускорения (рисунок 75б) позволила установить возможную причину неисправности – повреждения (забоина) на зубчатом колесе тихоходного вала проявившуюся, как удары с частотой вращения тихоходного вала. Подтверждение диагноза получено при визуальном осмотре и устранено после механической обработки повреждённого зуба.
|
(а) |
(б) |
Рисунок 75 – Спектрограмма виброскорости (а) и временной сигнал (б) виброускорения подшипника тихоходного вала редуктора механизма передвижения мостового крана
Цикл измерений содержал 12 измерений, с учётом 800 линий в спектре – 9600 значений, дополнительно проведены измерения временной формы вибрационного сигнала ‑ 4×16000 значений. Из этих данных получено два информационных сообщения: об общем уровне вибрации (соответствующего удовлетворительному состоянию) и о возможной причине неисправности, устранённой при ремонте.
Работа электродвигателей часто сопровождается биениями, которые, хорошо воспринимаются на слух. Эти биения соответствуют частоте скольжения ротора или разности частоты вращения ротора и частоты возбуждения двигателя. Частота биений очень низка, иногда ниже 0,1 Гц. Биения могут также возникать, когда машины, близко расположенные друг к другу, работают на слегка различающихся частотах вращения. Наблюдать биения лучше во временной области вибрационного сигнала, поскольку для вычисления спектральных составляющих на столь низких частотах требуется очень большое время и высокое разрешение.
Трудность анализа заключается в отсутствии правил формализации и обработки временных реализаций параметров быстропротекающих процессов. Во многом данный процесс субъективен и зависит от опыта специалиста. Спектральные составляющие вибрационного сигнала часто остаются практически без изменений из-за усреднения вибрационного сигнала, необходимого для получения достоверной оценки. Анализ фактического сигнала несет дополнительную информацию о техническом состоянии механизма. Наиболее эффективно использование анализа временной формы вибрационного сигнала для диагностирования переходных, нестационарных, ударных процессов. Для этого используются периоды 30…400 мкс, количество измерений 10000…16000 и более, режим – без усреднений.
Правила анализа временного сигнала
- Необходимо оценить повторяемость параметров колебательного процесса. Одинаковым воздействиям должны соответствовать одинаковые реализации параметров колебаний. Можно использовать сравнительный анализ однотипных процессов в различных точках при использовании двухканального анализатора вибрации.
- Оценка симметричности сигнала относительно нулевого (начального) уровня колебаний. Наличие симметричного сигнала свидетельствует о хорошем состоянии (идеальным случаем является синусоидальная форма колебаний – абсолютно симметричная), отклонения – увеличивают степень асимметрии. Диагностические параметры для анализа — положительные и отрицательные значения амплитуд колебаний. Причины асимметрии — нелинейность характеристик системы, анизотропия деталей подшипникового узла.
- Наиболее значимым является время успокоения системы после возмущающего воздействия. Системы с малой жесткостью и малыми демпфирующими свойствами будут иметь большее время затухания. Следует определить причины снижающие жесткость и демпфирующие свойства системы. Оценить стабильность демпфирующих свойств механической системы возможно при определении декремента колебаний как натурального логарифма отношения двух последующих амплитуд:
Характер вибрации при изменении частоты вращения механизма также является диагностическим признаком, требующим анализа временных реализаций:
- Если при изменении частоты вращения происходит увеличение вибрации в линейной зависимости, причиной повреждений являются механические повреждения деталей.
- Если при изменении частоты вращения происходит увеличение вибрации в квадратичной зависимости, причиной повреждений является дисбаланс ротора.
- Если при изменении частоты вращения происходит увеличение вибрации в экспоненциальной зависимости, причиной повреждений является трещина в корпусной детали или в основании.
- Резкое уменьшение вибрации электродвигателя при отключении питания – признак наличия повреждений, вызванных повреждениями в электрической части двигателя.
- Постепенное снижение вибрации при остановке механизма – признак наличия повреждений в механической системе.
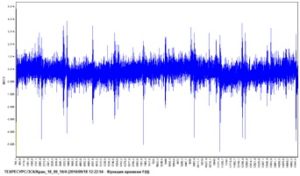
Примеры временной реализации виброускорения подшипников электродвигателя приведены на рисунке 76.
|
(а) |
(б) |
Рисунок 76 – Примеры временной реализации виброускорения подшипников электродвигателя
Рисунок 76а – размах колебаний около 14,0 м/с2, чётко выделяются колебания с периодом 20 мс – частотой вращения вала двигателя. Рисунок 76б – размах колебаний около 30,0 м/с2, на длинной выборке регистрируются отдельные удары до 63,0 м/с2, пропускаемые спектральным анализом в результате усреднения. Анализ временной реализации позволяет обнаружить первые признаки отклонений на более ранних стадиях, чем спектральный анализ.
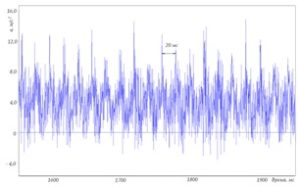
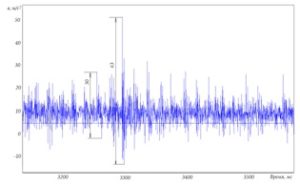
Различные временные интервалы при записи сигнала позволяют изменять анализируемую картину вибрации (рисунок 77).
Рисунок 77 – Примеры временной реализации виброускорения при различных временных интервалах
Рисунок 77а – интервал 5 секунд, сигнал стабильный, размах около 10,0 м/с2. Рисунок 77б – интервал 1 секунда, различаются колебания с оборотной частотой вращения вала двигателя. Рисунок 77в – интервал 100 миллисекунд, различимы синусоидальные колебания с оборотной частотой модулированные примерно 12-й гармоникой – повреждения колец подшипника, размах модуляции около 2,6 м/с2. Рисунок 77г – подшипник компрессора интервал 100 миллисекунд, различаются колебания первой и второй зубцовой частоты, амплитуда второй зубцовой частоты значительно ниже, чем первой.
Вопросы для самостоятельного контроля
- В каких случаях измеряют виброперемещение?
- Какой показатель характеризует виброскорость?
- Зачем необходимо измерять виброускорение?
- Что характеризует частота колебаний?
- Что важнее значение сдвига фаз или его изменение?
- Каким образом связаны параметры гармонических колебаний?
- Что такое точка вибрационного контроля?
- Какие характеристики определяют колебательные процессы?
- Что такое относительные единицы вибрации?
- Зачем необходим анализ временной реализации виброускорения?
Материал предоставил Сидоров Владимир Анатольевич.
3
4
голоса
Рейтинг статьи