Как найти размах набора данных

Была ли эта статья полезной?

Как найти размах в численных данных? Работа с большими численными данными тесно связана со статистикой. Размах — это статистический термин, который определяет простое действие над численными данными.

Статистика — раздел математики, в котором изучают информацию разного рода, а также проводят над ней всякие операции, чтобы:

• выявить закономерности;

• спрогнозировать вероятности;

• проанализировать результаты каких-либо действий;

• и др.

Сегодня мы не будем изучать все статистические операции над численной информацией, но подробнее остановимся на вопросе: как найти размах?

Как найти размах

Чтобы найти размах в статистике, нам нужно будет коротко остановиться еще на двух терминах: объем и выборка.

Для удобства давайте разработаем условный недельный бюджет расходов. Например:

• понедельник — 110;

• вторник — 140;

• среда — 100;

• четверг — 160;

• пятница — 260;

• суббота — 220;

• воскресенье — 50.

Допустим, такой бюджет мы составили на 1 месяц, чтобы понять наши ежемесячные расходы. Если мы возьмем из месячной статистики результаты одной недели, тогда это и будет выборкой. То есть выборка — это определенное количество информации из большого массива данных, которую вы извлекли для дальнейшего анализа. В выборке может участвовать любое количество элементов. 

Обычно элементам выборки для удобства присваивают индексы при помощи переменных. Например: x1, x2, x3 и др. То есть в нашем случае у нас будет х1 – х7 или 7 элементов. Количество элементов выборки — это и есть объем. По сути, мы имеет выборку объемом в 7 элементов. Теперь самое важное — как найти размах?

Размах в статистике 

Размах в статистике, он же размах в выборке — это разница между самым большим элементом выборки и самым маленьким. Глядя на наш еженедельный бюджет, мы видим, что самым большим элементом у нас является 260, а самым маленьким — 50.

Как найти размах нашей выборки: 260 – 50 = 210. Размах нашей выборки равен 210. Размах в статистике помогает определить амплитуду изменений наших статистических данных.

Как найти размах, используя программирование

Искать размах в статистике при помощи программирования — это базовые вещи, которые изучают все специалисты big data. Поиск осуществляется на том языке, при помощи которого вы взаимодействуете с данными. Например: Python, R, Java, Scala, Julia и др. Язык влияет только на реализацию поиска размаха, но алгоритм будет везде одинаковый.

Как найти размах в статистике при помощи программирования:

1. Вначале нужно сделать выборку данных из их общего массива.

2. Отсортировать элементы выборки по возрастанию, то есть от меньшего к большему.

3. После сортировки нужно определить наименьшее и наибольшее значения элементов. После сортировки элемент выборки с самым меньшим индексом будет иметь наименьшее значение, элемент с наибольшим индексом будет иметь наибольшее значение.

4. Математически вычислить разницу между большим и меньшим значениями выборки.

5. Вывести полученный размах на экран.

Заключение

Как найти размах в статистике? Для этого нужно определить наибольшее и наименьшее значения выборки и найти их разницу. Реализовать подобные действия можно при помощи любого языка программирования, который поддерживает работу с массивами данных.

План урока:

Понятие выборки и генеральной совокупности

Среднее арифметическое выборки

Упорядоченный ряд и таблица частот

Размах выборки

Мода выборки

Медиана выборки

Ошибки в статистике

Понятие выборки и генеральной совокупности

Слово статистика, образованное от латинского status(состояние дел), появилось только в 1746 году, когда его употребил немец Готфрид Ахенвалль. Однако ещё в Древнем Китае проводились переписи населения, в ходе которых правители собирали информацию о своих владениях и жителях, проживающих в них.

В основе любого статистического исследования лежит массив информации, который называют выборкой данных. Покажем это на примере. Пусть в классе, где учится 20 учеников, проводился тест по математике, содержавший 25 вопросов. В результате учащиеся показали следующие результаты:

Ряд чисел, приведенный во второй строке таблицы (12, 19, 19, 14, 17, 16, 18, 20, 15, 25, 13, 20, 25, 16, 17, 12, 24, 13, 21, 13), будет выборкой. Также ее могут называть рядом данных или выборочной совокупностью.

В примере с классом выборка состоит из 20 чисел. Эту величину (количество чисел в ряду) называют объемом выборки. Каждое отдельное число в ряду именуют вариантой выборки.

В примере со школьным классом в выборку попали все его ученики. Это позволяет точно определить, насколько хорошо учащиеся написали математический тест. Однако иногда необходимо проанализировать очень большие группы населения, состоящие из десятков и даже сотен миллионов человек. Например, необходимо узнать, какая часть населения страны курит. Опросить каждого жителя государства невозможно, поэтому в ходе исследования опрашивают лишь его малую часть. В этом случае статистики выделяют понятие генеральная совокупность.

Так, если с помощью опроса 10 тысяч человек ученые делают выводы о распространении курения в России, то все российское население будет составлять генеральную совокупность исследования, а опрошенные 10 тысяч людей вместе образуют выборку.

Среднее арифметическое выборки

Сбор информации о выборке является лишь первой стадией статистического исследования. Далее ее необходимо обобщить, то есть получить некоторые цифры, характеризующие выборку. Самой часто используемой статистической характеристикой является среднее арифметическое.

Другими словами, для подсчета среднего арифметического необходимо просто сложить все числа в ряде данных, а потом поделить получившееся значение на количество чисел в ряде. Так, в примере с тестом по математике (таблица 1) средний балл учащихся составит: (12+19+19+14+17+16+18+20+15+25+13+20+25+16+17+12+24+13+21+13):20=

= 349:20 = 17,45.

Среднее арифметическое позволяет одним числом характеризовать какое-либо качество всех объектов группы. Чем больше средний балл учащихся в классе, тем выше их успеваемость. Чем меньше среднее количество голов, пропускаемых футбольной командой за один матч, тем лучше она играет в обороне. Если средняя зарплата программистов в городе составляет 90 тысяч рублей, а дворников – 25 тысяч рублей, то это значит, что программисты значительно более востребованы на рынке труда, а потому при выборе будущей профессии лучше предпочесть именно эту специальность.

Упорядоченный ряд и таблица частот

В ряде данных в таблице 1 числа приведены в произвольном порядке. Перепишем ряд так, чтобы все числа шли в неубывающем порядке, то есть от самого маленького к самому большому:

12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.

Такую запись называют упорядоченным рядом данных.

Его характеристики ничем не отличаются от изначальной выборки, однако с ним удобнее работать. С его помощью можно видеть, что ни одному ученику не удалось набрать 22 или 23 балла на тесте, но сразу двое учащихся дали 25 правильных ответов. На основе упорядоченного ряда данных несложно составить таблицу частот, в которой будет указано, как часто та или иная варианта выборки встречается в ряде. Выглядеть она будет так:

При составлении этой таблицы мы исключили из нее те варианты количества набранных баллов, частота которых равна нулю (от 0 до 12, 22 и 23).Заметим, что сумма чисел в нижней строке таблицы частот должна равняться объему выборки. Действительно,

2+3+1+1+2+2+1+2+2+1+1+2 = 20.

С помощью таблицы частот можно быстрее посчитать среднее арифметическое выборки. Для этого каждую варианту надо умножить на ее частоту, после чего сложить полученные результаты и поделить их на объем выборки:

(12•2+13•3+14•1+15•1+16•2+17•2+18•1+19•2+20•2+21•1+24•1+25•2):20 =

(24+39+14+15+32+34+18+38+40+42+24+50):20 = 349:20 = 17,45.

Размах выборки

Следующий важная характеристика ряда данных – это размах выборки.

Если выборка представлена в виде упорядоченного ряда данных, то достаточно вычесть из последнего числа ряда первое число. Так, размах выборки результатов теста в классе равен:

25 – 12 = 13,

так как самые лучшие ученики смогли решить все 25 заданий, а наихудший учащийся ответил правильно только на 13 вопросов.

Размах выборки характеризует стабильность, однородность исследуемых свойств. Например, пусть два спортсмена-стрелка в ходе соревнований производят по 5 выстрелов по круговой мишени, где за попадание начисляют от 0 до 10 очков. Первый стрелок показал результаты 8, 9, 9, 8, 9 очков. Второй же спортсмен в своих попытках показал результаты 7, 10, 10, 6, 10. Средние арифметические этих рядов равны:

(8+9+9+8+9):5 = 43:5 = 8,6;

(7+10+10+6+10):5 = 43:5 = 8,6.

Получается, что в среднем оба стрелка стреляют одинаково точно, однако первый спортсмен демонстрирует более стабильные результаты. У его выборки размах равен

9 – 8 = 1,

в то время как размах выборки второго спортсмена равен

10 – 6 = 4.

Размах выборки может быть очень важен в метеорологии. Например, в Алма-Ате и Амстердаме средняя температура в течение года почти одинакова и составляет 10°С. Однако в Алма-Ате в январе и феврале иногда фиксируются температуры ниже -30°С, в то время как в Амстердаме за всю историю наблюдений она никогда не падала ниже -20°С.

Мода выборки

Иногда важно знать не среднее арифметическое выборки, а то, какая из ее вариант встречается наиболее часто. Так, при управлении магазином одежды менеджеру не важен средний размер продаваемых футболок, а необходима информация о том, какие размеры наиболее популярны. Для этого используется такой показатель, как мода выборки.

В примере с математическим тестом сразу 3 ученика набрали по 13 баллов, а частота всех других вариант не превысила 2, поэтому мода выборки равна 13. Возможна ситуация, когда в ряде есть сразу две или более вариант, которые встречаются одинаково часто и чаще остальных вариант. Например, в ряде

1, 2, 3, 3, 3, 4, 5, 5, 5

варианты 3 и 5 встречаются по три раза. В таком случае ряд имеет сразу две моды – 3 и 5, а всю выборку именуют мультимодальной. Особо выделяется случай, когда в выборке все варианты встречаются с одинаковой частотой:

6, 6, 7, 7, 8, 8.

Здесь числа 6, 7 и 8 встречаются одинаково часто (по два раза), а другие варианты отсутствуют. В таких случаях говорят, что ряд не имеет моды.

Медиана выборки

Иногда, например, при расчете средней зарплаты, среднее арифметическое не вполне адекватно отражает ситуацию. Это происходит из-за наличия в выборке чисел, очень сильно отличающихся от среднего. Так, из-за огромных зарплат некоторых начальников большинство рядовых сотрудников компаний обнаруживают, что их зарплата ниже средней. В таких случаях целесообразно использовать такую характеристику, как медиану ряда. Это такое значение, которое делит ряд данных пополам. В упорядоченном ряде 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25 медианой будет равна 12, так как именно она находится в середине ряда:

Однако таким образом можно найти только медиану ряда, в котором находится нечетное количество чисел. Если же их количество четное, то за медиану условно принимают среднее арифметическое двух средних чисел. Так, для ряда 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25, 30, содержащего 12 чисел, медиана будет равна среднему значению 12 и 15, которые занимают 6-ое и 7-ое место в ряду:

Вернемся к примеру с математическим тестом в школе. Так как его сдавали 20 учеников, а 20 – четное число, то для расчета медианы следует найти среднее арифметическое 10-ого и 11-ого числа в упорядоченном ряде

12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.

Эти места занимают числа 17 и 17 (выделены жирным шрифтом). Медиана ряда будет равна

(17+17):2 = 34:2 = 17.

Три приведенные основные статистические характеристики выборки, а именно среднее арифметическое, мода и медиана, называются мерами центральной тенденции. Они позволяют одним числом указать значение, относительно которого группируются все числа ряда.

Рассмотрим для наглядности ещё один пример. Врач в ходе диспансеризации измерил вес мальчиков в классе. В результате он получил 10 значений (в кг):

39, 41, 67, 36, 60, 58, 46, 44, 39, 69.

Найдем среднее арифметическое, размах, моду и медиану для этого ряда.

Решение. Сначала перепишем ряд в упорядоченном виде:

36, 39, 39, 41, 44, 46, 58, 60, 67, 69.

Так как в ряде 10 чисел, то объем выборки равен 10. Найдем среднее арифметическое. Для этого сложим все числа в ряде и поделим их на объем выборки (то есть на 10):

(36+39+39+41+44+46+58+60+67+69):10 =

= 499:10 = 49,9 кг.

Размах выборки равен разнице между наибольшей и наименьшей вариантой в ней. Самый тяжелый мальчик весит 69 кг, а самый легкий – 36 кг, а потому размах ряда равен

69 – 36 = 33 кг.

В упорядоченном ряде только одно число, 39, встречается дважды, а все остальные числа встречаются по одному разу. Поэтому мода ряда будет равна 39 кг.

В выборке 10 чисел, а это четное число. Поэтому для нахождения медианы надо найти два средних по счету значение найти их среднее. На 5-ом и 6-ом месте в ряде находятся числа 44 и 46. Их среднее арифметическое равно

(44+46):2 = 90:2 = 45 кг.

Поэтому и медиана ряда будет равна 45 кг.

Ошибки в статистике

Статистика является очень мощным инструментом для исследований во всех областях человеческой деятельности. Однако иногда ее иронично называют самой точной из лженаук. Известно и ещё одно высказывание, приписываемое политику Дизраэли, согласно которому существует просто ложь, наглая ложь и статистика. С чем же связана такая репутация этой дисциплины?

Дело в том, что некоторые люди и организации часто манипулируют данными статистики, чтобы убедить других в своей правоте или преимуществах товара, которые они продают. Требуются определенные навыки, чтобы правильно пользоваться статистикой. Одна из самых распространенных ошибок – это неправильный выбор выборки.

В 1936 году перед президентскими выборами в США был проведен телефонный опрос, который показал, что с большим преимуществом победу должен одержать Альфред Лендон. Однако на выборах Франклин Рузвельт набрал почти вдвое больше голосов. Ошибка была связана с тем, что в те годы телефон могли позволить себе только богатые люди, которые в большинстве своем поддерживали Лендона. Однако бедные люди (а их, конечно же, больше, чем богатых) голосовали за Рузвельта.

Ещё один пример – это агитация в конце XIX века в США к службе на флоте. Пропагандисты в своей рекламе указывали, что, согласно статистике, смертность на флоте во время войны (испано-американской) составляет 0,09%, в то время как среди населения Нью-Йорка она равнялась 0,16%. Получалось, что служить на флоте в военное время безопаснее, чем жить мирной жизнью. Однако на самом деле причина таких цифр заключается в том, что во флот всегда отбирали молодых мужчин с хорошим здоровьем, которые не могли умереть от «старческих» болезней, в то время как в население Нью-Йорка входят больные и старые люди.

При указании среднего значения исследователь может использовать разные характеристики – среднее арифметическое, медиана, мода. При этом почти всегда среднее арифметическое несколько больше медианы. Именно поэтому большинство людей, узнающих о средней зарплате в стране, удивляются, так как они столько не зарабатывают. Правильнее ориентироваться на медианную зарплату.

Ну и наконец, нельзя забывать, что любая статистика может показать только корреляцию между двумя величинами, но это не всегда означает причинно-следственную связь. Так, известно, что чем больше в городе продается мороженого, тем больше в это же время людей тонет на пляжах. Означает ли это, что поедание мороженого увеличивает риск во время плавания? Нет. Дело в том, что оба этих показателя, продажи мороженого и количество утонувших, зависят от третьей величины – температуры в городе. Чем жарче на улице, тем большее количество людей ходят на пляж и тем больше мороженого продается в магазинах.

Изучаем статистику: средние значения

Один из разделов описательной статистики посвящен знакомству
с характеристиками числового набора: минимальное значение, максимальное
значение, размах, среднее арифметическое и медиана. Ученики должны научиться
определять их для набора чисел, заданного списком, таблицей или диаграммой
рассеивания.

Мы изучали этот материал в течение трех уроков. На первых
двух были введены новые понятия и решались задачи из учебного пособия (авт.
Ю.Н. Тюрин, А.А. Макаров, И.Р. Высоцкий, И.В. Ященко). Например. Найдите
наибольшее и наименьшее значение, размах, среднее значение и медиану набора
чисел: 12; 7; 25; 3; 19; 15. (Ответ: 25; 3; 22; 13,5; 13,5).

Однако естественно показать учащимся, зачем мы все это
изучаем. На третьем уроке мы решали задачи, в которых требуется выбрать
такое среднее, которое наилучшим образом отражает особенности данного набора
чисел в соответствии с их природой и требованиями задачи. В одних задачах не
сказано, какую характеристику надо искать, поэтому, чтобы ответить на вопрос
задачи, приходится примерять к поставленной задаче поочередно разные средние и
выяснять, какое подходит больше других. В этом случае ответом к задаче является
не число, а название подходящей характеристики. В других задачах присутствует
необходимость правильно интерпретировать полученные результаты, отнестись к ним
критически, попытаться найти здравое зерно даже там, где, на первый взгляд, «все
сделано неверно». И наконец, предложен и третий вид задач, в которых природа
данных накладывает определенные дополнительные требования на найденное значение
среднего: например, оно должно быть целым.

Тем самым мы не только продолжаем закреплять навык подсчета
среднего, но и демонстрируем возможности применения изученного в реальных
жизненных ситуациях. Ведь для учащихся важным фактором освоения нового является
осознание необходимости знания этого нового, то есть не только как
найти, но и зачем находить.

Данная статья состоит из двух частей. В первой дается описание наиболее
употребительных средних. Во второй части предлагается набор задач для решения в
классе и для самостоятельной работы учащихся.

Знакомимся со средними

Наибольшее и наименьшее значения

Слова «минимальный», «максимальный», «меньший», «больший»
интуитивно понятны учащимся, поэтому первые две характеристики: наибольшее
и наименьшее значения оставим без определения. Скажем, что в наборе,
упорядоченном по возрастанию, наименьшее число стоит на первом месте, а
наибольшее — на последнем.

В пособии имеются задания, в которых требуется найти
наибольшее или наименьшее значения среди чисел, указанных в таблице. К ним
добавим задания с другой формой представления данных — в виде диаграммы
рассеивания.

Задание. Имеется диаграмма 1 рассеивания, показывающая
взаимосвязь роста и веса 15 опрошенных юношей. Найти рост самого высокого и рост
самого низкого юноши (т.е. определить минимальное и максимальное значения набора
чисел, заданного диаграммой рассеивания).

Для этого будем использовать следующее: минимальный рост
соответствует абсциссе точки, расположенной левее других, а
максимальный — абсциссе крайней точки справа. Получим:

min ≈ 167 см, max ≈ 181 см.

Интересно, что остальные 13 точек участия в «обсуждении»
вообще не принимают. Их можно стереть — результат от этого не изменится (см.
диаграмму 2).

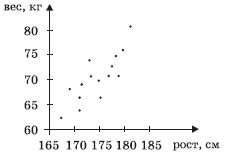
Диаграмма 1

Вторая особенность получаемого результата в том, что, в
отличие от работы с таблицей, данные, получаемые с помощью графиков и диаграмм,
являются не точными, а приближенными, то есть ответы могут отличаться.

Аналогично находим минимальное и максимальное значения веса,
как ординаты самой нижней и самой верхней точек.

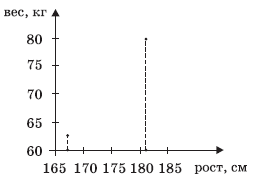
Диаграмма 2

С каким же видом представления данных удобнее работать?

Преимущество таблицы заключается в точности получаемых
результатов, но работа с ней требует концентрации внимания на протяжении
длительного времени: нельзя пропустить искомое число, а оно может попасть в
любой исследуемый столбец. И если таблица содержит не 15 чисел, а 5000, то этот
аргумент становится решающим в пользу наглядного представления данных. Оно дает
менее точные результаты, зато обработка такой информации происходит за
считанные секунды. Даже если диаграмма будет содержать 5000 точек, нас будут
интересовать только две крайние, на остальные мы даже не посмотрим.

Размах

В отличие от предыдущих понятий, размах — это
незнакомая учащимся характеристика набора. Он показывает протяженность набора
вдоль числовой оси, меру его разброса.

Определение. Размах набора чисел (R) — это
разность между наибольшим и наименьшим числом набора.

Например, в предыдущем задании размах равен: R = 181 –
167 = 14 см.

Что показывает размах значений?

Сравним диаграммы 3 и 4:

Диаграмма 3                 Диаграмма 4

Точки, изображенные на диаграмме 3, расположены ближе друг к
другу, соответственно, и максимальное и минимальное значение отличаются друг от
друга меньше, чем на диаграмме 4. Таким образом, размах показывает, сильно ли
отличаются числа набора друг от друга.

Маленький размах показывает, что исследуемая величина
принимала практически одинаковые значения. Большой размах показывает, что
некоторая величина принимает значительно отличающиеся друг от друга значения, то
есть нестабильность. Иногда большой размах свидетельствует о наличии
грубой ошибки измерений, о том, что какое-то из чисел попало в список случайно.

Если вычислить полусумму наименьшего и наибольшего значений
набора и обозначить ее с, а половину размаха обозначить то можно
утверждать, что все числа набора содержатся в промежутке На бытовом уровне
размах (а точнее, полуразмах) дает информацию о точности информации: расстояние
от дома до дачи (100 ± 5) км, цена на хлеб (14 ± 2) р. и т.д.

Среднее арифметическое

Определение. Средним арифметическим нескольких чисел () называется частное от деления суммы этих чисел на количество чисел.

Например, средним арифметическим чисел 4; 6; 11 является
число

Зачастую среднее арифметическое называют просто «средним» в
силу его наибольшей популярности. Говорят о среднем балле аттестата,
среднегодовом потреблении населением фруктов. «Потребительская корзина» для
определенного слоя граждан рассчитывается исходя из средних показателей.

Рассмотрим следующий пример. На олимпиаде по математике
предлагалось решить пять задач по 4 балла за каждую. В протоколе указана сумма
баллов каждого из восьми участников этой олимпиады:

12; 14; 14; 16; 17; 18; 19; 200.

Для ускорения подсчета имеется автоматизированная система
обработки данных, которая находит среднее арифметическое любых введенных чисел.
Какой средний балл набрали участники олимпиады?

У данного набора среднее равно 38,75. Однако такую сумму
баллов никто из участников набрать не мог. К тому же семь чисел из данных восьми
намного меньше его. Все значения этого набора, кроме крайнего правого,
достаточно кучно попадают в интервал [12; 19], а 38,75 в него не попадает. Все
это говорит о том, что полученное среднее арифметическое не только не передает
особенностей данного набора чисел, но и вообще противоречит здравому смыслу.
Значит, либо в условие, либо в решение вкралась ошибка! Посмотрим еще раз на
данные числа. Теперь, получив явно бессмысленный результат, мы сможем более
критически отнестись к условию: первые семь чисел вполне реальны, а вот
последнее… Откуда оно взялось?! Видимо, оно случайно попало в этот список:
возможно, в результате описки. Однако обнаружение ошибки в условии не избавляет
нас от необходимости довести решение до конца. Можно, конечно, посоветовать
комиссии снова переписать результаты учащихся и ввести числа из нового,
«правильного» протокола. Но где гарантия, что в нем снова не будет опечатки?

Когда все результаты более или менее кучно располагаются на
числовой оси, кроме, быть может, нескольких ненадежных значений, анализировать
результаты можно! Достаточно высокую точность полученных значений будет
гарантировать применение других средних — в частности, урезанного среднего.
Для его нахождения сначала упорядочивают набор по возрастанию, а затем
отбрасывают слева и справа равное небольшое количество чисел. При этом «выбросы»
(или ошибки наблюдений) в дальнейших вычислениях не участвуют. У полученного
«урезанного» набора обычным образом находят среднее арифметическое. Оно и
является урезанным средним исходного набора.

Вернемся к задаче. Если отбросить по одному числу с каждой
стороны, то есть числа 12 и 200, то у оставшегося набора из шести чисел среднее
равно

Это и есть урезанное среднее. Оно неплохо передает реальное
среднее количество баллов, набранных юными математиками.

Некоторая аналогия с нахождением урезанного среднего
просматривается в правилах судейства во многих видах спорта. Например, в
соревнованиях по прыжкам с трамплина технику каждого прыжка оценивают 5 судей.
Чтобы получить объективные оценки, две из них — высшую и низшую — отбрасывают, а
для трех оставшихся находят сумму. Такой подход не дает возможности судьям
повышать баллы своим соотечественникам, а спортсменам затрудняет нечестный путь
к медалям.

Медиана

Медианой числового набора является число, которое
разделяет этот набор на две одинаковые по части.

Если набор упорядочен и в нем имеется нечетное количество
чисел (2n + 1), то медиана стоит посередине этого набора, на (n +
1)-м месте. Если упорядоченный набор состоит из четного количества чисел (2n),
то медианой является любое число, находящееся между двумя числами, которые стоят
в середине (под номерами n и n + 1). Обычно берется их полусумма.

В наборе 12; 14; 14; 16; 17; 18; 19; 200 медианой является
любое число из интервала (16; 17), например, 16,5. Напомним, что урезанное
среднее равнялось 16,3. Похоже!

Перейдем к решению задач.

Вычисляем средние

1. Про отличника. У отличника Коли были отметки по математике
«5», «5», «5», «5».
И вдруг в конце четверти он получил «2». Он знает, что
учитель математики выставляет четвертную отметку как среднее всех отметок,
имеющихся у ученика, и не признает пересдач. Какое среднее было бы
предпочтительнее для Коли, если он, естественно, надеется на пятерку в четверти?

Решение. 1. Попробуем начать с такого очень
распространенного способа выставления четвертных отметок, как нахождение
среднего арифметического:

Естественно, что любой учитель округлит этот результат в
меньшую сторону и выставит итоговую отметку «4». Значит, это среднее Колю не
устраивает.

Мы видим, что один неудачный ответ на балл снизил четвертную
отметку. Ведь до этого среднее арифметическое равнялось 5.

2. Помочь Колиной мечте сбыться может другое среднее, и не
одно! Например, если в качестве среднего учитель Коли возьмет медиану или
урезанное среднее, то в четверти Коле обеспечена пятерка:

— медиана набора 2, 5, 5, 5, 5 равна 5;

— урезанное среднее набора 5, 5, 5, равно

Ответ: медиана или урезанное среднее.

2. Про лодку. Рыбаки собираются порыбачить на озере. Но не
везде им обеспечен хороший улов. Чтобы найти рыбное место, они решили
воспользоваться лодкой с мотором. На лодке установлен мотор, который можно
регулировать по высоте, поднимая или глубже погружая его. Известно, что мотор
работает надежно и не перегревается во время работы, если опустить его как можно
ниже в глубь воды. Но тогда возникает опасность зацепить им за дно водоема.
Мотор устанавливается на желаемую высоту на берегу, в воде менять глубину
погружения нельзя. Какой информацией о глубине воды в озере надо располагать
рыбакам, чтобы не повредить мотор о дно?

Решение. Рыбаки должны узнать глубину озера вдоль
предполагаемого маршрута следования. Затем у полученного набора чисел надо найти
минимальное значение. Оно обеспечит им удачное прохождение и других,
более глубоких участков.

Ответ: минимальное значение.

3. Библиотека. Известно, что детская библиотека выдает в день
в среднем 180 книг. Сколько книг выдает библиотека в среднем за неделю? за
месяц? за год?

Решение. Под средним в данной задаче подразумевается
среднее арифметическое. Так как библиотека работает 6 дней в неделю, значит,
за неделю она выдает около 1806
= 1080 книг. За 26 рабочих дней месяца она выдаст 18026
= 4700 книг. За 12 месяцев выдача составит 468012
= 56 000 книг.

Ответ: 1080 книг, около 4700 книг, около 56 000 книг.

Решая эту задачу, уместно обсудить вопрос точности полученных
результатов. Во-первых, из условия неясно, за какой период было получено
среднедневное значение. Если наблюдения велись лишь одну неделю, то к полученным
вычисленным значениям нужно относиться весьма скептически. Для получения более
точных результатов надо было проводить более длительное наблюдение, сопоставимое
по длительности с запрашиваемым периодом. А во-вторых, возможно, наблюдатели
«попали» на неделю «книжного бума», тогда результаты, распространенные на месяц
и тем более на год получатся явно завышенными. Возможна и обратная картина: нам
сообщили результаты, полученные в период летних каникул, значит, результаты
вычислений будут заниженными. Другими словами, к полученным числам нужно
относиться с большой осторожностью, если нет возможности уточнить, как было
проведено исследование, и за какой период было вычислено среднее значение 180
книг.

Этот пример показывает, что для получения достоверных
результатов исследований нужно соблюдать некоторые условия, следовать
определенным правилам, чтобы полученным выводам можно было доверять.

4. Метание молота. Спортивный клуб должен организовать
соревнования по метанию молота среди спортсменов с разной спортивной подготовкой
и разными достижениями. Для этого он должен пригласить необходимое количество
судей в сектор для метания. Судьи, с которыми сотрудничает клуб, точно отмечают
место падения молота, если находятся не далее четырех метров от него. Спортивный
клуб может запросить любую информацию о прошлых результатах приглашенных
спортсменов. Какой информацией должны располагать организаторы, чтобы пригласить
необходимое количество судей?

Решение. Надо запросить предыдущие результаты метания
молота всех участников и найти максимальный, минимальный результаты и размах.
Зная величину угла сектора для метания и максимальный результат, можно
вычислить длину дуги, вдоль которой через каждые 8 м надо расставить судей.

Количество таких рядов зависит от размаха результатов.
Если он окажется менее 8 м, то судьи могут стоять в один ряд. Если размах
окажется бóльшим, то чтобы успешно фиксировать как более далекие, так и близкие
результаты судей надо расставить в несколько рядов через каждые 8 м.

Ответ: максимальный результат, размах.

5. Отпуск на юге. Для успешной рекламы отдыха на Кипре
туристическая фирма запросила данные о погоде на острове за последние 10 лет.
Выяснилось, что за этот период было лишь 216 пасмурных или дождливых дней,
которые были равномерно распределены по запрашиваемым годам. Сколько дней в году
на острове Кипр светит солнце?

Решение. За 10 лет наблюдалось 3652 – 216 = 3436
солнечных дней. Значит, в среднем за один год — 343,6 дня. Поскольку в ответе
надо писать целое число дней, то можно округлить до целых, а можно и до
десятков: в рекламе круглые числа смотрятся лучше.

Ответ: около 340 дней.

Задачи для самостоятельного решения

1. а) Через речку хотят построить мост. Известно, что уровень
воды в реке меняется в течение года: весной при таянии снега повышается,
засушливым летом понижается. Какую характеристику уровня воды в реке надо
учитывать, чтобы построенный мост был над водой?

б) Периодически в средствах массовой информации нам сообщают
о стихийных бедствиях, в результате которых переполненные водой реки выходят из
своих берегов и даже затопляют улицы городов. Понимая возможность подобного
стихийного бедствия, не будет ли разумнее построить мост (а заодно и высокую
дамбу) как можно выше, насколько это будет технически возможно? Ведь гибель
людей несравнима ни с какими материальными затратами, позволяющими предупредить
беду.

2. За урок учительница вызывает в среднем 5 человек из класса
и каждому ставит отметку за устный ответ. Сколько отметок за устные ответы
выставит эта учительница за неделю, если она проводит в этом классе 5 уроков в
неделю? За четверть?

3. В забеге на 800 м принимали участие 19 спортсменов,
разделенных на группы, стартующие в разное время. Как судьи определили
победителя забега?

4. На зимние каникулы в одной из школ города Мурманска
учительница дала детям задание: следить за погодой и найти среднюю температуру.
Ежедневно в течение десяти дней в 15 часов Наташа записывала показания
термометра:

–13, –10, –15, 11, –9, –9, –11, –12, –10, –11.

А затем вычислила среднее арифметическое и получила –8,9.

а) Действительно ли в период наблюдений температура
колебалась вблизи этого числа?
б) Почему большинство значений (9 из 10) меньше найденного
среднего?
в) Как исправить ответ, если он неверный (заново повторить
наблюдение, естественно, нельзя)?

5.  Имеются данные об успеваемости по химии 8 «А» и 8 «Б» : о
количестве учащихся, получивших ту или иную четвертную отметку. Данные занесены
в таблице:

Отметка	8 «А»	8 «Б»
5	6 чел.	4 чел.
4	12 чел.	10 чел.
3	6 чел.	5 чел.

Какой класс в среднем имеет лучшие результаты?

6. Лучший нападающий баскетбольной команды «Луч» за восемь
прошедших матчей принес своей команде 61 очко. Сколько в среднем очков добавлял
своей команде этот игрок за каждую игру?

Подводя итог сказанному, хочется отметить, что решение задач,
приведенных в этой статье, было встречено учениками с большим интересом. В их
глазах просматривалось и удивление: оказывается школьные знания имеют прямое
отношение к реальной жизни. Длинные формулировки задач не только не мешали
воспринимать задачу, а напротив, учащиеся успевали глубже погрузиться в
ситуацию, пропустить ее через себя. Сюжеты не были надуманными, они
согласовывались с имеющимся у детей жизненным опытом, поэтому даже слабо
подготовленные ученики на этих уроках проявляли необычную для них активность.
Решение некоторых задач проходило в форме жаркой, но доброжелательной дискуссии,
и доказать свою правоту могла только та сторона, которая аргументированно
отстаивала свою позицию, опираясь на строгие математические факты и здравый
смысл!

Решения и ответы

1. а) Максимальное значение уровня воды в реке.
б) Все зависит от массы обстоятельств: географического
положения реки, «поведения» реки в прошлом и др. Конечно, раз в 100–150 лет даже
на самой «мирной» реке может быть катастрофический паводок. Однако стоит ли
строить очень высокий мост через каждую речку, ожидая ужасного, но
маловероятного катаклизма?

2. Около 25 отметок; около 200 отметок.

3. Победитель затратил на преодоление дистанции минимальное
время.

4. а) Нет, в период наблюдений температура колебалась в
промежутке [–15; –9], которому найденное среднее не принадлежит;
б) потому что имеется число 11, которое существенно
отличается от всех остальных и поэтому меняет среднее в большую сторону;
в) найти урезанное среднее данного набора:

–9, –9, –10, –10, –11, –11, –12, –13, –15,
11. Оно приближенно равно 11,4.

5. 8 «А».

6. Около 8 очков.

Багишова О.

Как легко найти выбросы в Excel

Выброс — это наблюдение, которое лежит аномально далеко от других значений в наборе данных. Выбросы могут быть проблематичными, поскольку они могут повлиять на результаты анализа.

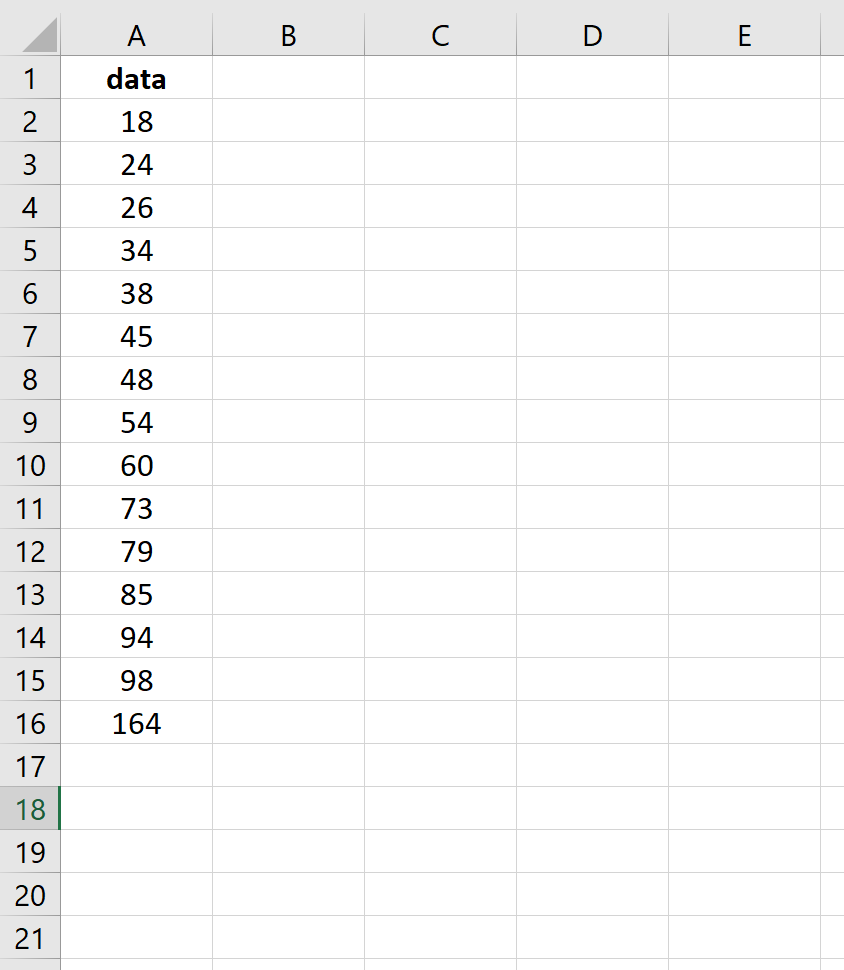
Мы будем использовать следующий набор данных в Excel, чтобы проиллюстрировать два метода поиска выбросов:

Метод 1: используйте межквартильный диапазон

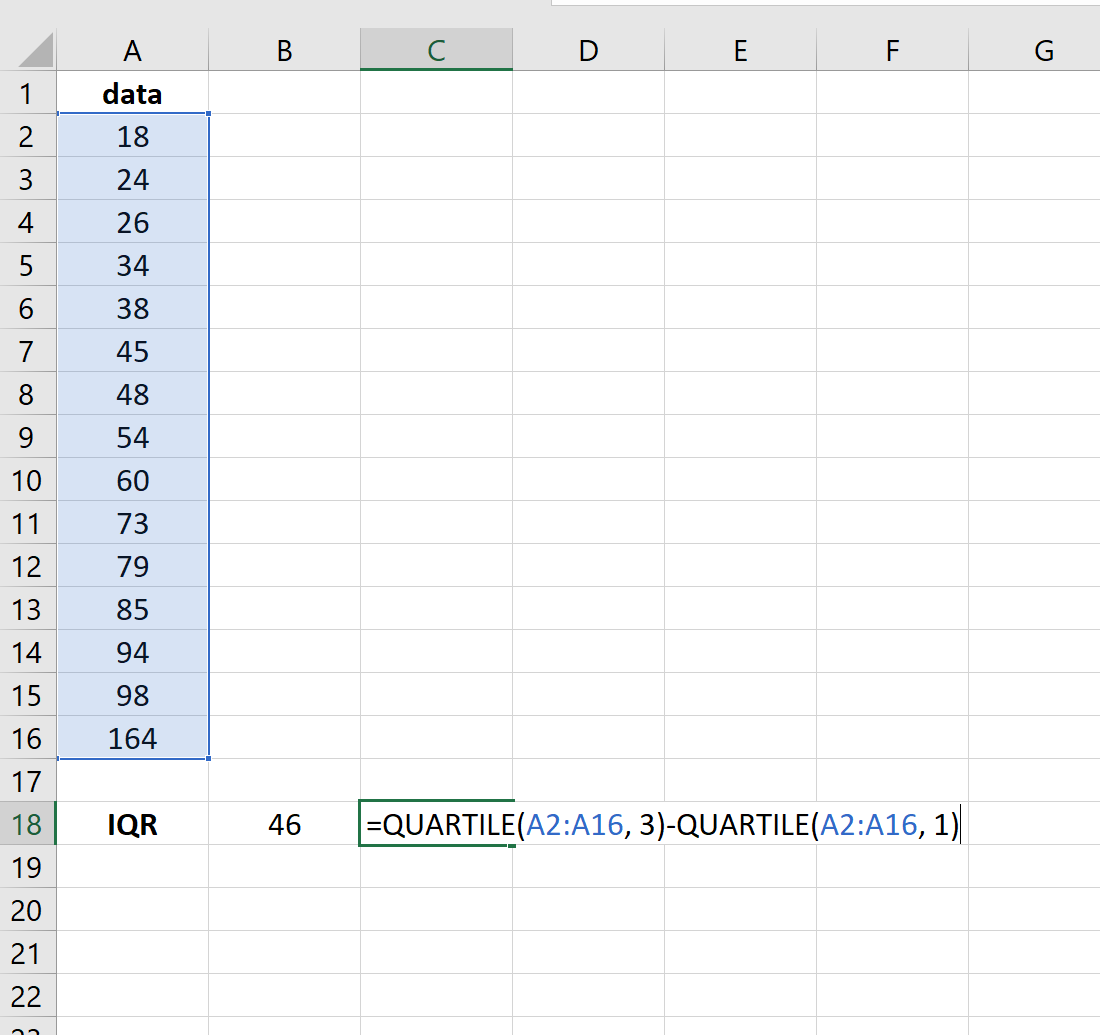
Межквартильный размах (IQR) — это разница между 75-м процентилем (Q3) и 25-м процентилем (Q1) в наборе данных. Он измеряет разброс средних 50% значений.

Мы можем определить наблюдение как выброс, если оно в 1,5 раза превышает межквартильный размах, превышающий третий квартиль (Q3), или в 1,5 раза превышает межквартильный размах меньше, чем первый квартиль (Q1).

На следующем изображении показано, как рассчитать межквартильный диапазон в Excel:

Затем мы можем использовать формулу, упомянутую выше, чтобы присвоить «1» любому значению, которое является выбросом в наборе данных:

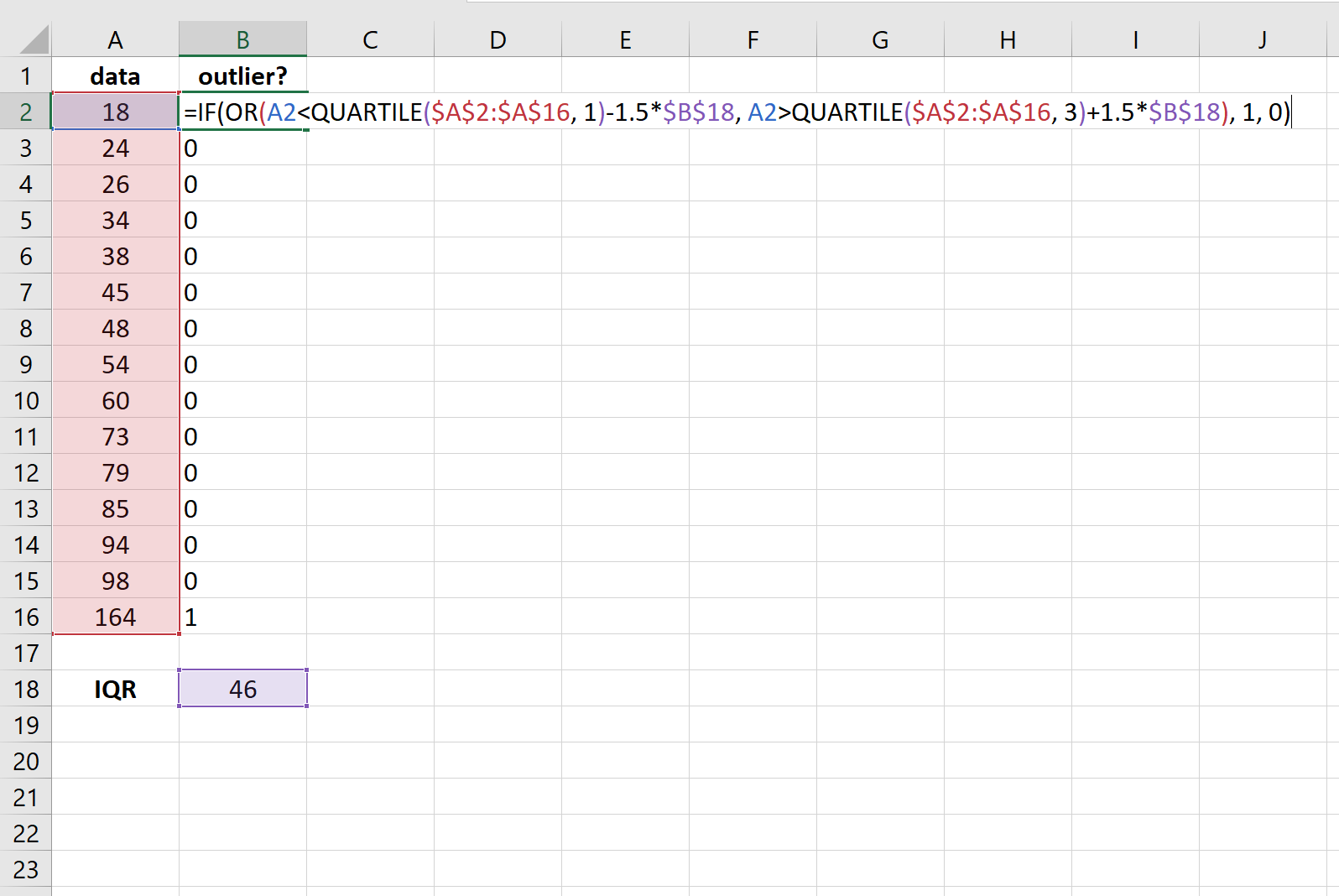
Мы видим, что только одно значение — 164 — оказывается выбросом в этом наборе данных.

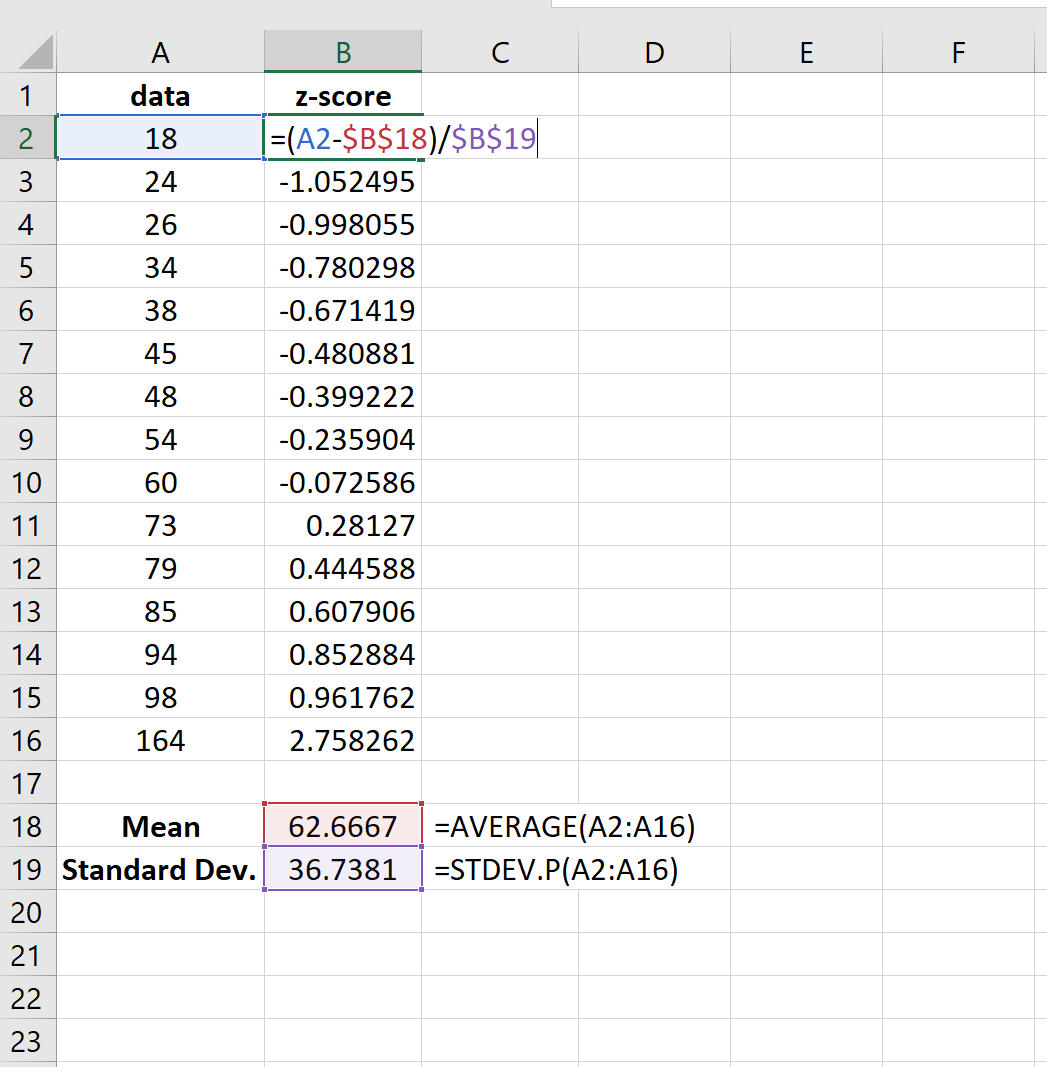
Способ 2: использовать z-показатели

Z-оценка показывает, сколько стандартных отклонений данного значения от среднего. Мы используем следующую формулу для расчета z-показателя:

z = (X — μ) / σ

• X — это одно необработанное значение данных.
• μ — среднее значение населения
• σ — стандартное отклонение населения

Мы можем определить наблюдение как выброс, если его z-оценка меньше -3 или больше 3.

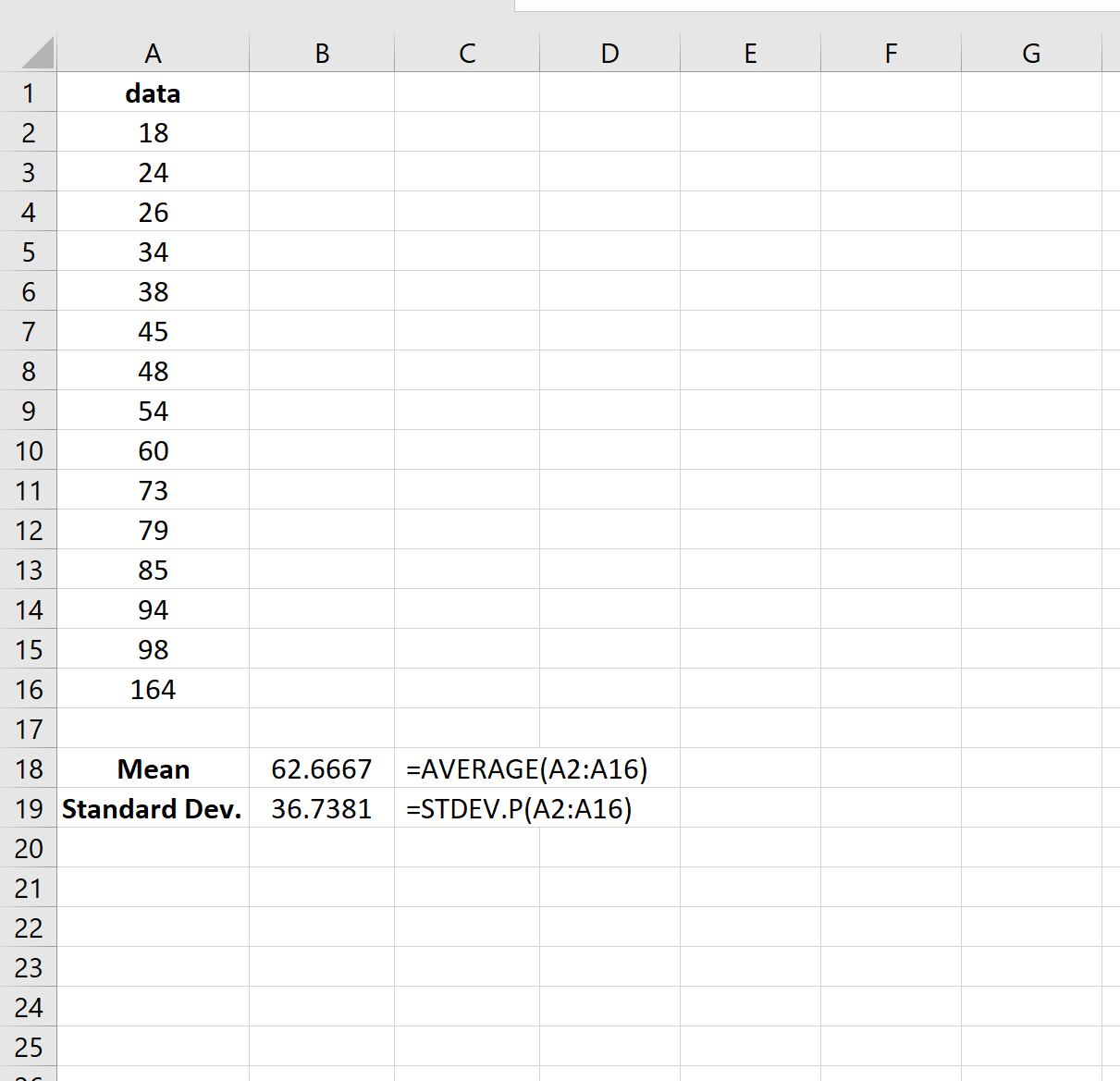
На следующем изображении показано, как рассчитать среднее значение и стандартное отклонение для набора данных в Excel:

Затем мы можем использовать среднее значение и стандартное отклонение, чтобы найти z-оценку для каждого отдельного значения в наборе данных:

Затем мы можем присвоить «1» любому значению, которое имеет z-оценку меньше -3 или больше 3:

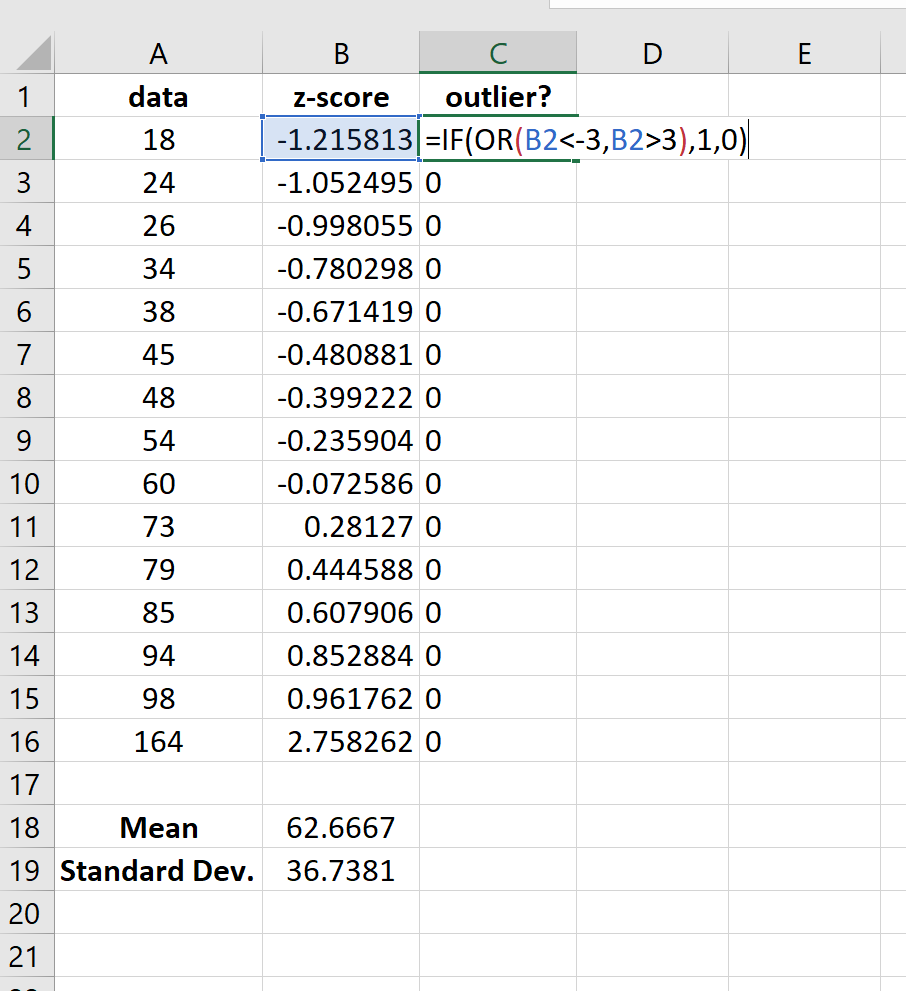
Используя этот метод, мы видим, что в наборе данных нет выбросов.

Примечание. Иногда вместо 3 используется z-показатель 2,5. В этом случае отдельное значение 164 будет считаться выбросом, поскольку его z-показатель больше 2,5. При использовании метода z-показателя руководствуйтесь своим здравым смыслом, какое значение z-показателя вы считаете выбросом.

Как обращаться с выбросами

Если в ваших данных присутствует выброс, у вас есть несколько вариантов:

1. Убедитесь, что выброс не является результатом ошибки ввода данных.

Иногда человек просто вводит неправильное значение данных при записи данных. Если присутствует выброс, сначала убедитесь, что значение было введено правильно и что это не ошибка.

2. Удалите выброс.

Если значение является истинным выбросом, вы можете удалить его, если оно окажет значительное влияние на общий анализ. Просто не забудьте упомянуть в своем окончательном отчете или анализе, что вы удалили выброс.

3. Присвойте новое значение выбросу .

Если выброс является результатом ошибки ввода данных, вы можете решить присвоить ему новое значение, такое как среднее или медиана набора данных.

Источник

Как найти объем выборки в excel

Использование Excel для расчета статистических характеристик случайной величины

Разделы: Математика

• Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
• применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.

1. Сегодня на уроке мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
2. Для начала вспомним:

– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)

– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)

– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).

– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).

– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).

1. Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.

Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):

1. Занести данные в EXCEL, каждое число в отдельную ячейку.

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем — статистические, в списке: МОДА

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_о = 29 (чел) – Фирм у которых в штате 29 человек больше всего.

Используя тот же путь вычисляем медиану.

Вставка – Функция – Статистические – Медиана.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_е = 29 (чел) – среднее значение сотрудников в фирме.

Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.

Вставка – Функция – Статистические – МАКС.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наибольшее значение = 36.

Вставка – Функция – Статистические – МИН.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наименьшее значение = 22.

36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.

Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения x_iслучайной величины меняются от 22 до 36 включительно шагом 1.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni

Чтобы сосчитать частоту каждого значения воспользуемся

Вставка – Функция – Статистические – СЧЕТЕСЛИ.

В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22

Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni	1	3	4	5	11	9	13	18	16	6	4	6	3	0	1

Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические — СУММА). Должно получиться 100 (количество всех фирм).

Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)

Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.

Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).

Диаграмма – Стандартные – Круговая.

Диаграмма – Стандартные – Гистограмма.

4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.

Как рассчитать размер выборки в Excel — Вокруг-Дом — 2021

Table of Contents:

Microsoft Excel имеет десять основных статистических формул, таких как размер выборки, среднее значение, медиана, стандартное отклонение, максимум и минимум. Размер выборки — это число наблюдений в наборе данных, например, если опрашивающая компания опрашивает 500 человек, то размер выборки данных составляет 500. После ввода набора данных в Excel формула = COUNT вычислит размер выборки. , Размер выборки полезен для вычислений, таких как стандартные ошибки и уровни достоверности. Использование Microsoft Excel позволит пользователю быстро рассчитать статистические формулы, поскольку статистические формулы, как правило, длиннее и сложнее, чем другие математические формулы.

Excel облегчает сложные статистические вычисления.

Шаг 1

Введите данные наблюдений в Excel, по одному наблюдению в каждой ячейке. Например, введите данные в ячейки с A1 по A24. Это обеспечит вертикальный столбец данных в столбце А.

Шаг 2

Введите «= COUNT (» в ячейку B1.

Шаг 3

Выделите диапазон ячеек данных или введите диапазон ячеек данных после «(», введенного на шаге 2 в ячейку B1, затем завершите формулу знаком «)». Диапазон ячеек — это любые ячейки, в которых есть данные. В этом примере диапазон ячеек от A1 до A24. Формула в примере — это «= COUNT (A1: A24)»

Шаг 4

Нажмите «Enter», и размер ячейки появится в ячейке с формулой. В нашем примере ячейка B1 будет отображать 24, поскольку размер выборки будет 24.

Источник