Загрузить PDF
Загрузить PDF
В статистике размах – разница между наибольшим и наименьшим результатами наблюдений. Размах показывает разброс значений в совокупности данных. Если размах большой, то значения в совокупности сильно разбросаны; если размах – небольшая величина, то значения в совокупности лежат близко друг к другу. Если вы хотите узнать, как вычислить размах, выполните следующие действия.
Шаги
-

1
Запишите значения совокупности данных. Чтобы найти размах, нужно перечислить все значения для определения максимального и минимального чисел. Например: 14 , 19, 20 , 24, 25, 28.
- Будет легче определить наибольшее и наименьшее значение в совокупности, если вы запишете значения в порядке возрастания. В нашем примере: 14, 19, 20, 24, 24, 25, 28 .
- Запись значений по возрастанию также может помочь вам сделать другие расчеты, как например моду, среднее или медиану совокупности.
-

2
Определите максимальное и минимальное числа. В нашем примере, это 14 и 28.
-

3
Вычтете наименьшее число из наибольшего. Теперь, когда вы определили самое маленькое и самое большое число в совокупности, вам нужно вычесть их друг из друга: 25 – 14 = 11 – это и есть размах.
-

4
Выделите размах. Как только вы нашли размах, четко выделите его. Это поможет вам избежать путаницы с любыми другими статистическими величинами, такими как среднее, медиана или мода.
Реклама
Советы
- Медиана статистической совокупности данных – такое значение, которое делит эту совокупность на две равные части. Таким образом, медиана не вычисляется путем деления размаха на 2. Чтобы найти медиану, необходимо перечислить значения данных по возрастанию и найти значение в середине списка. Это значение и является медианой. Например, если у Вас есть список из 29 значений (по возрастанию), пятнадцатое значение будет равноудалено от верхней и нижней части этого списка, так что пятнадцатое значение является медианой, независимо от того, как это значение соотносится с размахом.
- Вы также можете интерпретировать “размах” в алгебраических выражениях, но сначала Вы должны понять концепцию алгебраической функции. Так как функция может быть задана на любом числе, даже неизвестном, то это число представляется в виде переменной (обычно «х»). Область определения – множество всех возможных значений х. Область значения функции (размах) – множество всех возможных значений функции (у) при определенных значениях х. К сожалению, нет единого способа вычислить область значения функции. Иногда, построив график функции или вычислив несколько значений, можно получить четкую закономерность.
Реклама
Об этой статье
Эту страницу просматривали 51 992 раза.
Была ли эта статья полезной?
План урока:
Понятие выборки и генеральной совокупности
Среднее арифметическое выборки
Упорядоченный ряд и таблица частот
Размах выборки
Мода выборки
Медиана выборки
Ошибки в статистике
Понятие выборки и генеральной совокупности
Слово статистика, образованное от латинского status(состояние дел), появилось только в 1746 году, когда его употребил немец Готфрид Ахенвалль. Однако ещё в Древнем Китае проводились переписи населения, в ходе которых правители собирали информацию о своих владениях и жителях, проживающих в них.
В основе любого статистического исследования лежит массив информации, который называют выборкой данных. Покажем это на примере. Пусть в классе, где учится 20 учеников, проводился тест по математике, содержавший 25 вопросов. В результате учащиеся показали следующие результаты:

Ряд чисел, приведенный во второй строке таблицы (12, 19, 19, 14, 17, 16, 18, 20, 15, 25, 13, 20, 25, 16, 17, 12, 24, 13, 21, 13), будет выборкой. Также ее могут называть рядом данных или выборочной совокупностью.

В примере с классом выборка состоит из 20 чисел. Эту величину (количество чисел в ряду) называют объемом выборки. Каждое отдельное число в ряду именуют вариантой выборки.
В примере со школьным классом в выборку попали все его ученики. Это позволяет точно определить, насколько хорошо учащиеся написали математический тест. Однако иногда необходимо проанализировать очень большие группы населения, состоящие из десятков и даже сотен миллионов человек. Например, необходимо узнать, какая часть населения страны курит. Опросить каждого жителя государства невозможно, поэтому в ходе исследования опрашивают лишь его малую часть. В этом случае статистики выделяют понятие генеральная совокупность.

Так, если с помощью опроса 10 тысяч человек ученые делают выводы о распространении курения в России, то все российское население будет составлять генеральную совокупность исследования, а опрошенные 10 тысяч людей вместе образуют выборку.
Среднее арифметическое выборки
Сбор информации о выборке является лишь первой стадией статистического исследования. Далее ее необходимо обобщить, то есть получить некоторые цифры, характеризующие выборку. Самой часто используемой статистической характеристикой является среднее арифметическое.

Другими словами, для подсчета среднего арифметического необходимо просто сложить все числа в ряде данных, а потом поделить получившееся значение на количество чисел в ряде. Так, в примере с тестом по математике (таблица 1) средний балл учащихся составит: (12+19+19+14+17+16+18+20+15+25+13+20+25+16+17+12+24+13+21+13):20=
= 349:20 = 17,45.
Среднее арифметическое позволяет одним числом характеризовать какое-либо качество всех объектов группы. Чем больше средний балл учащихся в классе, тем выше их успеваемость. Чем меньше среднее количество голов, пропускаемых футбольной командой за один матч, тем лучше она играет в обороне. Если средняя зарплата программистов в городе составляет 90 тысяч рублей, а дворников – 25 тысяч рублей, то это значит, что программисты значительно более востребованы на рынке труда, а потому при выборе будущей профессии лучше предпочесть именно эту специальность.
Упорядоченный ряд и таблица частот
В ряде данных в таблице 1 числа приведены в произвольном порядке. Перепишем ряд так, чтобы все числа шли в неубывающем порядке, то есть от самого маленького к самому большому:
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Такую запись называют упорядоченным рядом данных.

Его характеристики ничем не отличаются от изначальной выборки, однако с ним удобнее работать. С его помощью можно видеть, что ни одному ученику не удалось набрать 22 или 23 балла на тесте, но сразу двое учащихся дали 25 правильных ответов. На основе упорядоченного ряда данных несложно составить таблицу частот, в которой будет указано, как часто та или иная варианта выборки встречается в ряде. Выглядеть она будет так:

При составлении этой таблицы мы исключили из нее те варианты количества набранных баллов, частота которых равна нулю (от 0 до 12, 22 и 23).Заметим, что сумма чисел в нижней строке таблицы частот должна равняться объему выборки. Действительно,
2+3+1+1+2+2+1+2+2+1+1+2 = 20.
С помощью таблицы частот можно быстрее посчитать среднее арифметическое выборки. Для этого каждую варианту надо умножить на ее частоту, после чего сложить полученные результаты и поделить их на объем выборки:
(12•2+13•3+14•1+15•1+16•2+17•2+18•1+19•2+20•2+21•1+24•1+25•2):20 =
(24+39+14+15+32+34+18+38+40+42+24+50):20 = 349:20 = 17,45.
Размах выборки
Следующий важная характеристика ряда данных – это размах выборки.

Если выборка представлена в виде упорядоченного ряда данных, то достаточно вычесть из последнего числа ряда первое число. Так, размах выборки результатов теста в классе равен:
25 – 12 = 13,
так как самые лучшие ученики смогли решить все 25 заданий, а наихудший учащийся ответил правильно только на 13 вопросов.
Размах выборки характеризует стабильность, однородность исследуемых свойств. Например, пусть два спортсмена-стрелка в ходе соревнований производят по 5 выстрелов по круговой мишени, где за попадание начисляют от 0 до 10 очков. Первый стрелок показал результаты 8, 9, 9, 8, 9 очков. Второй же спортсмен в своих попытках показал результаты 7, 10, 10, 6, 10. Средние арифметические этих рядов равны:
(8+9+9+8+9):5 = 43:5 = 8,6;
(7+10+10+6+10):5 = 43:5 = 8,6.
Получается, что в среднем оба стрелка стреляют одинаково точно, однако первый спортсмен демонстрирует более стабильные результаты. У его выборки размах равен
9 – 8 = 1,
в то время как размах выборки второго спортсмена равен
10 – 6 = 4.
Размах выборки может быть очень важен в метеорологии. Например, в Алма-Ате и Амстердаме средняя температура в течение года почти одинакова и составляет 10°С. Однако в Алма-Ате в январе и феврале иногда фиксируются температуры ниже -30°С, в то время как в Амстердаме за всю историю наблюдений она никогда не падала ниже -20°С.
Мода выборки
Иногда важно знать не среднее арифметическое выборки, а то, какая из ее вариант встречается наиболее часто. Так, при управлении магазином одежды менеджеру не важен средний размер продаваемых футболок, а необходима информация о том, какие размеры наиболее популярны. Для этого используется такой показатель, как мода выборки.

В примере с математическим тестом сразу 3 ученика набрали по 13 баллов, а частота всех других вариант не превысила 2, поэтому мода выборки равна 13. Возможна ситуация, когда в ряде есть сразу две или более вариант, которые встречаются одинаково часто и чаще остальных вариант. Например, в ряде
1, 2, 3, 3, 3, 4, 5, 5, 5
варианты 3 и 5 встречаются по три раза. В таком случае ряд имеет сразу две моды – 3 и 5, а всю выборку именуют мультимодальной. Особо выделяется случай, когда в выборке все варианты встречаются с одинаковой частотой:
6, 6, 7, 7, 8, 8.
Здесь числа 6, 7 и 8 встречаются одинаково часто (по два раза), а другие варианты отсутствуют. В таких случаях говорят, что ряд не имеет моды.
Медиана выборки
Иногда, например, при расчете средней зарплаты, среднее арифметическое не вполне адекватно отражает ситуацию. Это происходит из-за наличия в выборке чисел, очень сильно отличающихся от среднего. Так, из-за огромных зарплат некоторых начальников большинство рядовых сотрудников компаний обнаруживают, что их зарплата ниже средней. В таких случаях целесообразно использовать такую характеристику, как медиану ряда. Это такое значение, которое делит ряд данных пополам. В упорядоченном ряде 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25 медианой будет равна 12, так как именно она находится в середине ряда:

Однако таким образом можно найти только медиану ряда, в котором находится нечетное количество чисел. Если же их количество четное, то за медиану условно принимают среднее арифметическое двух средних чисел. Так, для ряда 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25, 30, содержащего 12 чисел, медиана будет равна среднему значению 12 и 15, которые занимают 6-ое и 7-ое место в ряду:


Вернемся к примеру с математическим тестом в школе. Так как его сдавали 20 учеников, а 20 – четное число, то для расчета медианы следует найти среднее арифметическое 10-ого и 11-ого числа в упорядоченном ряде
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Эти места занимают числа 17 и 17 (выделены жирным шрифтом). Медиана ряда будет равна
(17+17):2 = 34:2 = 17.
Три приведенные основные статистические характеристики выборки, а именно среднее арифметическое, мода и медиана, называются мерами центральной тенденции. Они позволяют одним числом указать значение, относительно которого группируются все числа ряда.
Рассмотрим для наглядности ещё один пример. Врач в ходе диспансеризации измерил вес мальчиков в классе. В результате он получил 10 значений (в кг):
39, 41, 67, 36, 60, 58, 46, 44, 39, 69.
Найдем среднее арифметическое, размах, моду и медиану для этого ряда.
Решение. Сначала перепишем ряд в упорядоченном виде:
36, 39, 39, 41, 44, 46, 58, 60, 67, 69.
Так как в ряде 10 чисел, то объем выборки равен 10. Найдем среднее арифметическое. Для этого сложим все числа в ряде и поделим их на объем выборки (то есть на 10):
(36+39+39+41+44+46+58+60+67+69):10 =
= 499:10 = 49,9 кг.
Размах выборки равен разнице между наибольшей и наименьшей вариантой в ней. Самый тяжелый мальчик весит 69 кг, а самый легкий – 36 кг, а потому размах ряда равен
69 – 36 = 33 кг.
В упорядоченном ряде только одно число, 39, встречается дважды, а все остальные числа встречаются по одному разу. Поэтому мода ряда будет равна 39 кг.
В выборке 10 чисел, а это четное число. Поэтому для нахождения медианы надо найти два средних по счету значение найти их среднее. На 5-ом и 6-ом месте в ряде находятся числа 44 и 46. Их среднее арифметическое равно
(44+46):2 = 90:2 = 45 кг.
Поэтому и медиана ряда будет равна 45 кг.
Ошибки в статистике
Статистика является очень мощным инструментом для исследований во всех областях человеческой деятельности. Однако иногда ее иронично называют самой точной из лженаук. Известно и ещё одно высказывание, приписываемое политику Дизраэли, согласно которому существует просто ложь, наглая ложь и статистика. С чем же связана такая репутация этой дисциплины?
Дело в том, что некоторые люди и организации часто манипулируют данными статистики, чтобы убедить других в своей правоте или преимуществах товара, которые они продают. Требуются определенные навыки, чтобы правильно пользоваться статистикой. Одна из самых распространенных ошибок – это неправильный выбор выборки.
В 1936 году перед президентскими выборами в США был проведен телефонный опрос, который показал, что с большим преимуществом победу должен одержать Альфред Лендон. Однако на выборах Франклин Рузвельт набрал почти вдвое больше голосов. Ошибка была связана с тем, что в те годы телефон могли позволить себе только богатые люди, которые в большинстве своем поддерживали Лендона. Однако бедные люди (а их, конечно же, больше, чем богатых) голосовали за Рузвельта.
Ещё один пример – это агитация в конце XIX века в США к службе на флоте. Пропагандисты в своей рекламе указывали, что, согласно статистике, смертность на флоте во время войны (испано-американской) составляет 0,09%, в то время как среди населения Нью-Йорка она равнялась 0,16%. Получалось, что служить на флоте в военное время безопаснее, чем жить мирной жизнью. Однако на самом деле причина таких цифр заключается в том, что во флот всегда отбирали молодых мужчин с хорошим здоровьем, которые не могли умереть от «старческих» болезней, в то время как в население Нью-Йорка входят больные и старые люди.
При указании среднего значения исследователь может использовать разные характеристики – среднее арифметическое, медиана, мода. При этом почти всегда среднее арифметическое несколько больше медианы. Именно поэтому большинство людей, узнающих о средней зарплате в стране, удивляются, так как они столько не зарабатывают. Правильнее ориентироваться на медианную зарплату.
Ну и наконец, нельзя забывать, что любая статистика может показать только корреляцию между двумя величинами, но это не всегда означает причинно-следственную связь. Так, известно, что чем больше в городе продается мороженого, тем больше в это же время людей тонет на пляжах. Означает ли это, что поедание мороженого увеличивает риск во время плавания? Нет. Дело в том, что оба этих показателя, продажи мороженого и количество утонувших, зависят от третьей величины – температуры в городе. Чем жарче на улице, тем большее количество людей ходят на пляж и тем больше мороженого продается в магазинах.
Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней

Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
n = 6
Элементы выборки обозначаются с помощью переменных с индексами ![]() . Последний
. Последний ![]() элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.
элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.

Обозначим элементы нашей выборки через переменные ![]()
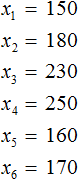
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
В нашем случае, самым большим элементом выборки является элемент 250, а самым маленьким — элемент 150. Разница между ними равна 100
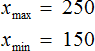
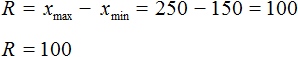
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Примеры:
- средняя зарплата жителей страны;
- средний балл учащихся;
- средняя скорость движения;
- средняя производительность труда.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
![]()
Вернемся к нашему примеру

Узнаем сколько в среднем мы тратили в каждом из шести дней:
![]()
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?

Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
![]()
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
66,2 × 3 = 198,6 км.
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
78,4 × 2 = 156,8 км.
Сложим эти расстояния и результат разделим на 5
![]()
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.

Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
![]()
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров

Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат

Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:

Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:

Выпишем рост спортсменов отдельно:
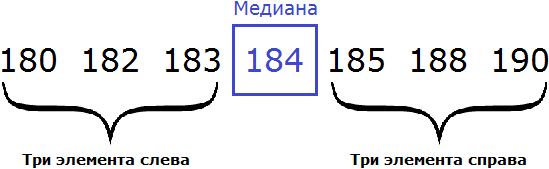
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:

Построим этих шестерых спортсменов по росту:

Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186

Найдем среднее арифметическое элементов 184 и 186
![]()
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
![]()
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
![]()
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.
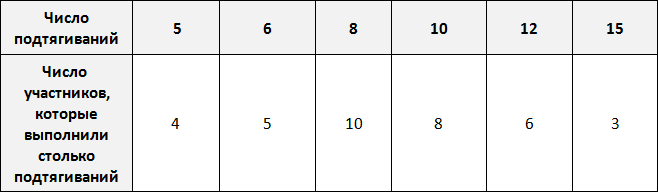
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:

Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:

Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:

Выполним деление в этих дробях:

Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:

Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Мода и медиана
Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.
Обратимся снова к нашему примеру со сборной по футболу:
Чему в данном примере равна мода? Какое число наиболее часто встречается в этой выборке?
Все верно, это число ( displaystyle 181), так как два игрока имеют рост ( displaystyle 181) см; рост же остальных игроков не повторяется.
Тут все должно быть ясно и понятно, да и слово знакомое, правда?
Перейдем к медиане, ты ее должен знать из курса геометрии. Но мне не сложно напомнить, что в геометрии медиана (в переводе с латинского- «средняя») — отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны.
Ключевое слово – СЕРЕДИНА. Если ты знал это определение, то тебе легко будет запомнить, что такое медиана в статистике.
Медианой ряда чисел с нечетным числом членов называется число, которое окажется посередине, если этот ряд упорядочить (проранжировать, т.е. расположить значения в порядке убывания или возрастания).
Медианой ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине, если этот ряд упорядочить.
Ну что, вернемся к нашей выборке футболистов?
Ты заметил в определении медианы важный момент, который нам еще здесь не встречался? Конечно, «если этот ряд упорядочить»!
Для того, чтобы в ряду чисел был порядок, можно расположить значения роста футболистов как в порядке убывания, так и в порядке возрастания. Мне удобней выстроить этот ряд в порядке возрастания (от самого маленького к самому большому).
Вот, что у меня получилось:
Так, ряд упорядочили, какой еще есть важный момент в определении медианы? Правильно, четное и нечетное количество членов в выборке.
Заметил, что для четного и нечетного количества даже определения отличаются? Да, ты прав, не заметить – сложно. А раз так, то нам надо определиться, четное у нас количество игроков в нашей выборке или нечетное?
Все верно – игроков ( displaystyle 11), значит, количество нечетное! Теперь можем применять к нашей выборке менее заковыристое определение медианы для нечетного количества членов в выборке.
Ищем число, которое оказалось посередине в нашем упорядоченном ряду:
Ну вот, чисел у нас ( displaystyle 11), значит, по краям остается по пять чисел, а рост ( displaystyle 183) см будет медианой в нашей выборке.
Не так уж и сложно, правда?
Частота и относительная частота
Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.
То есть частота определяет то, как часто повторяется та или иная величина в выборке.
Разберемся на нашем примере с футболистами. Перед нами вот такой вот упорядоченный ряд:
![]()
Частота – это число повторений какой-либо величины параметра. В нашем случае, это можно считать вот так. Сколько игроков имеет рост ( 176)?
Все верно, один игрок. Таким образом, частота встречи игрока с ростом ( 176) в нашей выборке равна ( 1).
Сколько игроков имеет рост ( 178)? Да, опять же один игрок. Частота встречи игрока с ростом ( 178) в нашей выборке равна ( 1).
Задавая такие вопросы и отвечая на них, можно составить вот такую табличку:
Ну вот, все довольно просто. Помни, что сумма частот должна равняться количеству элементов в выборке (объему выборки).
То есть в нашем примере: ( 1+1+1+2+1+1+1+1+1+1=11)
Перейдем к следующей характеристике – относительная частота.
Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах.
Обратимся опять к нашему примеру с футболистами. Частоты для каждого значения мы рассчитали, общее количество данных в ряду мы тоже знаем ( left( n=11 right)) .
Рассчитываем относительную частоту для каждого значения роста и получаем вот такую табличку:
А теперь сам составь таблицы частот и относительных частот для примера с 9-классниками, решающими задачи.
Раздел 11 Элементы теории вероятностей и математической статистики
Лекция № 208 Среднее арифметическое, медиана, размах, генеральная совокупность, выборка.
Основная литература:
-
Уч. пособие “Алгебра. Элементы статистики и теории вероятностей” авторов Ю.Н. Макарычева и Н.Г. Миндюк
-
Математика: учебник / М.И. Башмаков. — Москва: КноРус, 2017.
-
Башмаков М.И. Математика. Задачник: учебное пособие для студ. Учреждений сред проф. образования. – 5-е изд., стер.- М.: Издательский центр «Академия», 2017 год.
-
Математика: учебник для учреждений нач. и сред. проф. образования /М.И. Башмаков.- 7-е изд., стер.- М.: Издательский центр «Академия», 2012 год.
-
http://www.drofa.ru/ (Методические пособия, статьи для обучения математике)
-
http://podgotovka-ege.ru/education/ (Сайт для подготовки к ЕГЭ)
-
https://multiurok.ru/seropol-irina
ВНИМАНИЕ!!! Материалы, представленные в лекции взяты из книги Уч. пособие “Алгебра. Элементы статистики и теории вероятностей” авторов Ю.Н. Макарычева и Н.Г. Миндюк. Книгу можно открыть:
1. В материалах, представленных в папке преподавателя файл Учебник. Алгебра элементы статистики и теории вероятностей. Миндюк, Макарычев.pdf (Для открытия файла на вашем компьютере или телефоне, должна быть установлена программа Adobe Acrobat –распространяется бесплатно).
2. Книгу можно открыть по ссылкам вашем браузере
https://uch-lit.ru/matematika-2/dlya-shkolnikov/makaryichev-yu-n-algebra-elementyi-stati
https://www.description-pdf.ru/2020/01/31/%D0%B0%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0-%D1%8D%D0%BB%D0%B5%D0%BC%D0%B5%D0%BD%D1%82%D1%8B-%D1%81%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D0%BA%D0%B8-%D0%B8-%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D0%B8/
Мотивация.
Для изучения различных общественных и социально-экономических явлений, а также некоторых процессов, происходящих в природе, проводятся специальные статистические исследования. Всякое статистическое исследование начинается с целенаправленного сбора информации об изучаемом явлении или процессе. Этот этап называется этапом статистического наблюдения.
Для обобщения и систематизации данных, полученных в результате статистического наблюдения, их по какому-либо признаку разбивают на группы и результаты группировки сводят в таблицы.
Как уже было замечено, что результаты статистических исследований широко используются для практических и научных выводов, поэтому важно уметь собирать и группировать информацию по какому-либо признаку.
Задача 1: Администрация школы решила проверить математическую подготовку восьмиклассников. С этой целью был составлен тест, содержащий 9 заданий. Работу выполняли 40 учащихся школы. При проверке каждой работы учитель отмечал число верно выполненных заданий. В результате был составлен ряд чисел. После того, как его упорядочили получили:
0, 1, 2, 3,3, 4,4,4,4,4, 5,5,5,5,5,5, 6,6,6,6,6,6,6,6, 7,7,7,7,7,7,7, 8,8,8,8,8, 9,9,9,9.
Решение.
Представим полученные данные в виде таблицы. В верхней строке укажем число верно выполненных заданий, а в нижней количество появлений этого числа в ряду, т.е. частоту.
|
Число верно выполненных заданий |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Частота появления |
1 |
1 |
1 |
2 |
5 |
6 |
8 |
7 |
5 |
4 |
Такую таблицу называют таблицей частот
Замечание: сумма частот равна общему числу данных числового ряда.
При проведении статистического исследования после сбора и группировки данных переходят к их анализу, используя для этого различные обобщающие показатели. Простейшими из них являются такие известные вам статистические характеристики, как.
Задача 2: Проведите анализ результатов проведенной проверки работ учащихся задачи 1. Найдите среднее арифметическое, моду, медиану, размах.
Решение.
Проанализируем результаты проведенной проверки работ учащихся.
Чтобы найти среднее арифметическое, надо общее число верно выполненных заданий разделить на число учащихся, т. е. на 40. (Используем таблицу задачи 1). Получаем:
![]()
Значит, в среднем учащиеся выполнили по 5,8 заданий, т. е. примерно от общего объема работы.
Наибольшее число верно выполненных учащимися заданий равно 9, а наименьшее равно 0. Значит, размах ряда равен 9-0 = 9, т. е. различие в числе верно выполненных заданий достаточно велико.
Из таблицы ясно, что чаще всего встречаются работы, в которых верно выполнено 6 заданий, т. е. мода ряда равна 6.
Найдем медиану ряда. Так как в ряду всего 40 чисел, то медиана равна среднему арифметическому 20-го и 21-го членов соответствующего упорядоченного ряда. Для того чтобы определить, в какие группы попадают эти члены, будем последовательно суммировать частоты и сравнивать суммы с числами 20 и 21. Найдем, что 1 + 1 + 1+2 + 5 + 6=16, 1 + 1 + 1+2 + 5 + 6 + 8 = 24, т.е. 20-й и 21-й члены ряда попадают в ту группу, которую составляют учащиеся, верно выполнившие 6 заданий. Значит, медиана ряда равна (6+ 6): 2 = 6.
Ответ: среднее арифметическое 5,8, мода 6, медиана 6
Иногда составляют таблицу, в которой для каждого данного указывается не частота, а отношение частот к общему числу данных в ряду. Это отношение, выраженное в процентах, называется относительной частотой, а саму таблицу – таблицей относительных частот.
Определение: Относительно частотой (частостью) называют число
![]() ,
,
где M – частота, N –общее число данных.
Для данной задачи найдем относительные частоты и составим таблицу относительных частот:
|
Число верно выполненных заданий |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Относительная частота, % |
2,5 |
2,5 |
2,5 |
5 |
12,5 |
15 |
20 |
17,7 |
12,5 |
10 |
Замечание: сумма относительных частот равна 100%.
Если в ряду имеется большое число данных и одинаковые значения встречаются редко, то таблицы частот или относительных частот становятся излишне громоздкими. В таких случаях для анализа данных строят интервальный ряд. Для этого разность между наибольшим и наименьшим значениями делят на несколько равных частей (примерно 5 – 10) и, округляя полученный результат, определяют длину интервала. За начало первого интервала часто выбирают наименьшее данное или ближайшее к нему целое число, расположенное левее. Для каждого интервала указывают число данных, попадающих в этот интервал, или выраженное в процентах отношение этого числа к общей численности совокупности. При этом граничное число обычно считают относящимся к последующему интервалу.
Задача 3: На партии из 50 электроламп изучали продолжительность их горения (в часах). По результатам составили такую таблицу:
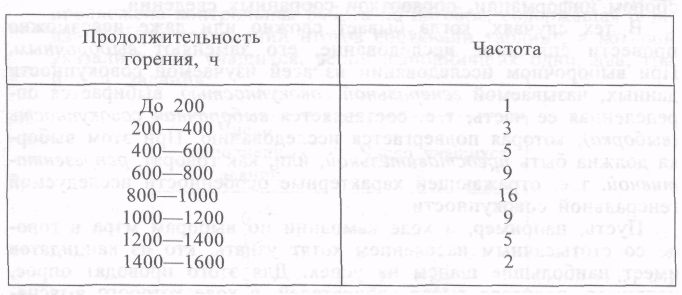
Найдите среднюю продолжительность горения ламп.
Решение.
Пользуясь составленной таблицей, найдем среднюю продолжительность горения. Для этого составим новую таблицу частот, заменив каждый интервал числом, которое является его серединой. Получим:

Для полученного ряда данных найдем среднее арифметическое:
(100∙1+300∙3+ 500∙5+ 700∙9+900∙16+1100∙9+1300∙5+1500∙2): 50 ≈ 870 (с точностью до десятков).
Значит, средняя продолжительность горения электроламп приближенно равна 870 ч.
Ответ: средняя продолжительность горения электроламп приближенно равна 870 ч.
В рассмотренном в начале пункта примере были проанализированы результаты выполнения теста восьмиклассниками одной школы. Тот же тест можно было бы использовать для более широкой проверки математической подготовки учащихся, например, предложить его восьмиклассникам всех школ города или региона. Заметим, что организация такой проверки связана с серьезными трудностями по пересылке текстов заданий в школы, сбору и проверке работ учащихся, обработке полученных результатов. Вообще, проведение любого массового исследования требует больших организационных усилий и финансовых затрат. Например, перепись населения страны связана с подготовкой разнообразной документации, выделением и инструктажем переписчиков, сбором информации, обработкой собранных сведений.
В тех случаях, когда бывает сложно или даже невозможно провести сплошное исследование, его заменяют выборочным. При выборочном исследовании из всей изучаемой совокупности данных, называемой генеральной совокупностью, выбирается определенная ее часть, т. е. составляется выборочная совокупность (выборка), которая подвергается исследованию. При этом выборка должна быть представительной, или, как говорят, репрезентативной, т. е. отражающей характерные особенности исследуемой генеральной совокупности.
Пусть, например, в ходе кампании по выборам мэра в городе со стотысячным населением хотят узнать, кто из кандидатов имеет наибольшие шансы на успех. Для этого проводят опрос, например, полутора тысяч избирателей, в ходе которого выясняется, за кого они собираются голосовать. При этом нельзя опрашивать только молодых избирателей или только пенсионеров, так как это может привести к неправильным выводам. Необходимо, чтобы среди опрашиваемых было примерно одинаковое число мужчин и женщин. Кроме того, должны быть представлены люди с разным социальным положением и образованием.
Выборочное исследование проводят также и тогда, когда проведение сплошного исследования связано с порчей или уничтожением продукции. Например, при исследовании продолжительности горения партии электроламп, выпущенных заводом, невозможно проверить всю партию, так как это просто привело бы к ее уничтожению.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ И РЕШЕНИЯ ДОМАШНЕГО ЗАДАНИЯ.
-
Определяя степень засоренности цветочных семян, выясняли, сколько семян сорных растений содержится в каждом из 100 произвольным образом выбранных пакетов с одинаковым числом семян. Получили такую таблицу:
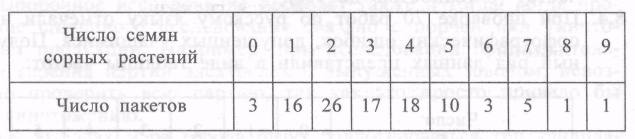
Для полученного ряда данных найдите среднее арифметическое и моду. Объясните практический смысл этих характеристик.
-
В ходе опроса 34 учащихся школы было выяснено, сколько времени (с точностью до 0,5 ч) в неделю они затрачивают на занятия в кружках и спортивных секциях. Получили следующие данные:
5, 1,5, 0, 2,5, 1, О, О, 2, 2,5, 3,5, 4, 5, 3,5, 2,5, 0, 1,5, 4,5, 3, 3, 5, 3,5, 4, 3,5, 3, 2,5, 2, 1, 2, 2, 4,5, 4, 3,5, 2, 5.
Представьте этот ряд данных в виде таблицы частот. Найдите, сколько времени в среднем тратят учащиеся на занятия в кружках и спортивных секциях.
-
Учащимся восьмых классов школ некоторого города была предложена контрольная работа по алгебре, содержащая 6 заданий. При подведении итогов составили таблицу, в которой указали число учащихся, верно выполнивших одно, два, три и т. д. задания:
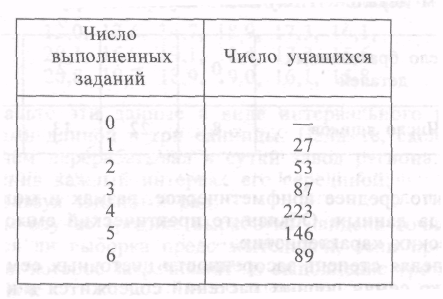
Пользуясь этой таблицей, составьте таблицу относительных частот (с точностью до 1%).
-
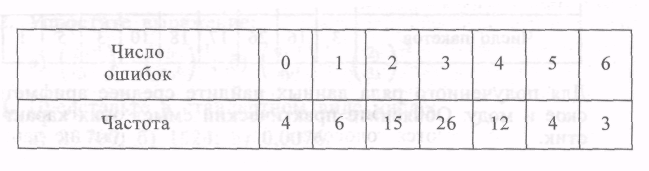
При проверке 70 работ по русскому языку отмечали число орфографических ошибок, допущенных учащимися. Полученный ряд данных представили в виде таблицы частот:
-
Каково наибольшее различие в числе допущенных ошибок?
-
Какое число ошибок является типичным для данной группы учащихся?
-
Укажите, какие статистические характеристики были использованы при ответе на поставленные вопросы.
-
При изучении учебной нагрузки учащихся попросили 32 восьмиклассников отметить время (с точностью до 0,1 ч), которое они затратили в определенный день на выполнение домашних заданий. Получили следующие данные:

Представьте полученные данные в виде интервального ряда с интервалами длиной 0,5 ч.
-
Ряд данных о количестве акций одинаковой стоимости, приобретенных сотрудниками лаборатории, представлен в виде таблицы частот:
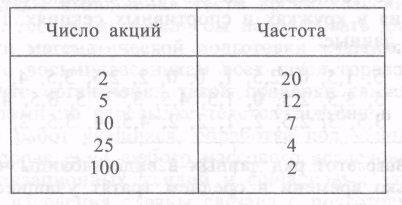
Для этого ряда данных найдите среднее арифметическое, размах и моду. Что характеризует каждый из этих показателей?
-
Имеются следующие данные о распределении участников похода по возрасту:

Заменив каждый интервал его серединой, найдите средний возраст участников похода.
-
Ниже показана среднесуточная переработка сахара (в тыс. ц) заводами сахарной промышленности некоторого региона:
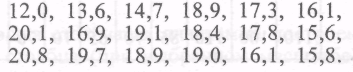
Представьте эти данные в виде интервального ряда с интервалами длиной в три единицы. Найдите, сколько сахара в среднем перерабатывал в сутки завод региона:
а) заменив каждый интервал его серединой;
б) используя заданный ряд.
В каком случае средняя выработка найдена точнее?
Является ли выборка представительной, если при изучении времени, которое затрачивают на выполнение уроков восьмиклассники:
а) опрашивали только девочек;
б) опрос проводили только по четвергам;
в) опрашивали только учащихся гимназий и лицеев?
Вопросы для повторения материала
-
Назовите формулу для нахождения относительных частот.
-
Объясните на примере, как по таблице частот находят среднее арифметическое.
-
Объясните на примере, как по таблице частот находят размах.
-
Объясните на примере, как по таблице частот находят моду.
-
Объясните на примере, как по таблице частот находят медиану.
