Среднее арифметическое, размах, мода и медиана
- Алгебра
- Среднее арифметическое, размах, мода и медиана
Статистические характеристики
количество чисел
Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда
чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите
рассчитать.
Среднее арифметическое, размах, мода и медиана
Средним арифметическим ряда чисел называется частное от деления суммы этих
чисел на число слагаемых.
Для ряда a1,a1,..,an среднее арифметическое вычисляется по
формуле:
begin{align}
& overline{a}=frac{a_1+a_2+…+a_n}{n}\
end{align}
Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.
begin{align}
& overline{a}=frac{5,24+6,97+8,56+7,32+6,23}{5}=6.864\
end{align}
Размахом ряда чисел называется разность между наибольшим и наименьшим из
этих чисел.
Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32
Модой ряда чисел называется число, которое встречается в данном ряду чаще
других.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.
В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.
Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.
Медианой упорядоченного ряда чисел с нечётным числом членов называется
число, записанное посередине, а медианой упорядоченного ряда чисел с чётным
числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного
ряда.
Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.
Примеры
Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды
ряда.
-
Среднее арифметическое чисел 30, 5, 23, 5, 28, 30
begin{align}
& overline{a}=frac{30+5+23+5+28+30}{6}=20frac{1}{6}\
end{align}Размах ряда: 30-5=25
Моды ряда: 5 и 30
Медиана ряда: 25.5
-
Среднее арифметическое чисел 40, 35, 30, 25, 30, 35
begin{align}
& overline{a}=frac{40+35+30+25+30+35}{6}=32frac{1}{2}\
end{align}Размах ряда: 40-25=15
Моды ряда: 30, 35
Медиана ряда: 32.5
-
Среднее арифметическое чисел 21, 18,5, 25,3, 18,5, 17,9
begin{align}
& overline{a}=frac{21+18,5+25,3+18,5+17,9}{5}=20,24\
end{align}Размах ряда: 25,3-17,9=7,4
Мода ряда: 18,5
Медиана ряда: 18,5
Примеры
Примеры нахождения среднего арифметического отрицательных и вещественных чисел.
-
Среднее арифметическое чисел 67,1, 68,2, 67,1, 70,4, 68,2
begin{align}
& overline{a}=frac{67,1+68,2+67,1+70,4+68,2}{5}=68,2\
end{align}Размах ряда: 70,4-67,1=3,3
Моды ряда: 67.1, 68.2
Медиана ряда: 68.2
-
Среднее арифметическое чисел 0,6, 0,8, 0,5, 0,9, 1,1
begin{align}
& overline{a}=frac{0,6+0,8+0,5+0,9+1,1}{5}=0.78\
end{align}Размах ряда: 1,1-0,5=0.6
Ряд не имеет моды
Медиана ряда: 0.8
-
Среднее арифметическое чисел -21, -33, -35, -19, -20, -22
begin{align}
& overline{a}=frac{(-21)+(-33)+(-35)+(-19)+(-20)+(-22)}{6}=-25\
end{align}Размах ряда: (-19)-(-35)=16
Ряд не имеет моды
Медиана ряда: -21,5
-
Среднее арифметическое чисел -4, -6, 0, -4, 0, 6, 8, -12
begin{align}
& overline{a}=frac{(-4)+(-6)+0+(-4)+0+6+8+(-12)}{8}=-1,5\
end{align}Размах ряда: 8-(-12)=20
Моды ряда: -4, 0
Медиана ряда: -2
-
Среднее арифметическое чисел 275, 286, 250, 290, 296, 315, 325
begin{align}
& overline{a}=frac{275+286+250+290+296+315+325}{7}=291\
end{align}Размах ряда: 325-250=75
Ряд не имеет моды
Медиана ряда: 290
-
Среднее арифметическое чисел 38, 42, 36, 45, 48, 45, 45, 42, 40, 47, 39
begin{align}
& overline{a}=frac{38+42+36+45+48+45+45+42+40+47+39}{11}=42frac{6}{11}\
end{align}Размах ряда: 48-36=12
Мода ряда: 45
Медиана ряда: 42
-
Среднее арифметическое чисел 3,8, 7,2, 6,4, 6,8, 7,2
begin{align}
& overline{a}=frac{3,8+7,2+6,4+6,8+7,2}{5}=6,28\
end{align}Размах ряда: 7,2-3,8=3,4
Мода ряда: 7,2
Медиана ряда: 6,8
-
Среднее арифметическое чисел 21,6, 37,3, 16,4, 12,6
begin{align}
& overline{a}=frac{21,6+37,3+16,4+12,6}{4}=21,025\
end{align}Размах ряда: 37,3-12,6=24,7
Мода ряда: 12,6
Медиана ряда: 17,1
Кроме среднего арифметического числовой ряд можно описать и с помощью других характеристик. Одной из них является размах ряда.
В статистике размахом ряда называют разницу между самым большим и самым маленьким результатами наблюдений. Другими словами, в совокупности данных размах отражает разброс значений.
Таким образом, если размах — большая величина, то и значения в совокупности будут сильно разбросаны, а если размах маленький, то, соответственно, значения будут располагаться рядом друг с другом.
На письме размах ряда обычно сокращенно обозначают буквой $R$.
Размах ряда — это разность между наибольшим и наименьшим значениями чисел.
Формула для расчета
Для того чтобы рассчитать размах ряда, можно применить следующую формулу:
$$textcolor{blue}{R}=textcolor{lightblue}{x}-textcolor{green}{y}$$
В свою очередь, $textcolor{blue}{R}$ — размах ряда, $textcolor{lightblue}{x}$ — максимальное значение, а $textcolor{green}{y}$ — минимальное. Используя эту формулу можно с легкостью решать задачи, где нужно найти значение $textcolor{blue}{R}$.
Чтобы найти размах ряда нужно из наибольшего значения вычесть наименьшее.
Рассмотрим на примере. Дровосек пилил бревно. Чтобы брёвна можно было аккуратно сложить, он старался делать их примерно одной длины. Когда работа была сделана, он решил проверить, как хорошо у него это получилось. Для этого он измерил все брёвна и получил такие значения:
$$43, 32, 36, 51, 48$$
Рассчитаем размах ряда. Выбираем самое большое и самое маленькое число.
$$43, textcolor{green}{32}, 36, textcolor{lightblue}{51}, 48$$
Вычитаем из наибольшего наименьшее:
$$textcolor{lightblue}{51}-textcolor{green}{32} = 19$$
$19$ — размах ряда.
Среднее арифметическое нескольких величин – это отношение суммы величин к их количеству.
Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.
Например: найдем среднее арифметическое чисел 2; 6; 9; 15.
У нас четыре числа, значит надо их сумму разделить на четыре. Это и будет среднее арифметическое данных чисел: (2 + 6 + 9 + 15) : 4 = 8.
Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.
Например: найдем размах чисел 2; 5; 8; 12; 33.
Наибольшее число здесь – 33, наименьшее – 2. Значит, размах составляет 31, т. е.: 33 – 2 = 31.
Мода ряда чисел – это число, которое встречается в данном ряду чаще других.
Например: найдем моду ряда чисел 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 8.
Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.
Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Например: в ряде чисел 2; 5; 9; 15; 21 медианой является число 9, находящееся посередине.
Найдем медиану в ряде чисел 4; 5; 7; 11; 13; 19.
Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел: (7 + 11) : 2 = 9. Число 9 является медианой данного ряда чисел.
-
В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3; 5; 5; 4; 4; 4; 3; 2; 4; 5.
Какую оценку получали чаще всего? Каков средний балл сдавшей зачет группы?
-
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите медиану и размах ряда.
-
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите моду ряда и среднее арифметическое ряда.
-
Имеются следующие данные о месячной заработной плате пяти рабочих (тг): 126000; 138000; 132000; 141000; 150000.
Найдите среднюю заработную плату.
-
Магазин продает 8 видов булочек по следующим ценам: 31; 22; 24; 27; 30; 36; 19; 27.
Найдите разность среднего арифметического и медианы этого набора.
-
Найдите объем и медиану числового ряда.
9; 7; 1; 1; 11; 5; 1.
-
Товарные запасы хлопчатобумажных тканей в магазине за первое полугодие составили (тыс. тг) на начало каждого месяца:
I II III IV V VI VII 37 34 35 32 36 33 38 Определите средний товарный запас хлопчатобумажных тканей за первое полугодие.
-
Провели несколько измерений случайной величины: 2,5; 2,2; 2; 2,4; 2,9; 1,8.
Найдите среднее арифметическое этого набора чисел.
-
Провели несколько измерений случайной величины: 6; 18; 17; 14; 4; 22.
Найдите медиану этого набора чисел.
-
Провели несколько измерений случайной величины:
800; 3200; 2000; 2600; 2900; 2000. Найдите моду этого набора чисел.
-
Магазин продает 8 видов хлеба по следующим ценам: 60, 75, 80, 85, 90, 100, 110, 120 тенге.
Найдите разность среднего арифметического и медианы этого набора.
-
Дан числовой ряд: 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 7,8.
Найдите среднее арифметическое, размах и моду.
Вопросы
занятия:
· ввести понятие «среднее арифметическое
числового ряда»;
· ввести понятия «размах ряда», «мода ряда»;
· разобрать, где находят применение рассмотренные
статические характеристики.
Материал
урока
Давайте
рассмотрим пример.
Пример.
Ежедневно
в течение 10 дней в полдень измеряли температуру воздуха (в градусах Цельсия) и
получили следующие данные.
Пользуясь
этим рядом, мы можем определить среднюю температуру воздуха, наблюдаемую в
течение этих десяти дней.
Число
25 называют средним арифметическим рассматриваемого ряда чисел.
Сформулируем
определение.
Определение.
Средним
арифметическим ряда чисел называется частное от деления
суммы этих чисел на число слагаемых.
Таким
образом, умея находить среднее арифметическое ряда чисел, мы можем найти
средний расход холодной воды семьёй в течение года
средний
балл ученика за четверть
среднюю
урожайность пшеницы за последние 5 лет и так далее.
Вернёмся
к нашему примеру. Обратите внимание, что температура воздуха в некоторые дни
существенно отличается от 25 градусов Цельсия (то есть от средней температуры).
Так, самая высокая температура равна 30 градусам, а самая низкая – 19 градусам.
Найдём
разность между наибольшим и наименьшим значениями:
Говорят,
что размах ряда равен 11.
Определение.
Размахом
ряда чисел называется разность между наибольшим и наименьшим
из этих чисел.
Размах
ряда находят, когда хотят узнать, насколько велик разброс данных в ряду. Так,
например, в нашем примере размах ряда показывает колебание температуры воздуха
в течение 10 дней.
Но
кроме среднего арифметического и размаха ряда данных, нас может заинтересовать
вопрос: какая температура воздуха чаще всего устанавливалась за 10 дней?
Заметим, что чаще всего в нашем ряду встречается число 25. Это число называют модой
рассматриваемого ряда.
Сформулируем
определение.
Определение.
Модой
ряда
называется число, которое встречается в данном ряду чаще других.
Стоит
отметить, что ряд может иметь более одной моды.
Например,
Также
ряд может и не иметь моды.
Например,
Моду
ряда находят, когда хотят выяснить некоторый характерный показатель. Например,
удобно воспользоваться этим показателем при изучении спроса покупателей на
мужскую обувь, чтобы определить какой размер самый популярный.
Рассмотрим
ещё один пример.
Пример.
Посмотрите,
среднее арифметическое ряда чисел может не совпадать ни с одним из чисел ряда,
а вот мода всегда совпадает хотя бы с одним из чисел. Причем, если среднее
арифметическое мы можем найти только для числового ряда, то понятие «мода»
относится не только к числовым рядам.
Например,
проведя опрос группы людей, можно определить, какой из видов спорта более
популярен. И модой будут служить те ответы, которые чаще всего встречаются.
Рассмотренные
на уроке характеристики (среднее арифметическое, размах и мода) применяются в
статистике.
Определение.
Статистика
(от латинского слова статус, что означает состояние, положение вещей) – это
наука, которая занимается получением, обработкой и анализом количественных
данных о разнообразных массовых явлениях, происходящих в обществе и
природе.
Основываясь
на примерах, которые мы с вами рассматривали на уроке, можно сказать, что
статистика используется в различных сферах деятельности человека.
Урок 1. «Среднее арифметическое, размах и мода»
Тип урока: ознакомление с новым материалом.
Цели:
- обучающая – формирование представления о простейших статистических характеристиках и их использовании при анализе данных, полученных в результате исследования;
- развивающая – знакомство с разделом математики: «статистика и теория вероятностей» и его местом в системе научного познания мира;
- воспитательная – подготовка учащихся к проблемам современной жизни (понимание и интерпретация результатов статистических исследований).
Оборудование: проектор.
Ход урока
I. Организационный момент
II. Сообщение темы и целей урока
Слышали ли вы когда-нибудь такую песню: «Потому что на десять девчонок по статистике девять ребят»? Как вы думаете, что это значит?
Сегодня мы познакомимся с новой наукой – статистикой. Узнаем, что она изучает и как можно применить те знания, которые вы сейчас получите.
<Презентация 1>
III. Актуализация знаний
– Какое число называют средним арифметическим нескольких чисел?
(Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых).
Задача: дан ряд чисел 5, 6, 8, 12, 15, 4, 17, 8, 10, 15.
- Найдите среднее арифметическое ряда чисел.
- Найдите наибольшее и наименьшее значение ряда чисел, вычислите их разность.
IV. Первичное усвоение, осознание и осмысление нового материала
– Ребята, вы начинаете изучать новый предмет: «Элементы статистики и теории вероятностей».
– Где в реальной повседневной жизни мы сталкиваемся с этими науками?
– Вы что-нибудь слышали об этом разделе математики?
– А разве вам не приходилось подсчитывать среднюю скорость движения, средний бал ученика, класса. Подготовку человека к таким проблемам во всем мире осуществляет школьный курс математики, и в частности ее раздел «Математическая статистика».
Статистика – наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Слово «статистика» происходит от латинского слова status, которое означает «состояние, положение вещей». Статистика изучает численность отдельных групп населения страны и ее регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и многое другое. Результаты статистических исследований широко используются для практических и научных выводов. Вам было дано задание: измерить время, затраченное на выполнение домашнего задания по алгебре.
Мы получили следующие результаты: 27, 25, 26, 25, 40, 38, 38, 25 и т.д.
Имея этот ряд данных, можно определить, сколько минут в среднем затратили учащиеся на выполнение домашнего задания.
– Что для этого нужно сделать? (сложить все числа и разделить полученную сумму на их количество).
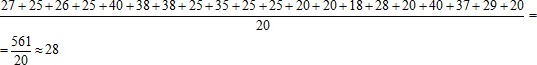
Число 28, полученное в результате, называют средним арифметическим рассматриваемого ряда. Обозначение: ![]() .
.
Мы вычислили, что на выполнение домашнего задания по алгебре учащиеся затратили в среднем 28 минут. Проводя аналогичные наблюдения, можно проследить, какова была средняя затрата времени на выполнение в какой-либо день домашнего задания по алгебре и русскому языку.
Заметим, что иногда вычисление среднего арифметического не дает полезной информации, так как время, затраченное некоторыми учащимися, значительно отличается от среднего арифметического.
Наибольший расход времени равен 40 минут, а наименьший расход времени равен 18 минут. Разность между наибольшим и наименьшим значением называется размахом ряда.
Размах ряда находят тогда, когда хотят определить, как велик разброс данных в ряду.
-Ребята, нас могут интересовать не только среднее арифметическое и размах, но и другие показатели.
Например, интересно знать, какое число встречается в ряду данных чаще всего.
Таким числом является число 25. Число, наиболее часто встречающееся в данном ряду, называется модой чисел.
Ряд может иметь две моды, а может не иметь моды. Например, 47, 46, 50, 52, 47, 49, 52, 55 – имеет две моды: 47 и 52.
69, 68, 66, 70, 67, 71, 74, 63, 73, 72 – этот ряд не имеет моды.
– Ребята, где еще можно встретить понятие моды ряда чисел?
– Данные о размерах мужских сорочек, проданных в определенный день в универмаге. Здесь мода – размер пользующихся спросом, мода – цены на товар распространенный на рынке и т.п.
V. Закрепление изученного материала
При выставлении оценок учитель также вычисляет среднее арифметическое ваших текущих оценок.
Сейчас вы получите выписку ваших оценок по алгебре за I четверть.
Вы должны вычислить среднее арифметическое, моду и размах.
VI. Подведение итогов урока
Выставление оценок за работу на уроке.
«В среднем в день ребёнок улыбается 400 раз, взрослый — 17. Теперь все улыбнулись, чтобы испортить статистику»
VIII. Рефлексия
Раздать карточки для рефлексии.
<Приложение 1>
VII. Постановка домашнего задания п. 9, 168 (а, б), 172, 178
Урок 2. «Медиана как статистическая характеристика»
Тип урока: ознакомление с новым материалом.
Цели:
- обучающая – ввести понятие медианы, организовать деятельность учащихся по закреплению медианы, среднего арифметического, размаха и моды, обеспечить отработку навыка их применения при выполнении различных заданий;
- развивающая – знакомство с разделом математики: «статистика и теория вероятностей» и его местом в системе научного познания мира;
- воспитательная – подготовка учащихся к проблемам современной жизни (понимание и интерпретация результатов статистических исследований).
Оборудование: проектор
Ход урока
I. Организационный момент
II. Проверка домашнего задания
<Приложение 2>
III. Сообщение темы и целей урока
Сегодня на уроке мы повторим алгоритм нахождения среднего арифметического, размаха и моды, и узнаем, как находится еще одна характеристика – медиана.
<Презентация 2>
IV. Актуализация опорных знаний учащихся
1. Фронтальный опрос.
- Что называется средним арифметическим ряда чисел? Может ли среднее арифметическое ряда чисел не совпадать ни с одним из этих чисел?
- Что называется размахом ряда чисел?
- Что называется модой ряда чисел? Любой ли ряд чисел имеет моду? Может ли ряд чисел иметь более одной моды? Может ли мода ряда чисел не совпадать ни с одним из этих чисел?
2. Устный счет.
а) Дан ряд чисел: 3, 5, 1, 7, 9. Найти среднее арифметическое, размах и моду.
б) Дан ряд чисел: 1, 2, 2, 5, 5. Найти среднее арифметическое, размах и моду.
V. Первичное усвоение, осознание и осмысление нового материала
Задача. В небольшой фирме 10 сотрудников: 7 рабочих, мастер, бухгалтер, директор. Зарплата у рабочих: 2000, у мастера 4000, у бухгалтера 16000, у директора 40000. Найдите чему будет равна средняя зарплата на этом предприятии?
Решение:
![]()
Но достаточно ли этой характеристики работнику, который устраивается работать рабочим? (Нет)
В этом случае используют другую статистическую характеристику – медиану.
Запишем алгоритм нахождения медианы набора чисел:
- Упорядочить числовой набор.
- Одновременно зачеркиваем “самое большое” и “самое маленькое” числа данного набора чисел до тех пор, пока не останется одно число или два числа.
- Если осталось одно число, то оно и есть медиана.
- Если осталось два числа, то медианой будет среднее арифметическое двух оставшихся чисел.
Медиану используют вместо средней арифметической, когда крайние варианты упорядоченного ряда (наименьшая и наибольшая) по сравнению с остальными оказываются чрезмерно большими или чрезмерно малыми.
VI. Закрепление изученного материала
Задача 2. В таблице приведена информация о длине основных рек, протекающих по территории округа Домодедово Московской области.
| Река | Длина, км |
| Пахра | 900 |
| Рожайка | 51 |
| Битца | 24 |
| Гнилуша | 31 |
| Северка | 98 |
| Конопелька | 13 |
а) Найдите среднюю длину рек (среднее арифметическое);
б) Найдите длину рек в среднем (медиану данных);
в) По вашему мнению, какая из этих характеристик – среднее арифметическое или медиана – лучше описывает длину рек, протекающих в Домодедовском районе? Ответ объясните.
Ответ: а) 186 км, б) 41 км, в) медиана, т.к. данные содержат значения сильно отличающиеся от всех прочих.
Итак, для характеристики статистической информации используют среднее арифметическое и медиану. Во многих случаях одна из характеристик может не иметь никакого содержательного смысла.
VI. Подведение итогов урока
У статистиков есть шутка: средняя глубина озера 0,5 м, а корова все-таки утонула. Как вы понимаете эту фразу?
Выставление оценок за работу на уроке.
VIII. Рефлексия
Раздать карточки для рефлексии.
<Приложение 1>
VII. Постановка домашнего задания п.10, 187, 190, 193
Урок 3. «Статистические характеристики»
Тип урока: закрепление изученного.
Цели:
- обучающая – закрепить полученные знания и умения, применять статистические характеристики при решении простейших задач;
- развивающая – развитие математически грамотной речи, логического мышления;
- воспитательная – подготовка учащихся к проблемам современной жизни, воспитание познавательной активности, культуры диалога.
Оборудование: карточки для выполнения проверочной работы.
Ход урока
I. Организационный момент
II. Проверка домашнего задания, уточнение направлений актуализации материала
<Приложение 2>
III. Сообщение темы, цели и задач урока, мотивация учения
Сегодня на уроке мы продолжим находить основные статистические характеристики числовых рядов.
IV. Воспроизведение изученного и их первичное применение в новых или измененных условиях с целью формирования умений
1. Фронтальный опрос
- Что такое статистика?
- Какие статистические характеристики вы знаете?
- Что называется средним арифметическим ряда чисел?
- Что называется размахом ряда чисел?
- Что называется модой ряда чисел?
- Любой ли ряд имеет моду?
- Может ли ряд иметь более одной моды?
- Может ли мода ряда чисел не совпадать ни с одним из этих чисел?
- Что называется медианой ряда чисел?
- Какой ряд называется упорядоченным рядом чисел?
2. Решение задач
В таблице приведены расходы учащегося 7 класса за 4 дня:
| День | Понедельник | Вторник | Среда | Четверг |
| Расходы | 100 | 75 | 50 | 75 |
Определить какая статистическая характеристика находится в каждом задании:
а) 100+75+50+75=30;
300:4=75;
___=75 р.б) 50, 75, 75, 100;
(75+75):2 = 75;
___=75 р.в) 100, 75, 50, 75;
___=75 р.г) 100-50=50;
___=50 р.
3. Решение заданий повышенной сложности
<Приложение 3>
V. Проверочная работа
<Приложение 4>
Выдаются карточки с заданием. Эти карточки подписываются учащимися. Задания выполняются на этих карточках в течение 3-5 минут.
Ребята меняются карточками. И по готовым ответам на доске проверяют работы друг друга и выставляют отметки согласно предложенным критериям.
Оценка: «5» – всё верно; «4» – 3 задания выполнены верно; «3» – 2 задания выполнены верно; «2» – выполнено верно менее двух зданий.
Работы сдаются учителю для просмотра и анализа усвоения материала.
VI. Подведение итогов урока
Выставление оценок за урок.
VII. Рефлексия
Раздать карточки для рефлексии.
<Приложение 1>
VIII. Постановка домашнего задания №182, №183, №193
Провести сбор информации на тему: «Размер обуви учеников 7 класса», «Рост учеников 7 класса», «Количество детей в семье учеников 7 класса» (в трех экземплярах) <Приложение 5>
Урок 4. «Статистические характеристики нашего класса»
Тип урока: обобщения и систематизации знаний.
Цели:
- обучающая – повторение и закрепление пройденного материала, введение понятия статистического исследования, продемонстрировать удобные способы упорядочивания и систематизации больших объёмов информации;
- развивающая – развитие математически грамотной речи, логического мышления;
- воспитательная – воспитание познавательной активности, культуры диалога.
Оборудование: таблицы для заполнения данных.
Ход урока
I. Организационный момент
II. Сообщение темы и целей урока
– На перемене я собрала ответы на все ваши вопросы. Все готовы приступить к групповому исследованию. Начинаем заключительный урок по теме “Статистические характеристики”.
III. Воспроизведение и коррекция опорных знаний
- Что такое статистика?
- Какие статистические характеристики вы знаете?
IV. Обобщение и систематизация понятий, усвоение системы знаний и их применение для объяснения новых фактов и выполнения практических заданий
Сегодня на уроке мы проведем с вами статистическое исследование.
Запишем основные этапы статистического исследования:
- Сбор данных.
- Систематизация данных – представление данные в табличном виде.
- Анализ данных – нахождение статистических характеристик, выводы.
Рассмотрим следующую задачу:
В женском обувном магазине провели статистические исследования и составили соответствующую таблицу по цене обуви и количества продаж:
| Цена (руб.) | 500 | 1200 | 1500 | 1800 | 2000 | 2500 |
| Количество | 8 | 9 | 14 | 15 | 3 | 1 |
Первый и второй этап статистического исследования уже пройдены: данные собраны и систематизированы. Осталось произвести анализ данных.
Для данных показателей надо найти статистические характеристики и объяснить их значение. После ученики должны ответить на следующие вопросы:
- Из данных ценовых категорий, обувь за какую цену не следует продавать магазину?
- Обувь, по какой цене следует распространять?
- К какой цене лучше стремиться?
По каким параметрам еще можно провести статистические исследования в обувном магазине?
V. Усвоение ведущих идей и основных теорий на основе широкой систематизации знаний
Проведем собственное статистическое исследование. У вас было домашнее задание: принести данные о своем росте, размере обуви и количестве детей в семье.
Сейчас каждый ряд получит свое задание <Приложение 5>:
- Провести статистическое исследование роста учащихся вашего класса.
- Провести статистическое исследование размера обуви.
- Провести статистическое исследование количества детей в семье.
Так как статистическое исследование состоит из трех этапов, а первый этап – сбор данных мы уже провели, то вы можете переходить ко второму этапу – систематизации данных. Для этого данные занесите в таблицы.
После того как вы провели систематизацию данных, можно переходить к следующему этапу – анализу данных. Найдите статистические характеристики: среднее арифметическую, моду, медиану и размах ряда. Сделайте выводы.
VI. Подведение итогов урока
Вы все отлично справились с заданием. Выставление оценок за работу на уроке.
VII. Постановка домашнего задания
Провести исследование на тему: «Рост учащихся 8 класса».
VII. Рефлексия
Раздать карточки для рефлексии.
<Приложение 1>
