Как найти размах ряда в excel

Цель:

• Совершенствование умений и навыков нахождения статистических
  характеристик случайной величины, работа с расчетами в Excel;
• применение информационно коммутативных технологий для анализа данных;
  работа с различными информационными носителями.

Ход урока

1. Сегодня на уроке мы научимся рассчитывать статистические характеристики
   для больших по объему выборок, используя возможности современных
   компьютерных технологий.
2. Для начала вспомним:

– что называется случайной величиной? (Случайной величиной называют
переменную величину, которая в зависимости от исхода испытания принимает одно
значение из множества возможных значений.)

– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)

– Приведите примеры непрерывных случайных величин (рост дерева), дискретных
случайных величин (количество учеников в классе).

– Какие статистические характеристики случайных величин мы знаем (мода,
медиана, среднее выборочное значение, размах ряда).

– Какие приемы используются для наглядного представления статистических
характеристик случайной величины (полигон частот, круговые и столбчатые
диаграммы, гистограммы).

1. Рассмотрим, применение инструментов Excel для решения статистических
   задач на конкретном примере.

Пример. Проведена проверка в 100 компаниях. Даны значения количества
работающих в компании (чел.):

23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28

рассчитать числовые характеристики: моду медиану размах ряда построить полигон частот построить столбчатую и круговую диаграммы раскрыть смысловую сторону каждой характеристики

Ход работы.

1. Занести данные в EXCEL, каждое число в отдельную ячейку.

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в
появившемся окне в строке категория выберем – статистические, в списке: МОДА

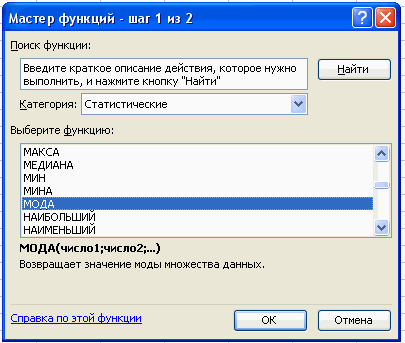
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

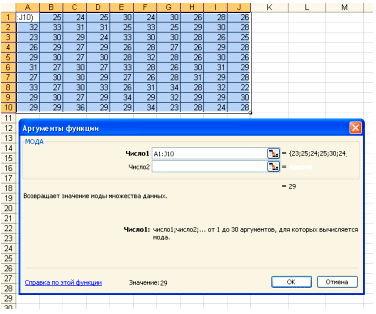
Нажимаем клавишу ОК. Получили М_о = 29 (чел) – Фирм у которых в
штате 29 человек больше всего.

Используя тот же путь вычисляем медиану.

Вставка – Функция – Статистические – Медиана.

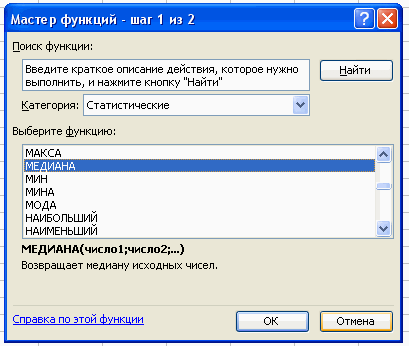
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

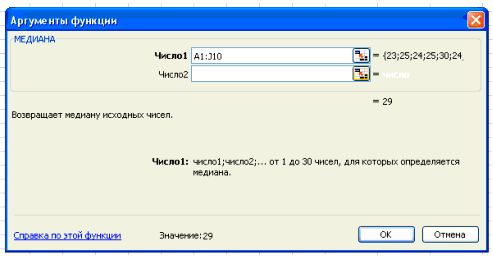
Нажимаем клавишу ОК. Получили М_е = 29 (чел) – среднее значение
сотрудников в фирме.

Размах ряда чисел – разница между наименьшим и наибольшим возможным значением
случайной величины. Для вычисления размаха ряда нужно найти наибольшее и
наименьшее значения нашей выборки и вычислить их разность.

Вставка – Функция – Статистические – МАКС.

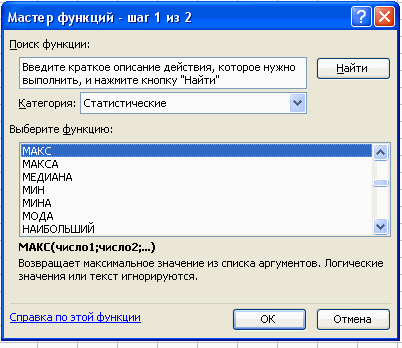
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

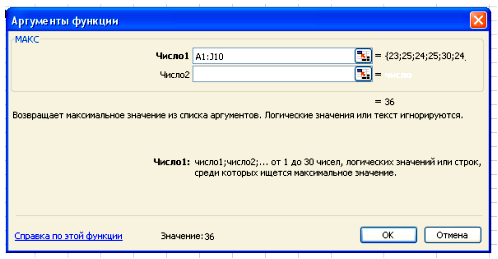
Нажимаем клавишу ОК. Получили наибольшее значение = 36.

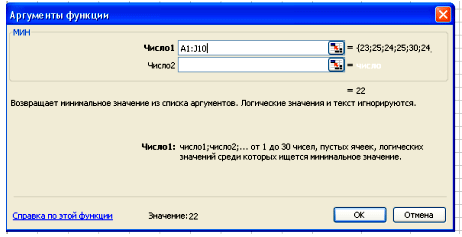
Вставка – Функция – Статистические – МИН.

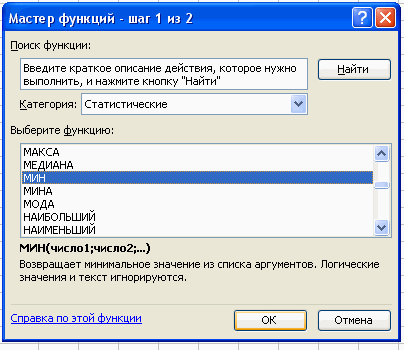
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

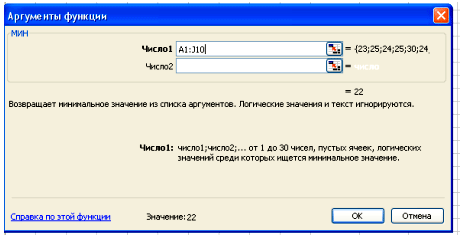
Нажимаем клавишу ОК. Получили наименьшее значение = 22.

36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и
фирмой с наименьшим штатом сотрудников.

Для построения диаграммы и полигона частот необходимо задать закон
распределения, т.е. составить таблицу значений случайной величины и
соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в
фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения x_i
случайной величины меняются от 22 до 36 включительно шагом 1.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni

Чтобы сосчитать частоту каждого значения воспользуемся

Вставка – Функция – Статистические – СЧЕТЕСЛИ.

В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий
ставим число 22

Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке
встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni	1	3	4	5	11	9	13	18	16	6	4	6	3	0	1

Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция –
Математические – СУММА). Должно получиться 100 (количество всех фирм).

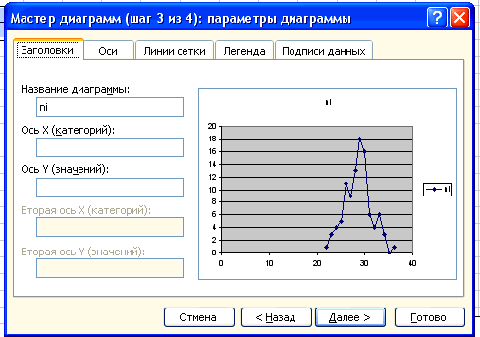
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма –
Стандартные – Точечная (точечная диаграмма на которой значения соединены
отрезками)

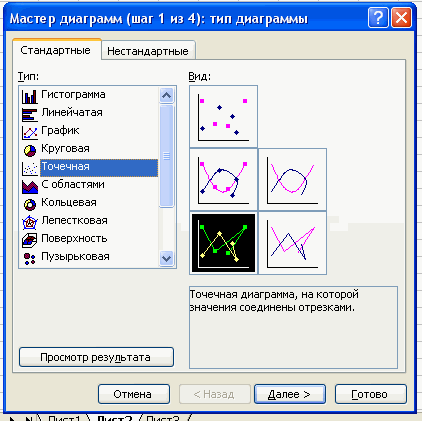
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы
(Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы
для наибольшей наглядности.

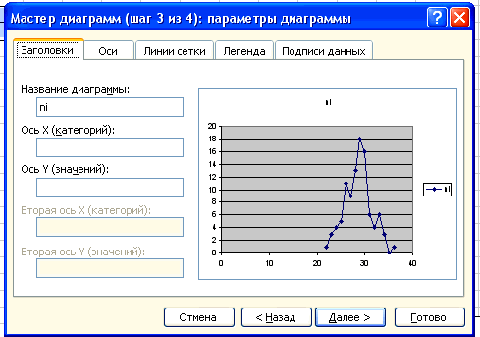
 Получаем:

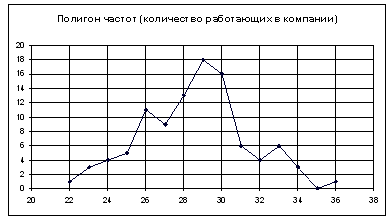
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая
нужный нам тип диаграммы).

Диаграмма – Стандартные – Круговая.

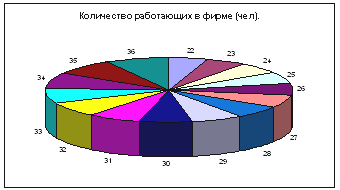
Диаграмма – Стандартные – Гистограмма.

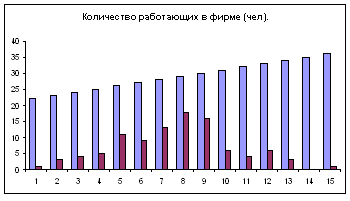
4. Сегодня на уроке мы научились применять компьютерные технологии для
анализа и обработки статистической информации.

Одним из основных статистических показателей последовательности чисел является коэффициент вариации. Для его нахождения производятся довольно сложные расчеты. Инструменты Microsoft Excel позволяют значительно облегчить их для пользователя.

Вычисление коэффициента вариации

Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.

В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.

Шаг 1: расчет стандартного отклонения

Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.

Синтаксис данных функций выглядит соответствующим образом:

= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)

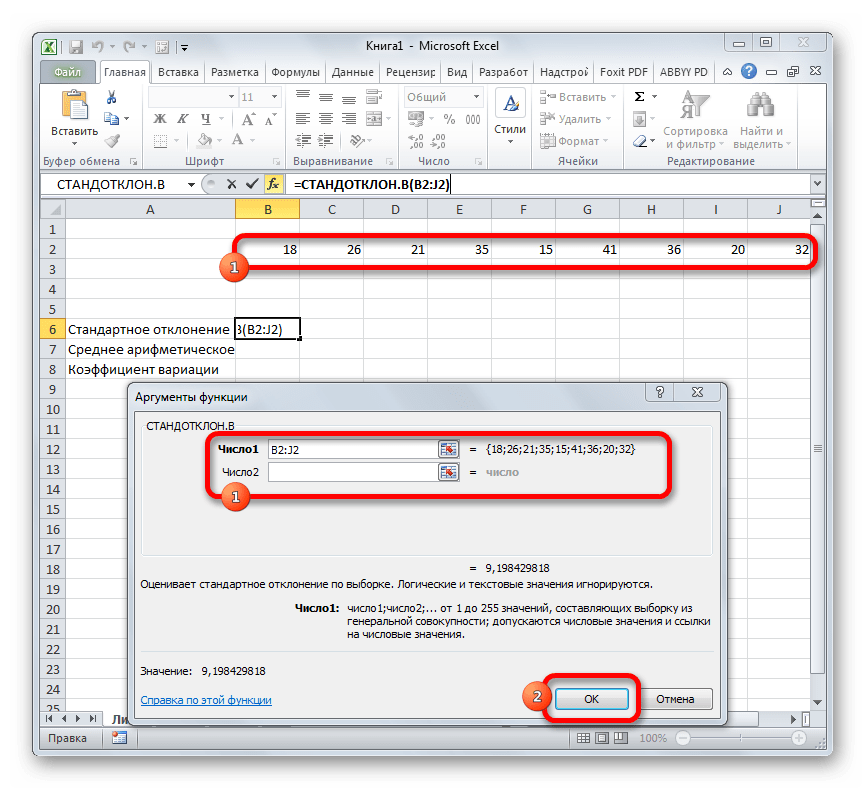
1. Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.

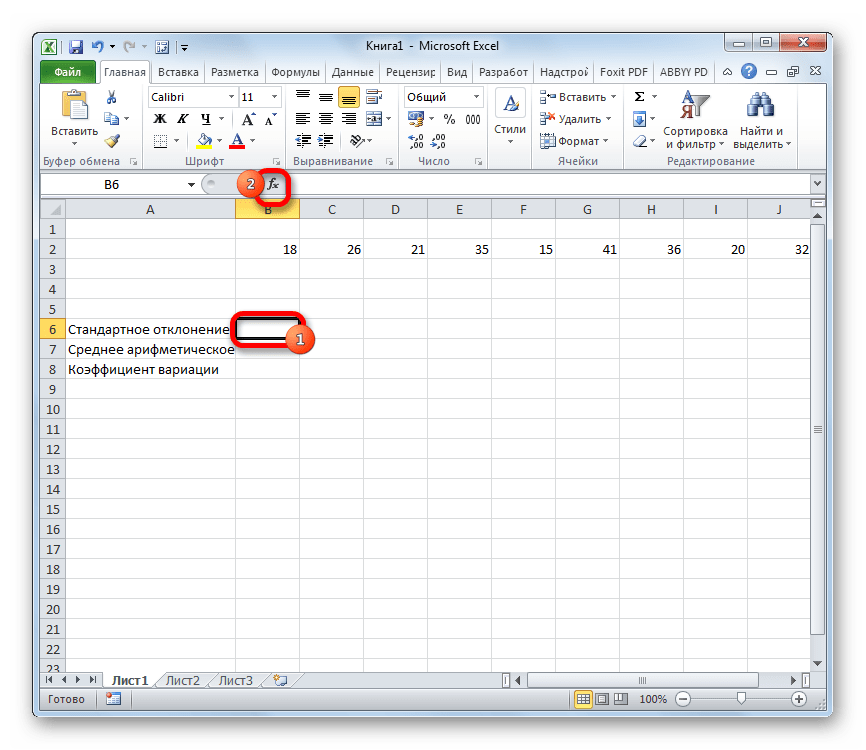
Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».

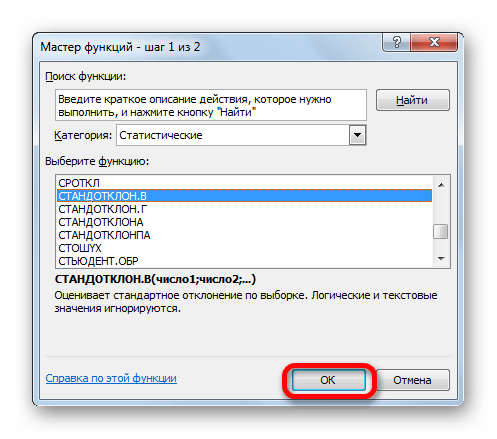
Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»

В предварительно выделенной ячейке отображается итог расчета выбранного вида стандартного отклонения.

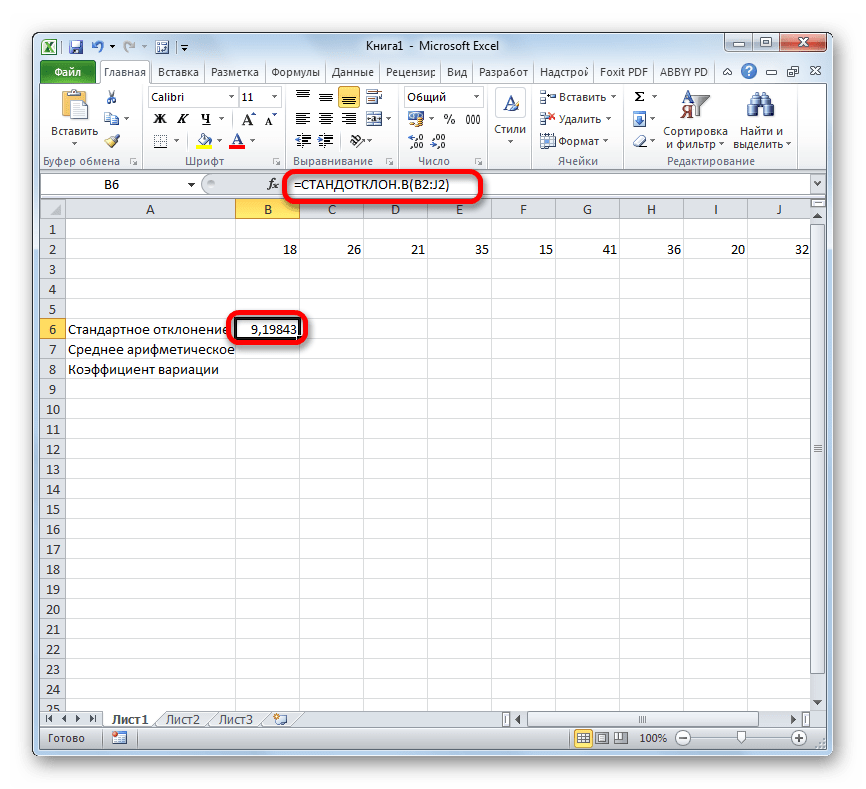
Шаг 2: расчет среднего арифметического

Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.

Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».

В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».

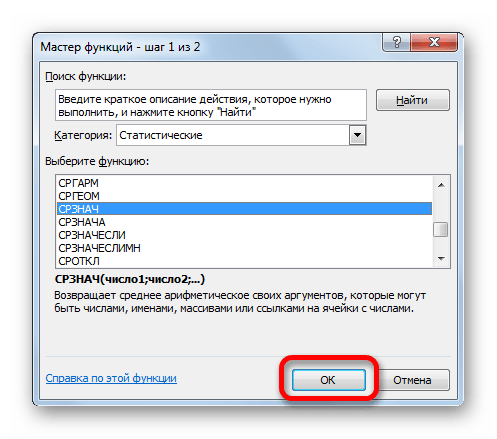
Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».

Результат вычисления среднего арифметического выводится в ту ячейку, которая была выделена перед открытием Мастера функций.

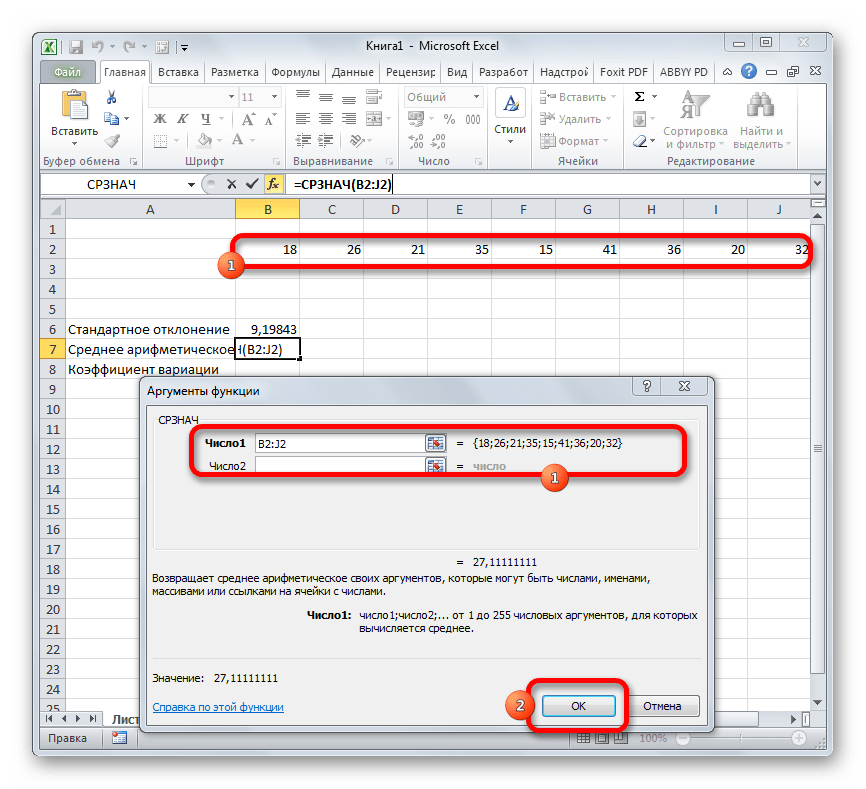
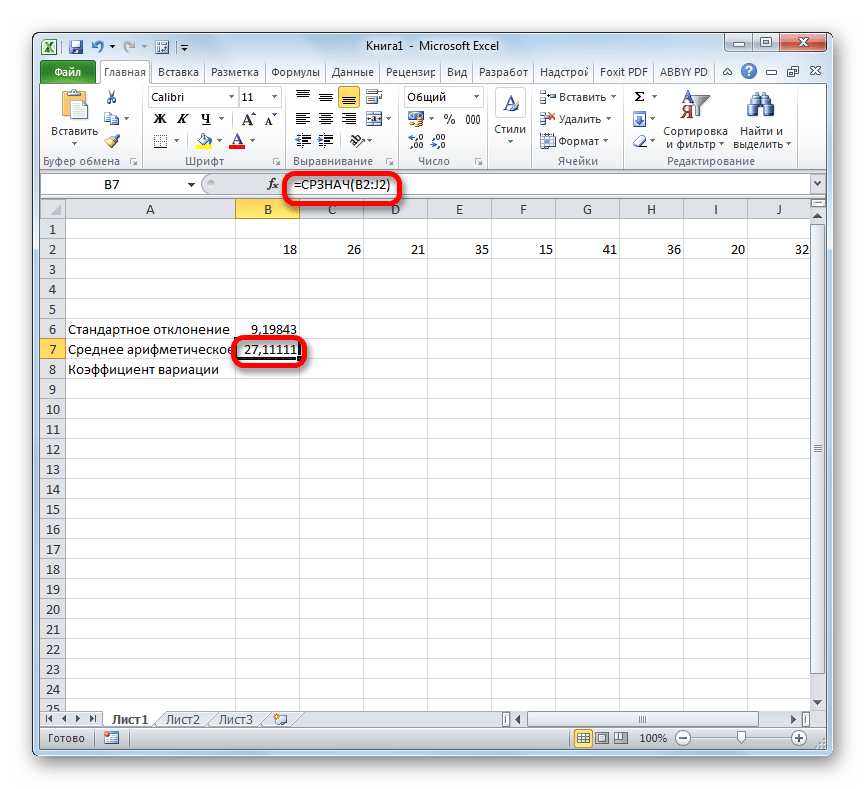
Шаг 3: нахождение коэффициента вариации

Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.

Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.

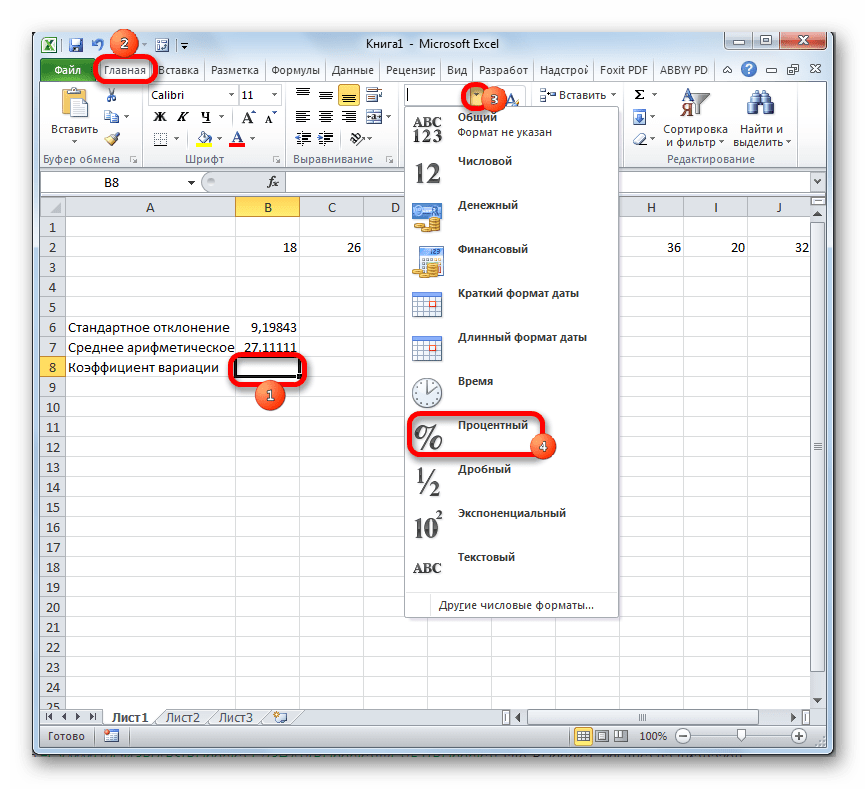
Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.

Как видим, результат расчета выведен на экран.

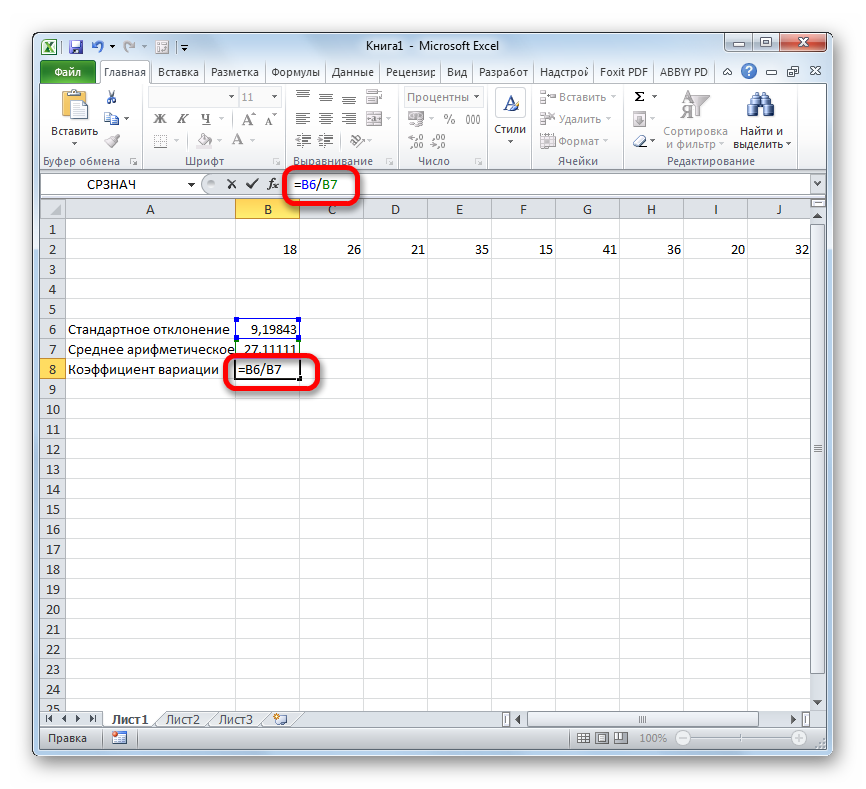
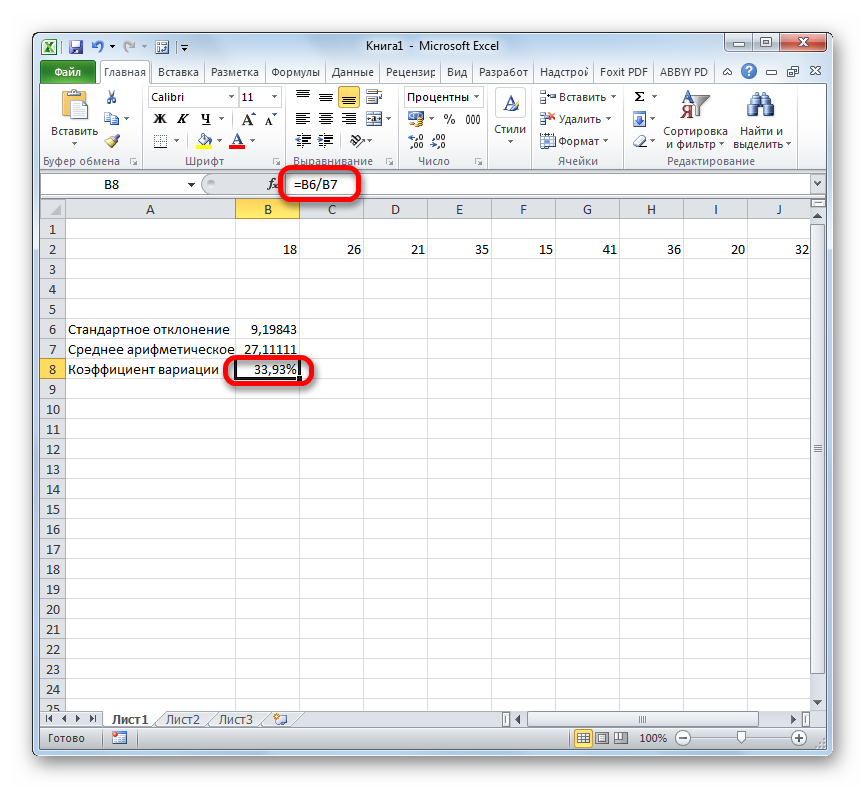
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.

Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:

Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.

После этого, чтобы рассчитать значение и показать результат на экране монитора, щелкаем по кнопке Enter.

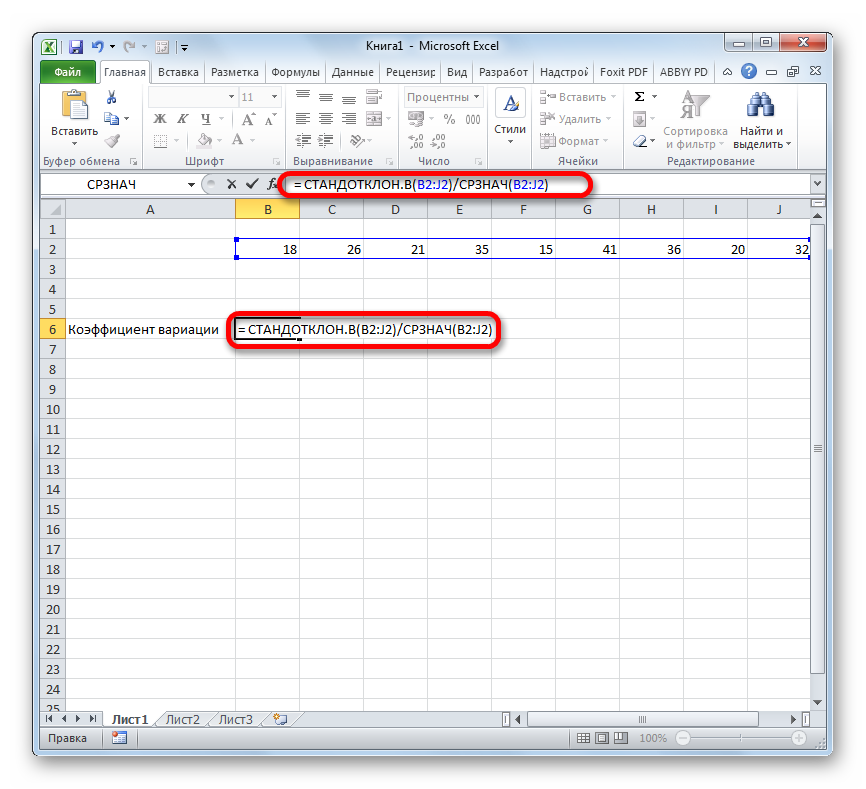
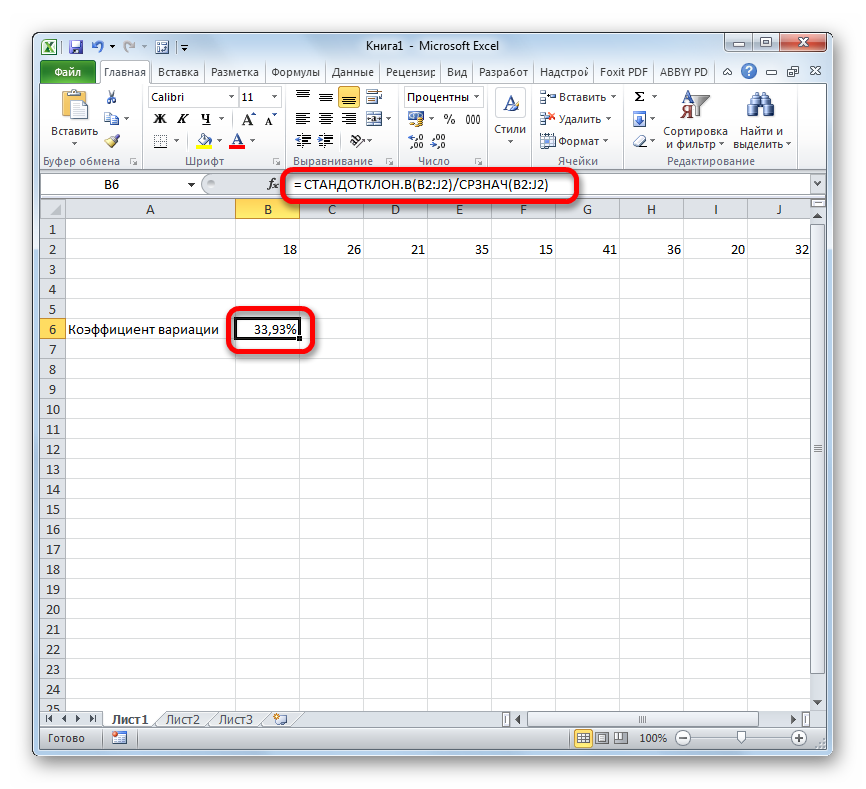
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.

Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Разделы: Математика

• Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
• применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.

1. Сегодня на уроке мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
2. Для начала вспомним:

– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)

– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)

– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).

– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).

– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).

1. Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.

Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):

23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28

рассчитать числовые характеристики: моду медиану размах ряда построить полигон частот построить столбчатую и круговую диаграммы раскрыть смысловую сторону каждой характеристики

1. Занести данные в EXCEL, каждое число в отдельную ячейку.

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

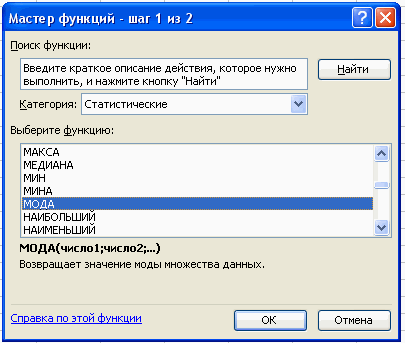
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем — статистические, в списке: МОДА

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

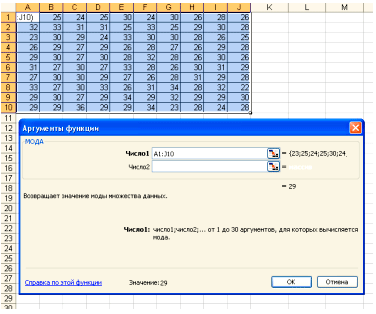
Нажимаем клавишу ОК. Получили М_о = 29 (чел) – Фирм у которых в штате 29 человек больше всего.

Используя тот же путь вычисляем медиану.

Вставка – Функция – Статистические – Медиана.

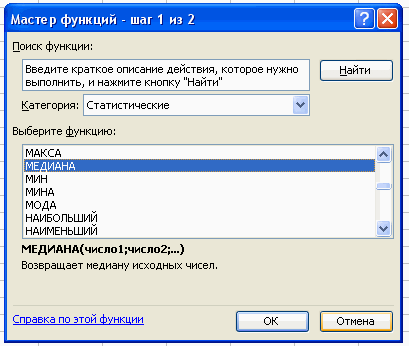
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

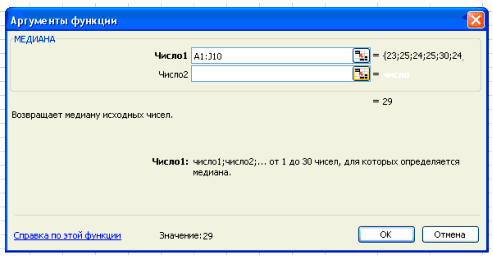
Нажимаем клавишу ОК. Получили М_е = 29 (чел) – среднее значение сотрудников в фирме.

Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.

Вставка – Функция – Статистические – МАКС.

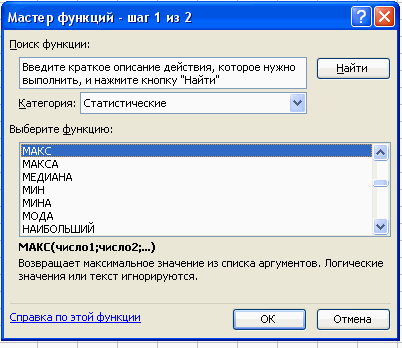
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

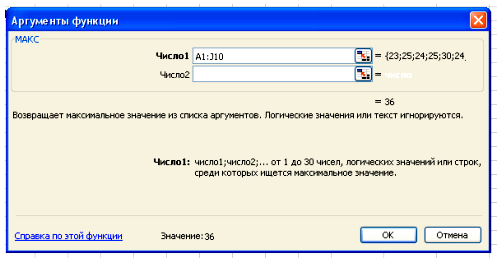
Нажимаем клавишу ОК. Получили наибольшее значение = 36.

Вставка – Функция – Статистические – МИН.

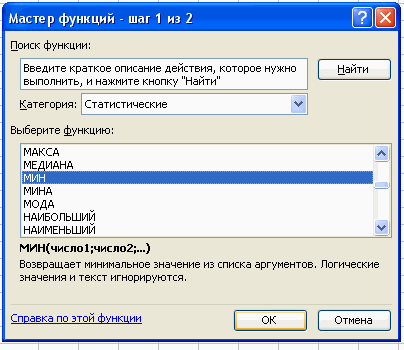
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

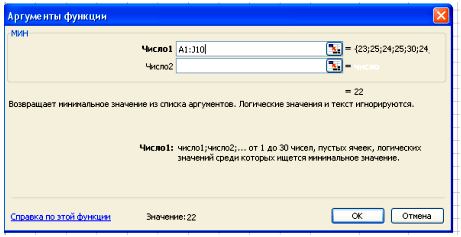
Нажимаем клавишу ОК. Получили наименьшее значение = 22.

36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.

Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения x_i случайной величины меняются от 22 до 36 включительно шагом 1.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni

Чтобы сосчитать частоту каждого значения воспользуемся

Вставка – Функция – Статистические – СЧЕТЕСЛИ.

В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22

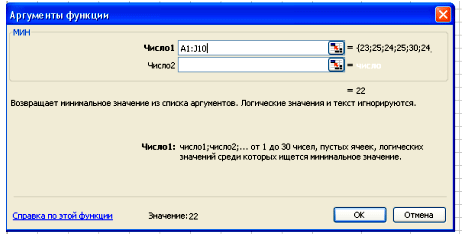
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni	1	3	4	5	11	9	13	18	16	6	4	6	3	0	1

Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические — СУММА). Должно получиться 100 (количество всех фирм).

Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)

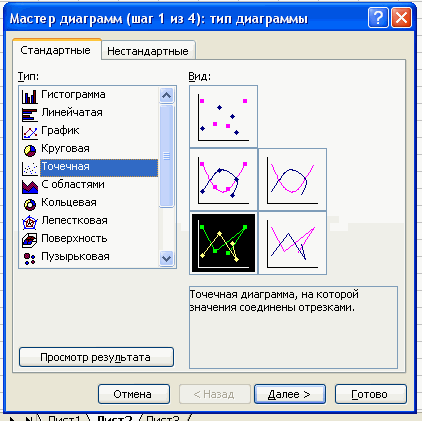
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.

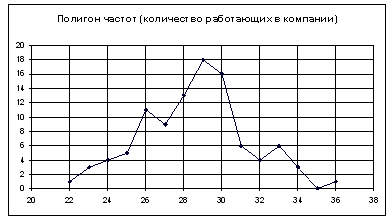
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).

Диаграмма – Стандартные – Круговая.

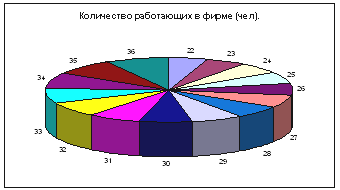
Диаграмма – Стандартные – Гистограмма.

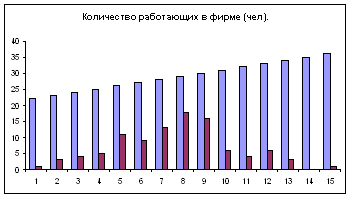
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.

Основная идея

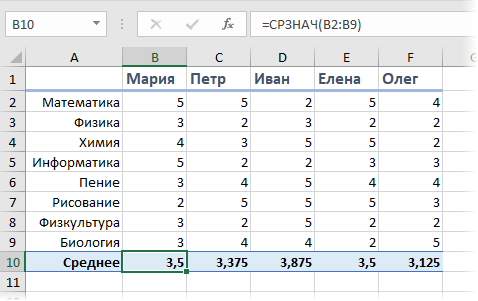
Предположим, что мы с вами сидим в приемно-экзаменационной комиссии и оцениваем абитуриентов, которые хотят поступить в наш ВУЗ. Оценки по различным предметам у наших кандидатов следующие:

Свободное место, допустим, только одно, и наша задача — выбрать достойного.

Первое, что обычно приходит в голову — это рассчитать классический средний балл с помощью стандартной функции Excel СРЗНАЧ (AVERAGE).

На первый взгляд кажется, что лучше всех подходит Иван, т.к. у него средний бал максимальный. Но тут мы вовремя вспоминаем, что факультет-то наш называется “Программирование”, а у Ивана хорошие оценки только по рисованию, пению и прочей физкультуре, а по математике и информатике как раз не очень. Возникает вопрос: а как присвоить нашим предметам различную важность (ценность), чтобы учитывать ее при расчете среднего? И вот тут на помощь приходит средневзвешенное значение.

Средневзвешенное — это среднее с учетом различной ценности (веса, важности) каждого из элементов.

В бизнесе средневзвешенное часто используется в таких задачах, как:

• оценка портфеля акций, когда у каждой из них своя ценность/рисковость
• оценка прогресса по проекту, когда у задач не равный вес и важность
• оценка персонала по набору навыков (компетенций) с разной значимостью для требуемой должности
• и т.д.

Расчет средневзвешенного формулами

Добавим к нашей таблице еще один столбец, где укажем некие безразмерные баллы важности каждого предмета по шкале, например, от 0 до 9 при поступлении на наш факультет программирования. Затем расчитаем средневзвешенный бал для каждого абитурента, т.е. среднее с учетом веса каждого предмета. Нужная нам формула будет выглядеть так:

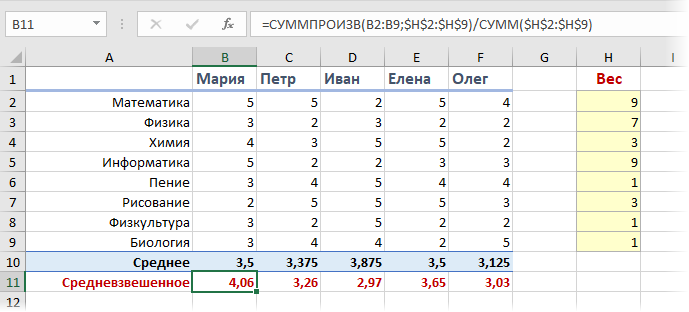
Функция СУММПРОИЗВ (SUMPRODUCT) попарно перемножает друг на друга ячейки в двух указанных диапазонах — оценки абитурента и вес каждого предмета — а затем суммирует все полученные произведения. Потом полученная сумма делится на сумму всех баллов важности, чтобы усреднить результат. Вот и вся премудрость.

Так что берем Машу, а Иван пусть поступает в институт физкультуры 😉

Расчет средневзвешенного в сводной таблице

Поднимем ставки и усложним задачу. Допустим, что теперь нам нужно подсчитать средневзвешенное, но не в обычной, а в сводной таблице. Предположим, что у нас есть вот такая таблица с данными по продажам:

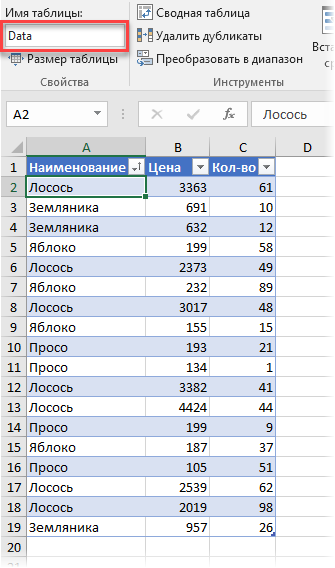
Обратите внимание, что я преобразовал ее в “умную” таблицу с помощью команды Главная — Форматировать как таблицу (Home — Format as Table) и дал ей на вкладке Конструктор (Design) имя Data.

Заметьте, что цена на один и тот же товар может различаться. Наша задача: рассчитать средневзвешенные цены для каждого товара. Следуя той же логике, что и в предыдущем пункте, например, для земляники, которая продавалась 3 раза, это должно быть:

=(691*10 + 632*12 + 957*26)/(10+12+26) = 820,33

То есть мы суммируем стоимости всех сделок (цена каждой сделки умножается на количество по сделке) и потом делим получившееся число на общее количество этого товара.

Правда, с реализацией этой нехитрой логики именно в сводной таблице нас ждет небольшой облом. Если вы работали со сводными раньше, то, наверное, помните, что можно легко переключить поле значений сводной в нужную нам функцию, щелкнув по нему правой кнопкой мыши и выбрав команду Итоги по (Summarize Values By) :

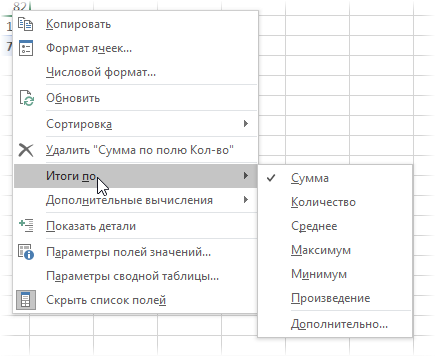
В этом списке есть среднее, но нет средневзвешенного 🙁

Можно частично решить проблему, если добавить в исходную таблицу вспомогательный столбец, где будет считаться стоимость каждой сделки:

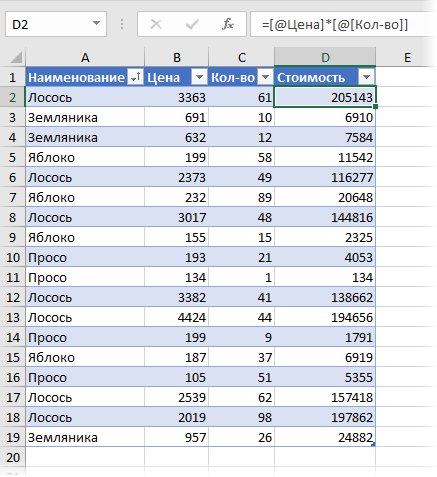
Теперь можно рядом закинуть в область значений стоимость и количество — и мы получим почти то, что требуется:

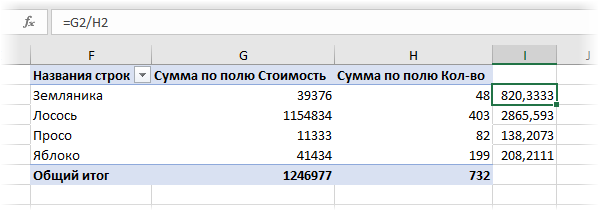
Останется поделить одно на другое, но сделать это, вроде бы, простое математическое действие внутри сводной не так просто. Придется либо добавлять в сводную вычисляемое поле (вкладка Анализ — Поля, элементы, наборы — Вычисляемое поле), либо считать обычной формулой в соседних ячейках или привлекать функцию ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ (GET.PIVOT.DATA) , о которой я уже писал. А если завтра изменятся размеры сводной (ассортимент товаров), то все эти формулы придется вручную корректировать.

В общем, как-то все неудобно, трудоемко и нагоняет тоску. Да еще и дополнительный столбец в исходных данных нужно руками делать. Но красивое решение есть.

Расчет средневзвешенного в сводной таблице с помощью Power Pivot и языка DAX

Если у вас Excel 2013-2016, то в него встроен супермощный инструмент для анализа данных — надстройка Power Pivot, по сравнению с которой сводные таблицы с их возможностями — как счеты против калькулятора. Если у вас Excel 2010, то эту надстройку можно совершенно бесплатно скачать с сайта Microsoft и тоже себе установить. С помощью Power Pivot расчет средневзвешенного (и других невозможных в обычных сводных штук) очень сильно упрощается.

1. Для начала, загрузим нашу таблицу в Power Pivot. Это можно сделать на вкладке Power Pivot кнопкой Добавить в модель данных (Add to Data Model) . Откроется окно Power Pivot и в нем появится наша таблица.

2. Затем щелкните мышью в строку формул и введите туда формулу для расчета средневзвешенного:

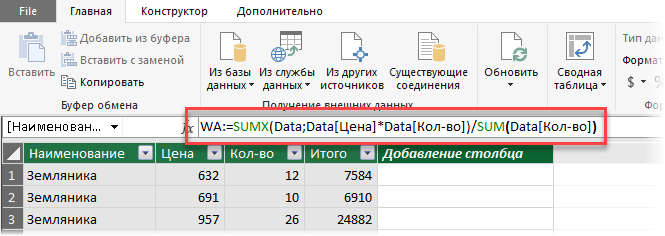
Несколько нюансов по формуле:

• В Power Pivot есть свой встроенный язык с набором функций, инструментов и определенным синтаксисом, который называется DAX. Так что можно сказать, что эта формула — на языке DAX.
• Здесь WA — это название вычисляемого поля (в Power Pivot они еще называются меры), которое вы придумываете сами (я называл WA, имея ввиду Weighted Average — “средневзвешенное” по-английски).
• Обратите внимание, что после WA идет не равно, как в обычном Excel, а двоеточие и равно.
• При вводе формулы будут выпадать подсказки — используйте их.
• После завершения ввода формулы нужно нажать Enter , как и в обычном Excel.

3. Теперь строим сводную. Для этого в окне Power Pivot выберите на вкладке Главная — Сводная таблица (Home — Pivot Table). Вы автоматически вернетесь в окно Excel и увидите привычный интерфейс построения сводной таблицы и список полей на панели справа. Осталось закинуть поле Наименование в область строк, а нашу созданную формулой меру WA в область значений — и задача решена:

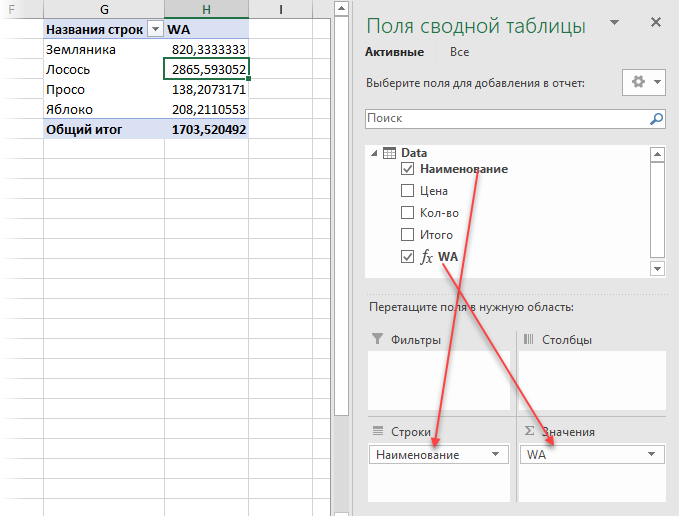
Вот так — красиво и изящно.

Общая мораль: если вы много и часто работаете со сводными таблицами и вам их возможности “тесноваты” — копайте в сторону Power Pivot и DAX — и будет вам счастье!

Видео с уроком:

Генерируем с помощью надстройки «анализа данных» -«генерация случайных чисел» нормально распределённую случайную величину мат.ожиданием равным 0 и стандартным отклонением 1.

В ячейках А1-А1000 получаем значения случайной величины, подчинённой нормальному закону распределения с параметрами: мат.ожиданием = 0 и стандартным отклонением =1.

Построим на основании полученных данных дискретный вариационный ряд.

С помощью функции МИН находим минимальное значение из полученных данных: D1 =МИН(A1:A1000).

С помощью функции МАКС находим максимальное значение из полученных данных: D2 =МАКС(A1:A1000).

Находим размах вариации (R= Хмакс – Хмин): D3 =D2-D1.

Число интервалов определяем по формуле Стерджесса:

D4 =1+3,322*LOG(1000).

Определяем величину интервала: l=R/n

Определяем границы интервалов.

Первый нижний интервал равен минимальному значению ряда (G2 =D1). Первый верхний интервал равен значение нижнего плюс величина интервала (H2= =D1+D5). И так далее.

Последний верхний интервал равен максимальному значению ряда.

С помощью функции ЧАСТОТА находим число попаданий случайной величины в полученные интервалы вариационного ряда.

Что бы заполнились все клетки частот необходимо одновременно нажать:

Получим частоты ряда распределения.

Видим, что сумма частот не равна 1000. Не хватает одного наблюдения. Это произошло из за того, что верхний интервал ряда не считается, и последний верхний интервал не был посчитан. Что бы его учесть прибавляем малое число к верхней границе последнего интервала.

H12 =H11+D$5+0,000001

Теперь сумма частот равна 1000.

Находим среднее значение массива данных с помощью функции СРЗНАЧ:

G16 =СРЗНАЧ(A1:A1000)

Стандартное отклонение массива данных находим с помощью функции СТАНДОТКЛОН.В:

G17 =СТАНДОТКЛОН.В(A1:A1000)

Найдём среднее и стандартное отклонение построенного интервального вариационного ряда. Находим середину интервала:

j2 =(G2+H2)/2

аналогично для других интервалов.

Находим произведение середины интервала на частоту:

K2 =J2*I2

аналогично для других интервалов.

Находим произведение квадрата середины интервала на частоту:

L2 = =J2^2*I2

аналогично для других интервалов.

Далее суммируем полученные столбцы и получаем таблицу.

Среднее значение определяем по формуле:

H16= =K13/I13

Стандартное отклонение определяем по формуле:

Полученные значения среднего и стандартного отклонения по массиву данных и по интервальному ряду имеют небольшое расхождение. Так и должно быть, так как методики определения различны.

Далее нами была построена гистограмма интервального ряда распределения.

P.S.

На следующем занятии мы проверим, подчиняется ли полученный интервальный ряд нормальному распределению, будем использовать функции НОРМРАСП и ХИ2.ОБР https://dzen.ru/a/Y4cyLlERd0hh00_s

Материал подготовлен сайтом: https://pro-smysl.ru/

Онлайн помощь в решении задач, консультации, создание обучающих роликов.

Подписывайтесь на наши каналы:

https://vk.com/sm_smysl

https://www.youtube.com/@SMYS_L

Размах варьирования. Наибольшее и наименьшее значения

Лабораторная работа № 1

Статистический анализ данных

Цель работы: научиться обрабатывать статистические данные с помощью встроенных функций.

Порядок выполнения работы:

1. Основные статистические характеристики:

— Выборочная дисперсия (вариабельность)

2. Самостоятельная работа

— Диаграмма рассеяния (задание 1)

— Основные статистические показатели (задание 2)

— Отклонение случайного распределения от нормального (задание 3)

1. Основные статистические характеристики.

Электронные таблицы Excel имеют огромный набор средств для анализа статистических данных. Наиболее часто используемые статистические функции встроены в основное ядро программы, то есть эти функции доступны с момента запуска программы.

Среднее значение.

Функция СРЗНАЧ (или AVERAGE) вычисляет выборочное (или генеральное) среднее, то есть среднее арифметическое значение признака выборочной (или генеральной) совокупности. Аргументом функции СРЗНАЧ является набор чисел, как правило, задаваемый в виде интервала ячеек, например, =СРЗНАЧ (А3:А201).

Дисперсия и среднее квадратическое отклонение.

Для оценки разброса данных используются такие статистические характеристики, как дисперсия D и среднее квадратическое (или стандартное) отклонение . Стандартное отклонение есть квадратный корень из дисперсии: . Большое стандартное отклонение указывает на то, что значения измерения сильно разбросаны относительно среднего, а малое – на то, что значения сосредоточены около среднего.

В Excel имеются функции, отдельно вычисляющие выборочную дисперсию D_ви стандартное отклонение _в и генеральные дисперсию D_г и стандартное отклонение _г. Поэтому, прежде чем вычислять дисперсию и стандартное отклонение, следует четко определиться, являются ли ваши данные генеральной совокупностью или выборочной. В зависимости от этого нужно использовать для расчета D_г и _г , D_в и _в.

Для вычисления выборочной дисперсии D_в и выборочного стандартного отклонения _в имеются функции ДИСП (или VAR) и СТАНДОТКЛОН (или STDEV). Аргументом этих функций является набор чисел, как правило, заданный диапазоном ячеек, например, =ДИСП (В1:В48).

Для вычисления генеральной дисперсии D_г и генерального стандартного отклонения _г имеются функции ДИСПР (или VARP) и СТАНДОТКЛОНП (или STDEVP), соответственно.

Аргументы этих функций такие же как и для выборочной дисперсии.

Объем совокупности.

Объем совокупности выборочной или генеральной – это число элементов совокупности. Функция СЧЕТ (или COUNT) определяет количество ячеек в заданном диапазоне, которые содержат числовые данные. Пустые ячейки или ячейки, содержащие текст, функция СЧЕТ пропускает. Аргументом функции СЧЕТ является интервал ячеек, например: =СЧЕТ (С2:С16).

Для определения количества непустых ячеек, независимо от их содержимого, используется функция СЧЕТ3. Ее аргументом является интервал ячеек.

Мода и медиана.

Мода – это значение признака, которое чаще других встречается в совокупности данных. Она вычисляется функцией МОДА (или MODE). Ее аргументом является интервал ячеек с данными.

Медиана – это значение признака, которое разделяет совокупность на две равные по числу элементов части. Она вычисляется функцией МЕДИАНА (или MEDIAN). Ее аргументом является интервал ячеек.

Размах варьирования. Наибольшее и наименьшее значения.

Размах варьирования R – это разность между наибольшим x_max и наименьшим x_min значениями признака совокупности (генеральной или выборочной): R=x_max–x_min. Для нахождения наибольшего значения x_max имеется функция МАКС (или MAX), а для наименьшего x_min – функция МИН (или MIN). Их аргументом является интервал ячеек. Для того, чтобы вычислить размах варьирования данных в интервале ячеек, например, от А1 до А100, следует ввести формулу: =МАКС (А1:А100)-МИН (А1:А100).

Задание 1

Имеются данные о размерах располагаемого дохода DPI и расходов на личное потребление С для n семей в условных единицах, так что DPI_i и С_i, соответственно, представляют располагаемый доход и расходы на личное потребление i-й семьи.

1. Построить диаграмму рассеяния, принимая за ось абсцисс — DPI_i,а за ось ординатС_i

Доходы_расходы
I	DPI	C	I	DPI	C

2. Выполнить настройку формата оси Х и оси Y в соответствии с образцом диаграммы.

Задание 2

Имеются данные об уровне безработицы (в %) среди «белого» (коренное) и «цветного» (эмигранты) населения страны с марта 2000г. по июль 2001г. (месячные данные), так что BEL_i и ZVET_i, соответственно, представляют уровни безработицы в i-м месяце.

1. Построить графики изменения уровней безработицы в обеих группах в течение указанного периода времени.

2. Вычислить средние значения уровней безработицы для BEL_i и ZVET_i населения страны.

Уровень безработицы
Исходные данные
I	BEL(%)	ZVET(%)
3,2	6,9
3,1	6,7
3,2	6,5
3,3	7,1
3,3	6,8
3,2	6,4
3,2	6,6
3,1	7,3
3,0	6,5
3,0	6,5
3,0	6,0
2,9	5,7
3,1	6,0
3,1	6,9
3,1	6,5
3,0	7,0
3,2	6,4

3. Вычислить выборочные дисперсии, характеризующие степень разброса значений BEL_i и ZVET_i вокруг своего среднего значения.

4. Вычислить стандартные отклоненияBEL_i и ZVET_i относительно среднего значения.

5. Вычислить наибольшее и наименьшее значения для BEL_i и ZVET_i.

6. Вычислить размах варьирования дляBEL_i и ZVET_i.

7. Вычислить Моду и Медиану дляBEL_i и ZVET_i.

Разделы: Математика

• Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
• применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.

1. Сегодня на уроке мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
2. Для начала вспомним:

– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)

– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)

– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).

– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).

– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).

1. Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.

Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):

1. Занести данные в EXCEL, каждое число в отдельную ячейку.

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем — статистические, в списке: МОДА

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_о = 29 (чел) – Фирм у которых в штате 29 человек больше всего.

Используя тот же путь вычисляем медиану.

Вставка – Функция – Статистические – Медиана.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_е = 29 (чел) – среднее значение сотрудников в фирме.

Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.

Вставка – Функция – Статистические – МАКС.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наибольшее значение = 36.

Вставка – Функция – Статистические – МИН.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наименьшее значение = 22.

36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.

Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения x_iслучайной величины меняются от 22 до 36 включительно шагом 1.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni

Чтобы сосчитать частоту каждого значения воспользуемся

Вставка – Функция – Статистические – СЧЕТЕСЛИ.

В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22

Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni	1	3	4	5	11	9	13	18	16	6	4	6	3	0	1

Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические — СУММА). Должно получиться 100 (количество всех фирм).

Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)

Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.

Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).

Диаграмма – Стандартные – Круговая.

Диаграмма – Стандартные – Гистограмма.

4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.

Математическая
статистика в MS
Excel.
Часть 1

Простейшие
статистические характеристики

Создайте
книгу Excel.
Сохраните под именем МАТСТАТ_1. Выполните
все задания.

Среднее арифметическое, размах и мода

При изучении
учебной нагрузки учащихся выделили
группу из 12 семиклассников. Их попросили
отметить в определенный день время (в
минутах), затраченное на выполнение
домашнего задания по алгебре. Получили
такие данные:

23, 18, 25, 20, 25, 25, 32,
37, 34, 26, 34, 25.

Имея этот ряд
данных, можно определить, сколько минут
в среднем затратили учащиеся на выполнение
домашнего задания по алгебре.

Для этого указанные
числа надо сложить и сумму разделить
на 12:

=

Число 27, полученное
в результате, называют средним
арифметическим
рассматриваемого ряда чисел.

Средним
арифметическим
ряда чисел называется частное от деления
суммы этих чисел на число слагаемых.

Мы нашли, что на
выполнение домашнего задания по алгебре
учащиеся затратили в среднем по 27 минут.
Проводя аналогичные наблюдения за
группой учащихся, можно проследить,
какова была средняя затрата времени на
выполнение домашнего задания по алгебре
в течение недели, сравнить среднюю
затрату времени на выполнение в какой-либо
день домашних заданий по алгебре и
русскому языку и т.п.

Обычно среднее
арифметическое находят тогда, когда
хотят определить среднее значение для
некоторого ряда данных. Заметим, что
среднее арифметическое находят только
для однородных величин. Не имеет,
например, смысла использовать в качестве
обобщающего показателя среднюю
урожайность зерновых и бахчевых культур
в фермерском хозяйстве. Причем и для
однородных величин вычисление среднего
арифметического бывает иногда лишено
смысла, например, нахождение средней
температуры больных в госпитале, среднего
размера обуви, которую носят учащиеся
школы.

В рассмотренном
примере мы нашли, что в среднем учащиеся
затратили на выполнение домашнего
задания по алгебре по 27 минут. Однако
анализ приведенного ряда данных
показывает, что время, затраченное
некоторыми учащимися, существенно
отличается от 27 минут, т.е. от среднего
арифметического. Наибольший расход
равен 37, а наименьший – 18 минутам.
Разность между наибольшим и наименьшим
расходом времени составляет 19 минут. В
этом случае говорят, что размах
ряда равен
19.

Размахом ряда
чисел
называется разность между наибольшим
и наименьшим из этих чисел.

Размах ряда находят
тогда, когда хотят определить, как велик
разброс данных в ряду. Пусть, например,
в течение суток отмечали каждый час
температуру воздуха в городе. Для
полученного ряда данных полезно не
только вычислить среднее арифметическое,
показывающее, какова среднесуточная
температура, но и найти размах ряда,
характеризующий колебания температуры
в течение этих суток.

При анализе сведений
о времени, затраченном семиклассниками
на выполнение домашнего задания по
алгебре, нас могут интересовать не
только среднее арифметическое и размах
полученного ряда данных, но и другие
показатели. Интересно, например, знать,
какой расход времени является типичным
для выделенной группы учащихся, то есть
какое число встречается в ряду данных
чаще всего. Нетрудно заметить, что таким
числом является число 25. говорят, что
число 25 – мода
рассматриваемого ряда.

Модой ряда
чисел
называется число, чаще других встречающееся
в данном ряду.

Ряд чисел может
иметь более одной моды или не иметь моды
совсем.

Например, в ряду
чисел

47, 46, 50, 52, 47, 52, 49,
45, 43, 53

две моды – это
числа 47 и 52,

а в ряду чисел 69,
68, 66, 80, 67, 65, 71, 74, 63, 73, 72 моды нет.

Моду ряда данных
обычно находят тогда, когда хотят выявить
некоторый типичный показатель. Например,
если изучаются данные о размерах мужских
сорочек, проданных в определенный день
в универмаге, то удобно воспользоваться
таким показателем, как мода, который
характеризует размер, пользующийся
наибольшим спросом. Находить в этом
случае среднее арифметическое не имеет
смысла. Мода является наиболее приемлемым
показателем при выявлении, например,
расфасовки некоторого товара, которой
отдают предпочтение покупатели; цены
на товар данного вида, наиболее
распространенный на рынке, и т.п.

Рассмотрим еще
пример. Пусть, проведя учет деталей,
изготовленных за смену рабочими одной
бригады, получили такой ряд данных:

36, 36, 36, 36, 37, 37, 36,
37, 38, 36, 36, 36, 39, 39, 37, 39, 38, 38, 36, 39, 36.

Найдем для него
среднее арифметическое, размах и моду.
Для этого удобно предварительно составить
из полученных данных упорядоченный
ряд чисел,
т.е. такой ряд, в котором каждое последующее
число не меньше (или не больше) предыдущего.
Получим: 35, 35, 36, 36, 36, 36, 36, 36, 36, 36, 37, 37, 37,
37, 38, 38, 38, 39, 39, 39, 39.

Вычислим среднее
арифметическое:

Размах ряда равен
39-35=4. Мода данного ряда равна 36, так как
число 36 чаще всего встречается в этом
ряду.

Итак, средняя
выработка рабочих за смену составляет
примерно 37 деталей; различие в выработке
рабочих не превосходит 4 деталей; типичной
является выработка, равная 36 деталям.

Заметим, что среднее
арифметическое ряда чисел может не
совпадать ни с одним из этих чисел, а
мода, если она существует, обязательно
совпадает с двумя или более числами
ряда. Кроме того, в отличие от среднего
арифметического, понятие «мода» относится
не только к числовым данным. Например,
проведя опрос учащихся, можно получить
ряд данных, показывающий, каким видом
спорта они предпочитают заниматься,
какую из развлекательных телевизионных
программ они считают наиболее интересной.
Модой будут служить те ответы, которые
встретятся чаще всего. Этим и объясняется
само название «мода».

1. Найдите среднее
   арифметическое и размах ряда чисел:

А	24	22	27	20	16	31
Б	11	9	7	6	2	0	1
В	30	5	23	5	28	30
Г	144	146	114	138

– Запустите табличный
процессор Excel.

– Заполните таблицу в соответствии с
образцом:

	А	В	С	D	Е
1		Исходные данные
2	1	24	11	30	144
3	2	22	9	5	146
4	3	27	7	23	114
5	4	20	6	5	138
6	5	16	2	28
7	6	31	0	30
8	7		1
9
10
11
12
13	Результаты
14	Мин	Формула 1	Заполнить вправо
15	Макс	Формула 2	Заполнить вправо
16	Срзнач	Формула 3	Заполнить вправо
17	Размах	Формула 4	Заполнить вправо

– Введение формул в расчетные ячейки:

Ячейка	Формула
В14	=МИН(В2:В7)	(1)
В15	=МАКС(В2:В7)	(2)
В16	=СРЗНАЧ(В2:В7)	(3)
В17	=МИН(В15-В14)	(4)

1. Для создания
   формул выполните следующие действия:

• щелкните по кнопке
  «мастер функций f_x»;

• далее выберите
  Статистические и далее МИН, МАКС или
  СРЗНАЧ, нажмите ОК;

• укажите диапазон
  клеток;

• Нажмите ОК.

1. Для нахождения
   размаха чисел необходимо в свободной
   ячейке создать формулу, находящую
   разность. Для этого:

• наберите на
  клавиатуре знак «=»;

• введите адрес
  ячейки, содержащей значение МАКС (В15);

• наберите на
  клавиатуре знак «-»;

• введите адрес
  ячейки, содержащей значение МИН (В14);

• нажмите «Enter».

1. Для заполнения
   вправо выделим диапазон В14:В17. Подведем
   указатель мыши к правому нижнему углу
   выделенного диапазона и протянем
   вправо.

1. Найдите среднее
   арифметическое, размах и моду ряда
   чисел:

А) 32, 26, 18, 26, 15, 21,
26;

Б) 21, 15.5, 25.3, 18.5,
17.9;

В) 67.1, 68.2, 67.1, 70.4,
68.2;

Г) 0.6, 0.8, 0.5, 0.9, 1.1.

– Запустите табличный
процессор Excel.

– Заполните таблицу в соответствии с
образцом:

	А	В	С	D	Е
1		Исходные данные
2	1	32	21	67.1	0.6
3	2	26	18.5	68.2	0.8
4	3	18	25.3	67.1	0.5
5	4	26	18.5	70.4	0.9
6	5	15	17.9	68.2	1.1
7	6	21
8	7	26
9
10
11
12
13	Результаты
14	Мин	Формула 1	Заполнить вправо
15	Макс	Формула 2	Заполнить вправо
16	Срзнач	Формула 3	Заполнить вправо
17	Размах	Формула 4	Заполнить вправо
18	Мода	Формула 5	Заполнить вправо

– Введение формул в расчетные ячейки:

Ячейка	Формула
В14	=МИН(В2:В7)	(1)
В15	=МАКС(В2:В7)	(2)
В16	=СРЗНАЧ(В2:В7)	(3)
В17	=МИН(В15-В14)	(4)
В18	=МОДА(В2:В7)	(5)

1. Для создания
   формул выполните следующие действия:

• щелкните по кнопке
  «мастер функций f_x»;

• далее выберите
  Статистические и далее МИН, МАКС, МОДА
  или СРЗНАЧ, нажмите ОК;

• укажите диапазон
  клеток;

• Нажмите ОК.

1. Для нахождения
   размаха чисел необходимо в свободной
   ячейке создать формулу, находящую
   разность. Для этого:

• наберите на
  клавиатуре знак «=»;

• введите адрес
  ячейки, содержащей значение МАКС (В15);

• наберите на
  клавиатуре знак «-»;

• введите адрес
  ячейки, содержащей значение МИН (В14);

• нажмите «Enter».

1. Для заполнения
   вправо выделим диапазон В14:В18. Подведем
   указатель мыши к правому нижнему углу
   выделенного диапазона и протянем
   вправо.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #