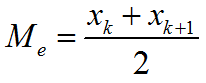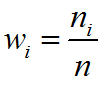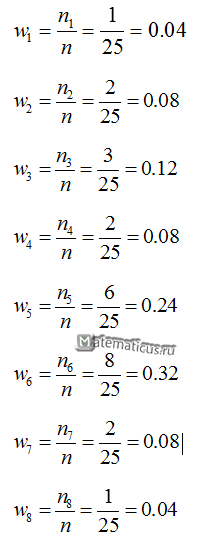Пусть из генеральной совокупности извлечена выборка объема П, в которой значение X1 некоторого исследуемого признака Х наблюдалось П1 раз, значение X2 — п2 раз, …, значение XK — Nk раз. Значения Xi называются Вариантами, а их последовательность, записанная в возрастающем порядке,— Вариационным рядом. Числа Ni называются Частотами, а их отношения к объему выборки
— Относительными частотами. При этом Ni = П. Модой Мo называется варианта, имеющая наибольшую частоту. Медианой те называется варианта, которая делит вариационный ряд на две части с одинаковым числом вариант в каждой. Если число вариант нечетно, т. е. K = 2L + 1, то Me = Xl+1; если же число вариант четно (k = 2L), То те = (Xl + Xl+1)/2. Размахом варьирования называется разность между максимальной и минимальной вариантами или длина интервала, которому принадлежат все варианты выборки:
Перечень вариант и соответствующих им частот называется Статистическим распределением выборки. Здесь имеется аналогия с законом распределения случайной величины: в теории вероятностей — это соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — это соответствие между наблюдаемыми вариантами и их частотами (относительными частотами). Нетрудно видеть, что сумма относительных частот равна единице: Wi = 1.
Пример 2. Выборка задана в виде распределения частот:
Найти распределение относительных частот и основные характеристики вариационного ряда.
Решение. Найдем объем выборки: П = 2 + 4 + 5 + 6 + 3 = 20. Относительные частоты соответственно равны W1 = 2/20 = 0,1; W2 = 4/20 = 0,2; W3 = 5/20 = 0,25; W4 = 6/20 = 0,3; W5 = 3/20 = 0,15. Контроль: 0,1 + 0,2 + 0,25 + 0,3 + 0,15 = 1. Искомое распределение относительных частот имеет вид
Мода этого вариационного ряда равна 12. Число вариант в данном случае нечетно: K = 2 ∙ 2 + 1, поэтому медиана Me = X3 = 8. Размах варьирования, согласно формуле (18.48), R = 17 – 4 = 13.
| < Предыдущая | Следующая > |
|---|
Пусть в результате
выборки объема n, т.е. приnнезависимых испытаниях,
исследуемый количественный признакдискретная случайная величинаXпринялn1раз значение x1,n2раззначение x2,
…,nkраззначение xk.
Таким образом,n1+n2+ …+nk
=n. Значения x1,
x2,…, хk,
называемые иногда наблюдаемыми значениями
случайной величиныX,
можно считать расположенными в порядке
возрастания: x1
x2…хk.
Последовательность
значений x1, x2,…, хk, исследуемой случайной величиныX,
расположенных в неубывающем порядке
и принимаемых ею в результате выборки
объема n с частотами соответственно n1, n2, …, nk, где n1+ n2+ …+ nk = n, называетсявариационным
рядом, а каждое значение
xi(i= 1, 2, …,k)вариантой. То есть, вариационный ряд
можно определить как последовательность
наблюдаемых значений исследуемой
случайной величины, расположенных в
неубывающем порядке. Частоты n1,
n2, …, nk, соотнесенные к
объему выборки, т.е.,
называются относительными частотами.
Теоретическим
законом распределения случайной величины
Xназывается закон
распределения количественного признака
в генеральной совокупности. Теоретический
закон распределения записывается в
виде таблицы, в верхней строке которой
расположены все значения случайной
величины (т.е. все объекты генеральной
совокупности), а в нижнейсоответствующие им вероятности.
Статистическим
распределением выборки называется
перечень вариант и соответствующих им
частот или относительных частот.
Пример.
Записать
в виде вариационного ряда выборку 5, 3,
7, 10, 5, 5, 2, 10, 7, 2, 7, 7, 4, 2, 4. Определить размах
и статистическое распределение выборки.
Объем
выборки n=15.
Упорядочив элементы выборки по величине,
получим вариационный ряд 2, 2, 2, 3, 4, 4, 5,
5, 5, 7, 7, 7, 7, 10, 10. Разность между максимальным
и минимальным элементами выборки
называется размахом
выборки,
который в нашем случае равен 10 –2 =8.
Различными в заданной выборке являются
элементы х1=2,
х2=3,
х3=4,
х4=5,
х5=7,
х6=10;
их частоты соответственно равны n1=3,
n2=1,
n3=2,
n4=3,
n5=4,
n6=2.
Следовательно, статистическое
распределение исходной выборки можно
записать в виде следующей таблицы:
-
xi
2
3
4
5
7
10
ni
3
1
2
3
4
2
Задания для
самостоятельного решения:
Для каждой из
приведенных ниже выборок определить
размах, построить вариационный ряд и
определить статистическое распределение
выборки.
-
11, 15, 12, 0, 16, 19, 6, 11,
12, 13, 16, 8, 9, 14, 5, 11, 3. -
17, 18, 16, 16, 17, 18, 19,
17, 15, 17, 19, 18, 16, 16, 18, 18.
Эмпирический закон
распределения отличается от теоретического
закона, прежде всего тем, что вместо
вероятностей значений величины в таблице
выписываются относительные частоты.
Эмпирической
функцией распределения, или функцией
распределения выборкиF*(x),
называется функциягдеnобщее число наблюдений, аn(x)число наблюдений,
для которых оказалосьX<x.
Эмпирическая
функция распределения F*(x)
отличается от теоретической интегральной
функции распределенияF(x)
тем, что вместо вероятности события {X<x} берется относительная
частота этого события.
Свойства эмпирической
функции распределения:
-
F*(x)[ 0, 1];
-
F*(x)неубывающая
функция; -
если x1наименьшая, а хkнаибольшая из
вариант, тоF*(x)
= 0 приx< x1иF*(x)=
1 приx> хk.
Пример.
Задан эмпирический
закон распределения.
-
xi
2
6
10
ni
12
18
30
Построим эмпирическую
функцию распределения.
Объем
выборки n=12+18+30=60.
Тогда эмпирическая функция распределения
имеет вид:
Задание для
самостоятельного решения:
Построить
эмпирическую функцию распределения
для выборки, представленной следующим
статистическим распределением.
|
хi |
15 |
16 |
17 |
18 |
19 |
|
ni |
1 |
4 |
5 |
4 |
2 |
Соседние файлы в папке Матан 2 семестр
- #
- #
Генеральная совокупность представляет собой всю совокупность исследуемых объектов (например население города, ) и обозначается N.
Выборка — это ограниченное по количество объектов n, извлечённых случайным образом из генеральной совокупности.
Вариантами называются значения выборки x1, x2,…,xi, а частоты — n1, n2,…,ni
Если варианты представлены в упорядоченном отсортированном виде, обычно от минимального значения к максимальному, то такие варианты называются вариационным рядом.
Представим вариационный ряд в виде таблицы:
| Xi | x1 | x2 | …… | xn |
| ni | n1 | n2 | …… | nn |
Размах выборки — это разность между минимальным и максимальным значениями выборки и вычисляется по формуле:
Мода М0 в статистике называется варианта, которая чаще всего встречается в данной выборки и имеет наибольшую частоту (повторяемость).
Медиана Me — это варианта, находящиеся в середине вариационного ряда, делящая его пополам.
Формула для вычисления медианы нечетного вариационного ряда n=2k+1:
Me=xk+1
Формула для определения медианы четного вариационного ряда n=2k:
Относительной wi частотой называется отношение частоты к объёму выборки и определяется по формуле
Примечание
Сумма относительных частот равна единице
∑wi=1
Таблица распределения относительных частот имеет вид:
В обувном магазине
Статистика покупки обуви в магазине за один день в соответствии с размерами равна:
42, 41, 43, 40, 39, 44, 38, 42, 41, 39, 43, 41, 42, 37, 42, 41, 39, 42, 42, 41, 40, 41, 42, 38, 42
Требуется найти моду, медиану, размах выборки, построить таблицу распределения частот и относительных частот.
Решение
Отсортируем выборку и запишем вариационный ряд:
37, 38, 38, 39, 39, 39, 40, 40, 41, 41, 41, 41, 41, 41, 42, 42, 42, 42, 42, 42, 42, 42, 43, 43, 44
Обозначим варианты и их частоты:
x1=37, х2=38, х3=39, х4=40, х5=41, х6=42, х7=43 и х8=44
n1=1, n2=2, n3=3, n4=2, n5=6, n6=8, n7=2 и n8=1
Объем выборки равен
n=1+2+3+2+6+8+2+1=25
Размах выборки равен:
R=х8-х1=44–37=7
Найдем моду, наибольшая частота в вариационном ряде равна n6=8, тогда мода равна
М0=42
Число вариант восемь, то есть четно, следовательно медиана равна:
$${M_e} = frac{{{x_4} + {x_5}}}{2} = frac{{40 + 41}}{2} = 40.5$$
Вычислим относительные частоты:
Составим таблицу частот
| Xi | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
| ni | 1 | 2 | 3 | 2 | 6 | 8 | 2 | 1 |
и таблицу относительных частот:
| Xi | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
| ni | 0.04 | 0.08 | 0.12 | 0.08 | 0.24 | 0.32 | 0.08 | 0.04 |
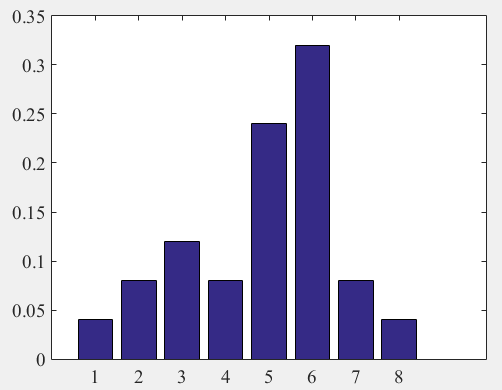
Гистограмма относительных частот
3323
Имеется выборка из генеральной совокупности
Исходные данные к задаче
№ вар. Выборка
4 14 13 10 11 4 9 12 9 11 1 5 11 14 5 12 8 10
7 12 11 12 13 6 5 2 1 8 1 8 10 7 10 12 12
11 13 16 3 13 8 6 11 5 14 12 8 10 10 12 11 12
а) Построить статистический ряд распределения, полигон частот, определить размах, моду, медиану.
б) Выполнить группировку, разбив на равные интервалы шириной h=2, построить гистограмму и график эмпирической функции распределения вероятностей.
в) найти точечные оценки математического ожидания, дисперсии, ско.
г) Определить доверительные интервалы для неизвестных математического ожидания и дисперсии , отвечающей заданной доверительной вероятности
() в предположении, что выборка взята из нормальной генеральной совокупности;
д) Построить графики теоретической функции распределения вероятностей и плотности распределения вероятности в предположении, что генеральная совокупность распределена по нормальному закону. Сравнить эти графики с гистограммой и эмпирической функцией распределения вероятностей. Сделать вывод.
е) Проверить гипотезу о нормальном законе распределения генеральной совокупности, используя критерий Пирсона при уровне значимости .
По результатам сформировать отчет, сделать выводы.
Отчет
а) Построить статистический ряд распределения, полигон частот, определить размах, моду, медиану.
Входные данные
14 13 10 11 4 9 12 9 11 1 5 11 14 5 12 8 10
7 12 11 12 13 6 5 2 1 8 1 8 10 7 10 12 12
11 13 16 3 13 8 6 11 5 14 12 8 10 10 12 11 12
Вариационный ряд (расположенные в порядке возрастания варианты):
1, 1, 1, 2, 3, 4, 5, 5, 5, 5, 6, 6, 7, 7, 8, 8, 8, 8, 8, 9, 9, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12, 12, 12, 12, 13, 13, 13, 13, 14, 14, 14, 16.
Статистический ряд
xi
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16
ni
3 1 1 1 4 2 2 5 2 6 7 9 4 3 1
Объем выборки n=ni=51
Полигоном частот называют ломаную, отрезки которой соединяют точки (x1;n1), (x2;n2)… (xi;ni), где xi– варианты выборки и ni—соответствующие им частоты.
Отложим на оси абсцисс варианты xi, а на оси ординат – соответствующие частоты. Соединив точки (xi;ni), отрезками прямых, получим искомый полигон частот.
Наименьшее значение в выборке xmin=1, наибольшее значение в выборке xmax=16.
Размах выборки: R=xmax-xmin=16-1=15.
Мода – наиболее часто встречаемая варианта – xMod=12
Медиана – середина вариационного ряда для n=51 xMed=10
б) Выполнить группировку, разбив на равные интервалы шириной h=2, построить гистограмму и график эмпирической функции распределения вероятностей.
Выполним группировку, разбив на равные интервалы
Шаг одного интервала h=2, тогда получим группированный статистический ряд
xi
1, 3
(3, 5]
(5, 7] (7, 9] (9, 11] (11, 13] (13, 15] (15, 17]
ni
5 5 4 7 13 13 3 1
Заполним таблицу 1, используя следующие формулы:
Середина интервала: ,
относительные частоты ,
Эмпирическая функция распределения .
Плотность относительной частоты .
Таблица 1
Номер интервала Границыинтервала Середина интервала Абсолютная частота Относительная частота Эмпирическая функция распределения Плотность относительной частоты
N
1 1, 3
2 5 0,10 0,10 0,05
2 (3, 5]
4 5 0,10 0,20 0,05
3 (5, 7] 6 4 0,08 0,27 0,04
4 (7, 9] 8 7 0,14 0,41 0,07
5 (9, 11] 10 13 0,25 0,67 0,13
6 (11, 13] 12 13 0,25 0,92 0,13
7 (13, 15] 14 3 0,06 0,98 0,03
8 (15, 17] 16 1 0,02 1,00 0,01
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению wi/h (плотность относительной частоты). Площадь частичного i-гo прямоугольника равна hwih=wi—сумме относительных частот вариант, попавших в i-й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице.
Построим на оси абсцисс данные частичные интервалы. Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от нее на расстояниях, равных соответствующим плотностям относительной частоты. Например, над интервалом 1, 3 проведем отрезок, параллельный оси абсцисс и находящийся от нее на расстоянии, равном 0,05; аналогично строят остальные отрезки.
Объем выборки n=51.
Наименьшая варианта равна 2, поэтому F*(x)=0 при x≤2.
Значение X<4, а именно x1=2 наблюдалось 5 раз, следовательно, F*(x)=5/51=0,1 при 2<x≤4.
Значения x<6, а именно x1=2 и x2=4, наблюдались 5+5=10 раз, следовательно, F*(x)=10/51=0,2 при 4<x≤6.
Значения x<8, а именно x1=2, x2=4 и x3=6, наблюдались 5+5+4=14 раз, следовательно, F*(x)=14/51=0,27 при 6<x≤8.
Значения x<10, а именно x1=2, x2=4, x3=6, x4=8 наблюдались 5+5+4+7=21 раз, следовательно, F*(x)=21/51=0,41 при 8<x≤10.
Значения x<12, а именно x1=2, x2=4, x3=6, x4=8, x5=10 наблюдались 5+5+4+7+13=34 раза, следовательно, F*(x)=34/51=0,67 при 10<x≤12.
Значения x<14, а именно x1=2, x2=4, x3=6, x4=8, x5=10 и x6=12 наблюдались 5+5+4+7+13+13=47 раз, следовательно, F*(x)=47/51=0,92 при 12<x≤14.
Значения x<16, а именно x1=2, x2=4, x3=6, x4=8, x5=10, x6=12, x7=14 наблюдались 5+5+4+7+13+13+3=50 раз, следовательно, F*(x)=50/51=0,98 при 14<x≤16.
Так как x=16 наибольшая варианта, то F*(x)=1 при x>16.
Искомая эмпирическая функция:
F*(x)=0 при x≤2; 0,10 при 2<x≤4;0,20 при 4<x≤6;0,27 при 6<x≤8;0,41 при 8<x≤10;0,67 при 10<x≤12;0,92 при 12<x≤14;0,98 при 14<x≤16;1 при x>16
График эмпирической функции распределения:
F*(x)
1
0,98
0,92
0,67
0,41
0,27
0,2
0,1
0 2 4 6 8 10 12 14 16
x
в) найти точечные оценки математического ожидания, дисперсии, ско.
Точечные оценки искомых числовых характеристик определяются по следующим формулам
, .
Для удобства расчетов последовательно заполним столбцы следующей таблицы.
Таблица 2
N
1 2 5 10 4 20
2 4 5 20 16 80
3 6 4 24 36 144
4 8 7 56 64 448
5 10 13 130 100 1300
6 12 13 156 144 1872
7 14 3 42 196 588
8 16 1 16 256 256
51 454
4708
На основании приведенных в таблице 2 данных можно найти точечные оценки: математического ожидания
.
Дисперсии
.
СКО:
.
г) Определить доверительные интервалы для неизвестных математического ожидания и дисперсии , отвечающей заданной доверительной вероятности () в предположении, что выборка взята из нормальной генеральной совокупности.
Для построения доверительного интервала для математического ожидания
используем формулы:
,,
– квантиль распределения Стьюдента с (n-1) степенью свободы;
В нашем случае для получим
,,
,
для дисперсии
,
д) Построить графики теоретической функции распределения вероятностей и плотности распределения вероятности в предположении, что генеральная совокупность распределена по нормальному закону. Сравнить эти графики с гистограммой и эмпирической функцией распределения вероятностей. Сделать вывод.
Для того, чтобы проверить гипотезу о том, что выборка из нормальной генеральной совокупности, подставим точечные оценки в место неизвестных параметров в плотность распределения вероятности и функцию распределения вероятности. Нормальная плотность распределения вероятности
.
Будем считать, что
.
Результаты расчетов будем заносить в таблицу 3.
Сначала найдем и занесем в третий столбец с округлением до сотых.
Далее по таблице ищем значения функции , соответствующие рассчитанным ранее значениям . При этом пользуемся четностью функции : . Результат заносим в четвертый столбец таблицы 3.
Найдем значения теоретической функции плотности вероятности . Результат заносим в пятый столбец таблицы 3.
Находим значения теоретической функции распределения , где . Значения функции находятся по таблице с учетом того, что . Результаты заносим в последний столбец таблицы 3.
Таблица 3
N
1 2 -1,89 0,0669 0,018 0,029
2 4 -1,34 0,1626 0,044 0,090
3 6 -0,79 0,2920 0,080 0,215
4 8 -0,25 0,3867 0,106 0,401
5 10 0,30 0,3814 0,104 0,618
6 12 0,85 0,2780 0,076 0,802
7 14 1,39 0,1518 0,041 0,918
8 16 1,94 0,0608 0,017 0,974
Строим на основании расчетов графики теоретических плотности вероятности и функции вероятности .
Гистограмма немного асимметрична, но можно сделать предположение, что совокупность распределена по нормальному закону. По графикам эмпирической и теоретической функции также можно сделать предположение, что данное распределение близко к нормальному.
е) Проверить гипотезу о нормальном законе распределения генеральной совокупности, используя критерий Пирсона при уровне значимости .
Методом Пирсона проверим гипотезу Н0 – генеральная совокупность распределена по нормальному закону. Альтернативная гипотеза НА – это не так.
Результаты расчетов будем сводить в таблицу 4.
Критерий использует тот факт, что приближенно нормальная величина. Чтобы это условие выполнялось в достаточной мере, необходимо, чтобы в каждом интервале было не менее пяти точек. Для этого интервалы, в которых это условие не выполняется, следует объединить с соседними. В таблице 4 пятый и шестой интервалы из таблицы 1 объединены в один интервал.
Определяем длину интервалов, середины, абсолютную и относительную частоты. По результатам расчета заполняем первые шесть колонок таблицы 4.
Рассчитываем значения и . Результаты заносим в седьмую и восьмую колонки таблицы 4.
Оценим теоретические вероятности попадания нормальной случайной величины с указанными параметрами в интервал .
.
Заполняем девятую колонку таблицы 4.
Далее считаем и заполняем десятую колонку таблицы 4.
Значения заносим в последний столбец таблицы 4.
№ Интервал Длина интервала Середина интервала Абсолютная частота Относительная частота
Теор. плотность вероятности Теоретич. вероятность
1 1, 3
2 2 5 0,1 -1,89 0,018 0,037 0,063 0,1101
2 (3, 7]
4 5 9 0,18 -1,07 0,062 0,246 0,066 0,017712
3 (7, 9] 2 8 7 0,14 -0,25 0,106 0,211 0,071 0,024066
4 (9, 11] 2 10 13 0,25 0,30 0,104 0,208 0,042 0,008297
5 (11, 17] 6 14 17 0,33 1,39 0,041 0,249 0,081 0,026461
51 1
0,186636
Таблица 4
Вычисляем , здесь r – число интервалов табл. 4. Для данной выборки .
.
По таблице находим квантиль , где l – число оцениваемых параметров. В нашем случае ( и ). находим из условия .
,
.
И так, по таблице находим .
Если , то справедлива гипотеза Н0. Если , то НА. В нашем случае , то есть гипотеза Н0 не принимается
Предположение о нормальном законе распределения не принимается.
Выводы: По данным выборки построили статистический ряд, определили моду, медиану и размах выборки, построили полигон частот. Составили интервальный статистический ряд, разбив данную выборку на 8 равных интервалов, шириной h=2, построили гистограмму относительных частот, которая оказалась немного асимметричной, но по ее виду можно сделать предположение, что данная совокупность распределена по нормальному закону. Построили график эмпирической функции распределения по накопленным относительным частотам. Нашли несмещенные точечные оценки параметров распределения:
x=8,9, и . Полученные результаты говорят о том, что среднее значение равно 8,9 с разбросом порядка 3,66, то есть примерно в 70% случаев значение должно попадать в интервал от 5,24 до 12,56 (в выборке в этот интервал попадает 73% значений).
Определили доверительные интервалы для математического ожидания и дисперсии с доверительной вероятностью 0,9. Доверительный интервал для математического ожидания: 7,87<m<9,93. Это означает, что среднее значение с вероятность 90% заключено в интервале 7,87-9,93.
Доверительный интервал для дисперсии: 9,9<σ2<19,22. Иными словами, среднее квадратическое отклонение величины X, характеризующее ее разброс относительно математического ожидания m=8,9, с вероятностью 90% заключено в пределах от 3,15 до 4,38.
Построили графики теоретической функции распределения вероятностей и плотности распределения вероятности. Сравнили полученные графики с эмпирическими. Сделали предположение о том, что данное распределение близко к нормальному. Но, проверив с помощью критерия Пирсона при уровне значимости гипотезу о нормальном распределении генеральной совокупности, пришли к выводу, что эмпирические и теоретические частоты различаются значимо, то есть, нулевую гипотезу о нормальном распределении генеральной совокупности отвергаем в пользу альтернативной.