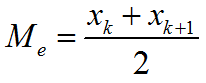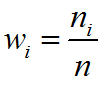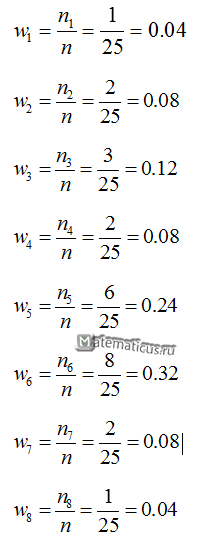Загрузить PDF
Загрузить PDF
В статистике размах – разница между наибольшим и наименьшим результатами наблюдений. Размах показывает разброс значений в совокупности данных. Если размах большой, то значения в совокупности сильно разбросаны; если размах – небольшая величина, то значения в совокупности лежат близко друг к другу. Если вы хотите узнать, как вычислить размах, выполните следующие действия.
Шаги
-
1
Запишите значения совокупности данных. Чтобы найти размах, нужно перечислить все значения для определения максимального и минимального чисел. Например: 14 , 19, 20 , 24, 25, 28.
- Будет легче определить наибольшее и наименьшее значение в совокупности, если вы запишете значения в порядке возрастания. В нашем примере: 14, 19, 20, 24, 24, 25, 28 .
- Запись значений по возрастанию также может помочь вам сделать другие расчеты, как например моду, среднее или медиану совокупности.
-
2
Определите максимальное и минимальное числа. В нашем примере, это 14 и 28.
-
3
Вычтете наименьшее число из наибольшего. Теперь, когда вы определили самое маленькое и самое большое число в совокупности, вам нужно вычесть их друг из друга: 25 – 14 = 11 – это и есть размах.
-
4
Выделите размах. Как только вы нашли размах, четко выделите его. Это поможет вам избежать путаницы с любыми другими статистическими величинами, такими как среднее, медиана или мода.
Реклама
Советы
- Медиана статистической совокупности данных – такое значение, которое делит эту совокупность на две равные части. Таким образом, медиана не вычисляется путем деления размаха на 2. Чтобы найти медиану, необходимо перечислить значения данных по возрастанию и найти значение в середине списка. Это значение и является медианой. Например, если у Вас есть список из 29 значений (по возрастанию), пятнадцатое значение будет равноудалено от верхней и нижней части этого списка, так что пятнадцатое значение является медианой, независимо от того, как это значение соотносится с размахом.
- Вы также можете интерпретировать “размах” в алгебраических выражениях, но сначала Вы должны понять концепцию алгебраической функции. Так как функция может быть задана на любом числе, даже неизвестном, то это число представляется в виде переменной (обычно «х»). Область определения – множество всех возможных значений х. Область значения функции (размах) – множество всех возможных значений функции (у) при определенных значениях х. К сожалению, нет единого способа вычислить область значения функции. Иногда, построив график функции или вычислив несколько значений, можно получить четкую закономерность.
Реклама
Об этой статье
Эту страницу просматривали 51 992 раза.
Была ли эта статья полезной?
Сегодня на уроке мы вспомним, что является модой, медианой и
средним арифметическим выборки. Узнаем, что называется размахом выборки.
Выясним, что называют отклонением от среднего. Познакомимся с величиной,
которую называют дисперсией. Узнаем, что называют средним квадратичным
отклонением.
Прежде, чем приступить к рассмотрению новой темы, давайте
вспомним, что совокупность данных иногда бывает полезно оценить одним числом – мерой
центральной тенденции числовых значений её элементов. К таким характеристикам
относятся мода, медиана и среднее.
Итак, мода – это значение случайной величины, имеющее
наибольшую частоту в рассматриваемой выборке.
Медиана – это число (значение
случайной величины), разделяющее упорядоченную выборку на две равные по
количеству данных части.
При этом если в упорядоченной выборке нечётное количество
данных, то медиана равна серединному из них. Если в упорядоченной выборке чётное
количество данных, то медиана равна среднему арифметическому двух
серединных чисел.
Среднее (или среднее
арифметическое) выборки – это число, равное отношению суммы всех чисел
выборки к их количеству. Если рассматривается совокупность значений случайной
величины , то её
среднее обозначают .
Отметим, что не каждую выборку имеет смысл оценивать с помощью
центральных тенденций.
Так, например, посмотрите на следующую выборку ,
,
,
Это выборка выигрышей (в рублях) четырёх человек. Здесь мода равна
. Медиана
также равна . Среднее
равно .
Очевидно, что ни мода, ни медиана, ни среднее не могут выступать в
роли единой объективной характеристики данной выборки. Это объясняется тем, что
наименьшие значения этой выборки существенно отличаются от наибольшего. А вот
разность наибольшего и наименьшего значений соизмерима с наибольшим значением ().
Сформулируем определение. Разность наибольшего и наименьшего
значений случайной величины выборки называется её размахом и
обозначается буквой R.
Для рассматриваемой выборки размах равен разности и
, то есть
равен .
Размах показывает, насколько велик разброс значений случайной
величины в выборке. Однако, зная размах выборки, невозможно охарактеризовать
отличие её элементов друг от друга, отличие каждого элемента от среднего
значения.
А как сравнить две выборки, которые имеют одинаковые размахи и
одинаковые средние значения?
Давайте рассмотрим пример. На место столяра претендуют двое
рабочих. Для каждого из них установили испытательный срок, в течение которого
они должны изготавливать одинаковые стулья из дерева. В следующей таблице приведены
результаты претендентов.
Каждый из рабочих за пять дней изготовил деталей. Следовательно, средняя производительность труда за день у
обоих рабочих одинаковая и равна стульев в
день.
Моды у предложенных совокупностей отсутствуют. Чтобы найти
медианы, расположим значения в порядке возрастания.
,
,
,
,
;
,
,
,
,
.
Количество данных в обоих случаях нечётно. Слева и справа от числа
находятся по
два элемента. Получается, что медианы одинаковые ( и
).
В качестве критерия сравнения совокупностей в данном случае может
выступать стабильность производительности труда. Её можно оценить с
помощью отклонений от среднего значения элементов совокупности.
Давайте сформулируем определение. Отклонением от среднего
называют разность между рассматриваемым значением случайной величины и средним
значением выборки.
Например, если значение , а значение
, то
отклонение от среднего
равно .
Отклонение от среднего может быть как положительным, так и
отрицательным.
Найдём отклонение от среднего и внесём найденные значения в
таблицу.
Покажем на нашем примере, что сумма отклонений всех значений
выборки от среднего значения равна .
,
.
Поэтому характеристикой стабильности элементов совокупности может
служить сумма квадратов отклонений от среднего.
Давайте найдём квадраты отклонений от среднего и суммы квадратов
отклонений.
Видим, что у второго рабочего сумма квадратов отклонений от
среднего больше, чем у первого, то есть можно записать неравенство .
На практике это означает, что второй рабочий имеет нестабильную
производительность труда: в какие-то дни он работает не в полную силу, а
какие-то навёрстывает упущенное, а это всегда сказывается на качестве
продукции.
Получается, что работодатель захочет взять на место столяра
первого рабочего, ведь у первого рабочего сумма квадратов отклонений от средней
производительности меньше.
В рассмотренном примере рабочие работали одинаковое количество
дней. Если бы рабочие работали разное количество дней и производили в среднем
за день одинаковое число деталей, то стабильность работы каждого из них можно
было бы оценить по величине среднего арифметического квадратов отклонений.
Такая величина называется дисперсией, что в переводе с латинского
означает «рассеяние», и обозначается буквой .
Для случайной величины , принимающей
различных
значений и имеющей среднее значение , дисперсия
находится по формуле
Давайте решим задачу. Два столяра изготавливали одинаковые
стулья из дерева. При этом первый столяр трудился полную рабочую неделю, а
второй – дня.
Сведения об их дневной выработке представлены в таблице. Сравните стабильность
работы столяров.
Итак, найдём средние значения выборок данных величин X и Y.
,
.
Таким образом, мы получили, что найденные значения равны.
Далее найдём отклонения от среднего для всех значений величин X и Y.
Затем найдём квадраты отклонений от среднего. Найдём сумму
квадратов отклонений от среднего всех значений величин X и Y.
Теперь найдём дисперсию совокупности значений случайной величины X, то есть среднее
арифметическое квадратов отклонений.
Найдём дисперсию совокупности значений случайной величины Y.
Таким образом мы получили, что .
Следовательно, второй столяр работает стабильнее первого.
Отметим, что если значения ,
, …,
случайной
величины повторяются
с частотами ,
, …,
соответственно,
то дисперсию величины можно
вычислить по формуле
,
где .
Используя знак суммы Ʃ, данную формулу можно записать более
компактно.
, где
.
Пусть величина имеет
некоторую размерность (например, миллиметры). Тогда её среднее значение и отклонение
от среднего имеют ту же
размерность, что и сама величина (в миллиметрах). А вот квадрат отклонения и дисперсия
имеют
размерности квадрата этой величины (в квадратных миллиметрах).
Для оценки степени отклонения от среднего значения удобно иметь
дело с величиной той же размерности, что и сама величина . С этой
целью используются значения .
Сформулируем определение. Корень квадратный из дисперсии называют средним
квадратичным отклонением и обозначают , то есть
.
Давайте найдём среднее квадратичное отклонение от среднего
значения выборки:
см,
см,
см,
см,
см.
Вообще, дисперсию и среднее квадратичное отклонение в статистике
называют также мерами рассеивания значений случайной величины около
среднего значения.
Генеральная совокупность представляет собой всю совокупность исследуемых объектов (например население города, ) и обозначается N.
Выборка — это ограниченное по количество объектов n, извлечённых случайным образом из генеральной совокупности.
Вариантами называются значения выборки x1, x2,…,xi, а частоты — n1, n2,…,ni
Если варианты представлены в упорядоченном отсортированном виде, обычно от минимального значения к максимальному, то такие варианты называются вариационным рядом.
Представим вариационный ряд в виде таблицы:
| Xi | x1 | x2 | …… | xn |
| ni | n1 | n2 | …… | nn |
Размах выборки — это разность между минимальным и максимальным значениями выборки и вычисляется по формуле:
Мода М0 в статистике называется варианта, которая чаще всего встречается в данной выборки и имеет наибольшую частоту (повторяемость).
Медиана Me — это варианта, находящиеся в середине вариационного ряда, делящая его пополам.
Формула для вычисления медианы нечетного вариационного ряда n=2k+1:
Me=xk+1
Формула для определения медианы четного вариационного ряда n=2k:
Относительной wi частотой называется отношение частоты к объёму выборки и определяется по формуле
Примечание
Сумма относительных частот равна единице
∑wi=1
Таблица распределения относительных частот имеет вид:
В обувном магазине
Статистика покупки обуви в магазине за один день в соответствии с размерами равна:
42, 41, 43, 40, 39, 44, 38, 42, 41, 39, 43, 41, 42, 37, 42, 41, 39, 42, 42, 41, 40, 41, 42, 38, 42
Требуется найти моду, медиану, размах выборки, построить таблицу распределения частот и относительных частот.
Решение
Отсортируем выборку и запишем вариационный ряд:
37, 38, 38, 39, 39, 39, 40, 40, 41, 41, 41, 41, 41, 41, 42, 42, 42, 42, 42, 42, 42, 42, 43, 43, 44
Обозначим варианты и их частоты:
x1=37, х2=38, х3=39, х4=40, х5=41, х6=42, х7=43 и х8=44
n1=1, n2=2, n3=3, n4=2, n5=6, n6=8, n7=2 и n8=1
Объем выборки равен
n=1+2+3+2+6+8+2+1=25
Размах выборки равен:
R=х8-х1=44–37=7
Найдем моду, наибольшая частота в вариационном ряде равна n6=8, тогда мода равна
М0=42
Число вариант восемь, то есть четно, следовательно медиана равна:
$${M_e} = frac{{{x_4} + {x_5}}}{2} = frac{{40 + 41}}{2} = 40.5$$
Вычислим относительные частоты:
Составим таблицу частот
| Xi | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
| ni | 1 | 2 | 3 | 2 | 6 | 8 | 2 | 1 |
и таблицу относительных частот:
| Xi | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
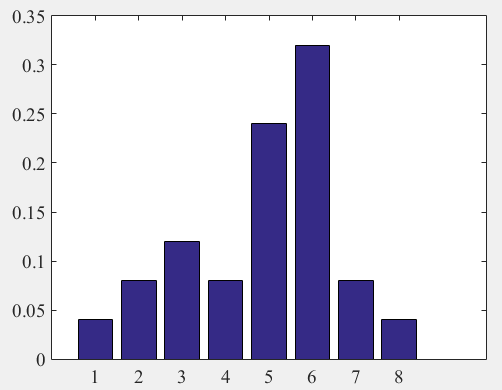
| ni | 0.04 | 0.08 | 0.12 | 0.08 | 0.24 | 0.32 | 0.08 | 0.04 |
Гистограмма относительных частот
3290
Как найти размах в численных данных? Работа с большими численными данными тесно связана со статистикой. Размах — это статистический термин, который определяет простое действие над численными данными.
Статистика — раздел математики, в котором изучают информацию разного рода, а также проводят над ней всякие операции, чтобы:
выявить закономерности;
спрогнозировать вероятности;
проанализировать результаты каких-либо действий;
и др.
Сегодня мы не будем изучать все статистические операции над численной информацией, но подробнее остановимся на вопросе: как найти размах?
Как найти размах
Чтобы найти размах в статистике, нам нужно будет коротко остановиться еще на двух терминах: объем и выборка.
Для удобства давайте разработаем условный недельный бюджет расходов. Например:
понедельник — 110;
вторник — 140;
среда — 100;
четверг — 160;
пятница — 260;
суббота — 220;
воскресенье — 50.
Допустим, такой бюджет мы составили на 1 месяц, чтобы понять наши ежемесячные расходы. Если мы возьмем из месячной статистики результаты одной недели, тогда это и будет выборкой. То есть выборка — это определенное количество информации из большого массива данных, которую вы извлекли для дальнейшего анализа. В выборке может участвовать любое количество элементов.
Обычно элементам выборки для удобства присваивают индексы при помощи переменных. Например: x1, x2, x3 и др. То есть в нашем случае у нас будет х1 – х7 или 7 элементов. Количество элементов выборки — это и есть объем. По сути, мы имеет выборку объемом в 7 элементов. Теперь самое важное — как найти размах?
Размах в статистике
Размах в статистике, он же размах в выборке — это разница между самым большим элементом выборки и самым маленьким. Глядя на наш еженедельный бюджет, мы видим, что самым большим элементом у нас является 260, а самым маленьким — 50.
Как найти размах нашей выборки: 260 – 50 = 210. Размах нашей выборки равен 210. Размах в статистике помогает определить амплитуду изменений наших статистических данных.
Как найти размах, используя программирование
Искать размах в статистике при помощи программирования — это базовые вещи, которые изучают все специалисты big data. Поиск осуществляется на том языке, при помощи которого вы взаимодействуете с данными. Например: Python, R, Java, Scala, Julia и др. Язык влияет только на реализацию поиска размаха, но алгоритм будет везде одинаковый.
Как найти размах в статистике при помощи программирования:
Вначале нужно сделать выборку данных из их общего массива.
Отсортировать элементы выборки по возрастанию, то есть от меньшего к большему.
После сортировки нужно определить наименьшее и наибольшее значения элементов. После сортировки элемент выборки с самым меньшим индексом будет иметь наименьшее значение, элемент с наибольшим индексом будет иметь наибольшее значение.
Математически вычислить разницу между большим и меньшим значениями выборки.
Вывести полученный размах на экран.
Заключение
Как найти размах в статистике? Для этого нужно определить наибольшее и наименьшее значения выборки и найти их разницу. Реализовать подобные действия можно при помощи любого языка программирования, который поддерживает работу с массивами данных.
План урока:
Понятие выборки и генеральной совокупности
Среднее арифметическое выборки
Упорядоченный ряд и таблица частот
Размах выборки
Мода выборки
Медиана выборки
Ошибки в статистике
Понятие выборки и генеральной совокупности
Слово статистика, образованное от латинского status(состояние дел), появилось только в 1746 году, когда его употребил немец Готфрид Ахенвалль. Однако ещё в Древнем Китае проводились переписи населения, в ходе которых правители собирали информацию о своих владениях и жителях, проживающих в них.
В основе любого статистического исследования лежит массив информации, который называют выборкой данных. Покажем это на примере. Пусть в классе, где учится 20 учеников, проводился тест по математике, содержавший 25 вопросов. В результате учащиеся показали следующие результаты:
Ряд чисел, приведенный во второй строке таблицы (12, 19, 19, 14, 17, 16, 18, 20, 15, 25, 13, 20, 25, 16, 17, 12, 24, 13, 21, 13), будет выборкой. Также ее могут называть рядом данных или выборочной совокупностью.
В примере с классом выборка состоит из 20 чисел. Эту величину (количество чисел в ряду) называют объемом выборки. Каждое отдельное число в ряду именуют вариантой выборки.
В примере со школьным классом в выборку попали все его ученики. Это позволяет точно определить, насколько хорошо учащиеся написали математический тест. Однако иногда необходимо проанализировать очень большие группы населения, состоящие из десятков и даже сотен миллионов человек. Например, необходимо узнать, какая часть населения страны курит. Опросить каждого жителя государства невозможно, поэтому в ходе исследования опрашивают лишь его малую часть. В этом случае статистики выделяют понятие генеральная совокупность.
Так, если с помощью опроса 10 тысяч человек ученые делают выводы о распространении курения в России, то все российское население будет составлять генеральную совокупность исследования, а опрошенные 10 тысяч людей вместе образуют выборку.
Среднее арифметическое выборки
Сбор информации о выборке является лишь первой стадией статистического исследования. Далее ее необходимо обобщить, то есть получить некоторые цифры, характеризующие выборку. Самой часто используемой статистической характеристикой является среднее арифметическое.
Другими словами, для подсчета среднего арифметического необходимо просто сложить все числа в ряде данных, а потом поделить получившееся значение на количество чисел в ряде. Так, в примере с тестом по математике (таблица 1) средний балл учащихся составит: (12+19+19+14+17+16+18+20+15+25+13+20+25+16+17+12+24+13+21+13):20=
= 349:20 = 17,45.
Среднее арифметическое позволяет одним числом характеризовать какое-либо качество всех объектов группы. Чем больше средний балл учащихся в классе, тем выше их успеваемость. Чем меньше среднее количество голов, пропускаемых футбольной командой за один матч, тем лучше она играет в обороне. Если средняя зарплата программистов в городе составляет 90 тысяч рублей, а дворников – 25 тысяч рублей, то это значит, что программисты значительно более востребованы на рынке труда, а потому при выборе будущей профессии лучше предпочесть именно эту специальность.
Упорядоченный ряд и таблица частот
В ряде данных в таблице 1 числа приведены в произвольном порядке. Перепишем ряд так, чтобы все числа шли в неубывающем порядке, то есть от самого маленького к самому большому:
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Такую запись называют упорядоченным рядом данных.
Его характеристики ничем не отличаются от изначальной выборки, однако с ним удобнее работать. С его помощью можно видеть, что ни одному ученику не удалось набрать 22 или 23 балла на тесте, но сразу двое учащихся дали 25 правильных ответов. На основе упорядоченного ряда данных несложно составить таблицу частот, в которой будет указано, как часто та или иная варианта выборки встречается в ряде. Выглядеть она будет так:
При составлении этой таблицы мы исключили из нее те варианты количества набранных баллов, частота которых равна нулю (от 0 до 12, 22 и 23).Заметим, что сумма чисел в нижней строке таблицы частот должна равняться объему выборки. Действительно,
2+3+1+1+2+2+1+2+2+1+1+2 = 20.
С помощью таблицы частот можно быстрее посчитать среднее арифметическое выборки. Для этого каждую варианту надо умножить на ее частоту, после чего сложить полученные результаты и поделить их на объем выборки:
(12•2+13•3+14•1+15•1+16•2+17•2+18•1+19•2+20•2+21•1+24•1+25•2):20 =
(24+39+14+15+32+34+18+38+40+42+24+50):20 = 349:20 = 17,45.
Размах выборки
Следующий важная характеристика ряда данных – это размах выборки.
Если выборка представлена в виде упорядоченного ряда данных, то достаточно вычесть из последнего числа ряда первое число. Так, размах выборки результатов теста в классе равен:
25 – 12 = 13,
так как самые лучшие ученики смогли решить все 25 заданий, а наихудший учащийся ответил правильно только на 13 вопросов.
Размах выборки характеризует стабильность, однородность исследуемых свойств. Например, пусть два спортсмена-стрелка в ходе соревнований производят по 5 выстрелов по круговой мишени, где за попадание начисляют от 0 до 10 очков. Первый стрелок показал результаты 8, 9, 9, 8, 9 очков. Второй же спортсмен в своих попытках показал результаты 7, 10, 10, 6, 10. Средние арифметические этих рядов равны:
(8+9+9+8+9):5 = 43:5 = 8,6;
(7+10+10+6+10):5 = 43:5 = 8,6.
Получается, что в среднем оба стрелка стреляют одинаково точно, однако первый спортсмен демонстрирует более стабильные результаты. У его выборки размах равен
9 – 8 = 1,
в то время как размах выборки второго спортсмена равен
10 – 6 = 4.
Размах выборки может быть очень важен в метеорологии. Например, в Алма-Ате и Амстердаме средняя температура в течение года почти одинакова и составляет 10°С. Однако в Алма-Ате в январе и феврале иногда фиксируются температуры ниже -30°С, в то время как в Амстердаме за всю историю наблюдений она никогда не падала ниже -20°С.
Мода выборки
Иногда важно знать не среднее арифметическое выборки, а то, какая из ее вариант встречается наиболее часто. Так, при управлении магазином одежды менеджеру не важен средний размер продаваемых футболок, а необходима информация о том, какие размеры наиболее популярны. Для этого используется такой показатель, как мода выборки.
В примере с математическим тестом сразу 3 ученика набрали по 13 баллов, а частота всех других вариант не превысила 2, поэтому мода выборки равна 13. Возможна ситуация, когда в ряде есть сразу две или более вариант, которые встречаются одинаково часто и чаще остальных вариант. Например, в ряде
1, 2, 3, 3, 3, 4, 5, 5, 5
варианты 3 и 5 встречаются по три раза. В таком случае ряд имеет сразу две моды – 3 и 5, а всю выборку именуют мультимодальной. Особо выделяется случай, когда в выборке все варианты встречаются с одинаковой частотой:
6, 6, 7, 7, 8, 8.
Здесь числа 6, 7 и 8 встречаются одинаково часто (по два раза), а другие варианты отсутствуют. В таких случаях говорят, что ряд не имеет моды.
Медиана выборки
Иногда, например, при расчете средней зарплаты, среднее арифметическое не вполне адекватно отражает ситуацию. Это происходит из-за наличия в выборке чисел, очень сильно отличающихся от среднего. Так, из-за огромных зарплат некоторых начальников большинство рядовых сотрудников компаний обнаруживают, что их зарплата ниже средней. В таких случаях целесообразно использовать такую характеристику, как медиану ряда. Это такое значение, которое делит ряд данных пополам. В упорядоченном ряде 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25 медианой будет равна 12, так как именно она находится в середине ряда:
Однако таким образом можно найти только медиану ряда, в котором находится нечетное количество чисел. Если же их количество четное, то за медиану условно принимают среднее арифметическое двух средних чисел. Так, для ряда 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25, 30, содержащего 12 чисел, медиана будет равна среднему значению 12 и 15, которые занимают 6-ое и 7-ое место в ряду:
Вернемся к примеру с математическим тестом в школе. Так как его сдавали 20 учеников, а 20 – четное число, то для расчета медианы следует найти среднее арифметическое 10-ого и 11-ого числа в упорядоченном ряде
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Эти места занимают числа 17 и 17 (выделены жирным шрифтом). Медиана ряда будет равна
(17+17):2 = 34:2 = 17.
Три приведенные основные статистические характеристики выборки, а именно среднее арифметическое, мода и медиана, называются мерами центральной тенденции. Они позволяют одним числом указать значение, относительно которого группируются все числа ряда.
Рассмотрим для наглядности ещё один пример. Врач в ходе диспансеризации измерил вес мальчиков в классе. В результате он получил 10 значений (в кг):
39, 41, 67, 36, 60, 58, 46, 44, 39, 69.
Найдем среднее арифметическое, размах, моду и медиану для этого ряда.
Решение. Сначала перепишем ряд в упорядоченном виде:
36, 39, 39, 41, 44, 46, 58, 60, 67, 69.
Так как в ряде 10 чисел, то объем выборки равен 10. Найдем среднее арифметическое. Для этого сложим все числа в ряде и поделим их на объем выборки (то есть на 10):
(36+39+39+41+44+46+58+60+67+69):10 =
= 499:10 = 49,9 кг.
Размах выборки равен разнице между наибольшей и наименьшей вариантой в ней. Самый тяжелый мальчик весит 69 кг, а самый легкий – 36 кг, а потому размах ряда равен
69 – 36 = 33 кг.
В упорядоченном ряде только одно число, 39, встречается дважды, а все остальные числа встречаются по одному разу. Поэтому мода ряда будет равна 39 кг.
В выборке 10 чисел, а это четное число. Поэтому для нахождения медианы надо найти два средних по счету значение найти их среднее. На 5-ом и 6-ом месте в ряде находятся числа 44 и 46. Их среднее арифметическое равно
(44+46):2 = 90:2 = 45 кг.
Поэтому и медиана ряда будет равна 45 кг.
Ошибки в статистике
Статистика является очень мощным инструментом для исследований во всех областях человеческой деятельности. Однако иногда ее иронично называют самой точной из лженаук. Известно и ещё одно высказывание, приписываемое политику Дизраэли, согласно которому существует просто ложь, наглая ложь и статистика. С чем же связана такая репутация этой дисциплины?
Дело в том, что некоторые люди и организации часто манипулируют данными статистики, чтобы убедить других в своей правоте или преимуществах товара, которые они продают. Требуются определенные навыки, чтобы правильно пользоваться статистикой. Одна из самых распространенных ошибок – это неправильный выбор выборки.
В 1936 году перед президентскими выборами в США был проведен телефонный опрос, который показал, что с большим преимуществом победу должен одержать Альфред Лендон. Однако на выборах Франклин Рузвельт набрал почти вдвое больше голосов. Ошибка была связана с тем, что в те годы телефон могли позволить себе только богатые люди, которые в большинстве своем поддерживали Лендона. Однако бедные люди (а их, конечно же, больше, чем богатых) голосовали за Рузвельта.
Ещё один пример – это агитация в конце XIX века в США к службе на флоте. Пропагандисты в своей рекламе указывали, что, согласно статистике, смертность на флоте во время войны (испано-американской) составляет 0,09%, в то время как среди населения Нью-Йорка она равнялась 0,16%. Получалось, что служить на флоте в военное время безопаснее, чем жить мирной жизнью. Однако на самом деле причина таких цифр заключается в том, что во флот всегда отбирали молодых мужчин с хорошим здоровьем, которые не могли умереть от «старческих» болезней, в то время как в население Нью-Йорка входят больные и старые люди.
При указании среднего значения исследователь может использовать разные характеристики – среднее арифметическое, медиана, мода. При этом почти всегда среднее арифметическое несколько больше медианы. Именно поэтому большинство людей, узнающих о средней зарплате в стране, удивляются, так как они столько не зарабатывают. Правильнее ориентироваться на медианную зарплату.
Ну и наконец, нельзя забывать, что любая статистика может показать только корреляцию между двумя величинами, но это не всегда означает причинно-следственную связь. Так, известно, что чем больше в городе продается мороженого, тем больше в это же время людей тонет на пляжах. Означает ли это, что поедание мороженого увеличивает риск во время плавания? Нет. Дело в том, что оба этих показателя, продажи мороженого и количество утонувших, зависят от третьей величины – температуры в городе. Чем жарче на улице, тем большее количество людей ходят на пляж и тем больше мороженого продается в магазинах.
