Как найти размер графа

Как найти размер графа

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 5 марта 2021 года; проверки требует 1 правка.

Размерность графа — наименьшее целое n такое, что существует «классическое представление» графа в евклидовом пространстве размерности n с единичными длинами рёбер.

В классическом представлении все вершины должны быть различны, но рёбра могут пересекаться[1].

Размерность графа G записывается как {displaystyle dim G}.

Например, граф Петерсена может быть нарисован с единичными рёбрами в E^{2}, но не в {displaystyle E^{1}}, его размерность поэтому равна 2 (см. рисунок справа).

Концепцию предложили в 1965 году Пал Эрдёш, Фрэнк Харари и Уильям Татт[2]. Она обобщает концепцию графа единичных расстояний для размерностей более 2.

Примеры[править | править код]

Для 4 равноудалённых точек нужна размерность 3.

Полный граф[править | править код]

В худшем случае каждая пара вершин соединена, что даёт полный граф.

Для погружения полного графа K_n со всеми рёбрами единичной длины нам необходимо евклидово пространство размерности n-1[3]. Например, нужно двухмерное пространство для погружения K_{3} (равносторонний треугольник) и трёхмерное для погружения K_{4} (правильный тетраэдр) как показано справа.

{displaystyle dim K_{n}=n-1}

Другими словами, размерность полного графа совпадает с размерностью симплекса, имеющего то же самое число вершин.

Полный двудольный граф {displaystyle K_{4,2}} нарисованный в евклидовом 3-мерном пространстве.

Полные двудольные графы[править | править код]

Граф-звезда, нарисованный на плоскости с рёбрами единичной длины.

Все звёзды {displaystyle K_{m,1}} для {displaystyle mgeqslant 3} имеют размерность 2 как показано на рисунке слева. Для звёзд с m равным 1 или 2 достаточна размерность 1.

Полный двудольный граф {displaystyle K_{m,2}} для {displaystyle mgeqslant 3} может быть нарисован как на рисунке справа путём расположения m вершин на окружности, радиус которой меньше единицы, другие две точки располагаем по обеим сторонам от плоскости окружности на соответствующем расстоянии. {displaystyle K_{2,2}} имеет размерность 2, так как он может быть нарисован на плоскости в виде ромба.

Размерность полного двудольного графа K_{{m,n}} для {displaystyle mgeqslant 3} и ngeqslant 3 равна 4.

Доказательство

Чтобы показать, что 4-мерного пространства достаточно, как и в предыдущем случае используем окружности.

Обозначим координаты 4-мерного пространства {displaystyle w,x,y,z}. Расположим один набор вершин произвольно на окружности {displaystyle w^{2}+x^{2}=a,y=0,z=0}, где 0<a<1, а другой произвольно на окружности {displaystyle y^{2}+z^{2}=1-a,w=0,x=0}. Мы видим, что расстояние между любой вершиной из первого множества и любой вершиной из второго множества равно {displaystyle {sqrt {w^{2}+x^{2}+y^{2}+z^{2}}}={sqrt {a+1-a}}=1}.

Мы также можем показать, что подграф K_{{3,3}} не позволяет такого представления в размерности, меньшей 4:

Если такое представление существует, то три точки A_{1}, A_{2} и A_{3} лежат на единичной сфере с центром B_1. Аналогично, они лежат на единичных сферах с центрами B_{2} и B_{3}. Первые две сферы должны пересекаться по окружности, в точке или не пересекаться вообще. Для размещения трёх различных точек A_{1}, A_{2} и A_{3} мы должны предположить пересечение по окружности. Либо эта окружность лежит полностью на третьей единичной сфере, откуда следует, что третья сфера совпадает с одной из первых двух, так что B_1, B_{2} и B_{3} не все различны. Если же окружности не пересекаются по окружности, они пересекаются с третьей сферой не более чем в двух точках, а этого недостаточно, чтобы расположить три точки A_{1}, A_{2} и A_{3}.

В итоге:

{displaystyle dim K_{m,n}=1,2,3,4}, в зависимости от значений m и n.

Размерность и хроматическое число[править | править код]

Размерность графа G всегда меньше или равна удвоенному хроматическому числу:

{displaystyle dim Gleqslant 2,chi (G)}

Доказательство

Это доказательство использует окружности.

Обозначим через n хроматическое число графа G и назначим целые числа {displaystyle (1..n)} для n цветов. В 2n-мерном евклидовом пространстве с размерностями, обозначенными через {displaystyle x_{1},x_{2},..x_{2n}}, мы располагаем все вершины цвета n произвольно на окружности, заданной формулой {displaystyle x_{2n-2}^{2}+x_{2n-1}^{2}=1/2,quad x_{i}|(ineq 2{n-2},ineq 2{n-1})=0}.

Тогда расстояние от вершины цвета p до вершины цвета q задаётся формулой {displaystyle {sqrt {x_{2p-2}^{2}+x_{2p-1}^{2}+x_{2q-2}^{2}+x_{2q-1}^{2}}}={sqrt {1/2+1/2}}=1}.

Евклидова размерность[править | править код]

Колесо с одной удалённой спицей имеет размерность 2.

То же самое колесо имеет евклидову размерность 3.

Определение размерности графа, данное выше, утверждает для n-минимального представления:

  • если две вершины графа G связаны ребром, они должны быть на расстоянии единица;
  • однако две вершины на расстоянии единица не обязательно должны быть соединены ребром.

Это определение отвергается некоторыми авторами. Другое определение предложил в 1991 годуАлександр Сойфер[en], которое он называет евклидовой размерностью графа[4]. Перед этим в 1980 году Пал Эрдёш и Миклош Шимонович[en] уже предложили это же определение под названием истинная размерность[5]. По этому определению n-минимальное представление — это то, в котором две вершины графа соединены тогда и только тогда, когда их представление находится на расстоянии 1.

Рисунок напротив показывает разницу между этими определениями для случая колеса, имеющего центральную вершину и шесть периферийных вершин с удалённой одной спицей. Представление графа на плоскости позволяет двум вершинам находиться на расстоянии 1, но при этом они не соединены.

Мы записываем евклидово расстояние как {displaystyle operatorname {Edim} G}. Оно никогда не меньше расстояния, определённого выше:

{displaystyle dim Gleqslant operatorname {Edim} G}

Евклидова размерность и максимальная степень[править | править код]

Пал Эрдёш и Миклош Шимонович доказали в 1980 году следующий результат[5]:

Евклидова размерность графа G не больше чем его удвоенная максимальная степень + 1:

{displaystyle operatorname {Edim} Gleqslant 2,Delta (G)+1}

Вычислительная сложность[править | править код]

Задача NP-трудна, и более конкретно, для экзистенциальной теории вещественных чисел полна задача определения, больше или нет размерность или евклидова размерность данного графа заданного значения.
Задача остаётся трудной даже для проверки, равна ли двум размерность или евклидова размерность[6].

Примечания[править | править код]

  1. ↑ Некоторые математики считают это «погружением», но многие теоретики графов, включая Эрдёша, Харари и Татта, использовали термин «вложение»
  2. ↑ Erdős, Harary, Tutte, 1965, с. 118–122.
  3. ↑ Kavangh, Ryan Explorations on the dimensionality of graphs. Дата обращения: 16 августа 2018.
  4. ↑ Soifer, 2009.
  5. ↑ 1 2 Erdős, Simonovits, 1980, с. 229–246.
  6. ↑ Schaefer, 2013, с. 461–482.

Литература[править | править код]

  • Erdős P., Harary F., Tutte W. T. On the dimension of a graph // Mathematika. — 1965. — Т. 12. — doi:10.1112/s0025579300005222.
  • Alexander Soifer. The Mathematical Coloring Book. — Springer, 2009. — ISBN 978-0-387-74640-1.
  • Erdős P., Simonovits M. On the chromatic number of geometric graphs // Ars Comb.. — 1980. — Вып. 9. — С. 229–246.
  • Marcus Schaefer. Realizability of graphs and linkages // Thirty Essays on Geometric Graph Theory / János Pach. — Springer, 2013. — С. 461–482. — doi:10.1007/978-1-4614-0110-0_24.
Источник

    1. Основные
      определения

Граф
– это совокупность двух множеств: вершини ребер,
между которыми определено отношениеинцидентности.

Каждое ребро e
из E
инцидентно ровно двум вершинам
и,
которые оно соединяет. При этом вершинаи реброe
называются инцидентными
друг другу, а вершины
иназываютсясмежными.

Принято обозначение
n
для числа вершин графа (мощность множества
):иm
для числа его ребер:
.
Говорят, что графG
есть (n,
m)
граф, где n
– порядок графа, m
– размер графа.

Если все ребра
графа неориентированные, т.е. пары
вершин, определяющие элементы множестваE,
неупорядочены, то такой граф называется
неориентированным графом, или неографом.
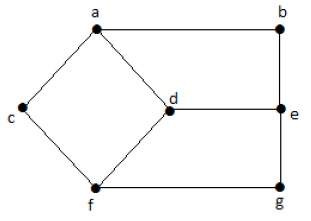
На рис. 12.1 показан пример неографа. Этот
граф имеет пять вершин и шесть ребер.

Рис. 12.1

Маршрут
– последовательность ребер, в которой
каждые два соседних ребра имеют общую
вершину. Граф связен,
если любые две вершины соединены хотя
бы одним маршрутом. Число ребер маршрута
определяет его длину.

Ребра, инцидентные
одной паре вершин, называются параллельными
или кратными.
Граф с кратными ребрами называется
мультиграфом.

Ребро
называетсяпетлей
(концевые вершины совпадают). Граф,
содержащий петли и кратные ребра,
называется псевдографом.
На рис. 12.2 показан псевдограф.

Рис. 12.2

Степень
deg(v)
вершины – это число ребер, инцидентных
v.
В неографе
сумма степеней всех вершин равна
удвоенному числу ребер
(лемма о рукопожатиях):

. (12.1)

Петля дает вклад,
равный 2, в степень вершины.

Степенная
последовательность
– последовательность степеней всех
вершин графа, записанная в определенном
порядке (по возрастанию или убыванию).

Пример
12.1. Степенная
последовательность неографа, изображенного
на рис. 12.1, записанная по возрастанию,
выглядит так:

=1,
=2,=3,=3,=3.

Сумма степеней
всех вершин графа равна:

.

Этот результат
не противоречит лемме о рукопожатиях,
поскольку граф имеет шесть ребер (m
= 6).

Матрица
смежности
графа – квадратная матрица A
порядка n,
где элемент
равен числу ребер, соединяющих вершиныi
и j.

Пример 12.2.
Граф, показанный на рис. 12.1, имеет
следующую матрицу смежности

.

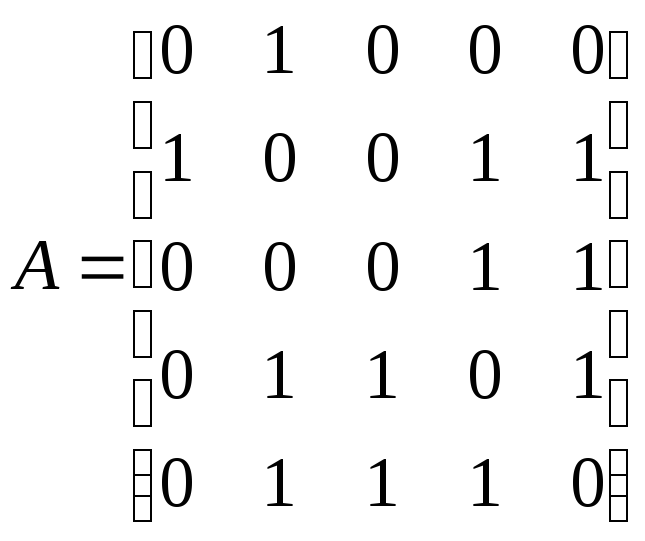
Матрица
инцидентности
I
– еще один способ описания графа. Число
строк этой матрицы равно числу вершин,
число столбцов – числу ребер;
=1,
если вершинаv
инцидентна ребру e;
в противном случае
=0.
В каждом столбце матрицы инцидентности
простого графа (без петель и без кратных
ребер) содержится по две единицы. Число
единиц в строке равно степени
соответствующей вершины.

Пример 12.3.
Граф, показанный на рис. 12.1, имеет
следующую матрицу инцидентности

.

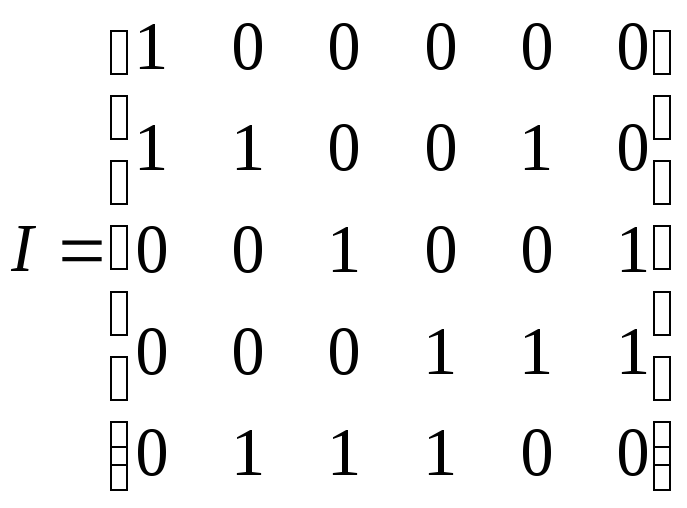
Граф
называетсяподграфом
графа
,
еслии.
Если,
то подграф называетсяостовным.

Компонента
связности
графа – максимальный по включению
вершин и ребер связной подграф.

Ранг
графа
,
гдеk
– число компонент связности.

Дерево
– связной граф, содержащий n
– 1 ребро.

Пример 12.4.
На рис. 12.3 показано дерево, которое
одновременно является остовным подграфом
графа, показанного на рис. 12.1.

Рис. 12.3

    1. Радиус, диаметр
      и центр графа

Вычисление
расстояний и определение маршрутов в
графе являются одной из наиболее
очевидных и практичных задач, которые
возникают в теории графов. Введем
некоторые необходимые определения.

Эксцентриситет
вершины графа – расстояние до максимально
удаленной от нее вершины. Для графа, для
которого не определен вес
его ребер, расстояние определяется в
виде числа ребер.

Радиус
графа – минимальный эксцентриситет
вершин, а диаметр
графа – максимальный эксцентриситет
вершин.

Центр
графа образуют вершины, у которых
эксцентриситет равен радиусу. Центр
графа может состоять из одной, нескольких
или всех вершин графа.

Периферийные
вершины имеют эксцентриситет, равный
диаметру.

Простая цепь с
длиной, равной диаметру графа, называется
диаметральной.

Теорема 12.1.
В связном графе диаметр не больше ранга
его матрицы смежности.

Теорема 12.2.
(Жордана) Каждое дерево имеет центр,
состоящий из одной или двух смежных
вершин.

Теорема 12.3.
Если диаметр дерева четный, то дерево
имеет единственный центр, и все
диаметральные цепи проходят через него,
если диаметр нечетный, то центров два
и все диаметральные цепи содержат ребро,
их соединяющее.

Очевидно практическое
значение центра графа. Если, например,
речь идет о графе дорог с вершинами-городами,
то в математическом центре целесообразно
размещать административный центр,
складские помещения и т.п. Этот же подход
можно применять и для взвешенного графа,
где расстояния – это веса ребер. В
качестве веса можно брать евклидовое
расстояние, время или стоимость
передвижения между пунктами.

Пример 12.5.
Найти радиус, диаметр и центр графа,
изображенного на рис. 12.1.

Решение.
В данной задаче удобно использовать
матрицу
расстояний S.
Элемент этой квадратной симметричной
матрицы
равен расстоянию между вершинойi
и вершиной j.
Для графа, показанного на рис. 12.1, матрица
расстояний имеет следующий вид:

. (12.2)

Вычислим
эксцентриситет
каждой вершины. Эту величину можно
определить как максимальный элемент
соответствующего столбца матрицы
расстояний (или строки – поскольку
матрицаS
симметрична).
Получаем

№

1

2

3

4

5

3

2

3

2

2

Радиус графа r
– минимальный эксцентриситет вершин.
В данном случае r
= 2. Такой эксцентриситет имеют вершины
№ 2, № 4 и № 5. Эти вершины образуют центр
графа. Диаметр графа d
– максимальный эксцентриситет вершин.
В данном случае d
= 3. Такой эксцентриситет имеют вершины
№ 1 и № 3, это периферия графа. В
исследованном графе вершины оказались
либо центральными, либо периферийными.
В графах большего порядка существуют
и другие вершины.

Эксцентриситеты
вершин небольшого графа легко вычислять
непосредственным подсчетом по рисунку.
Однако не всегда граф задан своим
рисунком. Кроме того, граф может иметь
большой размер. Поэтому необходим другой
способ решения предыдущей задачи.
Известна следующая теорема.

Теорема
12.4. Пусть
– матрица смежности графаG
без петель и
,
где.
Тогдаравно числу маршрутов длиныk
от вершины
к вершине.

Решение задач
теории графов с помощью различных
преобразований матрицы смежности
называют алгебраическим
методом.

Пример 12.6.
Найти матрицу расстояний графа,
изображенного на рис. 12.1, алгебраическим
методом.

Решение.
Матрица смежности данного графа равна:

.

Будем заполнять
матрицу расстояний, рассматривая степени
матрицы смежности. Единицы матрицы
смежности показывают пары вершин,
расстояние между которыми равно единице
(т.е. они соединены одним ребром).

.

Диагональные
элементы матрицы расстояний – нули.
Умножаем матрицу смежности на себя:

.

Согласно теореме
между вершинами 2 и 3, 1 и 4 и т.д. имеется
некоторое число маршрутов длиной 2
(поскольку степень матрицы равна двум).
Число маршрутов здесь не используется,
важен сам факт наличия маршрута и его
длина, на что и указывает ненулевой
элемент степени матрицы, не совпадающий
с элементом, отмеченным при вычислении
маршрута меньшей длины. Проставляем 2
в незаполненные элементы матрицы
расстояний и получаем следующее
приближение:

.

Осталось неизвестным
расстояние между вершинами 1 и 3. Будем
умножать матрицу смежности

саму на себя до тех пор, пока в матрице


не появится ненулевой элемент
.
Тогда соответствующий элемент матрицы
расстояний равен степени матрицы
смежности:
.
На следующем шаге получаем

,

следовательно,
,
и окончательно

.

Полученная матрица
совпадает с матрицей расстояний S
(12.2), найденной непосредственными
вычислениями по рисунку.

    1. Эйлерова цепь

Маршрут в неографе,
в котором все ребра разные, называется
цепью.
Цепь в графе называется эйлеровой,
если она содержит все ребра и все вершины
графа.

Рис. 12.4. Схема
Кенигсбергских мостов

Теория графов
многократно переоткрывалась разными
авторами при решении различных прикладных
задач. В их ряду – знаменитый математик
Леонард Эйлер (1707-1783). К созданию теории
графов его подтолкнула задача о
Кенигсберских мостах, которую он решил
в 1736 году. По условию задачи требовалось
пройти по всем семи мостам города
Кенигсберга через реку Преголь по одному
разу и вернуться к исходной точке. На
рис. 12.4 показана схема этих мостов (один
из них соединяет между собой два острова,
а остальные – острова с берегами). Этой
схеме соответствует приведенный на
следующем рисунке мультиграф с четырьмя
вершинами.

Рис. 12.5

Эйлер решил задачу
о Кенигсбергских мостах в отрицательном
смысле. Он доказал, что данная задача
не имеет решения. Для этого ему пришлось
доказать следующую теорему.

Теорема 12.5
(Эйлера).
Мультиграф обладает эйлеровой цепью
тогда и только тогда, когда он связен и
число вершин нечетной степени равно 0
или 2.

Вершины нечетной
степени в этой теореме, очевидно, являются
началом и концом цепи. Если таких вершин
нет, то эйлерова цепь становится эйлеровым
циклом.
Граф, обладающий эйлеровым циклом,
называется эйлеровым.
Если граф имеет эйлерову цепь, но не
обладает эйлеровым циклом (число вершин
нечетной степени равно 2), то он называется
полуэйлеровым
графом.

Предположим, что
граф имеет эйлеров цикл. Двигаясь по
нему, будем подсчитывать степени вершин,
полагая их до начала прохождения
нулевыми. Прохождение каждой вершины
вносит 2 в степень этой вершины. Поскольку
эйлеров цикл содержит все ребра, то
когда обход будет закончен, будут учтены
все ребра, а степени вершин – четные.

Все четыре вершины
мультиграфа, показанного на рис. 12.5,
имеют нечетные степени. Поэтому этот
граф не обладает эйлеровым циклом, а
задача о Кенигсбергских мостах не имеет
решения.

Рассмотрим для
сравнения граф, обладающий эйлеровой
цепью. В графе на рис. 12.6 только две
вершины имеют нечетную степень,
следовательно, эйлерова цепь есть.

Рис. 12.6

Цепей может быть
несколько. Например, граф на рис. 12.6
имеет две эйлеровы цепи: 1-2-3-4-1-3 и
1-2-3-1-4-3.

    1. Реберный граф

Рассмотрим два
графа G
и L(G).
Граф G
имеет произвольную форму, а вершины
графа L(G)
расположены на ребрах графа G.
В этом случае граф L(G)
называется реберным
графом по
отношению к графу G.

Английское название
реберного графа – line
graph,
отсюда и обозначение графа – L(G).
На рис. 12.7 показан реберный граф (он
выделен жирными линиями), построенный
для графа с рис. 12.1.

Рис. 12.7. Реберный
граф

Теорема 12.6.
Если
– степенная последовательность (n,
m)
графа G,
то L(G)
является (m,
)-графом,
где

. (12.3)

Для графа G,
показанного на рис. 12.7 (и рис. 12.1), его
степенная последовательность: 1-3-2-3-3.
Поэтому

.

    1. Раскраска графа,
      хроматический полином

Предположим, что
перед нами стоит задача: раскрасить
карту мира так, чтобы каждая страна
имела свой собственный цвет. Поскольку
на свете существует несколько сотен
государств, то, естественно, потребуется
достаточно много разных красок.

Упростим задачу.
Будем использовать меньшее количество
красок, но при этом не будем допускать,
чтобы соседние страны, имеющие общие
границы, были окрашены в один цвет.
Возникает вопрос: какое минимальное
количество красок требуется, чтобы
удовлетворить этому условию?

Ответить на этот
вопрос можно с помощью теории графов.
Для этого нужно представить карту мира
в виде графа, каждая вершина которого
соответствует отдельной стране, а ребро
между смежными вершинами соответствует
наличию между странами общей границы.

Произвольная
функция

на множестве вершин графа называется
раскраской
графа. Раскраска называется правильной,
если

для любых смежных вершин
и.
Минимальное числоk,
при котором граф G
является k-раскрашиваемым
называется хроматическим
числом
графа
.

Граф называется
пустым,
если в нем удалены все ребра и вершины
изолированы друг от друга. Граф называется
полным,
если в нем нельзя добавить новое ребро,
не добавив при этом одновременно новую
вершину.

Теорема 12.7
(Брукса).
Для любого графа G,
не являющегося полным,
,
если–максимальная
из степеней вершин графа.

Для определения
количества способов раскраски графа в
x
цветов, необходимо составить хроматический
полином
P(G,
x).
Значение полинома при некотором
конкретном
равно числу правильных раскрасок графа
вцветов.

Существует лемма,
утверждающая, что хроматический
полином графа имеет вид

,(12.4)

где
– граф, полученный изG
добавлением ребра (u,
v),
а граф
получается изG
отождествлением вершин u
и v.

Другой вариант
леммы:

, (12.5)

где
– граф, полученный изG
удалением ребра (u,
v),
а граф
получается изG
отождествлением вершин u
и v.

Операцию
отождествления вершин u
и
v
называют также стягиванием ребра (u,
v).

Оба варианта леммы
составляют основу для хроматической
редукции графа (reduction
– «сокращение» на английском).
Хроматическая редукция графа –
представление графа в виде нескольких
пустых или полных графов, сумма
хроматических полиномов которых равна
хроматическому полиному графа. Очевидно,
что хроматический полином пустого графа
равен(каждая вершина может быть раскрашена
независимо от других), а для полного
графа.
Последнее выражение называютфакториальной
степенью
переменной x:
.

Разложения по
пустым и полным графам связаны.
Факториальную степень можно представить
в виде полинома:

, (12.6)

где
– числа Стирлинга первого рода. И
наоборот, степеньможно выразить через факториальные
степени:

, (12.7)

где
– числа Стирлинга второго рода, обладающие
следующими свойствами:

при
, (12.8)

при
,при.

При получении
хроматического полинома могут быть
полезны следующие теоремы.

Теорема 12.8.
Коэффициенты хроматического полинома
составляют знакопеременную
последовательность.

Теорема 12.9.
Абсолютная величина второго коэффициента
хроматического полинома равна числу
ребер графа.

Теорема 12.10.
Наименьшее число i,
для которого отличен от нуля коэффициент
при

в хроматическом полиноме графа G,
равно числу компонент связности графа
G.

Кроме вершинной
раскраски, существует еще реберная
раскраска и раскраска граней.

Пример 12.7.
Найти хроматический полином графа,
показанного на рис. 12.8.

Рис. 12.8

Решение.
В зависимости от числа ребер графа можно
использовать разложение (12.4) или (12.5).
Если граф почти полный, то, добавив
несколько ребер по разложению (12.4),
получим хроматический полином в виде
суммы факториальных степеней. Если же
ребер мало и для получения пустого графа
требуется удалить только несколько
ребер, то следует использовать разложение
(12.5) с удалением ребер. Такие действия
называются хроматической редукцией.

1. Хроматическая
редукция по пустым графам.
Воспользуемся вначале леммой (12.5). Удаляя
ребра и отождествляя соответствующие
вершины (стягивая ребра), сведем исходный
граф к пустым графам. Сначала разложим
граф на два, убрав, а затем стянув ребро
1-3. Выполненное действие запишем в виде
условного равенства:

Здесь
операция вычитания относится не к самому
графу, а к его хроматическому полиному.
Таким образом, последнее равенство
означает, что
.
Для сокращения записи обозначениеP(…)
будем опускать. Далее разложим каждый
из графов

и
,
пользуясь той же леммой.

Приведем подобные
члены:

(12.9)

В итоге получим
искомый хроматический полином:

. (12.10)

Разложение (12.9)
называется хроматической редукцией
графа по пустым графам.

Очевидно, что
результат соответствует утверждениям
теорем 12.8-12.10. Коэффициенты в (12.10) образуют
знакопеременную последовательность,
а коэффициент при
равен четырем – числу ребер. Наименьшая
степеньx
в полиноме равна 1, т.е. числу компонент
связности графа.

2. Хроматическая
редукция по полным графам.
Добавив к изображенному на рис. 12.8 графу
ребро 1–4, получим граф с большим числом
ребер. Затем в исходном графе отождествим
вершины 1 и 4. В результате получим два
графа.

Отождествление
вершин приводит к уменьшению порядка
и иногда размера графа. Второй граф –
это полный граф
,
его преобразовывать больше не требуется.
К первому графу добавим ребро 1–2 и
отождествим вершины 1 и 2:

В итоге получим

(12.11)

Хроматический
полином примет вид

(12.12)

Разложение (12.11)
называется хроматической редукцией
графа по полным графам.

Оба способа дали
один результат, и из редукции по полным
графам легко получить редукцию по
пустым. Для этого достаточно раскрыть
скобки и привести подобные члены, как
в (12.12). Однако обратное действие не
очевидно. Для того чтобы полином
,
полученный из пустых графов, выразить
в виде суммы факториальных степеней,
необходимы числа Стирлинга 2-го рода.
Согласно рекуррентным формулам (12.8)
имеем следующие числа:

,

,

,

.

Пользуясь (12.7) и
найденными числами Стирлинга 2-го рода,
получим

,

,

.

Произведем
преобразование хроматического полинома:

Хроматическое
число
графа лучше всего получить, разложив
хроматический полином на множители:

.

Минимальное
натуральное число x,
при котором
не обращается в нуль, равно 3. Отсюда
следует.
Так как максимальная степень вершин
графа,
выполняется оценка.

    1. Ранг-полином
      графа

Ранг графа
определяется как
,
гдеn
– число вершин, k
– число компонент связности графа.
Коранг графа, или цикломатический ранг,
есть
,
гдеm
– число ребер.

Ранг-полином графа
G
имеет вид

,

где
– ранг графаG
, а
– корангостовного
(т.е. включающего в себя все вершины
графа) подграфа H,
а
– его ранг. Суммирование ведется по
всем остовным подграфам графаG.

Ранг полином
служит для анализа множества остовных
подграфов. Так, например, коэффициент
при
весть число подграфов размераk,
а значение
равно числу подграфов (включая
несобственный подграф), ранг которых
равен рангу самого графа.

Пример
12.8. Найти
ранг-полином графа, изображенного на
рис. 12.8.

Решение.
Найдем все 16 остовных подграфов графа
G
(рис. 12.9). Множество представим в виде
четырех графов размера 1 (т.е. с одним
ребром), шести графов размера 2, четырех
графов размера 3 и двух несобственных
графов (пустой граф и граф G).

Рис. 12.9

Учитывая, что ранг
графа равен 3, получаем сумму:

    1. Циклы

Маршрут, в котором
начало и конец совпадают, – циклический.
Циклический маршрут называется циклом,
если он – цепь.

Остовом
графа G
называется граф, не содержащий циклов
и состоящий из ребер графа G
и всех его вершин. Остов графа определяется
неоднозначно.

Ребра графа, не
входящие в остов, называются хордами.
Цикл, получающийся при добавлении к
остову графа его хорды, называется
фундаментальным
относительно
этой хорды.

Теорема 12.11.
Число ребер неографа, которые необходимо
удалить для получения остова, не зависит
от последовательности их удаления и
равно цикломатическому рангу графа.

Пример 12.8.
По заданной матрице смежности:

,

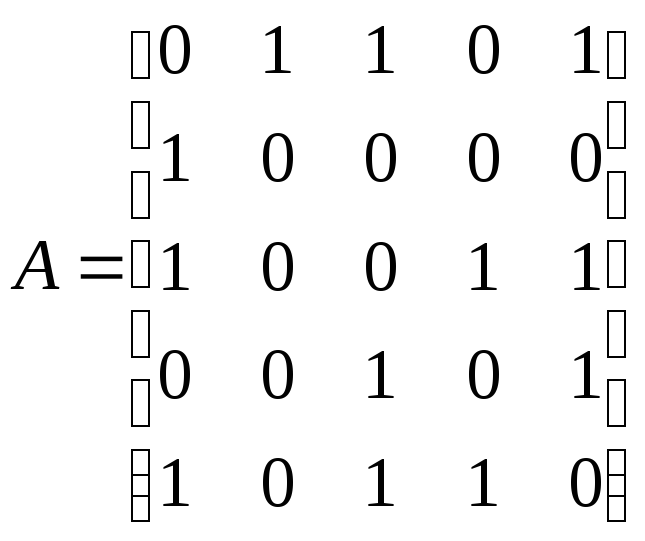
определить число
циклов длины 3 ()
и длины 4 ().
Записатьматрицу
фундаментальных циклов.

Решение.
Матрица смежности данного графа
симметричная, поэтому ей соответствует
неориентированный граф. Сумма ненулевых
элементов матрицы равна 12, следовательно,
по лемме о рукопожатиях в графе 6 ребер.
Построим этот граф (рис. 12.10). Очевидно,
в нем два цикла (3–4–5 и 1–3–5) длиной 3 и
один цикл (1–3–4–5) длиной 4. В данной
задаче решение получено прямым подсчетом
по изображению графа. Для более сложных
случаев существует алгоритм решения
задачи по матрице смежности.

Известно, что след
(trace)
матрицы смежности, возведенный в k-ю
степень, равен числу циклических
маршрутов длины k
(см. теорему 12.4). Это число включает в
себя и искомое число циклов. Цикл
отличается от циклического маршрута
тем, что в нем не повторяются ребра.
Кроме того, предполагается, что искомые
циклы не помечены, а в след матрицы
входят именно помеченные маршруты.

Рис. 12.10

Непомеченных
циклов длиной 3 в 6 раз меньше, чем
помеченных, так как каждый помеченный
цикл может отличаться началом (а их в
данном случае три) и двумя направлениями
обхода (по и против часовой стрелки).
Возведем заданную матрицу смежности в
третью степень:

,

и получим

.

Поскольку
циклических маршрутов длиной 3, отличных
от циклов длиной 3, не существует,
найденное число и есть ответ в поставленной
задаче.

С циклами длиной
4 немного сложнее. В след четвертой
степени матрицы смежности графа

,

входят не только
циклы, но и циклические маршруты с
двойным и четырехкратным прохождением
ребер. Обозначим количество таких
маршрутов через
исоответственно. Очевидно, число маршрутов
с четырехкратным прохождением одного
ребра для вершиныравно степени этой вершины:.
Число маршрутов с двукратным прохождением
ребра складывается из числас висячей вершинойи числамаршрутов с вершинойв центре.

Легко заметить,
что
.
Числозависит от степеней вершин, соседних с:

,

где
– ребро, инцидентное вершинамi
и k.

Для графа на рис.
12.10 получим

,

,

,

.

С учетом того, что
непомеченных циклов длиной 4 в 8 раз
меньше, получим

.

После преобразований
формула примет вид

.

Для нахождения
матрицы фундаментальных циклов
пронумеруем ребра графа, начиная
нумерацию с хорд, как показано на рис.
12.11 (а).

Рис. 12.11

Двум хордам, 1 и 2,
соответствуют два фундаментальных
цикла: 1–4–5 и 2–4–6 (рис. 12.11 (б и в)).
Матрица фундаментальных циклов имеет
две строки (число циклов) и шесть столбцов
(число ребер).

1

2

3

4

5

6

1

1

0

0

1

1

0

2

0

1

0

1

0

1

В первой строке
матрицы единицами отмечены столбцы с
номерами ребер, входящих в первый цикл,
а во второй строке – номера ребер из
второго цикла.

Источник

В математика, и особенно в теория графов, то размерность графа наименьшее целое число п такое, что существует “классическое представление” графа в Евклидово пространство измерения п со всеми краями единичной длины.

В классическом представлении вершины должны быть разными точками, но ребра могут пересекать друг друга.[1]

Размерность графа грамм написано: { displaystyle dim G}.

Например, Граф Петерсена может быть нарисован с ребрами единицы в E ^ {2}, но не в E ^ {1}: следовательно, его размер равен 2 (см. рисунок справа).

Эта концепция была представлена ​​в 1965 г. Пол Эрдёш, Фрэнк Харари и Уильям Тутте.[2] Это обобщает понятие график единичного расстояния до более чем двух измерений.

Примеры

С 4 равноотстоящими точками нам нужно 3 измерения.

Полный график

В худшем случае каждая пара вершин связана, что дает полный график.

К погружать полный график K_ {n} со всеми ребрами, имеющими единичную длину, нам понадобится евклидово пространство размерности п-1.[3] Например, для погружения требуется два измерения. К_ {3} (равносторонний треугольник) и три для погружения К_ {4} (правильный тетраэдр), как показано справа.

dim K_ {n} = n-1

Другими словами, размерность всего графа такая же, как у графа. симплекс с одинаковым количеством вершин.

Полный двудольный граф К _ {{4,2}} нарисованный в евклидовом трехмерном пространстве.

Полные двудольные графы

Все звездные графики К _ {{м, 1}}, за м geq 3, имеют размер 2, как показано на рисунке слева. Звездные графы с м равным 1 или 2, нужен только размер 1.

Размерность полный двудольный граф К _ {{м, 2}}, за м geq 3, можно нарисовать как на рисунке справа, поместив м вершины на окружности, радиус которой меньше единицы, и две другие вершины, расположенные по обе стороны от плоскости круга, на подходящем расстоянии от нее. К_ {2,2} имеет размер 2, так как его можно нарисовать как единичный ромб на плоскости.

Теорема — Размерность общего полного двудольного графа К_ {м, п}, за м geq 3 и п geq 3, равно 4.

Доказательство

Чтобы показать, что 4-мерного пространства достаточно, как и в предыдущем случае, мы используем круги.

Обозначая координаты четырехмерного пространства через ш, х, у, г, мы расположим один набор вершин произвольно на окружности, заданной w ^ {2} + x ^ {2} = a, y = 0, z = 0 куда 0 <а <1, а второй – произвольно на окружности y ^ {2} + z ^ {2} = 1-a, w = 0, x = 0. Тогда мы видим, что расстояние между любой вершиной в одном наборе и любой вершиной в другом наборе равно { sqrt {w ^ {2} + x ^ {2} + y ^ {2} + z ^ {2}}} = { sqrt {a + 1-a}} = 1.

Также можно показать, что подграф К_ {3,3} не допускает такого представления в пространстве размерности меньше 3:

Если такое представление существует, то три точки A_ {1}, A_ {2} и A_ {3} лежать на единичной сфере с центром B_ {1}. Точно так же они лежат на единичных сферах с центрами БИ 2} и B_ {3}. Первые две сферы должны пересекаться по кругу, в точке или вообще не пересекаться; для размещения трех различных точек A_ {1}, A_ {2} и A_ {3}, мы должны принять круг. Либо эта окружность полностью лежит на третьей единичной сфере, что означает, что третья сфера совпадает с одной из двух других, так что B_ {1}, БИ 2} и B_ {3} не все различны; или нет, поэтому его пересечение с третьей сферой составляет не более двух точек, недостаточных для размещения A_ {1}, A_ {2} и A_ {3}.

Обобщить:

{ displaystyle dim K_ {m, n} = 1,2,3 { text {или}} 4}, в зависимости от значений м и п.

Размерность и хроматическое число

Теорема — Размерность любого графа грамм всегда меньше или равно удвоенному значению хроматическое число:

{ Displaystyle тусклый G Leq 2 , чи (G)}

Доказательство

В этом доказательстве также используются круги.

Мы пишем п для хроматического числа грамми присваиваем целые числа (1..n) к п цвета. В 2n-мерное евклидово пространство, размеры которого обозначены x_ {1}, x_ {2}, .. x_ {2n}, расставляем все вершины цвета п произвольно на круге, данном x_ {2n-2} ^ {2} + x_ {2n-1} ^ {2} = 1/2, quad x_ {i} | (i neq 2 {n-2}, i neq 2 {n -1}) = 0.

Тогда расстояние от вершины цвета п к вершине цвета q дан кем-то { sqrt {x_ {2p-2} ^ {2} + x_ {2p-1} ^ {2} + x_ {2q-2} ^ {2} + x_ {2q-1} ^ {2}}} = { sqrt {1/2 + 1/2}} = 1.

Евклидово измерение

Колесная диаграмма с одной снятой спицей имеет размер 2.

Это же колесо имеет евклидово измерение 3.

Приведенное выше определение размерности графа говорит о минимальном –п представление:

  • если две вершины грамм соединены ребром, они должны находиться на единичном расстоянии друг от друга;
  • однако две вершины на единичном расстоянии друг от друга не обязательно соединены ребром.

Это определение отвергается некоторыми авторами. Другое определение было предложено в 1991 г. Александр Сойфер, за то, что он назвал Евклидово измерение графа.[4] Ранее, в 1980 г., Пол Эрдёш и Миклош Симоновиц уже предложил это с названием верное измерение.[5] По этому определению минимальныйп представление такое, что две вершины графа соединены если и только если их представления находятся на расстоянии 1.

На рисунках напротив показана разница между этими определениями в случае колесо графа имеющий центральную вершину и шесть периферийных вершин с удаленной одной спицей. Его представление на плоскости допускает две вершины на расстоянии 1, но они не связаны.

Запишем это измерение как { displaystyle operatorname {Edim} G}. Оно никогда не бывает меньше размера, указанного выше:

{ displaystyle dim G leq operatorname {Edim} G}

Евклидова размерность и максимальная степень

Пол Эрдёш и Миклош Симонович доказали в 1980 году следующий результат:[5]

Теорема — Евклидово измерение графа грамм не более чем в два раза больше максимального степень плюс один:

{ Displaystyle OperatorName {Edim} G leq 2 , Delta (G) +1}

Вычислительная сложность

это NP-жесткий, а точнее полный для экзистенциальная теория реальности, чтобы проверить, является ли размерность или евклидово измерение данного графа не более чем заданным значением. Проблема остается сложной даже для проверки того, равняется ли размерность или евклидово измерение двум.[6]

Рекомендации

  1. ^ Некоторые математики рассматривают это строго как “погружение “, но многие теоретики графов, включая Эрдеша, Харари и Тутте, используют этот термин”встраивание “.
  2. ^ Erdős, P .; Harary, F .; Тутте, У. Т. (1965). «О размерности графа» (PDF). Математика. 12 (2): 118–122. Дои:10.1112 / s0025579300005222.
  3. ^ Каванг, Райан. «Исследования размерности графиков» (PDF). Получено 16 августа, 2018.
  4. ^ Сойфер, Александр (2009). Математическая книжка-раскраска. Springer. ISBN  978-0-387-74640-1.
  5. ^ а б Erdős, P .; Симоновиц, М. (1980). «О хроматическом числе геометрических графов». Ars Comb. (9): 229–246.
  6. ^ Шефер, Маркус (2013), «Реализуемость графиков и связей», в Пах, Янош (ред.), Тридцать очерков по теории геометрических графов, Springer, стр. 461–482, CiteSeerX  10.1.1.220.9651, Дои:10.1007/978-1-4614-0110-0_24, ISBN  978-1-4614-0109-4.
Источник

Графы имеют различные свойства, которые используются для характеристики графов в зависимости от их структуры. Эти свойства определены в конкретных терминах, относящихся к области теории графов. В этой главе мы обсудим несколько основных свойств, которые являются общими для всех графиков.

Расстояние между двумя вершинами

Это число ребер в кратчайшем пути между вершиной U и вершиной V. Если существует несколько путей, соединяющих две вершины, то кратчайший путь рассматривается как расстояние между двумя вершинами.

Обозначение – d (U, V)

Может быть любое количество путей из одной вершины в другую. Среди них вам нужно выбрать только самый короткий.

пример

Посмотрите на следующий график –

Расстояние между двумя вершинами

Здесь расстояние от вершины ‘d’ до вершины ‘e’ или просто ‘de’ равно 1, поскольку между ними есть одно ребро. Существует много путей от вершины ‘d’ до вершины ‘e’ –

  • да, а, бе
  • дф, фг, гэ
  • де (считается для расстояния между вершинами)
  • дф, фц, ca, ab, be
  • да, ac, cf, fg, ge

Эксцентриситет вершины

Максимальное расстояние между вершиной и всеми остальными вершинами рассматривается как эксцентриситет вершины.

Обозначение – e (V)

Расстояние от конкретной вершины до всех других вершин графа берется, и среди этих расстояний эксцентриситет является наибольшим из расстояний.

пример

На приведенном выше графике эксцентриситет «а» равен 3.

Расстояние от «a» до «b» равно 1 («ab»),

от ‘a’ до ‘c’ равно 1 (‘ac’),

от «а» до «d» равно 1 («объявление»),

от ‘a’ до ‘e’ равно 2 (‘ab’ – ‘be’) или (‘ad’ – ‘de’),

от ‘a’ до ‘f’ равно 2 (‘ac’ – ‘cf’) или (‘ad’ – ‘df’),

от ‘a’ до ‘g’ равно 3 (‘ac’ – ‘cf’ – ‘fg’) или (‘ad’ – ‘df’ – ‘fg’).

Таким образом, эксцентриситет равен 3, что является максимумом от вершины «а» от расстояния между «ag», которое является максимальным.

Другими словами,

е (б) = 3

е (с) = 3

е (д) = 2

е (е) = 3

е (е) = 3

е (г) = 3

Радиус связного графа

Минимальный эксцентриситет от всех вершин рассматривается как радиус графа G. Минимальный среди всех максимальных расстояний между вершиной до всех остальных вершин рассматривается как радиус графа G.

Обозначение – r (G)

Из всех эксцентриситетов вершин графа радиус связного графа является минимумом всех этих эксцентриситетов.

Пример – На приведенном выше графике r (G) = 2, что является минимальным эксцентриситетом для «d».

Диаметр графика

Максимальный эксцентриситет от всех вершин рассматривается как диаметр графа G. Максимальный из всех расстояний между вершиной до всех других вершин рассматривается как диаметр графа G.

Обозначение – d (G)

Из всех эксцентриситетов вершин графа диаметр связного графа является максимальным из всех этих эксцентриситетов.

Пример. На приведенном выше графике d (G) = 3; что является максимальным эксцентриситетом.

Центральная точка

Если эксцентриситет графа равен его радиусу, то он называется центральной точкой графа. Если

e (V) = r (V),

тогда «V» является центральной точкой графа «G».

Пример – в примере графика ‘d’ является центральной точкой графика.

e (d) = r (d) = 2

Центр

Множество всех центральных точек «G» называется центром графа.

Пример. В примере графика {‘d’} является центром графика.

Длина окружности

Число ребер в самом длинном цикле «G» называется окружностью «G».

Пример. На графике примера длина окружности равна 6, что мы получили из самого длинного цикла acfgeba или acfdeba.

обхват

Число ребер в кратчайшем цикле G называется его обхват.

Обозначения – g (G).

Пример – в примере графика обхват графа равен 4, который мы получили из кратчайшего цикла acfda или dfged или abeda.

Теорема о сумме степеней вершин

Если G = (V, E) ненаправленный граф с вершинами V = {V 1 , V 2 ,… V n }, то

n ∑ i = 1 градус (V i ) = 2 | E |

Следствие 1

Если G = (V, E) ориентированный граф с вершинами V = {V 1 , V 2 ,… V n }, то

n ∑ i = 1 градус + (V i ) = | E | = n ∑ i = 1 град – (V i )

Следствие 2

В любом неориентированном графе число вершин с нечетной степенью является четным.

Следствие 3

В неориентированном графе, если степень каждой вершины равна k, то

к | V | = 2 | E |

Следствие 4

В неориентированном графе, если степень каждой вершины не меньше k, то

к | V | ≤ 2 | E |

Следствие 5

В неориентированном графе, если степень каждой вершины не более k, то

к | V | ≥ 2 | E |

Источник

From Wikipedia, the free encyclopedia

In mathematics, and particularly in graph theory, the dimension of a graph is the least integer n such that there exists a “classical representation” of the graph in the Euclidean space of dimension n with all the edges having unit length.

In a classical representation, the vertices must be distinct points, but the edges may cross one another.[1]

The dimension of a graph G is written: {displaystyle dim G}.

For example, the Petersen graph can be drawn with unit edges in E^{2}, but not in E^{1}: its dimension is therefore 2 (see the figure to the right).

This concept was introduced in 1965 by Paul Erdős, Frank Harary and William Tutte.[2] It generalises the concept of unit distance graph to more than 2 dimensions.

Examples[edit]

With 4 equally spaced points, we need 3 dimensions.

Complete graph[edit]

In the worst case, every pair of vertices is connected, giving a complete graph.

To immerse the complete graph K_{n} with all the edges having unit length, we need the Euclidean space of dimension n-1.[3] For example, it takes two dimensions to immerse K_{3} (an equilateral triangle), and three to immerse K_{4} (a regular tetrahedron) as shown to the right.

dim K_{n}=n-1

In other words, the dimension of the complete graph is the same as that of the simplex having the same number of vertices.

The complete bipartite graph K_{{4,2}} drawn in Euclidean 3-space.

Complete bipartite graphs[edit]

A star graph drawn in the plane with edges of unit length.

All star graphs K_{{m,1}}, for mgeq 3, have dimension 2, as shown in the figure to the left. Star graphs with m equal to 1 or 2 need only dimension 1.

The dimension of a complete bipartite graph K_{{m,2}}, for mgeq 3, can be drawn as in the figure to the right, by placing m vertices on a circle whose radius is less than a unit, and the other two vertices one each side of the plane of the circle, at a suitable distance from it. K_{2,2} has dimension 2, as it can be drawn as a unit rhombus in the plane.

Theorem — The dimension of a general complete bipartite graph K_{m,n}, for mgeq 3 and ngeq 3, is 4.

To summarise:

{displaystyle dim K_{m,n}=1,2,3{text{ or }}4}, depending on the values of m and n.

Dimension and chromatic number[edit]

Theorem — The dimension of any graph G is always less than or equal to twice its chromatic number:

{displaystyle dim Gleq 2,chi (G)}

Euclidean dimension[edit]

The wheel graph with one spoke removed is of dimension 2.

The same wheel is of Euclidean dimension 3.

The definition of the dimension of a graph given above says, of the minimal-n representation:

  • if two vertices of G are connected by an edge, they must be at unit distance apart;
  • however, two vertices at unit distance apart are not necessarily connected by an edge.

This definition is rejected by some authors. A different definition was proposed in 1991 by Alexander Soifer, for what he termed the Euclidean dimension of a graph.[4] Previously, in 1980, Paul Erdős and Miklós Simonovits had already proposed it with the name faithful dimension.[5] By this definition, the minimal-n representation is one such that two vertices of the graph are connected if and only if their representations are at distance 1.

The figures opposite show the difference between these definitions, in the case of a wheel graph having a central vertex and six peripheral vertices, with one spoke removed. Its representation in the plane allows two vertices at distance 1, but they are not connected.

We write this dimension as {displaystyle operatorname {Edim} G}. It is never less than the dimension defined as above:

{displaystyle dim Gleq operatorname {Edim} G}

Euclidean dimension and maximal degree[edit]

Paul Erdős and Miklós Simonovits proved the following result in 1980:[5]

Theorem — The Euclidean dimension of a graph G is no more than twice its maximal degree plus one:

{displaystyle operatorname {Edim} Gleq 2,Delta (G)+1}

Computational complexity[edit]

It is NP-hard, and more specifically complete for the existential theory of the reals, to test whether the dimension or the Euclidean dimension of a given graph is at most a given value.
The problem remains hard even for testing whether the dimension or Euclidean dimension is two.[6]

References[edit]

  1. ^ Some mathematicians regard this strictly as an “immersion”, but many graph theorists, including Erdős, Harary and Tutte, use the term “embedding”.
  2. ^ Erdős, P.; Harary, F.; Tutte, W. T. (1965). “On the dimension of a graph” (PDF). Mathematika. 12 (2): 118–122. doi:10.1112/s0025579300005222. hdl:2027.42/152495.
  3. ^ Kavangh, Ryan. “Explorations on the dimensionality of graphs” (PDF). Retrieved August 16, 2018.
  4. ^ Soifer, Alexander (2009). The Mathematical Coloring Book. Springer. ISBN 978-0-387-74640-1.
  5. ^ a b Erdős, P.; Simonovits, M. (1980). “On the chromatic number of geometric graphs”. Ars Combinatoria. 9: 229–246. CiteSeerX 10.1.1.210.6641. Zbl 0466.05031.
  6. ^ Schaefer, Marcus (2013), “Realizability of graphs and linkages”, in Pach, János (ed.), Thirty Essays on Geometric Graph Theory, Springer, pp. 461–482, CiteSeerX 10.1.1.220.9651, doi:10.1007/978-1-4614-0110-0_24, ISBN 978-1-4614-0109-4.
Источник

Добавить комментарий