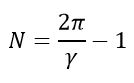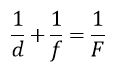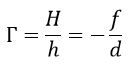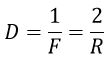Как найти размер изображения в зеркале

2017-11-29 23:05

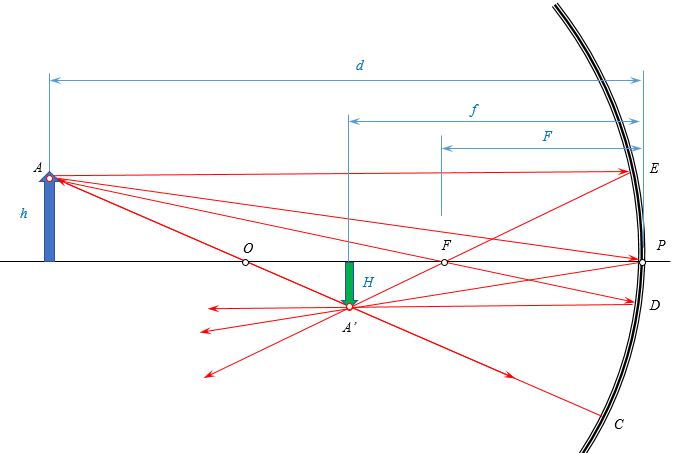
Теперь надо рассмотреть еще вопрос о размерах изображения, получающегося в зеркале и линзе. Выполненные на рис. 210 построения сразу указывают на то, что, в отличие от случая плоского зеркала, размер изображения, даваемого сферическим зеркалом, будет меняться в зависимости от положения объекта по отношению к фокусу зеркала. Так, например, если объект находится много дальше фокуса вогнутого зеркала, то его изображение получается уменьшенным. Если объект находится между зеркалом и фокусом, то изображение получается мнимым и увеличенным.

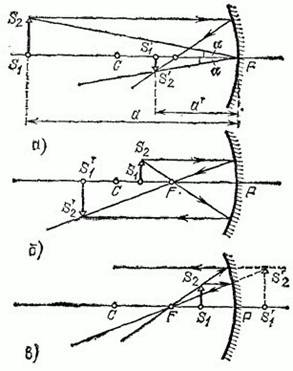
Рис. 210. Изображения протяженных объектов в вогнутом сферическом зеркале. Объект расположен: а) за центром зеркала (изображение действительное, обратное и уменьшенное); б) между центром и фокусом (изображение действительное, обратное и увеличенное); в) ближе фокуса ( изображение мнимое, прямое и увеличенное)

Отношение линейных размеров изображения

 к линейным размерам предмета

 называется линейным, или поперечным, увеличением:

.

Из подобия треугольников

 и

 (рис. 210, а) находим

(96.1)

Легко убедиться, что равенство (96.1) справедливо и в других случаях получения изображения при помощи сферических зеркал (рис. 210, б и в).

Изображения, получаемые с помощью линзы, могут быть также увеличенными и уменьшенными. Из подобия треугольников

 и

 (рис. 211) находим для увеличения линзы точно такое же выражение, какое мы получили для сферического зеркала:

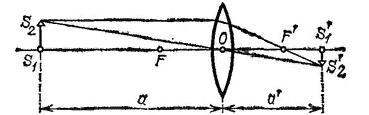
Рис. 211. Линейное увеличение

Наряду с линейным увеличением мы будем рассматривать также угловое увеличение линзы (или сферического зеркала). Угловым увеличением

 называется отношение тангенсов углов

 и

, составляемых лучом, выходящим из линзы, и лучом, падающим на линзу, с оптической осью, т.е.

. (96,3)

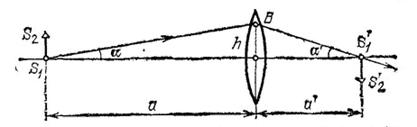
Рис. 212. Угловое увеличение

Из рис. 212 видно, что

;

отсюда

.

Сравнивая это соотношение с (96.1), находим

, (96.4)

т. е. угловое увеличение есть величина, обратная линейному увеличению. Из этого следует, что чем больше линейное увеличение, т.е. размеры изображения, тем меньше угловое увеличение, т. е. тем менее широки пучки световых лучей, образующих изображение. Это обстоятельство имеет важное значение для понимания вопроса о яркости изображения (см. гл. XI).

юя D 8 7 8 : 0

Каждый день по нескольку раз вы смотрите в зеркало и видите в нем своё изображение. Попробуем ответить на вопросы: где и на каком расстоянии от зеркала находится изображение? Какие его размеры по сравнению с размерами самого предмета? И как оно образуется?

Чтобы ответить на эти вопросы, проделаем такой опыт. На столе расположим вертикально стеклянную пластинку и зажжённую свечу. Стеклянная пластинка будет выполнять роль плоского зеркала.

Как видим, в стекле хорошо видно изображение свечи. Однако, заглянув за пластинку, мы свечи там не обнаружим.

Теперь возьмём такую же по размерам, но незажжённую свечу и будем перемещать с другой стороны пластинки вдоль линейки до тех пор, пока она не совместится с изображением, то есть не будет казаться зажжённой. По линейке определим расстояния от пластинки до свечи и до её изображения. Не трудно заметить, что эти расстояния оказались равными. А так как незажжённая свеча совместилась с изображением по высоте, то можно сделать вывод, что размеры изображения равны размерам предмета.

Если передвинуть свечу ближе к стеклянной пластинке, то её изображение тоже приблизится, причём ровно на столько же, на сколько приблизилась свеча.

Положение изображения не изменится, если вместо стеклянной пластинки использовать плоское зеркало.

Из проведённых опытов следует, что в плоском зеркале глаз видит изображение таких же размеров, что и предмет, и на таком же расстоянии за зеркалом.

Но что значит: «Глаз видит изображение»? Как глаз определяет местоположение предмета или его изображения? Чтобы ответить на возникшие вопросы, давайте рассмотрим, как получается изображение предмета в плоском зеркале. Итак, пусть перед зеркалом находится источник света S. Из множества лучей выделим два, например, SA и SB, падающих на зеркало. Пользуясь законом отражения света, построим отражённые лучи/

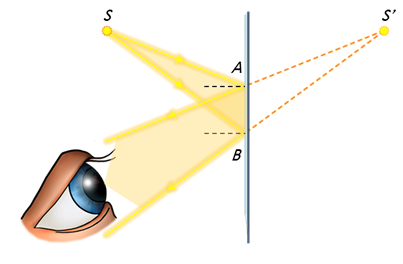
Не трудно заметить, что пучок света, ограниченный отражёнными лучами, будет расходящимся. Он то и попадает в глаз наблюдателя.

Если продолжить отражённые лучи за плоскость зеркала, то они пересекутся в точке S’. Глаз воспринимает отражённые лучи так, как будто они исходят из этой точки, которая является изображением светящейся точки S. То есть глазу кажется, что светящаяся точка находиться именно там. Такое изображение называют мнимым.

Мнимое изображение — изображение, получаемое на пересечении не самих отражённых (или преломлённых) лучей, а их продолжений.

Следовательно, плоское зеркало даёт мнимое изображение.

Теперь построим изображение протяжённого предмета, например, свечи в плоском зеркале. Для этого нам необходимо построить изображение двух её крайних точек. Для этого можно использовать любые два луча. Итак, пусть первый луч от точки А падает на зеркало в точку О перпендикулярно плоскости зеркала. Значит, угол падения равен 0^о. Следовательно, отражённый луч пойдёт вдоль падающего, но в обратном направлении, так как, согласно закону отражения света, угол падения и угол отражения равна.

Второй луч направим к зеркалу под некоторым углом. От зеркала он отразиться под таким же углом.

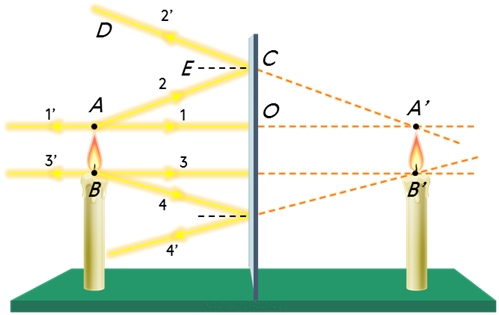
Из полученного рисунка видно, что отражённые лучи не пересекаются. Но пересекаются их продолжения в точке A’. Следовательно, эта точка и есть изображение точки A причём, как вы уже догадались, мнимое изображение.

Аналогично можно построить изображение любой точки предмета, в том числе и точки B.

Пользуясь признаками равенства треугольников, нетрудно доказать, что треугольники ACO и A’CO.

Это ещё раз подтверждает, что изображение предмета за зеркалом, находится на таком же расстоянии от него, как и сам предмет.

Важно запомнить, что предмет и его изображение в плоском зеркале представляют собой не тождественные, а симметричные фигуры. Например, посмотрим на изображение человека в зеркале. Правая рука на этом изображении расположена так, как будто это рука левая. То есть в зеркале «право» и «лево» меняются местами.

Таким образом, из опытов и построений следует, что изображение предмета в плоском зеркале является мнимым, прямым (то есть не перевёрнутым), по размерам равным предмету, находится на таком же расстоянии за зеркалом, на котором расположен предмет перед зеркалом и симметрично предмету.

Зеркала применяются в различных сферах жизнедеятельности человека: в быту, в медицине, на транспорте и в космической сфере.

Плоское зеркало используется и в перископе. Этот прибор устанавливают, например, на подводных лодках. Он позволяет с лодки, находящейся под водой, увидеть, что происходит на поверхности воды. Перископ представляет собой трубу, состоящую из трёх секций: двух горизонтальных и одной вертикальной. В местах соединения горизонтальных и вертикальной секций расположены зеркала. Зеркала взаимно параллельны и составляют угол сорок пять градусов с горизонталью.

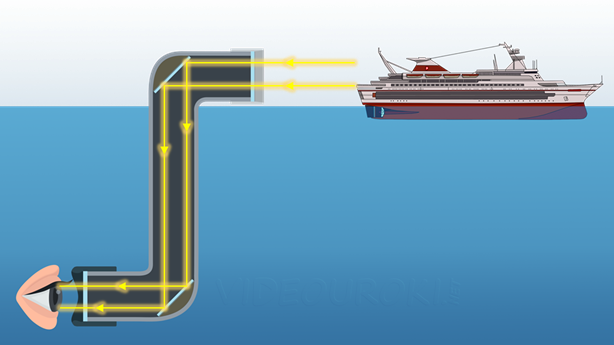
Принцип работы перископа следующий. На верхнее зеркало падают горизонтальные лучи света от предмета, например, от корабля. После отражения от зеркала лучи изменят своё направление на вертикальное и попадут на второе зеркало. После отражения в нём лучи света вновь изменят направление на девяносто градусов и попадут в глаз наблюдателя.

Пример решения задач.

Задача. В системе двух зеркал глаз увидел изображение светящейся точки благодаря лучам 1 и 2. Где оно расположено? Где находится сама светящаяся точка? Сколько всего будет изображений?

Домашняя работа

стр. 198 — 200

Упр. 46

Из прошлых уроков вы уже знаете, что свет распространяется прямолинейно в однородной среде, а при столкновении с какой-либо поверхностью — отражается.

Один из видов отражения называется зеркальным. При слове «зеркало» мы представляем себе плоское стекло, на одну сторону которого нанесено специальное покрытие, содержащее серебро. Но в физике зеркалом может считаться любой предмет, имеющий гладкую плоскую поверхность.

У зеркал есть одна интересная особенность, которая нас и будет интересовать в этом уроке. Мы видим в зеркале отражения — себя и окружающих нас предметов. 

Мы же видим предметы благодаря свету, но предметы в зеркале — ненастоящие. Что происходит на самом деле? Как это объясняет физика? На данном уроке вы узнаете много нового и интересного о, казалось бы, такой простой и привычной вещи, как зеркало.

Изображение в плоском зеркале

Плоское зеркало — это плоская поверхность, зеркально отражающая свет.

Рассмотрим изображение, которые мы получаем с помощью него. 

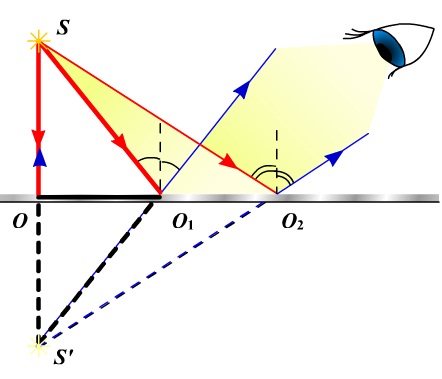
Возьмем плоское зеркало $MN$ (рисунок 1). У нас есть источник света $S$, от которого идет расходящийся пучок света. Мы изобразим его с помощью расходящихся лучей $SO$, $SO_1$ и $SO_2$.

Рассмотрим все лучи по очереди:

• Луч $SO$
  Луч достигает зеркала и отражается. Угол падения равен $0 degree$, значит (по закону отражения света) угол отражения тоже будет равен $0 degree$. Отраженный луч $OS$ совпадает с лучом $SO$, но имеет другое направление

• Луч $SO_1$
  Этот луч падает на зеркало под углом $alpha_1$ и отражается под углом $beta_1$. По закону отражения: $angle beta_1 = angle alpha_1$

• Луч $SO_2$
  Данный луч падает на плоское зеркало под углом $alpha_2$ и отражается под углом $beta_2$ ($angle beta_2 = angle alpha_2$)

Мы видим, что в глаз попадет расходящийся пучок света, который определяют лучи $SO_1$ и $SO_2$.

А теперь продолжим все отраженные лучи за зеркало. Они сойдутся в точке $S_1$. Эта точка называется мнимым изображением точки $S$.

Изображение в плоском зеркале называют мнимым, так как оно получается в результате пересечения не реальных лучей света, а их воображаемых продолжений.

В итоге, получается, что в глаз попадает расходящийся пучок света, исходящий как будто бы из точки $S_1$. Но в этой точке сходятся не сами лучи, а только их продолжения. В действительности изображения в этой точке нет: нам только кажется, что из этой точки исходят лучи.

Построение мнимого изображения светящейся точки

Источник света, подобный тому, что мы рассмотрели выше, принято называть светящейся точкой (точка $S$ на рисунке 1). Построить мнимое изображение такой точки очень просто. 

На рисунке 1 мы описали пучок света с помощью трех лучей, чтобы обратить ваше внимание на то изображение, которое попадает в глаза. Для построения такого изображения на чертеже нам хватит выделить всего два луча:
1. Луч, перпендикулярный зеркалу
2. Луч, падающий под углом

Второй луч мы выбираем удобным для нас образом, чтобы он попадал на зеркало под каким-то углом падения $alpha$.

Итак, возьмем светящуюся точку $S$ и плоское зеркало $MN$ (рисунок 2).

Из точки $S$ опустим перпендикуляр на зеркало. Мы отметили первый луч $SA$. Отраженный луч будет совпадать с ним, но иметь обратное направление — $AS$.

Отметим второй луч — $SB$, он падает на поверхность зеркала под углом $alpha$. Опустим на поверхность зеркала перпендикуляр $BC$ и отложим от него угол $beta$, по закону отражения света равный углу $alpha$. Мы получили отражённый луч $CD$.

Теперь необходимо продолжить лучи $AS$ и $CD$ за зеркало до их пересечения. Точка их пересечения $S_1$ — это мнимое изображение светящейся точки $S$.

Расположение и размеры предмета и его мнимого изображения относительно зеркала

Используя признаки равенства треугольников на рисунке 1, мы можем доказать, что $S_1O = OS$. То же самое можно проделать и с отрезками $AS$ и $AS_1$ на рисунке 2. Значит, изображение предмета находится на таком же расстоянии за зеркалом, на каком предмет расположен перед зеркалом.

Подтвердим этот факт простым, но очень показательным опытом. Возьмем обычную линейку и вертикально укрепим на ней кусок плоского стекла, как на рисунке 3. 

Стекло будет являться полупрозрачным зеркалом. С одной его стороны мы видим зеркальное отражение предметов, а с другой — то, что происходит за этим стеклом.

Также у нас имеются две одинаковые свечи. Одну поставим на расстоянии 3 см от зеркала и зажжем. Мы видим ее отражение в зеркале. Кажется, что оно находится позади стекла.

Наша задача — разместить вторую свечу с другой стороны зеркала так, чтобы она тоже казалась зажженой. Передвигая ее, найдем это положение.

Что мы получили? Незажженная свеча находится именно в том месте, где наблюдается изображение горящей свечи (рисунок 3, а). А теперь взгляните на линейку — за зеркалом свеча находится тоже на 3 см от него. Расстояние от свечи до стекла и от ее изображения до стекла одинаковы.

Итак, мы подошли к интересному выводу.

Мнимое изображение предмета в плоском зеркале находится на том же расстоянии от зеркала, на каком находится сам предмет.

Из этого опыта также очевидно, что высота изображения свечи равна высоте самой свечи (рисунок 3, б). Ведь, передвигая свечу за зеркалом, мы добились того, что она полностью совпала с изображением зажженной свечи.

Размеры изображения предмета в плоском зеркале равны реальным размерам предмета.

Из своего жизненного опыта каждый из нас знает, что когда мы смотрим на изображение предмета в зеркале, мы видим его симметричную форму (рисунок 4).

Это означает, что в зеркале «право» и «лево» меняются местами. Например, зеркальное изображение левой руки представляет для нас как бы правую руку.

Давайте подведем итоги.

Изображение предмета в плоском зеркале:

• Мнимое (находится на пересечении продолжений лучей, а не самих лучей)
• Прямое (не перевернутое)
• Равное по размеру самому предмету
• Находится за зеркалом на таком же расстоянии, как и предмет перед ним
• Симметричное предмету

Построение мнимого изображения предмета

Вы уже узнали определение плоского зеркала и установили его свойства. Теперь давайте рассмотрим, как самостоятельно построить мнимое изображение любого предмета в зеркале.

На чертеже у нас есть плоское зеркало и предмет $AB$ (рисунок 5).

Начнем построение изображения. Для этого опустим из точки $A$ перпендикуляр $АС$ на плоское зеркало. Теперь измерим и зафиксируем длину этого отрезка ($AC$).

Продлим отрезок $AC$ за зеркало и отложим расстояние, равное его длине. Так мы получили точку $A_1$ — мнимое изображение точки $A$.

Проделаем то же самое с точкой $B$. Опустим перпендикуляр на зеркало, продолжим и на определенном расстоянии отметим точку $B_1$.

Теперь осталось только соединить две полученные точки. Так мы получили мнимое изображение $A_1B_1$ предмета $AB$.

Пример задачи

Солнечные лучи при падении образуют с горизонтом угол $varphi = 40 degree$. Под каким углом к горизонту нужно расположить плоское зеркало, чтобы отраженные лучи пошли вертикально вверх?

Дано:
$varphi = 40 degree$

$eta — ?$

Для решения задачи нам понадобится рисунок 6.

Как мы получили такую картинку? Давайте разберемся.

Первым делом проводим линию горизонта $MN$ и отмечаем наш источник света ($S$). Солнечные лучи представим в виде одного падающего луча $SO$. Отмечаем угол между падающим лучом и линией горизонта — угол $varphi$.

Теперь нарисуем отраженный луч $OD$. По условию задачи $OD perp MN$.

По закону отражения света угол падения равен углу отражения. Поэтому мы разделим угол, образованный на картинке падающим и отраженными лучами, пополам — проведем биссектрису $OC$. Отметим угол падения $alpha$ и угол отражения $beta$.

Теперь вспомните, как мы строим отражённый луч. Для этого мы проводим перпендикуляр к отражающей поверхности. В нашем случае, эта поверхность — это зеркало, а перпендикуляр у нас уже есть — $OC$. Значит, поверхность зеркала должна располагаться перпендикулярно этому отрезку. 

Таким образом изобразим на рисунке зеркало и отметим искомый угол $eta$.

Теперь можно приступать к решению задачи.

Посмотреть решение и ответ

Скрыть

Применение плоских зеркал

В повседневной жизни нас окружает множество плоских зеркал. Они нашли очень широкое применение как в быту, так и в технике.

Например, плоские зеркала используют в фарах различных автомобилей, прожекторов. И помимо этого, мы можем упомянуть и о дорожных и автомобильных зеркалах (боковых и заднего вида). Многие оптические приборы содержат в своем устройстве одно или несколько зеркал: объективы фотоаппаратов, лазеры, телескопы, перископы).

Перископ — это специальный прибор для наблюдения за поверхностью моря с подводной лодки, идущей на небольшой глубине (рисунок 7).

Простейший перископ представляет собой трубу, в углах которой расположены зеркала. Они наклонены относительно трубы на $45 degree$. Сделано это для изменения хода световых лучей. Благодаря этому человек, находящийся у нижнего края трубы может видеть то, что находится у ее верхнего края.

Также в настоящее время зеркала используются в дизайне интерьеров. С их помощью создается иллюзия пространства — большой объем в небольших помещениях.

Интересный прием с зеркалами используют в магазинах. Один предмет помещают между несколькими зеркальным поверхностями, и создается впечатление, что предмет не один, а их много. Это возможно, если установить зеркала под определенным углом $alpha$ друг к другу. Здесь работает формула, позволяющая рассчитать количество изображений $n$: $n = frac{360 degree — alpha}{alpha}$.

Плоское зеркало — это плоская поверхность, зеркально отражающая свет.

Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света.

  

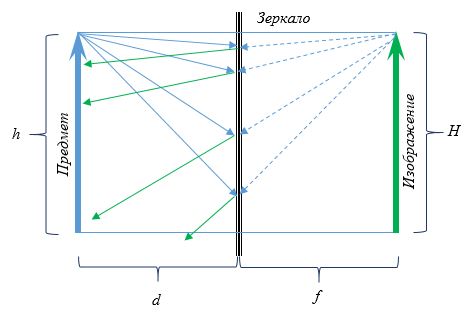
Изображение в плоском зеркале формируется за плоскостью зеркала на том же расстоянии от зеркала f, на каком находится предмет перед зеркалом d:

f = d

Изображение в плоском зеркале является:

• прямым;
• мнимым;
• равным по величине предмету: h = H.

Если плоские зеркала образуют между собой некоторый угол, то они формируют N изображений источника света, помещенного на биссектрису угла между зеркалами:

 

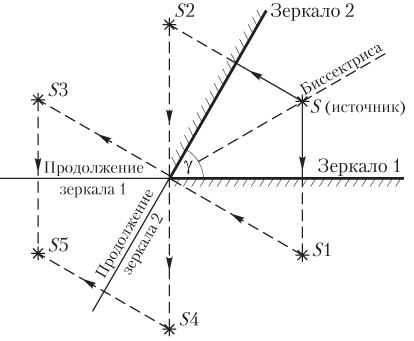
где γ — угол между зеркалами (в радианах).

Примечание: Формула справедлива для таких углов γ, для которых отношение 2π/γ является целым числом.

Сферическим зеркалом называют зеркально отражающую поверхность, имеющую форму сферического сегмента.

Центр сферы, из которой вырезан сегмент, называют оптическим центром зеркала. Вершину сферического сегмента называют полюсом. Прямая, проходящая через оптический центр и полюс зеркала, называется главной оптической осью сферического зеркала. Главная оптическая ось выделена из всех других прямых, проходящих через оптический центр, только тем, что она является осью симметрии зеркала.

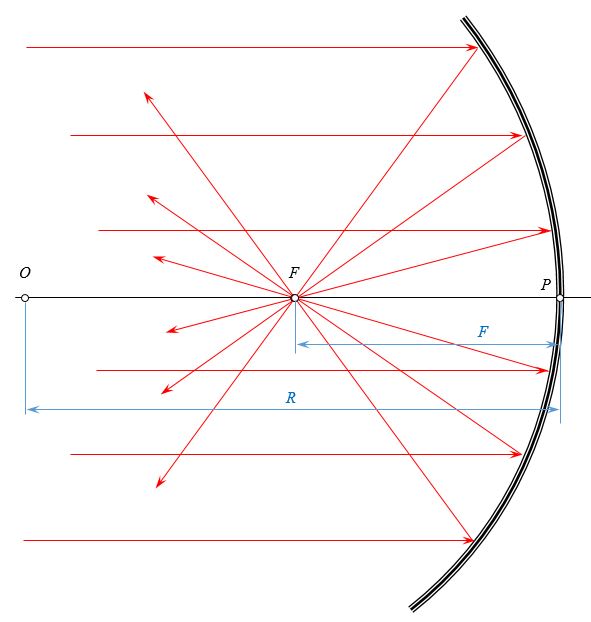
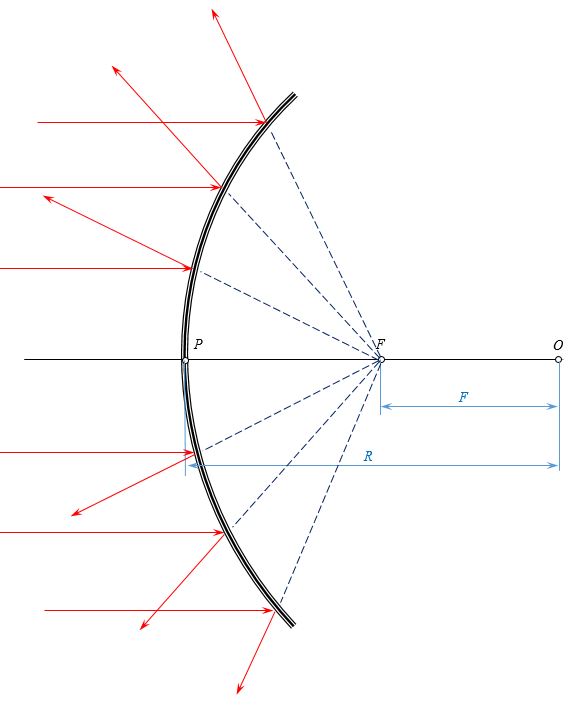
Сферические зеркала бывают вогнутыми и выпуклыми. Если на вогнутое сферическое зеркало падает пучок лучей, параллельный главной оптической оси, то после отражения от зеркала лучи пересекутся в точке, которая называется главным фокусом F зеркала. Расстояние от фокуса до полюса зеркала называют фокусным расстоянием и обозначают той же буквой F. У вогнутого сферического зеркала главный фокус действительный. Он расположен посередине между центром и полюсом зеркала.

Фокусное расстояние у сферического зеркала равно половине радиуса кривизны, причем у вогнутого зеркала F > 0, у выпуклого F < 0.

Изображение какой-либо точки A предмета в сферическом зеркале можно построить с помощью любой пары стандартных лучей:

• луч AOC, проходящий через оптический центр зеркала; отраженный луч COA идет по той же прямой;
• луч AFD, идущий через фокус зеркала; отраженный луч идет параллельно главной оптической оси;
• луч AP, падающий на зеркало в его полюсе; отраженный луч симметричен с падающим относительно главной оптической оси.
• луч AE, параллельный главной оптической оси; отраженный луч EFA₁ проходит через фокус зеркала.

 

Положение изображения и его размер можно также определить с помощью формулы сферического зеркала: 

Здесь d – расстояние от предмета до зеркала, f – расстояние от зеркала до изображения. Величины d и f подчиняются определенному правилу знаков:

• d > 0 и f > 0 – для действительных предметов и изображений;
• d < 0 и f < 0 – для мнимых предметов и изображений.

Линейное увеличение сферического зеркала Γ определяется как отношение линейных размеров изображения H и предмета h.

Величине H удобно приписывать определенный знак в зависимости от того, является изображение прямым (H > 0) или перевернутым (H < 0). Величина h всегда считается положительной. При таком определении линейное увеличение сферического зеркала выражается формулой

Оптическая сила зеркала – величина, обратная фокусному расстоянию, измеряется в диоптриях (дптр)

Задачи

                                        

Зеркало, поверхность которого представляет собой плоскость, называют плоским зеркалом. У сферических и параболических зеркал форма поверхности иная. Кривые зеркала мы изучать не будем. В обиходе чаще всего используют плоские зеркала, поэтому именно на них мы и остановимся.

Когда предмет находится перед зеркалом, то кажется, что за зеркалом находится такой же предмет. То, что мы видим за зеркалом, называется изображением предмета.

Почему мы видим предмет там, где его на самом деле нет?

Для ответа на этот вопрос выясним, как возникает изображение в плоском зеркале. Пусть перед зеркалом находится какая-либо светящаяся точка S (рис. 79). Из всех лучей, падающих из этой точки на зеркало, выделим для простоты три луча: SO, SO₁ и SO₂. Каждый из этих лучей отражается от зеркала по закону отражения света, т. е. под таким же углом, под каким падает на зеркало. После отражения эти лучи расходящимся пучком попадают в глаз наблюдателя. Если продолжить отраженные лучи назад, за зеркало, то они сойдутся в некоторой точке S₁. Эта точка и является изображением точки S. Именно здесь будет видеть наблюдатель источник света.

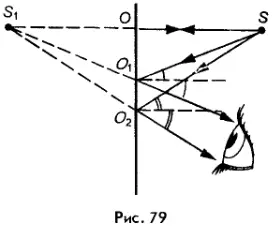
Изображение S₁ называется мнимым, так как получается оно в результате пересечения не реальных лучей света, которых за зеркалом нет, а их воображаемых продолжений. (Если бы это изображение было получено как точка пересечения реальных световых лучей, то оно называлось бы действительным.)

Итак, изображение в плоском зеркале всегда является мнимым. Поэтому когда вы смотритесь в зеркало, то видите перед собой не действительное, а мнимое изображение. Пользуясь признаками равенства треугольников (см. рис. 79), можно доказать, что S1O = OS. Это означает, что изображение в плоском зеркале находится на таком же расстоянии от него, на каком перед ним находится источник света.

Обратимся к опыту. Поместим на столе кусок плоского стекла. Часть света стекло отражает, и поэтому стекло можно использовать как зеркало. Но так как стекло прозрачно, мы сможем одновременно видеть и то, что находится за ним. Поставим перед стеклом зажженную свечу (рис. 80). За стеклом появится ее мнимое изображение (если поместить в изображение пламени кусочек бумаги, то он, конечно, не загорится).

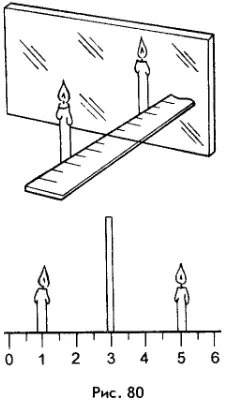
Поставим по другую сторону стекла (где мы видим изображение) такую же, но незажженную свечу и начнем передвигать ее до тех пор, пока она не совместится с полученным ранее изображением (при этом она покажется зажженной). Теперь измерим расстояния от зажженной свечи до стекла и от стекла до ее изображения. Эти расстояния окажутся одинаковыми.
Опыт также показывает, что высота изображения свечи равна высоте самой свечи.

Подводя итоги, можно сказать, что изображение предмета в плоском зеркале всегда является: 1) мнимым; 2) прямым, т. е. неперевернутым; 3) равным по размеру самому предмету; 4) находящимся на таком же расстоянии за зеркалом, на каком предмет расположен перед ним. Иными словами, изображение предмета в плоском зеркале симметрично предмету относительно плоскости зеркала.

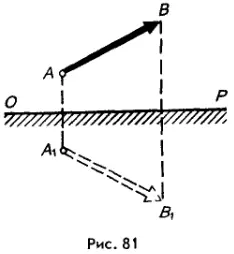
На рисунке 81 показано построение изображения в плоском зеркале. Пусть предмет имеет вид стрелки AB. Для построения его изображения следует:

1) опустить из точки A на зеркало перпендикуляр и, продлив его за зеркалом точно на такое же расстояние, обозначить точку A₁;

2) опустить из точки B на зеркало перпендикуляр и, продлив его за зеркалом точно на такое же расстояние, обозначить точку B₁;

3) соединить точки A₁ и B₁.

Полученный при этом отрезок A₁B₁ будет мнимым изображением стрелки AB.

На первый взгляд у предмета и его изображения в плоском зеркале нет никаких различий. Однако это не так. Посмотрите на изображение своей правой руки в зеркале. Вы увидите, что пальцы на этом изображении расположены так, как будто эта рука левая. Это не случайность: зеркальное отражение всегда меняет правое на левое и наоборот.

Не всем нравится различие правого и левого. Некоторые любители симметрии даже свои литературные произведения стараются написать так, чтобы они читались одинаково как слева направо, так и справа налево (такие фразы-перевертыши называют палиндромами), например: «Кинь лед зебре, бобер, бездельник».

Интересно, что животные по-разному реагируют на свое изображение в зеркале: некоторые его не замечают, у других оно вызывает явное любопытство. Наибольший интерес оно вызывает у обезьян. Когда на стене в одном из открытых вольеров для обезьян повесили большое зеркало, около него собрались все его обитатели. Обезьяны не отходили от зеркала, разглядывая свои изображения, в течение всего дня. И лишь когда им принесли их любимое лакомство, проголодавшиеся животные пошли на зов работницы. Но, как рассказал потом один из наблюдателей зоопарка, сделав несколько шагов от зеркала, они вдруг заметили, как их новые товарищи из «зазеркалья» тоже уходят! Страх больше не увидеть их оказался столь высоким, что обезьяны, отказавшись от пищи, вернулись к зеркалу. В конце концов зеркало пришлось убрать.

В жизни человека зеркала играют не последнюю роль, их используют как в быту, так и в технике.

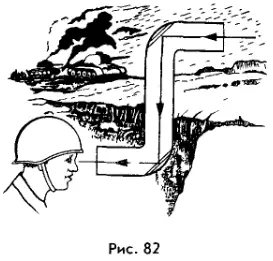
Получение изображения с помощью плоского зеркала может быть использовано, например, в перископе (от греч. «перископео» — смотрю вокруг, осматриваю) — оптическом приборе, служащем для наблюдений из танков, подводных лодок и различных укрытий (рис. 82).

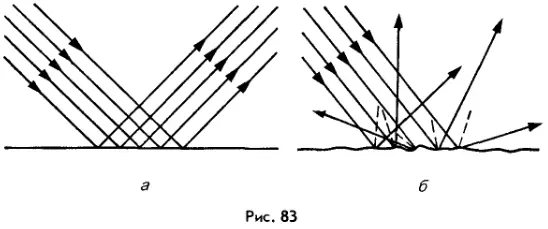
Параллельный пучок лучей, падающих на плоское зеркало, остается параллельным и после отражения (рис. 83, а). Именно такое отражение и называют зеркальным. Но помимо зеркального существует еще и другой вид отражения, когда параллельный пучок лучей, падающих на какую-либо поверхность, после отражения рассеивается ее микронеровностями по всевозможным направлениям (рис. 83, б). Такое отражение называют диффузным’, его создают негладкие, шероховатые и матовые поверхности тел. Именно благодаря диффузному отражению света становятся видимыми окружающие нас предметы.

??? 1. Чем отличаются плоские зеркала от сферических? 2. В каком случае изображение называют мнимым? действительным? 3. Охарактеризуйте изображение в плоском зеркале. 4. Чем отличается зеркальное отражение от диффузного? 5. Что мы увидели бы вокруг, если бы все предметы вдруг стали отражать свет не диффузно, а зеркально? 6. Что такое перископ? Как он устроен? 7. Используя рисунок 79, докажите, что изображение точки в плоском зеркале находится на таком же расстоянии от зеркала, на каком находится перед ним данная точка.

Экспериментальное задание. Встаньте дома перед зеркалом. Совпадает ли характер видимого вами изображения с тем, что описано в учебнике? С какой стороны у вашего зеркального двойника находится сердце? Отступите от зеркала на один-два шага. Что при этом произошло с изображением? Как изменилось его расстояние от зеркала? Изменилась ли при этом высота изображения?