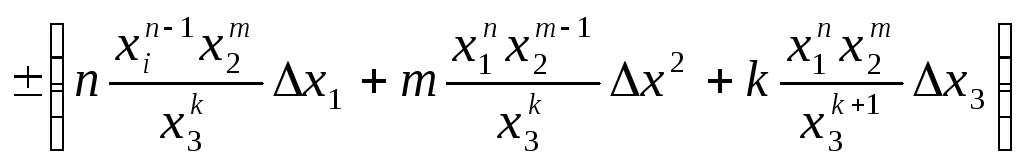Погрешности измерений, представление результатов эксперимента
- Шкала измерительного прибора
- Цена деления
- Виды измерений
- Погрешность измерений, абсолютная и относительная погрешность
- Абсолютная погрешность серии измерений
- Представление результатов эксперимента
- Задачи
п.1. Шкала измерительного прибора
Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.
Примеры шкал различных приборов:
п.2. Цена деления
Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.
Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.
Пример определения цены деления:
 |
Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
п.3. Виды измерений
Вид измерений
Определение
Пример
Прямое измерение
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Косвенное измерение
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.
Составляющие погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$
Если величина (a_0) – это истинное значение, а (triangle a) – погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$
Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$
Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.
Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}
п.6. Представление результатов эксперимента
Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то
- абсолютная погрешность их суммы равна сумме абсолютных погрешностей
$$ triangle (a+b)=triangle a+triangle b $$
- абсолютная погрешность их разности также равна сумме абсолютных погрешностей
$$ triangle (a-b)=triangle a+triangle b $$
Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:
- относительная погрешность их произведения равна сумме относительных погрешностей
$$ delta_{acdot b}=delta_a+delta_b $$
- относительная погрешность их частного также равна сумме относительных погрешностей
$$ delta_{a/b}=delta_a+delta_b $$
Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:
- относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности
$$ delta_{a^2}=2delta_a $$
- относительная погрешность куба (a^3) равна утроенной относительной погрешности
$$ delta_{a^3}=3delta_a $$
- относительная погрешность произвольной натуральной степени (a^n) равна
$$ delta_{a^n}=ndelta_a $$
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно? 
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac{b-a}{n+1}), мл |
| 1 | 20 | 40 | 4 | (frac{40-20}{4+1}=4) |
| 2 | 100 | 200 | 4 | (frac{200-100}{4+1}=20) |
| 3 | 15 | 30 | 4 | (frac{30-15}{4+1}=3) |
| 4 | 200 | 400 | 4 | (frac{400-200}{4+1}=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac{triangle}{2}), мл |
Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%}) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})
Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.
Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать
Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: 
. То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):
(5.1)
Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 
0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.
На точность измерения влияет много факторов, в частности:
- При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» – смотреть можно под разными углами.
- Не вполне ровно установили рулетку.
- Наша рулетка является копией эталона и может несколько отличаться от оригинала.
Все это необходимо учитывать при проведении измерений.
Итоги:
- Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
- Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
- Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины: и указывает на качество измерения. Ее можно выразить в процентах.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.
Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.
На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.
Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
- выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
- подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
- вычесть из большего значения меньшее (4 см – 3 см = 1 см) и результат разделить на число делений.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
- Для линейки 1:
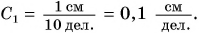
- Для линейки 2:
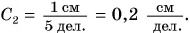
- Для линейки 3:
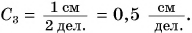
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:
Цена деления шкалы мензурки 2:
А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше 
Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы 
), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления 
). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.
Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
- Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
- Цена деления шкалы равна значению наименьшего деления шкалы.
- Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
- Заказать решение задач по физике
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.
Решение:
1) Цена деления нижней шкалы:
Цена деления средней шкалы:
Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10° 
определенный по средней шкале с точностью до 5° 
определенный по верхней шкале с точностью до 1° 
- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
Загрузить PDF
Загрузить PDF
При измерении чего-либо можно предположить, что есть некоторое «истинное значение», которое лежит в пределах диапазона значений, которые вы нашли. Для расчета более точной величины нужно взять результат измерения и оценить его при прибавлении или вычитании погрешности. Если вы хотите научиться находить такую погрешность, выполните следующие действия.
-
1
Выражайте погрешность правильно. Допустим, при измерении палки ее длина равна 4,2 см плюс-минус один миллиметр. Это означает, что палка примерно равна 4,2 см, но на самом деле может быть немного меньше или больше этого значения — с погрешностью до одного миллиметра.
- Запишите погрешность как: 4,2 см ± 0,1 см. Вы также можете переписать это как 4,2 см ± 1 мм, так как 0,1 см = 1 мм.
-
2
Всегда округляйте значения измерений до того же знака после запятой, что и в погрешности. Результаты измерений, которые учитывают погрешность, как правило, округляются до одной или двух значащих цифр. Наиболее важным моментом является то, что нужно округлить результаты до того же знака после запятой, что и в погрешности, чтобы сохранить соответствие.
- Если результат измерения 60 см, то и погрешность следует округлять до целого числа. Например, погрешность этого измерения может быть 60 см ± 2 см, но не 60 см ± 2,2 см.
- Если результат измерения 3,4 см, то погрешность округляется до 0,1 см. Например, погрешность этого измерения может быть 3,4 см ± 0,7 см, но не 3,4 см ± 1 см.
-
3
Найдите погрешность. Допустим, вы измеряете линейкой диаметр круглого шара. Это сложно, так как из-за кривизны шара будет трудно померить расстояние между двумя противоположными точками на его поверхности. Скажем, линейка может дать результат с точностью до 0,1 см, но это не значит, что вы можете измерить диаметр с той же точностью.[1]
- Изучите шар и линейку, чтобы получить представление о том, с какой точностью вы можете измерить диаметр. У стандартной линейки четко видна разметка по 0,5 см, но, возможно, вы сможете измерить диаметр с большей точностью, чем эта. Если вы думаете, что сможете измерить диаметр с точностью до 0,3 см, то погрешность в этом случае равна 0,3 см.
- Измерим диаметр шара. Допустим, вы получили результат около 7,6 см. Просто укажите результат измерения вместе с погрешностью. Диаметр шара составляет 7,6 см ± 0,3 см.
-
4
Рассчитайте погрешность измерения одного предмета из нескольких. Скажем, вам даны 10 компакт-дисков (CD), при этом размеры каждого одинаковы. Допустим, вы хотите найти толщину всего одного CD. Эта величина настолько мала, что погрешность практически невозможно вычислить. Тем не менее, чтобы вычислить толщину (и ее погрешность) одного CD, вы можете просто разделить результат измерения (и его погрешность) толщины всех 10 CD, сложенных вместе (один на другого), на общее количество CD.[2]
- Допустим, что точность измерения стопки CD с помощью линейки 0,2 см. Итак, ваша погрешность ± 0,2 см.
- Допустим, толщина всех CD равна 22 см.
- Теперь разделим результат измерения и погрешность на 10 (число всех CD). 22 см/10 = 2,2 см и 0,2 см/10 = 0,02 см. Это означает, что толщина одного компакт-диска 2,20 см ± 0,02 см.
-
5
Измерьте несколько раз. Для повышения точности измерений, будь то измерение длины или времени, замерьте искомую величину несколько раз. Вычисление среднего значения из полученных значений увеличит точность измерения и расчета погрешности.
Реклама
-
1
Проведите несколько измерений. Допустим, вы хотите найти, сколько времени падает мяч с высоты стола. Чтобы получить наилучшие результаты, измерьте время падения насколько раз, например, пять. Потом нужно найти среднее значение из пяти полученных значений измерений времени, а затем для наилучшего результата добавить или вычесть среднеквадратичное отклонение.[3]
- Допустим, в результате пяти измерений получены результаты: 0,43 с, 0,52 с, 0,35 с, 0,29 с и 0,49 с .
-
2
Найдите среднее арифметическое. Теперь найдите среднее арифметическое путем суммирования пяти различных результатов измерений и разделив результат на 5 (количество измерений). 0,43 + 0,52 + 0,35 + 0,29 + 0,49 = 2,08 с. 2,08 / 5 = 0,42 с. Среднее время 0,42 с.
-
3
Найдите дисперсию полученных значений. Для этого, во-первых, найдите разницу между каждой из пяти величин и средним арифметическим. Чтобы сделать это, вычтите из каждого результата 0,42 с.[4]
-
- 0,43 с – 0,42 с = 0,01 с
- 0,52 с – 0,42 с = 0,1 с
- 0,35 с – 0,42 с = -0,07 с
- 0,29 с – 0,42 с = -0,13 с
- 0,49 с – 0,42 с = 0,07 с
- Теперь сложите квадраты этих разниц: (0,01) 2 + (0,1) 2 + (-0,07) 2 + (-0,13) 2 + (0,07) 2 = 0,037 с.
- Найти среднее арифметическое этой суммы можно, разделив ее на 5: 0,037 / 5 = 0,0074 с.
-
-
4
Найдите среднеквадратичное отклонение. Чтобы найти среднеквадратичное отклонение, просто возьмите квадратный корень из среднего арифметического суммы квадратов. Квадратный корень из 0,0074 = 0,09 с, так что среднеквадратичное отклонение равно 0,09 с.[5]
-
5
Запишите окончательный ответ. Чтобы сделать это, запишите среднее значение всех измерений плюс-минус среднеквадратичное отклонение. Поскольку среднее значение всех измерений равно 0,42 с, а среднеквадратичное отклонение 0,09 с, то окончательный ответ 0,42 с ± 0,09 с.
Реклама
-
1
Сложение. Чтобы сложить величины с погрешностями, сложите отдельно величины и отдельно погрешности.[6]
- (5 см ± 0,2 см) + (3 см ± 0,1 см) =
- (5 см + 3 см) ± (0,2 см + 0,1 см) =
- 8 см ± 0,3 см
-
2
Вычитание. Чтобы вычесть величины с погрешностями, вычтите величины и сложите погрешности.[7]
- (10 см ± 0,4 см) – (3 см ± 0,2 см) =
- (10 см – 3 см) ± (0,4 см + 0,2 см) =
- 7 см ± 0,6 см
-
3
Умножение. Чтобы умножить величины с погрешностями, перемножьте величины и сложите ОТНОСИТЕЛЬНЫЕ погрешности (в процентах).[8]
Рассчитать можно только относительную погрешность, а не абсолютную, как и в случае со сложением и вычитанием. Чтобы узнать относительную погрешность, разделите абсолютную погрешность на измеренное значение, затем умножьте на 100, чтобы выразить результат в процентах. Например:- (6 см ± 0,2 см) = (0,2 / 6) x 100 — добавив знак процента, получаем 3,3 %.
Следовательно: - (6 см ± 0,2 см) х (4 см ± 0,3 см) = (6 см ± 3,3 % ) x (4 см ± 7,5 %)
- (6 см x 4 см) ± (3,3 + 7,5) =
- 24 см ± 10,8 % = 24 см ± 2,6 см
- (6 см ± 0,2 см) = (0,2 / 6) x 100 — добавив знак процента, получаем 3,3 %.
-
4
Деление. Чтобы разделить величины с погрешностями, разделите величины и сложите ОТНОСИТЕЛЬНЫЕ погрешности.[9]
- (10 см ± 0,6 см) ÷ (5 см ± 0,2 см) = (10 см ± 6 %) ÷ (5 см ± 4 %)
- (10 см ÷ 5 см) ± (6 % + 4 %) =
- 2 см ± 10 % = 2 см ± 0,2 см
-
5
Возведение в степень. Для того, чтобы возвести в степень величину с погрешностью, возведите величину в степень, а относительную погрешность умножьте на степень.[10]
- (2,0 см ± 1,0 см)3 =
- (2,0 см)3 ± (50 %) x 3 =
- 8,0 см3 ± 150 % или 8,0 см3 ±12 см3
Реклама
Советы
- Вы можете дать погрешность как для общего результата всех измерений, так и для каждого результата одного измерения в отдельности. Как правило, данные, полученные из нескольких измерений, менее достоверны, чем данные, полученные непосредственно из отдельных измерений.
Реклама
Предупреждения
- Точные науки никогда не работают с «истинными» величинами. Хотя правильное измерение, скорее всего, даст величину в пределах погрешности, нет никакой гарантии, что это будет так. Научные измерения допускают возможность ошибок.
- Погрешности, описанные здесь, применимы только для случаев нормального распределения (распределения Гаусса). Другие распределения вероятностей требуют других решений.
Реклама
Об этой статье
Эту страницу просматривали 104 724 раза.
Была ли эта статья полезной?
Абсолютная и относительная погрешность
4.2
Средняя оценка: 4.2
Всего получено оценок: 2177.
4.2
Средняя оценка: 4.2
Всего получено оценок: 2177.
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.
Опыт работы учителем математики – более 33 лет.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-
Светлана Лобанова-Асямолова
10/10
-
Валерий Соломин
10/10
-
Анастасия Юшкова
10/10
-
Ксюша Пономарева
7/10
-
Паша Кривов
10/10
-
Евгений Холопик
9/10
-
Guzel Murtazina
10/10
-
Максим Аполонов
10/10
-
Olga Bimbirene
9/10
-
Света Колодий
10/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 2177.
А какая ваша оценка?
15
Л а б о р а т о р н
а я р а б о т а № 1.
ОБРАБОТКА РЕЗУЛЬТАТОВ
ИЗМЕРЕНИЙ.
ОЦЕНКА
ПОГРЕШНОСТЕЙ.
Цель работы:
приобретение
навыков обработки результатов
измерений.
Погрешность измерений
Результат измерений
любой физической величины не может быть
абсолютно точен, обязательно имеется
некоторая погрешность. При оценке
результатов физического эксперимента
это обстоятельство имеет решающее
значение. Например, для некоторой
величины теория предсказывает значение
5.54, а в эксперименте получено 5.6. Можно
ли отсюда сделать вывод – верна теория
или нет? Все зависит от точности
теоретического предсказания и точности
экспериментального результата.
Предположим, что теория предсказывает
значение некоторой величины 5,54±0,01 и
экспериментальный результат получен
также с точностью до одной сотой:
5,60±0,01. Тогда мы делаем вывод, что теория
не подтверждается экспериментом. Если
же точность предсказания и результата
измерений меньше, например 5, 54±0,05 и
5,60±0,06
то вывод, соответственно, будет другой.
Отчего возникает
погрешность? Причины, кроме явных ошибок
экспериментатора, могут быть самые
разнообразные. Принято различать
приборные
погрешности, обусловленные точностью
измерительного прибора и его настройки
и погрешности, вызванные неконтролируемыми
внешними воздействиями, может быть,
даже воздействием самого прибора. Такие
ошибки называют случайными.
Например, при
измерении некоторого размера
штангенциркулем возможна деформация
измеряемого объекта самим штангенциркулем,
под “губки” штангенциркуля может
попасть посторонний микроскопический
предмет, может возникнуть перекос и
т.д. Причиной появления погрешности
может быть и несовершенство принятой
модели. Например, мы считаем объект
измерения телом вращения, а в
действительности его сечение может
иметь форму эллипса. При этом в зависимости
от конкретных условий эксперимента
погрешность может быть в одном случае
отнесена к приборным погрешностям, а в
другом – считаться вызванной внешними
воздействиями, точной границы при таком
разделении погрешностей нет.
Приборные погрешности
в свою очередь могут быть случайными
по величине и знаку или закономерными.
Если погрешность закономерна, ее называют
систематической
и в принципе ее можно учесть в виде
некоторой поправки к результату
измерений.
По форме представления
различают погрешность абсолютную
и относительную.
Смысл этих терминов очевиден. Например,
если результат измерения некоторого
промежутка времени записан так:
Т1=(1,2±0,1)
с; Т2=(214,5±0,1)
с,
то здесь величина
0,1с представляет собой абсолютную
погрешность, обозначается она, как и
измеряемая величина, но со знаком Δ. В
нашем примере: ΔТ=0,1с.
С другой стороны, ясно, что время во
втором случае определено точнее, так
как больший промежуток времени сложнее
определить с той же абсолютной
погрешностью. Чтобы отразить это
обстоятельство в записи величины
погрешности, вводят так называемую
относительную погрешность δТ=
.
Относительная погрешность может
измеряться в процентах, тогда эту
величину умножают на 100%.
Практическое определение погрешности измеряемой величины.
Измерение физической
величины может быть произведено
чувствительным прибором или не очень
чувствительным прибором.
Если измерительный
прибор не очень чувствительный,
погрешность измерений определяется
приборной погрешностью. При этом нет
необходимости проводить измерения
многократно, т.к. это не приводит к
повышению точности измерения. Приборная
погрешность, либо указывается в описании
прибора, либо за такую принимается
половина цены деления шкалы прибора.
Так, при измерении длины миллиметровой
линейкой принято в качестве погрешности
брать величину 0,5 мм. Результат измерения
длины некоторого объекта в этом случае
надо записывать в виде
(385,0 ±0,5) мм.
В дальнейшем
приборную погрешность будем обозначать
ΔTпр.Погрешность
может быть больше этой величины, если
объект не имеет точной границы (например,
при измерении размеров изображения
предмета на экране). Точной рекомендации,
какую при этом брать погрешность нет.
Все зависит от вида измеряемого объекта
и целей измерения.
При использовании
чувствительного прибора (например,
микрометра, миллисекундомера и т.д.) при
повторных измерениях могут получаться
неодинаковые результаты.
Например, измерения
времени падения шарика с некоторой
высоты с помощью миллисекундомера дают
следующие результаты (первая строчка
таблицы):
|
N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
ti, |
0,460 |
0,446 |
0,452 |
0,456 |
0,448 |
0,454 |
0,446 |
0,458 |
|
Δti, |
0,007 |
0,007 |
0,001 |
0,003 |
0,005 |
0,001 |
0,007 |
0,005 |
Простейший расчет
погрешности в этом случае следует
проводить следующим образом:
а) найти среднее
арифметическое значение измеряемой
величины
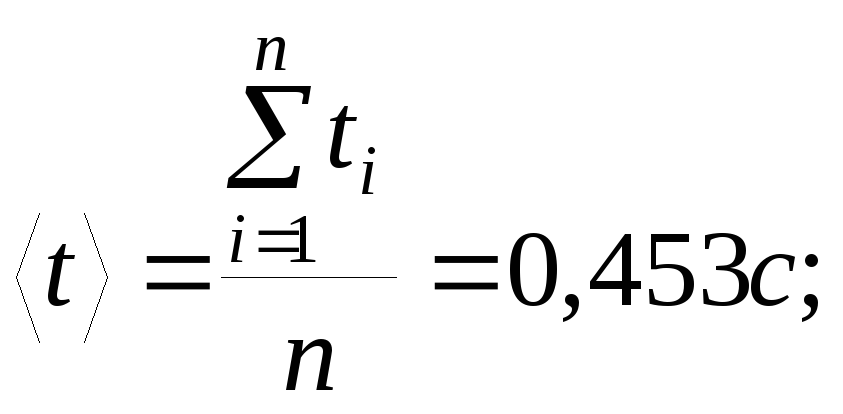
среднее арифметическое
должно содержать столько значащих цифр,
сколько их в измеряемой величине (в
нашем примере – три);
б) для каждого
измерения найти модуль разности среднего
значения
и измеренной величиныti
и занести в таблицу
(вторая строчка таблицы);
в) найти среднее
значение погрешности
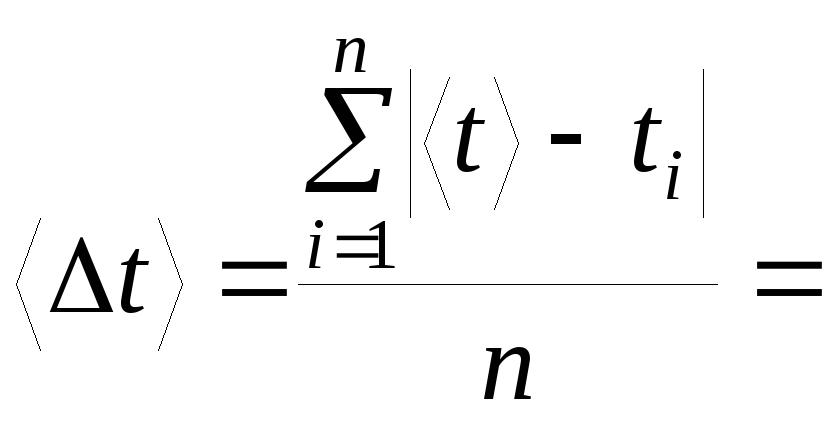
с;
г) сравнить
с приборной погрешностью миллисекундомера
Δtпр.
Если
>Δtпр
, то результат измерения следует записать
в виде
t=
±
Если
<Δtпр,
то результат измерения следует записать
в виде
t=
±
Δtпр.
Например, если
приборная погрешность равна Δtпр=0,002с,
– то
t=(0,453±0,005)
с,
если Δtпр=0,008с,
то
t=(0,453±0,008)
с.
Вообще говоря,
обоснованным для расчета погрешности
Δt является
выражение
Однако если
обратиться к числам, мы с большой степенью
точности получим правило изложенное
выше. Причем точность тем выше, чем
больше разность между Δt2пр
и
.
Действительно, если рассмотреть
предыдущий пример, то для первого случая
получим
c
для второго случая
c
При арифметическом
расчете средних значений измеряемой
величины и погрешности (особенно при
использовании калькулятора) может
получиться такой результат:
х=(12,785±0,4592)
см.
Приведенная запись
является неграмотной. Для того чтобы
правильно записать результат, поступают
следующим образом:
а) округляют
погрешность до двух значащих цифр, если
первой из них является единица, и до
одной значащей цифры во всех остальных
случаях. Например:
|
неправильно
Δх=3,2
Δх=133 Δх=0,387 |
правильно
Δх=3
Δх=1,3·102 Δх=0,4 |
б) при записи
измеренного значения последней должна
указываться цифра того десятичного
разряда, который использован при указании
погрешности. Например,
|
неправильно
х=(15,4±3)
х=(21,17±1,7)
х=(4,886±0,4)
х=(58419±238) |
правильно
х=(15±3)
х=(21,2±1,7)
х=(4,9±0,4)
х=(5,84±0,02)·104 |
Таким образом,
грамотной записью результата для
приведенного выше примера является
такая запись: х=(12,8±0,5) см.Задание 1: Рассчитать среднее
значение периода колебаний и погрешность
периода колебаний математического
маятника, если в результате измерений
получены такие результаты:
|
№ опыта |
1 |
2 |
3 |
4 |
5 |
|
Т, |
1.24 |
1,18 |
1,23 |
1,20 |
1,19 |
Результаты записать
для случаев, когда измерения произведены
секундомером, имеющим погрешности:
а) ΔТпр=0,01с;
б) ΔТпр=0,05с.
Определение
погрешности косвенных измерений.
Часто встречается
ситуация, когда интересующая нас величина
в эксперименте непосредственно не
измеряется, но может быть рассчитана с
помощью функциональной зависимости от
измеряемых величин. В этом случае говорят
о косвенных измерениях. Точность
определения этой величины зависит как
от точности эксперимента, так и от
конкретного вида ее зависимости от
измеряемых величин.
Пусть величину f
можно рассчитать, измерив непосредственно
некоторые физические величины х1,
х2
и т.д., и пусть погрешности этих величин
соответственно равны Δх1,
Δх2
и т.д. Погрешность величины f
можно рассчитать. Воспользовавшись
формулой
(1)
Здесь
– так называемые частные производные,
которые подсчитываются по обычным
правилам в предположении, что остальные
переменные (кроме той, по которой
осуществляется дифференцирование)
зафиксированы. Например, измеряя время
падения тела с некоторой высоты, можно
рассчитать ускорение свободного падения
по формуле
(здесь g
рассматривается как функция двух
переменных H
и t,
определяемых экспериментально).
Пусть Н=(1,00±0,01)
м, t=(0,453±0,005)
с, тогда
;
.
Воспользовавшись
выражением (1), получим
(3)
Подставляя численные
значения, получим 
м/с2.
Таким образом,
g=(9.7±0.3)
м/с2.
Полученные таким
способом формулы для подсчета погрешности
часто оказываются довольно громоздкими
(например, если вычисляемая величина
является функцией большого числа
переменных). На практике во многих
случаях можно избежать использования
таких громоздких формул, подсчитав
сначала относительную погрешность
вычисляемой величины. Например, выражение
(3) можно переписать в виде
,
или
,
(4)
где 
и 
– относительные погрешности измеряемых
величин, 
– относительная погрешность вычисляемой
величины.
Рассчитав g
и выражение, стоящее в скобках в (4), можно
вычислить Δg.
Приведем более
сложный пример. Модуль сдвига материала
проволоки N,из которого изготовлена
пружина жесткостьюk,можно подсчитать
по формуле
,
(5)
где R
– радиус
пружины, r
– радиус проволоки, n
– число витков пружины. Пусть погрешности
измерения этих величин соответственно
равны Δk,
ΔR,
Δr.
Если использовать формулу (1) для расчета
погрешности ΔN,
то получится следующее выражение
,
которым неудобно
пользоваться из-за его громоздкости.
Выражение же для расчета относительной
погрешности более компактно
Обратите внимание!
Относительная погрешность модуля сдвигa
N
равна сумме относительных погрешностей
измеряемых величин. Перед
и
стоят множители равные показателям
степени, с которыми эти величины входят
в формулу (5).Рассчитав
иN
легко определить ΔN
.
Видно, что последний
способ расчета абсолютной погрешности
менее трудоемкий, чем первый. В заключение
приведем таблицу формул для вычисления
погрешностей в некоторых частных
случаях. При ознакомлении с таблицей
обратите внимание на следующее правило:
при сложении (вычитании) некоторых
величин складываются абсолютные
погрешности (пример 3), при умножении
(делении) величин складываются
относительные погрешности (пример 4).
|
Математическая операция |
Погрешность |
|
|
абсолютная |
относительная |
|
|
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
Домашнее задание:
Получить выражение для расчета абсолютной
и относительной погрешности для следующих
математических операций:
а)
;
б)
;
в)
,
(х
и α
– измеряемые величины).
Задание 2.
Измеряя период колебания математического
маятника, можно рассчитать ускорение
свободного падения. Напомним, что
Пусть l=(0.500±0.005)
м, T=(1,42±0,02)
с.
Рассчитайте
ускорение свободного падения.
Соседние файлы в папке Лабораторные работы
- #
- #
- #
- #
- #
- #
