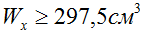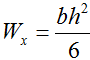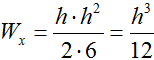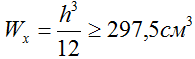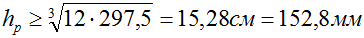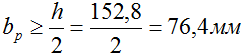Пример решения задачи по подбору минимальных размеров балки прямоугольного поперечного сечения, обеспечивающих её необходимую прочность.
Задача
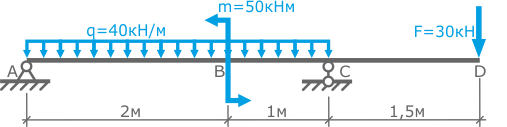
Для заданной стальной балки подобрать размеры прямоугольного поперечного сечения по условию прочности.
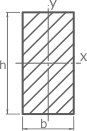
Соотношение сторон сечения h=2b (h – высота, b – ширина).
Полученные размеры принять согласно ГОСТ 6636.
Допустимые напряжения для материала балки [σ]=160МПа.
Другие примеры решений >
Помощь с решением задач >
Решение
Предыдущие пункты решения задачи:
- Определение опорных реакций
- Построение эпюр внутренних поперечных сил и изгибающих моментов
- Расчет момента сопротивления сечения балки по условию прочности
Минимально необходимый расчетный момент сопротивления сечения балки составил
В случаях, когда система изгибающих нагрузок действующих на балку расположена в вертикальной плоскости сечение тоже следует располагать вертикально.
По справочнику находим формулу осевого момента сопротивления прямоугольного сечения
Используя заданное соотношение сторон (h=2b), уменьшим количество переменных в выражении
и запишем необходимое неравенство
откуда находим расчетную высоту прямоугольного сечения
Из заданного соотношения сторон определяем расчетную ширину сечения
Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки.
При отсутствии дополнительных условий расчетные размеры можно округлить до целого значения в миллиметрах исключительно в большую сторону (h=153мм, b=77мм).
По ГОСТ 6636 нормальных линейных размеров выбираются ближайшие значения в сторону увеличения.
Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=155мм, b=80мм.
После принятия размеров согласно ГОСТ заданное соотношение сторон может несколько измениться. Это нормально.
Оценка экономичности сечений >
Построение эпюры нормальных напряжений >
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Расчет балки, подбор прямоугольного сечения

Определение опорных реакций
1. Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки.
ΣFx = 0: HA = 0
ΣMA = 0: Найдем сумму моментов относительно шарнирно-неподвижной опоры в точке A:
- q1*3*(3/2) + RB*3 - M1 + P1*4.5 = 0
ΣMB = 0: Найдем сумму моментов относительно шарнирно-подвижной опоры в точке B:
- RA*3 + q1*3*(3 - 3/2) - M1 + P1*1.5 = 0
2. Решаем полученную систему уравнений, находим неизвестные :
HA = 0 (кН)
3. Вычислим реакцию шарнирно-подвижной опоры в точке B
RB = ( q1*3*(3/2) + M1 - P1*4.5) / 3 = ( 40*3*(3/2) + 30 - 10*4.5) / 3 = 55.00 (кН)
4. Вычислим реакцию шарнирно-неподвижной опоры в точке A
RA = ( q1*3*(3 - 3/2) - M1 + P1*1.5) / 3 = ( 40*3*(3 - 3/2) - 30 + 10*1.5) / 3 = 55.00 (кН)
5. Выполним проверку ΣFy = 0: RA - q1*3 + RB + P1 = 55.00 - 40*3 + 55.00 + 10 = 0
Построение эпюр
Рассмотрим 1-й участок 0 ≤ x1 < 3
Поперечная сила Q:
Q(x1) = + RA - q1*(x1 - 0)
Значения Q на краях участка:
Q1(0) = + 55 - 40*0 = 55 (кН)
Q1(3) = + 55 - 40*3 = -65 (кН)На этом участке эпюра Q пересекает горизонтальную ось. Точка пересечения:
x = 1.38
Изгибающий момент M:
M(x1) = + RA*(x1) - q1*(x1)2/2
Значения M на краях участка:
M1(0) = + 55*(0) - 40*02/2 = 0 (кН*м)
M1(3) = + 55*(3) - 40*32/2 = -15 (кН*м)Локальный экстремум в точке x = 1.38:
M1(1.38) = + 55*(1.38) - 40*(1.38 - 0)2/2 = 37.81 (кН*м)
Рассмотрим 2-й участок 3 ≤ x2 < 4
Поперечная сила Q:
Q(x2) = + RA - q1*3 + RB
Значения Q на краях участка:
Q2(3) = + 55 - 40*3 + 55 = -10 (кН)
Q2(4) = + 55 - 40*3 + 55 = -10 (кН)
Изгибающий момент M:
M(x2) = + RA*(x2) - q1*3*[(x2 - 3) + 3/2] + RB*(x2 - 3)
Значения M на краях участка:
M2(3) = + 55*(3) - 40*3*(0 + 1.50) + 55*(3 - 3) = -15 (кН*м)
M2(4) = + 55*(4) - 40*3*(1 + 1.50) + 55*(4 - 3) = -25 (кН*м)
Рассмотрим 3-й участок 4 ≤ x3 < 4.5
Поперечная сила Q:
Q(x3) = + RA - q1*3 + RB
Значения Q на краях участка:
Q3(4) = + 55 - 40*3 + 55 = -10 (кН)
Q3(4.50) = + 55 - 40*3 + 55 = -10 (кН)
Изгибающий момент M:
M(x3) = + RA*(x3) - q1*3*[(x3 - 3) + 3/2] + RB*(x3 - 3) + M1
Значения M на краях участка:
M3(4) = + 55*(4) - 40*3*(1 + 1.50) + 55*(4 - 3) + 30 = 5 (кН*м)
M3(4.50) = + 55*(4.50) - 40*3*(1.50 + 1.50) + 55*(4.50 - 3) + 30 = 0 (кН*м)
Подбор сечения
Прямоугольное сечение балки подбираем из условия прочности при допускаемом напряжении: 





Момент сопротивления прямоугольного сечения определим по формуле:
Требуемый момент сопротивления 
Поскольку дано соотношение сторон
Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки. Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=145 (мм), b=75 (мм)
Расчет произведен при помощи онлайн-сервиса SOPROMATGURU.RU
Обычно в инженерной
практике проверку прочности балок
производят по нормальным наибольшим и
касательным напряжениям [2]. Нормальные
напряжения σ зависят от величины
изгибавшего момента, а касательные
τ – от величины поперечной силы.
Касательные напряжения в сечениях балки
обычно не играют существенной роли,
поэтому размеры сечения балок определяют
из условия прочности по нормальным
максимальным напряжениям:

где Мmax
–
наибольший (по абсолютной величине)
изгибающий момент, известный из эпюры
изгибающих моментов ().
Сечение балки
подбирается по моменту сопротивления
относительно нейтральной оси:

(3.10)
Для балки
прямоугольного сечения
.
Числовые значения
моментов сопротивления стандартных
профилей проката указаны в соответствующих
государственных стандартах на прокат,
а на балки двутавровые приведены в
таблицах приложения Г. Следует подбирать
номер профиля, имеющий большее стандартное
ближайшее значение. Допустимо принимать
и меньшее ближайшее значение WхСТ,
однако оно должно удовлетворять условию:
.
Момент сопротивления
при изгибе
Подходит швеллер
№ 8 (Wx=22,4
см3,
площадь сечения А=8,98 см2).
Определим
прямоугольное сечение (рисунок 3.10) при
Рисунок 3.10 –
Сечение швеллера и прямоугольное сечение
Площадь
прямоугольного сечения
A=bh=16,27
см2
≈
в 2 раза больше площади швеллера.
3.4 Совместное действие изгиба и кручения
Сочетание деформаций
изгиба и кручения испытывает большинство
валов, которые обычно представляют
собой прямые брусья круглого или
кольцевого сечения.
Возникающие от
изгиба нормальные напряжения достигают
максимального значения в волокнах,
наиболее удаленных от нейтральной оси:
,
где М – максимальный
изгибающий момент, Нм;
W
– осевой момент сопротивления сечения,
м3.
Для вала круглого
сечения
Максимальные
касательные напряжения при кручении
возникают в точках контура поперечного
сечения:
где Wp
– полярный момент сопротивления сечения
(Wp=2W),
м3;
Т
– крутящий момент, Нм.
Таким образом, при
сочетании изгиба и кручения опасными
будут точки (для конкретного поперечного
сечения), наиболее удаленные от нейтральной
оси.
Применив третью
теорию прочности, получим

Расчетная формула
для круглых валов принимает вид:

где М
экв.
– эквивалентный момент, Нм;
[σ]
– допускаемое
напряжение на растяжение для материала
вала, Па.
Если величина и
направление нагрузки во время работы
вращающегося вала остаются неизменными,
то напряжения изгиба в теле вала будут
изменяться во времени по симметричному
циклу – I циклу
нагружения (рисунок 3.11).
Рисунок 3.11 – График
изменения во времени напряжения изгиба
I
цикл
При действии на
вал нагрузок в разных плоскостях силы
раскладывают на две взаимно перпендикулярные
плоскости, за одну из которых выбирают
плоскость действия одной из сил.
Суммарный изгибающий
момент определится как геометрическая
сумма моментов, действующих во взаимно
перпендикулярных плоскостях
рассматриваемого сечения:
где Мiв
и Мiгор
– изгибающие
моменты в i
– м сечении,
действующие в вертикальной и в
горизонтальной плоскостях соответственно.
Эквивалентный
момент определится по формуле:
,
Диаметр вала в
опасном сечении
рассчитывается из условия прочности:

Примечание –
При решении задач все необходимые
вычисления следует сначала проделать
в общем виде, обозначая все данные и
искомые величины буквами, после чего
вместо буквенных обозначений подставить
их числовые значения и найти результат.
На расчетных эскизах размеры должны
быть проставлены теми же буквами, какие
имеются в расчетных формулах.
Пример 4.
Построить
эпюры изгибающих, крутящего, суммарного
изгибающего моментов и определить
диаметр вала (рисунок 3.12) в опасном
сечении.
Т = 0,2 кНм, F
= 2 кН, q
= 4 кН/м, a
= 0,2м, b
=1,2а = 0,24м,
с = 0,8а = 0,16м, [σ]
= 110МПа.
Решение:
Плоскость yz:
Плоскость хz:
Из условия прочности
наиболее нагруженного сечения А определим
диаметр вала.
Рисунок 3.12 –
Расчетная
схема и эпюры вала
ПРИЛОЖЕНИЕ А
ЗАДАЧА 1
Расчет бруса на
осевое растяжение (сжатие)
Сечение бруса
квадратное. Материал – сталь. Допускаемое
напряжение [σ]
= 100 МПа. Модуль продольной упругости Е
= 2·105
МПа. Исходные данные к расчету см. в
таблице + рисунок.
ИСХОДНЫЕ ДАННЫЕ
|
Вариант |
F1 |
F2 |
F3 |
l1 |
l2 |
l3 |
|
кН |
м |
|||||
|
1 |
32 |
18 |
24 |
0,7 |
0,4 |
0,8 |
|
2 |
28 |
16 |
12 |
0,6 |
0,5 |
0,7 |
|
3 |
22 |
8 |
26 |
0,5 |
0,6 |
0,9 |
|
4 |
19 |
24 |
15 |
0,8 |
0,6 |
0,5 |
|
5 |
30 |
12 |
16 |
0,4 |
0,9 |
0,6 |
|
6 |
27 |
15 |
10 |
0,6 |
0,7 |
0,8 |
|
7 |
24 |
14 |
8 |
0,3 |
0,8 |
0,7 |
|
8 |
26 |
16 |
11 |
0,7 |
0,9 |
0,4 |
|
9 |
25 |
12 |
18 |
0,5 |
0,5 |
0,9 |
|
10 |
31 |
26 |
14 |
0,7 |
0,3 |
0,5 |
|
11 |
18 |
15 |
12 |
0,6 |
0,6 |
0,8 |
|
12 |
23 |
25 |
12 |
0,8 |
0,4 |
0,7 |
|
13 |
16 |
8 |
12 |
0,4 |
0,7 |
0,9 |
|
14 |
18 |
10 |
14 |
0,6 |
0,5 |
0,8 |
|
15 |
22 |
12 |
14 |
0,5 |
0,6 |
0,7 |
|
16 |
20 |
9 |
12 |
0,7 |
0,4 |
0,8 |
|
17 |
24 |
16 |
12 |
0,9 |
0,3 |
0,6 |
|
18 |
18 |
10 |
14 |
0,8 |
0,2 |
0,7 |
|
19 |
25 |
18 |
14 |
0,7 |
0,6 |
0,9 |
|
20 |
19 |
11 |
10 |
0,8 |
0,5 |
0,6 |
|
21 |
30 |
13 |
10 |
0,4 |
0,8 |
0,5 |
|
22 |
27 |
15 |
12 |
0,6 |
0,9 |
0,4 |
|
23 |
22 |
11 |
10 |
0,7 |
0,7 |
0,6 |
|
24 |
20 |
9 |
10 |
0,5 |
0,9 |
0,7 |
|
25 |
24 |
12 |
14 |
0,7 |
0,4 |
0,9 |
|
26 |
19 |
10 |
11 |
0,8 |
0,3 |
0,6 |
|
27 |
25 |
13 |
13 |
0,4 |
0,7 |
0,8 |
|
28 |
21 |
16 |
12 |
0,5 |
0,5 |
0,7 |
|
29 |
22 |
20 |
10 |
0,8 |
0,6 |
0,8 |
|
30 |
23 |
15 |
11 |
0,7 |
0,3 |
0,9 |
Расчетные схемы
ПРИЛОЖЕНИЕ Б
ЗАДАЧА 2 РАСЧЕТ
ВАЛА НА КРУЧЕНИЕ
Сечение вала
круглое, сплошное и кольцевое. Допускаемое
напряжение кручения [τ]=25
МПа. Модуль сдвига G=8∙104
МПа
|
Вариант |
Т1, |
Т2, |
Т3, |
Т4, |
l1, |
l2, |
l3, |
l4, |
l5, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
200 |
300 |
400 |
0,8 |
0,7 |
0,4 |
0,6 |
0,3 |
|
|
2 |
300 |
500 |
500 |
0,7 |
0,6 |
0,5 |
0,8 |
0,4 |
|
|
3 |
400 |
400 |
300 |
0,9 |
0,5 |
0,6 |
0,3 |
0,2 |
|
|
4 |
100 |
200 |
300 |
0,5 |
0,8 |
0,9 |
0,4 |
0,3 |
|
|
5 |
300 |
400 |
100 |
0,6 |
0,4 |
0,6 |
0,5 |
0,4 |
|
|
6 |
100 |
100 |
500 |
0,8 |
0,6 |
0,7 |
0,3 |
0,2 |
|
|
7 |
300 |
200 |
200 |
0,7 |
0,3 |
0,8 |
0,4 |
0,3 |
|
|
8 |
500 |
600 |
500 |
0,4 |
0,7 |
0,9 |
0,5 |
0,4 |
|
|
9 |
600 |
800 |
700 |
0,9 |
0,5 |
0,5 |
0,3 |
0,2 |
|
|
10 |
400 |
200 |
300 |
0,5 |
0,7 |
0,8 |
0,2 |
0,3 |
|
|
11 |
300 |
500 |
600 |
0,8 |
0,6 |
0,6 |
0,4 |
0,3 |
|
|
12 |
100 |
200 |
200 |
0,7 |
0,8 |
0,4 |
0,3 |
0,4 |
|
|
13 |
700 |
500 |
200 |
0,9 |
0,4 |
0,7 |
0,2 |
0,3 |
|
|
14 |
800 |
400 |
300 |
0,8 |
0,6 |
0,5 |
0,3 |
0,3 |
|
|
15 |
900 |
600 |
400 |
0,7 |
0,5 |
0,6 |
0,4 |
0,4 |
|
|
16 |
100 |
200 |
300 |
0,8 |
0,7 |
0,4 |
0,2 |
0,5 |
|
|
17 |
200 |
800 |
100 |
0,6 |
0,9 |
0,3 |
0,3 |
0,6 |
|
|
18 |
300 |
800 |
100 |
0,7 |
0,8 |
0,2 |
0,4 |
0,7 |
|
|
19 |
400 |
500 |
300 |
200 |
0,9 |
0,7 |
0,6 |
0,2 |
|
|
20 |
500 |
500 |
200 |
300 |
0,6 |
0,8 |
0,5 |
0,3 |
|
|
21 |
600 |
900 |
400 |
100 |
0,5 |
0,4 |
0,8 |
0,4 |
|
|
22 |
700 |
800 |
300 |
200 |
0,4 |
0,6 |
0,9 |
0,2 |
|
|
23 |
800 |
700 |
100 |
400 |
0,6 |
0,7 |
0,7 |
0,3 |
|
|
24 |
900 |
600 |
200 |
300 |
0,7 |
0,5 |
0,9 |
0,4 |
|
|
25 |
100 |
500 |
300 |
200 |
0,9 |
0,7 |
0,4 |
0,2 |
|
|
26 |
200 |
300 |
500 |
300 |
0,6 |
0,8 |
0,3 |
0,4 |
|
|
27 |
300 |
300 |
400 |
200 |
0,8 |
0,4 |
0,7 |
0,3 |
|
|
28 |
400 |
200 |
600 |
100 |
0,7 |
0,5 |
0,5 |
0,2 |
|
|
29 |
500 |
100 |
700 |
200 |
0,8 |
0,8 |
0,6 |
0,3 |
|
|
30 |
600 |
200 |
800 |
300 |
0,9 |
0,7 |
0,3 |
0,4 |
Расчетные схемы
ПРИЛОЖЕНИЕ В
ЗАДАЧА 3
РАСЧЕТ НА ПРОЧНОСТЬ ДВУХОПОРНОЙ БАЛКИ
ПРИ ИЗГИБЕ
Для данной балки подобрать сечения
двутавра и прямоугольника (h/b=2).
Допускаемое напряжения изгиба [σ]=160
МПа
|
Вариант |
М,K |
F, |
q, |
l1, |
l2, |
l3, |
l4, |
l5, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
18 |
26 |
14 |
2 |
2 |
5 |
1 |
1 |
|
2 |
24 |
18 |
10 |
2 |
3 |
2 |
3 |
2 |
|
3 |
16 |
34 |
12 |
2 |
3 |
3 |
2 |
2 |
|
4 |
30 |
24 |
16 |
2 |
4 |
4 |
1 |
2 |
|
5 |
20 |
12 |
8 |
1,8 |
2,2 |
1 |
5 |
1 |
|
6 |
22 |
16 |
10 |
1,6 |
1 |
1,4 |
6 |
2 |
|
7 |
18 |
22 |
14 |
2,2 |
2 |
1,8 |
5 |
1 |
|
8 |
16 |
24 |
12 |
2,5 |
1 |
1,5 |
5 |
2 |
|
9 |
16 |
24 |
12 |
2,5 |
1 |
1,5 |
5 |
2 |
|
10 |
14 |
15 |
8 |
1,6 |
2 |
1,4 |
4 |
3 |
|
11 |
10 |
23 |
12 |
2 |
2 |
2 |
4 |
2 |
|
12 |
18 |
17 |
10 |
1,8 |
3 |
1,2 |
5 |
1 |
|
13 |
16 |
25 |
15 |
2 |
2 |
4 |
2 |
2 |
|
14 |
24 |
16 |
10 |
2 |
3 |
4 |
2 |
1 |
|
15 |
1 |
22 |
12 |
1,6 |
2,4 |
3,5 |
2,5 |
2 |
|
16 |
20 |
18 |
14 |
1,8 |
2,2 |
4,5 |
2,5 |
2 |
|
17 |
22 |
24 |
8 |
2 |
2 |
4 |
3 |
1 |
|
18 |
16 |
26 |
6 |
2 |
2 |
3,5 |
3,5 |
1 |
|
19 |
18 |
20 |
10 |
1,5 |
2,5 |
4,2 |
1,8 |
8 |
|
20 |
28 |
18 |
16 |
1,8 |
2,2 |
4,5 |
2,5 |
3 |
|
21 |
17 |
25 |
12 |
2 |
2 |
1 |
5 |
2 |
|
22 |
15 |
30 |
10 |
1,5 |
2,5 |
2 |
4 |
1 |
|
23 |
26 |
22 |
8 |
2 |
2 |
2 |
3 |
2 |
|
24 |
30 |
18 |
14 |
1,6 |
3,0 |
2 |
4 |
1 |
|
25 |
24 |
26 |
15 |
1,5 |
2,5 |
6 |
1 |
1 |
|
26 |
22 |
13 |
2,5 |
1,5 |
5 |
2 |
2 |
|
|
27 |
20 |
12 |
2,0 |
1,5 |
5,5 |
3 |
2 |
|
|
28 |
18 |
28 |
10 |
2,0 |
1,5 |
4,5 |
2 |
2 |
|
29 |
30 |
20 |
8 |
1,8 |
3,2 |
1 |
2 |
1 |
|
30 |
28 |
18 |
15 |
2 |
2,5 |
1,5 |
5 |
2 |
Расчетные схемы
задачи 3
ПРИЛОЖЕНИЕ Г
Сталь прокатная
– балки двутавровые (ГОСТ 8239-83)
h
– высота профиля;
b
– ширина;
d
– толщина;
t
– средняя толщина;
R
и r
– внутренний и наружный радиусы
скруглений;
J
– момент инерции;
W
– момент сопротивления;
i
– радиус инерции;
S
– статический момент полусечения
|
Номер профиля |
Масса |
Размеры, |
Площадь сечения, |
Jx, см4 |
Wx, см3 |
ix, см |
Sx, см3 |
Jy, см4 |
Wy, см3 |
iy, см |
|||||
|
h |
b |
d |
t |
R |
r |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
10 |
9,46 |
100 |
55 |
4,5 |
7,2 |
7 |
2,5 |
12 |
198 |
39,7 |
4,06 |
23 |
17,9 |
6,49 |
1,22 |
|
12 |
11,45 |
120 |
64 |
4,8 |
7,3 |
7,5 |
3 |
14,7 |
350 |
58,4 |
4,88 |
33,7 |
27,9 |
8,72 |
1,38 |
|
14 |
13,7 |
140 |
73 |
4,9 |
7,5 |
8 |
3 |
17,4 |
572 |
81,7 |
5,73 |
46,8 |
41,9 |
11,5 |
1,55 |
|
16 |
15,9 |
160 |
81 |
5,0 |
7,8 |
8,5 |
3,5 |
20,2 |
873 |
109,0 |
6,57 |
62,3 |
58,6 |
14,5 |
1,7 |
|
18 |
18,4 |
180 |
90 |
5,1 |
8,1 |
9,0 |
3,5 |
23,4 |
1290 |
143,0 |
7,42 |
81,4 |
82,6 |
18,4 |
1,88 |
|
18а |
19,9 |
180 |
100 |
5,1 |
8,3 |
9,0 |
3,5 |
25,4 |
1430 |
159,0 |
7,51 |
89,8 |
114,0 |
22,8 |
2,12 |
|
20 |
21,0 |
200 |
100 |
5,2 |
8,4 |
9,5 |
4,0 |
26,8 |
1840 |
184,0 |
8,28 |
104,0 |
115,0 |
23,1 |
2,07 |
|
20а |
22,7 |
200 |
110 |
5,2 |
8,6 |
9,5 |
4,0 |
28,9 |
2030 |
203,0 |
8,37 |
114,0 |
155,0 |
28,2 |
2,32 |
|
22 |
24,0 |
220 |
110 |
5,4 |
8,7 |
10,0 |
4,0 |
30,6 |
2550 |
232,0 |
9,13 |
131,0 |
157,0 |
28,6 |
2,27 |
|
22а |
25,8 |
220 |
120 |
5,4 |
8,9 |
10,0 |
4,0 |
32,6 |
2790 |
254,0 |
9,22 |
143,0 |
106,0 |
34,3 |
2,5 |
|
24 |
27,3 |
240 |
115 |
5,6 |
9,5 |
10,5 |
4,0 |
34,8 |
3460 |
289 |
9,97 |
163 |
198 |
34,5 |
2,37 |
|
24а |
29,4 |
240 |
125 |
5,6 |
9,8 |
20,5 |
4,0 |
37,5 |
3800 |
317 |
10,1 |
178 |
260 |
41,6 |
2,63 |
|
27 |
31,5 |
270 |
125 |
6,0 |
9,8 |
11,0 |
4,5 |
40,2 |
5010 |
371 |
11,2 |
210 |
260 |
41,5 |
2,54 |
|
27а |
33,9 |
270 |
135 |
6,0 |
10,2 |
11,0 |
4,5 |
43,2 |
5500 |
407 |
11,3 |
229 |
337 |
50,0 |
2,8 |
|
30 |
36,5 |
300 |
135 |
6,5 |
10,2 |
12,0 |
5 |
46,5 |
7080 |
472 |
12,3 |
268 |
337 |
49,9 |
2,69 |
|
30а |
39,2 |
300 |
145 |
6,5 |
10,7 |
12,0 |
5 |
49,9 |
7780 |
518 |
12,5 |
292 |
436 |
60,1 |
2,95 |
|
33 |
42,2 |
330 |
140 |
7,0 |
11,2 |
13,0 |
5 |
53,8 |
9840 |
597 |
13,5 |
339 |
419 |
59,1 |
3,79 |
|
36 |
48,6 |
360 |
145 |
7,5 |
12,3 |
14,0 |
6 |
61,9 |
13380 |
743 |
14,7 |
423 |
516 |
71,1 |
2,89 |
|
40 |
57,0 |
400 |
155 |
8,3 |
13,0 |
15,0 |
6 |
72,6 |
19062 |
953 |
16,2 |
545 |
667 |
86,1 |
3,08 |
|
45 |
66,5 |
450 |
160 |
9,0 |
14,2 |
16,0 |
7 |
84,7 |
27696 |
1231 |
18,1 |
708 |
808 |
101,0 |
3,09 |
|
50 |
78,5 |
500 |
170 |
10,0 |
15,2 |
17,0 |
7 |
100 |
39727 |
1589 |
19,9 |
919 |
1043 |
123,0 |
3,23 |
|
60 |
108,0 |
600 |
190 |
12,0 |
17,8 |
20,0 |
8 |
138 |
76806 |
2560 |
23,6 |
1491 |
1725 |
182,0 |
3,54 |
|
60б |
120,0 |
650 |
200 |
12,0 |
19,2 |
22,0 |
9 |
153 |
101400 |
3120 |
25,8 |
1800 |
2170 |
217,0 |
3,77 |
|
70 |
138,0 |
700 |
210 |
13,0 |
20,8 |
24,0 |
10 |
176 |
134600 |
3840 |
27,7 |
2230 |
2730 |
260,0 |
3,94 |
|
70а |
168,0 |
700 |
210 |
15,0 |
24,0 |
24,0 |
10 |
202 |
152700 |
4360 |
27,5 |
2550 |
3240 |
309,0 |
4,01 |
|
70б |
184,0 |
700 |
210 |
17,5 |
28,2 |
24,0 |
10 |
234 |
175770 |
5010 |
27,4 |
2940 |
3910 |
373,0 |
4,09 |
ПРИЛОЖЕНИЕ Д
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Расчет железобетонных балок прямоугольного сечения с одиночным армированием по прочности нормального сечения
Преподаватель ГБУ КО ПОО «КИТиС» А.Н.Панина
Различают 2 расчетных случая
Расчетная схема прочности нормальных сечений изгибаемых элементов (общий случай)
- Рассмотрим элемент прямоугольной формы. В общем случае элемент армируется предварительно напряженной ( Asp и A’sp ) и ненапрягаемой ( As и A’s ) арматурой в растянутой ( Asp, As ) и в сжатой зонах ( A’sp , A’s )
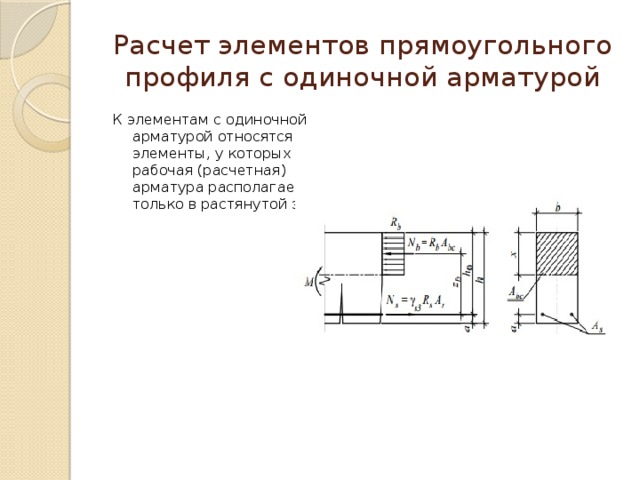
Расчет элементов прямоугольного профиля с одиночной арматурой
К элементам с одиночной арматурой относятся элементы, у которых рабочая (расчетная) арматура располагается только в растянутой зоне.
Порядок расчета
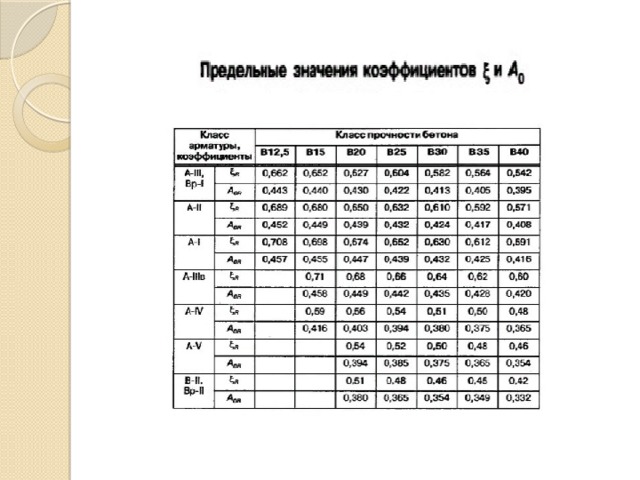
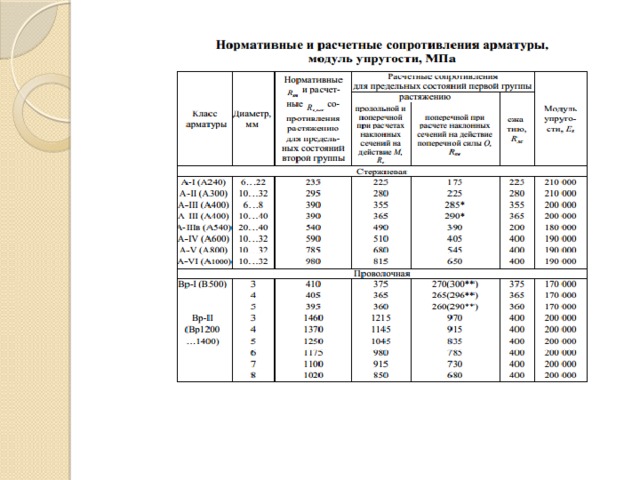
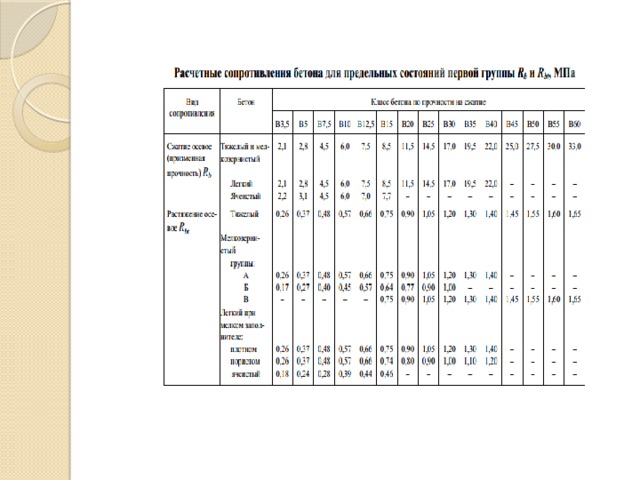
- 1.Определяем расчетное сопротивление бетона осевому сжатию (СП 52-101-2003 Бетонные и железобетонные конструкции без предварительного напряжения арматуры), по классу бетона, при расчете необходимо учесть коэффициент – условий работы бетона, тогда:
- 2.Определяем расчетную высоту сечения, по формуле:
- где: -высота сечения, см;
- a -расстояние, от центра тяжести рабочего стержня до крайнего нижнего волокна бетона, cм (2 …3 см).
- 3.Определением коэффициент α , по формуле:
- где: -ширина сечения, см;
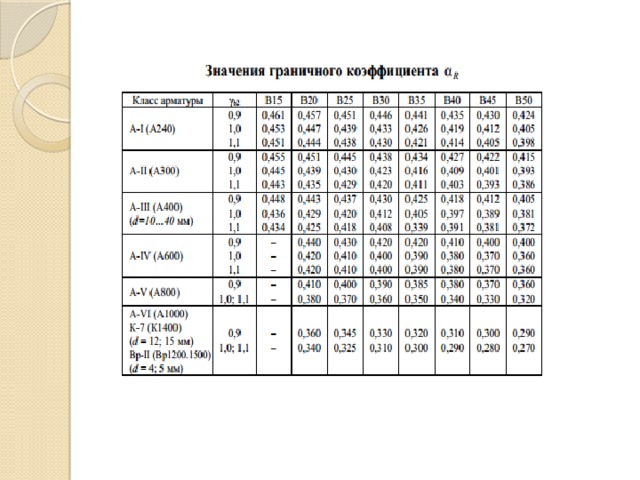
- α R -если условие выполняется, следовательно армирование одиночное, если не выполняется – двойное ( α R – граничный коэффициент, зависит от класса арматуры, коэффициента и класса бетона).
- 4.Производим расчет площади поперечного сечения рабочей арматуры, по формуле:
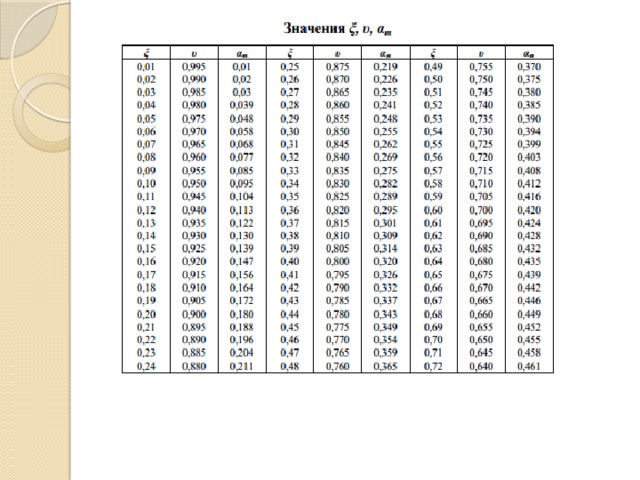
- где: -коэффициент зависящий от α , определяется по таблице;
- R s -расчетное сопротивление арматуры осевому растяжению (СП 52-101-2003 Бетонные и железобетонные конструкции без предварительного напряжения арматуры), кН/см 2 ;
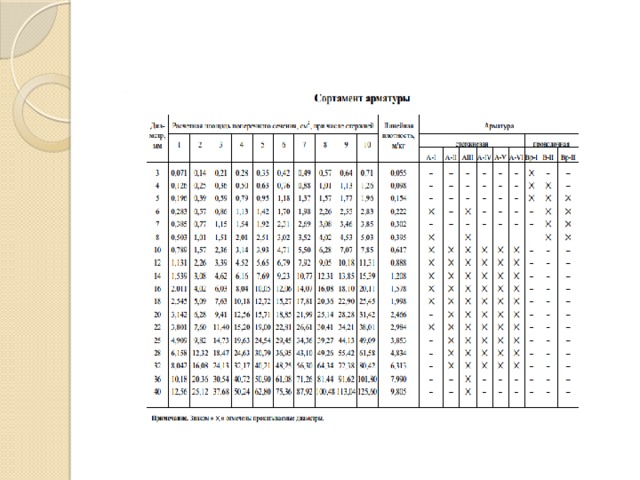
- 5.По значению A s , по сортаменту, определяем диаметр и количество стержней, конструктивно устанавливая их в элементе в зависимости от ширины сечения.
При расчете элементов с одиночным армированием встречаются задачи трех типов
- Задача типа 1. По заданному изгибающему моменту М от расчетных нагрузок, известным размерам поперечного сечения элемента b и h , при известных классах бетона и арматуры и условиях работы конструкции требуется определить площадь рабочей арматуры Аs ( Аsр ).
- Задача типа 2 . По заданному расчетному изгибающему моменту М , известным видам и классам материалов и условиям работы конструкции подобрать сечение элемента ( b и h ) и рабочую арматуру Аs.
- Задача типа 3. При всех известных данных: размерах сечения элемента, видах и классах материалов, количества и диаметров стержней рабочей арматуры требуется определить несущую способность элемента.
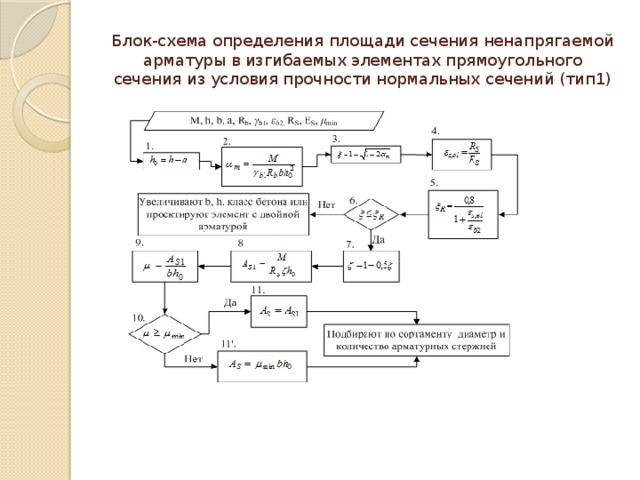
Блок-схема определения площади сечения ненапрягаемой арматуры в изгибаемых элементах прямоугольного сечения из условия прочности нормальных сечений (тип1)
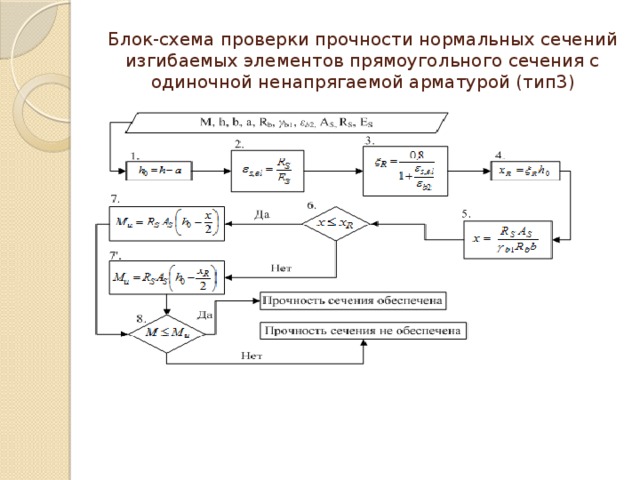
Блок-схема проверки прочности нормальных сечений изгибаемых элементов прямоугольного сечения с одиночной ненапрягаемой арматурой (тип3)
Вопросы для закрепления
1.Что учитывает коэффициент условий работы бетона γ b 1?
2. Какие классы арматурной стали вы знаете?
3. Каковы условия применения арматуры в конструкциях?
4. Что учитывает коэффициент условия работы арматуры γ s 3?
5. Что такое защитный слой бетона, как он определяется?
6.Что такое рабочая высота сечения и как она определяется?
7. Какой метод расчета используется для расчета железобетонных конструкций?
8. Каковы основы расчета прочности нормальных сечений изгибаемых элементов с одиночным армированием? Приведите схему действующих усилий в сечении.
Домашнее задание
- Решить задачу:
Подобрать одиночную арматуру в изгибаемом элементе. Геометрические размеры изгибаемого железобетонного элемента: b =200мм, h =500мм. Характеристики бетона и арматуры. Бетон тяжелый, класса В25, Rb 14.5 МПа . Продольная рабочая арматура класса А-400, Rs 355 МПа . Изгибающий момент M =159,9кН*м .
Калькулятор будет доступен после внесения изменений в соответствующие параметры.
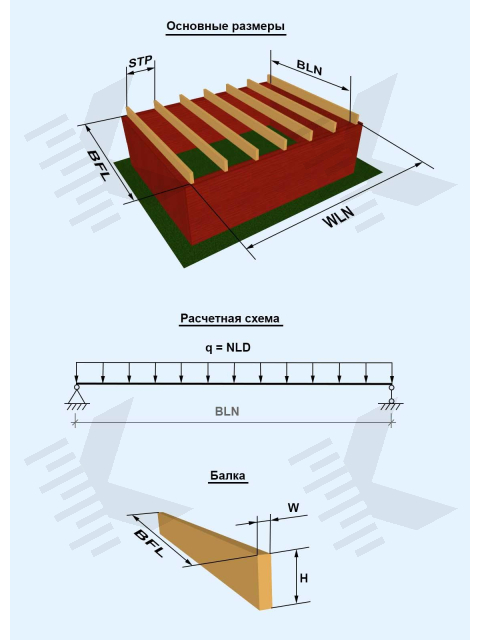
Длина/Пролет балки — расстояние между опорами балки:
BLN
м
Сорт и Класс древесины:
WCL
Срок службы, согласно СНиП II-25-80 (СП 64.13330.2011):
LFT
Температурный режим эксплуатации:
TMP
Эксплуатационная влажность древесины/Максимальная влажность воздуха при температуре 20 °С:
WML
Вести расчет для конструкций, в которых напряжения в элементах, возникающие от постоянных и временных длительных нагрузок, превышают 80% суммарного напряжения от всех нагрузок согласно СП 64.13330.2011 Деревянные конструкции. Актуализированная редакция СНиП II-25-80 п.5.2 (в):
MDC
Стоимость леса
Длина стены дома (внутренняя сторона), на которую укладываются балки:
WLN
м
Полная длина балки (с учетом краёв, упирающихся на стены):
BFL
м
Нагрузка действующая на балку (200 кг/м2 – чердачное перекрытие, 400 кг/м2 – перекрытия жилых зданий):
NLD
кг/м2
Предельный прогиб балки в долях пролета:
LID
1/350 – При наличии стяжки
- Вид сверху на расположение деревянных балок на перекрытии
Результаты расчета
Подобранная балка
-
Сечение: 275×100 мм
-
Площадь сечения: 27500 мм 2
-
Максимальный шаг между балками: 60 см
-
Fmax (максимальный прогиб балки): 1.54 см
-
I (момент инерции): 173.31 см 4
-
Mmax (максимальный изгибающий момент): 8581.79 MPaXcm 3
-
Wreq (момент сопротивления балки в соответствии с выбранным вариантом древесины и условиями эксплуатации): 612.98 см³
Минимальные параметры балки
-
Сечение: 273×100 мм
-
Площадь сечения: 27300 мм 2
Параметры балки при расчете на “прочность”
-
Сечение: 192×100 мм
-
Площадь сечения: 19200 мм 2
Параметры балки при расчете на “прогиб”
-
Сечение: 273×100 мм
-
Площадь сечения: 27300 мм 2
Материалы конструкции
Балки
-
Сечение: 275×100 мм
-
Площадь сечения: 27500 мм 2
-
Шаг между балками: 60 см
-
Расстояние между балками: 50 см
-
Длина: 6 м
-
Количество: 18 шт
-
Объём: 2.97 м³
-
Общая стоимость: 20790 rub
Указанные «Размеры»
Задача
-
Рассчитать сечение балки при известном шаге между балками: 60 см
Дополнительные данные
-
Известна ширина сечения балки – b: 100 мм
Характеристики балки
-
Длина/Пролет балки — расстояние между опорами балки: 5.4 м
-
Ширина сечения (b): 100 мм
-
Вид древесины: Сосна
-
Сорт и Класс древесины: Класс 1 (К26)
-
Пропитка: Нет пропитки
Конфигурация перекрытия
-
Длина стены дома (внутренняя сторона), на которую укладываются балки: 10 м
-
Полная длина балки (с учетом краёв, упирающихся на стены): 6 м
-
Нагрузка действующая на балку (200 кг/м2 – чердачное перекрытие, 400 кг/м2 – перекрытия жилых зданий): 400 м 2
-
Предельный прогиб балки в долях пролета: 1/350 – При наличии стяжки
Условия эксплуатации балки
-
Срок службы, согласно СНиП II-25-80 (СП 64.13330.2011): До 50 лет
-
Температурный режим эксплуатации: До 35 °С
-
Эксплуатационная влажность древесины/Максимальная влажность воздуха при температуре 20 °С: До 12% / До 65%
-
Вести расчет для конструкций, в которых напряжения в элементах, возникающие от постоянных и временных длительных нагрузок, превышают 80% суммарного напряжения от всех нагрузок согласно СП 64.13330.2011 Деревянные конструкции. Актуализированная редакция СНиП II-25-80 п.5.2 (в): Не учитывается
Стоимость леса
-
Цена за 1м3: 7000 rub
Добавить в закладки
Сохранить ссылку на результат расчёта в раздел “Мои закладки” в личном кабинете.
Сканировать QR-код
Получить ссылку на расчет с параметрами через сканирование QR-кода