Как найти размер ядра атома – Сайт, где вы сможете решить свои вопросы

Ядерная физика

Атомное ядро · Радиоактивный распад · Ядерная реакция · Термоядерная реакция
Основные термины Атомное ядро · Изотопы · Изобары · Капельная модель ядра · Период полураспада · Массовое число · Составное ядро · Цепная ядерная реакция · Ядерное эффективное сечение
Распад ядер Закон радиоактивного распада · Альфа-распад · Бета-распад · Кластерный распад
Сложный распад Электронный захват · Двойной бета-распад · Двойной электронный захват · Внутренняя конверсия · Изомерный переход
Излучения Ионизирующее излучение · Нейтронный распад · Позитронный распад · Протонный распад · Гамма излучение · Фоторасщепление
Захваты Электронный захват · Нейтронный захват (r-процесс · s-процесс) · Протонный захват (p-процесс · rp-процесс) · Нейтронизация
Деление ядра Спонтанное деление
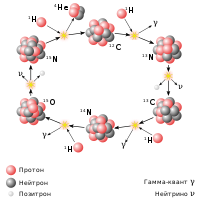
Нуклеосинтез Первичный нуклеосинтез · Протон-протонный цикл · CNO-цикл · Тройная гелиевая реакция · Гелиевая вспышка · Ядерное горение углерода · Углеродная детонация · Ядерное горение кислорода · Ядерное горение неона · Ядерное горение кремния · Реакции скалывания
См. также: Портал:Физика

А́томное ядро́ — центральная часть атома, в которой сосредоточена основная его масса (более 99,9 %). Ядро заряжено положительно, заряд ядра определяет химический элемент, к которому относят атом. Размеры ядер различных атомов составляют несколько фемтометров, что более чем в 10 тысяч раз меньше размеров самого атома. Атомные ядра изучает ядерная физика.

Атомное ядро состоит из нуклонов — положительно заряженных протонов и нейтральных нейтронов, которые связаны между собой при помощи сильного взаимодействия. Протон и нейтрон обладают собственным моментом количества движения (спином), равным $hbar /2=h/4pi$ ^{[сн 1]} и связанным с ним магнитным моментом. Единственный стабильный атом, не содержащий нейтронов в ядре — лёгкий водород (протий).

Атомное ядро, рассматриваемое как класс частиц с определённым числом протонов и нейтронов, принято называть нуклидом.

В некоторых редких случаях могут образовываться короткоживущие экзотические атомы, у которых вместо нуклона ядром служат иные частицы.

Количество протонов в ядре называется его зарядовым числом $Z$ — это число равно порядковому номеру элемента, к которому относится атом, в таблице (Периодической системе элементов) Менделеева. Количество протонов в ядре определяет структуру электронной оболочки нейтрального атома и, таким образом, химические свойства соответствующего элемента. Количество нейтронов в ядре называется его изотопическим числом $N$ ^{[источник не указан 1372 дня (обс.)]}. Ядра с одинаковым числом протонов и разным числом нейтронов называются изотопами. Ядра с одинаковым числом нейтронов, но разным числом протонов — называются изотонами. Термины изотоп и изотон используются также применительно к атомам, содержащим указанные ядра, а также для характеристики нехимических разновидностей одного химического элемента. Полное количество нуклонов в ядре называется его массовым числом $A$ ( ${displaystyle A=N+Z}$ ) и приблизительно равно средней массе атома, указанной в таблице Менделеева. Нуклиды с одинаковым массовым числом, но разным протон-нейтронным составом принято называть изобарами.

Как и любая квантовая система, ядра могут находиться в метастабильном возбуждённом состоянии, причём в отдельных случаях время жизни такого состояния исчисляется годами. Такие возбуждённые состояния ядер называются ядерными изомерами^[1]^[2]^[3].

История[править | править код]

В 1911 году Резерфорд в своём докладе «Рассеяние α- и β-лучей и строение атома» в философском обществе Манчестера заявил^[4]:

Рассеяние заряженных частиц может быть объяснено, если предположить такой атом, который состоит из центрального электрического заряда, сосредоточенного в точке и окружённого однородным сферическим распределением противоположного электричества равной величины. При таком устройстве атома α- и β-частицы, когда они проходят на близком расстоянии от центра атома, испытывают большие отклонения, хотя вероятность такого отклонения мала.

Таким образом Резерфорд открыл атомное ядро, с этого момента и ведёт начало ядерная физика, изучающая строение и свойства атомных ядер.

После обнаружения стабильных изотопов элементов, ядру самого лёгкого атома была отведена роль структурной частицы всех ядер. С 1920 года ядро атома водорода имеет официальный термин — протон. В 1921 году Лиза Мейтнер предложила^[5] первую, протон-электронную, модель строения атомного ядра, согласно которой оно состоит из протонов, электронов и альфа-частиц^[6]^:96. Однако в 1929 году произошла «азотная катастрофа» — В. Гайтлер и Г. Герцберг установили^[7], что ядро атома азота подчиняется статистике Бозе — Эйнштейна, а не статистике Ферми — Дирака, как предсказывала протон-электронная модель^[8]^[9]^:374. Таким образом, эта модель вступила в противоречие с экспериментальными результатами измерений спинов и магнитных моментов ядер^[10]. В 1932 году Джеймсом Чедвиком была открыта новая электрически нейтральная частица, названная нейтроном. В том же году Иваненко^[11] и, ссылаясь на работу первого^[12], Гейзенберг выдвинули гипотезу о протон-нейтронной структуре ядра. В дальнейшем, с развитием ядерной физики и её приложений, эта гипотеза была полностью подтверждена^[13].

Теории строения атомного ядра[править | править код]

В процессе развития физики выдвигались различные гипотезы строения атомного ядра; тем не менее, каждая из них способна описать лишь ограниченную совокупность ядерных свойств. Некоторые модели могут взаимоисключать друг друга.

Наиболее известными являются следующие:

Капельная модель ядра — предложена в 1936 году Нильсом Бором.
Оболочечная модель ядра — предложена в 30-х годах XX века.
Обобщённая модель Бора — Моттельсона
Кластерная модель ядра
Модель нуклонных ассоциаций
Оптическая модель ядра
Сверхтекучая модель ядра
Статистическая модель ядра

Ядерно-физические характеристики[править | править код]

Зарядовым числом $Z$ полностью определяется химический элемент. Парой чисел $Z$ и $A$ (массовое число) полностью определяется нуклид. Можно рассмотреть некоторые ядерно-физические характеристики нуклидов с заданными зарядовыми и массовыми числами.

Заряд[править | править код]

Число протонов в ядре $Z$ определяет непосредственно его электрический заряд; у изотопов одинаковое количество протонов, но разное количество нейтронов. Ядерные свойства изотопов элемента, в отличие от химических, могут различаться чрезвычайно резко^[1].

Впервые заряды атомных ядер определил Генри Мозли в 1913 году. Свои экспериментальные наблюдения учёный интерпретировал зависимостью длины волны рентгеновского излучения от некоторой константы $Z$ , изменяющейся на единицу от элемента к элементу и равной единице для водорода:

${displaystyle {sqrt {1/lambda }}=aZ-b}$ , где

$a$ и $b$ — постоянные.

Из чего Мозли сделал вывод, что найденная в его опытах константа атома, определяющая длину волны характеристического рентгеновского излучения и совпадающая с порядковым номером элемента, может быть только зарядом атомного ядра, что стало известно под названием закон Мозли^[2].

Масса[править | править код]

Из-за разницы в числе нейтронов ${displaystyle A-Z}$ изотопы элемента имеют разную массу ${displaystyle M(A,Z)}$ , которая является важной характеристикой ядра. В ядерной физике массу ядер принято измерять в атомных единицах массы (а. е. м.), за одну а. е. м. принимают 1/12 часть массы нуклида ¹²C^{[сн 2]}. Стандартная масса, которая обычно приводится для нуклида — это масса нейтрального атома. Для определения массы ядра нужно из массы атома вычесть сумму масс всех электронов (более точное значение получится, если учесть ещё и энергию связи электронов с ядром).

Кроме того, в ядерной физике часто используется энергетический эквивалент массы. Согласно соотношению Эйнштейна, каждому значению массы $M$ соответствует полная энергия:

${displaystyle E=Mc^{2}}$ , где $c$ — скорость света в вакууме.

Соотношение между а. е. м. и её энергетическим эквивалентом в джоулях:

${displaystyle E_{1}=1{,}660539cdot 10^{-27}cdot (2{,}997925cdot 10^{8})^{2}=1{,}492418cdot 10^{-10}}$ ,

а так как 1 электронвольт = 1,602176⋅10⁻¹⁹ Дж, то энергетический эквивалент а. е. м. в МэВ равен^[1]^[3]:

${displaystyle E_{1}=931{,}494}$ .

Радиус[править | править код]

Анализ распада тяжёлых ядер уточнил оценку Резерфорда^{[сн 3]} и связал радиус ядра $R$ с массовым числом $A$ простым соотношением:

${displaystyle R=r_{0}A^{1/3}}$ , где ${displaystyle r_{0}}$ — константа.

Так как радиус ядра не является чисто геометрической характеристикой и связан прежде всего с радиусом действия ядерных сил, то значение ${displaystyle r_{0}}$ зависит от процесса, при анализе которого получено значение $R$ , усреднённое значение ${displaystyle r_{0}=1{,}23cdot 10^{-15}}$ м, таким образом радиус ядра в метрах^[1]^[2]:

${displaystyle R=1{,}23cdot 10^{-15}A^{1/3}}$ .

Моменты ядра[править | править код]

Как и составляющие его нуклоны, ядро имеет собственные моменты.

Спин[править | править код]

Поскольку нуклоны обладают собственным механическим моментом, или спином, равным $1/2$ , то и ядра должны иметь механические моменты. Кроме того, нуклоны участвуют в ядре в орбитальном движении, которое также характеризуется определённым моментом количества движения каждого нуклона. Орбитальные моменты принимают только целочисленные значения $hbar$ (постоянная Дирака). Все механические моменты нуклонов, как спины, так и орбитальные, суммируются алгебраически и составляют спин ядра.

Несмотря на то, что число нуклонов в ядре может быть очень велико, спины ядер обычно невелики и составляют не более нескольких $hbar$ , что объясняется особенностью взаимодействия одноимённых нуклонов. Все парные протоны и нейтроны взаимодействуют только так, что их спины взаимно компенсируются, то есть пары всегда взаимодействуют с антипараллельными спинами. Суммарный орбитальный момент пары также всегда равен нулю. В результате ядра, состоящие из чётного числа протонов и чётного числа нейтронов, не имеют механического момента. Отличные от нуля спины существуют только у ядер, имеющих в своём составе непарные нуклоны, спин такого нуклона суммируется с его же орбитальным моментом и имеет какое-либо полуцелое значение: 1/2, 3/2, 5/2. Ядра нечётно-нечётного состава имеют целочисленные спины: 1, 2, 3 и т. д.^[2]

Магнитный момент[править | править код]

Измерения спинов стали возможными благодаря наличию непосредственно связанных с ними магнитных моментов. Они измеряются в магнетонах и у различных ядер равны от −2 до +5 ядерных магнетонов. Из-за относительно большой массы нуклонов магнитные моменты ядер очень малы по сравнению с магнитными моментами электронов, поэтому их измерение гораздо сложнее. Как и спины, магнитные моменты измеряются спектроскопическими методами, наиболее точным является метод ядерного магнитного резонанса.

Магнитный момент чётно-чётных пар, как и спин, равен нулю. Магнитные моменты ядер с непарными нуклонами образуются собственными моментами этих нуклонов и моментом, связанным с орбитальным движением непарного протона^[10].

Электрический квадрупольный момент[править | править код]

Атомные ядра, спин которых больше или равен единице, имеют отличные от нуля квадрупольные моменты, что говорит об их не точно сферической форме. Квадрупольный момент имеет знак плюс, если ядро вытянуто вдоль оси спина (веретенообразное тело), и знак минус, если ядро растянуто в плоскости, перпендикулярной оси спина (чечевицеобразное тело). Известны ядра с положительными и отрицательными квадрупольными моментами. Отсутствие сферической симметрии у электрического поля, создаваемого ядром с ненулевым квадрупольным моментом, приводит к образованию дополнительных энергетических уровней атомных электронов и появлению в спектрах атомов линий сверхтонкой структуры, расстояния между которыми зависят от квадрупольного момента^[2].

Энергия связи[править | править код]

Большая энергия связи нуклонов, входящих в ядро, говорит о существовании ядерных сил, поскольку известные гравитационные силы слишком малы, чтобы преодолеть взаимное электростатическое отталкивание протонов в ядре. Связь нуклонов осуществляется чрезвычайно короткодействующими силами, которые возникают вследствие непрерывного обмена частицами, называемыми пи-мезонами, между нуклонами в ядре.

Экспериментально было обнаружено, что для всех стабильных ядер масса ядра меньше суммы масс составляющих его нуклонов, взятых по отдельности. Эта разница называется дефектом массы или избытком массы и определяется соотношением:

${displaystyle Delta M(Z,A)=Zm_{p}+(A-Z)m_{n}-M(Z,A)}$ ,

где ${displaystyle m_{p}}$ и ${displaystyle m_{n}}$ — массы свободного протона и нейтрона, ${displaystyle M(Z,A)}$ — масса ядра.

Согласно принципу эквивалентности массы и энергии дефект массы представляет собой массу, эквивалентную работе, затраченной ядерными силами, чтобы собрать все нуклоны вместе при образовании ядра. Эта величина равна изменению потенциальной энергии нуклонов в результате их объединения в ядро.

Энергия, эквивалентная дефекту массы, называется энергией связи ядра и равна:

${displaystyle E_{c}=(Zm_{p}+(A-Z)m_{n}-M(Z,A))c^{2}}$ ,

где $c$ — скорость света в вакууме.

Другим важным параметром ядра является энергия связи, приходящаяся на один нуклон ядра, которую можно вычислить, разделив энергию связи ядра на число содержащихся в нём нуклонов:

${displaystyle varepsilon ={frac {E_{c}}{A}}}$

Эта величина представляет собой среднюю энергию, которую нужно затратить, чтобы удалить один нуклон из ядра, или среднее изменение энергии связи ядра, когда свободный протон или нейтрон поглощается в нём.

Как видно из поясняющего рисунка, при малых значениях массовых чисел удельная энергия связи ядер резко возрастает и достигает максимума при ${displaystyle Aapprox 50div 60}$ (примерно 8,8 Мэв). Нуклиды с такими массовыми числами наиболее устойчивы. С дальнейшим ростом $A$ средняя энергия связи уменьшается, однако в широком интервале массовых чисел значение энергии почти постоянно ( ${displaystyle epsilon approx 8}$ МэВ), из чего следует, что можно записать ${displaystyle E_{c}approx epsilon A}$ .

Такой характер поведения средней энергии связи указывает на свойство ядерных сил достигать насыщения, то есть на возможность взаимодействия нуклона только с малым числом «партнёров». Если бы ядерные силы не обладали свойством насыщения, то в пределах радиуса действия ядерных сил каждый нуклон взаимодействовал бы с каждым из остальных и энергия взаимодействия была бы пропорциональна ${displaystyle A(A-1)}$ , а средняя энергия связи одного нуклона не была бы постоянной у разных ядер, а возрастала бы с ростом $A$ .

Общая закономерность зависимости энергии связи от массового числа описывается формулой Вайцзеккера в рамках теории капельной модели ядра^[1]^[2]^[14]^[15].

Устойчивость ядер[править | править код]

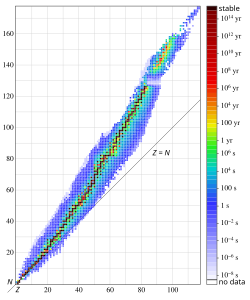
Зависимость числа нейтронов N от числа протонов Z в атомных ядрах (N=A-Z).

Из факта убывания средней энергии связи для нуклидов с массовыми числами больше или меньше 50-60 следует, что для ядер с малыми $A$ энергетически выгоден процесс слияния — термоядерный синтез, приводящий к увеличению массового числа, а для ядер с большими $A$ — процесс деления. В настоящее время оба этих процесса, приводящих к выделению энергии, осуществлены, причём последний лежит в основе современной ядерной энергетики, а первый находится в стадии разработки.

Детальные исследования показали, что устойчивость ядер также существенно зависит от параметра $N/Z$ — отношения чисел нейтронов и протонов. В среднем для наиболее стабильных ядер^[16] $N/Zapprox 1+0.015A^{{2/3}}$ , поэтому ядра лёгких нуклидов наиболее устойчивы при $Napprox Z$ , а с ростом массового числа всё более заметным становится электростатическое отталкивание между протонами, и область устойчивости сдвигается в сторону $N>Z$ (см. поясняющий рисунок).

Если рассмотреть таблицу стабильных нуклидов, встречающихся в природе, можно обратить внимание на их распределение по чётным и нечётным значениям $Z$ и $N$ . Все ядра с нечётными значениями этих величин являются ядрами лёгких нуклидов ${}_{{1}}^{{2}}{textrm {H}}$ , ${}_{{3}}^{{6}}{textrm {Li}}$ , ${}_{{5}}^{{10}}{textrm {B}}$ , ${}_{{7}}^{{14}}{textrm {N}}$ . Среди изобар с нечётными A, как правило, стабилен лишь один. В случае же чётных $A$ часто встречаются по два, три и более стабильных изобар, следовательно, наиболее стабильны чётно-чётные, наименее — нечётно-нечётные. Это явление свидетельствует о том, что как нейтроны, так и протоны, проявляют тенденцию группироваться парами с антипараллельными спинами, что приводит к нарушению плавности вышеописанной зависимости энергии связи от $A$ ^[1].

Z	N=A-Z	A	Число нуклидов
Чётное	Чётное	Чётное	167
Чётное	Нечётное	Нечётное	55
Нечётное	Чётное	Нечётное	53
Нечётное	Нечётное	Чётное	4

Таким образом, чётность числа протонов или нейтронов создаёт некоторый запас устойчивости, который приводит к возможности существования нескольких стабильных нуклидов, различающихся соответственно по числу нейтронов для изотопов и по числу протонов для изотонов. Также чётность числа нейтронов в составе тяжёлых ядер определяет их способность делиться под воздействием нейтронов^[2].

Ядерные силы[править | править код]

Ядерные силы — это силы, удерживающие нуклоны в ядре, представляющие собой большие силы притяжения, действующие только на малых расстояниях. Они обладают свойствами насыщения, в связи с чем ядерным силам приписывается обменный характер (с помощью пи-мезонов). Ядерные силы зависят от спина, не зависят от электрического заряда и не являются центральными силами^[2].

Уровни ядра[править | править код]

В отличие от свободных частиц, для которых энергия может принимать любые значения (так называемый непрерывный спектр), связанные частицы (то есть частицы, кинетическая энергия которых меньше абсолютного значения потенциальной), согласно квантовой механике, могут находиться в состояниях только с определёнными дискретными значениями энергий, так называемый дискретный спектр. Так как ядро — система связанных нуклонов, оно обладает дискретным спектром энергий. Обычно оно находится в наиболее низком энергетическом состоянии, называемым основным. Если передать ядру энергию, оно перейдёт в возбуждённое состояние.

Расположение энергетических уровней ядра в первом приближении:

${displaystyle D=ae^{-b{sqrt {E^{*}}}}}$ , где:

$D$ — среднее расстояние между уровнями,

$E^{*}$ — энергия возбуждения ядра,

$a$ и $b$ — коэффициенты, постоянные для данного ядра:

$a$ — среднее расстояние между первыми возбуждёнными уровнями (для лёгких ядер примерно 1 МэВ, для тяжёлых — 0,1 МэВ)

$b$ — константа, определяющая скорость сгущения уровней при увеличении энергии возбуждения (для лёгких ядер примерно 2 МэВ^−1/2, для тяжёлых — 4 МэВ^−1/2).

С ростом энергии возбуждения уровни сближаются быстрее у тяжёлых ядер, также плотность уровней зависит от чётности числа нейтронов в ядре. Для ядер с чётными (особенно магическими) числами нейтронов плотность уровней меньше, чем для ядер с нечётными, при равных энергиях возбуждения первый возбуждённый уровень в ядре с чётным числом нейтронов расположен выше, чем в ядре с нечётным.

Во всех возбуждённых состояниях ядро может находиться лишь конечное время, до тех пор, пока возбуждение не будет снято тем или иным путём. Состояния, энергия возбуждения которых меньше энергии связи частицы или группы частиц в данном ядре, называются связанными; в этом случае возбуждение может сниматься лишь гамма-излучением. Состояния с энергией возбуждения, превышающей энергию связи частиц, называются квазистационарными. В этом случае ядро может испустить частицу или гамма-квант^[1].

Ядерные реакции[править | править код]

Ядерная реакция — процесс превращения атомных ядер, происходящий при их взаимодействии с элементарными частицами, гамма-квантами и друг с другом.

Радиоактивность[править | править код]

Лишь небольшая часть нуклидов являются стабильными. В большинстве случаев ядерные силы оказываются неспособны обеспечить их постоянную целостность, и ядра рано или поздно распадаются. Это явление получило название радиоактивности.

Система обозначений ядер[править | править код]

Для обозначения атомных ядер используется следующая система:

Таким образом, состав ядра оказывается полностью определён, так как ${displaystyle N=A-Z}$ .

Пример такого обозначения:

${displaystyle {}^{238}{textrm {U}}}$ — ядро урана-238, в котором 238 нуклонов, из которых 92 — протоны, так как элемент уран имеет 92-й номер в таблице Менделеева.

Иногда, однако, для полноты вокруг обозначения элемента указывают все характеризующие ядро его атома числа:

слева снизу — зарядовое число $Z$ , то есть, то же самое, что указано символом элемента;
слева сверху — массовое число $A$ ;
справа снизу — изотопическое число $N$ ^{[источник не указан 1372 дня (обс.)]};
если речь идёт о ядерных изомерах, к массовому числу приписывается буква из последовательности m, n, p, q, … (иногда используют последовательность m1, m2, m3, …). Иногда эту букву указывают в качестве самостоятельного индекса справа сверху.

Примеры таких обозначений:

${}_{{92}}^{{238}}{textrm {U}}$ , ${}_{{92}}^{{238}}{textrm {U}}_{{146}}$ , ${}_{{92}}^{{238m}}{textrm {U}}$ , ${}_{{92}}^{{238}}{textrm {U}}^{{m}}$ .

Обозначения атомных ядер совпадают с таковыми для нуклидов.

По историческим и иным причинам, некоторые ядра имеют самостоятельные названия. Например, ядро ⁴He называется α-частицей, ядро дейтерия ²H (или D) — дейтроном, а ядро трития ³H (или T) — тритоном. Последние два ядра являются изотопами водорода и поэтому могут входить в состав молекул воды, давая в итоге так называемую тяжёлую воду.

Примечания[править | править код]

Использованная литература

↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ Бартоломей Г.Г., Байбаков В.Д., Алхутов М.С., Бать Г.А. Основы теории и методы расчета ядерных энергетических реакторов. — М.: Энергоатомиздат, 1982. — С. 512.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ Климов А. Н. Ядерная физика и ядерные реакторы. — М.: Энергоатомиздат, 1985. — С. 352.
↑ ¹ ² Ганев И. Х. Физика и расчёт реактора. — М.: Энергоиздат, 1981. — С. 368.
↑
Кудрявцев П. С. Открытие атомного ядра // Курс истории физики. — 2-е изд., испр. и доп. — М.: Просвещение, 1982. — 448 с.
↑ Meitner, L. Über die verschiedenen Arten des radioaktiven Zerfalls und die Möglichkeit ihrer Deutung aus der Kernstruktur (нем.) // Zeitschrift für Physik : magazin. — 1921. — Bd. 4. — S. 146—156.
↑ Мухин К. Привлекательный мир микрофизики // Наука и жизнь. — 2015. — № 10. — С. 96—103.
↑ W. Heitler, G. Herzberg. Gehorchen die Stickstoffkerne der Boseschen Statistik? (нем.) // Naturwissenschaften (англ.) (рус. : magazin. — 1929. — Bd. 17. — S. 673.
↑ А. И. Ахиезер, М. П. Рекало. Биография элементарных частиц. — Киев: Наукова думка, 1979. — С. 18.
↑ Ю. А. Храмов. Физики:Биографический справочник. — 2-е изд. — М.: Наука, 1983.
↑ ¹ ² Мухин К. Н. Экспериментальная ядерная физика. — М.: Энергоатомиздат, 1983.
↑ Iwanenko, D.D., The neutron hypothesis, Nature 129 (1932) 798.
↑ Г. А. Сарданашвили. Дмитрий Иваненко – суперзвезда советской физики. Ненаписанные мемуары. — Либроком. — 2010. — С. 12.
↑ Глесстон С. Атом. Атомное ядро. Атомная энергия. — М.: Изд-во иностр. лит., 1961.
↑ I.R.Cameron, University of New Brunswick. Nuclear fission reactors. — Canada, New Brunswick: Plenum Press, 1982.
↑ Камерон И. Ядерные реакторы. — М.: Энергоатомиздат, 1987. — С. 320.
↑ Rohlf, James William. Modern Physics from α to Z°. — John Wiley & Sons, 1994. — С. 664. — ISBN 0471572705.

Литература[править | править код]

М. Айзенберг, В. Грайнер. Модели ядер, коллективные и одночастичные явления. — М.: Атомиздат, 1975. — 454 c.
М. Айзенберг, В. Грайнер. Микроскопическая теория ядра. — М.: Атомиздат, 1976. — 488 с.
К. Бракнер Теория ядерной материи. — М., Мир, 1964. — 302 с.
О. Бор, Б. Моттельсон. Структура атомного ядра. — В 2-х т. — М.: Мир, 1971—1977.
В. П. Крайнов. Лекции по микроскопической теории атомного ядра. — М.: Атомиздат, 1973. — 224 с.
В. В. Маляров. Основы терии атомного ядра. 2-ое изд. — М.: Наука, 1967. — 512 с.
Р. Натаф. Модели ядер и ядерная спектроскопия. — М.: Мир, 1968. — 404 с.
С. М. Поликарпов. Необычные ядра и атомы. — М.: Наука, 1977. — 152 с.
Дж. Рейнуотер. Как возникла модель сфероидальных ядер. Успехи физических наук, 1976, Том 120. Вып. 4, с. 529—541. (Нобелевская лекция по физике 1975 г.)
А. Г. Ситенко. Теория ядерных реакций. — М.: Энергоатомиздат, 1983. — 352 с.
А. Г. Ситенко, В. К. Тартаковский. Лекции по теории ядра. — М.: Атомиздат, 1972. — 352 с.
Л. Слив М. И. Стрикман, Л. Л. Франкфурт. Проблемы построения микроскопической теории ядра и квантовая хромодинамика, Успехи физических наук, 1976, Том 145. Вып. 4, с. 553—592.
В. Г. Соловьев. Теория атомного ядра. Ядерные модели. — М.: Энергоиздат, 1981. — 296с.
В. Г. Соловьев. Теория сложных ядр. — М.: Наука, 1971. — 560 с.
Журнал: Физика элементарных частиц и атомного ядра (ЭЧАЯ) (Архив статей с 1970 г.)

Ссылки[править | править код]

Ядро атомное — Физическая энциклопедия
Колебательные возбуждения ядер — Физическая энциклопедия
Ядерные модели — Физическая энциклопедия
Капельная модель ядра — Физическая энциклопедия
Ядерная материя — Физическая энциклопедия
Ядерные цепные реакции — Физическая энциклопедия
Деформированные ядра — Физическая энциклопедия
Б. С. Ишханов, Э. И. Кэбин, Физика ядра и частиц, XX век. МГУ, 2000.
Ядерная энергия

Источник

Физика > Ядерный размер и плотность

Узнайте, каковы размер и плотность ядра. Читайте, как использовать радиус, эксперимент с золотой фольгой, формула плотности ядра, спектры излучения атома.

Размер ядра вычисляется по его радиусу, а плотность выходит из размера.

Задача обучения

Вывести связь ядерных радиуса, плотности и размера.

Основные пункты

Первую оценку радиуса выполнили Г. Гейгер и Э. Марсден в 1909 году в эксперименте с золотой фольгой.

Есть эмпирическая связь радиуса, заряда и массового числа для более тяжелых ядер (A > 20), где r – эмпирическая постоянная (1.2-1.5 фм).

Формула плотности ядра:

Термины

Альфа-частицы – два протона и два нейтрона, соединенных с частицей, соответствующей ядру гелия.
Атомные спектры – линии излучения или поглощения, появляющиеся при переходе электрона от одного энергетического уровня к другому.
Ядро – массивная центральная часть атома с положительным зарядом. Состоит из протонов и нейтронов.

Размер ядра вычисляется по радиусу. Его можно измерить путем рассеяния электронов в ядре. Определение радиуса атомного ядра напоминает проблему с расчетами атомного радиуса, так как они попросту не обладают четкими границами. Но ядро атома можно смоделировать в виде сферы с положительным зарядом, чтобы интерпретировать эксперименты рассеяния электронов: нет четкой границы и электроны «видят» диапазон поперечных сечений, для которых можно принять среднее значение. Ядерное сечение расположено пропорционально квадрату радиуса, определяющему рассеяние электронов.

Первую оценку радиуса в 1909 году сделали Г. Гейгер и Э. Марсден. Им принадлежит известный опыт с золотой фольгой, где некоторые частицы рассеивались с углом более 90°, из-за чего возвращались к той же стороне, что и альфа-источник. Резерфорду удалось определить верхний предел радиуса золотого ядра 34 фм.

В поздних исследованиях удалось выявить эмпирическую связь радиуса и массового числа для более тяжелых ядер (А > 20): R ≈ r⋅A^1/3 (r – эмпирическая постоянная, 1.2-1.5 фм). Отсюда радиус для золотого ядра (A = 197) – 7.5 фм.

Ядерная плотность составляет примерно 4 ⋅ 10¹⁷ кг/м³. Ее можно определить по размеру:

Источник

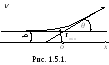Первые
представления о размерах ядра были
получены Резерфордом при экспериментальном
изучении рассеяния α-частиц с энергией~ 5МэВпри прохождении
через тонкие пленки золота. Наблюдалось,
что некоторое количество α-частиц
рассеивается на очень большие углыθ,
почти до 180º. На этом основании в 1911 г.
Резерфорд пришел к выводу, что в центре
атома (точкао
на рис. 1.5.1)
имеется область положительного
электрического заряда, связанная с
большой массой, сконцентрированной в
очень малом объеме (по сравнению с
объемом атома). На основании закона
Кулона для точечных зарядов можно
вычислить наименьшее расстояниеr_min,
на которое может подойти к центру ядра
α-частица, летящая точно по направлению
к ядру (прицельный параметрb= 0). Для этого следует приравнять ее
начальную кинетическую энергию к
потенциальной энергии взаимодействия
α-частицы с ядром в момент ее полной
остановки (в точке поворота):

(1.5.1)

Формула
(1.5.1) верна в предположении неподвижного
ядра, когда масса ядра М(A,Z)
>>m_α
– массы α-частицы. Приняв кинетическую
энергию α-частицы равной 5МэВи
положивZ= 79 (золото),
получимr_min= 4,5·10^-12см. Естественным было
принять эту величину за верхнюю оценку
радиуса ядра золота.

Однако
необходимо быть уверенным в том, что
отбрасываемая в обратном направлении
α-частица не
проникает в область положительного
заряда атома, поскольку равенство
(1.5.1) справедливо либо для точечных, либо
для сферически симметричных не
перекрывающихся зарядов конечных
размеров. Тщательная проверка этого
предположения была выполнена сотрудниками
Резерфорда в 1913 г. и было установлено
хорошее согласие экспериментальных
результатов рассеянияα-частиц
с расчетами по формуле (1.2.2), полученной
теоретически на основе закона Кулона.
Оказалось, что закон Кулона имеет место
дляr_min
> 3·10^-12см. Подобные
эксперименты, выполненные двадцатью
годами позже сα-частицами,
имеющими энергию в десять и вышеМэВ(получены на ускорителях), показали, что
когда расстояние между взаимодействующими
частицами уменьшается до 10^-12см,
наблюдаются резкие отклонения от закона
Кулона, а на расстояниях, меньших 10^-12см, обнаруживается действие быстро
убывающих с расстоянием сил притяжения,
которые перекрывают действие кулоновских
сил отталкивания.

В
дальнейшем размеры ядер определялись
разными способами. Говоря о размерах
ядра, нужно всегда иметь в виду, что это
достаточно условная величина. Ядро, как
квантовомеханическая система, не имеет
определенной границы. Наиболее точными
считаются оценки размеров ядра по
результатам рассеяния ядрами быстрых
нейтронов и электронов. Все опыты
подтвердили предположения о приблизительно
сферической форме ядра, радиус которого
определяется через массовое число А
как

(1.5.2)

где r₀= (1,2 ÷ 1,4)·10^-13см.

В
опытах по рассеянию быстрых нейтронов
на ядрах определяется не радиус ядра,
а несколько большее значение радиуса
области ядерного взаимодействия, поэтому
r₀= (1,3 ÷ 1,4)·10^-13см.

При
зондировании ядра быстрыми электронами
(опыты Хофштадтера) определяется сфера
радиусаR, в которой
находятся протоны. Поэтому получают
несколько меньшее значениеr₀= (1,2 ÷ 1,3)·10^-13см. Высокая
точность современных методов исследования
с помощью рассеяния быстрых электронов
с кинетической энергиейТ_е> 500МэВпозволяет оценить не только
размер области, занятой протонами, но
и распределение плотностиρ_ээлектрического заряда по ядру. Поскольку
нет причин стабильному ядру иметь
различное распределение плотности
протонов и нейтронов, то полученные
результаты для протонов представляют
по существу распределение плотности
ρ_яядерного вещества в ядре. Распределение
ядерного вещества хорошо согласуется
с формулой (модель Ферми)

(1.5.3)

где R₀=
1,08·10^-13·А^1/3см– расстояние
от центра ядра до места, где плотность
ядра падает вдвое, а δ ≈ 0,55·10^–13см– определяет скорость убывания
плотности ядерного вещества. Спад
плотности ядерного вещества от 0,9ρ₀до 0,1ρ₀для всех ядер происходит
в пределах одинаковых расстоянияхd= 4,4δ = 2,4·10^-13см. Поэтому у
легких ядер отсутствует область, где
плотность ядерного вещества примерно
постоянна (см. рис. 1.5.2).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Все, наверное, помнят со школы, что атомы, а тем более — атомные ядра, настолько маленькие, что их не увидеть и не пощупать. Из этого может сложиться впечатление, что раз эти размеры относятся к микромиру, то и определить их можно только с помощью очень сложных физических экспериментов. Но это вовсе не так. Существуют вполне макроскопические и даже повседневные явления, которые позволяют оценить эти размеры хотя бы по порядку величины. В одной из задач мы уже выясняли, как можно прикинуть размер атома, исходя из известных термодинамических характеристик вещества. Обратимся теперь к атомному ядру.

Ядра, конечно, изучать труднее, чем сами атомы. В формировании свойств материи они играют довольно-таки второстепенную роль. Они придают веществу массивность, держат около себя электроны, но сами ядра непосредственно друг с другом не взаимодействуют. Так получается потому, что они очень маленькие, намного меньше самих атомов (рис. 1). И по этой причине определить их размер труднее, чем размер атомов.

Рис. 1. Атомное ядро намного меньше самого атома

В этой задаче, однако, для оценки размера ядра мы воспользуемся одной подсказкой, которую нам предоставляет природа, — явлением радиоактивности.

Известно, что в ходе некоторых ядерных превращений из ядер вылетают нейтроны. В отличие от протонов или электронов, нейтроны электрически не заряжены. В своем полете сквозь вещество они практически не чувствуют электронные оболочки атомов. Они пролетают один атом за другим насквозь, не отклоняясь от своей траектории, пока не столкнутся лоб в лоб с каким-нибудь ядром вещества. Для простоты мы будем считать, что каждый быстрый нейтрон, врезающийся в ядро, вызывает какое-то существенное взаимодействие: это может быть поглощение, упругое рассеяние или какое-нибудь изменение внутри ядра.

Такое «наплевательское отношение» нейтронов к электромагнитным взаимодействиям приводит к тому, что нейтронный поток обладает высокой проникающей способностью (рис. 2). Длина свободного пробега нейтрона (то есть расстояние между отдельными актами столкновений) может быть довольно большой, намного больше, чем для электронов или рентгеновского излучения. Самое важное для нас тут то, что эта длина измеряется напрямую в простейшем лабораторном опыте по экранированию нейтронного потока пластинками разной толщины. Результаты получаются такие: для быстрых нейтронов с энергией порядка 1 МэВ длина свободного пробега в твердом веществе, например алюминии, составляет около 10 см — вполне макроскопический размер.

Рис. 2. Типичное соотношение между глубиной проникновения альфа-, бета-, гамма-излучения и нейтронов сопоставимой энергии

Задача

Опираясь на приведенные выше числа и рассуждения, оцените по порядку величины размер атомного ядра алюминия.

Подсказка 1

Нарисуйте схематично несколько атомов, плотно прижавшихся друг к другу своими электронными оболочками. Отметьте внутри них атомные ядра, не забывая о том, что они очень маленькие. Нейтроны не обращают внимание на электронные оболочки, для них сплошное вещество — это как бы очень разреженный и почти неподвижный «газ» из атомных ядер. С учетом этого нарисуйте прямую траекторию нейтрона и попытайтесь понять, как длина свободного пробега связана с размером ядра.

Подсказка 2

Вообще-то формула для связи длины свободного пробега с параметрами среды нам уже встречалась в задаче Столкновение фотонов. Там мы говорили про сечение рассеяния фотонов друг на друге, и это была довольно абстрактная величина. Сейчас всё проще: мы считаем, что сечение рассеяния для нейтрон-ядерного столкновения просто совпадает с геометрическим сечением системы «ядро + нейтрон».

Решение

На рис. 3 в очень упрощенном виде показано сплошное вещество с точки зрения заряженных частиц или фотонов, а также с точки зрения нейтрона. Нейтрон практически «не видит» электроны, для него существуют только атомные ядра. Радиус ядра мы обозначим через R, а характерное расстояние между ними — через a. Обратите внимание, что a — это типичное межатомное расстояние, оно много больше размера ядра R. Сам нейтрон мы для простейших оценок будем считать точечным. При желании оценку можно уточнить, связав размер нейтрона с размером ядра и его массовым числом. Однако оценку по порядку величины это уточнение не изменит.

Рис. 3. Схематичное изображение вещества с точки зрения заряженных частиц и с точки зрения нейтрона

Связь между длиной свободного пробега L, сечением столкновения σ и концентрацией ядер n уже подробно обсуждалась в решении задачи про столкновение фотонов. Записывается она просто: Lσn = 1. В нашем случае сечение столкновения — это просто поперечное сечение ядра, σ = πR², а концентрация выражается через расстояние между ядрами, n = 1/a³. Подставив эти выражения, мы получаем ответ для оценки радиуса ядра:

Межатомное расстояние a — это для сплошного вещества просто размер атомов, то есть несколько ангстрем. Для более точной оценки можно вычислить концентрацию ядер через плотность вещества и массу ядра; для алюминия это даст a = 2,5 Å. Взяв L = 0,1 м, получим R ≈ 7·10⁻¹⁵ м.

Найденное значение примерно вдвое превышает реальный радиус ядра алюминия. Это совершенно приемлемая точность для столь простой оценки по порядку величины.

Послесловие

Эта задача может послужить вступлением для самых разных рассказов о том, как нейтроны или, более широко, отдельные элементарные частицы, взаимодействуют с веществом. Мы здесь ограничимся только несколькими самыми общими набросками.

Во-первых, надо сразу сказать, что в реальном эксперименте размеры ядер измеряются совсем не такими методами. Самый стандартный способ — это улучшенная разновидность классического опыта Резерфорда: размер ядра можно узнать по тому, как на нем рассеиваются заряженные частицы. Но тут есть любопытный момент: оказывается, у ядра может быть несколько разных размеров: протонный радиус, материальный радиус, зарядовый радиус и т.д. В отдельных случаях, например для ядер с нейтронным гало, эти размеры могут существенно различаться. Поэтому современная экспериментальная физика использует сразу несколько разных методов для измерения размеров и изучения структуры ядер (см. введение в эту область физики в нашей новости Оптические исследования помогают изучать ядра с нейтронным гало).

Рис. 4. Траектории электрона и нейтрона в веществе

Далее, почему в этой задаче использовались нейтроны, а не электроны или протоны? Отчасти ответ уже понятен из решения. Заряженные частицы, а также фотоны, чувствуют не только и не столько ядра, сколько электронные оболочки атомов, а значит, использовать их движение для измерения размеров ядра затруднительно. Но тут есть и второй аспект. Взаимодействие нейтронов с ядрами короткодействующее; оно имеет место только в том случае, когда нейтрон приблизится к ядру на расстояние порядка ядерного размера. Поэтому траектория нейтрона в веществе представляет собой ломаную линию с четко определенными точками излома и прямыми участками (рис. 4). А вот траектория заряженных частиц из-за дальнодействующего электромагнитного взаимодействия постоянно отклоняется из стороны в сторону, но, правда, на небольшие углы. Более того, это взаимодействие приводит к ионизации вещества (выбиванию новых электронов) и к излучению фотонов. В итоге заряженная частица в веществе просто не имеет четко определенной длины свободного пробега. Подробнее про возникающие здесь явления см. в онлайн курсе Взаимодействие частиц с веществом.

В этой задаче мы для простоты считали, что сечение рассеяния нейтрона на ядре чисто геометрическое: столкновение происходит, если траектория нейтрона попадает строго в ядро. На самом деле в микромире, который описывается квантовыми законами, ситуация может сильно отличаться от этого предположения. Более того, это отличие сильно зависит от энергии нейтронов (рис. 5). Так, при энергиях около 1 МэВ сечение рассеяния обычно составляет несколько барн (1 б = 10⁻²⁴ см²; в нашей задаче сечение получилось примерно 0,5 б). Для тепловых нейтронов (энергия порядка 0,025 эВ) сечение захвата нейтрона составляет порой многие тысячи (!) барн, то есть на несколько порядков больше геометрического размера ядра (см. периодическую таблицу сечений захвата нейтрона). Существуют даже медицинские технологии, которые используют эту особенность ядерной физики, например, бор-нейтронозахватная терапия для борьбы с трудными формами рака. А в промежуточной области энергий наблюдаются резкие и узкие всплески сечения, которые возникают из-за сложной структуры ядра.

Рис. 5. Зависимость сечения захвата нейтрона изотопами урана, плутония, и тория от энергии нейтрона

Особняком стоят здесь холодные нейтроны. Благодаря своей малой скорости и большой длине волны, они чувствуют не отдельные атомные ядра, а сразу их большой коллектив (см. новость Холодные нейтронные лучи прощупывают предметы, не внося никаких возмущений). Из-за этого при достаточно низкой скорости они могут вообще коллективно отражаться от вещества; материал словно выталкивает из себя такие нейтроны. Это позволяет в буквальном смысле держать ультрахолодные нейтроны в «металлической бутылке» и проводить с ним разные эксперименты (см. например новости Измерения времени жизни нейтрона, выполненные разными методами, по-прежнему расходятся и Нейтроны в гравитационном поле Земли позволяют проверить модели темной энергии и темной материи, а также задачу Нейтроны в ловушке).

Рис. 6. Изображение охлаждающих каналов внутри турбинной лопасти, полученные с помощью нейтронной радиографии

Ну и наконец, нейтроны открывают бесчисленные возможности не только для фундаментальной физики, но и для прикладных исследований. Не пытаясь даже перечислить все конкретные области применения, просто упомянем индустриальную диагностику устройств, внутрь которых не заглянешь другими методами (рис. 6), материаловедение, биомедицинские науки вкупе с фармакологией, геофизику. Все эти применения так или иначе опираются на высокую проникающую способность нейтронов в веществе.

Источник

Вот казалось бы, радиус атома – штука хорошо известная и кажется уже чем-то очевидным. Значение это приведено даже в таблице Менделеева. Правда ни в каждой, но есть такие “прокаченные” варианты, где отражены основные параметры каждого приведенного элемента. Ну и исходя из таких данных, мы вполне можем выбрать самый большой атом и самый маленький.

Размер атома

В чём сложность?

Однако, тут нужно помнить, что размер атома – величина весьма условная. Одной из главных проблем тут является нестабильность самого атома. Под термином нестабильность тут мы будем понимать не его склонность к постоянному распаду, а ряд сопутствующих проблем.

Например, вроде бы очевидно, что измерять размер следует исходя из радиуса, который является отрезком прямой, соединяющий центр ядра атома и наиболее стабильную электронную орбиталь, где вероятность появления электрона наибольшая. Но это очень красиво, пока мы рисуем планетарную модель. На самом же деле, орбиты электронов, движущихся вокруг атома выглядят примерно так 🙂

Траектории электронов

Соответственно, уже “с порога” встаёт вопрос точности измерения. При этом нужно понимать, что переход атома в возбужденное состояние при таком раскладе сможет изменить его размер.

Но даже если исходить из усреднения измерений, есть и ещё одна важная проблема. На данный момент не существует объективной методики, которая позволяет измерять размер атома, как мы измеряем гайку штангенциркулем. Все измерения размера атомов косвенные.

Какие методики измерения существуют?

В энциклопедии довольно мудрёно объясняется, что нормальных в нашем понимании измерений пока нет. Существующие методики строятся на логическом предположении, которое позволяет утверждать, что мы измеряем размер атома.

Например, существует методика измерения размера атома, исходя из плотности потока отражения бомбардируемых частиц. По атому стреляют частичкам и там где есть атом, эти частички отлетают в обратном направлении. Пятно, появившееся на сенсоре, фиксирующем такие отраженные частицы, считается соответствующим размеру измеряемого атома.

Есть теоретическая методика, которая исходит из измерения размера атома посредством определения межатомных расстояний. Исходя из принципа плотнейшей упаковки, расстояние между атомами для каждого элемента фиксировано и прямо соотносится с размером самого атома. Это даёт возможность предположить, что реальный размер атома такой-то. Ну а измерить расстояние между самими атомами технически проще, чем измерять радиус атома. Тут достаточно точечных рефлексов.

Наиболее точной методикой измерения размеров атома сегодня считается методика спектроскопии. Спектроскопические методы основаны на взаимодействии электромагнитной волны с веществом. При некоторых условиях, вещество выступает как дифракционная решетка, а параметры решетки могут быть высчитаны. При этом, размер самой решетки прямо соотносится с размерами межатомных пространств. Ну а исходя из знаний о строении вещества, можно прикинуть и размер самого атома.

Есть и ещё одна интересная методика. Она расчётная. Исходя из атомной массы высчитывается размер атома. Плотность можно измерить, массу высчитать. Дальше простая арифметика позволяет рассчитать и радиус атома. Правда тут приближений ещё больше, чем во всех описанных ранее методиках.

Ну и из серии совсем экстравагантных измерений – на одном из конкурсов научной фотографии победила фотография “Одинокий атом стронция в ионной ловушке”. Там на простой фотоаппарат был сфотографирован атом и выглядит он как светящаяся точка. Сопоставляя размеры этой точки и любого объекта, вполне можно прикинуть реальный размер.

Автор фото студент Оскфорда Дэвид Надлингер

Важно отметить, что в основном все методики дают сопоставимые результаты. Казалось бы, это означает, что размер атома определен верно и однозначно. Но, возвращаемся к началу статьи и вспоминаем, что сама по себе однозначная форма атома – это научное приближение и абстракция. В реальных условиях может меняться как реальная форма, так характерный размер.

Так, если измерять атом внутри кристаллической решетки, то мы получим один размер, а если измерять атом того же вещества, свободно путешествующий в пространстве – другой. Логично предположить, что размер свободного атома больше размера связанного атома. Он ведет себя подобно резиновому мячику. Пока мячик сжимается внешними силами, он имеет меньший радиус, нежели мячик, который находится в свободном положении.

Так есть ли точная информация?

В итоге можно сказать, что однозначно определенных значений атомных радиусов не существует. Ведь помимо того, что все методики измерений дают хоть и коррелирующий, но не одинаковый результат, есть ещё и конфигурация самого атома. Отсюда следует очень простой и, отчасти печальный, вывод.

Размер атома, известный нам – это всего лишь научная абстракция, используемая для удобной работы с моделью строения вещества. Радиус атома, приведенный в справочнике подразумевает измерение в одинаковых условиях одинаковым методом. Нельзя сказать, что это полная ахинея, ведь размеры соизмеримы с реальностью, но и нельзя утверждать о высокой точности.

Обязательно подпишитесь на проект, оцените статью лайком и напишите комментарий! Это поможет развитию канала, а вы не пропустите новые интересные статьи

Советую также прочитать на нашем канале:

—–

Смотрите нас на YouTube и присоединяйтесь к телеге!

Источник

История[править | править код]

Теории строения атомного ядра[править | править код]

Ядерно-физические характеристики[править | править код]

Заряд[править | править код]

Масса[править | править код]

Радиус[править | править код]

Моменты ядра[править | править код]

Спин[править | править код]

Магнитный момент[править | править код]

Электрический квадрупольный момент[править | править код]

Энергия связи[править | править код]

Устойчивость ядер[править | править код]

Ядерные силы[править | править код]

Уровни ядра[править | править код]

Ядерные реакции[править | править код]

Радиоактивность[править | править код]

Система обозначений ядер[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Задача обучения

Основные пункты

Термины

Задача

Подсказка 1

Подсказка 2

Решение

Послесловие

В чём сложность?

Какие методики измерения существуют?

Так есть ли точная информация?

Советую также прочитать на нашем канале:

Смотрите нас на YouTube и присоединяйтесь к телеге!

Вам также может понравиться

Как найти одноклассников без регистрации бесплатно

Как найти посылку если нет номера отправления

Как найти свой способ мышления

Добавить комментарий Отменить ответ