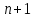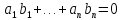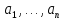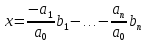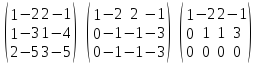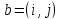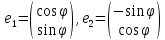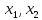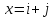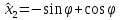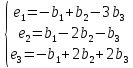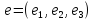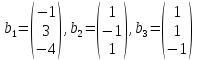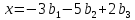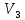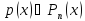The calculator will find a basis of the space spanned by the set of given vectors, with steps shown.
Related calculators:
Linear Independence Calculator,
Matrix Rank Calculator
Your Input
Find a basis of the space spanned by the set of the vectors $$$left{left[begin{array}{c}1\2\3end{array}right], left[begin{array}{c}9\12\5end{array}right], left[begin{array}{c}5\7\4end{array}right]right}.$$$
Solution
The basis is a set of linearly independent vectors that spans the given vector space.
There are many ways to find a basis. One of the ways is to find the row space of the matrix whose rows are the given vectors.
Thus, the basis is $$$left{left[begin{array}{c}1\0\- frac{13}{3}end{array}right], left[begin{array}{c}0\1\frac{11}{3}end{array}right]right}$$$ (for steps, see row space calculator).
Another way to find a basis is to find the column space of the matrix whose columns are the given vectors.
Thus, the basis is $$$left{left[begin{array}{c}1\2\3end{array}right], left[begin{array}{c}9\12\5end{array}right]right}$$$ (for steps, see column space calculator).
If two different bases were found, they are both the correct answers: we can choose any of them, for example, the first one.
Answer
The basis is $$$left{left[begin{array}{c}1\0\- frac{13}{3}end{array}right], left[begin{array}{c}0\1\frac{11}{3}end{array}right]right}approx left{left[begin{array}{c}1\0\-4.333333333333333end{array}right], left[begin{array}{c}0\1\3.666666666666667end{array}right]right}.$$$A
1.6.
Размерность линейного пространства
Эта
важнейшая характеристика линейного
пространства связана
со свойствами систем векторов в этом
пространстве.
Определение
1.5. Максимальное
количество линейно
независимых векторов в
данном линейном пространстве называют
размерностью
линейного пространства.
Если
размерность линейного пространства С
равна
n,
т.е. существует линейно независимая
система из п
векторов,
а любая система
векторов, содержащая
вектор или более, линейно
зависима, то
говорят, что это линейное пространство
п-мерно.
Размерность
такого линейного пространства обозначают
Существуют
линейные пространства, в которых можно
выбрать линейно независимую систему,
содержащую сколь угодно большое
количество векторов. Такие линейные
пространства называют бесконечномерными.
В
отличие от них, n-мерные
линейные пространства называют
конечномерными.
Мы
будем рассматривать конечномерные
линейные пространства.
Пример
1.12. Линейное
пространство
функций, непрерывных на отрезке [0,1] (см.
1.1),
является
бесконечномерным, так как для любого
натурального п
система
многочленов

являющихся
элементами этого линейного пространства,
линейно независима. В самом деле, линейная
комбинация этих
многочленов, отвечающая набору
коэффициентов

есть многочлен

который
является нулевым (т.е. равен постоянной
функции 0), только если все его коэффициенты
(они же коэффициенты
линейной комбинации) равны
нулю.
Оказывается,
что размерность линейного пространства
тесно связана с количеством векторов,
которое может иметь базис
линейного
пространства.
Теорема
1.4. Если
линейное пространство
n-мерно,
то любая линейно независимая система
из п
векторов
является его базисом.
Пусть
система векторов
линейно независима. Тогда для любого
вектора
система
векторов
линейно
зависима, так как она содержит
вектор, т.е. количество большее, чем
размерность линейного пространства.
Это значит, что существуют такие
коэффициенты

одновременно не равные нулю, что

Заметим,
что

так как в противном случае равенство
(1.6) сводится к равенству
причем
среди коэффициентов
есть
хотя бы один ненулевой (так как
Но это означало бы, что система векторов
линейно
зависима. Учитывая, что

из (1.6) находим
Так
как вектор х
был
выбран произвольно, заключаем, что любой
вектор в линейном пространстве
можно
представить в виде линейной комбинации
системы векторов
Поэтому
эта система векторов, по предположению
линейно независимая, является базисом
в

Теорема
1.5. Если
в линейном пространстве
существует
базис из п
векторов,
то

(Без
доказательства)
Из
теорем 1.4 и 1.5 следует, что в каждом
линейном пространстве любые два базиса
содержат одно и то же количество векторов,
и это количество равно размерности
линейного пространства.
Пример
1.13. В
линейном
арифметическом пространстве
стандартный базис (1.5)
состоит из п
векторов,
поэтому

что и отражено в обозначении этого
линейного пространства.
Пример
1.14. Рассмотрим
однородную СЛАУ
множество
решений которой образует линейное
пространство. Найдем размерность этого
линейного пространства и какой-либо
базис в нем.
Решим
эту систему, определив ее фундаментальную
систему решений. Для
этого запишем матрицу системы и при
помощи элементарных
преобразований строк приведем
ее к треугольному виду:
Из
полученного находим, что

качестве свободных неизвестных можно
взять
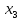

а
в качестве базисных неизвестных –


система имеет вид
Полагая


находим
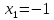

а
при

имеем


Записав
найденные решения в виде столбцов,
получим фундаментальную систему решений:
Согласно
теории систем линейных алгебраических
уравнений, эти два решения линейно
независимы, а любое другое решение СЛАУ
представляется в виде их линейной
комбинации. Другими словами, столбцы
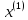
образуют
базис в линейном пространстве решений
рассматриваемой однородной СЛАУ.
Размерность этого линейного пространства
равна двум – количеству векторов в
базисе.
1.7.
Преобразование координат вектора при
замене базиса
В
линейном
пространстве все
базисы
равноправны.
Тот или иной базис выбирают исходя из
конкретных обстоятельств, а может быть,
и вообще произвольно. Иногда удобно
использовать для представления элементов
линейного пространства несколько
базисов, но тогда естественным образом
возникает задача преобразования
координат
векторов, которое
связано с изменением базиса.
Пусть
в n-мерном
линейном пространстве
заданы
два базиса: старый
и
новый
Любой вектор можно разложить по базису
b.
В
частности, каждый вектор из базиса с
может быть представлен в виде линейной
комбинации
векторов
базиса b:
Запишем
эти представления в матричной форме:
или

где
(1.7)
Определение
1.6. Матрицу
(1.7) называют матрицей
перехода от
старого базиса b
к
новому
базису с.
Согласно
данному определению, i-й
столбец матрицы перехода есть столбец
координат i-го
вектора нового базиса в старом. Поэтому
говорят, что матрица перехода состоит
из координат векторов нового базиса в
старом, записанных по столбцам.
Обсудим
некоторые свойства матрицы перехода.
1°.
Матрица перехода невырождена и всегда
имеет обратную.
Действительно,
столбцы матрицы перехода – это столбцы
координат векторов нового базиса в
старом. Следовательно, они, как и векторы
базиса, линейно
независимы. Значит,
матрица U
невырожденная
и имеет обратную матрицу
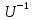
2°.
Если в n-мерном
линейном пространстве задан базис b,
то для любой невырожденной квадратной
матрицы U
порядка
п
существует
такой базис с
в
этом линейном пространстве, что U
будет
матрицей перехода от базиса b
к
базису с.
Из
невырожденности матрицы U
следует,
что ее ранг равен n,
и поэтому ее столбцы, будучи базисными,
линейно независимы. Эти столбцы являются
столбцами координат векторов системы

Линейная
независимость столбцов матрицы U
равносильна
линейной независимости системы векторов
с.
Так
как система с
содержит
п
векторов,
причем линейное пространство п-мерно,
то, согласно теореме 1.4, эта система
является базисом.
Пример
1.15. Пусть
–
базис линейного пространства. Тогда
система векторов
тоже является базисом в этом линейном
пространстве. Это следует из того, что

где
диагональная матрица
невырождена.
3°.
Если U
—
матрица перехода от старого базиса b
к
новому базису с
линейного пространства, то
— матрица перехода от базиса с
к базису b.
Матрица
невырождена,
и поэтому из равенства
следует, что

Последнее
равенство означает, что столбцы матрицы
являются
столбцами координат векторов базиса b
относительно
базиса с,
т.е., согласно определению 1.6,
—
это матрица перехода от базиса с
к
базису
b.
4°.
Если в линейном пространстве заданы
базисы b,
с
и d,
причем
U
—
матрица перехода от базиса b
к
базису с,
а V
— матрица
перехода от базиса с
к базису d
то
произведение этих матриц
—
матрица перехода от базиса b
к
базису d.
Согласно
определению 1.6
матрицы перехода, имеем равенства

откуда

т.е.
—
матрица перехода от базиса b
к
базису d.
Рассмотрим
теперь, как преобразуются координаты
произвольного вектора в линейном
пространстве при переходе от старого
базиса к новому. Выберем произвольный
вектор
и
разложим его в старом базисе:

Разложение
того же вектора в новом базисе имеет
вид.

Найдем
связь
между старыми координатами х
вектора
х
и
новыми его координатами
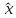
Из
соотношений (1.8), (1.9) следует, что

Учитывая,
что

получаем
или

Последнее равенство можно рассматривать
как запись двух разложений одного и
того же вектора х
в
данном базисе b.
Разложениям
соответствуют столбцы координат х
и
которые,
согласно теореме 1.2
о единственности разложения вектора
по базису, должны быть равны:
или

Итак,
чтобы получить координаты вектора в
старом базисе, необходимо столбец
координат этого вектора в новом базисе
умножить слева на матрицу перехода из
старого базиса в новый. Матрица перехода
из старого базиса в новый позволяет
пересчитывать новые координаты в старые.
cos^A
sin<p y
Пример
1.16. Рассмотрим
в
ортонормированный базис
из
векторов осей
координат.
Обозначим
через
новый
базис, который получается поворотом
старого базиса b
на
заданный угол

Исходя
из заданного угла поворота, мы можем
найти координаты векторов
нового
базиса относительно старого
Эти
разложения позволяют составить матрицу
перехода U
из
старого базиса b
в
новый e,
а
также обратную матрицу:
Найденные
матрицы перехода U
(из
старого базиса в новый) и
(из нового базиса в старый) позволяют
записать соотношения между старыми
и
новыми

координатами
произвольного вектора х
из

Например,
вектор
в старом базисе имеет координаты

а в новом базисе –

Вопросы
и задачи
1.1.
Найдите координаты вектора х
в
базисе

если известны его координаты
в базисе
а
базисы связаны соотношениями
1.2.
В
линейном пространстве две системы
векторов
и
заданы своими координатами в некотором
базисе:
Докажите,
что эти системы являются базисами.
Найдите:
а)
матрицу
перехода
от базиса b
к
базису е;
б)
матрицу
обратного перехода от базиса е
к базису b;
в)
координаты вектора
в
обоих базисах;
г)
координаты вектора
в базисе е.
1.3.
Найдите
размерность
линейного пространства матриц типа
с
элементами из R.
1.4. Является
ли матрица
матрицей перехода от одного базиса
трехмерного линейного пространства к
его другому базису?
1.5.
Какой
вид имеет матрица перехода от старого
базиса к новому, если матрица перехода
от нового базиса к старому является:
а)
треугольной; б) симметрической; в)
кососимметрической?
1.5.
Может ли в пространстве
матрица перехода быть кососимметрической?
1.6.
При
каких условиях векторы
в пространстве
образуют базис?
1.7.
Докажите,
что в линейном пространстве
многочлены
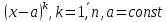
образуют
базис. Найти координаты произвольно
взятого многочлена
в
этом базисе.
Соседние файлы в папке re
- #
- #
- #
- #
- #
- #
- #
- #
В статье о n-мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n-мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n-векторов. Размерность его соответственно равна n. Возьмем систему из n-единичных векторов:
e(1)=(1, 0,…,0)e(2)=(0, 1,…,0)e(n)=(0, 0,…,1)
Используем эти векторы в качестве составляющих матрицы A: она будет являться единичной с размерностью n на n. Ранг этой матрицы равен n. Следовательно, векторная система e(1), e(2),…, e(n) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n, то размерность пространства n-мерных векторов равна n, а единичные векторы e(1), e(2),…, e(n) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n-мерных векторов, в которой число векторов меньше n, не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e(2), e(1),…, e(n). Она также будет являться базисом n-мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n. Система e(2), e(1),…, e(n) линейно независима и является базисом n-мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n-мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n-мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a=(3, -2, 1)b=(2, 1, 2)c=(3, -1, -2)
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A=323-21-112-2A=3-212123-1-2=3·1·(-2)+(-2)·2·3+1·2·(-1)-1·1·3-(-2)·2·(-2)-3·2·(-1)==-25≠0⇒Rank(A)=3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a=(3, -2, 1)b=(2, 1, 2)c=(3, -1, -2)d=(0, 1, 2)
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a=(3, -2, 1), b=(2, 1, 2), c=(3, -1, -2) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a=(1, 2, 3, 3)b=(2, 5, 6, 8)c=(1, 3, 2, 4)d=(2, 5, 4, 7)
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A=1233256813242547
По методу Гаусса определим ранг матрицы:
A=1233256813242547~1233010201-1101-21~~1233010200-1-100-2-1~1233010200-1-10001⇒⇒Rank(A)=4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a(1)=(1, 2, -1, -2)a(2)=(0, 2, 1, -3)a(3)=(1, 0, 0, 5)
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e(1), e(2),…, e(n) являются базисом векторного n-мерного пространства. Добавим к ним некий n-мерный вектор x→: полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n-мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n-мерного векторного пространства – e(1), e(2),…, e(n). Сделаем систему линейно зависимой, добавив к ней n-мерный вектор x→. Этот вектор может быть линейно выражен через исходные векторы e:
x=x1·e(1)+x2·e(2)+…+xn·e(n) , где x1, x2,…, xn – некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
x=x~1e(1)+x2~e(2)+…+x~ne(n), где x~1, x~2,…, x~n – некие числа.
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x=x1·e(1)+x2·e(2)+…+xn·e(n) . Получим:
0=(x~1-x1)·e(1)+(x~2-x2)·e(2)+…(x~n-xn)·e(2)
Система базисных векторов e(1), e(2),…, e(n) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты (x~1-x1), (x~2-x2),…, (x~n-xn) будут равны нулю. Из чего справедливым будет: x1=x~1, x2=x~2,…, xn=x~n. И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x1, x2,…, xn называются координатами вектора x→ в базисе e(1), e(2),…, e(n).
Доказанная теория делает понятным выражение «задан n-мерный вектор x=(x1, x2,…, xn)»: рассматривается вектор x→ n-мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n-мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n-мерного векторного пространства задана система из n линейно независимых векторов
e(1)=(e1(1), e2(1),…, en(1))e(2)=(e1(2), e2(2),…, en(2))⋮e(n)=(e1(n), e2(n),…, en(n))
а также задан вектор x=(x1, x2,…, xn).
Векторы e1(1), e2(2),…, en(n) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x→ в базисе e1(1), e2(2),…, en(n), обозначаемые как x~1, x~2,…, x~n.
Вектор x→ будет представлен следующим образом:
x=x~1·e(1)+x~2·e(2)+…+x~n·e(n)
Запишем это выражение в координатной форме:
(x1, x2,…, xn)=x~1·(e(1)1, e(1)2,…, e(1)n)+x~2·(e(2)1, e(2)2,…, e(2)n)+…++x~n·(e(n)1, e(n)2,…, e(n)n)==(x~1e1(1)+x~2e1(2)+…+x~ne1(n), x~1e2(1)+x~2e2(2)++…+x~ne2(n), …, x~1en(1)+x~2en(2)+…+x~nen(n))
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x~1, x~2,…, x~n:
x1=x~1e11+x~2e12+…+x~ne1nx2=x~1e21+x~2e22+…+x~ne2n⋮xn=x~1en1+x~2en2+…+x~nenn
Матрица этой системы будет иметь следующий вид:
e1(1)e1(2)⋯e1(n)e2(1)e2(2)⋯e2(n)⋮⋮⋮⋮en(1)en(2)⋯en(n)
Пусть это будет матрица A, и ее столбцы – векторы линейно независимой системы векторов e1(1), e2(2),…, en(n). Ранг матрицы – n, и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x~1, x~2,…, x~n вектора x→ в базисе e1(1), e2(2),…, en(n).
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e(1)=(1,-1,1)e(2)=(3, 2, -5)e(3)=(2, 1, -3)x=(6, 2, -7)
Необходимо подтвердить факт, что система векторов e(1), e(2), e(3) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e(1), e(2), e(3) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A, строки которой – заданные векторы e(1), e(2), e(3).
Используем метод Гаусса:
A=1-1132-521-3~1-1105-803-5~1-1105-800-15
Rank (A) = 3. Таким образом, система векторов e(1), e(2), e(3) линейно независима и является базисом.
Пусть в базисе вектор x→ имеет координаты x~1, x~2, x~3. Связь этих координат определяется уравнением:
x1=x~1e1(1)+x~2e1(2)+x~3e1(3)x2=x~1e2(1)+x~2e2(2)+x~3e2(3)x3=x~1e3(1)+x~2e3(2)+x~3e3(3)
Применим значения согласно условиям задачи:
x~1+3x~2+2x~3=6-x~1+2x~2+x~3=2x~1-5x~2-3×3=-7
Решим систему уравнений методом Крамера:
∆=132-1211-5-3=-1∆x~1=632221-7-5-3=-1, x~1=∆x~1∆=-1-1=1∆x~2=162-1211-7-3=-1, x~2=∆x~2∆=-1-1=1∆x~3=136-1221-5-7=-1, x~3=∆x~3∆=-1-1=1
Так, вектор x→ в базисе e(1), e(2), e(3) имеет координаты x~1=1, x~2=1, x~3=1.
Ответ: x=(1,1,1)
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c(1)=(c1(1), c2(1),…, cn(1))c(2)=(c1(2), c2(2),…, cn(2))⋮c(n)=(c1(n), e2(n),…, cn(n))
И
e(1)=(e1(1), e2(1),…, en(1))e(2)=(e1(2), e2(2),…, en(2))⋮e(n)=(e1(n), e2(n),…, en(n))
Указанные системы являются также базисами заданного пространства.
Пусть c~1(1), c~2(1),…, c~n(1) – координаты вектора c(1) в базисе e(1), e(2),…, e(3), тогда связь координат будет задаваться системой линейных уравнений:
с1(1)=c~1(1)e1(1)+c~2(1)e1(2)+…+c~n(1)e1(n)с2(1)=c~1(1)e2(1)+c~2(1)e2(2)+…+c~n(1)e2(n)⋮ сn(1)=c~1(1)en(1)+c~2(1)en(2)+…+c~n(1)en(n)
В виде матрицы систему можно отобразить так:
(c1(1), c2(1),…, cn(1))=(c~1(1), c~2(1),…, c~n(1))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)
Сделаем по аналогии такую же запись для вектора c(2):
(c1(2), c2(2),…, cn(2))=(c~1(2), c~2(2),…, c~n(2))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)
И, далее действуя по тому же принципу, получаем:
(c1(n), c2(n),…, cn(n))=(c~1(n), c~2(n),…, c~n(n))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)
Матричные равенства объединим в одно выражение:
c1(1)c2(1)⋯cn(1)c1(2)c2(2)⋯cn(2)⋮⋮⋮⋮c1(n)c2(n)⋯cn(n)=c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)·e1(1)e2(1)⋯en(1)e1(2)e2(2)⋯en(2)⋮⋮⋮⋮e1(n)e2(n)⋯en(n)
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e(1), e(2),…, e(3) через базис c(1), c(2),…, c(n):
e1(1)e2(1)⋯en(1)e1(2)e2(2)⋯en(2)⋮⋮⋮⋮e1(n)e2(n)⋯en(n)=e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)·c1(1)c2(1)⋯cn(1)c1(2)c2(2)⋯cn(2)⋮⋮⋮⋮c1(n)c2(n)⋯cn(n)
Дадим следующие определения:
Матрица c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n) является матрицей перехода от базиса e(1), e(2),…, e(3)
к базису c(1), c(2),…, c(n).
Матрица e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n) является матрицей перехода от базиса c(1), c(2),…, c(n)
к базису e(1), e(2),…, e(3).
Из этих равенств очевидно, что
c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)·e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)=10⋯001⋯0⋮⋮⋮⋮00⋯1e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)·c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)=10⋯001⋯0⋮⋮⋮⋮00⋯1
т.е. матрицы перехода взаимообратны.
Рассмотрим теорию на конкретном примере.
Исходные данные: необходимо найти матрицу перехода от базиса
c(1)=(1, 2, 1)c(2)=(2, 3, 3)c(3)=(3, 7, 1)
к базису
e(1)=(3, 1, 4)e(2)=(5, 2, 1)e(3)=(1, 1, -6)
Также нужно указать связь координат произвольного вектора x→ в заданных базисах.
Решение
1. Пусть T – матрица перехода, тогда верным будет равенство:
314521111=T·121233371
Умножим обе части равенства на
121233371-1
и получим:
T=31452111-6·121233371-1
2. Определим матрицу перехода:
T=31452111-6·121233371-1==31452111-6·-18537-2-15-1-1=-2794-712012-4198
3. Определим связь координат вектора x→:
допустим, что в базисе c(1), c(2),…, c(n) вектор x→ имеет координаты x1,x2,x3, тогда:
x=(x1,x2,x3)·121233371,
а в базисе e(1), e(2),…, e(3) имеет координаты x~1,x~2,x~3, тогда:
x=(x~1,x~2,x~3)·31452111-6
Т.к. равны левые части этих равенств, мы можем приравнять и правые:
(x1,x2,x3)·121233371=(x~1,x~2,x~3)·31452111-6
Умножим обе части справа на
121233371-1
и получим:
(x1,x2,x3)=(x~1,x~2,x~3)·31452111-6·121233371-1⇔⇔(x1,x2,x3)=(x~1,x~2,x~3)·T⇔⇔(x1,x2,x3)=(x~1,x~2,x~3)·-2794-712012-4198
С другой стороны
(x~1,x~2,x~3)=(x1,x2,x3)·-2794-712012-4198
Последние равенства показывают связь координат вектора x→ в обоих базисах.
Ответ: матрица перехода
-2794-712012-4198
Координаты вектора x→ в заданных базисах связаны соотношением:
(x1,x2,x3)=(x~1,x~2,x~3)·-2794-712012-4198
или
(x~1,x~2,x~3)=(x1,x2,x3)·-2794-712012-4198-1
Примеры решений. Линейные пространства
В этом разделе вы найдете бесплатные решения задач о линейных пространствах по темам: проверка линейности подпространства, базис пространства и подпространства, ортогональное подпространство, размерность.
Понравилось? Добавьте в закладки
Решения задач: линейные пространства
Задача 1. Образует ли линейное подпространство пространства $R^4$ множество $V$, заданное по правилу:
$$
V={(x_1, x_2, x_3, x_4): x_1-2x_3=0 };quad V={(x_1, x_2, x_3, x_4): x_3+x_4=1 }.
$$
Задача 2. Даны векторы $e_1, e_2, e_3, e_4$ и $a$ в стандартном базисе пространства $R^4$.
Требуется:
а) убедиться, что векторы $e_1, e_2, e_3, e_4$ образуют базис пространства $R^4$;
б) найти разложение вектора $a$ по этому базису;
в) найти угол между векторами $e_1$ и $e_2$.
$$
e_1=(1,0,-2,3); e_2=(0,1,3,2); e_3=(1,0,0,1); e_4=(2,3,12,2); a=(9,12,5,8).
$$
Задача 3.Найти ортогональный базис подпространства $L$, заданного системой уравнений, и базис подпространства $L^{perp}$
$$
left{
begin{aligned}
x_1+x_2+x_3+x_4+x_5&=0,\
x_1-2x_2+2x_3+x_4-2x_5&=0.\
end{aligned}
right.
$$
Задача 4. Для каждого из следующих множеств геометрических векторов определить, будет ли это множество линейным подпространством пространства $V_3$ :
1) радиус-векторы точек данной плоскости;
2) векторы, образующие с данным ненулевым вектором $overline{a}$ угол $alpha$;
3) множество векторов, удовлетворяющих условию $|overline{x}|=1$ .
Задача 5. Пусть $L$ – множество многочленов степени не выше 2, удовлетворяющих условию $p(1)+p'(1)+p”(1)=0$. Доказать, что $L$ – линейное подпространство в пространстве $P_2$. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.
Задача 6. Образуют ли многочлены $p_1(x)=x^3+x^2-1$, $p_2(x)=x^2-2x$, $p_3(x)=x^3+x$, $p_4(x)=x^2-3$ базис в пространстве $P_3$?
Задача 7. Доказать, что матрицы вида
$$
begin{pmatrix}
2a & a+3b-2c\
b & 5c\
end{pmatrix}
$$
образуют линейное подпространство в пространстве матриц $M_{22}$. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.
Не получаются задачи? Решим подробно и понятно
Базисом
в
-мерном пространстве называется упорядоченная система из
линейно-независимых векторов.
Введём также некоторые дополнительные понятия, необходимые для дальнейшего изложения.
Выражение вида:
, где
−
некоторые числа и
называется
линейной комбинацией
векторов
.
Если существуют такие числа
из которых хотя бы одно не равно нулю (например
) и при этом выполняется равенство:
, то система векторов
−
является
линейно-зависимой.
Если же указанное равенство выполняется лишь при условии, что все числа
,
тогда система векторов
−
является
линейно-независимой.
Базис
может образовывать только
линейно-независимая
система векторов. Понятие линейной зависимости/независимости системы векторов, тесно связано с понятием
ранга матрицы.
Наш онлайн калькулятор позволяет проверить образует ли система векторов
базис.
При этом калькулятор выдаёт подробное решение на русском языке.