Определение. Подпространством линейного пространства Х называется любое его подмножество Х0, которое само является линейным пространством.
Очевидно, что у каждого линейного пространства есть два так называемых несобственных подпространства: состоящее из одного нулевого элемента и состоящее из всех элементов данного пространства. Все остальные подпространства называются собственными. В дальнейшем, если не оговорено противное, все рассматриваемые подпространства мы будем считать собственными. Таким образом, у п-мерного линейного пространства собственные подпространства могут иметь любую размерность от 1 до п – 1. Например, в обычном трехмерном векторном пространстве подпространства могут иметь размерности лишь 1 и 2. Очевидно, что одномерные подпространства – это всевозможные векторы, лежащие на какойнибудь прямой, проходящей через начало координат, а двумерные – всевозможные векторы, лежащие в какой-нибудь плоскости, проходящей через начало координат и, при этом, не лежащие на одной прямой.
Определение. Множество всех элементов линейного пространства, имеющих вид z = x0 + x, где х0 – фиксированный элемент пространства, а х пробегает некоторое подпространство, называется линейным многообразием.
Например, в пространстве трехмерных векторов одномерные линейные многообразия – всевозможные прямые, а двумерные – это всевозможные плоскости. Поэтому в любом конечномерном (п-мерном) линейном пространстве одномерные линейные многообразия обычно называют прямыми, а (п–1)-мерные линейные многообразия – гиперплоскостями. Прямая в линейном пространстве, проходящая через 2 элемента х1 и х2, задается уравнением: х = х1 + t(x2 – x1), где t пробегает всю вещественную ось.
Замечание. Для того, чтобы выяснить, является ли подмножество М линейного пространства подпространством, достаточно проверить следующее: если элементы а М и b M, то и (a + b) M, а так же, что для любого числа λ элемент λа М. Проверять выполнение аксиом Вейля не нужно, так как если они выполняются во всем пространстве, то автоматически выполняются и на его подмножествах. Например, вещественная ось является подпространством в множестве комплексных чисел, а первый квадрант (т. е. множество чисел x + yi, у которых x > 0 и y > 0) – не является, так как при умножении этих чисел на (–1) произведение не входит в 1-й квадрант.
Определение. Линейной оболочкой набора элементов х1, х2, …, хт на-
зывается множество всевозможных линейных комбинаций этих элементов. Стандартное обозначение линейной оболочки: L(x1, x2, …, xm).
21
Замечание. Линейные подпространства чаще всего задаются как линейные оболочки некоторых элементов или как множества решений однородных систем линейных уравнений.
Замечание. То, что линейная оболочка является подпространством – очевидно, так как сумма двух линейных комбинаций тоже есть линейная комбинация тех же элементов и умножение линейной комбинации на число есть также линейная комбинация тех же элементов.
Замечание. Очевидно и то, что линейная оболочка одного вектора а есть множество векторов вида λа (в пространстве векторов – это прямая, проходящая через начало координат и содержащая данный элемент, т. е. данный вектор). Линейная оболочка двух неколлинеарных векторов – это плоскость, содержащая данные векторы и проходящая через начало координат. Ясно также, что все пространство является линейной оболочкой любого своего базиса.
Теорема 1. Если элементы пространства заданы своими координатами в некотором базисе, то размерность их линейной оболочки равна рангу матрицы из их координат.
Доказательство.
Пусть пространство Х есть линейная оболочка элементов х1, х2, …, хm: Х = L(х1, х2, …, хm), и пусть координаты этих элементов в некотором базисе
таковы: хk = (ak1, ak2, …, akn). Составим матрицу из этих координат: А = (аij). Пусть ранг этой матрицы равен числу r: r(A) = r.
Требуется доказать, что dim X = r. Так как r(A)=r, то в матрице А найдется минор ∆r порядка r, не равный нулю: ∆r ≠ 0. За счет перестановки строк и столбцов можно добиться того, чтобы этот минор занимал левый
|
верхний угол матрицы А: |
r |
det(a )r |
(эта перестановка равносильна |
|
ij i, j 1 |
перенумерации данных элементов и элементов базиса). Из этого следует, что первые r элементов (т. е. первые r строк матрицы А) линейно независимы. Действительно, если бы они оказались линейно зависимы, то, в частности, оказались бы линейно зависимы и строки минора ∆r, т. е. он был бы равен 0 вопреки предположению. Осталось доказать, что все остальные строки матрицы А линейно зависимы с первыми r, т. е. являются линейными комбинациями первых r строк. Зафиксируем какую-нибудь из этих строк, например, строку с номером i > r. Найдем сначала такие коэффициенты λ1, λ2,…, λr, чтобы первые r элементов i-й строки оказались линейной комбинацией с этими коэффициентами строк минора ∆r. Для этого необходимо, чтобы выполнялись r равенств:
|
λ1а1j + λ2a2j +…+ λrarj = aij, |
(4.1) |
где j = 1, 2,…, r.
22

Но эти равенства есть система r линейных уравнений с r неизвестными λ1, λ2,…, λr. Определитель этой системы – транспонированной матрицы минор ∆rT ≠ 0. Таким образом, по теореме Крамера эта система имеет единственное решение, и коэффициенты λ1, λ2,…, λr находятся однозначно. Осталось доказать, что равенства (4.1) справедливы и при j > r. Для этого вспомним, что все миноры матрицы А порядка, большего r, равны 0. Рассмотрим минор r + 1 порядка:
|
a11 a12 |
a1r a1 j |
||
|
a21 a22 |
a2r a2u |
||
|
r 1 |
= 0 |
||
|
ar1 ar 2 |
arr arj |
||
|
ai1 ai2 |
air aij |
(к минору ∆r добавлена i-я строка и j-й столбец). Вычтем из его последней строки 1-ю строку, умноженную на λ1, 2-ю – умноженную на λ2, …, r-ю – умноженную на λr. Из равенств (4.1) следует, что получится равенство:
|
a11 a12 |
a1r a1 j |
|||
|
a21 a22 |
a2r a2u |
|||
|
r 1 |
= 0, |
(4.2) |
||
|
ar1 ar 2 |
arr arj |
|||
|
0 0 |
0 b |
|||
где b = aij – (λ1a1j + λ2a2j + …+ λrj). Раскладывая определитель (4.2) по последней строке, получим ∆r+1 = b∆r = 0. Но ∆r ≠ 0. Отсюда b = 0, т. е.
aij = λ1a1j + λ2a2j +…+ λrj. Это и значит, что j-я строка матрицы А является линейной комбинацией первых r ее строк. Что и требовалось доказать.
Следствие 1. Элементы хк (k = 1,…,п) образуют базис в п-мерном пространстве тогда и только тогда, когда определитель из их координат не равен нулю.
Теорема 2. Множество решений однородной системы линейных уравнений является линейным подпространством п-мерного векторного пространства, где п – число неизвестных системы.
Доказательство.
Пусть однородная система задается матричным уравнением АХ = 0, и пусть Х1 и Х2 – какие-то два ее решения, т. е. выполняются равенства: АХ1 = 0, АХ2 = 0, тогда выполняются и равенства: А(Х1 + Х2) = АХ1 + АХ2 = 0 + 0 = 0 и А(λХ1) = λ АХ1 = λ 0 = 0, т. е. сумма решений системы снова является ее
23
решением и произведение решения на число тоже является ее решением. Это и означает, что множество решений однородной системы является подпространством.
Теорема 3. Размерность множества решений однородной системы равна n–r, где п – число неизвестных системы, а r – ранг матрицы из коэффициентов.
Доказательство. Размерность множества решений однородной системы и базис этого подпространства определяются теоремой Кронекера – Капелли и методом Гаусса решения такой системы. А именно, из теоремы Кронекера – Капелли следует, что размерность множества решений равна n – r, где п – число неизвестных системы, а r – ранг матрицы из коэффициентов при неизвестных этой системы. Для того чтобы найти базис этого пространства, мы должны найти n – r линейно независимых решений системы, но n – r неизвестных по теореме Кронекера – Капелли можно взять произвольными числами (формула (0.4), в которой правые части bk, k = 1, 2, …, r, равны нулю). Чтобы гарантировать линейную независимость полученных решений, можно каждому из этих произвольных неизвестных по очереди одному дать значение равное 1, а остальным неизвестным значения 0. При каждом таком наборе значений неизвестных (равных единице и нулям) найти соответствующее решение системы. Получим n–r линейно независимых решений, т. е. базис в множестве решений. Таким образом, множество решений однородной линейной системы уравнений является линейным пространством размерности n – r. Теорема доказана.
Теорема 4. Множество всех решений системы линейных уравнений АХ = В является линейным многообразием Z, элементы которого имеют вид z = x0 + x, где х0 – какое-то фиксированное решение данной системы:
при этом х пробегает множество всех решений соответствующей однородной системы:
Доказательство.
То, что все элементы указанного вида являются решениями, очевидно: если выполняются (4.3) и (4.4), то Аz = А(x0 + x) = А x0 + А x = В + 0 = В.
Докажем обратное, т. е. что любое решение данной системы можно представить таким образом. Действительно, любое решение можно пред-
ставить в виде z = x0 + (z – х0) = x0 + у, где у = z – x0, и осталось доказать, что у – решение однородного уравнения (4.10). Но Ау = А(z – x0) = Аz –Ах0 = = В – В = 0.
Следствие 2. Любое линейное многообразие размерности п – 1 в п-мер- ном векторном пространстве (такие подпространства называются гиперп-
24
лоскостями) может быть задано как множество векторов (х1, х2, …, хп), удовлетворяющих одному линейному уравнению а1х1 + а2х2 +… + апхп = с, где хотя бы один из числовых коэффициентов а1, а2,…, ап не равен 0.
Определение. Пересечением двух подпространств X и Y называется новое подпространство, состоящее из всех тех элементов, которые входят и в X, и в Y. Оно обозначается символом Z X Y.
Определение. Суммой этих подпространств называется новое подпространство S X Y, состоящее из всех тех элементов, которые представимы в виде s = x + y, где х Х, у Y.
Замечание. То, что Z и S действительно являются подпространствами, легко проверить самим. Например, если s1 S и s2 S, т. е. s1 = x1 + y1, s2 =
= x2 + y2, то s = s1 + s2 = x1 + y1 + x2 + y2 = (x1 + х2) + (у1 + y2) Х + Y. Ана-
логично проверяется, что из s S следует, что λs S при любом λ. Замечание. Если подпространства X и Y задаются как линейные обо-
лочки некоторых множеств: Х = L(x1, x2, …, xm), Y = L(у1, у2, …, ук), то, очевидно, что Х + Y является линейной оболочкой всего набора заданных
элементов, т. е. Х + Y = L(x1, x2, …, xm, у1, у2, …, ук). И размерность, и базис этого подпространства находятся стандартным методом. Пересечение этих
|
подпространств Z X Y есть множество элементов вида: |
|
|
Z = α1x1 + α2x2 + …+ αmxm = β1y1+ β2y2+ …+ βkyk, |
(4.5) |
|
т. е. множество решений однородной системы линейных уравнений |
|
|
α1x1 + α2x2 + …+ αmxm + (–β1)y1 + (–β2)y2 + … (–βk)yk = 0. |
(4.6) |
Если известны координаты данных векторов x1, x2, …, xm, у1, у2, …, ук, то подставляя их в (4.6), получим однородную систему п линейных уравнений с неизвестными α1, α2, …, αm, β1, β2,…, βk. Решая эту систему методом Гаусса и находя базисные элементы множества решений (т. е. конкретные линейно независимые наборы чисел α1, α2, …, αm, β1, β2,…, βk), подставим их в левые (или правые) части уравнений (4.5). Получим базисные элементы пространства Z X Y. Если же пространства X и Y задаются как множества решений однородных систем линейных уравнений, то их пересечение задается как множество решений однородной системы, полученной объединением всех уравнений обеих данных систем, поэтому размерность и базис пересечения находятся стандартным методом Гаусса по теореме Кронекера – Капелли.
Замечание. Сумма двух подпространств X и Y называется прямой суммой, если пересечение этих двух подпространств есть нулевой элемент: X Y 0 . Таким образом, прямая сумма подпространств – это обычная сумма, а термин «прямая» несет дополнительную информацию об их пересечении.
25
Теорема 5 (о связи размерностей подпространств, их суммы и пере-
сечения). Для любых двух линейных подпространств X и Y линейного про-
|
странства Z справедливо равенство: |
|||
|
dim(X Y ) dim( X |
Y ) dim X dimY . |
(4.7) |
|
|
Доказательство. Обозначим: |
|||
|
dim X k, dimY m, dim(X Y ) s, dim(X |
Y ) r . |
(4.8) |
|
|
В обозначениях (4.8) требуется доказать, что: |
|||
|
s = k + m – r. |
(4.9) |
Для этого выберем какой-нибудь базис е1, е2, …, еr в пространстве
Z X Y и дополним его элементами еr+1’, er+2’, …, ek’ и е1’’, е2’’, …, еm’’ до базисов в пространствах X и Y соответственно. Докажем, что набор
|
элементов: |
|
|
е1, е2, …, еr, еr+1’, er+2’, …, ek’, е1’’, е2’’, …, еm’’ |
(4.10) |
является базисом в X + Y. Для этого надо доказать, что система (4.10) полная и линейно независима. Полнота этой системы очевидна, так как если s X + Y, то s = x + y = (α1е1 + α2е2 +…+ αrеr + αr+1 еr+1’ + αr+2 er+2’ +…+ αkek’) +
+ (β1е1 + β2е2 +…+ βrеr + βm+1е1’’+ βm+2е2’’+…+ βmеm’’), т. е. является ли-
нейной комбинацией элементов (4.10).
Докажем линейную независимость этих элементов. Предположим противное, т. е. что выполняется равенство:
|
с1е1 + с2е2 +…+ сrеr + cr+1’еr+1’ + cr+2’er+2’ +…+ ck’ek’ + c1’’е1’’+ |
|
|
+ c2’’е2’’ +…+ cm’’еm’’= 0. |
(4.11) |
|
Из (4.11) следует: |
|
|
а = с1е1 + с2е2 + …+ сrеr + cr+1’еr+1’ + cr+2’er+2’ +..+ ck’ek’= |
|
|
= –(c1’’е1’’+ c2’’е2’’+ …+ cm’’еm’’) |
(4.12) |
принадлежит одновременно и X, и Y. Значит, он принадлежит и их пересечению. Следовательно, а раскладывается только по базису пространства
|
Z X Y, т. е.: |
|
|
а = b1е1 + b2е2 + …+ brеr. |
(4.13) |
В силу единственности разложения элемента по базису из (4.12) и (4.13) следует, что все коэффициенты cr+1’ = cr+2’ = … = ck’ = 0. Аналогично доказывается, что c1’’= c2’’= …= cm’’= 0. Но тогда из (4.11) следует,
что с1е1 + с2е2 + …+ сrеr = 0 . Так как элементы базиса линейно независимы, то в последнем равенстве все коэффициенты равны 0. Итак, если запи-
26

сать равенство (4.11), то в нем все коэффициенты обязательно равны 0. А это и значит, что элементы (4.10) линейно независимы и, следовательно, образуют базис в X + Y. Так как в базисе (4.11) число элементов равно r + (k – r) + (т – r) = k + m – r, то равенство (4.9), а значит, и равенство (4.7) доказано.
Следствие 3. Если сумма подпространств X и Y прямая, то dim X Y dim X dimY .
Следствие 4. Если dim X Y dim X , то dim X Y dimY .
Заметим, что в этом случае пространство Y является подпространством пространства X, и следовательно, их сумма совпадает с Х, а пересечение – с Y.
Замечание. Нахождению размерностей и базисов данных подпространств, а также их суммы и пересечения посвящен разбор 2-го типового задания в разд. 9 («Решение типовых примеров»).
27
5.МЕТРИЧЕСКИЕ, НОРМИРОВАННЫЕ
ИУНИТАРНЫЕ ПРОСТРАНСТВА. ОРТОГОНАЛИЗАЦИЯ
Определение. Расстоянием (метрикой) в данном множестве объектов М называется сопоставление каждым двум объектам х М и у М некоторого вещественного числа ρ(х, у), называемого «расстоянием между х и у», по любому фиксированному правилу, лишь бы выполнялись следующие три аксиомы:
1)ρ(х, у) ≥ 0, причем ρ(х, у) = 0 тогда и только тогда, когда х = у;
2)ρ(х, у) = ρ(у, х);
3)ρ(х, у) ≤ ρ(х, z) + ρ(z, у), где x, y, z – любые элементы данного множества М.
Замечание. Обычно первую из перечисленных аксиом называют «неотрицательностью метрики», вторую – «симметричностью метрики», третью – «неравенством треугольника».
Определение. Метрическим пространством называется множество объектов любой природы, в котором введена метрика, или (что, то же)
расстояние.
Наличие в множестве М метрики позволяет ввести в нем важные новые понятия: открытый и замкнутый шар, сферу, окрестность элемента (элементы метрического пространства часто называют его точками).
Определение. Открытым шаром радиуса r с центром в элементе х0 называется множество всех тех элементов х М, которые удалены от центра меньше, чем на r, т. е. для которых выполняется неравенство ρ(х, х0) < r.
Определение. Замкнутым шаром радиуса r с центром в элементе х0 называется множество всех тех элементов х М, которые удалены от центра не больше, чем на r, т. е. для которых выполняется неравенство
ρ(х, х0) ≤ r.
Определение. Сферой радиуса r с центром в элементе х0 называется множество всех тех элементов х М, которые удалены от центра на расстояние r, т. е. для которых выполняется равенство ρ(х, х0) = r.
Замечание. Очевидно, что замкнутый шар состоит из открытого шара и граничной сферы.
Определение. Окрестностью элемента х0 называется любой открытый шар с центром в данном элементе.
В частности, ε-окрестностью элемента х0 называется открытый шар радиуса ε с центром в точке х0.
Замечание. Наличие понятий «расстояние», «окрестность» позволяет ввести в метрических пространствах понятие «предела».
28
|
Определение. Элемент |
y называется пределом последовательности |
|
элементов хп (записывается |
lim x y ), если выполняется равенство для |
|
n n |
|
|
обычной числовой последовательности lim xn , y 0 . |
|
|
n |
|
|
Определение. Нормой в линейном пространстве М называется сопос- |
тавление каждому элементу х М вещественного числа ||х|| по любому фиксированному правилу, лишь бы выполнялись следующие три аксиомы:
1)||x|| ≥ 0, причем ||x|| = 0 тогда и только тогда, когда х = 0;
2)||αx|| = |α|∙||x||;
3)||x + у|| ≤ ||x|| + ||у||.
Замечание. Обычно первую из перечисленных аксиом называют «неотрицательностью нормы», вторую – «однородностью нормы», третью – «неравенством треугольника».
Определение. Нормированным пространством называется линейное
пространство, в котором введена норма.
Упражнение. Покажите, что функция x, y , определенная на множестве вещественных чисел по формуле
|
x, y |
x y |
, если |
x y |
1, |
||||||||||
|
1, если |
x |
y |
1, |
|||||||||||
|
является нормой на этой прямой. |
Утверждение. Нормированное пространство одновременно можно рассматривать и как метрическое, так как в нем всегда можно ввести метрику по следующей формуле:
|
ρ(х, у) = ||x – y||. |
(5.1) |
Доказательство.
Надо проверить, что функция (5.1) удовлетворяет всем трем аксиомам метрики. Выполнение первых двух аксиом метрики с очевидностью следует из первых двух аксиом нормы. Докажем, что для нее выполняется и правило треугольника:
ρ(х, у) = ||x – y|| = ||x – z + z – y|| ≤ ||x – z|| + ||z – y|| = ρ(х, z) + ρ(z, у).
Замечание. Сходимость в нормированном пространстве, т. е. выполне-
|
ние равенства lim x |
у , означает, что lim |
|| x у || 0 . |
|
n n |
n |
n |
Замечание. Так как по определению нормированное пространство Х обязательно линейно, то в нем можно рассматривать ряды из его элементов:
n 1
29

Определение. Ряд называется сходящимся, если существует предел по-
n
следовательности его частных сумм Sn xk , т. е. существует предел
k 1
S lim Sn , где элемент S, называется суммой данного ряда.
n
Такие ряды обладают многими привычными свойствами числовых рядов, в частности, для них справедлив (и также доказывается) необходимый признак сходимости.
Пример 1. Обычное трехмерное векторное пространство является нормированным (а значит, и метрическим), так как в нем в качестве нормы можно взять длину вектора (она удовлетворяет всем трем аксиомам нормы). Таким образом, понятие нормы является обобщением понятия длины вектора.
Аналогично, нормированным является и пространство строк длины п (столбцов высоты п), если ввести в нем норму по формуле
|
x |
||||||||||||||||
|
1 |
||||||||||||||||
|
x2 |
||||||||||||||||
|
x |
(x1, x2 ,…, xn ) |
2 |
2 |
2 |
(5.2) |
|||||||||||
|
x1 |
x2 |
… xn . |
||||||||||||||
|
xn |
То, что функция (5.2) удовлетворяет первым двум аксиомам нормы – очевидно; неравенство треугольника следует из того, что эти пространства являются унитарными, что будет доказано позднее.
Упражнение. Проверить самостоятельно, что в пространстве строк (столбцов) можно ввести и другие нормы, а именно, что нормами являются
|
n |
||
|
|| x || |
max | xk | и || x ||1 | xk | . Что является единичной сферой с цен- |
|
|
k 1, 2,…,n |
k 1 |
|
тром в начале координат на плоскости, в которой введена одна из этих норм? Пример 2. Линейное пространство С[a, b], состоящее из непрерывных
на [a, b] функций, является нормированным с нормой
|
f |
max | f (t) | |
(5.3) |
|||
|
t [a, b] |
и, следовательно, с метрикой
( f , ) || f || max | f (t) (t) | .
t [a, b]
Первые 2 аксиомы нормы для (5.3) выполняются с очевидностью; неравенство треугольника следует из свойств абсолютной величины: для каждого t [a, b] выполняется неравенство:
|
| f(t) + φ(t)| ≤ | f(t)| + | φ(t)| ≤ max | f (t) | + |
max | (t) | = || f || + || φ||. |
|
t [a, b] |
t [a, b] |
30

Переходя в этом неравенстве к максимуму по t, получим неравенство треугольника.
Открытый шар радиуса R с центром в элементе f0(t) в этом пространстве – это множество всех непрерывных на [a, b] функций f(t), графики которых расположены между графиками функций f0(t) – R и f0(t) + R. Сфера радиуса R с центром в элементе f0(t) состоит из функций f(t), графики которых расположены между графиками функций f0(t) – R и f0(t) + R и (обязательно) имеют общие точки с этими графиками. Замкнутый шар состоит из объединения открытого шара и его граничной сферы.
Например, в пространстве С[0, 1] ε-окрестность функции х2 состоит из всевозможных непрерывных функций, графики которых целиком лежат в полосе между кривыми у = х2 – ε и у = х2 + ε. Сходимость последовательностей и рядов в пространстве С[a, b] называется равномерной сходимостью и иногда обозначается не одной, а двумя стрелочками: xn x0 .
Пример 3. Пространство Lp[a, b] (где р – заданное число, удовлетворяющее неравенству 1 ≤ р ≤ ∞) состоит из функций, у которых существует
и конечен интеграл (может быть, несобственный)
торых задаются равенством:
|
1 |
|||||||||
|
b |
|||||||||
|
p |
|||||||||
|
f |
f (x) |
p dx |
|||||||
|
a |
b
| f (x) |p dx , нормы ко-
a
(5.4)
при р < ∞ (при р = ∞ формула для нормы сложнее). То, что (5.4) действительно задает норму, примем без доказательства. В частности, функции
b
из L1[a, b] (т. е. функции, у которых сходится интеграл || f || | f (x) | dx )
a
называются абсолютно интегрируемыми на [a, b].
Замечание. Выяснению вопроса о том, входит ли данная функция или данная последовательность в то или иное пространство и, если входит, то какова норма этого элемента в рассматриваемом пространстве, посвящено задание № 6 в разд. 10 «Индивидуальные задания» этого пособия, и разбор соответствующего примера в разд. 9 «Решение типовых примеров».
Пример 4. Элементами пространства lp (где р – заданное число, удовлетворяющее неравенству 1 ≤ р ≤ ∞) являются числовые последовательности х = (х1, х2, …, хп, …), но не все, а только те, у которых сходится ряд
| x |p ; и норма такого элемента при р > 1 задается равенством:
n 1
31

|
1 |
||||||||
|
p |
||||||||
|
x |
p |
| xn |p |
, |
(5.5) |
||||
|
n 1 |
||||||||
а при р = ∞ – равенством:


n 1, 2,…
Например, l1 состоит из последовательностей, для которых сходится
ряд 

n 1
стве при р=2 нормы (5.2) и (5.6), очевидно, совпадают.
Определение. Скалярным произведением в линейном пространстве М называется функция, сопоставляющая каждым двум элементам х, у М число (х, у), удовлетворяющая следующим аксиомам:
1)(х, х) ≥ 0, причем (х, х) = 0 тогда и только тогда, когда х есть нулевой элемент;
2)(х, у) = ( y, x) , где черта сверху означает комплексное сопряжение;
3)(αх + βу, z) = α(x, z) + β(y, z), для любых чисел α, β и любых элементов х, у, z М.
Замечание. Если линейное пространство М вещественно, то скалярное произведение (х, у) принимает вещественные значения, и во второй аксиоме не надо ставить знак комплексного сопряжения.
Следствие (свойство полулинейности по второму множителю):
(x, αy + βz) = (x, y) (x, z) .
Доказательство.
По 2-й и 3-й аксиомам скалярного произведения выводим
(x, αy + βz) =
( y z, x) ( y, x) (z, x) ( y, x) (z, x) (x, y) (x, z) .
Пример. Если (х, у) = 2 + 3i, тогда ((1 – 2i)x, (2 + i)y) = (1 – 2i)(2 – i) (х, у) = = (2 – i – 4i + 2i2)(2 + 3i) = (–5i)(2 + 3i) = 15 – 10i.
Определение. Унитарным (гильбертовым) пространством называ-
ется линейное пространство, в котором введено скалярное произведение. В гильбертовом пространстве можно ввести норму по формуле:
|
x |
(x, x) |
(5.6) |
|||
значит, и метрику по формуле:
(x, y) 

32

То, что функция, задаваемая (5.6), удовлетворяет первым двум аксиомам нормы, очевидно. Но для того, чтобы установить, что для нее справедливо также неравенство треугольника, нужно доказать очень важное неравенство Коши – Буняковского – Шварца (кратко – неравенство КБШ).
Теорема (о неравенстве КБШ). Модуль скалярного произведения двух элементов не превосходит произведения норм сомножителей, т. е.:
|
| (x, y) | || x || || y || |
(5.7) |
При этом равенство в (5.7) достигается тогда и только тогда, когда элементы х и у пропорциональны.
Доказательство.
Зафиксируем некоторые элементы x, y. Пусть α – вещественное число. Рассмотрим скалярное произведение вектора х + αу самого на себя (оно неотрицательно по определению):
A(α) = ||x + αy||2 = (х + αу, х + αу) = (х, х) + (αу, х) + (х, αу) + (αу, αу).
Так как α вещественно, его можно выносить из любого сомножителя.
Поэтому A(α) = ||x||2 + α(y, x) + α(x, y) + α2||y||2. Но ( y, x) (x, y) и (y, x) + (x, y) = 2Re(x, y).
Значит, A(α) = ||x||2 + 2α Re(x,y) + α2||y||2 ≥ 0. Так как квадратный трехчлен A(α) ≥ 0 при всех α, то его дискриминант ≤ 0, и поэтому:
|
[Re(x, y)]2 – ||x||2||y||2 ≤ 0, ||x||2||y||2 ≥ [Re(x, y)]2 |
||
|
или |
|| Re(x, y)| ≤ ||x||∙||y|| |
(5.8) |
Из (5.8) следует (5.7). Действительно, пусть r = |(x,y)|, a arg(x,y) = φ.
Тогда (x, y) = reiφ. Вместо x возьмем x1= x∙e–iφ, а так как φ – вещественно,
то ||x1||=||x||. Поэтому Re(x1, y) = Re(xe–iφ, y) = Re(e–iφ(x, y)) = Re(e–iφ reiφ) =
= Re(r) = r = |(x, y)|. Из (5.8) с х1 вместо х получаем
||x||ּ||y|| = ||x1||ּ||y|| ≥ |Re(x1, y)| = |(x, y)|,
и неравенство (5.10) доказано.
При этом равенство в (5.7) означает, что дискриминант квадратного трехчлена А(α) равен 0. Следовательно, квадратный трехчлен имеет только один корень α0, т. е. А(α0) = ||x + α0 у||2 = 0. По первой аксиоме нормы от-
сюда следует, что x + α0у = 0, т. е. что x = –α0у, а это и значит, что х и у пропорциональны.
Теорема доказана полностью.
Следствие. Функция (5.6) удовлетворяет неравенству треугольника и, следовательно, является нормой.
33

Доказательство.
По неравенству КБШ:
||x + y||2 = (x + y, x + y) = ||x||2 + 2Re(x, y) + ||y||2 ≤ ||x|| + 2|(x, y)| + ||y||2 ≤ ≤ ||x||2 + 2||x|| ∙ ||y|| + ||y||2 = (||x|| + ||y||)2,
извлекая корень из полученного неравенства, получаем неравенство треугольника.
Замечание. В унитарных пространствах ввиду неравенства КБШ можно ввести понятие угла между элементами, а именно:
|
(x, y) arccos |
(x, y) |
|
|
|| x || || y || . |
(5.9) |
Абсолютная величина дроби в формуле (5.9) ввиду (5.7) всегда не превосходит единицы.
Определение. Конечномерное (п-мерное) вещественное унитарное пространство называется евклидовым (п-мерным) пространством.
Определение. Элементы х и у унитарного пространства называются ортогональными (и записывается это так: х у), если их скалярное произведение равно нулю, т. е. если выполняется равенство:
(х, у) = 0.
Пример. Введем в пространстве L2[а, b] (частный случай пространства Lр[а, b] при р = 2) скалярное произведение функций x(t) и y(t) формулой:
|
b |
||||||
|
(x, y) x(t) |
dt , |
|||||
|
y(t) |
(5.10) |
|||||
|
a |
||||||
|
а значит, и норму по (5.5): |
||||||
|
b |
||||||
|
| x(t) |2dt . |
||||||
|
|| x || (x, x) |
||||||
|
a |
Легко проверить, что (5.10) действительно задает скалярное произведение, т. е. что выполняются соответствующие аксиомы. Вычислим, например, скалярное произведение функций x(t) = t2 и y(t) = t3 в пространстве
|
1 |
1 |
t6 |
1 |
||||
|
L2[0, 1]: (t2, t3) = t2t3dt t5dt |
10 |
. |
|||||
|
6 |
6 |
||||||
|
0 |
0 |
||||||
Так как (t2, t3) ≠ 0, то элементы t2 и t3 не ортогональны на (0, 1). Тем не менее, легко проверить, что они ортогональны на (–1, 1). Вычислим для примера норму функции x= t2:
34
|
1 |
t5 |
||||||||||||||
|
|| t |
2 |
|| |
(t |
2 |
, t |
2 |
) |
t |
4 |
dt |
1 |
||||
|
5 |
0 |
||||||||||||||
|
0 |
|||||||||||||||

Определение. Последовательность е1, е2, …, еп,… ненулевых элементов унитарного пространства называется ортогональной системой элементов, если любые два элемента этой системы ортогональны между собой: (еi, ej) = 0 при i ≠ j; она называется ортонормальной (или декартовой), если нормы всех ее элементов равны единице: ||ek|| = 1, k = 1, 2,…
Замечание. Для того, чтобы ортогональную систему превратить в ортонормальную, достаточно каждый ее элемент поделить на его норму.
Утверждение. Если элементы х и у заданы своими координатами в ортонормальном базисе е1, е2, …, еп: х = (х1, х2, …, хп), у = (у1, у2, …, уп), то их скалярное произведение обязательно вычисляется по формуле:
n
(x, y) xk yk ,
k1
вчастности, в вещественном (т. е. в евклидовом) пространстве – по формуле:
n
(x, y) xk yk .
k 1
Доказательство.
Так как (ei, ej) = 0 при i ≠ j и (ei, ei) = 1, то
|
n |
n |
n n |
||
|
(x, y) |
xiei , y je j |
xi y j |
||
|
i 1 |
j 1 |
i 1 j 1 |
n
(ei , e j ) xk yk .
k 1
Что и требовалось доказать.
Теорема (единственность разложения). Если элемент х разложен по
(конечной или бесконечной) ортогональной системе е1, е2, …, еп, …:
|
х = с1е1 + с2е2 + …+ спеп + … |
(5.11) |
то коэффициенты в этом разложении определяются однозначно формулой
|
c |
(x, en ) |
, |
(5.12) |
||||||
|
n |
e |
2 |
|||||||
|
n |
в частности, если система {en} ортонормальна, то сп = (х, еп).
Доказательство.
Пусть выполняется равенство (5.11). Домножим его скалярно справа на еп. Умножение по свойству линейности скалярного произведения можно
35

производить в случае конечного числа слагаемых почленно (для бесконечного числа слагаемых примем это без доказательства). Получим:
|
(х, еп) = с1(е1, еп) + с2(е2, еп) + …+ сп(еп, еп) + … |
(5.13) |
В силу ортогональности системы {en} все слагаемые справа, кроме сп(еп, еп), равны 0, а сп(еп, еп) = сп||еп||2, т. е. равенство (5.13) имеет вид:
(х, еп) = сп|| еп||2,
а это и есть равенство (5.12), что и требовалось доказать.
Определение. Представление элемента х в виде линейной комбинации элементов ортогональной системы называется разложением х по этой системе. В бесконечномерном унитарном пространстве такое разложение называется рядом Фурье элемента х по этой системе, а коэффициенты разложения сп называются коэффициентами Фурье.
Можно показать, что в бесконечномерном гильбертовом пространстве ряд Фурье сходится. Это основывается на неравенстве Бесселя
|
x,en |
2 |
|||||||||||
|
x |
2 |
. |
||||||||||
|
en |
2 |
|||||||||||
|
n 1 |
||||||||||||
Если система элементов en – ортогональный базис пространства, то справедливо равенство Парсеваля (аналог теоремы Пифагора)
|
x,en |
2 |
|||||||||||
|
x |
2 |
. |
||||||||||
|
en |
2 |
|||||||||||
|
n 1 |
||||||||||||
Пример. Тригонометрической системой функций на (–l, l) называется бесконечный набор функций следующего вида:
|
x |
x |
2 x |
2 x |
n x |
n x |
||||||||
|
1, cos |
, sin |
, cos |
, sin |
,…, cos |
, sin |
,… |
. (5.14) |
||||||
|
l |
l |
l |
l |
l |
l |
Докажем, что тригонометрическая система (5.23) ортогональна в пространстве L2[–l, l]. Так как скалярное произведение в этом пространстве вводится формулой (5.10), то доказательство сводится к проверке шести равенств:
|
l |
nx dx 0 |
l |
nx dx 0 |
l |
nx cos |
mx dx 0 |
|||
|
cos |
; |
sin |
; |
cos |
; |
||||
|
l |
l |
l |
l |
l |
l |
l |
|||
36

|
l |
nx sin |
mx dx 0 ; |
l |
nx sin |
mx dx 0 |
||
|
sin |
cos |
, т ≠ п; |
|||||
|
l |
l |
l |
l |
l |
l |
||
|
l |
nx sin |
nx dx 0 , (т, п = 0, 1, 2, …). |
|||||
|
cos |
|||||||
|
l |
l |
l |
|||||
Проверка предоставляется читателю. Нормы элементов системы (5.14) вычисляются по формулам:
|
1 cos |
2 nt |
||||||||||||||||||||||||||||||||
|
l |
nx |
l |
nt |
l |
|||||||||||||||||||||||||||||
|
l |
|||||||||||||||||||||||||||||||||
|
||1|| |
(1, 1) |
1 1dt |
2l , || cos |
|| |
cos |
2 |
dt |
l , |
|||||||||||||||||||||||||
|
l |
l |
2 |
|||||||||||||||||||||||||||||||
|
l |
l |
l |
|||||||||||||||||||||||||||||||
|
l 1 cos |
2 nt |
||||||||||||||||||||||||||||||||
|
nx |
l |
nt |
|||||||||||||||||||||||||||||||
|
l |
|||||||||||||||||||||||||||||||||
|
|| sin |
|| |
sin |
2 |
dt |
l . |
||||||||||||||||||||||||||||
|
l |
l |
2 |
|||||||||||||||||||||||||||||||
|
l |
l |
||||||||||||||||||||||||||||||||
Так как система (5.14) ортогональна, то можно функции из L2[–l, l] раскладывать в ряды Фурье по этой системе. Кроме того эта система функций является базисом в пространстве L2[–l, l]. Такие ряды называются
тригонометрическими рядами Фурье. Эти ряды имеют вид
|
f (x) ~ a |
a cos x |
b sin x |
a |
cos |
2 x |
b sin |
2 x |
… |
|||||
|
0 |
1 |
l |
1 |
l |
2 |
l |
2 |
l |
|||||
|
, (5.15) |
|||||||||||||
|
n x |
n x |
||||||||||||
|
a |
cos |
b sin |
… |
||||||||||
|
n |
l |
n |
l |
||||||||||
где коэффициенты вычисляются по следующим формулам:
|
a |
1 |
l |
f (t)dt , |
a |
1 l |
f (t) cos |
nt |
dt , |
b |
1 l |
f (t)sin |
nt |
dt . |
||
|
2l |
2l |
||||||||||||||
|
0 |
n |
l |
n |
l |
l |
||||||||||
|
l |
l |
l |
Вопрос о том, для каких точек х в формуле (5.15) можно поставить знак равенства вместо «~», окончательно не решен до сих пор. Достаточные условия даются условиями Дирихле, которые здесь не обсуждаются. Однако знак равенства здесь понимают в смысле среднеквадратичной сходимости ряда Фурье к функции f(x).
Если система элементов {en} не ортогональна, то ее можно ортогонализовать. Это часто выполняют с помощью процесса Грама – Шмидта.
Если система элементов {en} не ортогональна, то говорить о рядах Фурье по ней не приходится. Однако ее можно попытаться ортогонализовать.
Определение. Ортогонализацией системы элементов {en} называется отыскание таких коэффициентов αij, при которых новая система элементов {en΄}:
37
e1‘ 11e1 ,
e2‘ 21e1 22e2 ,
. . . . . . . . . . . . . . (5.16) en‘ n1e1 n2e2 … nnen ,
. . . . . . . . . . . . . .
является ортонормальной.
Теорема. Если при любом натуральном п первые п элементов данной системы {en} линейно независимы, то эта система допускает ортогонализацию.
Для доказательства потребуются новые понятия.
Определение. Матрицами Грама данной системы называются матрицы:
|
(e , e ) |
(e , e ) … (e , e ) |
||||
|
1 1 |
1 2 |
1 n |
|||
|
G |
(e2 , e1) |
(e2 , e2 ) … (e2 , en ) , |
|||
|
n |
. . . . . . . . . . . . . . . . . . . . . . . . . . |
||||
|
(en , e1) (en , e2 ) … (en , en ) |
|||||
|
определителями Грама |
п называются определители этих матриц: |
||||
|
0 = 1, |
п = detGn, |
элементами Грама en‘ называются элементы, вычисляемые по формуле:
|
(e1, e1) (e1, e2 ) … (e1, en 1) e1 |
||
|
e* (e2 , e1) |
(e2 , e2 ) … (e2 , en 1) e2 . |
(5.17) |
|
n |
(en , e1) (en , e2 ) … (en , en 1) en
Доказательство теоремы.
Докажем, что искомыми элементами вида (5.16) являются элементы:
|
e‘ |
1 |
e* . |
(5.18) |
|||
|
n |
n 1 n |
n |
||||
То, что (5.17) есть элементы вида (5.16), видно из разложения определителя (5.17) по последнему столбцу. Ортогональность элементов (5.17) элементам данной системы, т. е. равенства:
следует из того, что для скалярного умножения элемента (5.17) на еk надо каждый элемент последнего столбца определителя (5.17) скалярно умножить на еk, но при этом получится определитель с двумя одинаковыми
38

столбцами – п-м и k-м, а такой определитель равен нулю. Отсюда уже следует ортогональность системы (5.17), т. е. равенства (en* , ek* ) 0 . Действительно,
k
en* , ek* Ajk en* , e j 0 ввиду (5.19) (здесь Ajk – алгебраические дополне-
j 1
ния соответствующих элементов определителя (5.17), а k < п). Наконец,
e* 2 e* , e* A e A e … A e A e , e*
n n n 1n 1 2n 2 n 1,n n 1 nn n n
n1
Ajn e j , en* Ann en , en* .
j1
Но в силу (5.19) все слагаемые суммы в последнем равенстве равны
|
нулю, а Апп = п–1, откуда: |
|
|
en* 2 n 1 en , en* n 1 n . |
(5.20) |
Отсюда и следует, что элементы (5.18) имеют единичную норму и, следовательно, образуют ортонормальную систему элементов. Теорема доказана.
Следствие 1. Если элементы {en} линейно независимы, то все их определители Грама п, положительны.
Доказательство. Действительно, так как норма любого ненулевого элемента положительна, то из (5.20) следует, что все эти определители – одного знака. При этом, 0 = 1 > 0, поэтому и все п > 0. Следствие доказано.
Следствие 2. Признак линейной зависимости. Элементы {e1, e2,…,en}
унитарного пространства линейно зависимы тогда и только тогда, когда их определитель Грама равен нулю.
Доказательство.
Необходимость. Пусть данные элементы линейно зависимы. Тогда один из них есть линейная комбинация остальных. Для определенности,
пусть это en 1e1 2e2 … n 1en 1. Подставим это выражение в каждое
скалярное произведение последней строки определителя п и дважды воспользуемся свойством линейности: сначала свойством линейности скалярного произведения, а затем свойством линейности определителя. Получим из п серию из п–1 определителя, каждый из которых имеет две одинаковых строки и, следовательно, равен нулю, что и требовалось доказать.
|
Достаточность. Пусть |
п = 0. Тогда из (5.20) следует, что норма |
|||||
|
элемента (5.17) равна нулю: |
|| e* ||2 |
n |
0 |
. По определению нормы |
||
|
n |
n 1 |
тогда и сам элемент (5.17) является нулевым. А это и значит, что данные элементы – линейно зависимы (явную линейную зависимость можно
39

получить, раскладывая определитель в равенстве en* = 0 по последнему
столбцу Ап1е1 + Ап2е2 +…+ Аппеп = 0). Следствие доказано.
Пример 1. В 3-мерном векторном пространстве заданы декартовы ко-
ординаты трех векторов: а1 = (1, 2, –2), а2 = (–1, 0, 2), а3 = (0, 2, –3). Требу-
ется их ортогонализовать. Для этого вычислим элементы Грама по форму-
ле (5.17), а затем элементы (5.18): (а1, а2) = 1(–1) + 2 ∙ 0 + (–2) ∙ 2 = –5, (а1, а3) = 10, (а2, а3) = –6, (а1, а1) = 9, (а2, а2) = 5, (а3, а3) = 13, 0 = 1,
|
9 5 |
5 |
10 |
36 , e1* a1 , |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
9 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 = |(а1, а1)| = 9, |
2 |
= |
20, |
3 = |
5 |
5 6 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
5 5 |
10 |
6 |
13 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
e* |
a1 |
9 |
a1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
(a1, a1) |
5a 9a |
( 4,10, 8) , |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
(a2 |
, a1) a2 |
5 a2 |
1 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
a1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
e3* = |
5 |
5 |
a2 |
20a1 4a2 |
20a3 ( 24, 0, 12) . |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
10 |
6 |
a3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Отсюда по формуле (5.18): |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
‘ |
1 |
* |
1 |
2 |
2 |
‘ |
1 |
* |
2 |
5 |
4 |
|||||||||||||||||||||||||||||||||||||||||||
|
e1 |
e1 |
, |
, |
, e2 |
e2 |
, |
, |
, |
||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 3 3 |
6 5 |
3 5 3 5 3 5 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
e3‘ |
1 |
e3* |
2 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
, 0, |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
5 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
12 |
5 |
Пример 2. Пусть р(х) – заданная на (a, b) функция, принимающая на (a, b) только положительные значения (в дальнейшем будем называть ее «весом»).
Пространством L2 [( a, b), р(х)] («пространством с весом») называ-
ется множество всех тех функций f(x), для которых сходится интеграл
b
p(x) | f (x) |2 dx , в котором введено скалярное произведение по формуле:
a
b
(f(x), g(x)) = p(x) f (x)g(x)dx ,
a
и, следовательно, норма по формуле:
|
b |
|
|
|| f (x) || |
p(x) | f (x) |2dx. |
|
a |
40
Рассмотрим множество вещественнозначных функций и возьмем в качестве веса р(х) = 1 на (–1, 1). Ортогонализуем функции {1, x, x2,…, xn,…}. Полученные многочлены называются многочленами Лежандра.
В индивидуальных заданиях будут предложены другие веса, по которым нужно будет ортогонализовать те же функции и получить соответствующие ортогональные многочлены.
Найдем хотя бы 4 первые многочлена Лежандра:
|
1 |
1 |
1 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
(1, 1) = 1dx 2 , (1, х) = (х, 1) = xdx 0 , (1, х2) = x2dx |
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
(1, х3) = (х3, 1) = x3dx = 0, (х, х) = x2dx |
, (х, х2) = (х2, х) = 0, |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
(x2 x2) = (x3, x) = (x,x3)= |
2 |
, (х3, х2) = (х2, х3) = 0, (х3, х3) = |
2 |
. |
||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
7 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Поэтому: |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 0 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
2 |
32 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
∆0 = 1, ∆1 = |(1, 1)| = 2, ∆2 = |
2 |
= |
, ∆3 = |
0 |
0 |
= |
, |
|||||||||||||||||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
3 |
135 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
5 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
2 |
0 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
∆4= |
3 |
5 |
= |
256 |
. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
0 |
23625 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
5 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
2 |
0 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
7 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Соответственно: |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 0 1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
4 |
х2 –. |
4 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Р (х) = 1, Р (х) = |
21 |
=2х, Р (х) = |
0 |
х |
= |
, |
||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
1 |
0 х |
2 |
3 |
3 |
9 |
||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
0 х2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
41
|
2 |
0 |
2 |
1 |
||||||||||||
|
3 |
|||||||||||||||
|
0 |
2 |
0 |
x |
||||||||||||
|
Р3(х) = |
3 |
= |
32 |
х |
3 |
– |
32 |
. |
|||||||
|
2 |
0 |
2 |
x2 |
135 |
225 |
||||||||||
|
3 |
5 |
||||||||||||||
|
0 |
2 |
0 |
x3 |
||||||||||||
|
5 |
|||||||||||||||
Отсюда по формуле (5.31) получаем полиномы Лежандра:
L0(x)= 12 , L1(x)= 
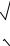

Замечание. Можно доказать, что полиномы Лежандра задаются равенством Ln(x) = cn[(x2 – 1)n](n), где сп – нормирующие коэффициенты [7].
42

6.ЛИНЕЙНЫЕ ОПЕРАТОРЫ
ВЛИНЕЙНЫХ ПРОСТРАНСТВАХ.
СОБСТВЕННЫЕ ЧИСЛА И СОБСТВЕННЫЕ ЭЛЕМЕНТЫ ЛИНЕЙНЫХ ОПЕРАТОРОВ
Под термином «оператор» в математике понимают сопоставление каждому элементу из одного данного пространства некоторого элемента из другого или того же данного пространства. Операторы обычно обозначаются большими латинскими буквами. Символ А: Х→Y означает, что оператор А отображает элементы пространства Х в элементы пространства Y. Если А отображает элементы множества Х в элементы того же множества Х, то говорят, что А действует на множестве Х. Если оператор отображает некоторое множество Х в множество вещественных чисел R или в множество комплексных чисел С, то он называется функционалом. Если оператор А сопоставляет элементу х из Х элемент у из Y, то этот факт записывается символом у = Ах, при этом элемент у называется образом элемента х, а элемент х называется прообразом элемента у.
Определение. Оператор А, действующий из линейного пространства Х в линейное пространство Y, называется линейным оператором, если для любых элементов х и у из Х и любых чисел α и β выполняется равенство:
|
А(αх + βу) = αА(х) + βА(у). |
(6.1) |
В частности, функционал называется линейным функционалом, если Y есть R или C.
Замечание. Из определения следует, что числовой множитель можно выносить за знак линейного оператора: при β = 0 (6.1) превращается в:
Так же следует, что линейный оператор переводит нулевой элемент
в нулевой же элемент (при α = 0 (6.2) превращается в А( 0 ) = 0).
Замечание. Множество всех линейных операторов в пространстве Х обычно обозначается символом L(Х→Х), а из Х→Y – символом L(Х→Y).
Определение. Множество элементов, которые линейный оператор отображает в нулевой элемент, называется ядром этого оператора.
Не вдаваясь в подробности, отметим, что ядро оператора является линейным пространством. Например, множество решений линейного однородного дифференциального уравнения (ЛОДУ) является ядром линейного дифференциального оператора (ЛДО). Теорему о структуре общего решения ЛОДУ можно переформулировать так: ядро приведенного ЛДО п-го порядка с непрерывными на (a, b) коэффициентами – п-мерно (его базисом являются любые п линейно независимых частных решений).
43

Пример. Оператор дифференцирования в пространстве дифференцируемых функций является линейным, так как (αf(x) + βg(x))΄= αf ΄(x) +
βg΄(x), оператор возведения функции в квадрат не является линейным, так как (αf(x) + βg(x))2 ≠ αf 2(x) + βg2(x).
Линейным функционалом является определенный интеграл по фиксированному отрезку; он задан на множестве всех функций, интегрируемых по этому отрезку (любой другой интеграл, например, двойной по фиксированному множеству, также является линейным функционалом). Линейными операторами в соответствующих пространствах являются преобразования Фурье и Лапласа, z-преобразование и т. д.
Теорема (матричное представление линейных операторов). Если Х и
Y – конечномерные (п-мерное и т-мерное) линейные пространства и в них выбраны базисы {е1, е2, …, еп} и {е1΄, е2΄, …, ет΄} соответственно, тогда любой линейный оператор А: Х→Y можно задать матрицей (она тоже обозначается символом А) в том смысле, что для любого элемента х из Х, заданного своими координатами в выбранном базисе: х = (х1, х2, …, хп), и его образа у = Ах = (у1, у2, …, ут) в выбранном базисе пространства Y их координаты связаны матричным равенством у = Ах, или (что то же) равенством:
|
y |
a |
a |
||
|
1 |
11 |
12 |
||
|
y2 |
a21 a22 |
|||
|
ym |
am1 am2 |
|
a |
x |
||||
|
1n |
1 |
||||
|
a2n |
x2 |
; |
(6.3) |
||
|
amn |
xn |
при этом столбцами матрицы А служат координаты образов базисных векторов, т. е.:
Ае1 = а11е1΄+ a21e2΄+ …+ am1em΄,
Ае2 = а12е1΄+ a22e2΄+ …+ am2em΄,
. . . . . . . . . . . . . . . . . . . . . . . . . . . (6.4)
Аеn = а1nе1΄+ a2ne2΄+ …+ am1em΄.
Доказательство.
Всилу линейности А справедливы равенства:
у= Ах = А(х1е1 + х2е2 +…+ хпеп) = х1Ае1 + х2Ае2 +…+ хпАеп =
=х1(а11е1΄+ a21e2΄+…+ am1em΄) + х2(а12е1΄+ a22e2΄+ …+ am2em΄) +
+…+ хп(а1nе1΄+ a2ne2΄+ …+ am1em΄) =
=(а11х1 + а12х2 + …+а1пхп)е1΄+ (a21x2 + a22x2 + …+ a2nxn)e2΄+…+
+(am1x1 + am2x2 +…+ amnxn)em΄.
С другой стороны, у = Ах = у1 е1΄+ у2 e2΄+ …+ уm em΄, откуда в силу единственности разложения элемента пространства по базису следует, что:
44
|
у1 = а11х1 + a12х2 + …+ a1пхп, |
|
|
у2 = а21х1 + a22х2 + …+ a2пхп, |
(6.5) |
|
. . . . . . . . . . . . . . . . . . . . . . . . |
|
|
ут = ат1х1 + aт2х2 + …+ aтпхп. |
Матричная запись системы (6.5) есть требуемое равенство (6.3) и, кроме того, она доказывает справедливость (6.4).
Теорема (о преобразовании матрицы оператора при переходе к новому базису). Пусть в линейном пространстве Х выбраны два базиса: {е1, е2, …, еп} и {е1΄, е2΄, …, еn΄}, и пусть матрица перехода от первого из них ко второму есть С. Пусть в этом пространстве действует линейный оператор А: Х→Х, матрица которого в первом базисе есть А, а во втором есть А’.
|
Тогда матрицы A и A’ связаны равенством: |
|
|
A’ = C–1AC. |
(6.6) |
Доказательство.
Для любых элементов х и у, у которых векторы из координат в первом базисе есть Х и Y, а во втором – X’ и Y’ соответственно, из определений следуют равенства Y = CY’= CA’X’= CA’ C–1X, а с другой стороны Y = AX. Так как это верно для любых Х и Y, то
Очевидно, что равенства (6.6) и (6.7) равносильны, что и требовалось доказать.
Пример 1. Очевидно, что если в конечномерном векторном пространстве оператор задается как оператор умножения данной фиксированной матрицы на вектор, то матрица этого оператора совпадает с данной.
Пример 2. Пусть Х – пространство многочленов степени не выше трех со стандартным базисом е0 = 1, е1 = х, е2 = х2, е3 = х3. В этом 4-мерном пространстве рассмотрим два оператора: А – оператор дифференцирования, В – оператор, задаваемый формулой: ВР = (x2 – 2x)P’’– (3x + 1)P’+ 2P, где P – многочлен. Найдем матрицы этих операторов. Для этого, по теореме о матричной записи операторов нужно найти координаты образов базисных векторов (напоминаем, что координаты – это коэффициенты в разложении по базису):
Ае0 = (1)’= 0 = (0, 0, 0, 0), Ae1 = (x)’= 1 = (1, 0, 0, 0), Ae2 = (x2)’= 2x = (0, 2, 0, 0), Ae3 = (x3)’= 3x2 = (0, 0, 3, 0).
Поэтому матрица оператора дифференцирования имеет вид:
|
0 1 0 0 |
||||
|
A |
0 0 2 0 |
. |
||
|
0 0 0 3 |
||||
|
0 0 0 0 |
45
Ве0 = (x2 – 2x)(1)’’ – (3x + 1)(1)’+ 2ּ1 = 2 = (2, 0, 0, 0);
Be1 = (x2 – 2x)(x)’’ – (3x + 1)(x)’+ 2ּx = 5x + 1 = (1, 5, 0, 0); Be2 = (x2 – 2x)(x2)’’ – (3x + 1)(x2)’+ 2ּx2 = –2x2 – 6x = (0, –6, –2, 0);
Be3 = (x2 – 2x)(x3)’’ – (3x + 1)(x3)’+ 2ּx3 = –x3 – 15x2 = (0, 0, –15, –1).
Матрица оператора В имеет вид:
|
2 1 |
0 |
||||
|
0 |
5 |
6 |
|||
|
B |
|||||
|
0 |
0 |
2 |
|||
|
0 |
0 |
0 |
Теперь, чтобы узнать результат действия оператора В на данный многочлен, можно умножить матрицу В на столбец коэффициентов этого многочлена и получить столбец коэффициентов образа.
Пример 3. В пространстве матриц размером 2 × 2 со стандартным ба-
|
10 |
01 |
0 0 |
0 0 |
||||||||||||||||
|
зисом |
e1 |
, |
e2 |
, |
e3 |
, |
e4 |
рассмотрим оператор А, |
|||||||||||
|
0 0 |
0 0 |
10 |
01 |
который переставляет строчки между собой, после чего умножает второй столбец на три.
Найдем матрицу этого оператора:
|
0 0 |
e3 =(0, 0, 1, 0); А e2 |
0 0 |
||||||
|
Ae1 |
= 3е4=(0, 0, 0, 3); |
|||||||
|
10 |
0 3 |
|
10 |
0 3 |
||||||||
|
А e3 |
0 0 |
=е1=(1, 0, 0, 0); А e4 |
0 0 |
=3е2 |
= (0, 3, 0, 0). |
||||
Значит, матрица оператора А имеет вид:
|
0 01 0 |
||
|
0 0 0 3 |
||
|
A |
. |
|
|
1 0 0 0 |
||
|
0 3 0 0 |
Замечание. Оператор, который все элементы переводит в нулевой элемент, называется нулевым оператором и обозначается О. Очевидно, что его матрица в любом базисе является нулевой матрицей. Оператор Е, который все элементы Х оставляет на месте, т. е. такой, что ЕХ = Х, называется единичным оператором. Очевидно, что его матрица в любом базисе является единичной матрицей.
46

Определение. Собственным числом данного линейного оператора А называется число λ, для которого найдется ненулевой элемент Х, что выполняется равенство:
Этот ненулевой элемент Х называется собственным элементом (или собственным вектором) оператора А, соответствующим собственному числу λ.
Замечание. Очевидно, что если равенству (6.8) удовлетворяют два элемента Х1 и Х2, то ему удовлетворяет и любая их линейная комбинация.
Действительно, если Х = αХ1 + βХ2, АХ1 = λХ1, АХ2 = λХ2, то
АХ = А(αХ1 + βХ2) = αАХ1 + βАХ2 = αλХ1 + βλХ2 = λ(αХ1 + βХ2) = АХ,
т. е. Х = αХ1 + βХ2 тоже является собственным вектором. Таким образом, множество элементов, являющихся собственными векторами оператора А, соответствующими собственному числу λ, образуют линейное подпространство; оно называется собственным подпространством оператора А, соответствующим собственному числу λ, и обычно обозначается символом Хλ.
Определение. Характеристическим многочленом данного конечно-
мерного линейного оператора А в данном базисе называется многочлен:
|
a11 |
a12 . |
a1n |
|||
|
χ(λ) = det(A – λE)= |
a21 |
a22 |
a2n |
. |
(6.9) |
|
an1 |
an2 |
ann |
|||
|
При раскрытии определителя (6.9) по определению определителя вид- |
|||||
|
но, что это действительно многочлен: |
|||||
|
χ(λ) = (–1)пλп+ р1λп–1+ …+ рп-1 λ + рп, |
(6.10) |
||||
|
Определение. Характеристическим уравнением оператора А называ- |
|||||
|
ется уравнение: |
|||||
|
χ(λ) = 0. |
(6.11) |
Утверждение. Число λ является собственным числом оператора А тогда и только тогда, когда оно является корнем его харктеристического уравнения (6.11).
Доказательство.
Уравнение (6.8), определяющее собственные числа, можно переписать в следующем виде:
47
Оно является матричной записью однородной системы линейных алгебраических уравнений. Как известно, такая система имеет нетривиальное решение тогда и только тогда, когда ее определитель равен нулю, т. е. когда выполняется равенство (6.11), что и требовалось доказать.
Замечание. Чтобы найти соответствующие λ собственные векторы, надо подставить найденный корень в уравнение (6.8) или (6.12)) и найти какие-нибудь нетривиальные решения (т. е. координаты этих векторов).
Утверждение. Характеристический многочлен линейного оператора не меняется при переходе к новому базису (поэтому предпочитают говорить о харктеристическом многочлене оператора, а не о харктеристическом многочлене его матрицы).
Доказательство.
Обозначим матрицу данного оператора в старом базисе через А, в но-
вом – через A’, а матрицу перехода – через С.
Тогда χA’(λ) = det(A’ – λE) = det(C–1AC – λE) = det(C–1AC –λ C–1EC) = = det[C–1 (A – λE)C] = detC–1 det(A – λE) detC = det(C–1C) det(A – λE) =
= detEχA(λ) = χA(λ).
Что и требовалось доказать.
Замечание. Таким образом, доказано, что все коэффициенты рk у многочлена (6.10) сохраняются в любом базисе. В частности, сохраняется р1. Он называется следом оператора и обозначается trA = a11 + a22 +…+ ann (очевидно, он равен сумме элементов главной диагонали матрицы оператора). Так же сохраняется и величина определителя матрицы данного оператора в любом базисе, так как detA = pn.
Утверждение. Собственные векторы оператора, соответствующие различным собственным числам, линейно независимы.
Доказательство.
Пусть собственные числа оператора А есть λ1, λ2,…, λk,…, а им соответствуют собственные векторы Х1, Х2,…, Хk,… Предположим, что они линейно зависимы. Будем перебирать их до тех пор, пока не получим линейную зависимость. Для определенности будем считать, что Х1, Х2,…, Хт еще линейно независимы, а Х1, Х2,…, Хт, Хт+1 уже линейно зависимы. Тогда Хт+1 является линейной комбинацией остальных векторов, т. е. найдутся такие коэффициенты α1, α2, …, αт, что выполняется равенство:
|
Хт+1 = α1Х1 + α2Х2 +… + αтХт. |
(6.13) |
Применим к этому равенству оператор А. В силу его линейности получим АХт+1 = α1А Х1 + α2А Х2 +… + αтА Хт, а так как рассматриваемые вектора – собственные, то из него следует, что
48

|
λт+1 Хт+1 = α1λ1 Х1 + α2λ2 Х2 +… + αтλт Хт. |
(6.14) |
Умножим равенство (6.13) на λт+1 и вычтем полученное равенство из (6.14). Получим:
α1 (λ1 – λт+1) Х1+ α2(λ2 – λт+1) Х2+… + αт (λт – λт+1) Хт = 0. (6.15)
Так как все собственные числа по условию различны, и хотя бы один из коэффициентов аk ≠ 0 (иначе из (6.13) следовало бы, что Хт+1= 0), то (6.16) означает, что векторы Х1, Х2,…, Хт линейно зависимы, что противоречит предположению. Значит, предположение неверно, и утверждение доказано.
Следствие. Если все корни харктеристического уравнения – простые (или, что то же, все собственные подпространства одномерны), то из собственных векторов оператора можно составить базис.
Утверждение. В базисе из своих собственных векторов е1, е2, …, еп оператора, соответствующая ему матрица имеет диагональный вид, т. е.
на ее главной диагонали стоят собственные числа, а все остальные ее элементы равны 0:
|
1 |
0 |
0 |
||||
|
0 |
2 |
0 |
||||
|
D |
. |
(6.16) |
||||
|
0 |
0 |
. n |
Доказательство.
Вбазисе из собственных векторов Ае1 = λ1е1 = (λ1, 0, 0,…,0), Ае2 =
=λ2е2 = (0, λ2, 0,…,0), …, Аеп = λпеп = (0, 0, 0,…, λп). Это и означает равен-
ство (6.16).
Замечание. Как было отмечено, коэффициенты хар. мн-на одинаковы в любом базисе. В частности, не меняются след оператора и его определи-
тель. Но след матрицы (6.16) trD = λ1 + λ2 +…+ λn, а определить detD = λ1λ2ּ…ּ λn. Поэтому в любом базисе след оператора есть сумма всех его собственных чисел, а величина его определителя равна произведению всех его собственных чисел.
Замечание. Если характеристический многочлен имеет кратные корни, то соответствующих собственных векторов может не хватить для построения базиса. Однако, как доказал Жордан, для любого оператора существует базис из собственных и «присоединенных» векторов, но это материал для другой работы, здесь жорданова форма матрицы не понадобится.
49
7. СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ
Определение. Суммой двух линейных операторов А и В, действующих в линейном пространстве Х, называется линейный оператор С =А + В, действующий на любой элемент х по формуле (А + В)х = Ах + Вх.
Аналогично определяются: разность (А – В)х = Ах– Вх и произведе-
ние (λА)х = λּАх, (АВ)х = А(Вх).
Отметим, что при умножении операторов сначала действует второй множитель, а на полученный результат – первый. Если при умножении операторов результат не зависит от того, какой оператор считать первым, а какой – вторым, т. е. если АВ = ВА, то такие операторы называются пере-
становочными, или коммутирующими. Оператор С = АВ – ВА называется
коммутатором операторов А и В.
Замечание. В частности, степени операторов Ат действуют по формуле А2х = А(Ах), А3х = А(А2х), …, Атх = А(Ат-1х),…. При этом очевидно равенство Ат Ап = Ат+п.
Очевидно, что в конечномерном пространстве действиям над операторами соответствуют те же действия над их матрицами.
Нахождению матриц данных операторов и их произведений посвящен разбор 4-го типового задания в разд. 9 («Решение типовых примеров»).
Пример 1. Если в пространстве дифференцируемых функций А – опе-
ратор дифференцирования: Af = f ΄(x), то A2f = f ΄΄(x), A3f = f ΄΄΄(x),…….,
An(f) = f (n)(x),….
Пример 2. Если в том же пространстве А – тот же оператор, а В – оператор умножения на независимую переменную х, то коммутатором этих операторов является оператор Сf(x) = (AB – BA)f(x) = (xf(x))΄ – xf ΄(x) = f(x) + + xf ΄(x) – xf ΄(x) = f(x), т. е. коммутатор С – есть единичный оператор, С = Е.
Определение. Нормой оператора А, действующего в нормированном пространстве Х, называется супремум нормы его значений на единичном шаре (или, что то же, на единичной сфере):
|
|| A || sup || Ax || sup || Ax || |
(7.1) |
||||||||
|
||x|| 1 |
||x|| 1 |
||||||||
|
Если ||x|| < 1, то |
|||||||||
|
x |
x |
x |
|||||||
|
|| Ax || || A |
|| || x || || A |
|| || Az ||, |
где || z || || |
|| 1. |
|||||
|
|| x || |
|| x || |
|| x || |
Замечание. Равенство (7.1) означает, что норма оператора – это инфимум тех С, у которых для всех элементов х пространства справедливо неравенство:
50

Иными словами, для всех х выполняется неравенство ||Ax|| ≤ ||A||ּ||x||, но при коэффициенте меньшем, чем ||A|| оно верно не для всех x.
Легко проверить, что норма операторов, введенная формулами (7.1) или (7.2), является настоящей нормой, т. е. удовлетворяет всем трем аксиомам нормы. Операторы, у которых норма является конечным числом, называются ограниченными, те же, у которых норма бесконечна, называются неограниченными. В конечномерных пространствах все линейные операторы ограничены.
Определение. Оператор А*, действующий в унитарном пространстве, называется сопряженным к оператору А, если для всех элементов х и у
|
пространства выполняется равенство: |
|
|
(Ах, у) = (х, А*у). |
(7.3) |
Можно доказать, что у любого линейного оператора существует (и единствен) сопряженный оператор, что он тоже линейный и что его норма совпадает с нормой исходного оператора. Кроме того, очевидно, что А** = А. Ясно также, что (αА ± βВ)* = αА*± βВ* и что (АВ)*= В*А* (по определе-
нию (АВх, у) = (Вх, А*у) = (х, В*А*у)).
Утверждение. Если в конечномерном унитарном пространстве Х линейный оператор А задан (в некотором базисе) своей матрицей А, то сопряженный к нему оператор задается (в том же базисе) матрицей А*, которая является транспонированной по отношению к матрице А, а ее эле-
|
менты комплексно сопряжены элементам матрицы A: |
|
|
А* = AT . |
(7.4) |
В вещественном пространстве матрица сопряженного оператора совпадает с транспонированной матрицей этого оператора: А*=АТ.
Доказательство.
Выпишем скалярное произведение ( Ax, y) и поменяем порядок суммирования:
|
n |
n |
||
|
( Ax, y) |
aij x j yi |
||
|
i 1 |
j 1 |
Заменим в последней сумме индекс i на индекс j, а индекс j на индекс i и воспользуемся тем, что aijT = aji, а также свойствами комплексно сопряженных чисел. Тогда последнее равенство перепишется в виде:
|
n |
n |
n |
n |
x, |
T y . |
|||||
|
(Ax, y)= xi |
aijT y j |
xi |
aijT y j |
|||||||
|
A |
||||||||||
|
i 1 |
j 1 |
i 1 |
j 1 |
Сравнивая с (7.3) в силу единственности сопряженного оператора получаем (7.4), что и требовалось доказать.
51

Определение. Линейный оператор А называется самосопряженным,
если он совпадает со своим сопряженным, т. е. если А=А*.
Замечание. Таким образом, для самосопряженного оператора при всех х и у выполняется равенство:
В комплексном конечномерном пространстве такому оператору соот-
ветствует матрица, у которой AT =А. Такая матрица называется эрмитовой. В вещественном пространстве самосопряженному оператору соответствует матрица, которая совпадает со своей транспонированной: А=АТ. Такая матрица называется симметричной (поскольку равны ее элементы, симметричные относительно ее главной диагонали).
Теорема (о собственных числах и собственных векторах самосопря-
женных операторов). У самосопряженных операторов все собственные числа вещественны, а собственные вектора, соответствующие различным собственным числам, ортогональны между собой; в пространстве существует декартов (ортонормальный) базис из собственных векторов.
Доказательство.
Пусть А – самосопряженный оператор, λ – его собственное число, а х – соответствующий собственный вектор. Тогда (Ах, х) = (λх, х) = λ(х, х) = λ||x||2,
|
с другой стороны, в силу |
(7.5) имеем (Ах, х) = (x, Ax) |
= (х, |
λ х) |
= |
||||||||
|
(x, x) |
|| x ||2 . Поэтому |
|||||||||||
|
= |
что |
, |
а |
|||||||||
|
( |
) || x ||2 0 . Отсюда следует, |
|||||||||||
|
это означает, что λ – вещественное число, что и требовалось доказать. |
Пусть теперь λ1 ≠ λ2 – два различных собственных числа самосопряженного оператора А, а х1 и х2 – соответствующие собственные векторы.
Тогда (Ах1, х2) = (λ1х1, х2) = λ1(х1, х2), (Ах1, х2) = (х1, Ах2) = (х1, λ2х2) = λ2(х1, х2).
Сравнивая эти равенства, получим (λ1 – λ2)(х1, х2) = 0. Так как по условию λ1 ≠ λ2, то из этого равенства следует, что (х1, х2) = 0. Это и значит,
что x1 x2 .
Последнюю часть утверждения теоремы можно доказать, используя одно свойство самосопряженного оператора. Это свойство состоит в том, что самосопряженный оператор, определенный на ортогональном дополнении к собственному подпространству будет самосопряженным. Таким образом, определив несколько взаимно ортогональных собственных векторов самосопряженного оператора, можно достроить эту систему до базиса, рассмотрев оператор на ортогональном дополнении к уже построенной системе. Подробности доказательства можно найти в [1], [3], [6]. Очевидно, матрица оператора в этом базисе диагональна. Теорема доказана.
Нам понадобится еще классы матриц – ортогональные и унитарные. Определение. Матрица перехода от одного ортонормального базиса
к другому в евклидовом пространстве называется ортогональной матрицей, а в унитарном конечномерном пространстве – унитарной матрицей.
52
Замечание. Таким образом, у таких матриц все столбцы имеют норму, равную единице, а разные столбцы ортогональны между собой, что легко проверяется на практике. Например, так называемая матрица Адамара порядка 2п ортогональна. Матрица Адамара 4-го порядка имеет вид:
|
1 |
1 |
1 |
1 |
|||
|
1 |
1 |
1 |
1 |
1 |
||
|
A |
. |
|||||
|
1 |
1 |
|||||
|
2 |
1 |
1 |
||||
|
1 |
1 |
1 |
1 |
Утверждение. У ортогональной матрицы обратная матрица совпадает с транспонированной: C–1= CT, а у унитарной – с транспонированной ком-
плексно сопряженной: C 1 CT .
Доказательство.
Столбцами матрицы перехода C служат координаты новых базисных векторов в старом базисе. В случае унитарной матрицы ее столбцы – координаты векторов ортонормального базиса {е1΄, е2΄, …, еп΄} в ортонормальном же базисе {е1, е2, …, еп}. Мы уже выясняли (в формуле (5.20)), что эти координаты вычисляются по формуле (еj΄, ei), т. е. что j-й столбец матрицы С состоит из этих скалярных произведений. Аналогично, столбцы обратной матрицы С–1, т. е. матрицы перехода от нового базиса к старому, состоят из координат старых базисных векторов в новом базисе, т. е. из ска-
лярных произведений (еj, ei΄)= (ei , e j ) . Это и означает, что C 1 CT , что и
требовалось доказать.
Пример. Так как матрица Адамара одновременно ортогональна и симметрична, то для нее А–1= А, т. е. А2 = Е (проверьте самостоятельно!). Матрица F перехода к дискретному преобразованию Фурье (к ДПФ), рассмотренная в конце раздела 3, становится унитарной и симметричной, если ее
|
(т. е. все ее элементы) |
умножить на |
1 |
. |
Поэтому обратная к ней есть |
|||||||||||||
|
N |
|||||||||||||||||
|
комплексно сопряженная к ней: |
|||||||||||||||||
|
1 |
1 |
1…………… |
1 |
||||||||||||||
|
z 2 |
z N 1 |
||||||||||||||||
|
1 |
z |
||||||||||||||||
|
1 |
1 |
2 |
4 |
2( N 1) |
|||||||||||||
|
F |
1 |
z |
z |
……….. |
z |
. |
|||||||||||
|
N |
|||||||||||||||||
|
………………………………. |
|||||||||||||||||
|
( N 1)2 |
|||||||||||||||||
|
N 1 |
2( N 1) |
||||||||||||||||
|
1 |
z |
z |
…… |
z |
53
8.ПРИВЕДЕНИЕ КВАДРАТИЧНОЙ ФОРМЫ
КГЛАВНЫМ ОСЯМ
Обзор канонических уравнений второго порядка от двух и трех переменных.
Определение. Квадратичной формой от п переменных называется функция от п переменных, задаваемая формулой:
|
n n |
|
|
F(x1, x2, …, xn)= aij xi x j , |
(8.1) |
i 1 j 1
где аij – заданные числа, называемые коэффициентами формы, а матрица из этих чисел A = (aij) называется матрицей квадратичной формы. В дальнейшем будем предполагать, что коэффициенты формы вещественные числа и матрица A квадратичной формы симметрична, т. е. аij = aji.
С помощью матрицы A квадратичную форму можно записать короче:
|
n n |
|
|
F(x1, x2, …, xn) = aij xi x j = (Ах, х) = хТАх, |
(8.2) |
|
i 1 j 1 |
где х = (x1, x2, …, xn), а хТ – транспонированная строка (т. е. столбец). Квадратичную форму (8.1) можно записать также равенством:
|
n |
n n |
|
|
F(x) = F(x1, x2, …, xn) = (Ах, х)= akk xk2 |
2 aij xi x j . |
(8.3) |
|
k 1 |
i 1 j i 1 |
Утверждение. Для любой квадратичной формы существует декартов базис (а именно, базис из собственных векторов ее матрицы), в котором она записывается в виде суммы квадратов независимых переменных с некоторыми числовыми коэффициентами.
Доказательство.
В (8.3) матрица А симметричная, поэтому в пространстве существует ортонормальный базис из собственных векторов. В этом базисе матрица А кв. формы диагональная. Обозначим ее через D. Она имеет вид (6.16). Матрица перехода к этому базису (т. е. матрица С, столбцами которой являются координаты собственных векторов матрицы А в исходном базисе) ортогональна, так как является матрицей перехода от одного декартова базиса к другому, поэтому С–1= СТ. По формуле (6.7) А = С DС–1= CDCT, следовательно, кв. форма (8.1) может быть записана в виде:
|
F(x) = F(x1, x2, …, xn) = хТАх = хТCDCTx = (CTx)TD(CTx). |
(8.4) |
Мы воспользовались известным фактом, что (АВ)Т=ВТАТ.
54
Перейдем к новым координатам x’=(x1’, x2’, …, xn’), связанным со старыми формулами
В силу (8.4) и (8.5) данная квадратичная форма в новом базисе имеет вид:
|
F(x’) = x’TDx’ = λ x ’ |
2+ λ х ’ |
2+ … + λ х |
’2. |
(8.6) |
|
1 1 |
2 2 |
n п |
Утверждение доказано.
Определение. Уравнением второго порядка (квадратичным уравнени-
ем) от п переменных называется уравнение вида:
где А = (аij) – заданная ненулевая симметричная матрица, b=(b1, b2, …, bn) – заданная строка чисел, с – заданное число, х = (х1, х2, …, хп) – столбец из переменных.
Замечание. В уравнениях от 2 и 3 переменных обычно переменные обозначают так: х1 = х, х2 = у, х3 = z. Поэтому из (8.7) получаем общий вид квадратичного уравнения от двух переменных:
|
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0, |
(8.8) |
|
|
а от 3 переменных – таков: |
||
|
Ax2 + By2 + Cz2 + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Kz + L = 0, |
(8.9) |
|
|
где A, B, C, D, E, F, G, H, K, L – некоторые заданные числа. |
||
|
Общий же вид кв. ур-ия от п переменных таков: |
||
|
n n |
n |
|
|
aij xi x j bk xk c 0 . |
(8.10) |
|
|
i 1 j 1 |
k 1 |
Определение. Квадратичная форма называется невырожденной, если все ее собственные числа отличны от нуля, кв. форма называется вырожденной, если хотя бы одно из ее собственных чисел равно нулю.
Утверждение. Если у квадратичного уравнения от п переменных квадратичная форма невырожденая, то существует декартовая система координат, в которой это уравнение имеет вид:
|
2 |
2 |
2 |
(8.11) |
|||||
|
1x1 |
2 x2 |
… n xn |
c . |
|||||
|
Доказательство. |
||||||||
|
В базисе из собственных векторов матрицы А уравнение (8.10) прини- |
||||||||
|
2 |
2 |
2 |
В этом урав- |
|||||
|
мает вид 1x1 |
2 x2 |
… n xn |
b1x1 |
b2 x2 … bn xn c . |
нении слагаемые с одинаковыми переменными дополним до полного квадрата по формуле
55

|
2 |
2 |
||||||||||||||||||||||||||
|
2 |
2 |
bk |
bk |
bk |
|||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||
|
k |
k |
k |
k |
k |
k |
2 k |
k |
2 |
4 k |
||||||||||||||||||
|
4 k |
|||||||||||||||||||||||||||
|
2 |
2 |
2 |
|||||||||||||||||||||||||
|
b |
bk |
2 |
bk |
||||||||||||||||||||||||
|
k |
. |
||||||||||||||||||||||||||
|
xk |
4 k |
k xk |
|||||||||||||||||||||||||
|
2 k |
4 k |
Проделав это с каждой парой слагаемых с одинаковыми индексами,
|
n |
k |
k |
n |
b 2 |
||||||||
|
перепишем (8.10) и виде |
4 |
c (новые координаты связаны |
||||||||||
|
x 2 |
k |
|||||||||||
|
k 1 |
k 1 |
k |
||||||||||
|
со старыми формулами x |
x |
b |
, |
к = 1, 2, …, п). Обозначив число |
||||||||
|
k |
||||||||||||
|
k |
k |
2 k |
||||||||||
в правой части за c’, получим (8.11), что и требовалось доказать.
Замечание. Переход к координатам x означает перенос начала коор-
k
|
b |
b |
b |
|||||||||||||||
|
динат в точку O |
1 |
, |
2 |
, |
, |
n |
. |
||||||||||
|
2 1 |
2 2 |
2 n |
|||||||||||||||
|
Замечание. Если c’ ≠ 0, то уравнение (8.11) обычно переписывают |
|||||||||||||||||
|
в виде: |
|||||||||||||||||
|
x 2 |
x 2 |
x 2 |
1, |
(8.12) |
|||||||||||||
|
1 |
2 |
n |
|||||||||||||||
|
a2 |
a2 |
a2 |
|||||||||||||||
|
1 |
2 |
n |
где знаки выбираются в соответствии со знаками собственных чисел, а
|
a2 |
| c | |
. Числа а |
называются главными полуосями квадратичной формы |
|||
|
k |
||||||
|
k |
| k |
| |
||||
(если представлять (8.11) в виде гиперповерхности, то она, очевидно, пересекает k-ю координатную ось в точке аk). Если же в (8.11) c’ = 0, то (8.11) тоже обычно переписывают в виде:
|
x 2 |
x 2 |
x 2 |
0 , |
(8.13) |
|||||||||||
|
1 |
2 |
n |
|||||||||||||
|
a2 |
a2 |
a2 |
|||||||||||||
|
1 |
2 |
n |
|||||||||||||
|
где a2 |
1 |
. В этом случае гиперповерхность (8.13) называют п-мерным |
|||||||||||||
|
k |
| k | |
||||||||||||||
|
конусом 2-го порядка (очевидно – если точка |
, |
лежит на по- |
|||||||||||||
|
(x1, x2 |
, xn ) |
верхности (8.13), т. е. удовлетворяет этому уравнению, то и вся прямая
|
, |
|||
|
(tx1, tx2 |
,txn ) , t R, тоже лежит на этой поверхности (т. е. удовлетворяет |
этому уравнению при всех t, что и оправдывает название «конус»). Утверждение. Если у квадратичного уравнения от п переменных ква-
дратичная форма вырождена, то существует декартовая система координат, в которой это уравнение имеет вид:
|
2 |
2 |
2 |
(8.14) |
|
|
1x1 |
2 x2 |
… m xm |
2xm 1 |
где т – число ненулевых собственных чисел матрицы квадратичной формы данного уравнения.
56
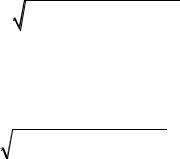
Доказательство. В декартовом базисе из собственных векторов матрицы А кв. формы из данного уравнения эта матрица становится диагональной, причем п–т элементов главной диагонали по условию равны нулю.
|
2 |
2 |
… |
||||
|
Поэтому данное уравнение в этом базисе имеет вид 1x1 |
2 x2 |
|||||
|
2 |
||||||
|
m xm |
b1x1 |
b2 x2 |
… bn xn c . Как и в случае с невырожденной мат- |
рицей, мы можем выделить полные квадраты, т. е. переписать данное уравнение в новой системе координат в виде
|
m |
m |
2 |
|||||||
|
2 |
bk |
c , |
|||||||
|
k xk |
bm 1xm 1 |
bm 2xm 2 |
… bn xn |
4 |
|||||
|
k 1 |
k 1 |
k |
|||||||
|
где по-прежнему |
bk |
, к = 1, 2, …, т. В подпространстве Х0, со- |
|||||||
|
xk |
xk |
2 k |
|||||||
ответствующем нулевому собственному числу, тоже введем новые декартовы координаты, а именно:
|
bm 1xm 1 bm 2 xm 2 |
… bn xn |
. |
||||||||
|
xm 1 |
2 |
2 |
2 |
2 |
||||||
|
bm 1 |
bm 2 |
… bn |
То есть в Х0 вместо старого декартова базиса из собственных векторов введем новый, тоже декартов и тоже из собственных векторов:
|
bm 1em 1 |
bm 2em 2 |
… bnen |
|||||
|
em 1 |
, |
||||||
|
2 |
2 |
2 |
|||||
|
bm 1 bm 2 |
… bn |
(деление на корень требуется для того, чтобы базис остался декартовым, то есть чтобы нормы его элементов остались равными единице). Осталь-
|
ные базисные вектора |
получим из ет+1, ет+2, …, еп при |
|||
|
em 2 |
, em 2 |
,… , en |
помощи ортогонализации. В этом базисе данное уравнение превратится
|
m |
|||||||
|
2 |
, где с’ – некоторая новая постоянная. Введем новую |
||||||
|
в k xk |
2xm 1 |
c |
|||||
|
k 1 |
|||||||
|
c |
, но ее по-прежнему будем обозна- |
||||||
|
переменную по формуле xm 1 |
xm 1 |
2 |
|||||
чать х΄΄. Исходное уравнение превратится в (8.14), и утверждение доказано. Предполагается, что читатели данного учебно-методического пособия
знакомы с элементами теории кривых и поверхностей второго порядка (т. е. задаваемых уравнением 2-го порядка.).
Теорема (классификация кривых 2-го порядка, данная Декартом). Лю-
бое уравнение 2-го порядка от двух переменных за счет преобразования к новой декартовой системе координат на плоскости приводится к одному из следующих 9 видов, и, следовательно, задает одну из следующих семи линий:
57
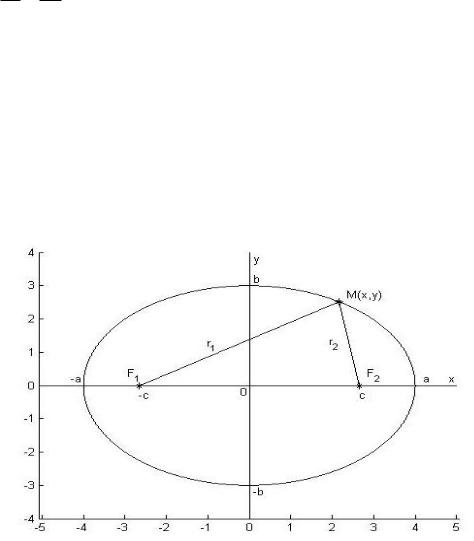
|
1) |
x2 |
y2 |
1 |
– эллипс (рис. 8.1); |
||||||||||||||
|
a2 |
b2 |
|||||||||||||||||
|
2) |
x2 |
y2 |
1 |
– гипербола (рис. 8.2); |
||||||||||||||
|
a2 |
||||||||||||||||||
|
b2 |
||||||||||||||||||
|
3) у2=2рх |
– парабола (рис. 8.3); |
|||||||||||||||||
|
x2 |
y2 |
0 |
x |
y |
0 и |
x |
y |
0 |
||||||||||
|
4) |
– две пересекающиеся прямые |
; |
||||||||||||||||
|
a2 |
b2 |
|||||||||||||||||
|
a |
b |
a |
b |
5)x2 y2 0 – одна точка – начало канонической системы координат; a b 22
|
6) |
x2 |
y2 |
1 |
– пустое множество точек, условно называемое «мни- |
||
|
a2 |
b2 |
|||||
|
мым эллипсом»; |
||||||
|
7) |
х2 = а2 |
– две параллельные прямые (х = а и х = –а); |
||||
|
8) |
х2 = 0 |
– одна прямая – ось ординат канонической системы; |
9) х2 = –1 – пустое множество точек, условно называемое «парой мнимых параллельных прямых» (название, разумеется, относится не к пустому множеству, а к типу уравнения).
Рис. 8.1. Эллипс
58
Рис. 8.2. Гипербола
Рис. 8.3. Парабола
Доказательство.
Как было доказано ранее, уравнение (8.10) за счет преобразования координат приводится к одному из видов (8.12), (8.13), (8.14), которые в слу-
|
x2 |
y2 |
1 |
x2 |
y2 |
0 |
2 |
|||||
|
чае двух переменных (8.8) принимают вид |
, |
, у = 2рх. |
|||||||||
|
a2 |
b2 |
a2 |
b2 |
||||||||
Перебирая всевозможные знаки у слагаемых в этих уравнениях (знак первого слагаемого всегда можно считать положительным), получим приведенные выше 9 типов уравнений. Что и требовалось доказать.
Заметим, что эти уравнения не могут быть переведены друг в друга линейными преобразованиями, что легко следует из геометрических соображений. Так, например, эллипс ограничен: |x| ≤ a, |y| ≤ b, а значит, его образ останется ограниченным при любом линейном преобразовании
59

плоскости, и он не может быть преобразован, например, в гиперболу. Аналогичные рассуждения верны и для любой другой пары из приведенных выше девяти уравнений.
Замечание. Определить вид кривой (8.8) можно, не вычисляя ее собственных чисел. Действительно, определитель матрицы ее квадратичной
|
формы |
A B |
AC B2 =λ λ |
, где λ |
и λ |
2 |
собственные числа этой мат- |
|
|
B C |
1 |
2 |
1 |
||||
рицы. Если ∆ > 0, то λ1 и λ2 – одного знака, и, следовательно, (8.8) задает эллипс или точку или пустое множество точек, если ∆ < 0, то (8.8) – гипербола или две пересекающиеся прямые, если ∆ = 0, то это – вырожденный случай, (8.8) задает параболу или две параллельные прямые или одну прямую или пустое множество точек. Равенство ∆ = 0 означает, что квадратичная форма в (8.8) есть полный квадрат: Ах2 + 2Вху + Су2 = (αх + βу)2.
Теорема (классификация поверхностей 2-го порядка, данная Эйлером).
Любое уравнение 2-го порядка от трех переменных (уравнение (82)) за счет преобразования к новой декартовой системе координат в пространстве приводится к одному из следующих 17 видов, и, следовательно, задает одну из следующих 14 поверхностей:
|
1) |
x2 |
y2 |
z2 |
1 |
– эллипсоид (рис. 8.4); |
||||||||||
|
a2 |
b2 |
c2 |
|||||||||||||
|
2) |
x2 |
y2 |
z2 |
1 |
– однополостный гиперболоид (рис. 8.5); |
||||||||||
|
a2 |
b2 |
||||||||||||||
|
c2 |
|||||||||||||||
|
3) |
x2 |
y2 |
z2 |
1 |
– двуполостный гиперболоид (рис. 8.6); |
||||||||||
|
a2 |
b2 |
||||||||||||||
|
c2 |
4)x2 y2 2z – эллиптический параболоид (рис. 8.7); a b2 2
|
5) |
x2 |
y2 |
2z |
– гиперболический параболоид или седлообраз- |
|||||||||||
|
a2 |
b2 |
||||||||||||||
|
ная поверхность (коротко – седло) (рис. 8.8); |
|||||||||||||||
|
6) |
x2 |
y2 |
z2 |
0 |
– конус второго порядка (рис. 8.9); |
||||||||||
|
a2 |
b2 |
c2 |
|||||||||||||
|
7) |
x2 |
y2 |
z2 |
1 |
– пустое множество точек, (или «мнимый эллипсоид); |
||||||||||
|
a2 |
|||||||||||||||
|
b2 |
c2 |
8)x2 y2 1 – эллиптический цилиндр (рис. 8.10); a2 b2
60
9)x y 1 – гиперболический цилиндр (рис. 8.11);
a2 b22 2
|
10) у2 = 2рх |
– параболический цилиндр (рис. 8.12); |
|||||||
|
x2 |
y2 |
0 |
x |
y |
0 и |
|||
|
11) |
– две пересекающиеся плоскости |
|||||||
|
a2 |
b2 |
|||||||
|
a |
b |
x y 0 ; a b
12)x2 y2 0 – одна прямая – ось аппликат канонической системы a b 22
координат;
13)x y 1 – пустое множество точек (условно называемое «мни-
a2 b222
мым эллиптическим цилиндром»);
|
14) |
х2 = а2 |
– две параллельные плоскости (х = а и х = –а); |
||||||
|
15) |
х2 |
= 0 |
– одна координатная плоскость YOZ канонической |
|||||
|
системы); |
||||||||
|
16) |
х2 |
= –1 |
– пустое множество точек (условно называемое «па- |
|||||
|
рой мнимых параллельных плоскостей»); |
||||||||
|
17) |
x2 |
y2 |
z2 |
0 – одна точка – начало канонической системы ко- |
||||
|
a2 |
b2 |
c2 |
||||||
ординат).
Доказательство.
Доказывается аналогично предыдущей теоремы.
|
Рис. 8.4. Эллипсоид |
Рис. 8.5. Однополостный |
|
гиперболоид |
61
|
Рис. 8.6. Двуполостный |
Рис. 8.7. Эллиптический |
|
гиперболоид |
параболоид |
|
Рис. 8.8. Гиперболический параболоид |
Рис. 8.9. Конус |
|
второго порядка |
|
Рис. 8.10. Эллиптический |
Рис. 8.11. Гиперболический |
|
цилиндр |
цилиндр |
62
Рис. 8.12. Параболический цилиндр
Замечание 1. Из перечисленных выше 14 поверхностей две поверхности – однополостный гиперболоид и гиперболический параболоид интересны тем, что они составлены из прямолинейных образующих. Действи-
|
тельно, уравнение |
x2 |
y2 |
z2 |
можно представить как произведение |
||||
|
a2 |
b2 |
c2 |
1 |
|||||
двух множителей:
|
x |
z |
y |
|||||||||||
|
t 1 |
, |
||||||||||||
|
c |
|||||||||||||
|
a |
b |
||||||||||||
|
y |
|||||||||||||
|
x |
z |
1 |
|||||||||||
|
1 |
|||||||||||||
|
c |
t |
b |
|||||||||||
|
a |
Каждая пара множителей задает пару пересекающихся плоскостей, т. е. прямую, целиком лежащую на поверхности гиперболоида, причем при разных t – разные прямые. Таким образом, через каждую точку такого гиперболоида проходят две прямые – по одной из первого и из второго семейства (они и называются прямолинейными образующими). При изменении t от –∞ до +∞ каждое семейство пробегает всю поверхность. (Инженер Шухов заметил, что если создать конструкцию из балок, расположенных вдоль прямолинейных образующих гиперболоида, то при ее нагрузке, балки будут работать на растяжение, а не на сжатие; поэтому такая конструкция прочнее стандартной, в которой балки устанавливают вертикально. Так Шуховым была сконструирована, например, знаменитая башня на Шаболовке, которая используется как телевизионная).
|
Аналогично, уравнение |
x2 |
y2 |
можно представить (двумя спо- |
|||
|
a2 |
b2 |
2z |
||||
собами) в виде произведения линейных множителей
63

|
x |
z |
tz, |
x |
z |
2t, |
|||||||||
|
c |
c |
. |
||||||||||||
|
a |
или a |
|||||||||||||
|
x |
z |
2 |
x |
z |
z |
. |
||||||||
|
c t |
c |
t |
||||||||||||
|
a |
a |
Как и выше, это два семейства прямолинейных образующих гиперболического параболоида.
Замечание 2. По формуле Тейлора любая функция от двух переменных, если она трижды непрерывно дифференцируема в окрестности точки М0(х0,у0), может быть представлена в этой окрестности в виде
|
z f (x, y) f (x , y ) + f |
(x x ) f |
M0 |
( y y ) … |
||||||||||||
|
o |
0 |
x |
M0 |
0 |
y |
0 |
|||||||||
|
2 f |
(x x )2 |
2 |
2 f |
(x x |
)( y y ) |
2 f |
( y y )2 |
o(r2 ), (8.18) |
|||||||
|
x2 |
M0 |
0 |
x y |
M0 |
0 |
0 |
y2 |
M0 |
0 |
||||||
где r 
уравнения (8.8). Поэтому (вместе с z из левой части) за счет преобразования координат оно может быть преобразовано в одно из уравнений вида 4) или 5) из предыдущей теоремы. Таким образом, с точностью до бесконечно малых более высокого порядка, чем r2, график всякой трижды дифференцируемой функции в окрестности любой точки представляет собой параболоид (эллиптический или гиперболический). Он называется соприкасающимся параболоидом. Если в качестве плоскости X’O’Y’ новой системы взять касательную плоскость, а начало новой системы O’ совместить с точкой касания М0, то в новой системе f(M0) = 0, первые частные производные в точке М0 тоже обратятся в 0 (т. е. точка М0 становится точкой, подозрительной на экстремум), и уравнение (8.18) примет вид: z = A’ x’2 +B’ x’ y’+ C’ y’2 + o(r2), где A’, B’, C’ – значения вторых частных производных в точке М0. Напоминаем, что это (приближенно) либо эллиптический параболоид, либо «седло», касающиеся плоскости X’O’Y’ (в анализе такие точки называются точками перевала). В первом случае экстремум есть, во втором – его нет. Доказан достаточный признак существования экстремума для функции двух переменных: если в точке, подозрительной на экстремум, D A C B 2 0, то экстремум есть, а при А’> 0 – мини-
мум, при A’< 0 – максимум, при D A C B 2 0 – экстремума нет, есть точка перевала. Аналогично можно исследовать и функции от большего числа переменных.
Замечание 3. Если квадратичная форма содержит лишь 2 переменные, то она задает эллиптический (при равных полуосях – прямой круговой),
64

гиперболический или параболический цилиндр. Касательная плоскость к поверхности S в точке М (х0, у0 ,z0), как известно, задается уравнением
|
F |
M0 |
x x |
F |
M0 |
x x |
F |
M0 |
z z |
0 , |
||
|
x |
0 |
y |
0 |
z |
0 |
||||||
где F(x, y, z) = 0 – уравнение поверхности S. Например, если поверхность S вляется эллипсоидом с полуосями a, b, c и каноническим уравнением
|
x2 |
y2 |
z2 |
1, то, как известно, нормаль к этой поверхности в точке М |
|||||||||||||||||||||||||||||||||
|
a2 |
b2 |
c2 |
0 |
|||||||||||||||||||||||||||||||||
|
с координатами (х0, у0, z0) имеет вид: |
||||||||||||||||||||||||||||||||||||
|
x2 |
y2 |
z2 |
||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
||||||||||||||||||||||||||||||||||
|
n |
a |
, |
b |
, |
c |
, |
||||||||||||||||||||||||||||||
|
M |
||||||||||||||||||||||||||||||||||||
|
x |
y |
z |
||||||||||||||||||||||||||||||||||
|
0 |
||||||||||||||||||||||||||||||||||||
|
x |
y |
z |
||||||||||||||||||||||||||||||||||
|
т. е. |
в данном случае n |
, |
, |
M |
, |
или, |
так как точка М0 лежит |
|||||||||||||||||||||||||||||
|
a2 |
b2 |
c2 |
0 |
|||||||||||||||||||||||||||||||||
на данном эллипсоиде, и, следовательно, удовлетворяет его уравнению, то
|
x |
y |
z |
|||||||||||||||||||||||||
|
n |
0 |
, |
0 |
, |
0 |
, а сама касательная плоскость имеет уравнение |
|||||||||||||||||||||
|
b2 |
c2 |
||||||||||||||||||||||||||
|
a2 |
|||||||||||||||||||||||||||
|
x0 |
x x |
y0 |
y y |
z0 |
z z |
0 |
0 . |
||||||||||||||||||||
|
a2 |
0 |
b2 |
0 |
c2 |
|||||||||||||||||||||||
|
x |
y |
z |
0 |
x2 |
y2 |
z2 |
|||||||||||||||||||||
|
Раскрывая скобки, получаем: |
0 |
x |
0 |
y |
z |
0 |
0 |
0 |
. Так как |
||||||||||||||||||
|
a2 |
b2 |
c2 |
|||||||||||||||||||||||||
|
b2 |
c2 |
a2 |
точка М0 лежит на данном эллипсоиде, и, значит, удовлетворяет его уравнению, то правая часть последнего равенства равна единице. Окончательно получаем, что уравнение касательной плоскости к эллипсоиду в точке М0,
лежащей на его поверхности, имеет вид: x0 x y0 y z0 z 1. a2 b2 c2
Если уравнение поверхности S содержит лишь 2 независимые переменные, например, имеет вид F(x, y)=0, то его касательная плоскость, в точке М0(х0, у0, z0), в соответствии с предыдущим изложением, задается
|
формулой |
F |
M0 |
(x x ) F |
M0 |
( y y ) 0 . Проекция этой плоскости |
||
|
x |
0 |
y |
0 |
||||
на плоскость XOY является касательной прямой к поверхности S в точке М0(х0, у0, z0), или, что то же, касательной прямой к кривой F(x, y) = 0 в точке
65

М0(х0, у0, z0). Для эллипса с полуосями a и b, заданного его каноническим
|
уравнением, касательная в точке М (х |
, у |
, z |
) такова: |
x0 x |
y0 y |
1. Анало- |
|
|
0 |
0 |
0 |
0 |
a2 |
b2 |
||
гично для гиперболы с полуосями a и b, заданной каноническим уравнением, касательная в ее точке М0(х0, у0, z0) определяется равенством
x0 x y0 y 1. a2 b2
Найдем теперь уравнение касательной к параболе, заданной канонически формулой у2 = 2рх. Нормаль к ней в точке М0(х0, у0, z0) (после сокращения на 2) такова: (у0, –рх0). Значит, направляющий вектор касательной имеет вид: (рх0, у0). Отсюда уравнение этой касательной таково: р(х – х0) + + (у – у0) = 0. Раскрывая скобки, находим: рх + у = рх0 + у0. Учитывая, что точка М0 тоже лежит на касательной и, следовательно, удовлетворяет ее уравнению, окончательно находим: рх + у = 0, или у = –рх.
Итак, следует запомнить, что если эллипс или гипербола заданы своими каноническими уравнениями, и их полуоси равны a и b, а парабола задана канонически с параметром р, то в точке М0(х0, у0, z0) на этой кривой касательная к ней задается соответствующим уравнением
|
x0 x |
y0 y |
z0 z |
1, |
x0 x |
y0 y |
z0z |
1, |
y px . |
|||||
|
a2 |
b2 |
c2 |
a2 |
b2 |
c2 |
||||||||
Замечание 4. Приведению данного уравнения 2-го порядка от двух и трех переменных к главным осям и выяснению их геометрического содержания посвящен разбор 5-го типового задания в разд. 9 («Решение типовых примеров»).
66
Свойства собственных векторов линейных операторов (преобразований)
1. Собственные векторы линейного преобразования, принадлежащие различным собственным значениям, линейно независимы.
Аналогичное утверждение было доказано для собственных векторов матрицы (см. свойство 1).
2. Все собственные векторы линейного преобразования , принадлежащие одному собственному значению, совместно с нулевым вектором образуют линейное подпространство, инвариантное относительно преобразования
. Такое линейное подпространство называется собственным для преобразования
.
В самом деле, условие (9.5) можно записать в виде , где
— тождественное преобразование. Множество векторов
, удовлетворяющих последнему равенству, составляет ядро линейного преобразования
, т.е. является линейным подпространством
(собственное подпространство, отвечающее собственному значению
). Покажем, что это подпространство инвариантно относительно преобразования
. Действительно, любой вектор
в силу равенств
отображается в коллинеарный ему вектор
, также принадлежащий
.
3. Для собственного значения линейного преобразования
существует цепочка инвариантных подпространств
(9.8)
где ;
— некоторое натуральное число
.
Все перечисленные в цепочке (9.8) множества , являются линейными подпространствами по свойству ядра линейного преобразования. Каждое из подпространств
инвариантно относительно преобразования
, поскольку для любого вектора
его образ
, так как в силу перестановочности многочленов от одного и того же линейного преобразования (см. пункт 2 замечаний 9.3)
так как согласно определения ядра оператора.
Докажем включение . Если
, то
, при этом очевидно, что
то есть
Остальные включения доказываются аналогично.
Из цепочки (9.8) “расширяющихся” подпространств следует, что их размерности не убывают
поэтому в силу конечномерности пространства существует такое
, что
, т.е.
. Покажем, что дальнейшего “увеличения” подпространств нет, т.е.
для любого натурального
. Предположим противное. Пусть
и для некоторого
пространства не совпадают:
, то есть существует вектор
, который не принадлежит пространству
. Обозначим
. Тогда, с одной стороны,
, так как
, поскольку
. С другой стороны,
, так как
, поскольку
. Следовательно, и
и
одновременно, что противоречит предположению
.
Таким образом, в цепочке (9.8) размерности пространств , возрастают. Поэтому
.
Корневым подпространством линейного преобразования для собственного значения
называется линейное подпространство
с наименьшим натуральным показателем
, для которого
.
4. Если — собственное значение линейного преобразования
, то пространство
можно представить в виде прямой суммы
, где
— корневое подпространство, а
— инвариантное относительно
подпространство, в котором нет собственных векторов, принадлежащих собственному значению
.
В самом деле, покажем, что пересечение этих подпространств есть нулевой вектор: . Выберем вектор
. Так как вектор
, то существует такой вектор
, что
. Поскольку
, то
. Тогда
. Следовательно, вектор
, но
, так как
— корневое подпространство. Значит,
то есть
По теореме 9.1 о размерности ядра и образа получаем, что . Следовательно, пространство
можно представить в виде прямой суммы подпространств
(см. признаки прямых сумм подпространств).
Докажем, что в нет собственных векторов, принадлежащих собственному значению
. Действительно, пусть
— собственный вектор, соответствующий собственному значению
. Тогда
и в силу (9.8)
. Подпространство
имеет с
только один общий вектор (нулевой). Поэтому
, так как
. Инвариантность подпространства
следует из перестановочности операторов
и
(см. пункт 2 замечаний 9.3). В самом деле, для любого вектора
существует прообраз
. Поэтому в силу перестановочности операторов
поскольку и
. Таким образом, инвариантность подпространства
доказана, так как
.
Теорема (9.5) о разложении пространства в сумму корневых подпространств
Если все различные корни характеристического уравнения линейного преобразования
являются его собственными значениями, то пространство
можно разложить в прямую сумму инвариантных (корневых) подпространств:
(9.9)
где — корневое подпространство, соответствующее собственному значению
.
В самом деле, по свойству 4 можно “отщепить” корневое подпространство , т.е. представить пространство
в виде прямой суммы инвариантных подпространств
, причем в
нет собственных векторов, принадлежащих собственному значению
. В пространстве
определено сужение
преобразования
. Применяя свойство 4 к сужению
, аналогичным образом можно “отщепить” корневое подпространство
, т.е. представить пространство
в виде прямой суммы инвариантных подпространств:
. Этот процесс следует продолжить до тех пор, пока не исчерпаются все корни характеристического уравнения.
Следствие. Если все различные корни характеристического уравнения линейного преобразования
являются его собственными значениями, то существует базис пространства
, в котором матрица
линейного преобразования имеет блочно-диагональный вид
где — матрицы сужений
, преобразования
на корневые подпространства.
Согласно следствию из теоремы 9.2, такой базис можно получить, записывая последовательно базисы корневых подпространств (9.9).
Алгебраическая и геометрическая кратности собственных значений
Алгебраической кратностью собственного значения линейного оператора (преобразования)
называется кратность корня
характеристического многочлена
(или, что то же самое, кратность корня характеристического уравнения
).
Геометрической кратностью собственного значения линейного оператора (преобразования)
называется размерность собственного подпространства
, соответствующего этому собственному значению.
Теорема 9.6 о кратностях собственных значений оператора. Геометрическая кратность собственного значения не превосходит его алгебраической кратности.
Представим пространство в виде прямой суммы
(см. свойство 4) и обозначим
. Выбрав базис пространства
, дополним его до базиса всего пространства. В этом базисе, согласно следствию теоремы 9.5, матрица
преобразования
будет иметь блочно-диагональный вид
, где квадратная матрица
порядка
является матрицей сужения
преобразования
на подпространство
, а матрица
является матрицей сужения
. Характеристический многочлен матрицы
имеет вид (см. определитель блочно-диагональной матрицы)
где — многочлены степеней
и
соответственно. Так как сужение
не имеет собственных значений, отличных от
, то
, в силу того, что
и основной теоремы алгебры. Поскольку сужение
не имеет собственных векторов, принадлежащих собственному значению
, то
. Следовательно,
-алгебраическая кратность собственного значения
. Тогда утверждение теоремы следует из включения (9.8):
, так как
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Теорема 5.5. Пусть собственные значения λ1, …, λr линейного оператора А попарно различны. Тогда система соответствующих им собственных векторов е1, … , еr линейно независима.
◄ Доказательство опирается на метод математической индукции, проводимый по количеству r векторов в системе. При r = 1 утверждение теоремы верно, так как линейная независимость системы из одного вектора означает, что этот вектор ненуле-вой, а собственный вектор, согласно определению 5.3, является ненулевым.
Пусть утверждение верно при r = m, т.е. для произвольной системы из т собственных векторов e1, …, еm. Добавим к системе векторов еще один собственный вектор em+1, отвечающий собственному значению λm+1, и докажем, что расширенная таким способом система векторов останется линейно независимой. Рассмотрим произвольную линейную комбинацию полученной системы собственных векторов и предположим, что она равна нулевому вектору:
α1е1 + … + αmеm + αm+1em+1 = 0. (5.7)
К равенству (5.7) применим линейный оператор А и в результате получим еще одно векторное равенство
α1Ае1 +… + αmАеm + αm+1Aem+1 = 0.
Учтем, что векторы e1, …, em+1 являются собственными:
α1λ1e1 + … + αmλmem + αm+1λm+1em+1 = 0. (5.8)
Умножив равенство (5.7) на коэффициент λm+1 и вычтя его из равенства (5.8), получим линейную комбинацию векторов е1, …, em, равную нулевому вектору:
α1(λ1 – λm+1)e1 + … + αm(λm – λm+1)em = 0.
Вспоминая, что система векторов e1, …, em, по предположению, линейно независима, делаем вывод, что у полученной линейной комбинации все коэффициенты равны нулю:
αk (λk – λm+1) = 0, k = 1,m. (5.9)
Поскольку все собственные значения λi попарно различны, то из равенств (5.9) следует, что α1 = α2 = … = αm = 0. Значит соотношение (5.7) можно записать в виде αm+1em+1 = 0, а так как вектор em+1 ненулевой (как собственный вектор), то αm+1 = 0. В итоге получаем, что равенство (5.7) выполняется лишь в случае, когда все коэффициенты ai, i = 1, m+1, равны нулю. Тем самым мы доказали, что система векторов e1, …, em, em+1 линейно независима. ►
Теорема 5.6. Матрица линейного оператора А, действующего в линейном пространстве, в данном базисе является диагональной тогда и только тогда, когда все векторы этого базиса являются собственными для оператора А.
◄ Пусть А – матрица линейного оператора А в базисе b = (b1 … bn). Согласно определению 4.4, j-м столбцом матрицы А является столбец координат вектора Abj.
Если матрица А является диагональной, то произвольно взятый ее j-и столбец имеет вид (0 … 0 μj 0 … 0)T (единственный ненулевой элемент может стоять на j-м месте). Для вектора Abj получаем представление
Abj = b(0 … 0 μj 0 … 0)T = μjbj,
которое как раз и означает, что вектор bj является собственным с собственным значением μj. Значит, все базисные векторы являются собственными, а все диагональные элементы матрицы А являются собственными значениями.
Верно и обратное. Если каждый вектор bj является собственным для линейного оператора А и ему отвечает собственное значение λj, то
Abj = λjbj = b(0 … 0 λj 0 … 0)T,
т.е. в матрице оператора А в этом базисе равны нулю все элементы, кроме диагональных, а диагональный элемент в j-м столбце равен λj. ►
Следствие 5.1. Если характеристическое уравнение линейного оператора, действующего в n-мерном линейном пространстве, имеет n попарно различных действительных корней, то существует базис, в котором матрица этого оператора является диагональной.
◄ Каждый действительный корень характеристического урав-нения является собственным значением линейного оператора.
Каждому из таких корней можно сопоставить хотя бы по одно-му собственному вектору. Система выбранных таким образом векторов, согласно теореме 5.5, является линейно независимой, а так как количество n векторов в ней равно размерности линейного пространства, она является базисом. Этот базис состоит из собственных векторов. Согласно теореме 5.6, матрица линейного оператора в этом базисе имеет диагональный вид. ►
Следствие 5.2. Если характеристическое уравнение квадратной матрицы порядка n имеет n попарно различных действительных корней, то эта матрица подобна некоторой диагональной.
◄ Пусть матрица А порядка n имеет n различных действительных корней. Выберем произвольное n-мерное линейное пространство L, зафиксируем в нем некоторый базис b = (b1 … bn) и рассмотрим линейный оператор А, матрицей которого в базисе b является матрица А. По теореме 5.6 существует базис, в котором матрица A’ этого оператора диагональна. Согласно теореме 4.6, матрицы А и А’ подобны. Отметим, что на диагонали матрицы А’ стоят все попарно различные собственные значения матрицы А. ►
Если характеристическое уравнение линейного оператора имеет кратные действительные корни, то такой линейный оператор может иметь диагональную матрицу в некотором базисе, но так бывает не всегда.
Пример 5.7. В двумерном линейном пространстве (например, в R2) рассмотрим линейные операторы, матрицы которых в некотором базисе имеют вид
Характеристические уравнения этих операторов совпадают и имеют вид (λ – 2)2 = 0. Поэтому оба оператора имеют единственное собственное значение λ = 2 кратности 2. Матрица первого линейного оператора уже имеет диагональный вид, т.е. исходный базис состоит из собственных векторов этого оператора. Можно показать, что любой ненулевой вектор для этого оператора является собственным и потому для него любой базис есть базис из собственных векторов. У второго линейного оператора все собственные векторы отвечают собственному значению 2, но собственное подпространство линейного оператора для этого собственного значения одномерно. Следовательно, найти два линейно независимых собственных вектора для этого линейного оператора невозможно и базиса из собственных векторов не существует. #
При изучении заданного линейного оператора появляется мысль выбрать такой базис, в котором его матрица выглядит наиболее просто. Из вышеизложенного следует, что в определенных ситуациях линейный оператор в некотором базисе имеет диагональную матрицу. Чтобы это было так, оператор должен иметь базис из собственных векторов. Изменение бази-са вызывают замену матрицы оператора подобной ей. Замену матрицы А диагональной матрицей А’, подобной А, называют приведением матрицы А к диагональному виду.
Задача приведения матрицы к диагональному виду может рассматриваться самостоятельно, вне зависимости от изучения конкретного линейного оператора. Она состоит в подборе для данной матрицы А такой невырожденной матрицы Р, что матрица А’ = Р-1АР является диагональной.
Пример 5.8. Выясним, можно ли привести к диагональному виду матрицу
Если это возможно, найдем соответствующую диагональную матрицу и матрицу Р преобразования подобия.
Найдем собственные значения данной матрицы. Ее характеристическое уравнение имеет вид
Раскрывая определитель и решая характеристическое уравнение, находим его корни: λ1 = -1, λ2 = λ3 = 1. Видим, что имеются два собственных значения, причем одно из них кратности 2.
Матрицу можно привести к диагональному виду, если сумма размерностей всех собственных подпространств (в данном случае матрицы, см. замечание 5.1) равна размерности линейного пространства, в нашем случае – трем. Отметим без доказательства, что размерность собственного подпространства линейного оператора (матрицы) не превышает кратности соответствующего собственного значения. Проверим это на собственном подпространстве, отвечающем собственному значению λ1, для чего вычислим ранг матрицы А – λ1Е:
Значит, размерность первого собственного подпространства равна 3 – 2 = 1.
Аналогично находим размерность второго собственного подпространства. Вычисляем ранг соответствующей матрицы А – λ2Е:
Размерность второго собственного подпространства равна 3 – 1 = 2.
Сумма размерностей обоих подпространств равна трем. Следовательно, базис из собственных векторов существует. Он собирается из базисов собственных подпространств. Чтобы его построить, нужно для каждого собственного значения А найти фундаментальную систему решений СЛАУ (А – λЕ)х = 0. Фундаментальная система решений представляет собой базис линейного пространства решений однородной СЛАУ, в нашем случае собственного подпространства матрицы.
Для собственного значения λ1 = – 1 получаем систему
Ранг матрицы системы равен двум, поэтому фундаментальная система состоит из одного столбца. Например, можно взять столбец (3 5 6)T.
Для собственного значения λ2 = 1 получаем систему
Ранг матрицы системы равен единице, поэтому фундаментальная система состоит из двух столбцов. Например, фундаментальную систему решений составляют столбцы (2 1 0)T и (0 1 2)T.
Таким образом, базисом из собственных векторов матрицы А является система
а сама матрица А подобна диагональной матрице
Отметим, что матрица Р преобразования подобия представляет собой матрицу перехода из одного базиса в другой, т.е. ее столбцы представляют собой столбцы координат векторов нового базиса, записанные в старом. В нашем случае столбцы матрицы Р определяются векторами “нового” базиса e1, e2, е3:
Пример 5.9. Линейный оператор, действующий в трехмерном линейном пространстве, в некотором базисе имеет матрицу
Можно ли, изменив базис, привести матрицу этого оператора к диагональному виду?
Составляем характеристическое уравнение линейного оператора:
Раскрывая определитель, получаем
λ3 – 4λ2 + 5λ – 2 = 0.
Корнями характеристического уравнения являются числа λ1 = 1 кратности 2 и λ2 = 2. Для определения размерностей собственных подпространств линейного оператора, отвечающих этим двум значениям, вычислим ранги соответствующих матриц:
Оба собственных подпространства линейного оператора, отвечающие двум собственным значениям, имеют размерность 3 – 2 = 1. Поэтому линейно независимая система из собственных векторов данного оператора может содержать максимум два вектора и по соображениям размерности не может быть базисом.
Дополнение 5.1. Жорданова нормальная форма
При исследовании линейного оператора, действующего в линейном пространстве, желательно выбирать базис так, чтобы матрица линейного оператора имела наиболее простой вид. Если линейный оператор имеет базис из собственных векторов, то его матрица в некотором базисе является диагональной (теорема 5.6). В частности, это верно в случае, когда все корни характеристического уравнения линейного оператора действительные и различные (см. следствие 5.1).
Матрица диагонального вида – наиболее простая, но не всякий линейный оператор может иметь такую матрицу (см. пример 5.7). Линейный оператор, который не может быть приведен к диагональному виду (т.е. его матрица ни в одном базисе не является диагональной), имеет характеристическое уравнение, у которого есть комплексные или кратные действительные корни.
Приведение матрицы линейного оператора к простому виду связано со структурой его инвариантных подпространств.
Теорема 5.7. Пусть Н1 и H2 – инвариантные подпространства линейного оператора А: L → L, причем Н1 ⊕ Н2 = L. Тогда в некотором базисе b матрица А этого оператора А имеет блочно-диагональный вид:
где 0 обозначает нулевые блоки соответствующего типа, а квадратные блоки H1, Н2 имеют порядки dimH1 и dimН2 соответственно.
◄ Выберем в линейных подпространствах H1 и Н2 базисы f = (f1 … fl) и g = (g1 … gk). В совокупности эти два базиса дают базис b всего пространства L (см. доказательство теоремы 2.5). Так как H1 – инвариантное подпространство линейного оператора А, вектор Аfi, i = 1,l, попадает в H1 и поэтому является линейной комбинацией системы векторов f. Другими словами, координаты вектора Afi в базисе b, соответствующие векторам равны нулю. Аналогично координаты векторов Agj, j = 1,k, в базисе b, соответствующие векторам fi, также равны нулю. Значит, в базисе b матрица А оператора А имеет вид (5.10). ►
Следствие 5.3. Если H1, … , Нs – инвариантные подпространства линейного оператора А: L → L, причем Н1 ⊕ … ⊕ Hs = L, то в некотором базисе матрица оператора А имеет блочно-диагональный вид
где квадратный блок Hi имеет порядок dimHi, i = 1,s, а остальные блоки являются нулевыми.
◄ Выберем в каждом из инвариантных подпространств Hi базис. Все базисы в совокупности образуют базис пространства L, в котором оператор А будет иметь матрицу указанного вида. ►
Остановимся на случае, когда характеристическое уравне-ние линейного оператора имеет лишь простые корни, среди которых, вообще говоря, есть и комплексные. Так как характеристическое уравнение линейного оператора имеет действительные коэффициенты, каждому комплексному корню α + iβ этого уравнения соответствует комплексно сопряженный корень α – iβ той же кратности [I].
Теорема 5.8. Любой паре комплексно сопряженных корней характеристического уравнения линейного оператора соответствует двумерное инвариантное подпространство этого оператора.
◄ Зафиксируем в линейном пространстве L некоторый базис b и рассмотрим матрицу А линейного оператора А в этом базисе. Пусть λ = α + iβ, β ≠ 0, – комплексный корень характеристического уравнения линейного оператора А. Тогда det(A – λЕ) = 0 и система линейных алгебраических уравнений (СЛАУ) (А – λЕ)х = 0 с комплексными коэффициентами имеет ненулевое решение x, которое можно записать в виде х = u + iϑ, разделив действительные и мнимые части у элементов столбца х.
Столбец ϑ не является нулевым, так как в противном случае х = u, и Аu = λu. Мы видим, что действительные элементы столбца Аu получаются из действительных элементов столбца и умножением на комплексное число λ, а это возможно лишь в случае, когда u = 0. Но это заключение противоречит выбору столбца х.
Столбцы u и ϑ линейно независимы. Действительно, если они линейно зависимы, то μu + vϑ = 0, где одно из чисел μ и v отлично от нуля. Мы можем утверждать, что μ ≠ 0, так как в противном случае vϑ =0. Но ϑ ≠ 0, значит v = 0. Получилось, что оба коэффициента μ и v являются нулевыми.
Итак, μ ≠ 0, и поэтому u = kϑ, где к = – v/μ ∈ R. Следовательно, x = u + iϑ = (k + i)ϑ. Так как Ах = λх, то А((k + i)ϑ) = λ(k + i)ϑ, и мы, сокращая равенство на k + i, находим, что Aϑ = λϑ. Как мы уже знаем, для комплексного λ такое равенство невозможно.
В равенстве Ах = λх сделаем замены λ = α + iβ, х = u + iϑ: А(u + iϑ) = (α + iβ) (u + iϑ). Разделив действительные и мнимые части, получим два матричных уравнения
Аu = αu – βϑ, Aϑ = βu + αϑ. (5.11)
Рассмотрим векторы u и ϑ, которые в базисе b имеют столбцы координат u и ϑ. Эти векторы образуют линейно независимую систему, так как линейно независимы столбцы u и ϑ. Кроме того, Аu = αu – βϑ, Aϑ = βu + αϑ, так как в матричной записи это совпадает с (5.11). Полученные соотношения означают, что двумерное линейное подпространство Н = span{u, ϑ} является инвариантным подпространством линейного оператора А. ►
Для любых действительных α и β обозначим
Теорема 5.9. Если характеристическое уравнение линей-ного оператора А: L → L имеет р различных пар комплексно сопряженных корней αj ± iβj, j = 1,p, и q различных действительных корней μj, j = 1,q, 2p + q = n = dimL, то в некотором базисе матрица А этого оператора А имеет вид
◄ Каждой паре комплексно сопряженных корней αj ± iβj характеристического уравнения соответствует двумерное инвариантное подпространство Pj оператора А с базисом uj, ϑj (см. доказательство теоремы 5.8). Каждому собственному значению μj соответствует одномерное собственное подпространство Qj линейного оператора А. Можно показать, что все эти подпространства образуют прямую сумму, так как пе-ресечение любой пары таких подпространств содержит лишь нулевой вектор. Учитывая, что сумма размерностей этих подпространств равна 2р + q = n = dimL, заключаем, что
P1⊕ … ⊕ Pp ⊕ Q1 ⊕ … ⊕ Qq = L.
Согласно следствию 5.3, в некотором базисе матрица А оператора А имеет блочно-диагональный вид, причем каждый диагональный блок представляет собой матрицу ограничения оператора А на соответствующее инвариантное подпространство. В случае двумерного подпространства Pj в базисе uj, ϑj эта матрица равна C(αj,βj) (см. (5.12)), а в случае одномерного инвариантного пространства Qj такой блок есть просто число, представляющее собой собственное значение μj. ►
Следствие 5.4. Если характеристическое уравнение квадратной матрицы А порядка n имеет р различных пар комплексно сопряженных корней αj ± iβj, j = 1,p, р, и q различных действительных корней μj, j = 1,q, 2p + q = n, то эта матрица подобна некоторой блочно-диагональной матрице вида (5.13).
◄ Указанная матрица А является матрицей некоторого линейного оператора А, характеристическое уравнение которого имеет различные корни. Согласно теореме 5.9, в некотором базисе оператор А имеет матрицу А’ блочно-диагонального вида (5.13) . Матрицы А’ и А подобны как матрицы одного оператора. ►
Если характеристическое уравнение оператора имеет кратные корни, действительные или комплексные, то инвариантные подпространства такого оператора имеют более сложную структуру. Рассмотрим два типа специальных матриц.
Для произвольного действительного числа μ введем обозначение матрицы порядка s:
У этой матрицы все диагональные элменты равны ц, над главной диагональю расположены элементы 1, а все остальные равны нулю. В случае s = 1 рассматриваемая матрица сводится к единственному числу μ.
Для любого комплексного числа λ = α + iβ (β ≠ 0) введем обозначение блочной матрицы порядка 2r:
где C1(α,β) = С(α,β) – квадратная матрица порядка 2 вида (5.12). Все остальные блоки также являются квадратными матрицами порядка 2, Е обозначает единичную матрицу, а 0 – нулевую.
Блочно-диагональную матрицу вида
где αj, βj (j = 1,m) и μl (l = 1,k) – действительные числа, называют жордановой, ее диагональные блоки – жордановыми клетками. Жорданову матрицу А’, подобную данной матрице А, называют жордановой нормальной формой (жордановой канонической формой) матрицы А.
Жорданова нормальная форма определяется неоднозначно, так как подходящими преобразованиями подобия можно пере-ставлять диагональные блоки (перестановка блоков в матрице линейного оператора вызывается перёстановкой соответствую-щих векторов базиса). Среди жордановых клеток жордановой матрицы могут встречаться одинаковые. Однако можно утвер-ждать, что если две жордановы матрицы подобны, то одна получается из другой перестановкой диагональных блоков. Это объясняется тем, что каждая жорданова клетка вида Jj(μj) определяется собственным значением μj матрицы, а жорданова клетка Cj (αj, βj) – комплексным корнем λj = αj + iβj характеристического уравнения матрицы. Частным случаем жорда-новой матрицы является матрица вида (5.13) (когда все корни характеристического уравнения простые) и диагональная матрица (все корни действительные, а все жордановы клетки имеют порядок 1).
Теорема 5.10. Каждая матрица имеет жорданову нормальную форму.
Вопросы и задачи
- Найдите собственные векторы и собственные значения линейного оператора, имеющего в некотором базисе матрицу:
- В примерах в), д)-к) постройте базис из собственных векторов и запишите матрицу линейного оператора в этом базисе.
- Выясните, приводится ли к диагональному виду данная матрица:
- Пусть линейный оператор, действующий в n-мерном линейном пространстве, имеет в некотором базисе матрицу А. Пусть λ1, λ2, …, λn – собственные значения этого оператора. Найдите собственные значения и собственные векторы линейного оператора, матрицей которого в том же базисе является: а) A2; б) А-1
- В линейном пространстве квадратных матриц порядка 2 содержится линейная оболочка матриц Аk, k = 0,100. Найдите размерность этой линейной оболочки для матрицы
- Докажите, что для каждого собственного значения А линейного оператора λ имеет место равенство £(А, А) = ker(A – λI).
- Докажите, что кратность собственного значения Л линейного оператора А не меньше размерности соответствующего собственного подпространства £(А, λ) этого оператора.
- Докажите теорему Кэли – Гамильтона в случае квадратной матрицы, все корни характеристического уравнения которой действительны и попарно различны.
- Сформулируйте теорему Кэли – Гамильтона для линейных операторов и доказать ее в случае линейного оператора, имеющего базис из собственных векторов.
- Докажите, что поворот вектора на плоскости на угол 2φ можно реализовать за три последовательно выполняемых шага: поворот вектора на угол φ; растяжение с коэффициентом 2 cosφ; прибавление вектора, противоположного исходному.
- Докажите, что любой линейный оператор в пространстве V3 имеет собственный вектор.
- Приведите пример линейного оператора, не имеющего собственных векторов. Какой может быть размерность линейного пространства, в котором есть такие операторы?
- Докажите, что для любого ненулевого вектора с ∈ V3 линейный оператор А: V3 → V3, определяемый соотношением Ах = x × с, имеет единственное собственное значение, равное нулю.
- Пусть Н – линейное подпространство евклидова пространства Ε. Рассмотрим линейный оператор ортогонального проектирования Рх = х°, где х = х° + x⊥, х° ∈ H, х⊥ ∈ Н⊥, – разложение произвольного вектора х на его ортогональную проекцию х° и ортогональную составляющую x⊥. Найдите собственные значения и собственные векторы этого линейного оператора.
- Докажите, что нуль является собственным значением любой кососимметрической матрицы нечетного порядка.
-
Линейные операции над векторами
-
Базис. Cкалярное произведение
-
Векторное и смешанное произведения векторов
-
Декартова система координат. прямая на плоскости
-
Плоскость в пространстве
-
Прямая в пространстве
-
Кривые второго порядка — I
-
Кривые второго порядка — II
-
Поверхности второго порядка
-
Матрицы и операции с ними
-
Обратная матрица
-
Ранг матрицы
-
Системы линейных алгебраических уравнений
-
Свойства решений однородных и неоднородных СЛАУ
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Размерность собственного подпространства
|
||
07/01/10 |
Докажите, что кратность собственного значения линейного оператора не меньше размерности соответствующего собственного подпространства этого оператора. (Оффтоп) Собственное подпространство Пусть имеются с. з. Я понимаю, что тут со строгостью проблемы. Но не понимаю, с чем вообще можно связать кратность , чтобы сделать нормальное доказательство?
|
||
|
|
|||
|
caxap |
Re: Размерность собственного подпространства
|
||
07/01/10 |
Может как-то надо использовать жорданову форму?
|
||
|
|
|||
|
Xaositect |
Re: Размерность собственного подпространства
|
||
06/10/08 |
Ну, если Вы жорданову форму уже знаете, то кратность – это кол-во Ну а проще можно сказать, что ограничение оператора на собственное пространство есть
|
||
|
|
|||
|
Ales |
Re: Размерность собственного подпространства
|
|
20/12/09 |
Рассмотрите оператор в следующем базисе: базис собственного пространства + базис его дополнения.
|
|
|
|
|
ewert |
Re: Размерность собственного подпространства
|
||
11/05/08 |
Это — весьма нетривиальное утверждение, и ни из каких общих соображений так просто не следует. Из жордановой формы следует, разумеется, мгновенно, однако надо ещё доказать существование такой формы. Собственно, всё сводится вот к чему. Собственное подпространство — это часть корневого подпространства, т.е. такого, каждый элемент которого обнуляется хоть какой-то степенью
|
||
|
|
|||
|
caxap |
Re: Размерность собственного подпространства
|
||
07/01/10 |
кратность – это кол-во Ух ты. А в моей книжке (Канатников, Крищенко) просто конец параграфа про жордановы формы замят и этого факта я не знал. Спасибо. Тогда всё просто. а у ограничения л-н с.в. А что такое л-н? Рассмотрите оператор в следующем базисе: базис собственного пространства + базис его дополнения. А как это можно связать с кратностью? (Оффтоп) Это как Пойа в “Как решать задачу” писал, что если, например, нужно доказать параллельность двух прямых в геометрической задаче, надо вообще подумать — а какие я теоремы знаю, которые заканчиваются на “тогда прямые параллельны” или наоборот — у каких теорем начало совпадает с условием задачи. (Оффтоп) ewert , если четсно, ничего не понял
|
||
|
|
|||
|
Ales |
Re: Размерность собственного подпространства
|
|
20/12/09 |
А как это можно связать с кратностью? Если “кратность” – это кратность корня характеристического многочлена, то надо посчитать характеристический многочлен.
|
|
|
|
|
ewert |
Re: Размерность собственного подпространства
|
||
11/05/08 |
Рассмотрите оператор в следующем базисе: базис собственного пространства + базис его дополнения. Ничего не выйдет — это пара подпространств, вообще говоря, не приводящая (и не может быть выбрана таковой).
|
||
|
|
|||
|
Ales |
Re: Размерность собственного подпространства
|
|
20/12/09 |
Рассмотрите оператор в следующем базисе: базис собственного пространства + базис его дополнения. Ничего не выйдет — это пара подпространств, вообще говоря, не приводящая (и не может быть выбрана таковой). “не приводящая” к чему?
|
|
|
|
|
ewert |
Re: Размерность собственного подпространства
|
||
11/05/08 |
“не приводящая” к чему? Два или несколько подпространств называются приводящими, если всё пространство есть их прямая сумма и при этом каждое из них инвариантно. В этом (и только в этом) случае матрица оператора в соответствующем базисе принимает блочно-диагональный вид.
|
||
|
|
|||
|
Ales |
Re: Размерность собственного подпространства
|
|
20/12/09 |
“не приводящая” к чему? Два или несколько подпространств называются приводящими, если всё пространство есть их прямая сумма и при этом каждое из них инвариантно. В этом (и только в этом) случае матрица оператора в соответствующем базисе принимает блочно-диагональный вид. Чтобы решить этот вопрос, не обязателен блочно-диагональный вид.
|
|
|
|
|
ewert |
Re: Размерность собственного подпространства
|
||
11/05/08 |
Ведь надо считать определитель, достаточно блочно-треугольный вид. Вот последний термин для меня загадка. Но, тем не менее — возражение снимаю. Вы правы, достаточно иметь подбазис в собственном подпространстве. Чего-то я не в ту сторону задумался.
|
||
|
|
|||
|
Ales |
Re: Размерность собственного подпространства
|
|
20/12/09 |
Вот последний термин для меня загадка. Я его сам придумал.
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |










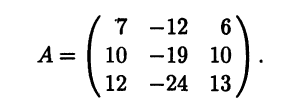
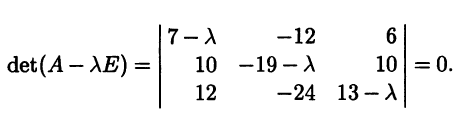
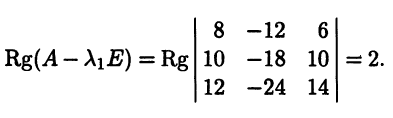
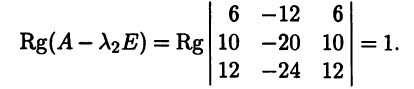
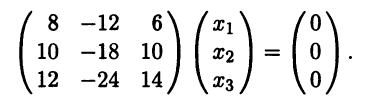
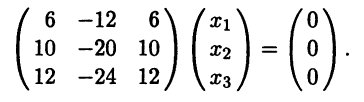
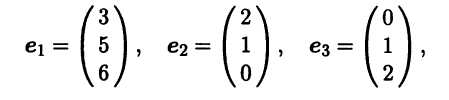
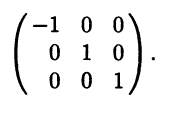
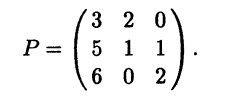
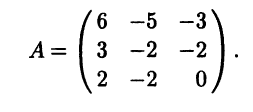
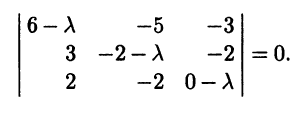
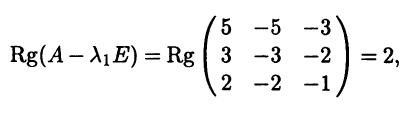
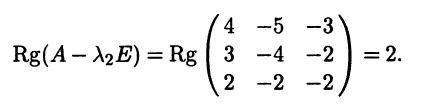
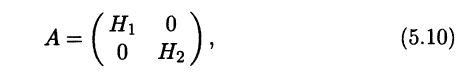
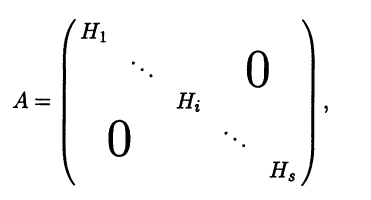
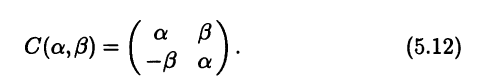
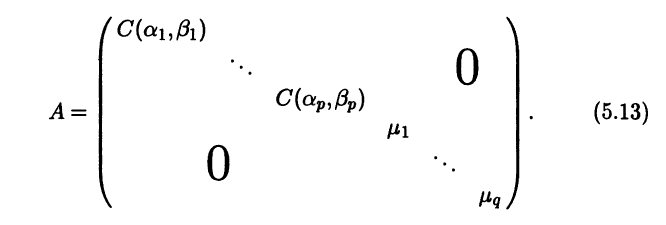
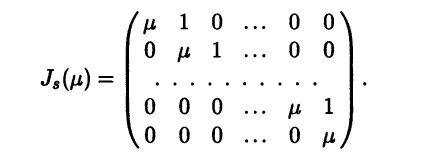
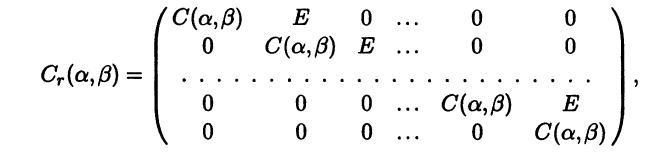
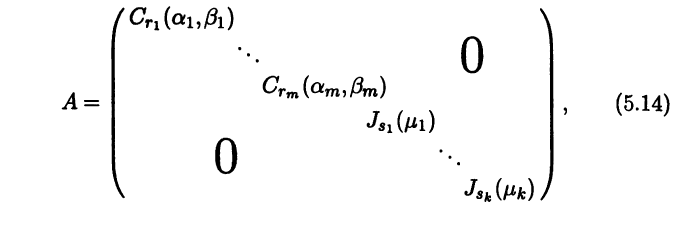
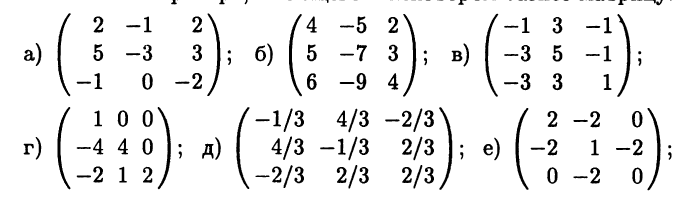
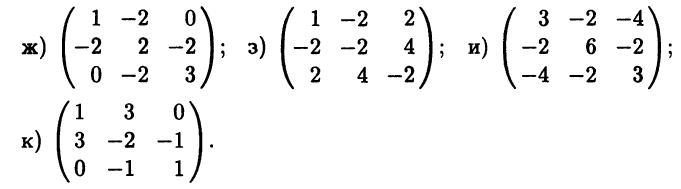
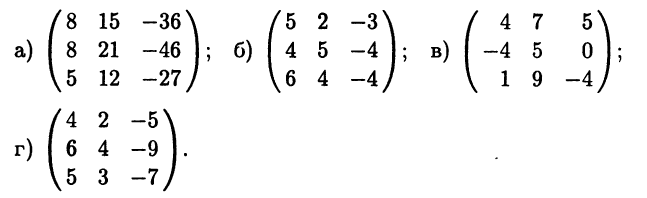
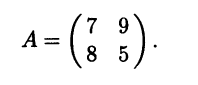
 линейного оператора
линейного оператора  — это множество собственных векторов, отвечающих собственному значению
— это множество собственных векторов, отвечающих собственному значению  , а также нулевой вектор.
, а также нулевой вектор. . Для
. Для  (как будто была бы кратность 1) собственное подпространство будет одномерно. Для
(как будто была бы кратность 1) собственное подпространство будет одномерно. Для  — тоже, но т. к.
— тоже, но т. к.  , то их собственные векторы могут совпадать и поэтому объединённое множество собственных векторов, соответствующих
, то их собственные векторы могут совпадать и поэтому объединённое множество собственных векторов, соответствующих  может быть как одномерно, так и двумерно. И т. д.: размерность объединённого множество с.в., соответствующих
может быть как одномерно, так и двумерно. И т. д.: размерность объединённого множество с.в., соответствующих  будет в диапазоне от
будет в диапазоне от  от
от  .
. , а у ограничения л-н с.в. с данным значением не может быть больше, чем у исходного.
, а у ограничения л-н с.в. с данным значением не может быть больше, чем у исходного. . Корневое подпространство, разумеется, инвариантно (как и собственное). Так вот: доказываемое утверждение сводится к тому, что это подпространство — не только инвариантное, но и приводящее, т.е. что существует такое дополнение к нему, которое также является инвариантным. А это нетривиально.
. Корневое подпространство, разумеется, инвариантно (как и собственное). Так вот: доказываемое утверждение сводится к тому, что это подпространство — не только инвариантное, но и приводящее, т.е. что существует такое дополнение к нему, которое также является инвариантным. А это нетривиально.