Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).

Рисунок 1
Определение
Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.
Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.
У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.
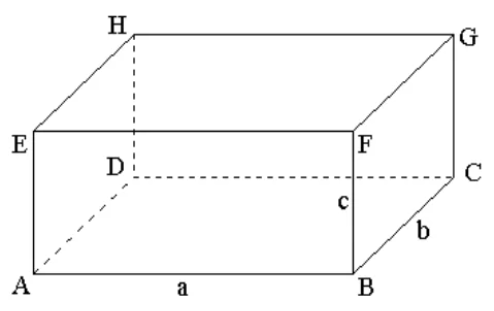
Рисунок 2
Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.
Длина, ширина, высота
Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.
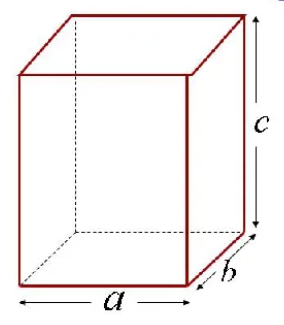
Рисунок 3
Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.
Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.
Куб
Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).
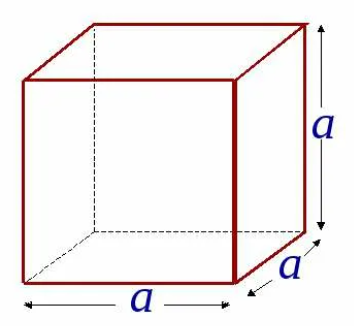
Рисунок 4
Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a2. Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a2
Объем прямоугольного параллелепипеда

Рисунок 5
С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.
Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.
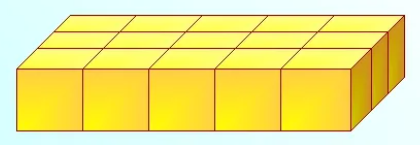
Рисунок 6
За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.
Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм3; с ребром 1 см – кубическим сантиметром (см3) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.
Формула объема прямоугольного параллелепипеда
Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.
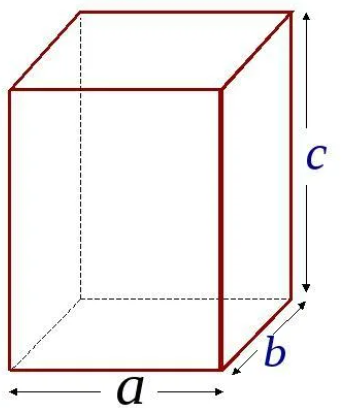
Рисунок 7
Объем куба
Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:
V=a3
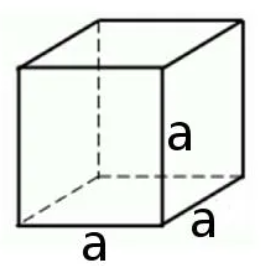
Рисунок 8
Пирамида

Рисунок 9
Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).
Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).
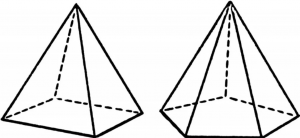
Рисунок 10
Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.
Рисунок 11
Даниил Романович | Просмотров: 957
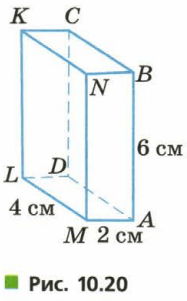
На рисунке 10.20 изображен параллелепипед. Известны длины его ребер:
AB = 6 см,
ML = 4 см,
AM = 2 см.
1) Определите длины всех ребер данного параллелепипеда.
2) Каковы размеры граней AMNB, BNKС, MLKN? Для каждой из них назовите равные ей грани.
3) Начертите три различные грани параллелепипеда в натуральную величину.
4) Найдите сумму площадей всех граней параллелепипеда.

reshalka.com
Математика 5 класс Дорофеев. 10.2 Параллелепипед. Номер №941
Решение 1
AB = MN = KL = CD = 6 см;
AM = NB = KC = LD = 2 см;
ML = AD = KN = CB = 4 см.
Решение 2
AMNB: 6 см и 2 см;
BNKС: 4 см и 2 см;
MLKN: 6 см и 4 см.
Решение 3
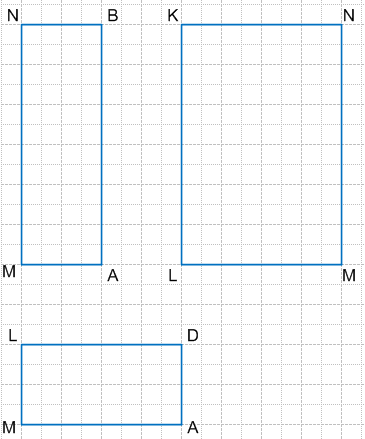
Решение 4
4 * 2 + 6 * 4 + 6 * 2 = 8 + 24 + 12 = 24 + 20 = 44
(
с
м
2
)
− сумма площадей всех граней параллелепипеда.
Как найти площадь грани параллелепипеда
Пространственная фигура под названием параллелепипед имеет несколько числовых характеристик, в том числе площадь поверхности. Чтобы ее определить, нужно найти площадь каждой грани параллелепипеда и сложить получившиеся величины.

Инструкция
Начертите параллелепипед с помощью карандаша и линейки, расположив основания горизонтально. Это классическая форма представления фигуры, с помощью которой можно наглядно показать все условия задачи. Тогда решить ее будет гораздо легче.
Посмотрите на рисунок. У параллелепипеда – шесть попарно параллельных граней. Каждая пара представляет собой равные двухмерные фигуры, которые в общем случае являются параллелограммами. Соответственно, их площади также равны. Таким образом, полная поверхность складывается из суммы трех удвоенных величин: площади верхнего или нижнего основания, фронтальной или задней грани, правой или левой грани.
Чтобы найти площадь грани параллелепипеда, нужно рассмотреть ее как отдельную фигуру с двумя измерениями, длиной и шириной. По общеизвестной формуле площадь параллелограмма равна произведению основания на высоту.
У прямого параллелепипеда только основания являются параллелограммами, все его боковые грани имеют форму прямоугольника. Площадь этой фигуры получается путем умножения длины на ширину, поскольку она совпадает с высотой. Кроме того, существует прямоугольный параллелепипед, все грани которого – прямоугольники.
Куб – тоже параллелепипед, который обладает уникальным свойством – равенством всех измерений и числовых характеристик граней. Площадь каждой его стороны равна квадрату длины любого ребра, а полная поверхность получается умножением этой величины на 6.
Форму параллелепипеда с прямыми углами часто можно встретить в повседневной жизни, например, при строительстве домов, создании предметов мебели, бытовой техники, детских игрушек, канцелярских принадлежностей и т.д.
Пример: найдите площадь каждой боковой грани прямого параллелепипеда, если известно, что высота равна 3 см, периметр основания – 24 см, а длина основания больше ширины на 2 см.Решение.Запишите формулу периметра параллелограмма P = 2•а + 2•b. По условию задачи b = а + 2, следовательно, P = 4•а + 4 = 24, откуда а = 5, b = 7.
Найдите площадь боковой грани фигуры со сторонами 5 и 3 см. Это прямоугольник:Sб1 = 5•3 = 15 (см²).Площадь параллельной боковой грани, по определению параллелепипеда, также равна 15 см². Осталось определить площадь другой пары граней со сторонами 7 и 3:Sб2 = 3•7 = 21 (см²).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Лучший ответ
Наталья Симахина
Оракул
(68255)
11 лет назад
6 граней, 3 разных прямоугольника, а как находить площадь прямоугольника всем известно – длину умножить на ширину.
Остальные ответы
дарья картушина
Знаток
(386)
11 лет назад
6 граней, умножь
!@#$%^&*())__+Darcside+__))(*&^%$#@!))))))))))))))))))))))))))))))))))))))))
Ученик
(139)
11 лет назад
12 граней, площадь по формулам площадей прямоугольника (квадрата, если это куб) , а общая площадь путем сложения площадей
!@#$%^&*())__+Darcside+__))(*&^%$#@!))))))))))))))))))))))))))))))))))))))))Ученик (139)
11 лет назад
а если реально, то S = 2(ab+bc+ac)
Alena Kimiko
Гуру
(3613)
11 лет назад
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД ИМЕЕТ:
6 граней
12 ребер
8 вершин
Прямой параллелепипед
Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота
Площадь полной поверхности Sп=Sб+2Sо, где Sо — площадь основания
Объём V=Sо*h
Взято с ru.wikipedia.ru
Прямоугольный параллелепипед строится на ребрах трех длин, расположенных под прямым углом друг к другу. Зная ребра параллелепипеда, можно найти все возможные параметры, характеризующие его. В первую очередь, каждая грань параллелепипеда представляет собой прямоугольник с двумя одинаковыми сторонами, периметр же всего объемного тела ищется как умноженная на четыре сумма всех сторон-ребер параллелепипеда.
P=4(a+b+c)
Площадь прямоугольного параллелепипеда складывается из площадей всех его граней, то есть шести прямоугольников, попарно конгруэнтных. Площадь каждого прямоугольника равна произведению его сторон, поэтому чтобы найти площадь параллелепипеда, необходимо сложить эти произведения.
S=2ab+2bc+2ac=2(ab+bc+ac)
Чтобы вычислить объем прямоугольного параллелепипеда, зная его ребро, нужно перемножить их между собой, так как объем любого прямого тела с двумя основаниями равен произведению площади основания на высоту тела, а в основании параллелепипеда находится прямоугольник, площадь которого также равна произведению – его сторон.
V=abc
У прямоугольного параллелепипеда есть четыре диагонали – диагонали его боковых граней и основания, и диагональ самого параллелепипеда, проходящая через его внутреннее пространство. Все диагонали рассчитывается через прямоугольные треугольники по теореме Пифагора, где они являются гипотенузами. Для диагоналей боковых граней и основания катетами являются ребра параллелепипеда, а для четвертой диагонали, катеты представляют собой боковое ребро и диагональ основания. (рис. 22.1,22.2,22.3,22.4)
d_1=√(a^2+c^2 )
d_2=√(a^2+b^2 )
d_3=√(b^2+c^2 )
d_4=√(a^2+〖d_3〗^2 )=√(a^2+b^2+c^2 )
Угол α, образованный внутренней диагональю прямоугольного параллелепипеда и диагональю основания, можно вычислить через отношение тангенса – бокового ребра а и диагонали основания d3.(рис.22.5)
tanα=a/d_3 =a/√(b^2+c^2 )
