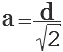Как найти размеры квадратов

Как найти размеры квадратов

текст при наведении

Квадрат самая простая и красивая, после окружности конечно, геометрическая фигура. Для нахождения его периметра или площади надо всего лишь знать длину любой стороны – ведь у квадрата эти стороны одинаковые, да к тому же параллельны. Зная сторону квадрата его площадь находим как квадрат стороны:

Периметр квадрата в этом случае равен длине четырех сторон или учетверенной длине одной стороны:

Ну и наконец еще один способ определения площади квадрата – через его диагональ, которая по совместительству является гипотенузой прямоугольных равнобедренных треугольников, каждый из которых равен половине квадрата. Площадь квадрата через диагональ считается по формуле:

автор вопроса выбрал этот ответ лучшим

Winik­i
[166K]

2 года назад 

Начертив небольшой квадрат – дюжина на дюжину сантиметров, я как бы посмотрел на него со стороны и увидел для себя одно. Постоянные у него только углы – четыре угла по 90º. Если их поделить диагоналями, они уменьшатся вдвое – два по 45º. Но при измерении периметра и площади от них ничего не зависит. Всё напрямую зависит только от длины стороны (a). Значение это может быть не известно, но его можно без труда вычислить, зная длину диагонали (d). Таким образом мы можем выразить периметр (P) и площадь (S) через длины стороны или той самой диагонали квадрата.

Длина и диагональ, а также площадь и периметр квадрата

Всё так, но ведь на практике может сложиться такая ситуация, когда мы уже будем знать значение площади квадрата, а необходимо будет посчитать его периметр. Или, наоборот, потребуется вычислить значение площади, исходя из сведений о периметре. Стало быть для каждого из (P) и (S) нам потребуется определиться не с двумя, а с тремя формулами. Что же, давайте приступим. Только одно маленькое замечание: очень неудобно рисовать буквами знак “квадратный корень” и я предлагаю использовать функцию “Корень()”, как это делается в электронной таблице Excel, если вы не против. Тогда мы можем получить следующие записи формул:

Периметр (P)

  • P = 4 * a
  • P = 4 * Корень( d² / 2 )
  • P = 4 * Корень( S )

Площадь (S)

  • S = a²
  • S = d² / 2
  • S = ( P / 4 )²

Вроде бы всё готово и можно было бы на этом остановиться. Но, друзья мои, как в таком деле обойтись без проверки? Я предлагаю подставить в качестве длины число 12, как в нашем квадрате на картинке. Тогда значение диагонали для него составит = Корень(2*a²) = 16,97. Тогда мы можем подставить эти данные в найденные формулы и получим следующие результаты:

Вычисление через длину стороны:

  • P = 4 * a = 4 * 12 = 48
  • S = a² = 12² = 144

Вычисление через длину диагонали:

  • P = 4 * Корень( 16,97² / 2 ) = 4 * Корень( 288 / 2 ) = 4 * Корень(144) = 4 * 12 = 48
  • S = 16,97² / 2 = 288 / 2 = 144

Вычисление через площадь или периметр, соответственно:

  • P = 4 * Корень( S ) = 4 * Корень(144) = 4 * 12 = 48
  • S = ( P / 4 )² = 12² = 144

Вот, теперь с чистой совестью можно отправляться на заслуженный отдых.

И р и н а
[129K]

6 лет назад 

Поскольку квадрат является геометрической фигурой, у которой все стороны равны, то для нахождения его площади достаточно знать длину всего одной его стороны.

Как известно, чтобы найти площадь квадрата, нужно значение одной его стороны возвести в квадрат. Формула площади квадрата может выглядеть, например, вот так:

, где S – площадь, а – сторона квадрата.

Периметр квадрата равен сумме длин всех его сторон, а мы знаем, что у квадрата четыре стороны, значит просто берем длину одной из сторон квадрата и умножаем ее на четыре, так как это количество сторон.

Формула нахождения периметра квадрата:

,где Р – обозначение периметра, а – длина стороны квадрата.

Елена Шамси­ева
[20.5K]

9 лет назад 

Эти формулы мне сейчас проше вывести, чем вспомнить. У квадрата 4 грани или стороны. Если длину каждой из них назвать например, буквой h, то не долго думая можно записать формулы расчета: Площадь (S), прямоугольника любого равна произведению высоты на ширину, а квадрат- это и есть прямоугольник, у которого Высота равна ширине, то есть S=h*h= h в квадрате.

Периметр (P) любого многоугольника- это сумма длин всех его сторон, у квадрата 4 стороны длиной h, то есть его периметр P= 4h

Oleg7­4
[202K]

8 лет назад 

Очень простой вопрос из курса школьной программы, ведь многие точно знают, как определить площадь и периметр квадрата, тем более, что у квадрата все стороны равны.

Итак, площадь квадрата :

  • S = a x a = a ², где а – это сторона нашего квадрата.

Периметр квадрата – это сумма всех четырех сторон квадрата :

  • P = a + a + a + a = 4 x a = 4a, где а – это сторона квадрата.

88Sky­Walke­r88
[428K]

8 лет назад 

Периметром любой фигуры называют сумму длин всех его сторон.

Как известно, у квадрата все стороны равны. Следовательно, чтобы найти периметр, достаточно длину одной стороны умножить на четыре.

Формула такая:

P = 4a, а – это длина стороны квадрата.

Можно просто сложить все стороны.

P = a + a + a + a

Карол­ина Мельн­икова
[159]

9 лет назад 

S=a2 ,Р=4а. Других формул для нахождения площади не знаю)можно попробовать через площадь двух прямоугольных треугольников,проведя диагональ.Sпрямоугольного треугольника=половина произведения катетов,т.е. S=а2/2

Ksyus­ha26
[26.8K]

8 лет назад 

Площадь квадрата, насколько я помню, находится достаточно просто. Для этого необходимо знать, сколько составляет сторона квадрата. И это число возвести в квадрат. Чтобы найти периметр квадрата, нужно сложить все его стороны, либо же попросту одну сторону умножить на 4

Чосик
[208K]

более года назад 

Периметр – это сумма длин всех сторон. Потому можно посчитать для квадрата периметр двумя способами:

  • Сложить все стороны. Р = а + а + а + а;
  • Умножить размер стороны на число сторон. Р = 4а.

Если речь о площади, то методов также несколько:

  • Квадрат является прямоугольником, потому перемножаем две стороны. S = a • a;
  • Если все стороны равны, то просто возводим стороны в квадрат. S = a2;
  • Если мы не знаем размер сторон, но знаем диагональ, то видоизменяет теорему Пифагора. S = d2/2.

У квадрата все стороны равны.

Это значит,что нужно знать,чему равна одна сторона и данное число просто возвести в квадрат, т.е. число умножить на само себя. Все! Это мы узнали площадь.

Теперь о периметре.

Точно также узнаем,чему равна сторона квадрата и умножаем данное число на 4.(стороны потому что 4 у квадрата.

Знаете ответ?
Источник

Площадь квадрата через сторону

{S = a ^2}

На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.

Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.

Содержание:
  1. калькулятор площади квадрата
  2. формула площади квадрата через сторону
  3. формула площади квадрата через диагональ
  4. формула площади квадрата через радиус вписанной окружности
  5. формула площади квадрата через радиус описанной окружности
  6. формула площади квадрата через периметр
  7. примеры задач

Формула площади квадрата через сторону

Площадь квадрата через сторону

S = a ^2

a – сторона квадрата

Формула площади квадрата через диагональ

Площадь квадрата через диагональ

S=dfrac{d^2}{2}

d – диагональ квадрата

Формула площади квадрата через радиус вписанной окружности

Площадь квадрата через радиус вписанной окружности

S = 4r^2

r – радиус вписанной окружности

Формула площади квадрата через радиус описанной окружности

Площадь квадрата через радиус описанной окружности

S = 2R^2

R – радиус описанной окружности

Формула площади квадрата через периметр

Площадь квадрата через периметр

S = dfrac{P^2}{16}

P – периметр квадрата

Примеры задач на нахождение площади квадрата

Задача 1

Найдите площадь квадрата если его диагональ равна 1.

Решение

Для решения задачи воспользуемся формулой.

S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2

Ответ: 0.5 см²

Проверим ответ на калькуляторе .

Задача 2

Найдите площадь квадрата, описанного вокруг окружности радиуса 83.

Решение

Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.

S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2

Ответ: 13778 см²

Проверим ответ с помощью калькулятора .

Задача 3

Найдите площадь квадрата если его сторона равна 8 см.

Решение

Используем первую формулу.

S = a ^2 = 8 ^2 = 64 : см^2

Ответ: 64 см²

Проверим результат на калькуляторе .

Задача 4

Найдите площадь квадрата периметр которого равен 456 см.

Решение

Используем формулу для площади квадрата через периметр.

S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2

Ответ: 12996 см²

Проверка .

Задача 5

Найдите площадь квадрата со стороной 15 см.

Решение

Воспользуемся формулой площади квадрата через сторону.

S = a ^2 = 15 ^2 = 225 : см^2

Ответ: 225 см²

Проверка .

Источник
  • Все калькуляторы

    • /

  • Учеба и наука

    • /

  • Математика

    • /   Длина стороны квадрата

    Длина стороны квадрата

    Установить Длина стороны квадрата на мобильный

    Найти длину стороны квадрата
    зная площадь

    Длина стороны квадрата по площади
    Площадь квадрата S
    Результат

    Вычислить длину стороны квадрата
    зная диагональ

    длину стороны квадрата зная диагональ
    Диагональ квадрата d
    Результат

    Скачать калькулятор

    Рейтинг: 2.5 (Голосов 24)

    ×

    Пожалуйста напишите с чем связна такая низкая оценка:

    ×

    Для установки калькулятора на iPhone – просто добавьте страницу
    «На главный экран»

    Для установки калькулятора на Android – просто добавьте страницу
    «На главный экран»

    Сообщить об ошибке

    Смотрите также

    Сторона треугольника Стороны прямоугольного Стороны равнобедренного Стороны равностороннего
    Стороны прямоугольника Стороны ромба Стороны параллелограмма Ребро куба

    Александра

    521 дн. назад

    Клас клас клас!!! Не могла понять (сломала голову

    • reply

    Наталья

    819 дн. назад

    Класс!!! Не люблю считать. Вообще… Спасибо!!!

    • reply

    Николай

    1018 дн. назад

    Супер. И быстро. Мне нравится.

    • reply

    Добавить комментарий:

    Я не робот

    Источник
    Квадрат
    Квадрат со стороной '"`UNIQ--postMath-00000001-QINU`"' и диагональю '"`UNIQ--postMath-00000002-QINU`"'
    Квадрат со стороной a и диагональю d
    Рёбра 4
    Символ Шлефли {4}
    Вид симметрии Диэдрическая группа (D4)
    Площадь a2
    Внутренний угол 90°
    Свойства
    Выпуклый многоугольник, Изогональная фигура, изотоксальная фигура
    Логотип Викисклада Медиафайлы на Викискладе

    Квадра́т (от лат. quadratus, четырёхугольный[1]) — правильный четырёхугольник, то есть плоский четырёхугольник, у которого все углы и все стороны равны. Каждый угол квадрата — прямой {displaystyle (90^{circ })}[2].

    Варианты определения[править | править код]

    Квадрат может быть однозначно охарактеризован разными способами[3][4].

    • Четырёхугольник, диагонали которого равны и взаимно перпендикулярны, причём точка пересечения делит их пополам.
    • Четырёхугольник, являющийся одновременно прямоугольником и ромбом.
    • Прямоугольник, у которого длины двух смежных сторон равны.
    • Прямоугольник, у которого диагонали пересекаются под прямым углом.
    • Ромб, у которого диагонали равны.
    • Ромб, у которого два соседних угла равны.
    • Ромб, один из углов которого — прямой (прочие углы, как легко доказать, тогда также прямые).
    • Параллелограмм, у которого длины двух смежных сторон равны, а угол между ними — прямой.
    • Параллелограмм, у которого диагонали равны, а угол между ними — прямой.
    • Дельтоид, все углы которого прямые.

    Свойства[править | править код]

    Основной источник: [4]

    Далее в этом разделе a обозначает длину стороны квадрата, d — длину диагонали, R — радиус описанной окружности, r — радиус вписанной окружности.

    Стороны и диагонали[править | править код]

    Диагонали квадрата равны, взаимно перпендикулярны, делятся точкой пересечения пополам и сами делят углы квадрата пополам (другими словами, являются биссектрисами внутренних углов квадрата). Длина каждой диагонали {displaystyle d=a{sqrt {2}}.}

    Периметр квадрата P равен:

    {displaystyle P=4a=4{sqrt {2}}R=8r}.

    Вписанная и описанная окружности[править | править код]

    Вписанная и описанная окружности для квадрата

    Центр описанной и вписанной окружностей квадрата совпадает с точкой пересечения его диагоналей.

    Радиус вписанной окружности квадрата равен половине стороны квадрата:

    {displaystyle r={frac {a}{2}}.}

    Радиус описанной окружности квадрата равен половине диагонали квадрата:

    {displaystyle R={frac {sqrt {2}}{2}}a.}

    Из этих формул следует, что площадь описанной окружности вдвое больше площади вписанной.

    Площадь[править | править код]

    • Площадь квадрата

    • Соединив середины сторон квадрата, получаем квадрат вдвое меньшей площади

      Соединив середины сторон квадрата, получаем квадрат вдвое меньшей площади

    Площадь S квадрата равна

    {displaystyle S=a^{2}=2R^{2}=4r^{2}={1 over 2}d^{2}}.

    Из формулы {displaystyle S=a^{2},} связывающей сторону квадрата с его площадью, видно, почему возведение числа во вторую степень традиционно называется «возведением в квадрат», а результаты такого возведения называются «квадратными числами» или просто квадратами. Аналогично корень 2-й степени называется квадратным корнем.

    Квадрат имеет два замечательных свойства[5].

    1. Из всех четырёхугольников с заданным периметром квадрат имеет наибольшую площадь.
    2. Из всех четырёхугольников с заданной площадью квадрат имеет наименьший периметр.

    К уравнению квадрата; здесь {displaystyle R=2,x_{0}=y_{0}=0}

    Уравнение квадрата[править | править код]

    В прямоугольной системе координат уравнение квадрата с центром в точке {displaystyle {x_{0},y_{0}}} и диагоналями, параллельными осям координат (см. рисунок), может быть записано в виде[6]:

    {displaystyle |x-x_{0}|+|y-y_{0}|=R,}

    где R — радиус описанной окружности, равный половине длины диагонали квадрата. Сторона квадрата тогда равна {displaystyle R{sqrt {2}},} его диагональ равна {displaystyle 2R,} а площадь квадрата равна {displaystyle 2R^{2}.}

    Уравнение квадрата с центром в начале координат и сторонами, параллельными осям координат (см. рисунок), может быть представлено в одной из следующих форм:

    1. {displaystyle |x-y|+|x+y|=a} (легко получается применением поворота на 45° к предыдущему уравнению)
    2. {displaystyle max(x^{2},y^{2})=r^{2}}
    3. (в полярных координатах[7]) {displaystyle quad r(varphi )=min left({frac {r}{|cos varphi |}},{frac {r}{|sin varphi |}}right)}

    Математические проблемы[править | править код]

    С квадратами связаны ряд проблем, часть из которых до сих пор не имеет решения.

    • Квадратура круга — древняя проблема построения циркулем и линейкой квадрата, равновеликого по площади заданному кругу. В 1882 году Фердинанд Линдеман доказал, что это невозможно.

    Пример квадрирования квадрата {displaystyle 112times 112}

    • Квадрирование квадрата — задача о разбиении квадрата на конечное число меньших квадратов, без «дырок», причём длины сторон квадратов должны отличаться друг от друга (в идеале должны быть все различны). Найден ряд решений этой задачи.
    • Долгое время математики пытались доказать, что непрерывное отображение отрезка прямой в квадрат невозможно, пока Джузеппе Пеано не построил свой контрпример.
    • Гипотеза Тёплица: на всякой замкнутой плоской жордановой кривой можно отыскать четыре точки, образующие вершины квадрата. Не доказана и не опровергнута.
    • Разбиение квадрата сеткой одинаковых более мелких квадратов также приводит к множеству проблем, используемых, в частности, в теории латинских и греко-латинских квадратов, магических квадратов, в игре судоку.

    Симметрия[править | править код]

    Квадрат обладает наибольшей осевой симметрией среди всех четырёхугольников. Он имеет:

    • одну ось симметрии четвёртого порядка — ось, перпендикулярную плоскости квадрата и проходящую через его центр;
    • четыре оси симметрии второго порядка (то есть относительно них квадрат отражается сам в себя), из которых две проходят вдоль диагоналей квадрата, а другие две — параллельно сторонам.

    Применение[править | править код]

    В математике[править | править код]

    Единичный квадрат используется как эталон единицы измерения площади, а также в определении площади произвольных плоских фигур. Фигуры, у которых можно определить площадь, называются квадрируемыми.

    Теорема Пифагора первоначально формулировалась геометрически: площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

    Квадратами являются грани куба — одного из пяти правильных многогранников.

    В математической физике символ квадрата может означать «оператор Д’Аламбера» (даламбериан) — дифференциальный оператор второго порядка:

    {displaystyle square u:={frac {partial ^{2}u}{partial x^{2}}}+{frac {partial ^{2}u}{partial y^{2}}}+{frac {partial ^{2}u}{partial z^{2}}}-{frac {1}{c^{2}}}{frac {partial ^{2}u}{partial t^{2}}}}

    Из теоремы Бойяи — Гервина следует, что любой многоугольник равносоставлен квадрату, то есть его можно разрезать на конечное число частей, из которых составляется квадрат (и обратно)[8].

    Графы:
    K4 полный граф часто изображается как квадрат с шестью рёбрами.

    Орнаменты и паркеты[править | править код]

    • Мозаики, включающие квадраты

    • «Пифагорова мозаика»

    • Bond brick hexagonal tiling.png

    • Square rhombic tiling.png

    Мозаики, орнаменты и паркеты, содержащие квадраты, широко распространены.

    Другие применения[править | править код]

    Шахматная доска имеет форму квадрата и поделена на 64 квадрата двух цветов. Квадратная доска для международных шашек поделена на 100 квадратов двух цветов. Квадратную форму имеет боксёрский ринг, площадка для игры в квадрат.

    Квадратный флаг Лима поделён на два чёрных и два жёлтых квадрата, будучи поднятым на корабле в гавани, означает, что корабль находится на карантине.

    Графика[править | править код]

    Символы со сходным начертанием: ロ · ⼝ · ⼞

    Ряд символов имеют форму квадрата.

    • Символы Юникода U+25A0 — U+25CF
    • U+20DE ◌⃞ COMBINING ENCLOSING SQUARE
    • ロ (Японский иероглиф «Ро» (катакана))
    • 口 (Китайский иероглиф «рот»)
    • 囗 (Китайский иероглиф «ограда»)

    В Latex для вставки символа квадрата служат конструкции Box или square.

    В HTML, чтобы заключить произвольный текст в квадрат или прямоугольник, можно использовать конструкцию:

    • <span style=”border-style: solid; border-width: 1.5px 1.5px 1.5px 1.5px; padding-left: 4px; padding-right: 4px;”>text</span>; результат: text.

    Вариации и обобщения[править | править код]

    Многомерное пространство[править | править код]

    Квадрат можно рассматривать как двумерный гиперкуб.

    Неевклидова геометрия[править | править код]

    В неевклидовой геометрии квадрат (в более широком смысле) — многоугольник с четырьмя равными сторонами и равными углами. По величине этих углов можно судить о кривизне плоскости — в евклидовой геометрии и только в ней углы прямые, в сферической геометрии углы сферического квадрата больше прямого, в геометрии Лобачевского — меньше.

    Построение квадрата с использованием циркуля и линейки

    Складывание квадрата из произвольного куска бумаги

    См. также[править | править код]

    • Алгоритм «движущиеся квадраты»
    • Квадрат Полибия
    • Квадратная матрица
    • Квадратриса
    • Первая теорема Тебо
    • Площадь произвольного четырёхугольника

    Примечания[править | править код]

    1. ↑ Квадрат // Советский энциклопедический словарь. — 2-е изд.. — М.: Советская энциклопедия, 1982. — С. 561. — 1600 с.
    2. ↑ Квадрат // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. — С. 776. — 1184 с.
    3. ↑ Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6.
    4. ↑ 1 2 Каплун, 2014, с. 171—173.
    5. ↑ Понарин Я. П. Элементарная геометрия: В 2 т. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — С. 117, 119. — 312 с. — ISBN 5-94057-171-9.
    6. ↑ Уравнение квадрата в декартовой системе координат. Дата обращения: 9 ноября 2021. Архивировано 9 ноября 2021 года.
    7. ↑ What is the polar equation for a square, if any?
    8. ↑ Болтянский В. Г. Третья проблема Гильберта. — М.: Наука, 1977. — 208 с. Архивировано 28 июня 2021 года.

    Литература[править | править код]

    • Каплун А. И. Математика, Учебно-практический справочник. — Ростов н/Д.: ООО “Феникс”, 2014. — 240 с. — ISBN 978-5-222-20926-3.

    Ссылки[править | править код]

    • Квадрат, геометрическая фигура // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
    Источник

    Добавить комментарий