Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).

Рисунок 1
Определение
Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.
Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.
У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.
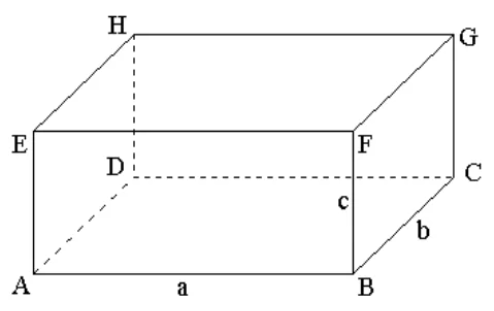
Рисунок 2
Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.
Длина, ширина, высота
Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.
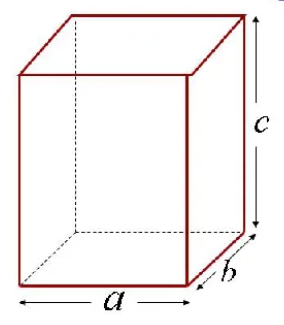
Рисунок 3
Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.
Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.
Куб
Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).
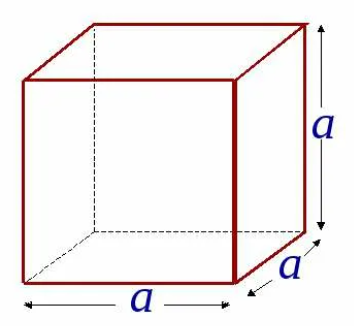
Рисунок 4
Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a2. Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a2
Объем прямоугольного параллелепипеда

Рисунок 5
С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.
Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.
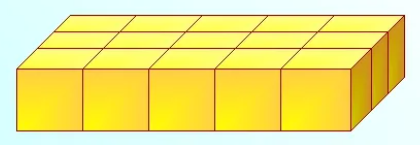
Рисунок 6
За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.
Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм3; с ребром 1 см – кубическим сантиметром (см3) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.
Формула объема прямоугольного параллелепипеда
Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.
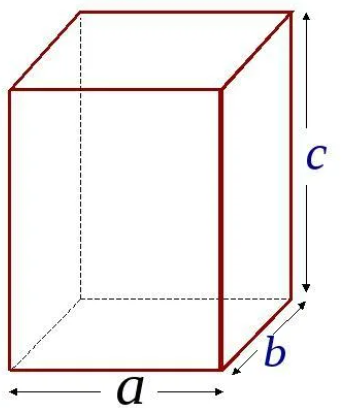
Рисунок 7
Объем куба
Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:
V=a3
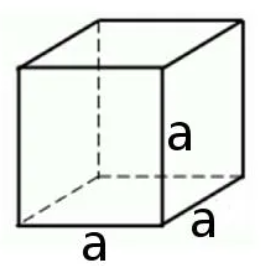
Рисунок 8
Пирамида

Рисунок 9
Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).
Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).
Рисунок 10
Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.
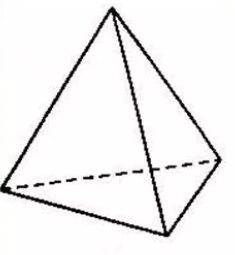
Рисунок 11
Даниил Романович | Просмотров: 965
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
- Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)

Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.
Математика
5 класс
Урок №31
Прямоугольный параллелепипед
Перечень рассматриваемых вопросов:
– куб;
– параллелепипед;
– элементы параллелепипеда;
– развёртка параллелепипеда.
Тезаурус
Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками.
Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью.
Основания параллелепипеда – это его верхняя и нижняя грани.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 класс. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Мир, в котором мы живём, состоит из огромного количества разных по форме, цвету и размеру предметов. Изучая их свойства, люди открывают что-то новое. Например, математики в окружающем пространстве обращают внимание на геометрические тела: цилиндры, кубы и так далее.
Сегодня мы рассмотрим прямоугольный параллелепипед – многогранник, название которого с древнегреческого переводится как «идущие рядом плоскости».
Прямоугольный параллелепипед ограничен шестью прямоугольниками, то есть шестью гранями. Грань, на которую поставлен параллелепипед, и ей противоположную называют нижним и верхним основаниями.

Остальные четыре грани называют боковыми гранями.
Стороны граней параллелепипеда называют рёбрами. Их двенадцать.
Концы рёбер называют вершинами. Их в параллелепипеде восемь.
Каждая вершина является общим концом трёх рёбер.
Длины двух рёбер основания, выходящих из одной вершины, называют длиной и шириной прямоугольного параллелепипеда.
Длину бокового ребра называют высотой.
Таким образом, длины трёх рёбер, выходящих из одной вершины, называют длиной, шириной, высотой. Иначе длину, ширину и высоту называют измерениями прямоугольного параллелепипеда.
Прямоугольный параллелепипед, у которого три ребра, выходящие из одной вершины, равны между собой, называется кубом. Каждая грань куба – квадрат.
Рассмотрим свойства прямоугольного параллелепипеда и куба.
У прямоугольного параллелепипеда противоположные грани равны.
Все грани куба равны между собой.
Построим прямоугольник заданной длины а и высоты h.
Для этого от каждой вершины отложим отрезок, равный половине ширины b под углом 45 градусов. И соединим концы отрезков, причём невидимые грани – пунктирной линией.

Изготовить параллелепипед можно несколькими способами. Например, с помощью развёртки. Для этого на бумаге вычерчивается макет, который выглядит как приведённый шаблон. Обратите внимание, что на картинке даны припуски для того, чтобы можно было склеить параллелепипед.

Другой способ изготовления параллелепипеда – модульная сборка. Она требует ряда последовательных действий.
1) Вырежьте из бумаги шесть одинаковых квадратов.
2) Согните их к середине, как показано на картинке.
3) Согните верхние и нижние края заготовки, как показано на рисунке.
4) Верхний уголок опустите вниз, а нижний – загните наверх. После этого получится квадрат.
5) Сделайте шесть таких заготовок и соедините их в один параллелепипед. Для этого каждый острый уголок вставьте в кармашек соседней части кубика.

Тренировочные задания
№ 1. Какова площадь верхней грани параллелепипеда?
S = ___ см2

Решение: площадь верхней грани параллелепипеда соответствует площади прямоугольника. Верхняя грань параллелепипеда имеет длину 15см и ширину 3см. Значит, далее по формуле вычисляем площадь:
S = а ·b = 15 см · 3 см = 45 см2
Ответ: 45 см2
№ 2. На рисунке изображен куб, состоящий из нескольких маленьких кубиков. Сколько маленьких кубиков ушло на построение данного куба?

Решение: для решения задачи нужно посмотреть, сколько маленьких кубиков расположено на одной грани куба. Их 9 штук. Всего на рисунке изображено три грани. Таким образом, чтобы найти общее количество маленьких кубиков, следует умножить количество кубиков, умещающихся на одной грани, на количество граней: 9 · 3= 27 штук.
Ответ: 27 штук.
Площадь поверхности прямоугольного параллелепипеда


4.6
Средняя оценка: 4.6
Всего получено оценок: 493.
4.6
Средняя оценка: 4.6
Всего получено оценок: 493.
В 5 классе в курсе математики изучается тема прямоугольного параллелепипеда. Сегодня мы поговорим о формулах для нахождения площади боковой поверхности и площади полной поверхности этой фигуры, которые наиболее часто вызывают затруднения у учеников.

Материал подготовлен совместно с учителем первой категории Камушковой Натальей Владимировной.
Опыт работы учителем математики – 27 лет.
Определения
Параллелепипед – это фигура в пространстве, которая состоит из шести четырехугольников.
Каждый четырехугольник – это грань параллелепипеда. Среди граней различают четыре боковые и два основания. Если в основании фигуры находится прямоугольник, то многогранник называется прямоугольным параллелепипедом.
Стороны граней – это ребра. У параллелепипеда всего 12 ребер.
Параллелепипед имеет 8 вершин, для их обозначения используют заглавные латинские буквы.
Если две грани не имеют общего ребра, то они называются противоположными. Так как каждая грань прямоугольного параллелепипеда – это прямоугольник, у которого противоположные стороны равны, то и противоположные грани прямоугольного параллелепипеда также равны.
Длина ребер определяет основные характеристики прямоугольного параллелепипеда: площадь, периметр, объем.
Примеры таких фигур мы часто встречаем в нашей жизни: кирпич, коробка, системный блок компьютера.
Математическая фигура – прямоугольный параллелепипед активно используется в искусстве, архитектуре и прочих областях.
Различают несколько видов параллелепипедов, с основанием в виде квадрата, параллелограмма или прямоугольника.
Формула для нахождения площади
Для того, чтобы найти площадь боковой поверхности прямоугольного параллелепипеда, необходимо вычислить по отдельности площадь каждой боковой грани, а затем просуммировать получившиеся значения.
$S = ab$;
$S = ac$; где a, b, c – стороны фигуры.
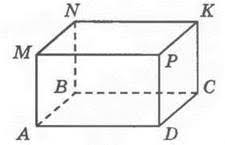
А так как противоположные грани равны, то есть $AMPD = BNKC$, $AMNB = DPKC$, их сумма и будет площадью боковой поверхности многоугольника.
$S= 2(ab + ac)$
Соответственно, чтобы вычислить площадь полной поверхности прямоугольного параллелепипеда необходимо сложить площадь боковой поверхности и две площади основания. В итоге получится формула площади прямоугольного параллелепипеда.
$S = 2(ab + ac) + 2 bc = 2(ab + ac + bc)$
Иногда для уточнения возле знака площади пишут краткое обозначение например, S п.п. – площадь полной поверхности, либо S б.п. – площадь боковой поверхности. Это помогает во время выполнения задания не перепутать нужные данные.
Пример задания
Найти площадь полной поверхности прямоугольного параллелепипеда, если длина и ширина основания 4 см и 3 см соответственно, а высота равна 2 см.
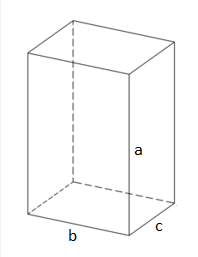
Решение:
S п.п. = 2(ab + ac + bc)
S п.п. = 2(4*3 + 4*2 + 3*2) = 52 см2
Таким образом, S п.п. = 52 см2.
Для площади поверхности прямоугольного параллелепипеда используют те же единицы измерения, в которых были приведены длины ребер. Если длины ребер прямоугольного параллелепипеда даны в разных единицах измерения, то их нужно перевести в одинаковые.

Что мы узнали?
Мы познакомились с элементами прямоугольного параллелепипеда: грани, ребра, основание. А также ознакомились с формулами для нахождения площади его боковой и полной поверхности, которые можно использовать для решения заданий.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Марина Яговцева
8/10
-

Розочка Ангелиночка
10/10
-

Слава Сироткин
10/10
-

Тома Зимина
7/10
-

Artem Sevastanov
10/10
-

Влад Чибиряев
10/10
-

Александр Селезнев
10/10
-

Акрам Сафарбеков
10/10
-

Вера Машковцева
10/10
-

Александр Семёнов
9/10
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 493.
А какая ваша оценка?
На прошлых занятиях мы рассматривали плоские фигуры.
В реальности же каждый предмет, какой бы он формы не был, занимает некоторую часть пространства.
Даже у самого тонкого листа бумаги имеется толщина.
Если взять стопку таких листов, то объем стопки бумаги будет хорошо заметен.
Эта информация доступна зарегистрированным пользователям
Раздел геометрии, в котором изучаются фигуры и их свойства в пространстве, называется стереометрией.
Слово стереометрия происходит от древнегреческого «стериос»- объемный, пространственный и «метрио»- измерять.
Базовыми фигурами в пространстве, как и на плоскости, является точка, прямая и плоскость, из которых образуются объемные геометрические фигуры, тела, пространства.
Геометрическое тело, состоящее из плоских многоугольников, называют многогранником.
Существует огромное множество многогранников: выпуклые, невыпуклые, правильные и т.д.
На данном уроке познакомимся с выпуклым прямоугольным многоугольником, который называется параллелепипед.
Эта информация доступна зарегистрированным пользователям
Выясним, как прямоугольный параллелепипед выглядит и из каких элементов он состоит.
Рассмотрим его свойства.
Научимся изображать данный многоугольник на плоскости и вычислять площадь его поверхности.
Разберем несколько примеров решения задач.
Каждый может себе представить и знает, как выглядят детские кубики.
С кубиками и конструктором из брусочков прямоугольной формы многие знакомы с раннего детства: строили домики, башенки, дороги, затем все это радостно рушили.
Эта информация доступна зарегистрированным пользователям
Всем известно, как выглядит коробка конфет или долька шоколада. Многие получали подарки в красивой красочной коробке с ярким бантом, читали книги с увлекательными рассказами и сказками.
Эта информация доступна зарегистрированным пользователям
Все эти знакомые вам предметы – это объемные тела, которые в реальности можно посмотреть, потрогать со всех сторон.
Если обратим внимание на форму, то заметим, что все изображенные объекты имеют некоторое сходство, они представляют собой прямоугольный параллелепипед.
Слово «параллелепипед» происходит от двух греческих слов: «параллелос» – идущие рядом и «опипедон» – плоскость.
Прямоугольный параллелепипед-это объемная геометрическая фигура, многогранник, состоящий из шести прямоугольников.
Прямоугольный параллелепипед – это пространственная фигура.
Плоские фигуры, такие как квадрат, прямоугольник, треугольник изобразить на плоскости легко, они являются её частью.
Любую объемную фигуру изобразить на плоскости затруднительно.
Многогранник необходимо изобразить так, чтобы была заметна объемность фигуры.
Для этого все линии многогранника, невидимые глазу, принято изображать на рисунке пунктирными линиями, а видимые – сплошными линиями.
Пунктирная линия дает возможность понять наблюдателю, как расположен многогранник и определить, откуда необходимо смотреть на него.
Если мы изобразим параллелепипед только сплошной линией, то на рисунке будут изображены различные четырехугольники, соединенные между собой, а объемного представления многоугольника данный рисунок не даст.
Эта информация доступна зарегистрированным пользователям
Даже если нам известно, что изображен прямоугольный параллелепипед, то все равно непонятно какой стороной расположен многогранник к наблюдателю.
Если невидимые линии на рисунке изобразить пунктирными линиями, то у фигуры сразу будет заметен объем.
Прямоугольный параллелепипед изображают так:
Эта информация доступна зарегистрированным пользователям
Прямоугольники, из которых состоит прямоугольный параллелепипед, называют гранями, причем противоположные грани его попарно равны.
Эта информация доступна зарегистрированным пользователям
Верхняя грань равна нижней, правая равна левой, передняя грань равна задней.
Грань, на которой стоит прямоугольный параллелепипед, называют нижним основанием, противоположную грань называют верхним основанием параллелепипеда.
Остальные четыре грани называют боковыми гранями.
Стороны граней называют ребрами параллелепипеда.
Эта информация доступна зарегистрированным пользователям
Концы ребер, т.е. вершины граней, называют вершинами параллелепипеда.
На рисунке вершины изображены точками.
Эта информация доступна зарегистрированным пользователям
Прямоугольный параллелепипед имеет три линейные величины (три измерения): ширину, длину и высоту.
Величину прямоугольного параллелепипеда определяют длинами трех ребер, исходящих из одной вершины.
Эта информация доступна зарегистрированным пользователям
Если все три величины прямоугольного параллелепипеда равны, то такой параллелепипед называют кубом.
Другими словами, куб – это частный случай параллелепипеда.
Куб – это правильный многоугольник, состоящий из шести одинаковых квадратов.
Куб по-другому называют правильный гексаэдр (от греческого «hex»- шесть и «hedra»- грань).
Куб выглядит так:
Эта информация доступна зарегистрированным пользователям
Он имеет все те же элементы, что и прямоугольный параллелепипед.
Эта информация доступна зарегистрированным пользователям
Все шесть граней куба равны, следовательно, и все 12 ребер между собой равны.
Куб так же имеет 2 основания: нижнее, на котором он стоит, и противоположное ему – верхнее.
Остальные четыре его грани – это боковые грани.
Эта информация доступна зарегистрированным пользователям
Платоновские тела
|
Тетраэдр |
Гексаэдр |
Октаэдр |
Додекаэдр |
Икосаэдр |
|
|
Внешний вид |
 |
 |
 |
 |
 |
|
Число и вид граней |
4 правильных треугольника |
6 квадратов |
8 правильных треугольников |
12 правильных пятиугольников |
20 правильных треугольников |
|
Число ребер |
6 |
12 |
12 |
30 |
30 |
|
Число вершин |
4 |
8 |
6 |
20 |
12 |
|
Число ребер, сходящихся в вершине |
3 |
3 |
4 |
3 |
5 |
|
Символьное значение |
Огонь |
Земля |
Воздух |
Все сущее (все мироздание) |
Вода |
Эта информация доступна зарегистрированным пользователям
Если посмотреть вокруг, то мы можем заметить огромное множество объектов, имеющих форму прямоугольного параллелепипеда или напоминающих его форму.
Так, например, большинство зданий и помещений, шкаф (тумбочка), столешница, аквариум, коробка, кирпичи и многое другое представляют собой прямоугольный параллелепипед.
Эта информация доступна зарегистрированным пользователям
Такой многогранник имеет широкое применение в различных областях нашей жизни, и это неспроста:
1) прямоугольная форма параллелепипеда удобна для деления целого на части
2) объекты прямоугольной формы легко надстраивать и совмещать
3) прямоугольный параллелепипед является одним из самых устойчивых многогранников
Часто приходится определять площадь поверхности объекта, имеющего форму прямоугольного параллелепипеда.
Давайте разберемся, как и с помощью каких формул можно вычислить площадь его поверхности.
Допустим, у нас есть коробка, имеющая форму прямоугольного параллелепипеда.
Попробуем изобразить развертку данного геометрического тела.
Развертка параллелепипеда – это изображение его поверхности в виде плоской фигуры, составленной из двух равных оснований: прямоугольников и четырех боковых граней (прямоугольников, попарно равных друг другу).
Эта информация доступна зарегистрированным пользователям
Площадь этой развертки- это и есть площадь поверхности прямоугольного параллелепипеда.
Так как прямоугольный параллелепипед состоит из шести граней, имеющих форму прямоугольников, причем противоположные грани равны по величине, то площадь поверхности прямоугольного параллелепипеда будет равна сумме площадей всех его шести граней.
Пусть для нашего прямоугольного параллелепипеда три ребра, выходящие из одной вершины, имеют значения а, b, h.
Эта информация доступна зарегистрированным пользователям
а– ширина прямоугольного параллелепипеда
b– длина прямоугольного параллелепипеда
h– высота прямоугольного параллелепипеда
Найдем площадь всех граней.
Воспользуемся формулой для расчета площади прямоугольника: площадь прямоугольника равна произведению его ширины на длину.
Ребра, лежащие напротив ребер а, b, h, будут иметь такие же значения длины, так как противолежащие ребра прямоугольного параллелепипеда равны.
В таком случае получаем:
1) Площадь нижнего основания равна произведению (a ∙ b)
2) Площадь верхнего основания также равна произведению (a ∙ b)
3) Площадь левой боковой и правой боковой граней равны, как противолежащие, площадь каждой из них определяется произведением (b ∙ h)
4) Передняя и задняя боковые грани равны, а значение площади каждой из них будет определяться произведением (а ∙ h)
Сложим площади всех граней прямоугольного параллелепипеда, получим общую площадь его поверхности.
Эта информация доступна зарегистрированным пользователям
Упростим выражение, вынесем 2 за скобку.
Формула площади поверхности прямоугольного параллелепипеда будет выглядеть так:
Эта информация доступна зарегистрированным пользователям
Площадь двух оснований прямоугольного параллелепипеда (это два прямоугольника) найдем по формуле:
Sосн = 2 (a ∙ b).
Площадь боковой поверхности прямоугольного параллелепипеда можно найти по формуле:
Sбок = 2h ∙ (a + b).
В нашем случае а, b– это стороны основания, h– это высота прямоугольного параллелепипеда (боковое ребро).
Так как основанием прямоугольного параллелепипеда является прямоугольник, то периметр основания прямоугольного параллелепипеда определяется равенством
Роснов = 2 ∙ (a + b).
Подставим Роснов в формулу Sбок = 2h ∙ (a + b) вместо выражения 2 ∙ (a + b).
Тогда площадь боковой поверхности можно найти так:
Sбок = Роснов ∙ h.
Определим площадь поверхности куба.
Известно, что куб – это прямоугольный параллелепипед, поверхность которого состоит из шести одинаковых граней, имеющих форму квадрата.
Чтобы найти площадь поверхности куба, необходимо сложить площади всех его граней.
Площадь одной грани куба найдем по формуле площади квадрата:
S = a2
а– это сторона квадрата (ребро куба).
Так как все 6 граней куба представляют собой равные по площади квадраты, следовательно, чтобы найти площадь всей поверхности куба, необходимо площадь одной грани умножить на их количество.
Формула площади поверхности куба выглядит так:
Эта информация доступна зарегистрированным пользователям
Рассмотрим решение нескольких практических задач.
В процессе любого строительства или ремонта очень часто встает вопрос о том, сколько необходимо потратить строительного и отделочного материала или как рассчитать расход краски.
Задача №1.
Какое количество краски понадобится, чтобы полностью покрасить бак прямоугольной формы?
Ширина бака 2 метра, длина 3 метра, высота 1 метр.
Известно, что на 1 м2 расходуется 200 г краски.
Эта информация доступна зарегистрированным пользователям
Чтобы рассчитать количество краски, которое нужно затратить на покраску бака, необходимо определить площадь окрашиваемой поверхности, затем, зная норму расхода краски на единицу площади, можно рассчитать расход краски на всю окрашиваемую поверхность.
Пусть m1– масса краски, которая расходуется на 1 м2
m2– масса краски, которая необходима для покраски всего бака.
Эта информация доступна зарегистрированным пользователям
Задача №2
Сколько квадратных метров стекла понадобится на изготовление аквариума кубической формы длиной 100 см?
Эта информация доступна зарегистрированным пользователям
Для вычисления площади поверхности аквариума в квадратных метрах необходимо длину аквариума перевести из сантиметров в метры.
Вспомним, 1 м = 100 см.
Эта информация доступна зарегистрированным пользователям
Если бы аквариум необходимо было изготовить только из боковых стенок и основания, то из стекла пришлось бы вырезать всего 5 квадратных граней.
В таком случае формула для вычисления площади поверхности аквариума приняла бы вид
S = 5 а2.
Задача №3
Хозяйка решила покрасить стены в комнате.
Вычислите площадь поверхности стен комнаты, в которой имеется дверной проем площадью 2 м2 и оконный проем площадью 1 м2.
Комната имеет форму прямоугольного параллелепипеда.
Ширина комнаты 3 метра, длина комнаты 4 метра, высота комнаты 3 метра.
Эта информация доступна зарегистрированным пользователям
Пусть Sc– общая площадь стен комнаты.
Sд– площадь дверного проема.
Sо– площадь оконного проема.
S– площадь стен комнаты за исключением площади дверного и оконного проемов.
Эта информация доступна зарегистрированным пользователям
