Правильный шестиугольник, многоугольнике с 6 вершинами, вычислить его параметры. Шестиугольник-это фигура, из которой можно складывать мозаику (черепицу). Введите одно из известных значений. Затем нажмите кнопку вычислить.
.
Поделиться расчетом:
Калькулятор шестиугольников
Длина стороны(a)
Большая диагональ(d1)
Меньшая диагональ(d2)
Периметр(p)
Площадь(S)
Радиус вписанной окружности(r)
Вычислить
Очистить
Формулы:
 d = 2 * a
d = 2 * a
d2 = √3 * a
p = 6 * a
S = 3/2 * √3 * a2
r = √3 / 2 * a
Высота = d2 = 2 * r
Радиус окружности = a
Внутренние углы: 120°, 9 диагоналей





Как рассчитать площадь правильного шестиугольника
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник – многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
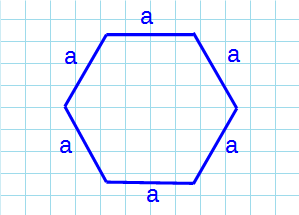
a:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через сторону:
a – сторона шестиугольника.
Через радиус описанной окружности
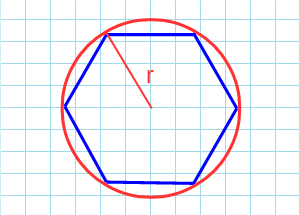
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
r – радиус описанной окружности.
Через радиус вписанной окружности
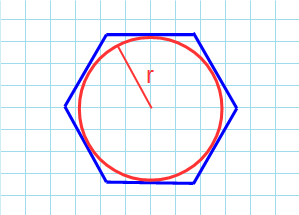
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности:
r – радиус вписанной окружности.
Калькулятор
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 февраля 2022 года; проверки требуют 2 правки.
| Шестиугольник | |
|---|---|
 Правильный шестиугольник |
|
| Тип | Правильный многоугольник |
| Рёбра | 6 |
| Символ Шлефли | {6}, t{3} |
| Диаграмма Коксетера — Дынкина |
|
| Вид симметрии | Диэдрическая группа (D6) |
| Площадь |
   |
| Внутренний угол | 120° |
| Свойства | |
| выпуклый, вписанный, Равносторонний, равноугольный[en], изотоксальный | |
Правильный шестиугольник (или гексагон от греч. εξάγωνο) — правильный многоугольник с шестью сторонами.
Свойства[править | править код]
Построение[править | править код]
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.

Правильный шестиугольник в природе, технике и культуре[править | править код]
- Пчелиные соты показывают разбиение плоскости на правильные шестиугольники.
- Некоторые сложные молекулы углерода (напр., графит) имеют гексагональную кристаллическую решётку.
- Гигантский гексагон — атмосферное явление на Сатурне.
- Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
- Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
- Гексаграмма — шестиконечная звезда, образованная двумя правильными треугольниками. Под названием звезда Давида она является символом иудаизма.
- Гексагоном[fr] иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.
Примечания[править | править код]
- ↑ А. М. Райгородский. Проблема Борсука. — М.: Издательство МЦНМО, 2006. — С. 9. — 56 с. — (Библиотека „Математическое просвещение“). — ISBN ISBN 5-94057-249-9.
См. также[править | править код]
- Шестиугольник
- Упаковка кругов на плоскости
Ссылки[править | править код]
- Шестиугольный мир (ЖЖ-сообщество)
Оглавление:
- Площадь правильного шестиугольника
- Площадь неправильного шестиугольника
- Площадь равностороннего шестиугольника
Умение определять площадь различных фигур играет немалую
роль в жизни каждого человека. Рано или поздно приходится иметь дело с этими
знаниями. К примеру, в процессе ремонта помещения для определения необходимого
количества рулонов обоев, линолеума, паркета, плитки в ванную или на кухню
нужно уметь рассчитывать необходимую площадь.
Знаниями в области геометрии пользовались еще в древнем
Вавилоне и других странах. На первых шагах к культуре всегда возникала
необходимость измерить участок, расстояние. При строительстве первых
значительных сооружений требовались умения выдерживать вертикаль,
спроектировать план.
Роль эстетических потребностей людей также имела немалое
значение. Украшение жилища, одежды, рисование картин способствовало процессу
формирования и накопления сведений в области геометрии, которые люди тех времён
добывали опытным путем, по крупицам и передавали из поколения в поколение.
Сегодня знания геометрии необходимы и закройщику, и строителю,
и архитектору и каждому простому человеку в быту.
Поэтому нужно учиться рассчитывать площадь различных
фигур, и помнить, что каждая из формул может пригодиться впоследствии на
практике, в том числе, и формула правильного шестиугольника. Шестиугольником называется
такая многоугольная фигура, общее количество углов которой равно шести.
Площадь правильного шестиугольника
Правильным шестиугольником называют шестиугольную фигуру,
которая имеет равные стороны. Углы у правильного шестиугольника также между
собой равны.
В повседневной жизни мы часто можем встретить предметы,
имеющие форму правильного шестиугольника. Это и металлическая гайка, и ячейки
пчелиных сот, и структура снежинки. Шестиугольными фигурами отлично заполняются
плоскости. Так, например, при мощении тротуарной плитки мы можем наблюдать, как
плитка укладывается одна возле другой, не оставляя пустых мест.
Свойства
правильного шестиугольника
- Правильный шестиугольник всегда будет иметь равные углы,
каждый из которых составляет 120˚. - Сторона фигуры равняется радиусу описанной окружности.
- Все стороны в правильном шестиугольнике равны.
- Правильный шестиугольник плотно заполняет плоскость.
Как посчитать
площадь правильного шестиугольника?
Площадь правильного шестиугольника можно рассчитать,
разбив его на шесть треугольников, каждый из которых будет иметь равные
стороны.
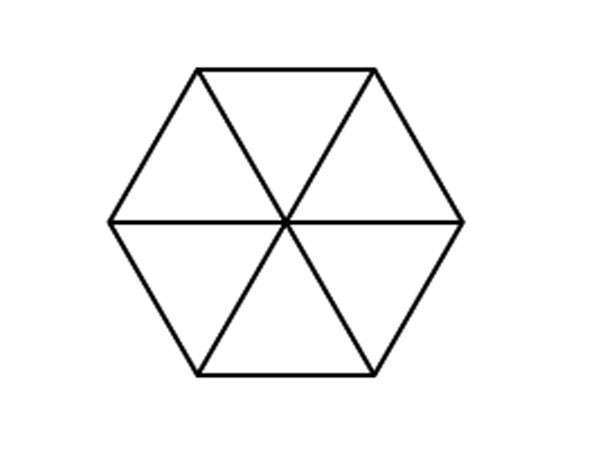
Для расчета площади правильного треугольника используется
следующая формула:
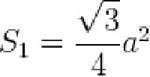
Зная площадь одного из треугольников, можно легко
рассчитать площадь шестиугольника. Формула для ее расчета проста: поскольку
правильный шестиугольник — это шесть равных треугольников, следует площадь
нашего треугольника умножить на 6.
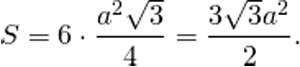
Если провести от центра фигуры к любой из ее сторон
перпендикуляр, получим отрезок, который называется апофема. Рассмотрим, как
найти площадь шестиугольника при известной апофеме:
- Площадь = 1/2*периметр*апофему.
- Предположим, наша апофема равняется 5√3 см.

- Используя апофему, находим периметр: Поскольку апофема
расположена перпендикулярно к стороне шестиугольника, то углы треугольника,
созданного при помощи апофемы, будут равняться 30˚—60˚—90˚. Каждая сторона
полученного треугольника будет соответствовать: x-x√3-2x,
где короткая сторона, которая расположена напротив угла в 30˚— это x, длинная сторона,
расположенная напротив угла в 60˚ — это x√3,
а гипотенуза — 2x. - Поскольку апофема представлена, как x√3, можно подставить ее в формулу a = x√3 и решить. Если, к примеру,
апофема = 5√3, тогда подставим эту
величину в формулу и получим: 5√3 см = x√3, или x = 5
см. - Итак, короткая сторона треугольника равняется 5 см.
поскольку эта величина является половиной длины стороны шестиугольника,
умножаем 5 на 2 и получим 10 см, которая является длиной стороны. - Зная длину стороны, умножим её на 6 и получим периметр
шестиугольника:10 см х 6 = 60 см - Подставим полученные результаты в нашу формулу:
Площадь =
1/2*периметр*апофему
Площадь = ½*60см*5√3
Решаем:

Теперь осталось упростить
ответ, чтобы избавиться от квадратных корней, а полученный результат укажем в
квадратных сантиметрах:
½ * 60 см * 5√3 см =30 * 5√3
см =150 √3 см =259.8 см²
Видео о том, как найти площадь правильного шестиугольника
Площадь неправильного шестиугольника
Существует несколько вариантов определения площади
неправильного шестиугольника:
- Метод трапеции.
- Метод расчета площади неправильных многоугольников при
помощи оси координат. - Метод разбивания шестиугольника на другие фигуры.
В зависимости от исходных данных, которые вам будут
известны, подбирается подходящий метод.
Метод трапеции
Площадь шестиугольника, имеющего произвольную
(неправильную) форму, рассчитывается методом трапеции, суть которого состоит в
разделении шестиугольника на отдельные трапеции и последующим вычислением
площади каждой из них.
Метод с осями
координат
Кроме этого, площадь неправильного шестиугольника можно рассчитать
при помощи метода расчета площади неправильных многоугольников. Рассмотрим его
на следующем примере:
Вычисление будем выполнять методом использования
координат вершин многоугольника:
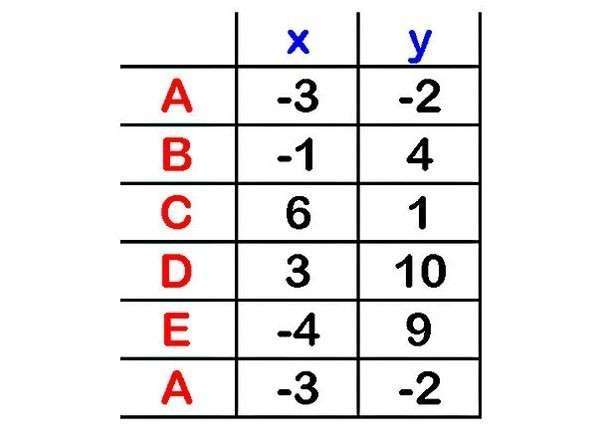
- На этом этапе следует сделать таблицу и записать
координаты вершин x и y. Выбираем вершины в
последовательном порядке по направлению против часовой стрелки, завершив конец
списка повторной записью координаты первой вершины:
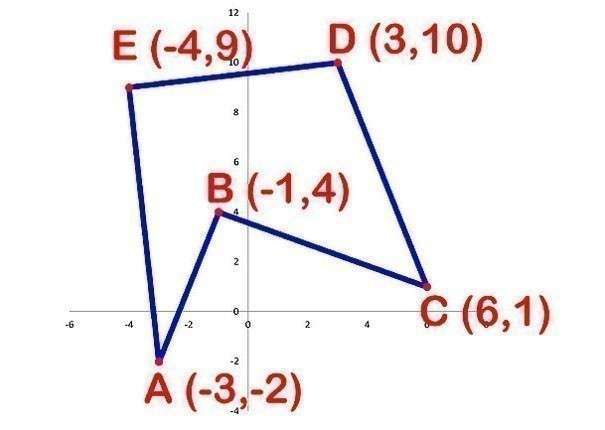
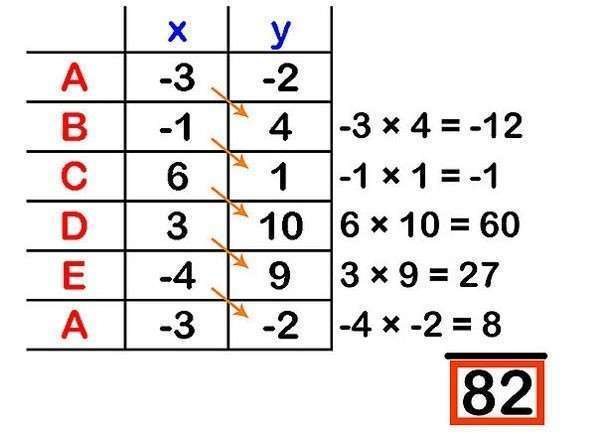
- Теперь следует умножить значения координаты х 1-й вершины
на y 2-й
вершины и продолжить таким образом умножение далее. Затем необходимо сложить
полученные результаты. В нашем случае получилось 82:
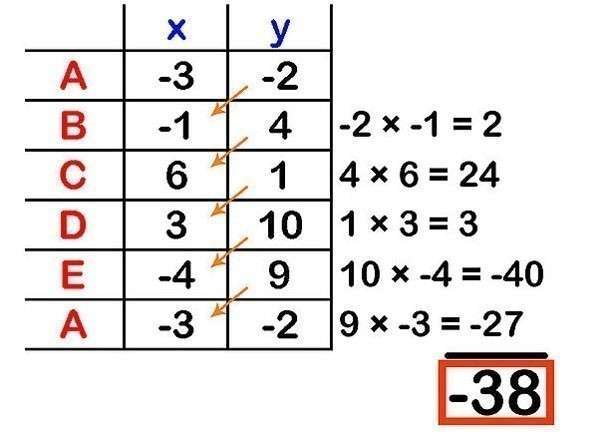
- Последовательно умножаем значения координат y1-й
вершины на значения координат х 2-й вершины. Суммируем полученные результаты. В
нашем случае получилось 38:
- Вычитаем сумму, которую получили на четвертом этапе из
суммы, которая получилась на третьем этапе: 82 – (-38) = 120
- Теперь необходимо разделить результат, который был
получен на предыдущем этапе и найдем площадь нашей фигуры: S= 120/2 = 60
см²
Метод разбивания
шестиугольника на другие фигуры
Каждый многоугольник можно разделить на несколько других
фигур. Это могут быть треугольники, трапеции, прямоугольники. Исходя из
известных данных, пользуясь формулами определения площадей перечисленных фигур,
последовательно вычисляются их площади и затем суммируются.
Некоторые неправильные шестиугольники состоят из двух
параллелограммов. Для определения площади параллелограмма следует умножить его
длину на ширину и затем сложить две уже известные площади.
Видео о том, как найти площадь многоугольника
Площадь равностороннего шестиугольника
Равносторонний шестиугольник имеет шесть равных сторон и
является правильным шестиугольником.
Площадь равностороннего шестиугольника равняется 6
площадям треугольников, на которые разбита правильная шестиугольная фигура.
Все треугольники в шестиугольнике правильной формы равны,
поэтому для нахождения площади такого шестиугольника достаточно будет знать
площадь хотя бы одного треугольника.
Для нахождения площади равностороннего шестиугольника
используется, конечно же, формула площади правильного шестиугольника, описанная
выше.
А Вы знали, как найти площадь шестиугольника? Как думаете, где эти знания пригодятся Вам в жизни? Поделитесь своим мнением в комментариях.
Правильный шестиугольник: свойства, формулы, площадь
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.

Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.

Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где
— сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольника.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной
.

Радиус такой окружности равен .
Ответ: .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Ответ: .
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Правильный шестиугольник: свойства, формулы, площадь» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
