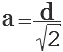как определить длину и ширину комнаты на чертиже зная площадь
Ученик
(187),
закрыт
7 лет назад
Паша
Мастер
(1589)
10 лет назад
через пропорции сторон ))
расскажу как ))))
Отношение длин сторон комнаты в метрах, будет таким-же как отношение длин сторон на чертеже.
Составляешь 2 уравления:
a и b – стороны комнаты, площадь комнаты – S, X= отношение a/b на чертеже (равное отношению сторон в комнате)
1) a/b=X
2) a*b=S
отсюда b=корень из (S/X)
a=корень из (S*X)
отрицательные значения отбрасываешь как не имеющие смысла.
Варенцов Антон
Мыслитель
(9349)
10 лет назад
Если известна площадь, то необходимо и достаточно знать соотношение длины и ширины комнаты.
Допустим, что A и B – ширина и длина комнаты соответственно, S – площадь комнаты, M – соотношение ширины и длины (не важно где – на чертеже или в натуре) . То есть:
S=A*B;
M=A/B;
Тогда A=M*B; S=M*B*B=M*B^2;
Отсюда находим B=(S/M)^1/2; A=M*B; или A=S/B;
Иван Петренко
Знаток
(256)
7 лет назад
вопрос старый но мало ли кому поможет! зная площадь S!и масштабные размеры сторон a и b!мы можем узнать реальные размеры сторон A и B!для начала нам нужно узнать масштаб x,составляем уравнение :ax*bx=S
(a*b)x²=S
x=√S/a*b
получив масштаб x…можем узнать реальные размеры A=ax и B=bx соответственно!
Екатерина
Профи
(873)
6 лет назад
Столкнулась с той же проблемой. Решила вопрос следующим образом.
1. Первое, что нам надо – распечатать план квартиры и найти на нём одну любую комнату правильной прямоугольной формы. Измеряем на распечатанном плане длину и ширину комнаты в см. В моём случае это было 2,5 см и 2,75 см.
2. Складываем 2,5 и 2,75 = 5,25. Соответственно, у нас есть сумма длин двух стен.
3. Вычисляем сколько в процентном соотношении от 5,25 занимает каждая стена. Составляем пропорцию.
5,25 – 100%
2,5 – х%
х = (2,5*100)/5,25 = 47,62% (округлила)
Соответственно вторая стена, которая 2,75 см на плане – 100% – 47,62% = 52,38%
3. Теперь берём известную нам по плану реальную площадь комнаты, в моём случае 2,51 метра квадратных. Находим корень из этого числа, для этого можно обратиться к Святому Гуглу, вбиваем в поисковик “корень квадратный из 2,51” и вуаля – 1,5842.
Что значит это число? Это значит, что если бы наша комната была идеально квадратной, то каждая стена была бы длиной 1,5842 м. Проверяем: 1,5842*1,5842 = 2,509.
4. Теперь мы можем найти реальную длину наших стен. Складываем длины двух стен 1,5842+1,5842 = 3,1684. – Сумма длин двух стен.
Благодаря процентному соотношению стен, которое мы нашли в первом пункте, мы можем узнать длину каждой из них.
Открываем калькулятор: 3,1684*47,62% = 1,5087м.
Вторую стену найти легко: 3,1684-1,50 = 1,6597м.
Итого у нас комната размером 1,5*1,66 метра.
5. Чтобы не париться так с измерением следующих комнат, вычисляем масштаб!
Стена на плане длиной 2,5 см имеет реальную длину 150 см. Составляем пропорцию:
2,5 см – 150,87 см
1 см – х %
х = 60,34
Теперь мы знаем, что у нас масштаб плана 1: 60,3.
То есть 1 см на распечатанном плане соответствует 60,3 см в реальности. И теперь вы можете измерить всю квартиру по плану.
Скажу сразу, что масштаб данным способом получается примерный и может отличаться от настоящего на несколько сантиметров.
Как по площади определить стороны
С каждым годом задачи по геометрии становятся сложнее. Уже недостаточно знать, как считать по готовым формулам. Необходимо уметь из уже готовой вывести новую формулу, чтобы узнать ту или иную величину.

Инструкция
Вычисление сторон квадрата. Формула площади квадрата а², где а – сторона данной фигуры. Для вычисления площади квадрата нужно знать лишь одну сторону, так как все его стороны равны. Отсюда вычислить сторону очень просто: √а. Пример: Площадь равна 49. Выделите квадратный корень из 49. Ответ: 7.
Вычисление сторон прямоугольника. Найти стороны этой фигуры, зная лишь значение площади, невозможно. Нужно знать еще одну величину – его периметр. Вот пример, площадь равна 12, а периметр 14.
Обозначьте стороны прямоугольника «х» и «у». Из формулы вычисления периметра P=2(a+b) подставьте значения нашей задачи 2(х+у)=14.
Из формулы вычисления площади S=ab подставьте значения нашей задачи ху=12, т. е. х=12/у. Подставьте значение «х» в уравнение 2(х+у)=14.
Получится 2(12/у+у)=14. Перенесите подобные 12/y+y=14/2. 12/у+у=7. Умножьте обе части уравнения на «у». Получится 12+у^2=7у. у^2-7у+12=0 – квадратное уравнение, считайте через дискриминант. У уравнения 2 корня у=4; у=3.
Ответ: стороны прямоугольника равны 3 и 4 см соответственно.
Вычисление сторон ромба. Для того чтобы узнать стороны ромба (EWYP), помимо площади нужно иметь еще какое-нибудь значение. Например, высота – WH, она же длина перпендикуляра, опущенного из вершины (W) на сторону (EP). Следует помнить, что стороны ромба равны между собой. В этом случае очень легко определить сторону ромба (EW). Как известно, ромб можно представить как два треугольника EWP и PWY, площадь каждого из которых равняется половине произведения высоты на основание. Можно сделать вывод, что площадь ромба будет равна произведению высоты на длину стороны. Отсюда получается простая формула для вычисления длины стороны ромбы: нужно его площадь разделить на длину высоты – |EW|=S/|WH|. Пример: Пусть площадь ромба EWYP равна 20. А высота WH=5. Подставьте значения в приведенную формулу: |EW|=20/|5 . Ответ: сторона равна 4.
Вычисление сторон равностороннего треугольника. Для того чтобы узнать его сторону (а все его стороны равны), помимо площади необходимо знать высоту. Если известны две эти величины, то расчет можно совершить по этой формуле: b=2S/h, где b – сторона треугольника, S – площадь, h – высота. Пример: Пусть площадь равностороннего треугольника ABC равна 25. Высота BH = 5.
Подставьте значения в формулу: b=2*25/5. Ответ: сторона равна 10.
Обратите внимание
Расчет сторон остальных фигур, имеющих стороны различные по длине друг к другу, требует знания большего количества величин.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
|
Площадь – 56 квадратных см. Периметр – 30 см.
Сторона А=7, сторона В=8 S=AxB P=2A+2B S=56 P=30 автор вопроса выбрал этот ответ лучшим Можно попробовать решить данную задачу, составив систему уравнений. Периметр прямоугольника равен: p=2a+2b; Площадь прямоугольника равна: s=a*b; Так как мы знаем периметр и площадь, то сразу подставляем числа: 30=2a+2b; 56=a*b; Выражаем b через a во втором уравнении: b=56/a; И подставляем 56/a вместо b в первое уравнение: 30=2a+2(56/a); 15=a+56/a; Домножаем обе части на a: 15a=a²+56; Получаем квадратное уравнение: a²-15a+56=0; Находим корни этого квадратного уравнения: (15±√(15²-4*1*56))/2*1 = (15±√(225-224))/2 = (15±√1)/2 = (15±1)/2 Получилось, что корни этого уравнения: a1=(15+1)/2=16/2=8; a2=(15-1)/2=14/2=7; Получается, что у нас 2 возможных варианта прямоугольников. Вспомним, что мы выразили: b=56/a; Отсюда находим возможные b: b1=56/a1=56/8=7; b2=56/a2=56/7=8; Как оказалось эти два разных прямоугольника – это один и тот же, просто достигнуть периметра в 30 при площади в 56 можно: Если a=7 и b=8. Либо наоборот: a=8 и b=7. То есть в сущности у нас один и тот же прямоугольник, просто в одном варианте вертикальная сторона больше горизонтальной, а в другом наоборот – горизонтальная больше вертикальной. Ответ: одна сторона 7 сантиметров, а вторая 8 сантиметров.
Oleg74 9 лет назад Если периметр прямоугольника Р = 30 см, а его площадь S = 56 см, то его стороны будут равны : а – одна сторона, в – другая сторона прямоугольника. S = а * в P = 2а + 2в Решив эту систему, приходим к тому, что сторона а будет равна 7 см, а сторона в будет равна 8 см. а = 7 см в = 8 см. Чтобы решить поставленную задачу, нужно составить систему уравнений и решить ее S = а*b P = 2(а+b) получим квадратное уравнение, которое легко решается, если подставить в него значения периметра и площади
Дискриминант равен 1 и уравнение имеет два корня 7 и 8, следовательно одна из сторон равна 7 см, другая 8 см или наоборот. Я специально выписал здесь дискриминант, так как по нему очень хорошо ориентироваться если в условии задачи на нахождение сторон прямоугольника значение периметра и площади заданы так, что этот дискриминант больше ноля, тогда мы имеем прямоугольник; если дискриминант равен нолю – тогда имеем квадрат (P=30, S=56,25, квадрат со стороной 7,5); если дискриминант меньше ноля, то тогда такой прямоугольник не существует (P=20, S=56 – решения нет)
Galina7v7 7 лет назад Дано: S = 56 смР = 30 смСтороны=?Решение:Пусть стороны прямоугольника a и b. Тогда: площадь S = a * b , периметр Р=2*(a + b), Получим систему уравнений: {a*b=56 ? {ab=56 {2(a+b)=30, {a+b=15 ,выражая b через а получим квадратное уравнение: b=15-a, a^2 -15a +56 =0 ,решая которое ,получим : a1=7, a2=8, b1=8, b2=7. То есть стороны прямоугольника: a=7,b=8 ,или наоборот:a=8,b=7.
Zolotynka 7 лет назад Нашла еще такое решение, Известно, что периметр прямоугольника 30 а площадь 56, далее: периметр = 2*(длина + ширина) или 2L + 2W площадь= длина * ширина или L * W 2L + 2W = 30 (делим обе части на 2) L + W = 15 L * W = 56 L * (15 – L) = 56 Честно говоря, не совсем поняла решение, но думаю, тот, кто не совсем подзабыл математику, разберется.
Azamatik 7 лет назад Вспоминаем школьную геометрию: Периметр прямоугольника – это будет сумма длин всех сторон, а площадь прямоугольника – это уже произведение двух смежных его сторон (длину на ширину). В данном случае нам известны и Площадь и Периметр прямоугольника. Они равны 56 см^2 и 30 см соответственно. Итак, решение: S – площадь = а x b; 56 = a x b; Р – периметр = а + b + a + b = 2a + 2b; 30 = 2 (а + b); 15 = a + b; a = 15 – b; Делаем подставление: 56 = (15 – b) x b; 56 = 15 b – b^2; b^2 – 15b + 56 = 0. Получили квадратное уравнение, решая которое получаем: b1 = 8, b2 = 7. Находим и другую сторону прямоугольника: a1 = 15 – 8 = 7; a2 = 15 – 7 = 8. Ответ: стороны прямоугольника равны 8 и 7 см или же 7 и 8 см.
Зная формулы периметра прямоугольника и его площади, стороны ищутся в виде решения системы двух уравнений. Для начала выражаем значение одной стороны через другую и например площадь.Это выглядит так А=S/В=56/В Затем подставляем это выражение вместо буквы А в уравнении для периметра: Р=2(56/В + В)=30 Получаем что 56/В+В=15 В этом уравнении даже решать его не надо – любому человеку знакомому с таблицей умножения сразу видно, что 56 это произведение 7 и 8, а поскольку и сумма этих цифр как раз 15, то они и есть нужные нам значения сторон прямоугольника.
Хеленочка 8 лет назад Обозначим одну сторону буквой Х, другую – буквой Y. Площадь прямоугольника вычисляется умножением длин сторон, следовательно, мы можем составить первое уравнение: Х*Y=56 Периметр – это сумма длин сторон, следовательно, второе уравнение такое: 2Х+2Y=30 Получаем систему двух уравнений. По первому уравнению выделяем Х: Х=56:Y, подставляем это во второе уравнение: 2*56:Y+2Y=30 Отсюда уже легко найти значение Y: Y=7, тогда Х=8. Lilechka 9 лет назад Периметр 30, площадь 56. Назовем стороны прямоугольника а и с. Тогда можем составить такие уравнения: (а+c)х2=30 ахс=56 Далее решаем систему уравнений и находим, что стороны прямоугольника составляют 7 и 8 см.
moreljuba 7 лет назад Итак, для начала рассмотрим формулы для нахождения площади и периметра: 1) S = a * b = 56 см2; 2) Р = 2а + 2b = 30 см. Ведь мы знаем, что прямоугольник имеет по две одинаковых стороны. Таким образом нам требуется решить систему из двух уравнений: a * b = 56 2а + 2b = 30 Отсюда получаем, что одна сторона равна 7, а другая 8. Знаете ответ? |
Сторона прямоугольника по площади и другой стороне в м

Введите длину стороны a в м:
0.00м
S = a • b ⇒ b = S : a
S — площадь прямоугольника в м2 (квадратных метрах);
a — известная длина одной из сторон прямоугольника в м (метрах).
b — неизвестная длина другой стороны прямоугольника в м (метрах)
Например:
Площадь прямоугольника равна 192 м2, одна сторона равна 8 м. Найдите длину другой стороны прямоугольника.
Краткое решение: b = S : a = 192 : 8 = 24 м.
Площадь прямоугольника равна 144 м2, длина прямоугольника равна 18 м. Найдите его ширину.
Краткое решение: ширина прямоугольника b = S : a = 144 : 18 = 8 м.
/
/
/ Длина стороны квадрата
Длина стороны квадрата
Установить Длина стороны квадрата на мобильный
Найти длину стороны квадрата
зная площадь
|
||
| Площадь квадрата S | ||
|
|
||
| Результат |
Вычислить длину стороны квадрата
зная диагональ
|
||
| Диагональ квадрата d | ||
| Результат |
Скачать калькулятор
Рейтинг: 2.5 (Голосов 24)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного | Стороны равнобедренного | Стороны равностороннего |
| Стороны прямоугольника | Стороны ромба | Стороны параллелограмма | Ребро куба |
Александра
527 дн. назад
Клас клас клас!!! Не могла понять (сломала голову
- reply
Наталья
824 дн. назад
Класс!!! Не люблю считать. Вообще… Спасибо!!!
- reply
Николай
1023 дн. назад
Супер. И быстро. Мне нравится.
- reply
Добавить комментарий:
Я не робот