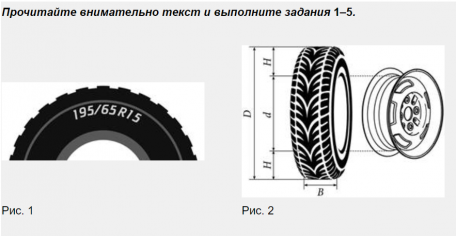
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине. Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис.1). Первое число (число 195 в приведенном примере) обозначает ширину шины в миллиметрах (параметр В на рисунке 2). Второе число (65 в приведенном примере) – процентное отношение высоты боковины (параметр Н на рисунке 2) к ширине шины, то есть 100•НВ . Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идет число, указывающее диаметр d диска колеса в дюймах ( в 1 дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит внедорожники определенной модели и устанавливает на них колеса с шинами маркировки 215/65 R16.
📜Теория для решения:
Посмотреть решение
Задание №1. Завод допускает установку шин с другими маркировками. В таблице показаны разрешенные размеры шин.
| Ширина шины (мм) | Диаметр диска (дюймы) | ||
| 16 | 17 | 18 | |
| 215 | 215/65 | 215/60 | – |
| 225 | 225/65; 225/60 | 225/55 | – |
| 235 | 235/60 | 235/55; 235/50 | 235/50 |
Шины какой наибольшей ширины можно устанавливать на автомобиль, если диаметр диска равен 17 дюймам? Ответ дайте в миллиметрах.
Решение
Смотрим по таблице на столбец, где указан диаметр диска – 17 дюймов. Движемся по столбцу вниз и просматриваем первые числа (ширину шины) в маркировках, нам надо найти наибольшую, в последней строке – это число 235. Значит наш ответ 235.
Ответ: 235
Задание №2. На сколько миллиметров радиус колеса с шиной маркировки 215/55 R17 меньше, чем радиус колеса с шиной маркировки 275/50 R17?
Решение
Прежде всего мы должны понимать, что высота колеса (диаметр колеса D) состоит из высоты шины Н, а их две, а также из диаметра диска . Если изобразить это в виде геометрического рисунка, то он будет выглядеть так, как показано на рисунке 2:
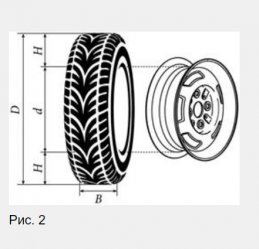
Значит, D=2H + d. Для удобства и последовательного решения задачи лучше составить таблицу, в которой и будем всё решать. В верхней строке записаны данные из условия. В первом столбце выписаны все параметры, которые будем находить.
Таблица 1
| 1 колесо
215/55 R17 |
2 колесо
275/50 R17 |
|
| Высота Н | ||
| Диаметр диска d | ||
| Диаметр колеса D | ||
| Радиус колеса | ||
| Разница в радиусах |
Теперь начинаем заполнять каждую строчку для 1 и 2 колеса, проводя вычисления.
| 1 колесо
215/55 R17 |
2 колесо
275/50 R17 |
|
| Высота Н | Запоминаем: для нахождения высоты выражаем второе число десятичной дробью и умножаем на первое число (так как второе число – процентное отношение высоты боковины к ширине шины). Чтобы выразить число % десятичной дробью, надо разделить его на 100! | |
| 55/100∙215=0,55∙215=118,25 | 50/100∙275=0,5∙275=137,5 | |
| Диаметр диска d | Так как диаметр диска дан в дюймах, то надо умножить последнее число маркировки шины (17) на количество дюймов в 1 мм, т.е. на 25,4 | |
| 17∙ 25,4=431,8 | 431,8 | |
| Диаметр колеса D | В начале решения нашей задачи, мы выяснили как найти диаметр колеса, это надо запомнить! D=2H + d. Находим диаметр в каждом случае, используя данные, которые нашли выше. | |
| 2∙118,25 + 431,8=668,3 | 2∙137,5 + 431,8=706,8 | |
| Радиус колеса | Помним, что радиус, это половина диаметра | |
| 668,3:2=334,15 | 706,8:2=353,4 | |
| Разница между радиусами | Для того, чтобы ответить на вопрос задания, надо найти разность между найденными радиусами | |
| 353,4 – 334,15=19,25 |
Ответ: 19,25
Задание №3. На сколько миллиметров увеличится диаметр колеса, если заменить колеса, установленные на заводе, колесами с шинами маркировки 235/50 R18?
Решение
Решение данного задания будем строить по принципу задания 2, так как требуется найти разницу в диаметрах между шинами заводской маркировки (смотрим в условии) 215/65 R16 и шинами маркировки 235/50 R18.
Сделаем таблицу, аналогичную таблице 1 (до строки диаметр колеса) и заполним её. Объяснения смотрим по заданию 2.
| 1 колесо
215/65 R16 |
2 колесо
235/50 R18 |
|
| Высота Н | 0,65∙215=139,75 | 0,5∙235=117,5 |
| Диаметр диска d | 16∙ 25,4=406,4 | 18∙ 25,4=457,2 |
| Диаметр колеса D | 2∙139,75 + 406,4=685,9 | 2∙117,5 + 457,2=692,2 |
| Разница между диаметрами колеса | Для того, чтобы ответить на вопрос задания, надо найти разность между найденными диаметрами | |
| 692,2 – 685,9=6,3 |
Ответ: 6,3
Задание №4. Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
Решение
С данными про колесо автомобиля, выходящего с завода (215/65 R16) мы встретились в задании 3. Надо найти диаметр, он найден в этом же задании 3 (смотрим таблицу с решением этого задания и находим соответствующее значение диаметра). Это значение равно 685,9.
Ответ: 685,9
Задание №5. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колеса, установленные на заводе, колесами с шинами маркировки 225/65 R16? Результат округлите до десятых.
Решение
Пробег автомобиля при одном обороте колеса – это длина окружности колеса. Значит, необходимо найти длину окружности, зная формулу l=2πR (данная формула есть в справочном материале ОГЭ). Зная, что диаметр – это два радиуса, формулу можем записать короче l=πD. Значение числа π не обязательно подставлять в формулу при решении задачи, удобнее использовать буквенное выражение.
Итак, нам надо найти диаметры двух колес, затем найти длины окружностей этих колес и сравнить их в процентном отношении. С маркировкой заводского колеса мы встречались, а данные ко второму колесу нужно найти. Итак, составим таблицу, аналогичную таблице 1, впишем в нее уже найденные значения заводского колеса (из задания 3) и найдем недостающие про «новое» колесо.
| 1 колесо (заводское)
215/65 R16 |
2 колесо
225/65 R16 |
|
| Высота Н | 139,75 | 0,65∙225=146,25 |
| Диаметр диска d | 406,4 | 406,4 (одинаковый с заводским) |
| Диаметр колеса D | 685,9 | 2∙146,25+406,4=698,9 |
| Длина окружности l=πD | 685,9π | 698,9π |
Итак, имеем две длины окружности, теперь надо найти, на сколько процентов увеличится пробег автомобиля при одном обороте колеса.
Заводское колесо 685,9π – 100%
Колесо на замену 698,9π – х %
Найдем значение х, используя правило пропорции: 698,9π ∙100685,9π=101,895…При решении числа π сократились, а значение % будет приближенное. Теперь найдем разницу между длинами окружностей 100% – 101, 895%=1,895%, округлим его, как сказано в условии – до десятых, получим 1,9 %. Наш ответ 1,9%.
Ответ: 1,9%
Общие советы и рекомендации по данному виду задач
Главное, с чем мы работаем в условии данной задачи, это маркировка шины.
Помните о том, что высота колеса – это его диаметр, состоящий из двух высот и одного диаметра диска (внутренняя металлическая часть колеса). Формулой D=2H+d придется пользоваться на протяжении нескольких заданий.
Для нахождения высоты переводим второе число маркировки в десятичную дробь (разделив на 100) и умножить его на первое число.
Используйте для решения таблицу, чтобы не запутаться при нахождении каких-либо данных.
Желаем удачи!
Ответ: см. решение
Алла Василевская | Просмотров: 11.5k
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
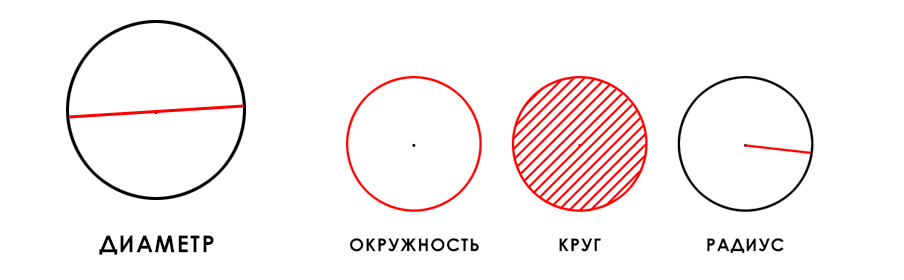
Что такое диаметр круга?
Диаметр круга – это отрезок, соединяющий две точки на окружности и проходящий через центр круга.
Если же говорить, про другие фигуры, то диаметром называется максимальное расстояние между точками этой фигуры. Диаметр круга – не исключение, так как это самый длинный отрезок, который можно провести в границах окружности.
Если нарисовать диаметр, то он будет выглядеть следующим образом (выделен красным на рисунке ниже).
Теперь давайте рассмотрим, как можно найти диаметр и какие для этого существуют формулы.
Формулы определения диаметра круга
Для определения диаметра существует несколько разных способов в зависимости от известных частей круга.
По радиусу
Самая простая формула определения диаметра может быть использована, если известен радиус круга. Радиус — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности. Диаметр равен двум радиусам.
d = r × 2
Где d – это диаметр, а r – радиус.
По длине окружности
Второй способ нахождения диаметра можно использовать тогда, когда известна длина окружности. Окружность — это замкнутая плоская кривая, все точки которой равноудалены от центра. Тако вот, диаметр равен длине окружности, делённой на число Пи.
d = L / π
Где d – это диаметр, а L – длина окружности, а π – константа, равная 3,14.
Эта формула, основывает на том, что отношение длины окружности к её диаметру всегда является постоянным числом, которое равняется примерно 3,14 и называется π (пи).
Через площадь круга
Чуть более изощренной и сложной является формула вычисления диаметра через площадь круга. Чаще всего требуется, наоборот, посчитать площадь круга, если известен диметр. Но если задача стоит обратная, то формула расчёта будет выглядеть следующим образом:
d = 2 × (S/π)1/2
Где d – диаметр, S – площадь круга, а π – константа, которая примерно равна 3,14.
То есть диаметр равен удвоенному корню частного площади круга к числу пи. Стоит отметить, что корень и степень ½ – это одно и то же.
Примеры вычисления диаметра
Давайте для закрепления рассмотрим несколько примеров.
Пример 1. Диаметр по длине окружности трубы 🚿
Предположим, у вас под рукой не оказалось штангенциркуля (устройства для измерения ширины изделий).

А вам требуется рассчитать диаметр действующей трубы, конца которой не видно. Для этого с помощью рулетки или сантиметра, вы можете измерить длину окружности, просто обернув рулетку вокруг трубы. А потом эту длину нужно будет разделить на 3,14. Если длина окружности трубы оказалась 31,4 сантиметра, тогда диаметр будет равен частному этой длинны к числу Пи, то есть:
d = 31,4 / 3,14 = 10 см.
Это и есть правильный ответ – 10 сантиметров.
Пример 2. Диаметр по колеса радиусу 🚲
Тут всё гораздо проще. Предположим, что вы знаете радиус колеса велосипеда – 10 дюймов. Какой будет диаметр?
Диаметру будет равен двум радиусам, то есть 20 дюймов.
Кстати, для справки, 1 дюйм = 2,54 сантиметра. То есть 10 дюймов = 25,4 сантиметра. В итоге диаметр колеса равен: 2 × 25,4 = 50,8 см.
❓Вопросы и ответы
И конечно же обратите внимание на ответы на часто задаваемые вопросы относительно расчёта длины диаметра круга.
Как работает ваш онлайн-калькулятор?
Просто. Вы выбираете, что известно: радиус, длина окружности или площадь круга (1), затем вписываете известное значение (2), выбираете размерность из мм, см, м, км (3) и нажимаете кнопку «рассчитать»?
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть различные калькуляторы, в частности калькуляторы: площади круга, длины окружности и диаметра. Для последнего калькулятор находится на данной странице.
Достаточно ли у меня данных для расчёта?
Для вычисления диаметра круга нужно что-то одно: радиус, длина окружности или площадь круга. Остальное вычислит наш калькулятор по специальным формулам, которые описаны выше.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Если у автомобильного колеса параметр R16, то какой у него диаметр?
16 дюймов, а радиус 8 дюймов. Как ни странно, диаметр такого колеса (точнее диска колеса) составляет 16 дюймов, то есть 40,64 см. Очень часто люди называют радиус в качестве единицы измерения: мол, радиус 16 дюймов. Но тогда представьте, для какого трактора диаметр диска будет более 80 сантиметров.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Наружный диаметр полого вала с учетом основного напряжения
Идти
Внешний диаметр полого вала = ((16*(Изгибающий момент в полом валу+sqrt(Изгибающий момент в полом валу^2+Крутящий момент в полом валу^2))/(pi*Максимальное основное напряжение в полом валу*(1-Отношение внутреннего к внешнему диаметру полого вала^4))))^(1/3)
Соотношение диаметров с учетом главного напряжения
Идти
Отношение внутреннего к внешнему диаметру полого вала = (1-(16*(Изгибающий момент в полом валу+sqrt(Изгибающий момент в полом валу^2+Крутящий момент в полом валу^2))/(pi*Внешний диаметр полого вала^3*Максимальное основное напряжение в полом валу)))^(1/4)
Главное напряжение – теория максимума главного напряжения
Идти
Максимальное основное напряжение в полом валу = 16*(Изгибающий момент в полом валу+sqrt(Изгибающий момент в полом валу^2+Крутящий момент в полом валу^2))/(pi*Внешний диаметр полого вала^3*(1-Отношение внутреннего к внешнему диаметру полого вала^4))
Соотношение диаметров с учетом угла поворота полого вала и жесткости на кручение
Идти
Отношение внутреннего к внешнему диаметру полого вала = (1-(584*Крутящий момент в полом валу*Длина полого вала/(Модуль жесткости полого вала*(Внешний диаметр полого вала^4)*Угол поворота полого вала)))^(1/4)
Наружный диаметр полого вала с учетом угла крутильной жесткости
Идти
Внешний диаметр полого вала = (584*Крутящий момент в полом валу*Длина полого вала/(Модуль жесткости полого вала*Угол поворота полого вала*(1-Отношение внутреннего к внешнему диаметру полого вала^4)))^(1/4)
Длина вала при заданном угле закручивания полого вала на основе жесткости на кручение
Идти
Длина полого вала = Угол поворота полого вала*(Модуль жесткости полого вала*(Внешний диаметр полого вала^4)*(1-Отношение внутреннего к внешнему диаметру полого вала^4))/(584*Крутящий момент в полом валу)
Момент кручения при заданном угле кручения на основе жесткости на кручение
Идти
Крутящий момент в полом валу = Угол поворота полого вала*(Модуль жесткости полого вала*(Внешний диаметр полого вала^4)*(1-Отношение внутреннего к внешнему диаметру полого вала^4))/(584*Длина полого вала)
Модуль жесткости при заданном угле закручивания полого вала на основе жесткости на кручение
Идти
Модуль жесткости полого вала = 584*Крутящий момент в полом валу*Длина полого вала/(Угол поворота полого вала*(Внешний диаметр полого вала^4)*(1-Отношение внутреннего к внешнему диаметру полого вала^4))
Угол поворота полого вала на основе жесткости на кручение
Идти
Угол поворота полого вала = 584*Крутящий момент в полом валу*Длина полого вала/(Модуль жесткости полого вала*(Внешний диаметр полого вала^4)*(1-Отношение внутреннего к внешнему диаметру полого вала^4))
Соотношение диаметров с учетом растягивающего напряжения в полом валу
Идти
Отношение внутреннего к внешнему диаметру полого вала = sqrt((1-(Осевая сила на полом валу/((pi/4)*Растягивающее напряжение в полом валу*Внешний диаметр полого вала^2))))
Отношение диаметра к заданному напряжению сдвига при кручении в полом валу
Идти
Отношение внутреннего к внешнему диаметру полого вала = (1-(16*Крутящий момент в полом валу/(pi*(Внешний диаметр полого вала^3)*Напряжение сдвига при кручении в полом валу)))^(1/4)
Наружный диаметр вала с учетом напряжения сдвига при кручении
Идти
Внешний диаметр полого вала = (16*Крутящий момент в полом валу/(pi*Напряжение сдвига при кручении в полом валу*(1-Отношение внутреннего к внешнему диаметру полого вала^4)))^(1/3)
Напряжение сдвига при кручении, когда вал подвергается воздействию чистого крутящего момента
Идти
Напряжение сдвига при кручении в полом валу = 16*Крутящий момент в полом валу/(pi*(Внешний диаметр полого вала^3)*(1-(Отношение внутреннего к внешнему диаметру полого вала^4)))
Крутящий момент при напряжении сдвига в полом валу
Идти
Крутящий момент в полом валу = Напряжение сдвига при кручении в полом валу*(pi*Внешний диаметр полого вала^3*(1-Отношение внутреннего к внешнему диаметру полого вала^4))/16
Наружный диаметр полого вала с учетом напряжения изгиба полого вала
Идти
Внешний диаметр полого вала = (32*Изгибающий момент в полом валу/(pi*Напряжение изгиба в полом валу*(1-Отношение внутреннего к внешнему диаметру полого вала^4)))^(1/3)
Соотношение диаметров с учетом напряжения изгиба полого вала
Идти
Отношение внутреннего к внешнему диаметру полого вала = (1-(32*Изгибающий момент в полом валу/(pi*Внешний диаметр полого вала^3*Напряжение изгиба в полом валу)))^(1/4)
Изгибающий момент при изгибающем напряжении полого вала
Идти
Изгибающий момент в полом валу = Напряжение изгиба в полом валу*(pi*(Внешний диаметр полого вала^3)*(1-(Отношение внутреннего к внешнему диаметру полого вала^4)))/32
Напряжение изгиба полого вала
Идти
Напряжение изгиба в полом валу = 32*Изгибающий момент в полом валу/(pi*Внешний диаметр полого вала^3*(1-Отношение внутреннего к внешнему диаметру полого вала^4))
Осевая сила растяжения при заданном растягивающем напряжении в полом валу
Идти
Осевая сила на полом валу = Растягивающее напряжение в полом валу*((pi/4)*(Внешний диаметр полого вала^2-Внутренний диаметр полого вала^2))
Растягивающее напряжение в полом валу под действием осевой силы
Идти
Растягивающее напряжение в полом валу = Осевая сила на полом валу/((pi/4)*(Внешний диаметр полого вала^2-Внутренний диаметр полого вала^2))
Внутренний диаметр полого вала при заданном соотношении диаметров
Идти
Внутренний диаметр полого вала = Отношение внутреннего к внешнему диаметру полого вала*Внешний диаметр полого вала
Наружный диаметр при заданном соотношении диаметров
Идти
Внешний диаметр полого вала = Внутренний диаметр полого вала/Отношение внутреннего к внешнему диаметру полого вала
Отношение внутреннего диаметра к внешнему диаметру
Идти
Отношение внутреннего к внешнему диаметру полого вала = Внутренний диаметр полого вала/Внешний диаметр полого вала
При помощи нашего калькулятора вы легко сможете узнать диаметр круга или окружности.
Для того что бы вычислить диаметр круга необходимо знать его длину или площадь. Если нам известа одна из указаннх величин, для нас не составит труда вычислить диаметр круга.
Диаметр круга рассчитывается по следующим формулам:
- Если нам известна длина:
Формула для расчета диаметра круга через его длину:
D=P/π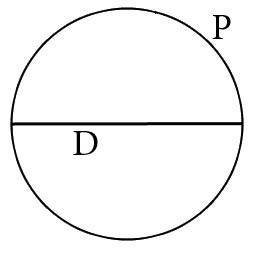
- Если нам известна площадь:
Формула для расчета диаметр круга через площадь:
D=2√
S/π
- Если нам известен диаметр:
Формула для расчета диаметр круга через радиус:
D=2R
Где D – диаметр круга, S – площадь круга, P – длина круга, R – радиус, π – число Пи которое всегда примерно равно 3,14.
#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳
Здравствуйте, уважаемые читатели канала Хакнем Школа!
По многочисленным просьбам читателей в комментариях к статье с задачами из ОГЭ по математике на «мобильную связь» публикуем статью с решением задач «с шинами».
Обращаю внимание читателей (особенно тех, кто не знаком с этими задачами) на то, что есть общее условие к заданиям №№ 1- 5, и к каждому заданию есть отдельное условие, будьте внимательны. Задачи взяты с сайта СтатГрад 2020 − 2021 уч. г.).
Но прежде, чем решать задачи, давайте выпишем из условия все величины и формулы, которые нам понадобятся. Итак,
По условию шина с завода имеет маркировку 175/70 R12:
В (первое число) — обозначает ширину шины, в мм, В = 175 мм;
Н (второе число) — высота боковины, при этом Н/В×100 % = 70 % ,
70 % = 0,70, отсюда можно выразить Н = В × 0,70
d — диаметр диска в дюймах, d = 12 дюймов, 1 дюйм = 25,4 мм
D — диаметр колеса, в мм, из рис. 2 видно, что
D = 2H + d. Итак, приступаем к решению задач.
Задание 1
Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
Шины какой наибольшей ширины можно устанавливать на автомобиль, если диаметр диска равен 13 дюймам? Ответ дайте в миллиметрах.
Решение:
Эта задача не требует даже никаких вычислений. Ширина шины (в мм) это B — первое число в обозначении маркировки шины. Если диаметр диска равен 13 дюймам, мы видим из таблицы, к нему допускается ширина шины 175,185,195 мм. И наибольшее из них число — 195. Это и есть искомое число.
Ответ : 195.
Задание 2
Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
Решение
Итак, требуется найти диаметр колеса D из условия: 175/70 R12. Напомню, что D = 2H + d. Таким образом, нам нужно прежде всего найти H и d .
1) Из условия значение d = 12 дюймов, переведём его в мм (по условию 1 дюйм = 25,4 мм).
d = 12× 25,4 = 304,8 мм;
2) Найдём Н (помним, что В = 175 мм , Н = В×0,70)
Н = 175×0,7 = 122,5 мм;
3) Найдём D = 2H + d = 2×122,5 + 304,8 = 549,8 мм.
Ответ : 549,8 мм.
По сути своей, эта задача содержит всего 3 действия на вычисления десятичных дробей, фактически это задача для 5-го класса.
Задание 3
На сколько миллиметров радиус колеса с шиной маркировки 185/60 R 13 меньше, чем радиус колеса с шиной маркировки 175/65 R 13 ?
Решение
Это задание практически повторяет задание 2, только во 2 задании мы находили диаметр колеса D, а в этом нужно найти радиусы. Но все мы помним, что r = D / 2 .
Усложнена задача только тем, что нужно найти r колеса с маркировкой 185/60 R 13 и сравнить его с радиусом колеса с завода с маркировкой 175/65 R 13.
1) Найдём r колеса с маркировкой 185/60 R 13 (B = 185 мм, Н = В×0,60, d = 13 дюймов или 13 дюймов = 13 × 25,4 = 330,2 мм).
H = 185 × 0,60 = 111 мм.
D = 2H + d = 2 × 111 + 330,2 = 552,2 мм
r = 552,2 / 2 = 276,1 мм.
2) Найдём r колеса с маркировкой 175/65 R 13 (В = 175 мм и H = B × 0,65, d тот же и равен 330,2 мм). Ход решения тот же:
H = 175 × 0,65 = 113,75 мм.
D = 2H + d = 2 × 113,75 + 330,2 = 557,7 мм
r = 557,2 / 2 = 278,85 мм.
3) Найдём разницу между полученными радиусами:
278,85 – 276,1 = 2,75 мм.
Ответ : 2,75.
Задание 4
На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 195/60 R13?
Решение
Ход рассуждения, аналогичен задаче № 3. Кроме того, D колеса с завода мы находили в задаче № 2, воспользуемся её данными: D = 549,8 мм.
1) Найдём диаметр колеса D с шиной маркировки 195/60 R13:
H = 195 × 0,60 = 117 мм;
d = 13 дюймов или 330,2 мм (находили в задаче 3);
D = 2H + d = 2 × 117 + 330,2 = 564,2 мм.
2) Найдём разницу:
564,2 – 549,8 = 14,4 мм.
Ответ : 14,4.
Задание 5
На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 175/65 R 13? Результат округлите до десятых.
Решение
В этой задаче мы должны применить свои знания из курса геометрии, ну и задачи на проценты.
Что такое 1 оборот колеса? Это длина окружности (колеса) .
Длина окружности вычисляется по формуле: С = 2π r, где r — радиус колеса, D = 2 r , и формулу длины окружности можно записать как: С = Dπ
1) Диаметр колеса, установленного на заводе, мы находили в задаче
№ 2, D = 549,8 мм.
Тогда, оборот 1 колеса равен: C = Dπ = 549,8π (не спешите умножать на 3,14, нам это не понадобится).
2) Диаметр колеса с маркировкой 175/65 R 13 возьмём из задачи 3:
D = 557,7 мм,
тогда, оборот 1 колеса равен: C = Dπ = 557,7π.
3) Итак,
549,8π — 100 %
557,7π — x %
Составим и решим уравнение:
549,8πx = 557,7π×100
х = 101,4 (приближенно до десятых)
2) Найдём изменение 101,4 %– 100 % = 1,4 %.
Ответ : 1,4 .
Итак, мы прорешали с Вами 5 из 25 задач из ОГЭ по математике. Напоминаю читателям о том, что каждое из заданий №№ 1-5 оценивается по 1 баллу.
НО! Хочу напомнить, что для прохождения аттестационного порога необходимо набрать не менее 8 баллов, из которых не менее 2-х баллов должны быть получены за решение задач по геометрии (задания 15 – 19, 23 – 25).
Кроме первой, во всех задачах наше решение «крутилось» вокруг диаметра колеса D, и вычисления были очень похожи. К сожалению, надо отметить, что именно вычисления и пугают девятиклассников, ведь даже, если вы хорошо считаете, вычисления достаточно объёмные и требуют значительных временных затрат, ну и конечно достаточно объёмное первоначальное условие к задачам. Если вы не можете решить все 5 заданий (хотя бы из-за отсутствия времени), решите для начала 3, потом можно к ним вернуться.
Если Вы прорешаете хотя бы 2-3 таких варианта заранее, я уверена, вы справитесь с ними и на экзамене! Удачи в подготовке! И я надеюсь, моя статья Вам в этом поможет!
Читайте наш канал в телеграм – по этой ссылке
Автор: #ирина_чудневцева руководитель канала Хакнем Школа, 42 года, город Ярославль
