-

1
Запишите двоичные числа друг под другом — меньшее число под большим. Если меньшее число имеет меньше цифр, выровняйте его по правому краю (так, как вы записываете десятичные числа при их вычитании).
-

2
Некоторые задачи на вычитание двоичных чисел ничем не отличаются от вычитания десятичных чисел. Запишите числа друг под другом и, начиная справа, найдите результат вычитания каждой пары чисел. Вот несколько простых примеров:
- 1 – 0 = 1
- 11 – 10 = 1
- 1011 – 10 = 1001
-

3
Рассмотрим более сложную задачу. Необходимо запомнить только одно правило, чтобы решать задачи на вычитание двоичных чисел. Это правило описывает заимствование цифры слева, чтобы вы могли вычесть 1 из 0 (0 – 1). Решим две задачи при помощи метода заимствования.
- 110 – 101 = ?
-

4
В первом столбце справа вы получаете разность 0 – 1. Для ее вычисления необходимо позаимствовать цифру слева (из разряда десятков).
- Во-первых, зачеркните 1 и замените ее на 0, чтобы получить такую задачу: 10
10 – 101 = ? - Вы вычли («позаимствовали») 10 из первого числа, поэтому вы можете написать это число вместо цифры, стоящей справа (в разряд единиц). 10
1100– 101 = ?
- Во-первых, зачеркните 1 и замените ее на 0, чтобы получить такую задачу: 10
-

5
Вычтите цифры в правом столбце. В нашем примере:
- 10
1100– 101 = ? - Правый столбец: 10 – 1 = 1. Если вы не поняли, как получить такой ответ, прочитайте эту статью:
- 102 = (1 x 2) + (0 x 1) = 210 (цифры нижнего регистра обозначают систему счисления, в которой записаны числа).
- 12 = (1×1) = 110.
- Таким образом, в десятичной системе эта разность записывается в виде: 2 – 1 = 1.
- 10
-

6
Вычтите цифры в оставшихся столбцах. Теперь это легко сделать (работайте со столбцами, двигаясь справа налево):
- 10
1100– 101 = __1 = _01 = 001 = 1.
- 10
-

7
Решите сложную задачу. В таких задачах придется «заимствовать» цифры несколько раз только для того, чтобы вычесть цифры в одном столбце. Например, решите следующую задачу: 11000 – 111. Нельзя «заимствовать» цифры у 0, поэтому передвигайтесь к следующей цифре слева (до тех пор, пока вы не достигнете 1).
- 10
110000 – 111 = -
10
111001000 – 111 = (запомните: 10 – 1 = 1) - 10
111001100100– 111 = - Вот как это записывается в более понятном виде: 101110
0– 111 = - Вычислите разность цифр во всех столбцах (двигаясь справа налево): _ _ _ _ 1 = _ _ _ 0 1 = _ _ 0 0 1 = _ 0 0 0 1 = 1 0 0 0 1
- 10
-

8
Проверьте ответ. Есть три способа сделать это.[1]
Быстрый способ — откройте двоичный онлайн калькулятор и введите в него условия задачи. Два других метода подразумевают проверку ответа вручную (они могут пригодиться вам на экзамене).- Сложите двоичные числа, чтобы проверить ответ. Сложите ответ с меньшим числом; вы должны получить большее число. В последнем примере (11000 – 111 = 10001): 10001 + 111 = 11000, то есть ответ правильный.
- Кроме того, вы можете преобразовать двоичные числа в десятичные и проверить ответ. В последнем примере (11000 – 111 = 10001) при преобразовании вы получите: 24 – 7 = 17, то есть ответ правильный.
Реклама
-

1
Запишите двоичные числа друг под другом так, как вы записываете десятичные числа при их вычитании. Этот метод используется компьютерами для вычитания двоичных чисел, так как он основан на более эффективном алгоритме. Однако простому человеку, привыкшему вычитать десятичные числа, этот метод может показаться более сложным (если вы программист, обязательно ознакомьтесь с этим методом вычитания двоичных чисел).[2]
- Рассмотрим пример: 101 – 11 = ?
-

2
Если значность чисел разная, к числу с меньшей значностью слева припишите соответствующее количество 0. Например, если даны числа 101 (трехзначное) и 11 (двузначное), превратите двузначное число в трехзначное, приписав ему слева один 0: 011.
- 101 – 011 = ?
-

3
В вычитаемом числе поменяйте цифры: каждую 1 поменяйте на 0, а каждый 0 на 1. В нашем примере вычитаемое превращается в:
011→ 100.- На самом деле мы «забираем дополнение у единицы», то есть вычитаем каждую цифру из 1. Это работает в двоичной системе, так как у такой «замены» может быть только два возможных результата: 1 – 0 = 1 и 1 – 1 = 0.
-

4
-

5
Теперь вместо вычитания сложите два двоичных числа.
- 101 + 101 = 1010
- Если вы не знаете, как складывать двоичные числа, прочитайте эту статью.
-

6
В полученном результате игнорируйте любую цифру, стоящую первой слева (так как вы получили число не той значности). В нашем примере вы складывали трехзначные числа (101 + 101), а получили четырехзначный ответ (1010). Поэтому зачеркните первую цифру слева, и вы получите окончательный ответ вашей задачи.[3]
-
1010 = 10 - Таким образом, 101 – 011 = 10
- Если лишней цифры нет, то вы вычитали большее число из меньшего. Смотрите раздел «Советы» о том, как решать такие задачи.
-
-

7
Попробуйте применить этот метод к десятичным числам. Этот метод называется «дополнение к двойке», так как замена цифр приводит к «дополнению к единице», а затем к полученному числу прибавляется 1.[4]
Для лучшего уяснения этого метода рассмотрим следующий пример:- 56 – 17
- Так как в примере рассматриваются десятичные числа, то каждую цифру вычитаемого (17) вычтите из 9: 99 – 17 = 82.
- Сложите два числа: 56 + 82. Если вы сравните это суммирование с исходной задачей (56 – 17), то вы увидите, что к исходной задаче прибавили 99.
- 56 + 82 = 138. Так как к исходной задаче прибавили 99, нужно вычесть 99 из ответа. Необходимо действовать аналогично вычислениям с двоичными числами: прибавьте к результату 1, а затем игнорируйте первую цифру слева.
-
138 + 1 = 139 →
139 → 39. Это решение исходной задачи (56 – 17 = 39).
Реклама
Советы
- Для вычитания большего числа из меньшего, вычтите меньшее число из большего, а к ответу припишите знак «минус». Например, чтобы вычислить 11 – 100, вычислите 100 – 11, а затем к ответу припишите знак «минус» (это правило относится к вычитанию чисел в любой системе счисления, а не только в двоичной системе).
- Метод дополнения работает следующим образом: a – b = a + (2n – b) – 2n. Если n равно разрядности b, то 2n – b на единицу больше результата вычитания каждого разряда.
Реклама
Об этой статье
Эту страницу просматривали 132 608 раз.
Была ли эта статья полезной?
Операция вычитания является обратной к операции сложения. В разных системах счисления выполняется почти одинаково. Самое важное отличие, которое меняет процесс вычитания это количество чисел.
Поскольку во всех системах счисления цифры начинаются с нуля, то количество цифр сводится к максимально допустимой цифре.
К примеру, в десятичной системе счисления максимальная цифра девять, а вот в троичной – двойка.
При вычитании (в столбик) когда вычитаем большее число из меньшего, то занимаем у старшего разряда “десяток”. Значение “десяток” будет меняться в зависимости от системы счисления, в которой будем производить операцию вычитания.
Для начала повторим, как работает вычитание в десятичной системе счисления, чтобы стало понятнее, как работает это в разных системах счисления.
Вычитание в десятичной системе счисления
Посчитаем разность 178 и 89. Операцию будем выполнять в столбик для наглядности.
Действия распишем поэтапно:
- 8 – 9 (вычесть не можем, занимаем у старшего разряда) → 18 – 9 = 9;
- 6 – 8 (вычесть не можем, занимаем у старшего разряда) → 16 – 8 = 8;
- Поскольку у единицы тоже занимали, то она превратилась в ноль
Вычитание в двоичной системе счисления
Когда будем занимать “десяток” в двоичной системе счисления из старшего разряда, то прибавляться будет уже не 10, а всего лишь двойка. Рассмотрим так же на примере. Посчитаем разность 10000 и 111 в двоичной системе счисления. Операцию опять же выполним в столбик.
Распишем действия поэтапно:
- 0 – 1 (вычесть не можем, занимаем у самого старшего разряда, т.к. все остальные тоже нули) → 2 – 1 = 1;
- 1 – 1 = 0 (тут единица поскольку заняли у единицы, а потом постепенно перешло по младшим разрядам);
- 1 – 1 = 0;
- Единицу спускаем;
- Спускаем ноль, так как занимали
Получили ответ в двоичной системе счисления.
Вычитание в шестнадцатеричной системе счисления
Хорошим примером будет также и шестнадцатеричная система счисления. Здесь операция вычитания выглядит сложнее из-за “буквенных” цифр. Главное — их сразу представлять с их значениями, и тогда счёт будет легче.
Здесь уже в качестве десятка выступает число шестнадцать. Посчитаем разность 1AB и FE.
Распишем действия поэтапно:
- B – E → 11 – 14 (вычесть не можем, занимаем у старшего разряда) → 27 – 14 = 13 (D);
- 9 – F → 9 – 15 (вычесть не можем, занимаем у старшего разряда) → 25 – 15 = 10 (A);
- Спускаем ноль, так как занимали.
В операции вычитания при занятии у старшего разряда в любой системе счисления, в младший разряд прибавляется число, равное основанию системы счисления.
Понравилась статья? Хочешь разбираться в информатике, программировании и уметь работать в разных программах? Тогда ставь лайк, подпишись на канал и поделись статьей с друзьями!
Читайте также:
#информатика #системы счисления #школьная информатика #образование #арифметика #вычитание
#статьи
- 27 фев 2023
-
0
Двоичная арифметика: сложение, умножение, вычитание, деление бинарных чисел
Учимся складывать, вычитать, умножать и делить двоичные числа — работаем с фундаментальными законами современной цифровой электроники.
Иллюстрация: Катя Павловская для Skillbox Media

Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.
Мы привыкли считать всё в десятичной системе, потому что у нас 10 пальцев — и это удобно. Но если бы у нас было больше пальцев, например 12, то система могла бы быть двенадцатиричной и мы бы воспринимали её как обычную.
Когда дело доходит до двоичной системы счисления, сложно вот так сразу переключиться на её арифметику — хотя, казалось бы, принципы такие же, как для десятичной. Ведь там есть все привычные операции: сложение, вычитание, умножение, деление. Единственное отличие: в двоичных числах используются всего две цифры — ноль и единица.
Давайте избавимся от страха и наконец узнаем, как проводить знакомые нам математические операции в двоичной системе.
Правила сложения двоичных чисел похожи на привычные нам: сложение происходит поразрядно справа налево, при этом важно помнить о переносе чисел в новый разряд.
В десятичной системе у нас всего 10 цифр: от 0 до 9. Когда мы складываем 1 и 9, у нас получается переполнение, так как больше 9 в одном разряде нельзя записать. Поэтому мы переносим единицу в следующий, получаем 10.
Двоичная система работает аналогично: чтобы понять, как складывать числа, нужно помнить об этом переполнении. Всего в двоичной системе две цифры — 0 и 1. Если сложить 1 и 1, мы получим переполнение, а значит, единица пойдёт в следующий разряд, результатом станет 10 (только не «десять», а «один-ноль»).
Если представить правила сложения двоичных чисел в общем виде, получим такую таблицу:
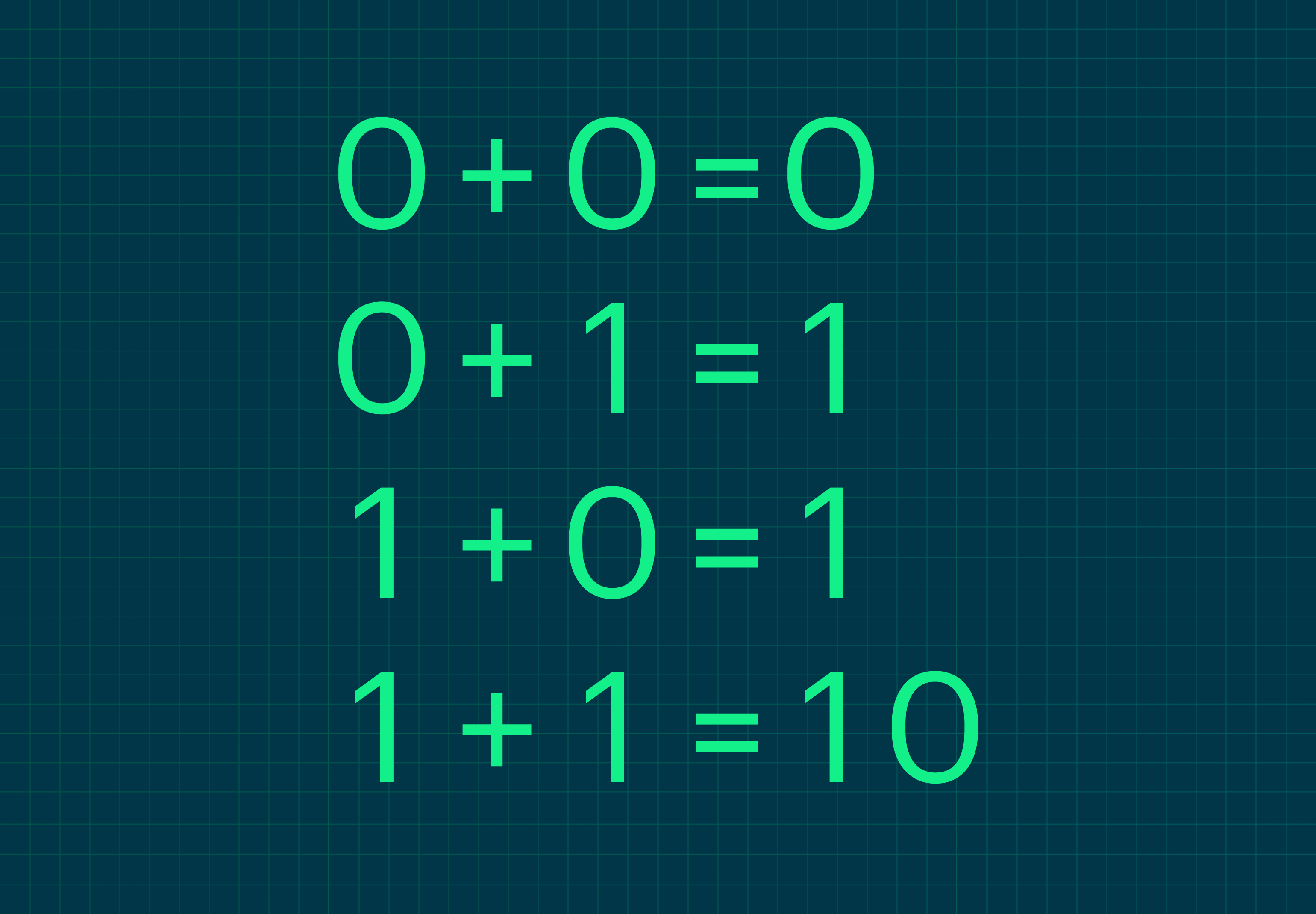
Но лучше разобраться на примерах.
Пример 1. Давайте сложим 1100 и 101.
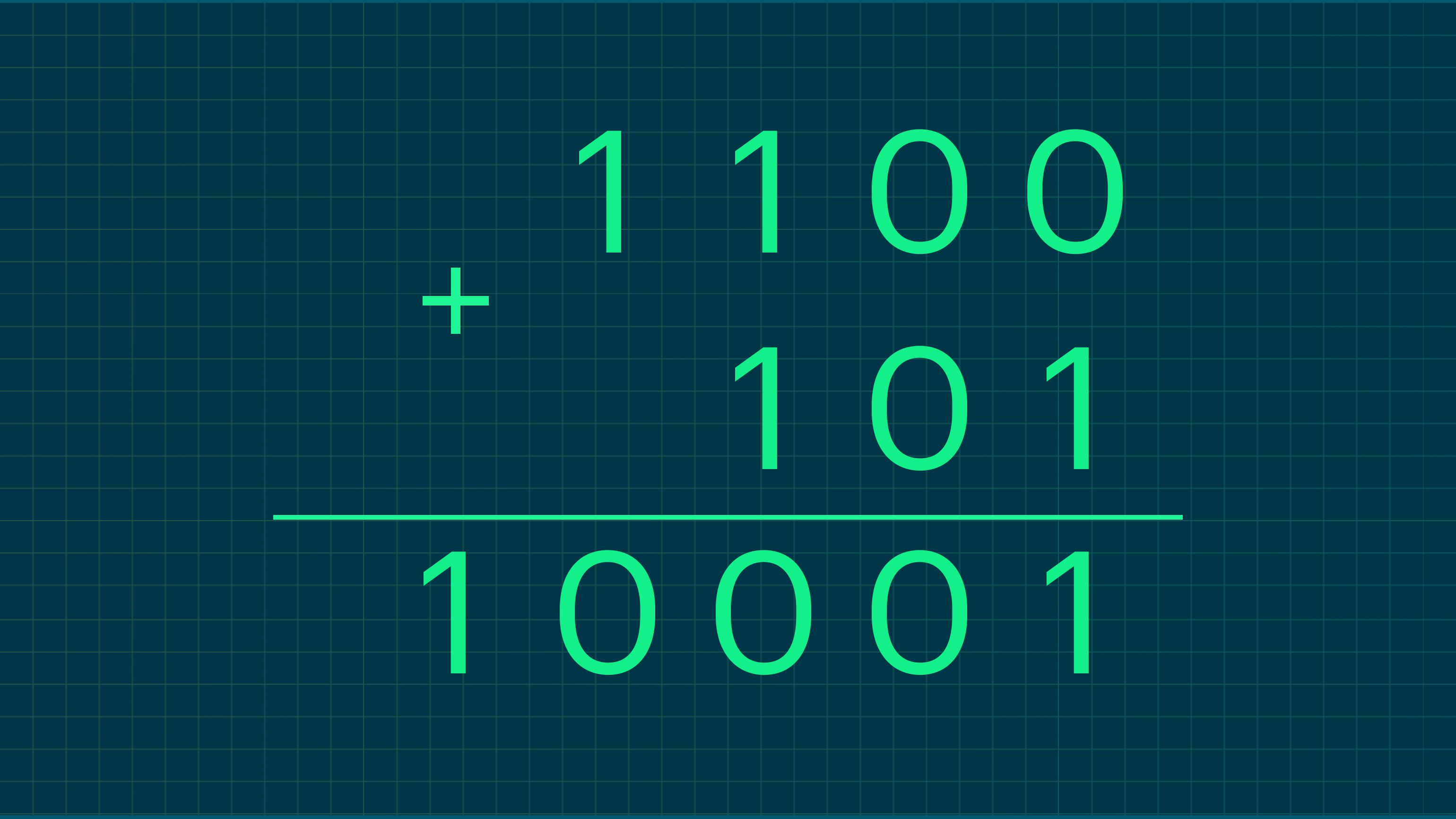
Рассмотрим пример подробнее. Как мы уже упоминали ранее, сложение происходит справа налево. Разряды считаются тоже справа налево:
- Первый: 0 + 1 = 1.
- Второй: 0 + 0 = 0.
- Третий: 1 + 1 = 10 — переполнение, единица переходит в следующий разряд.
- Четвёртый: 1 + 0 + 1 = 10 — добавляем единицу из прошлого разряда, получаем переполнение, единица переходит в следующий разряд.
- Пятый: 0 + 0 + 1 = 1 — единица пришла из предыдущего разряда.
Пример 2. Сложим 1111 и 111.

Теперь поразрядно:
- Первый: 1 + 1 = 0 — единица переходит в следующий разряд.
- Второй: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Третий: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Четвёртый: 1 + 0 + 1 = 0 — единица переходит в следующий разряд.
- Пятый: 0 + 0 + 1 = 1.
Вроде бы пока несложно. Так что попробуйте сами сложить 1101 и 1011, чтобы закрепить знания.
Ответ
1101 + 1011 = 11000.
Умножение в двоичной системе, как в десятичной, основано на сложении — и умении считать в столбик.
Сведём в таблицу правила умножения двоичных чисел:
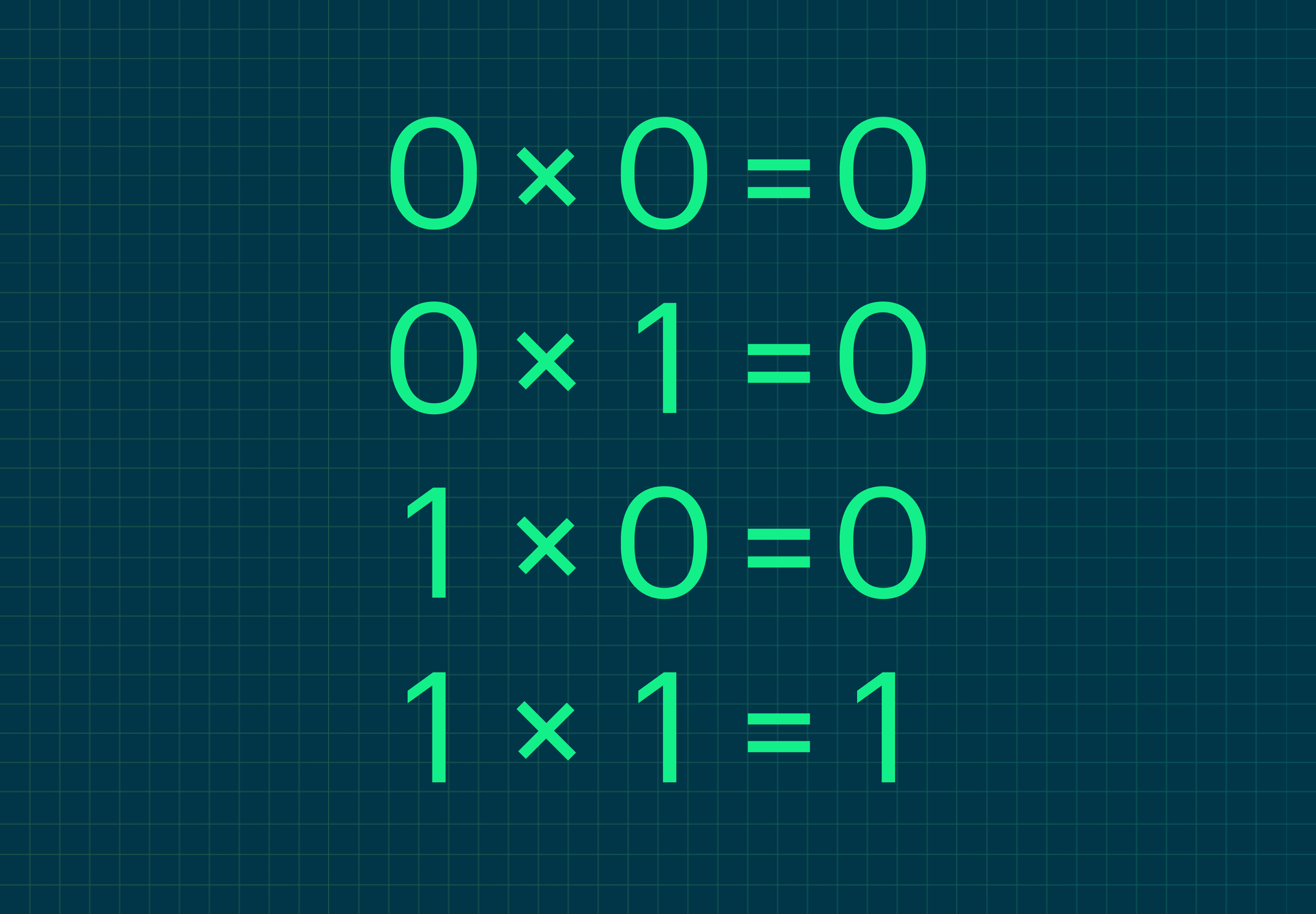
Давайте теперь посмотрим на реальных примерах, как правильно умножать двоичные числа.
Пример 1. Умножим 110 на 10.
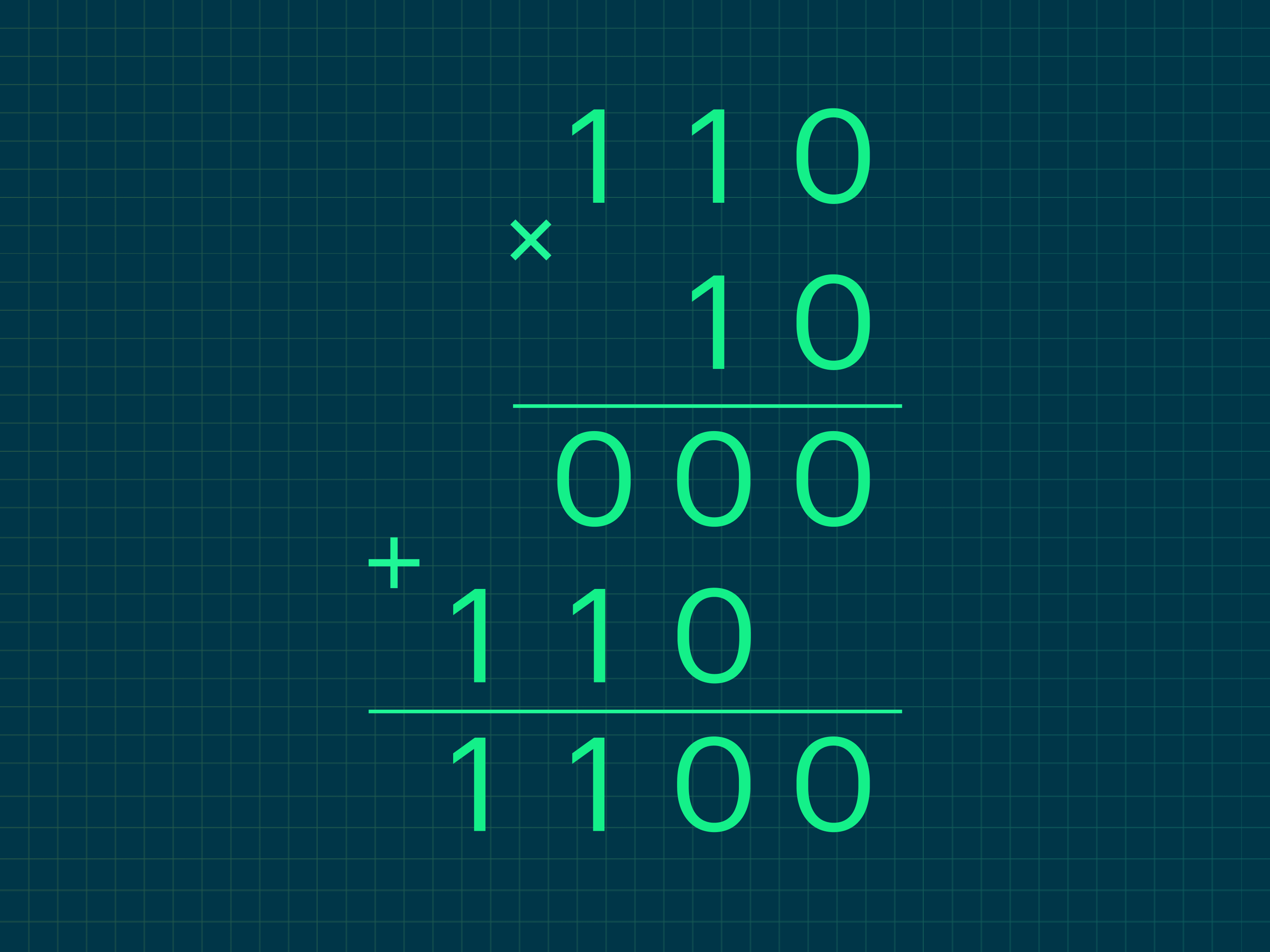
Здесь мы воспользуемся привычным школьным «столбиком»: сначала умножаем верхнее число, 110, на 0, затем на 1, а потом складываем полученные два и получаем результат.
По сути, если мы умножаем число на ноль, то оно превращается в ноль, а если на единицу — остаётся неизменным, но сдвигается на число разрядов, равное номеру разряда этой единицы, как в обычном умножении:
- 110 × 0 = 000;
- 110 × 1 = 110.
Сдвигаем 110 на один разряд влево и складываем результаты промежуточных умножений:
- 000 + 1100 = 1100.
Мы получили 1100, потому что сместили результат умножения 110 × 1 на один разряд влево, а затем добавили один 0 справа — как в обычном умножении.
Пример 2. Давайте теперь умножим 101 на 101.

Не пугайтесь, что у нас получилось три числа, которые нужно сложить: правила остаются теми же. Ещё можно приписывать дополнительные нули туда, где находится пустое пространство — это поможет не запутаться.
Разберём пошагово:
- 101 × 1 = 101;
- 101 × 0 = 000;
- 101 × 1 = 101.
Снова сдвигаем влево промежуточные результаты и складываем:
- 101 + 0000 + 10100 = 11001.
Попробуйте сами умножить 1101 на 111.
Ответ
1011011.
Правила двоичного вычитания тоже ничем не отличаются от десятичного. Мы также вычитаем поразрядно и, если нужно, занимаем единицу из старшего разряда.
Таблица вычитания выглядит так:
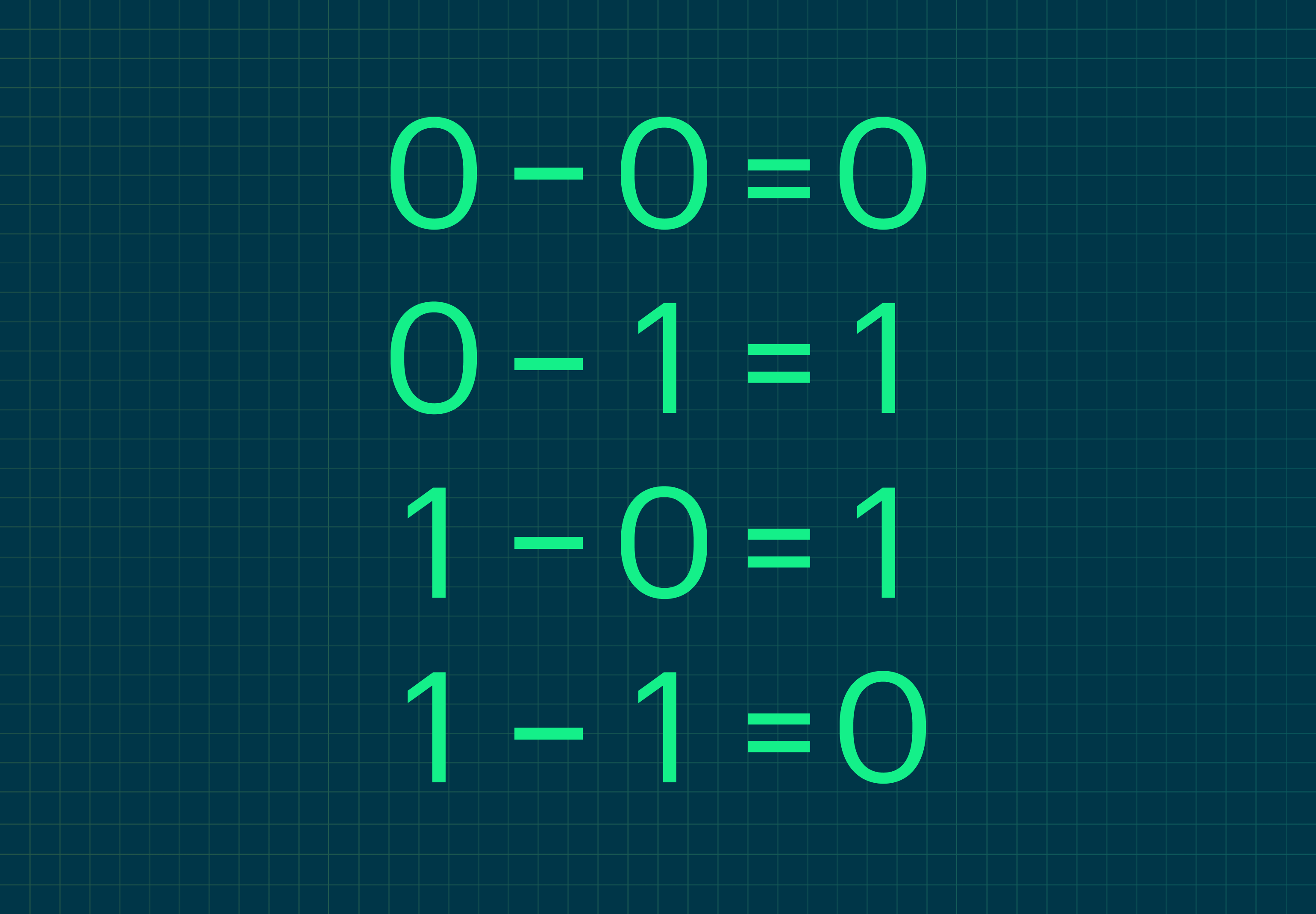
Заметьте, что 0 − 1 = 1. Это всё потому, что мы занимаем единицу из старшего разряда и получаем 10, или 2 в десятичной системе, а если вычесть из 10 число 1, получим 1 (ведь 2 − 1 = 1).
Перейдём к примерам, чтобы понять, как вычитать одно число из другого.
Пример 1. Вычтем из 1100 число 11.
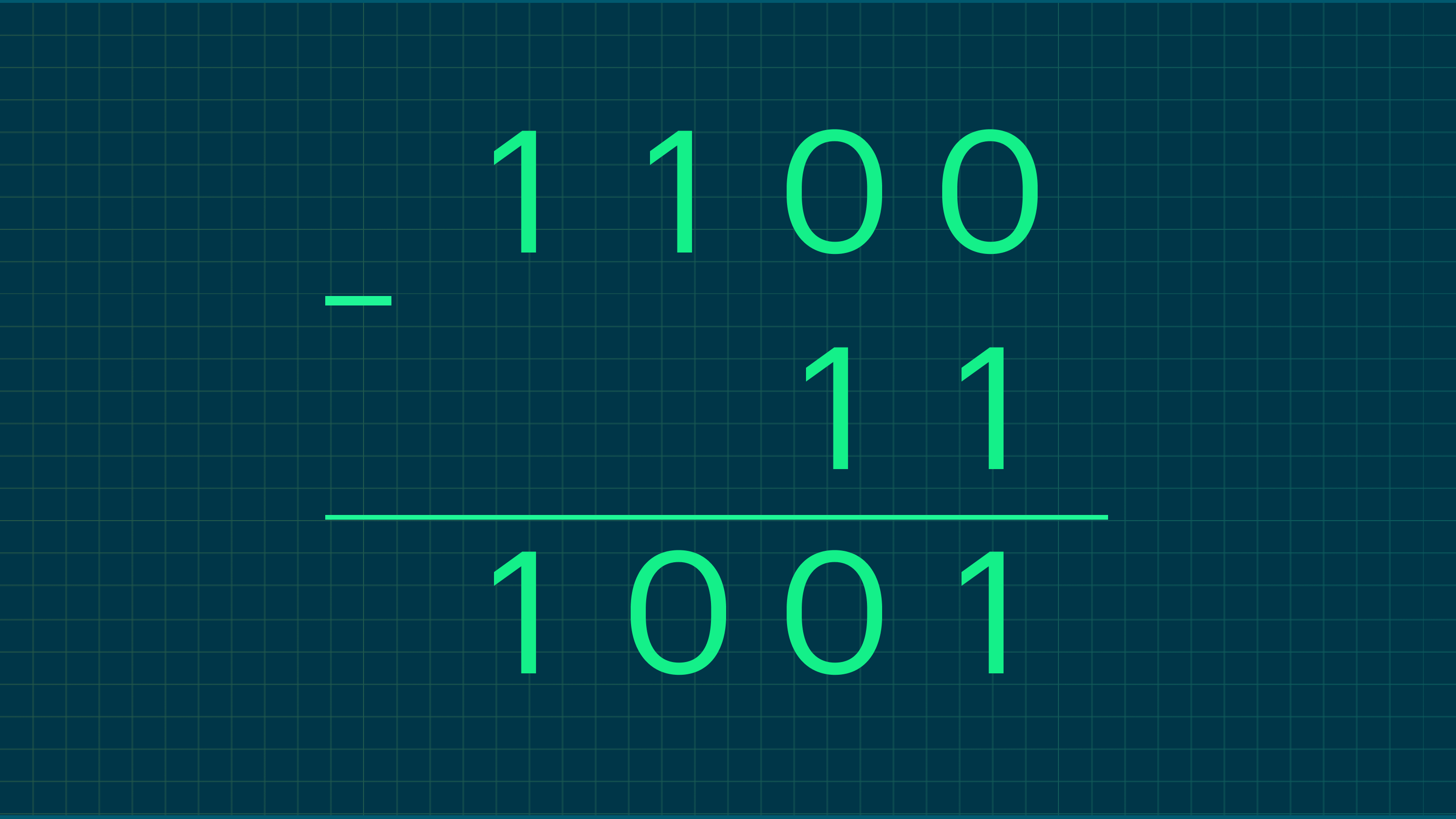
Разберём подробнее поразрядно:
- Первый: 0 − 1 = 1 — занимаем единицу из старшего разряда.
- Второй: 1 − 1 = 0 — так как отсюда заняли единицу, но у нас её не было, мы взяли её из следующего разряда и вычли единицу из этого.
- Третий: 0 − 0 = 0 — из этого разряда единица ушла в первый.
- Четвёртый: 1 − 0 = 1 — здесь всё нормально.
Всё то же знакомое нам вычитание.
Пример 2. Вычтем из 1011 число 101.

Тот же алгоритм по разрядам:
- Первый: 1 − 1 = 0.
- Второй: 1 − 0 = 1.
- Третий: 0 − 1 = 1 — заняли единицу из следующего разряда.
- Четвёртый: 0 − 0 = 0 — отдали единицу в предыдущий разряд.
Кажется, что всё несложно. Попробуйте теперь сами вычесть из 11010 число 1111.
Ответ
1011.
Вы удивитесь, но правила деления двоичных чисел похожи на деление десятичных. Рисуем привычный «столбик», умножаем, вычитаем, получаем результат.
Таблицы тут нет, потому что она бессмысленна — давайте сразу на примерах разбирать, как делить двоичные числа.
Пример 1. Поделить 1100 на 10.

У нас есть только два варианта: умножить делитель на 1 или на 0. Поэтому алгоритм будет таким:
- Смотрим на делимое, видим, что первые две его цифры — 11. Умножаем делитель на 1 и вычитаем из 11 число 10.
- Получили 1, дописываем справа следующую по порядку цифру — 0. Теперь 10 равно делителю, значит, тоже умножаем его на 1 и вычитаем.
- Получаем 0. Но у нас ещё остался один 0 у делимого — дописываем его справа от полученного 0.
- Число 0 меньше, чем 10, поэтому умножаем делитель на 0. Получаем конечный ответ — 110.
Пример 2. Поделить 10010 на 110.

Пошаговый алгоритм:
- Первые три числа делимого меньше, чем делитель — значит, умножаем делитель на 0 и вычитаем. Получаем 100.
- Дописываем 1 справа от 100, видим, что 1001 больше, чем 110, поэтому умножаем делитель на 1 и вычитаем его из 1001. Получаем 11.
- Дописываем 0 справа. Полученное 110 равно делителю, поэтому тоже умножаем его на 1, получаем конечный результат.
Попробуйте сами теперь поделить 10100 на 100.
Ответ
101.
Двоичная арифметика во многом похожа на десятичную: мы так же можем складывать, вычитать, делить и умножать числа столбиком. Правда, в двоичной системе всего две цифры: 0 и 1 — поэтому привычные математические операции в ней могут показаться немного странными. К счастью, в основе двоичной арифметики лежат простые принципы, которые нужно запомнить.

Научитесь: Профессия Python-разработчик
Узнать больше
Двоичный калькулятор онлайн
- Главная
- /
- Информатика
- /
- Двоичный калькулятор онлайн
Если вам необходимо произвести математические операции над двоичными числами воспользуйтесь нашим двоичным онлайн калькулятором:
Просто введите целые двоичные числа, выберите операцию и получите результат.
Данный калькулятор может производить следующие действия над двоичными числами:
- сложение +
- вычитание −
- умножение ×
- деление ÷
- логическое И (AND)
- логическое ИЛИ (OR)
- исключающее ИЛИ (XOR)
Сложение двоичных чисел
Сложение двух двоичных чисел производится столбиком поразрядно. Начиная с младшего разряда (справа на лево), как и при сложении столбиком десятичных чисел. Но так как цифр всего две (0 и 1), их сложение происходит по следующим правилам:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Пример
Для примера сложим 1011 и 101:
| + | 1 | 0 | 1 | 1 | |
| 1 | 0 | 1 | |||
| 1 | 0 | 0 | 0 | 0 |
10112 + 1012 = 100002
(1110 + 510 = 1610)
Вычитание двоичных чисел
Вычитание двоичных чисел производится аналогично сложению – столбиком, но по следующим правилам:
0 – 0 = 0
1 – 0 = 1
1 – 1 = 0
10 – 1 = 1
Пример
Для примера вычтем из числа 1011 число 101:
| − | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | ||
| 1 | 1 | 0 |
10112 − 1012 = 1102
(1110 − 510 = 610)
Умножение двоичных чисел
Умножение двоичных чисел производится в столбик аналогично умножению в десятичной системе, но по следующим правилам:
0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
Пример
Для примера перемножим числа 1011 и 101:
| × | 1 | 0 | 1 | 1 | ||
| 1 | 0 | 1 | ||||
| + | 1 | 0 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | |||
| 1 | 0 | 1 | 1 | |||
| 1 | 1 | 0 | 1 | 1 | 1 |
10112 × 1012 = 1101112
(1110 × 510 = 5510)
Деление двоичных чисел
Внешне деление двоичных чисел похоже на деление десятичных чисел, но тут есть свои нюансы: такое деление производится вычитанием делителя со сдвигом вправо, если остаток больше нуля. Чтобы понять этот процесс рассмотрим пример:
Пример
Для примера разделим число 11110 на 110:

111102 ÷ 1102 = 1012
(3010 ÷ 610 = 510)
См. также
ДВОИЧНЫЕ
КОДЫ И
СИСТЕМЫ
СЧИСЛЕНИЯ
Введение
С
помощью цифровых схем производятся
различные вычисления. Поэтому необходимо
представлять все десятичные цифры и
все необходимые числа в виде комбинации
0 и 1. Представление числа только двумя
знаками называется бинарным
представлением.
|
Коды, |
Существует
множество бинарных кодов. Но на практике
применяются только некоторые из них.
Бинарные коды имеют регламентированную
разрядность. Каждая десятичная цифра
в определенном коде представляется
определенным количеством так называемых
бинарных разрядов. Бинарный разряд
может принимать значение 0 или 1. Бинарный
разряд, или базовая единица данных
называется бит (от англ.: binary
digit
—
двоичная цифра).
|
Бит |
В
двоичном коде представляются прежде
всего десятичные числа. Однако
оказалось целесообразным использовать
также другие системы счисления.
Особенное значение имеет шестнадцатеричная
система счисления. Наряду с этим часто
используется восьмеричная система
счисления. Особенное значение имеет
двоичная система счисления. Двоичная
система счисления одновременно
является бинарным кодом, так как состоит
только из цифр 0 и 1.
Двоичная
система счисления
Структура
двоичной системы счисления
Все
используемые системы счисления являются
так называемыми позиционными системами
счисления. В позиционной системе
счисления позиция цифры однозначно
связана со значением числа посредством
особого фактора увеличения в виде
степенного числа.
В
десятичной системе счисления каждый
разряд числа умножается на 10 в
соответствующей степени (рис. 8.1). Чтобы
посчитать от нуля до 9, нужен ноль и
девять цифр в колонке единиц. Число
десять запишется как 1 в колонке десятков
и 0 в колонке единиц.
Если
в распоряжении имеются только цифры 0
и 1, то каждый разряд числа умножается
на степень числа два (рис. 8.2). В первом
столбце справа могут
быть записаны только числа от 0 до 1. Для
записи числа необходимо использовать
2 столбца справа. Число 2 получается
путем записи 0 в первом столбце справа
и 1 во втором столбце справа (рис. 8.3). Для
представления числа 7 требуется записать
111. Первая 1 справа представляет значение
1, вторая 1 — значение 2, и третья 1 —
значение 4. В итоге получается 4
+
2 + 1 = 7.
Перевод
двоичных чисел в
десятичную
систему счисления
Перевести
двоичное число в десятичное очень
просто. Для этого используют таблицу
согласно рис. 8.4. Эта таблица может быть
по желанию продолжена влево.
Двоичное
число заносится в таблицу (рис. 8.4).
Столбцы, в которых должны быть 0, не
представляют интереса. Важными являются
столбцы, в которых стоит 1. Первое двоичное
число на рис. 8.4 имеет 1 в столбце 25.
Эта 1 представляет значение 32. Следующая
1 стоит в столбце 22.
Эта 1 представляет значение 4. Общее
значение двоичного числа составляет
32 + 4 = 36.
Второе
двоичное число имеет 1 в столбце 27.
Эта 1 представляет значение 128.
Следующая 1 стоит в столбце 25.
Эта 1 представляет значение 32. Обе
следующие единицы представляют значения
4 и 2. Общее значение двоичного числа в
итоге 128 + 32 + 4 + 2 = 166.
Определим
значения третьего и четвертого двоичных
чисел на рис. 8.4. Для третьего двоичного
числа должно получиться значение 1633.
Четвертое двоичное число имеет значение
752.
Перевод
десятичных чисел
в
двоичную систему счисления
Преобразование
десятичных чисел в двоичные может также
быть проведено при помощи таблицы.
Таблица должна иметь достаточно большое
количество столбцов. При преобразовании
определяют прежде всего единицу с
наибольшим значением, затем единицы с
меньшими значениями. Общее значение
десятичного числа разделяется на
столбцы. Рассмотрим пример.
Переведем
десятичное число 900 в двоичное число. 1
со значением 1024 не подходит, так как
десятичное число имеет значение только
900. Наибольшая единица для этого
примера 29.
Она имеет значение 512. Итак, мы задействовали
512 из 900. Остается еще 388. Следующая 1 в
столбце 2* имеет значение 256. Теперь
остаток составляет только 388 — 256 ** 132.
1 в столбце 27
имеет значение 128, так что остается 4.
Остаток 4 дает I в столбце 22.
В другие столбцы записывается 0. В итоге
десятичное число 900 преобразовано в
двоичное число 1110000100. Теперь попробуем
преобразовать двоичное число в
десятичное.
Преобразуйте
десятичные числа 1300 и 1877 в двоичные.
Получают следующие результаты:
1300
* 10100010100;
1877
– 11101010101.
Вещественные
двоичные числа
(правильные
дроби)
Двоичные
числа бывают, как и десятичные, с цифрами
после запятой. Первому разряду справа
от запятой ставится в соответствие 2-1
.Второму
разряду справа от запятой — 2-2.
На рис. 8.6 показано распределение степеней
числа 2 по разрядам справа от запятой.
Двоичные
числа с запятой (дробные) пересчитываются
в десятичные числа таким же способом,
как и двоичные числа без запятой.
Соответственно можно и дробные
десятичные числа перевести в двоичную
систему.
Пример———————————————————————————————————
|
Десятичное |
25 32 |
24 16 |
23 8 |
22 4 |
21 2 |
20 1 |
2-1 0,5 |
2-2 0,25 |
2-3 0,125 |
2-4 0,0625 |
|
22,6875 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |

Может
так случиться, что десятичное число
с запятой
не может быть преобразовано в двоичное
число без остатка. Тогда нужно решить,
на сколько разрядов после запятой
следует производить преобразование
и по достижении этой разрядности
закончить пересчет. Для облегчения
пересчета можно использовать таблицу
на рис. 8.7.
24 23 22 21 20
16 8 4 2 1
1 1 Перенос
1 0 1 1 1.
Число
1 0 0 1 1
2.
Число
Если
преобразовать двоичные числа в десятичные,
можно легко проверить правильность
проведенного сложения.
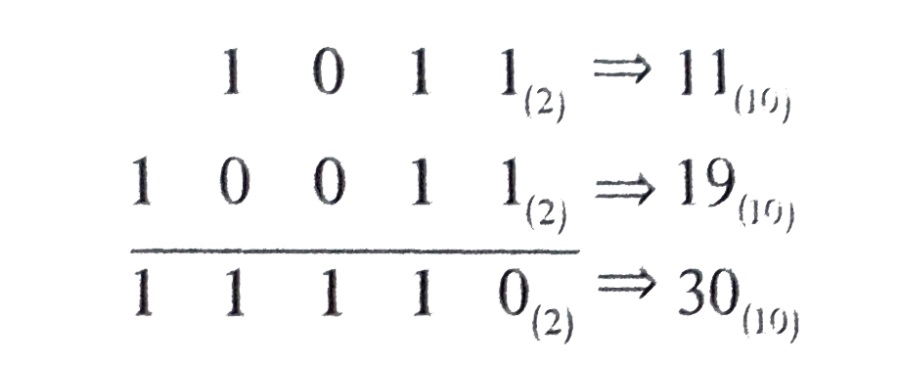
Маленькое
2 в скобках внизу обозначает двоичное
число. Число с 10 в скобках внизу является
десятичным числом. Эта идентификация
применяется только в случае возможных
недоразумений.
Вычитание двоичных чисел
Непосредственное
вычитание
Двоичное
число может, как и в десятичной системе,
вычитаться из другого двоичного числа.
Такое вычитание называется нормальным.
Для него действуют следующие правила.
Правила:
0
– 0 = 0
1
– 0 = 1
1
– 1 = 0
Вычитание
0—1 приводит к отрицательному результату.
Здесь возникает несколько трудностей.
При
непосредственном вычитании вычитаемое
число пишется прямо под числом, от
которого оно отнимается (уменьшаемым).
Пример
—————————————————————————————
1 1 0 1 1 Уменьшаемое
-1 0 0 0 1 Вычитаемое
1 0 0 1 1 Разность
Вычитание
начинают со столбца с наименьшей
степенью, с самого правого. Цифра
вычитаемого вычитается из цифры
уменьшаемого ( 1 – 1 = 0 в примере).
Затем происходит вычитание во втором
столбце справа (1-0=1),
затем
в 3 столбце справа и т. д. Этот пример не
представляет никакой трудности, так
как не возникает ситуации 0 — 1. В следующем
примере иначе.
Пример
—————————————————————————————

Чтобы
провести вычитание в третьем столбце
справа, «одолжим» 1 из 4-го столбца.
Получается: 10 – 1 = 1. Единица в сером круге,
таким образом,. становится 0.
Вычитание в дополнительном коде
В
компьютерной технике вычитание
производится преимущественно добавлением
дополнения к вычитаемому числу.
Вычитание
с дополнением также возможно в десятичной
системе. Предположим, что пятиразрядный
спидометр машины показывает 95000 (рис.
8.8). Если машина проедет еще 15 000 км, то
спидометр покажет 10 000. Такое же число
получится, если от 95 000 отнять 85 000. Число
15 000 называется дополнением к числу
85 000. Конечно, этот способ функционирует
только при выполнении условия, что при
прибавлении дополнения результат не
отображается в шестом разряде. То есть
спидометр на рис. 8.8 не может быть
шестиразрядным. В компьютерной технике
можно просто осуществлять запрет
переносов.
При
пятиразрядном представлении в десятичной
системе дополнение и вычитаемое в сумме
дают число 100000, т. е. 105.
При шестиразрядном представлении в
десятичной системе дополнение и
вычитаемое в сумме дают 106.
Общий принцип гласит:
|
В |
Найденное
дополнение называется B-дополнением.
В
двоичной системе вычитание в дополнительном
коде производится аналогичным образом.

В
приведенном примере нужно вычесть из
числа 15 число 7. Результат будет 8.
Какое число должно быть прибавлено к
15(10)
= 1111(2),
чтобы в результате получилось 8(10)
= 1000(2)
при условии, что перенос в 5 разряде
запрещен? Методом подбора находим число
1001(2)=
9(10).
Это число является дополнением к
111(2)
= 7(10).
При
четырехзначном представлении дополняют
вычитаемое число до 16 =24.
При пятизначном представлении— до 25
= 32. В следующем примере показано, как
дополнение (25) и вычитаемое (7) дополняют
друг друга до 32.
Пример
—————————————————————————————
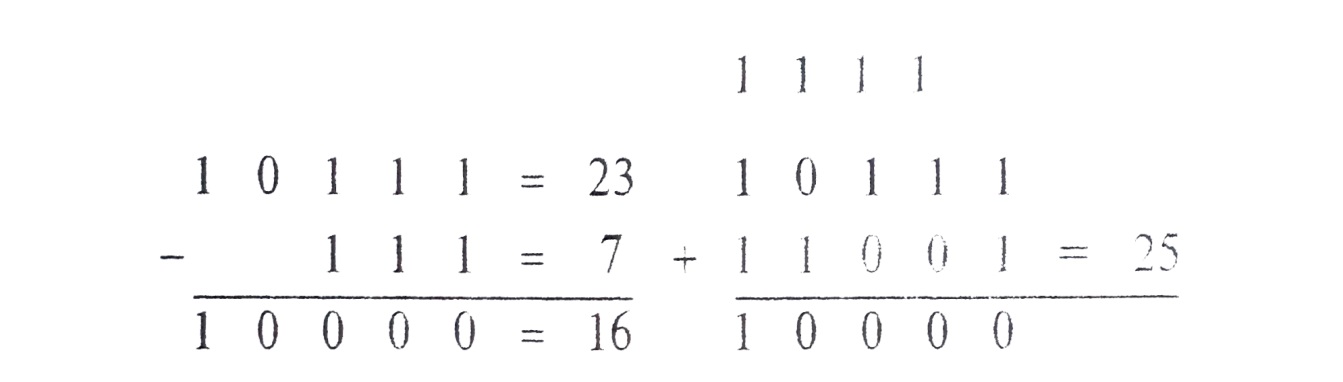
Итак,
можно сформулировать следующее правило.
|
В |
Если
требуется найти дополнение вычитаемого
числа, то прежде всего нужно знать, с
каким количеством разрядов предстоит
работать. В компьютерной технике
разрядность известна заранее. Для наших
примеров мы принимаем разрядность 6.
Если вычитаемое число имеет меньше
значащих цифр, чем 6, то оно расширяется
ведущими нулями до достижения заданного
6-разрядного формата.
Пример
—————————————————————————————
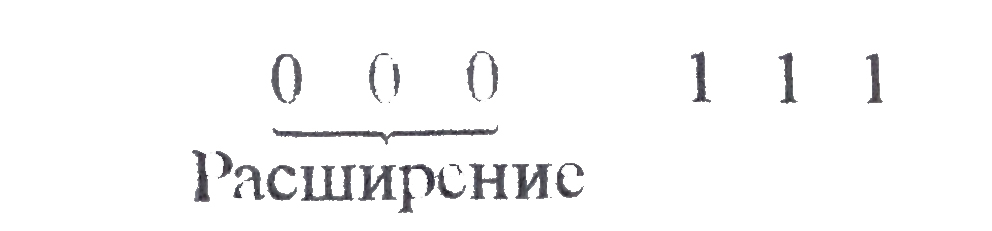
При
6 разрядах сумма дополнения и вычитаемого
должна быть равна 26 – 64. Если вычитаемое
число 7, то дополнение должно быть 57.
Если
теперь проинвертировать расширенное
число, т. е. вместо всех 0 записать 1 и
вместо всех 1 записать 0, то получится
число, которое только на 1 меньше искомого
дополнения. Получается число 56.
Пример
—————————————————————————————
32
16 8 4 2 1
0
0 0 1 1 1 = 7
↓ ↓ ↓ ↓ ↓ ↓
1
1 1 0 0 0 = 56
Это
не случайность, а закономерность, которую
можно проверить на следующих примерах.
|
После |
Если
к полученному коду добавить 1, то
получается искомое дополнение.
|
Для
|
Справедливость
этого метода доказана на следующих
примерах.
Пример
(6-разрядное
представление)___________________________________
1
0 1 1 1 1 = 47
–
1 1 0 1 1 = 27
?
0
1 1 0 1 1 Уменьшаемое
число
↓
↓ ↓ ↓ ↓ ↓
1
0
0 1 0 0 Инвертированное
уменьшаемое число
+
1
1
0 0 1 0 1 Дополнение
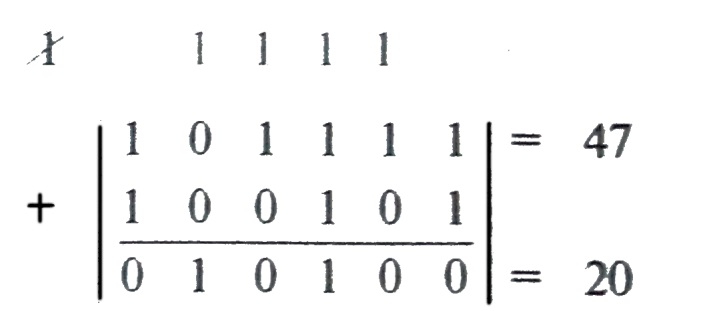
Перенос
Дополнение
Результат
Пример
(8-разрядное представление)
—————————————————
1
0 1 1 1 1
=
47
— 1
1
0
1
1
=
27
?
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
Уменьшаемое |
|
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
|
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
Инвертированное |
|
+ |
1 |
|||||||
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
Дополнение |
|
Перенос |
1 |
1 |
1 |
І |
1 |
1 |
1 |
||
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
||
|
Дополнение |
+ |
1 |
1 |
1 |
0. |
0 |
1 |
0 |
1 |
|
Результат: |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
=20
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
