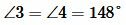Как найти разницу между углами

9 ответов

Лучший ответ

a = targetA - sourceA
a = (a + 180) % 360 - 180

mod = (a, n) -> a - floor(a/n) * n

mod = (a, n) -> (a % n + n) % n

a = targetA - sourceA
a += (a>180) ? -360 : (a<-180) ? 360 : 0

a = targetA - sourceA
a -= 360 if a > 180
a += 360 if a < -180

min((2 * PI) - abs(x - y), abs(x - y))

PI = math.pi
TAU = 2*PI
def smallestSignedAngleBetween(x, y):
    a = (x - y) % TAU
    b = (y - x) % TAU
    return -a if a < b else b

def f(x,y):
  import math
  return min(y-x, y-x+2*math.pi, y-x-2*math.pi, key=abs)

inline double getAbsoluteDiff2Angles(const double x, const double y, const double c)
{
    // c can be PI (for radians) or 180.0 (for degrees);
    return c - fabs(fmod(fabs(x - y), 2*c) - c);
}

angle = Pi - abs(abs(a1 - a2) - Pi);

double deltaOrientation = angle1 - angle2;
double delta =  remainder(deltaOrientation, 2*M_PI);

#include <math.h>
#define PIV2 M_PI+M_PI
#define C360 360.0000000000000000000
double difangrad(double x, double y)
{
double arg;

arg = fmod(y-x, PIV2);
if (arg < 0 )  arg  = arg + PIV2;
if (arg > M_PI) arg  = arg - PIV2;

return (-arg);
}
double difangdeg(double x, double y)
{
double arg;
arg = fmod(y-x, C360);
if (arg < 0 )  arg  = arg + C360;
if (arg > 180) arg  = arg - C360;
return (-arg);
}

dif = difangrad(a,b);

dif = difangdeg(a,b);

difangdeg(180.000000 , -180.000000) = 0.000000
difangdeg(-180.000000 , 180.000000) = -0.000000
difangdeg(359.000000 , 1.000000) = -2.000000
difangdeg(1.000000 , 359.000000) = 2.000000

atan2(sin(x-y), cos(x-y))

Сравнение углов. Сложение и вычитание углов

Углы различают по их величине. Большим считается не тот угол, стороны которого длиннее, а тот, стороны которого сильнее расходятся врозь. На черт. 13 уг. EDF больше, чем угол 2, потому, что у первого стороны сильней расходятся врозь. Встречаются углы, стороны которых расходятся врозь совершенно одинаково; такие углы можно наложить один на другой так, что их вершины совпадут, а стороны сольются. Углы, которые можно таким образом наложить друг на друга, считаются равными, хотя бы стороны их были неодинаковой длины.

На черт. 13 равны, например, уг. DEH и уг. DFH, уг. 2 и уг. а; вы можете убедиться в этом, есля обведете один угол на прозрачной бумаге и покроете им другой.

Если при наложении сравниваемых углов их вершины и одна сторона совпали, вторая же сторона накладываемого угла оказалась внутри или вне другого угла, то такие углы, конечно, не равны. Тот угол, который оказался внутри другого, считается меньшим.

Рассмотрите на том же черт. 13 углы, вершины которых лежат в точке D. Здесь три угла: уг. EDF, уг. EDH и уг. HDF. Вы видите, что оба меньших угла как раз заполняют собою уг. EDF, который составляется из них, как целое из своих частей. Когда углы так расположены, то говорят, что уг. EDF есть с у м м а углов EDH и HDF. С л о ж и т ь два угла значит найти их сумму, т. е. тот угол, который составится, если приложить их друг к другу, как показано на чертеже 13.

Если на черт. 13 от угла EDF отнять угол EDH, то останется уг. HDF; этот. угол называется р а з н о с т ь ю углов EDF и EDH. Вычесть один угол из другого значит найти их разность.

Повторительные вопросы

Какие углы называются равными? – Зависит ли величина угла от длины сторон? – Покажите на чертеже, что называется суммой и разностью двух углов.

Развернутый угол

Представьте себе, что мы разводим врозь стороны какого-нибудь угла, – напр. уг. 1 (черт. 14). От этого угол станет увеличиваться: он превратится сначала в уг. 2, потом в уг. 3 и, наконец, в уг. 4, стороны которого составляют одну прямую линию. Такие углы, как уг. 4, называются р а з в е р н у т ы м и углами.

Может ли один развернутый угол быть больше или меньше другого развернутого? Конечно, нет: ведь всякие прямые линии, если их наложить одну на другую, сливаются между собою; значит, должны слиться при наложении и всякие развернутые углы. Итак:

В с е р а з в е р н у т ы е у г л ы р а в н ы м е ж д у с о б о ю.

Смежные углы. Прямой угол

На черт. 15 вы видите углы 1 и 2, которые расположены так, что вершины их совпадают (в точке А) и одна сторона (AD) у них общая, т. е. принадлежит одновременно обоим углам, другие же стороны АВ и АС этой пары углов составляют одну прямую линию. Углы, которые так расположены, называются с м е ж н ы м и. На черт. 16 вы видите несколько пар смежных углов: уг. 1 и уг. 2; уг. 3 и уг. 4; уг. 5 и у г. 6; у г. а и у г. b; уг. с и у г. d, и др.

Если углы, составляющие одну пару смежных углов, равны между собою, – как уг. 7 и 8 на черт. 16, – то каждый из них называется прямым углом. Значит:

П р я м о й у г о л е с т ь о д и н и з д в у х р а в н ы х с м е ж н ы х у г л о в.

Так как оба равных смежных угла составляют вместе один развернутый угол, то прямой угол есть половина развернутого угла. Но все развернутые углы равны друг другу; поэтому равны и их половины, т. е. прямые углы. Значит:

В с е п р я м ы е у г л ы р а в н ы д р у г д р у г у.

Прямые линии, встречающиеся под прямым углом (черт. 17), называются перпендикулярными друг к другу. На черт. 17, например, уг. 1 = уг. 2, а так как эти углы смежные и притом равные, то они – прямые. Поэтому CD перпендикулярно к АВ и АВ перпендикулярно к CD.

Слово «перпендикулярный» не надо смешивать со словом «вертикальный». В е р т и к а л ь н о й, или о т в е с н о й, называют всякую прямую линию, имеющую направление свободно свешивающейся нагруженной нити.

Все те линии, которые составляют с вертикальной линией прямой угол, называются г о р и з о н т а л ь н ым и. Горизонтальны, например, все линии, проведенные по поверхности воды (черт. 18). Отвесное направление проверяют отвесом (черт. 18); горизонтальное – плотничьим ватерпасом.

На бумаге прямой угол чертят помощью линейки и чертежного треугольника (черт. 19). Проверить, правильно ли изготовлен чертежный треугольник, можно так. Проведя по линейке прямую линию и начертив с помощью треугольника другую прямую к ней, перпендикулярную, прикладывают чертежный треугольник прямым углом к смежному углу: если эти углы равны, то треугольник изготовлен правильно.

Углы, меньшие, чем прямой, называются о с т р ы м и; большие, чем прямой, – т у п ы м и.

Повторительные вопросы к §§ 6 и 7

Какой угол называется развернутым? – Какие углы называются смежными (начертите несколько таких углов)? – Какой угол называется прямым? – Как называется угол, который равен смежному с ним? – Могут ли прямые углы иметь различную величину? – Объясните значение слов: перпендикулярный, вертикальный, отвесный, горизонтальный. – Как чертить перпендикулярные прямые помощью чертежного треугольника? – Какие углы называются острыми? Тупыми? Начертите несколько острых и несколько тупых углов.

1. Уменье чертить взаимно-перпендикулярные прямые позволяет строить так наз. «графики», т. е. ломаные (или кривые) линии, наглядно показывающие ход изменения явлений. Пусть требуется построить график температуры за неделю по следующим данным:

Изобразим эти температуры рядом перпендикуляров к одной прямой, приведенных на равных расстояниях друг от друга: длина перпендикулярных отрезков будет изображать температуру дня. Верхушки перпендикуляров соединим прямыми линиями: полученная ломаная линия и есть «график температур».

2. На черт. 20 изображены графики годового хода температуры воздуха в разных местах земного шара: на о-ве Цейлон, в Ницце, в Самаре, во Владивостоке и в Верхоянске. Рассматривая эти графики, мы можем ответить себе на ряд могущих возникнуть вопросов, например:

a) Какова температура в среднем за много лет во всех на званных местах 1 мая?

О т в е т. На Цейлоне +27° в Ницце +18°, в Самаре +15°, во Владивостоке +10°, в Верхоянске 0°.

b) Какие дни в году (в среднем) самые жаркие и самые холодные в Верхоянске?

О т в е т. 1-е июля + 15°1-е января – минус 50°

c) В каких городах в апреле средняя температура ниже0°?

О т в е т. В Верхоянске, Владивостоке и Самаре.

d) Какова разница между самой высокой и самой низкой средней температурой в Ницце? В Самаре?

О т в е т ы. В Ницце средняя температура колеблется от +9° до +24°; в Самаре – от минус 10° до +21°.

Свойство смежных углов

Сумма обоих смежных углов, очевидно, равна развернутому углу. Но развернутый угол равен двум прямым углам, взятым вместе. Поэтому:

С у м м а о б о и х с м е ж н ы х у г л о в р а в н а д в у м п р я м ы м у г л а м.

Например, на черт. 21 уг. 1 +уг. 2 = двум прямым углам.

Бывает, что по одну сторону прямой расположено не два угла, как в случае смежных углов, а несколько углов, – как на черт. 22. Легко убедиться, что сумма этих углов также равна двум прямым: из них всегда можно составить одну пару смежных углов (на черт. 22 углы АОD и DOВ, или АОЕ и ЕОВ).

Подобным же образом можно найти, чему равна сумма углов,! расположенных вокруг общей вершины, как на черт. 23. Продолжив одну из сторон за общую вершину (черт. 24), получим две группы углов: группу 1 и а, сумма которых равна двум прямым (почему?), и группу углов 2, 3, Ь, сумма которых равна также двум прямым углам; значит, сумма всех углов вокруг общей вершины равна 4 прямым углам.

Повторительные вопросы

Чему равна сумма смежных углов? – Сумма нескольких углов, расположенных по одну сторону прямой линии? – Сумма всех углов, расположенных вокруг общей вершины?

Противоположные углы

Предварительные упражнения

1) На черт. 25 уг. 1 = 48°. Найти прочие углы.

2) На черт. 25 уг. b = 136 °. Найти прочие углы.

Когда две прямые линии пересекают друг друга (черт. 25), они образуют две пары углов, стороны которых составляют продолжение одни других: одна пара – уг. 1 и уг. 2; другая – уг. а и уг. b. Особенность противоположных углов та, что углы, составляющие такую пару, всегда равны между собою: у г. 1 = уг. 2, уг. а = у г. b. Действительно, если например (черт. 25) уг. 1 = 40°, то уг. b = 180° – 40° = 140°, уг. 2 = 180° – 140° = 40°, и уг. а = 180° – 40° = 140°; мы видим, что уг. 1 = уг. 2, и уг. а = уг. b. Вообще, так как уг. 1 вместе с углом а равен двум прямым (почему?), а уг. 2 вместе с тем же углом а тоже равен двум прямым, то ясно, что уг. 1 должен равняться уг. 2. Итак:

П р о т и в о п о л о ж н ы е у г л ы р а в н ы.

Повторительные вопросы.

Какие углы называются противоположными? знаете свойство противоположных углов?

Окружность

До сих пор мы говорили только о прямых линиях. Из к р и в ы х линий остановимся на о к р у ж н о с т и (черт. 26). Окружность чертят циркулем. Острие ножки раздвинутого циркуля втыкают в бумагу, другую же ножку с карандашом вращают вокруг первой; когда карандаш сделает полный оборот, он проведет на бумаге замкнутую кривую – окружность. Та точка, в которую было воткнуто острие циркуля, называется ц е н т р о м окружности. Понятно, что все точки окружности удалены от центра на одинаковое расстояние; это расстояние называется р а д и у с о м окружности. Значит:

О к р у ж н о с т ь е с т ь к р и в а я л и н и я, в с е т о ч к и к о т о р о й о д и н а к о в о у д а л е н ы о т о д н о й

т о ч к и, н а з ы в а е м о й ц е н т р о м.

Прямая, соединяющая две точки окружности через центр, называется д и а м е т р о м.

Всякая часть окружности называется ее д у г о ю (черт. 27).

Плоская фигура, ограниченная окружностью, называется к р у г о м.

Повторительные вопросы

Что такое окружность? Центр? Радиус? Дуга? – Покажите все это на чертеже. – Все ли радиусы одной окружности равны между собою? – Что больше: диаметр или радиус? Во сколько раз?

Применения

3. Гудок завода слышен на 4 км. Начертить в масштабе 1 км в 1 см границу местности, где слышен гудок этого завода.

Р е ш е н и е. Вокруг точки, обозначающей положение завода, начертить окружность радиусом 4 см.

4. Радиус круга 100 см. Некоторая точка удалена от центра на 40 см. Лежит ли она внутри круга или вне его? Каково ближайшее расстояние от этой точки до окружности?

Р е ш е н и е. Точка лежит внутри круга. Ближайшее расстояние ее от окружности надо считать вдоль диаметра, проведенного через эту точку; оно равно 60 см. Дальнейшее расстояние (вдоль того же диаметра) – 140 см.

Источник

Вертикальные углы. Свойства вертикальных углов

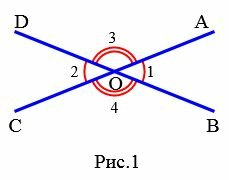
Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.

На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.

Свойства вертикальных углов

1. Вертикальные углы равны.

2. Две пересекающие прямые образуют две пары вертикальных углов.

Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем

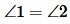
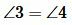
Следовательно . Аналогично доказывается, что .

Задачи и решения

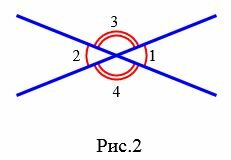
Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).

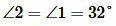
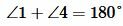
Решение. Так как углы 1 и 2 вертикальны, то . Углы 1 и 4 смежные. Следовательно . Тогда

Углы 3 и 4 вертикальные. Тогда

Ответ. .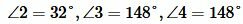

Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.

Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:

.

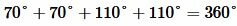
Ответ. .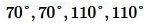

Источник

Degrees minutes seconds subtraction calculator is used to find the difference between angles in Trigonometric applications. An angle is a shape, formed by two lines diverging from a common point. An angle may be classified as acute, obtuse, right, reflex, straight and full angle. The angles are the sections of a full 360-degree circle. Use this online angle subtraction calculator or DMS subtraction calculator to subtract the angles expressed in degrees, minutes and seconds.

Degrees minutes seconds subtraction calculator is used to find the difference between angles in Trigonometric applications. An angle is a shape, formed by two lines diverging from a common point. An angle may be classified as acute, obtuse, right, reflex, straight and full angle. The angles are the sections of a full 360-degree circle. Use this online angle subtraction calculator or DMS subtraction calculator to subtract the angles expressed in degrees, minutes and seconds.