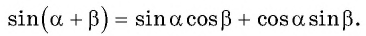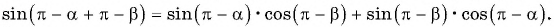Содержание
- Сравнение углов. Сложение и вычитание углов
- Вертикальные углы. Свойства вертикальных углов
- Свойства вертикальных углов
- Задачи и решения
Сравнение углов. Сложение и вычитание углов
Углы различают по их величине. Большим считается не тот угол, стороны которого длиннее, а тот, стороны которого сильнее расходятся врозь. На черт. 13 уг. EDF больше, чем угол 2, потому, что у первого стороны сильней расходятся врозь. Встречаются углы, стороны которых расходятся врозь совершенно одинаково; такие углы можно наложить один на другой так, что их вершины совпадут, а стороны сольются. Углы, которые можно таким образом наложить друг на друга, считаются равными, хотя бы стороны их были неодинаковой длины.
На черт. 13 равны, например, уг. DEH и уг. DFH, уг. 2 и уг. а; вы можете убедиться в этом, есля обведете один угол на прозрачной бумаге и покроете им другой.

Если при наложении сравниваемых углов их вершины и одна сторона совпали, вторая же сторона накладываемого угла оказалась внутри или вне другого угла, то такие углы, конечно, не равны. Тот угол, который оказался внутри другого, считается меньшим.
Рассмотрите на том же черт. 13 углы, вершины которых лежат в точке D. Здесь три угла: уг. EDF, уг. EDH и уг. HDF. Вы видите, что оба меньших угла как раз заполняют собою уг. EDF, который составляется из них, как целое из своих частей. Когда углы так расположены, то говорят, что уг. EDF есть с у м м а углов EDH и HDF. С л о ж и т ь два угла значит найти их сумму, т. е. тот угол, который составится, если приложить их друг к другу, как показано на чертеже 13.
Если на черт. 13 от угла EDF отнять угол EDH, то останется уг. HDF; этот. угол называется р а з н о с т ь ю углов EDF и EDH. Вычесть один угол из другого значит найти их разность.
Повторительные вопросы
Какие углы называются равными? – Зависит ли величина угла от длины сторон? – Покажите на чертеже, что называется суммой и разностью двух углов.
Развернутый угол
Представьте себе, что мы разводим врозь стороны какого-нибудь угла, – напр. уг. 1 (черт. 14). От этого угол станет увеличиваться: он превратится сначала в уг. 2, потом в уг. 3 и, наконец, в уг. 4, стороны которого составляют одну прямую линию. Такие углы, как уг. 4, называются р а з в е р н у т ы м и углами.

Может ли один развернутый угол быть больше или меньше другого развернутого? Конечно, нет: ведь всякие прямые линии, если их наложить одну на другую, сливаются между собою; значит, должны слиться при наложении и всякие развернутые углы. Итак:
В с е р а з в е р н у т ы е у г л ы р а в н ы м е ж д у с о б о ю.
Смежные углы. Прямой угол
На черт. 15 вы видите углы 1 и 2, которые расположены так, что вершины их совпадают (в точке А) и одна сторона (AD) у них общая, т. е. принадлежит одновременно обоим углам, другие же стороны АВ и АС этой пары углов составляют одну прямую линию. Углы, которые так расположены, называются с м е ж н ы м и. На черт. 16 вы видите несколько пар смежных углов: уг. 1 и уг. 2; уг. 3 и уг. 4; уг. 5 и у г. 6; у г. а и у г. b; уг. с и у г. d, и др.
Если углы, составляющие одну пару смежных углов, равны между собою, – как уг. 7 и 8 на черт. 16, – то каждый из них называется прямым углом. Значит:
П р я м о й у г о л е с т ь о д и н и з д в у х р а в н ы х с м е ж н ы х у г л о в.

Так как оба равных смежных угла составляют вместе один развернутый угол, то прямой угол есть половина развернутого угла. Но все развернутые углы равны друг другу; поэтому равны и их половины, т. е. прямые углы. Значит:
В с е п р я м ы е у г л ы р а в н ы д р у г д р у г у.
Прямые линии, встречающиеся под прямым углом (черт. 17), называются перпендикулярными друг к другу. На черт. 17, например, уг. 1 = уг. 2, а так как эти углы смежные и притом равные, то они – прямые. Поэтому CD перпендикулярно к АВ и АВ перпендикулярно к CD.
Слово «перпендикулярный» не надо смешивать со словом «вертикальный». В е р т и к а л ь н о й, или о т в е с н о й, называют всякую прямую линию, имеющую направление свободно свешивающейся нагруженной нити.
Все те линии, которые составляют с вертикальной линией прямой угол, называются г о р и з о н т а л ь н ым и. Горизонтальны, например, все линии, проведенные по поверхности воды (черт. 18). Отвесное направление проверяют отвесом (черт. 18); горизонтальное – плотничьим ватерпасом.
На бумаге прямой угол чертят помощью линейки и чертежного треугольника (черт. 19). Проверить, правильно ли изготовлен чертежный треугольник, можно так. Проведя по линейке прямую линию и начертив с помощью треугольника другую прямую к ней, перпендикулярную, прикладывают чертежный треугольник прямым углом к смежному углу: если эти углы равны, то треугольник изготовлен правильно.

Углы, меньшие, чем прямой, называются о с т р ы м и; большие, чем прямой, – т у п ы м и.
Повторительные вопросы к §§ 6 и 7
Какой угол называется развернутым? – Какие углы называются смежными (начертите несколько таких углов)? – Какой угол называется прямым? – Как называется угол, который равен смежному с ним? – Могут ли прямые углы иметь различную величину? – Объясните значение слов: перпендикулярный, вертикальный, отвесный, горизонтальный. – Как чертить перпендикулярные прямые помощью чертежного треугольника? – Какие углы называются острыми? Тупыми? Начертите несколько острых и несколько тупых углов.
1. Уменье чертить взаимно-перпендикулярные прямые позволяет строить так наз. «графики», т. е. ломаные (или кривые) линии, наглядно показывающие ход изменения явлений. Пусть требуется построить график температуры за неделю по следующим данным:

Изобразим эти температуры рядом перпендикуляров к одной прямой, приведенных на равных расстояниях друг от друга: длина перпендикулярных отрезков будет изображать температуру дня. Верхушки перпендикуляров соединим прямыми линиями: полученная ломаная линия и есть «график температур».
2. На черт. 20 изображены графики годового хода температуры воздуха в разных местах земного шара: на о-ве Цейлон, в Ницце, в Самаре, во Владивостоке и в Верхоянске. Рассматривая эти графики, мы можем ответить себе на ряд могущих возникнуть вопросов, например:
a) Какова температура в среднем за много лет во всех на званных местах 1 мая?
О т в е т. На Цейлоне +27° в Ницце +18°, в Самаре +15°, во Владивостоке +10°, в Верхоянске 0°.
b) Какие дни в году (в среднем) самые жаркие и самые холодные в Верхоянске?
О т в е т. 1-е июля + 15°1-е января – минус 50°
c) В каких городах в апреле средняя температура ниже0°?
О т в е т. В Верхоянске, Владивостоке и Самаре.
d) Какова разница между самой высокой и самой низкой средней температурой в Ницце? В Самаре?
О т в е т ы. В Ницце средняя температура колеблется от +9° до +24°; в Самаре – от минус 10° до +21°.

Свойство смежных углов
Сумма обоих смежных углов, очевидно, равна развернутому углу. Но развернутый угол равен двум прямым углам, взятым вместе. Поэтому:
С у м м а о б о и х с м е ж н ы х у г л о в р а в н а д в у м п р я м ы м у г л а м.
Например, на черт. 21 уг. 1 +уг. 2 = двум прямым углам.

Бывает, что по одну сторону прямой расположено не два угла, как в случае смежных углов, а несколько углов, – как на черт. 22. Легко убедиться, что сумма этих углов также равна двум прямым: из них всегда можно составить одну пару смежных углов (на черт. 22 углы АОD и DOВ, или АОЕ и ЕОВ).
Подобным же образом можно найти, чему равна сумма углов,! расположенных вокруг общей вершины, как на черт. 23. Продолжив одну из сторон за общую вершину (черт. 24), получим две группы углов: группу 1 и а, сумма которых равна двум прямым (почему?), и группу углов 2, 3, Ь, сумма которых равна также двум прямым углам; значит, сумма всех углов вокруг общей вершины равна 4 прямым углам.

Повторительные вопросы
Чему равна сумма смежных углов? – Сумма нескольких углов, расположенных по одну сторону прямой линии? – Сумма всех углов, расположенных вокруг общей вершины?
Противоположные углы
Предварительные упражнения
1) На черт. 25 уг. 1 = 48°. Найти прочие углы.
2) На черт. 25 уг. b = 136 °. Найти прочие углы.

Когда две прямые линии пересекают друг друга (черт. 25), они образуют две пары углов, стороны которых составляют продолжение одни других: одна пара – уг. 1 и уг. 2; другая – уг. а и уг. b. Особенность противоположных углов та, что углы, составляющие такую пару, всегда равны между собою: у г. 1 = уг. 2, уг. а = у г. b. Действительно, если например (черт. 25) уг. 1 = 40°, то уг. b = 180° – 40° = 140°, уг. 2 = 180° – 140° = 40°, и уг. а = 180° – 40° = 140°; мы видим, что уг. 1 = уг. 2, и уг. а = уг. b. Вообще, так как уг. 1 вместе с углом а равен двум прямым (почему?), а уг. 2 вместе с тем же углом а тоже равен двум прямым, то ясно, что уг. 1 должен равняться уг. 2. Итак:
П р о т и в о п о л о ж н ы е у г л ы р а в н ы.
Повторительные вопросы.
Какие углы называются противоположными? знаете свойство противоположных углов?
Окружность
До сих пор мы говорили только о прямых линиях. Из к р и в ы х линий остановимся на о к р у ж н о с т и (черт. 26). Окружность чертят циркулем. Острие ножки раздвинутого циркуля втыкают в бумагу, другую же ножку с карандашом вращают вокруг первой; когда карандаш сделает полный оборот, он проведет на бумаге замкнутую кривую – окружность. Та точка, в которую было воткнуто острие циркуля, называется ц е н т р о м окружности. Понятно, что все точки окружности удалены от центра на одинаковое расстояние; это расстояние называется р а д и у с о м окружности. Значит:
О к р у ж н о с т ь е с т ь к р и в а я л и н и я, в с е т о ч к и к о т о р о й о д и н а к о в о у д а л е н ы о т о д н о й
т о ч к и, н а з ы в а е м о й ц е н т р о м.
Прямая, соединяющая две точки окружности через центр, называется д и а м е т р о м.
Всякая часть окружности называется ее д у г о ю (черт. 27).

Плоская фигура, ограниченная окружностью, называется к р у г о м.
Повторительные вопросы
Что такое окружность? Центр? Радиус? Дуга? – Покажите все это на чертеже. – Все ли радиусы одной окружности равны между собою? – Что больше: диаметр или радиус? Во сколько раз?
Применения
3. Гудок завода слышен на 4 км. Начертить в масштабе 1 км в 1 см границу местности, где слышен гудок этого завода.
Р е ш е н и е. Вокруг точки, обозначающей положение завода, начертить окружность радиусом 4 см.
4. Радиус круга 100 см. Некоторая точка удалена от центра на 40 см. Лежит ли она внутри круга или вне его? Каково ближайшее расстояние от этой точки до окружности?
Р е ш е н и е. Точка лежит внутри круга. Ближайшее расстояние ее от окружности надо считать вдоль диаметра, проведенного через эту точку; оно равно 60 см. Дальнейшее расстояние (вдоль того же диаметра) – 140 см.
Источник
Вертикальные углы. Свойства вертикальных углов
Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.
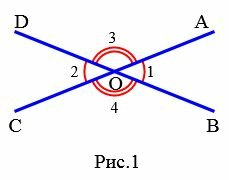
На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.
Свойства вертикальных углов
1. Вертикальные углы равны.
2. Две пересекающие прямые образуют две пары вертикальных углов.
Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем
Следовательно 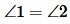 . Аналогично доказывается, что
. Аналогично доказывается, что 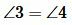 .
.
Задачи и решения
Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).
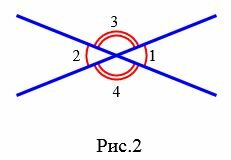
Решение. Так как углы 1 и 2 вертикальны, то 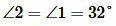 . Углы 1 и 4 смежные. Следовательно
. Углы 1 и 4 смежные. Следовательно 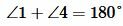 . Тогда
. Тогда
Углы 3 и 4 вертикальные. Тогда 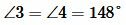
Ответ. 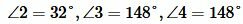 .
.
Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.
Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:
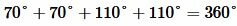 .
.
Ответ. 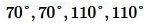 .
.
Источник
как рассчитать разность углов???
Знаток
(385),
на голосовании
11 лет назад
Дополнен 11 лет назад
а как вычесть? )
я умею складывать в столбик всё это,
а вот вычитать не знаю как..
Дополнен 11 лет назад
типо
291 градус 2,5 мин
вычесть
140 градусов 32,5 мин
Дополнен 11 лет назад
воот,
так сначала и делала,
но если проверит это действие
получается неправильный ответ!!
Голосование за лучший ответ
Leonid
Высший разум
(388685)
11 лет назад
1 градус = 60 минут. Так что если число минут в вычитаемом меньше, чем число минут в уменьшаемом, надо просто 1 градус преобразовать в минуты. То есть 291 гр. 2,5 мин = 290 град. 62,5 мин. После чего вычитание становится элементарным.
Синус, косинус, тангенс суммы и разности с примерами решения
Известные значения синуса, косинуса, тангенса углов можно использовать для вычисления значений синуса, косинуса, тангенса других углов.
Угол 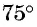
Выведем формулу 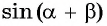 — синуса суммы двух углов. Рассмотрим случай, когда
— синуса суммы двух углов. Рассмотрим случай, когда 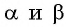 — острые углы в треугольнике
— острые углы в треугольнике  (рис. 115).
(рис. 115). 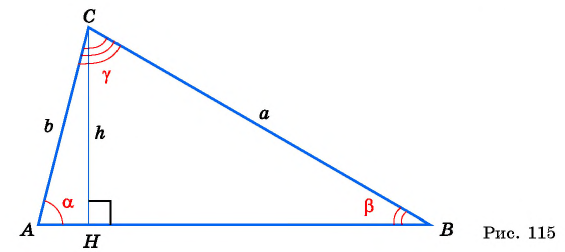
Выразим площадь треугольника  дважды:
дважды:
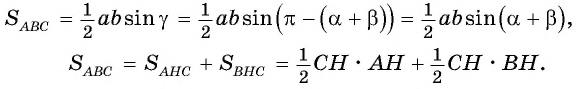
Треугольник 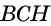 — прямоугольный, тогда
— прямоугольный, тогда 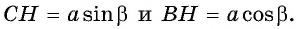 Из прямоугольного треугольника
Из прямоугольного треугольника  имеем:
имеем: 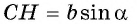 и
и 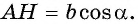 Тогда
Тогда
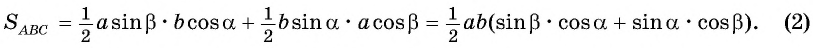
Приравняем правые части равенств (1) и (2):
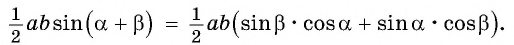
Разделим обе части равенства на 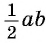 и получим формулу синуса суммы двух углов:
и получим формулу синуса суммы двух углов:
Если углы 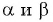 не являются острыми, то можно воспользоваться свойством периодичности синуса и формулами приведения.
не являются острыми, то можно воспользоваться свойством периодичности синуса и формулами приведения.
Например, если 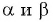 являются углами второй четверти, то
являются углами второй четверти, то 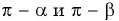 — острые углы.
— острые углы.
Применим к ним выведенную для острых углов формулу синуса суммы:
Воспользуемся формулами приведения в левой части равенства (3) и получим: 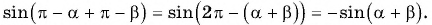
Применим формулы приведения к правой части равенства (3): 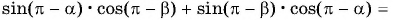
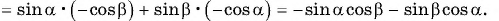
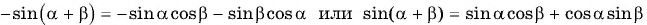 — формула синуса суммы двух углов.
— формула синуса суммы двух углов.
Остальные случаи принадлежности углов различным четвертям рассматриваются аналогично предыдущему.
Синус суммы
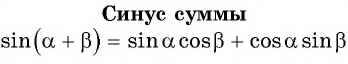
Воспользуемся полученной формулой 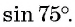
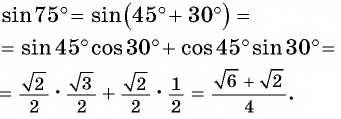
Выведем формулу синуса разности двух углов.
Для этого 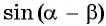 представим в виде
представим в виде 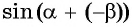 и применим формулу синуса суммы двух углов:
и применим формулу синуса суммы двух углов:
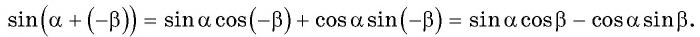
Получили формулу синуса разности двух углов:
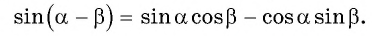
Синус разности
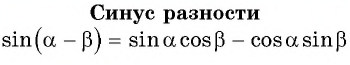
Вычислим, например, 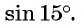
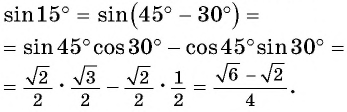
Для вывода формулы косинуса суммы двух углов воспользуемся формулами приведения и получим: 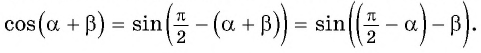
Тогда по формуле синуса разности двух углов имеем:
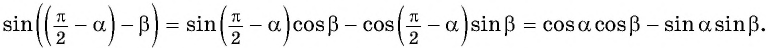
Получили формулу косинуса суммы двух углов:
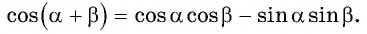
Косинус суммы

Применим полученную формулу и вычислим, например, 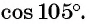
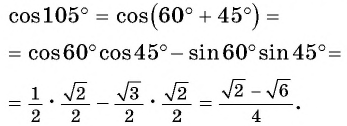
Представив разность  в виде суммы
в виде суммы 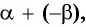 можно получить формулу косинуса разности двух углов:
можно получить формулу косинуса разности двух углов: 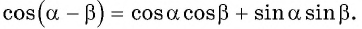
Косинус разности
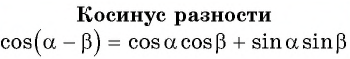 Найдем, например,
Найдем, например, 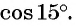
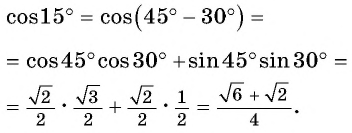
Пример №1
Решение:
Применим полученные формулы «справа налево»: 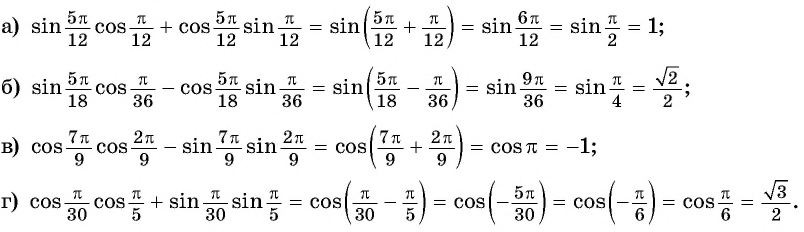 Выведем формулы тангенса суммы и тангенса разности двух углов.
Выведем формулы тангенса суммы и тангенса разности двух углов.
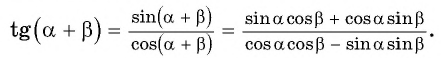 Разделим числитель и знаменатель дроби на
Разделим числитель и знаменатель дроби на 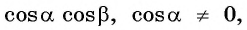
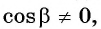 тогда:
тогда:
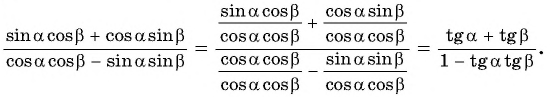
Таким образом, получили формулу тангенса суммы двух углов:
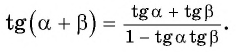
Воспользуемся формулой тангенса суммы и вычислим, например, 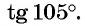
Тангенс суммы
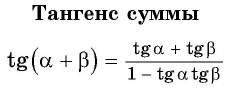 Представив разность
Представив разность 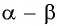 в виде суммы
в виде суммы 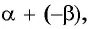 можно получить формулу тангенса разности двух углов:
можно получить формулу тангенса разности двух углов:
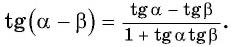 Найдем, например,
Найдем, например, 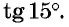
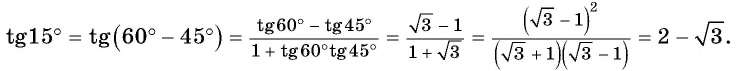
Тангенс разности
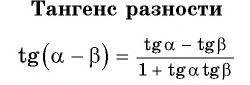
Пример №2
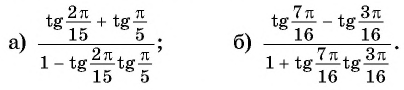
Решение:
Применим формулы тангенса суммы и тангенса разности «справа налево»:
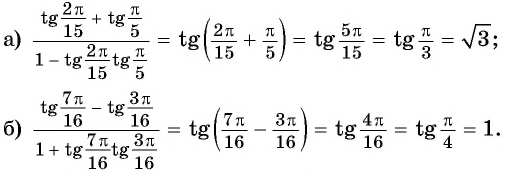
Полученные формулы синуса суммы, синуса разности, косинуса суммы, косинуса разности, тангенса суммы, тангенса разности двух углов называют формулами сложения.
Примеры заданий и их решения
Пример №3
С помощью формул сложения преобразуйте выражение:

Решение:
а) По формуле синуса разности получим:
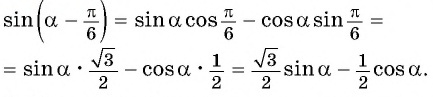
б) Применим формулу тангенса суммы:
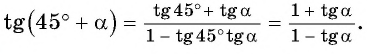
Пример №4
Найдите значение выражения:
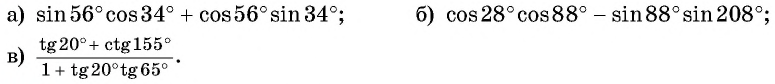
Решение:
а) По формуле синуса суммы получим:
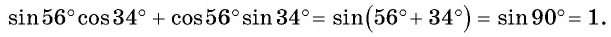
б) По формулам приведения получим, что 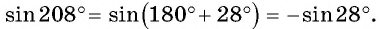
Тогда 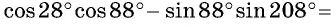
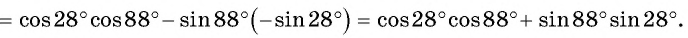 Воспользуемся формулой косинуса разности и получим:
Воспользуемся формулой косинуса разности и получим:
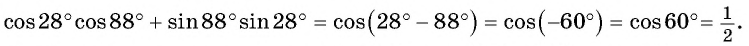
в) По формулам приведения 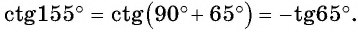
Тогда 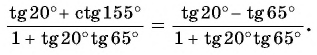
По формуле тангенса разности:
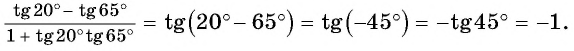
Пример №5

Решение:
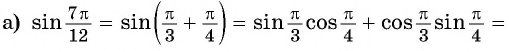
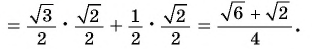
б) По формулам приведения: 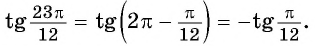
По формуле тангенса разности получим:
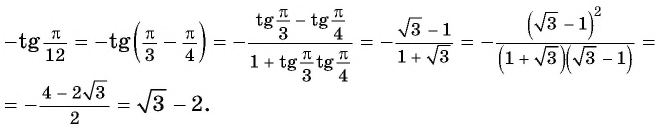
Таким образом, 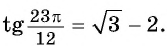
Пример №6
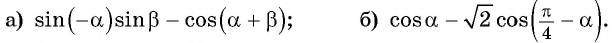
Решение:
а) Воспользуемся нечетностью синуса и формулой косинуса разности:
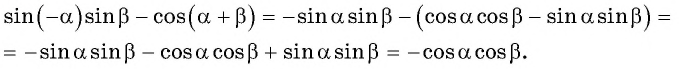
б) Применим формулу косинуса разности и получим: 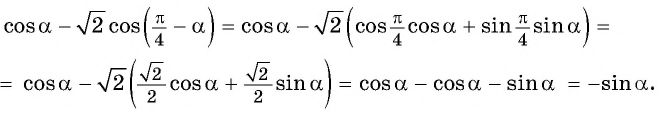
Пример №7
Решите уравнение 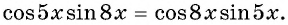
Решение:
Запишем уравнение в виде 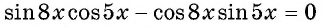 и по формуле синуса разности получим:
и по формуле синуса разности получим: 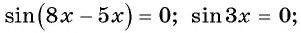
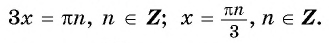
Ответ: 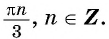
Пример №8
Вычислите 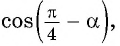 если
если 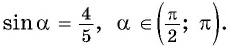
Решение:
Применим формулу косинуса разности:
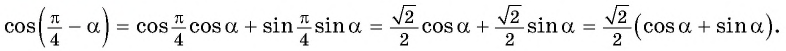
Из основного тригонометрического тождества выразим 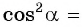
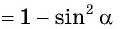 и найдем
и найдем 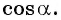 Так как
Так как 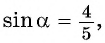 то
то 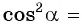
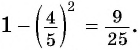 Значит,
Значит, 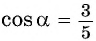 или
или 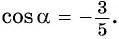 Поскольку
Поскольку 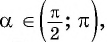 т. е.
т. е. 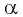 угол второй четверти, то
угол второй четверти, то 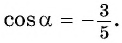 Тогда
Тогда
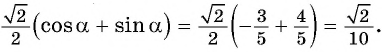
Пример №9
Докажите тождество 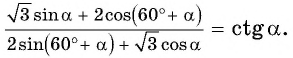
Решение:
Воспользуемся формулами сложения и получим:
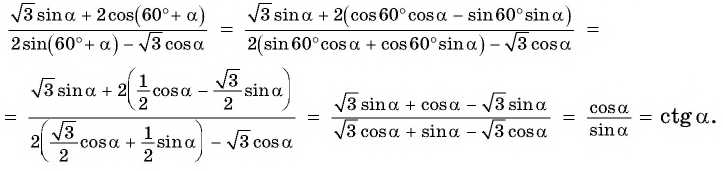
Пример №10
Найдите значение выражения:
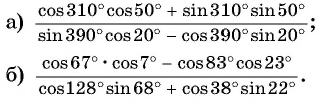
Решение:
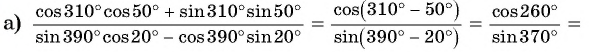
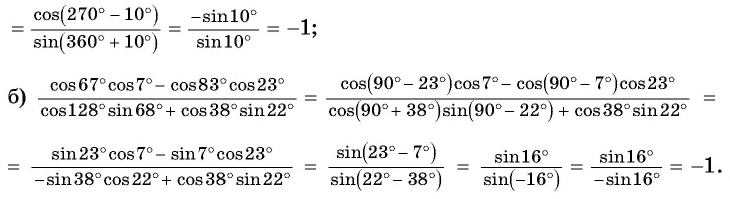 9.
9.
Пример №11
Найдите множество значений функции
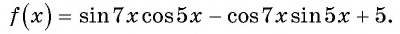
Решение:
Применим формулу синуса разности и запишем функцию в виде 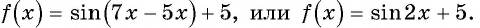
Так как 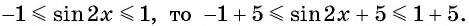 Таким образом, имеем:
Таким образом, имеем: 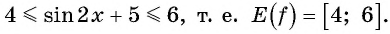
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Как найти разность углов
Разделы 
Дополнительно


Пример 1. На рис. изображены два угла с общей начальной стороной $bar $ и общей конечной стороной $bar $: один равен $+270^$, другой $-90^$.

Сумма двух углов. На координатной плоскости $Oxу$ рассмотрим окружность единичного радиуса с центром в начале координат (рис.). Пусть произвольный угол $alpha$ (на чертеже положительный) получен в результате вращения некоторото подвижного радиуса-вектора от его начального положения $bar$, совпадающего с положительным направлением оси $Ox$, до его конечного положения $bar$. Примем теперь положение радиуса-вектора $bar$ за начальное и отложим от него произвольный угол $beta$ (на чертеже положительный), который получим в результате вращения некоторого подвижного радиуса-вектора от его начального положения $bar$ до его конечного положения $bar$. В результате этих действий мы получим угол, который будем называть суммой углов $alpha$ и $beta$. (Начальное положение подвижного радиуса-вектора $bar$, конечное положение радиуса-вектора $bar $.)
Разность двух углов. 
Под разностью двух углов $alpha$ и $beta$, которую обозначим $alpha — beta$, мы будем понимать такой третий угол $gamma$, который в сумме с углом $beta$ дает угол $alpha$, т. е. $gamma = alpha — beta$, если $beta + gamma = alpha$. Разность двух углов $alpha$ и $beta$ можно трактовать как сумму углов $alpha$ и $- beta$. В самом деле, $[alpha + (- beta)] + beta = alpha$ (рис.). Вообще, для любых углов их сумма измеряется алгебраической суммой действительных чисел, измеряющих эти углы.
Виды углов
Каждый угол, в зависимости от его величины, имеет своё название:
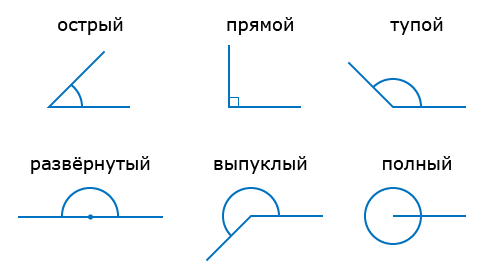
- Острый угол — это угол, который меньше прямого угла (<90°).
- Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол обозначается буквой d и равен 90°.
Если два смежных угла равны между собой, то каждый из них называется прямым углом. Прямой угол обычно обозначается не дугой, а уголком:

∠AOC и ∠COB — прямые углы. Общая сторона прямых углов OC называется перпендикуляром к прямой AB, а точка O — основанием перпендикуляра.
Развёрнутый угол равен сумме двух прямых углов или, короче, двум прямым углам. Следовательно, развёрнутый угол равен 180° или 2d.
Все развёрнутые углы равны между собой.
180° < выпуклый угол < 360°.
Полный угол равен сумме четырёх прямых углов, то есть 4d (360°).
Прилежащие углы
Прилежащие углы — это пара углов, имеющих общую вершину и общую сторону, другие стороны которых лежат по разные стороны от общей стороны.

∠AOB и ∠BOC — прилежащие углы, O — общая вершина, OB — общая сторона.
Если из вершины любого угла провести луч, разделяющий угол на два угла, то образованные углы будут прилежащими.
Угол, разделённый лучом, будет называться суммой полученных углов, например угол AOB является суммой углов AOC и COB:
∠AOB = ∠AOC + ∠COB.

Каждый из прилежащих углов, ∠AOC и ∠COB, называется разностью углов AOB и другого прилежащего, то есть:
Формулы суммы и разности углов тригонометрических функций онлайн
С помощю этого онлайн калькулятора можно получить формулы суммы и разности углов тригонометрических функций. Для получения формулы выберите нужную тригонометрическую функцию, нажав на “sin”, выберите нужный аргумент, нажав на аргумент в формуле. В результате получится формула для этой функции и аргумента. Теоретическую часть и численные примеры смотрите ниже.
Формулы суммы и разности углов тригонометрических функций − теория, доказательство, примеры
Выведем формулы суммы и разности углов тригонометрических функций. Начнем с формулы
Как мы знаем, угол между векторами не может быть больше 180° (π). На рисунке Рис.1 угол между векторами  и
и  равен
равен  . На рисунке Рис.2 угол между векторами
. На рисунке Рис.2 угол между векторами  и
и  равен
равен  .
.
Рассмотрим, теперь косинусы этих углов. Из формул приведения мы знаем (подпрбнее о формулах приведения смотрите на странице Формулы приведения тригонометрических функций онлайн):
Cкалярное произведение векторов  и
и  равно:
равно:
Так как точка  имеет координаты
имеет координаты  , а
, а  имеет координаты
имеет координаты  (смотрите статью на странице Синус и косинус. Онлайн калькулятор), то скалярное произведения векторов
(смотрите статью на странице Синус и косинус. Онлайн калькулятор), то скалярное произведения векторов  и
и  по координатам равно:
по координатам равно:
Поскольку левые части формул (2) и (3) равны, то равны и правые части этих формул. Следовательно выполнено равенство (1).
Докажем, далее, справедливость следующей формулы
Представим косинус суммы углов α и β в виде косинуса разности двух углов и воспользуемся формулой (1) и тем, что косинус четная функция а синус нечетная функция:
Перейдем к доказательству формул синусов суммы и разности углов:
Для доказательства формулы (5) воспользуемся формулами приведения тригонометрических функций и формулой (1):
Для доказательства формулы (6), представим разность углов в виде суммы и воспользуемся тем, что косинус четная функция а синус нечетная функция:
Формулы тангенса суммы и разности углов имееют следующий вид:
Докажем формулу (7):
Разделим числитель и знаменатель дроби в правой части уравнения (9) на  (
( ,
,  ):
):
Для доказательства формулы (9) представим разность углов в виде суммы, воспользуемся формулой (8) и учтем, что тангенс нечетная функция:
Формулы котангенса суммы и разности углов имееют следующий вид:
Докажем формулу (10):
Разделим числитель и знаменатель дроби в правой части уравнения (12) на  (
( ,
,  ):
):
Для доказательства формулы (11), представим разность углов α и β в виде суммы и учтем, что котангенс нечетная функция:
Умножив числитель и знаменатель в правой части уравнения (13) на −1, получим формулу (11).
Примеры использования формул суммы и разности углов тригонометрических функций
Пример 1. Найти точное значение  .
.
Решение:
Ответ:
Пример 2. Найти косинус для угла 15°.
Решение:
Ответ:
Пример 3. Найти точное значение тангенса для угла 15° .
Решение:
Тангенсы для углов 45° и 15° известны. Подставим эти значения в (14):
Дробь в правой части уравнения (15) можно упростить, умножив числитель и знаменатель дроби на  :
:
Ответ:
Degrees minutes seconds subtraction calculator is used to find the difference between angles in Trigonometric applications. An angle is a shape, formed by two lines diverging from a common point. An angle may be classified as acute, obtuse, right, reflex, straight and full angle. The angles are the sections of a full 360-degree circle. Use this online angle subtraction calculator or DMS subtraction calculator to subtract the angles expressed in degrees, minutes and seconds.
Degrees minutes seconds subtraction calculator is used to find the difference between angles in Trigonometric applications. An angle is a shape, formed by two lines diverging from a common point. An angle may be classified as acute, obtuse, right, reflex, straight and full angle. The angles are the sections of a full 360-degree circle. Use this online angle subtraction calculator or DMS subtraction calculator to subtract the angles expressed in degrees, minutes and seconds.
Code to add this calci to your website 

Formula:
A1 = d1 + ( m1 x 0.0166666667 ) + ( s1 x 0.000277778 )
A2 = d2 + ( m2 x 0.0166666667 ) + ( s2 x 0.000277778 )
A = A1 – A2
Where,
A1 = Angle 1
d1, d2 = Degree
m1, m2 = Minutes
s1, s2 = Seconds
A2 = Angle 2
A = Difference Between A1 and A2
Angle Subtraction Calculation
Find the Difference between two angles such as 74 ° 25′ 20′ and 24 ° 1′ 10′ ?
The resultant Angle of degree minutes seconds (DMS) subtraction is 50 ° 24′ 10′
Related Calculators:
- Right Triangle Calculator
- Double Angle Identity Solver, Formula – Trig Calculator
- Half Angle Formula Calculator
- Triangle Law Of Forces
- Wire Gauge Calculator
- Aquarium Glass Thickness Calculator