Как найти разность арифметической прогрессии все формулы - Сайт, где вы сможете решить свои вопросы

У этого термина существуют и другие значения, см. Прогрессия.

Арифмети́ческая прогре́ссия — числовая последовательность вида

${displaystyle a_{1}, a_{1}+d, a_{1}+2d, ldots , a_{1}+(n-1)d, ldots ,}$

то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа (шага, или разности прогрессии):

${displaystyle a_{n}=a_{n-1}+d.}$ ^[1]

Любой член арифметической прогрессии равен первому её члену, сложенному с произведением разности прогрессии на число членов, предшествующих определяемому, т. е. он выражается формулой^[2]:

${displaystyle a_{n}=a_{1}+(n-1)d.}$

Арифметическая прогрессия является монотонной последовательностью. При d>0 она является возрастающей, а при d<0 — убывающей. Если d=0 , то последовательность будет стационарной. Эти утверждения следуют из соотношения $a_{n+1}-a_n=d$ для членов арифметической прогрессии.

Свойства[править | править код]

Общий член арифметической прогрессии[править | править код]

Член арифметической прогрессии с номером может быть найден по формулам

${displaystyle a_{n}=a_{m}-(m-n)d}$

где $a_{1}$

— первый член прогрессии,

— её разность, a_m

— член арифметической прогрессии с номером

Доказательство формулы общего члена арифметической прогрессии

Пользуясь соотношением $a_{n+1}=a_n+d$ выписываем последовательно несколько членов прогрессии, а именно:

Заметив закономерность, делаем предположение, что . С помощью математической индукции покажем, что предположение верно для всех :

База индукции (n=1) :

— утверждение истинно.

Переход индукции:

Пусть наше утверждение верно при n=k , то есть . Докажем истинность утверждения при n=k+1 :

$a_{k+1}=a_k+d=a_1+(k-1)d+d=a_1+kd$

Итак, утверждение верно и при n=k+1 . Это значит, что для всех .■

Отметим, что в формулах общего члена -й член прогрессии есть линейная функция. Об этом говорит следующая теорема.

Доказательство

Необходимость. Пусть ${displaystyle left{a_{n}right}}$ арифметическая прогрессия. Тогда, как было уже показано, , то есть ${displaystyle a_{n}=nd+a_{1}-d}$ . Так как есть линейная функция и , это значит, что и ${displaystyle b=a_{1}-d}$ , т. е. a_n — линейная функция, где ${displaystyle fleft(nright)=nd+a_{1}-d}$ .

Достаточность. Пусть a_n есть линейная функция, т. е. ${displaystyle a_{n}=acdot x+b}$ . Так как и , то ${displaystyle a_{n}=acdot n+b}$ , тогда ${displaystyle a_{n+1}=acdot left(n+1right)+b}$ .
Рассмотрим ${displaystyle a_{n+1}-a_{n}=left(acdot left(n+1right)+bright)-left(an+bright)}$ .
Отсюда следует, что ${displaystyle a_{n+1}-a_{n}=a}$ , где — величина постоянная. Тогда ${displaystyle a_{n+1}=a_{n}+a}$ , а это значит по определению, что ${displaystyle left{a_{n}right}}$ — арифметическая прогрессия.■

Суммы членов арифметической прогрессии с равными суммами номеров равны, т. е. ${displaystyle a_{n}+a_{m}=a_{k}+a_{l}Longleftrightarrow n+m=k+lquad vert ;forall left(n,,m,,k,,lin mathbb {N} right)}$ .

Характеристическое свойство арифметической прогрессии[править | править код]

Последовательность есть арифметическая прогрессия для любого её элемента выполняется условие

${displaystyle a_{n}={dfrac {a_{n-1}+a_{n+1}}{2}},ngeqslant 2.}$

Доказательство характеристического свойства арифметической прогрессии

Необходимость.

Поскольку — арифметическая прогрессия, то для выполняются соотношения:

$a_n=a_{n-1}+d$

$a_n=a_{n+1}-d$ .

Сложив эти равенства и разделив обе части на 2, получим ${displaystyle a_{n}={dfrac {a_{n-1}+a_{n+1}}{2}}}$ .

Достаточность.

Имеем, что для каждого элемента последовательности, начиная со второго, выполняется $a_n=frac{a_{n-1}+a_{n+1}}2$ . Следует показать, что эта последовательность есть арифметическая прогрессия. Преобразуем эту формулу к виду $a_{n+1}-a_n=a_n-a_{n-1}$ . Поскольку соотношения верны при всех , с помощью математической индукции покажем, что $a_2-a_1=a_3-a_2=ldots =a_n-a_{n-1}=a_{n+1}-a_n$ .

База индукции (n=2) :

— утверждение истинно.

Переход индукции:

Пусть наше утверждение верно при n=k , то есть $a_2-a_1=a_3-a_2=ldots =a_k-a_{k-1}=a_{k+1}-a_k$ . Докажем истинность утверждения при n=k+1 :

$a_{k+1}-a_{k}=a_{k+2}-a_{k+1}$

Но по предположению индукции следует, что $a_2-a_1=a_3-a_2=ldots =a_k-a_{k-1}=a_{k+1}-a_k$ . Получаем, что $a_2-a_1=a_3-a_2=ldots =a_k-a_{k-1}=a_{k+1}-a_k=a_{k+2}-a_{k+1}$

Итак, утверждение верно и при n=k+1 . Это значит, что $a_n=frac{a_{n-1}+a_{n+1}}2, n geqslant 2 Rightarrow a_2-a_1=a_3-a_2=ldots =a_n-a_{n-1}=a_{n+1}-a_n$ .

Обозначим эти разности через . Итак, $a_2-a_1=a_3-a_2=ldots =a_n-a_{n-1}=a_{n+1}-a_n=d$ , а отсюда имеем $a_{n+1}=a_n+d$ для . Поскольку для членов последовательности выполняется соотношение $a_{n+1}=a_n+d$ , то это есть арифметическая прогрессия.■

Тождество арифметической прогрессии[править | править код]

Доказательство тождества арифметической прогрессии

С помощью формулы общего члена выразим -й, -й, -й члены:

${displaystyle a_{k}=a_{1}+(k-1)d,quad a_{l}=a_{1}+(l-1)d,quad a_{m}=a_{1}+(m-1)d.}$

Вычитая почленно из первого равенства второе, а из второго третьего, получим:

${displaystyle a_{k}-a_{l}=(k-l)d,quad a_{l}-a_{m}=(l-m)d.}$

Выражая из этих равенств и приравнивая полученные выражения, получим:

${displaystyle {dfrac {a_{k}-a_{l}}{k-l}}={dfrac {a_{l}-a_{m}}{l-m}}.}$

По основному свойству пропорции:

${displaystyle (l-m)(a_{k}-a_{l})=(k-l)(a_{l}-a_{m}).}$

Откуда следует доказываемое тождество:

${displaystyle (k-l)a_{m}+(m-k)a_{l}+(l-m)a_{k}=0.}$

■

Следствие 1. Всякий член арифметической прогрессии вырази́м^[5] через любую пару других членов.

Доказательство

Преобразовав тождество арифметической прогрессии

${displaystyle (k-l)a_{m}+(m-k)a_{l}+(l-m)a_{k}=0}$

к виду

${displaystyle a_{m}={dfrac {(l-m)a_{k}+(m-k)a_{l}}{l-k}},}$

можно заметить, что -й член есть линейная комбинация двух других членов ( $a_{{k}}$ и ${displaystyle a_{l}}$ ), поскольку оно равносильно

${displaystyle a_{m}={dfrac {l-m}{l-k}}a_{k}+{dfrac {m-k}{l-k}}a_{l}.}$

■

Следствие 2. Для того, чтобы число ${displaystyle a_{m}}$ являлось членом данной арифметической прогрессии с членами $a_{{k}}$ и ${displaystyle a_{l}}$ , необходимо и достаточно, чтобы было натуральным число

${displaystyle m={dfrac {(a_{l}-a_{m})k+(a_{m}-a_{k})l}{a_{l}-a_{k}}}.}$

Формулировка ещё одного признака арифметической прогрессии.

Следствие 3 [критерий]. Числовая последовательность является арифметической прогрессией в том и только в том случае, если выполняется тождество арифметической прогрессии для всех членов данной последовательности. Другими словами, чтобы каждый член был вырази́м через любую пару остальных членов последовательности.

${displaystyle left{a_{n}right}~-~div Longleftrightarrow left(k-lright)a_{m}+left(m-kright)a_{l}+left(l-mright)a_{k}=0mid forall k,forall l,forall min mathbb {N} .}$

Доказательство

Необходимость. Утверждение

${displaystyle left{a_{n}right}~-~div Rightarrow left(k-lright)a_{m}+left(m-kright)a_{l}+left(l-mright)a_{k}=0mid forall k,forall l,forall min mathbb {N} }$

очевидно (см. доказательство тождества арифметической прогрессии).

Достаточность. Докажем, что

${displaystyle left{a_{n}right}~-~div Leftarrow left(k-lright)a_{m}+left(m-kright)a_{l}+left(l-mright)a_{k}=0mid forall k,forall l,forall min mathbb {N} .}$

Равенство

${displaystyle (k-l)a_{m}+(m-k)a_{l}+(l-m)a_{k}=0}$

можно преобразовать к виду

${displaystyle (l-m)(a_{k}-a_{l})=(k-l)(a_{l}-a_{m}).}$

Если все три номера различны, тогда

${displaystyle {dfrac {a_{k}-a_{l}}{k-l}}={dfrac {a_{l}-a_{m}}{l-m}}.}$

Обозначим выражение, например, в левой части равенства за , то есть

${displaystyle d={dfrac {a_{k}-a_{l}}{k-l}}.}$

Откуда можно прийти к следующему предложению:

${displaystyle a_{k}=a_{l}+{left(k-lright)}d.}$

Наконец, методом математической индукции, например, по нетрудно убедиться, что данное соотношение описывает именно арифметическую прогрессию.

Действительно, при l=1 (база индукции) получаем формулу общего члена арифметической прогрессии:

${displaystyle a_{k}=a_{1}+{left(k-1right)}d.}$

Предположим истинность утверждения (для ): формула ${displaystyle a_{k}=a_{l}+{left(k-lright)}d}$ характеризует арифметическую прогрессию. Тогда покажем, что и при l+1 формула верна для арифметической прогрессии (переход, или шаг, индукции). Рассмотрим левую часть формулы

${displaystyle a_{k}=a_{l+1}+{left(k-left(l+1right)right)}d.}$

По предположению индукции ( ${displaystyle a_{k}=a_{l}+{left(k-lright)}d}$ ) заменим $a_{k}$ на выражение ${displaystyle a_{l}+{left(k-lright)}d}$ . Итак, получим следующее:

${displaystyle a_{l}+{left(k-lright)}d=a_{l+1}+{left(k-left(l+1right)right)}d.}$

Методом тождественных преобразований имеем равносильное предложение

${displaystyle a_{l+1}=a_{l}+d.}$

А это, в свою очередь, рекуррентное соотношение для арифметической прогрессии.

Значит, по принципу математической индукции можно утвердать, что для всякого соотношение ${displaystyle a_{k}=a_{l}+{left(k-lright)}d}$ верно только и только для членов арифметической прогрессии.

Аналогичные рассуждения проводятся для формулы ${displaystyle d={dfrac {a_{l}-a_{m}}{l-m}}}$ .

Данное следствие целиком и полностью считается доказанным.■

Сумма первых n членов арифметической прогрессии[править | править код]

Сумма первых членов арифметической прогрессии ${displaystyle S_{n}=sum _{i=1}^{n}a_{i}=a_{1}+a_{2}+ldots +a_{n}}$ может быть найдена по формулам

${displaystyle S_{n}={dfrac {a_{1}+a_{n}}{2}}cdot n}$

, где $a_{1}$

— первый член прогрессии, a_n

— член с номером

— количество суммируемых членов.

${displaystyle S_{n}={dfrac {a_{1}+a_{n}}{2}}cdot ({dfrac {a_{n}-a_{1}}{a_{2}-a_{1}}}+1)}$

— где $a_{1}$

— первый член прогрессии, $a_{2}$

— второй член прогрессии ${displaystyle ,a_{n}}$

— член с номером

${displaystyle S_{n}={dfrac {2a_{1}+d(n-1)}{2}}cdot n}$

, где $a_{1}$

— первый член прогрессии,

— разность прогрессии,

— количество суммируемых членов.

${displaystyle S_{n}=a_{frac {n+1}{2}}cdot n}$

, если

— нечётное натуральное число.

Доказательство
Запишем сумму двумя способами: $S_n=a_1+a_2+a_3+ ldots +a_{n-2}+a_{n-1}+a_n$ $S_n=a_n+a_{n-1}+a_{n-2}+ ldots +a_3+a_2+a_1$ — та же сумма, только слагаемые идут в обратном порядке. Теперь сложим оба равенства, последовательно складывая в правой части слагаемые, которые стоят на одной вертикали: $2S_n=(a_1+a_n)+(a_2+a_{n-1})+(a_3+a_{n-2})+ ldots +(a_{n-2}+a_3)+(a_{n-1}+a_2)+(a_n+a_1)$ Покажем, что все слагаемые (все скобки) полученной суммы равны между собой. В общем виде каждое слагаемое можно подать в виде $a_i+a_{n-i+1}, i=1,2,ldots,n$ . Воспользуемся формулой общего члена арифметической прогрессии: $a_i+a_{n-i+1}=a_1+(i-1)d+a_1+(n-i+1-1)d=2a_1+(n-1)d, i=1,2,ldots,n$ Получили, что каждое слагаемое не зависит от и равно . В частности, . Поскольку таких слагаемых , то ${displaystyle 2S_{n}=(a_{1}+a_{n})cdot nRightarrow S_{n}={dfrac {a_{1}+a_{n}}{2}}cdot n}$ Третья формула для суммы получается подстановкой вместо . Что и так непосредственно следует из выражения для общего члена. Замечание: Вместо в первой формуле для суммы можно взять любое из других слагаемых $a_i+a_{n-i+1}, i=2,3,ldots,n$ , так как они все равны между собой.

Доказательство

Запишем сумму двумя способами:

$S_n=a_1+a_2+a_3+ ldots +a_{n-2}+a_{n-1}+a_n$

$S_n=a_n+a_{n-1}+a_{n-2}+ ldots +a_3+a_2+a_1$ — та же сумма, только слагаемые идут в обратном порядке.

Теперь сложим оба равенства, последовательно складывая в правой части слагаемые, которые стоят на одной вертикали:

$2S_n=(a_1+a_n)+(a_2+a_{n-1})+(a_3+a_{n-2})+ ldots +(a_{n-2}+a_3)+(a_{n-1}+a_2)+(a_n+a_1)$

Покажем, что все слагаемые (все скобки) полученной суммы равны между собой. В общем виде каждое слагаемое можно подать в виде $a_i+a_{n-i+1}, i=1,2,ldots,n$ . Воспользуемся формулой общего члена арифметической прогрессии:

$a_i+a_{n-i+1}=a_1+(i-1)d+a_1+(n-i+1-1)d=2a_1+(n-1)d, i=1,2,ldots,n$

Получили, что каждое слагаемое не зависит от и равно . В частности, . Поскольку таких слагаемых , то

${displaystyle 2S_{n}=(a_{1}+a_{n})cdot nRightarrow S_{n}={dfrac {a_{1}+a_{n}}{2}}cdot n}$

Третья формула для суммы получается подстановкой вместо a_1+a_n . Что и так непосредственно следует из выражения для общего члена.

Замечание:

Вместо a_1+a_n в первой формуле для суммы можно взять любое из других слагаемых $a_i+a_{n-i+1}, i=2,3,ldots,n$ , так как они все равны между собой.

Формулировка ещё одного факта: для всякой арифметической прогрессии при любом выполняется равенство:

${displaystyle S_{2n}=S_{n}+{dfrac {1}{3}}S_{3n}.}$

Примечание: $S_{k}$ — сумма первых членов арифметической прогрессии.

Доказательство
1. Очевидно, что ${displaystyle {dfrac {S_{2n}}{2n}}-{dfrac {S_{n}}{n}}={dfrac {a_{1}+a_{2n}-left(a_{1}+a_{n}right)}{2}}={dfrac {a_{2n}-a_{n}}{2}},}$ или ${displaystyle S_{2n}-2S_{n}=ncdot (a_{2n}-a_{n}).}$ Прибавим к обеим частям $S_{n}$ и получим, что ${displaystyle S_{2n}-S_{n}=S_{n}+ncdot (a_{2n}-a_{n}).}$ 2. Покажем, что ${displaystyle S_{n}+ncdot (a_{2n}-a_{n})={dfrac {1}{3}}S_{3n}.}$ Это так, поскольку можно написать верное равенство: ${displaystyle {dfrac {S_{3n}}{3n}}-{dfrac {S_{n}}{n}}={dfrac {a_{3n}-a_{n}}{2}}.}$ Из него следует, что ${displaystyle {dfrac {S_{3n}}{3}}=S_{n}+{dfrac {a_{3n}-a_{n}}{2}}cdot n.}$ 3. Теперь докажем, что ${displaystyle a_{2n}-a_{n}={dfrac {a_{3n}-a_{n}}{2}}.}$ Перепишем последнее как ${displaystyle a_{2n}={dfrac {a_{3n}+a_{n}}{2}}.}$ Но гораздо лучше представить это равенство в виде ${displaystyle a_{2n}={dfrac {a_{2n+1}+a_{2n-1}}{2}}.}$ Видно, что это характеристическое свойство арифметической прогрессии. Значит, действительно ${displaystyle a_{2n}-a_{n}={dfrac {a_{3n}-a_{n}}{2}}.}$ 4. А следовательно, ${displaystyle S_{n}+ncdot (a_{2n}-a_{n})={dfrac {1}{3}}S_{3n}.}$ 5. Тем самым, ${displaystyle S_{2n}=S_{n}+{dfrac {1}{3}}S_{3n},}$ что и требовалось доказать.

Доказательство

1. Очевидно, что ${displaystyle {dfrac {S_{2n}}{2n}}-{dfrac {S_{n}}{n}}={dfrac {a_{1}+a_{2n}-left(a_{1}+a_{n}right)}{2}}={dfrac {a_{2n}-a_{n}}{2}},}$ или ${displaystyle S_{2n}-2S_{n}=ncdot (a_{2n}-a_{n}).}$

Прибавим к обеим частям $S_{n}$ и получим, что ${displaystyle S_{2n}-S_{n}=S_{n}+ncdot (a_{2n}-a_{n}).}$

2. Покажем, что ${displaystyle S_{n}+ncdot (a_{2n}-a_{n})={dfrac {1}{3}}S_{3n}.}$

Это так, поскольку можно написать верное равенство:

${displaystyle {dfrac {S_{3n}}{3n}}-{dfrac {S_{n}}{n}}={dfrac {a_{3n}-a_{n}}{2}}.}$

Из него следует, что ${displaystyle {dfrac {S_{3n}}{3}}=S_{n}+{dfrac {a_{3n}-a_{n}}{2}}cdot n.}$

3. Теперь докажем, что ${displaystyle a_{2n}-a_{n}={dfrac {a_{3n}-a_{n}}{2}}.}$
Перепишем последнее как ${displaystyle a_{2n}={dfrac {a_{3n}+a_{n}}{2}}.}$

Но гораздо лучше представить это равенство в виде ${displaystyle a_{2n}={dfrac {a_{2n+1}+a_{2n-1}}{2}}.}$ Видно, что это характеристическое свойство арифметической прогрессии.
Значит, действительно ${displaystyle a_{2n}-a_{n}={dfrac {a_{3n}-a_{n}}{2}}.}$

4. А следовательно, ${displaystyle S_{n}+ncdot (a_{2n}-a_{n})={dfrac {1}{3}}S_{3n}.}$

5. Тем самым, ${displaystyle S_{2n}=S_{n}+{dfrac {1}{3}}S_{3n},}$ что и требовалось доказать.

Предыдущее свойство имеет обобщение.

Для любых натуральных , , выполняется комплементарное свойство сумм:

${displaystyle {dfrac {l-m}{k}}cdot S_{k}+{dfrac {m-k}{l}}cdot S_{l}+{dfrac {k-l}{m}}cdot S_{m}=0.}$

Ещё один признак арифметической прогрессии.

Сумма членов арифметической прогрессии от n-го до m-го[править | править код]

Сумма членов арифметической прогрессии с номерами от до ${displaystyle S_{m,n}=sum _{i=n}^{m}a_{i}=a_{n}+a_{n+1}+ldots +a_{m}}$ может быть найдена по формулам

${displaystyle S_{m,n}={dfrac {a_{m}+a_{n}}{2}}cdot (m-n+1)}$

, где

— член с номером

— член с номером

— количество суммируемых членов.

${displaystyle S_{m,n}={dfrac {2a_{n}+dleft(m-nright)}{2}}cdot left(m-n+1right),}$

где a_n — член с номером , — разность прогрессии, — количество суммируемых членов.

Произведение членов арифметической прогрессии[править | править код]

Произведением первых членов арифметической прогрессии ${displaystyle left{a_{n}right}}$ называется произведение от $a_{1}$ до a_n , то есть выражение вида ${displaystyle prod limits _{i=1}^{n}a_{i}=a_{1}cdot a_{2}cdot a_{3}cdot ldots cdot a_{n-2}cdot a_{n-1}cdot a_{n}.}$ Обозначение: $P_{n}$ .

Свойство произведения:

Число множителей-скобок ${displaystyle {left(a_{frac {n+1}{2}}^{2}-{left[idright]}^{2}right)}}$ равно ${displaystyle {dfrac {n-1}{2}}}$ , а в самом произведении ${displaystyle a_{frac {n+1}{2}}cdot prod limits _{i=1}^{frac {n-1}{2}}{left(a_{frac {n+1}{2}}^{2}-{left[idright]}^{2}right)}}$ их составляет ${displaystyle {dfrac {n+1}{2}}}$ «штук».^[10]

Сходимость арифметической прогрессии[править | править код]

Арифметическая прогрессия расходится при dne 0 и сходится при d=0 . Причём

$lim_{nrightarrowinfty} a_n=left{ begin{matrix} +infty, d>0 \ -infty, d<0 \ a_1, d=0 end{matrix} right.$

Доказательство
Записав выражение для общего члена и исследуя предел $lim_{nrightarrowinfty} (a_1+(n-1)d)$ , получаем искомый результат.

Связь между арифметической и геометрической прогрессиями[править | править код]

Пусть — арифметическая прогрессия с разностью и число a>0 . Тогда последовательность вида $a^{a_1}, a^{a_2}, a^{a_3}, ldots$ есть геометрическая прогрессия со знаменателем a^d .

Доказательство
Проверим характеристическое свойство для образованной геометрической прогрессии: $sqrt{a^{a_{n-1}}cdot a^{a_{n+1}}}= a^{a_n}, ngeqslant 2$ Воспользуемся выражением для общего члена арифметической прогрессии: $sqrt{a^{a_{n-1}}cdot a^{a_{n+1}}}=sqrt{a^{a_1+(n-2)d}cdot a^{a_1+nd}}=sqrt{a^{2a_1+2(n-1)d}}=sqrt{(a^{a_1+(n-1)d})^2}=a^{a_1+(n-1)d}=a^{a_n}, ngeqslant 2$ Итак, поскольку характеристическое свойство выполняется, то $a^{a_1}, a^{a_2}, a^{a_3}, ldots$ — геометрическая прогрессия. Её знаменатель можно найти, например, из соотношения $q=frac{a^{a_2}}{a^{a_1}}=frac{a^{a_1+d}}{a^{a_1}}=a^d$ .

Доказательство

Проверим характеристическое свойство для образованной геометрической прогрессии:

$sqrt{a^{a_{n-1}}cdot a^{a_{n+1}}}= a^{a_n}, ngeqslant 2$

Воспользуемся выражением для общего члена арифметической прогрессии:

$sqrt{a^{a_{n-1}}cdot a^{a_{n+1}}}=sqrt{a^{a_1+(n-2)d}cdot a^{a_1+nd}}=sqrt{a^{2a_1+2(n-1)d}}=sqrt{(a^{a_1+(n-1)d})^2}=a^{a_1+(n-1)d}=a^{a_n}, ngeqslant 2$

Итак, поскольку характеристическое свойство выполняется, то $a^{a_1}, a^{a_2}, a^{a_3}, ldots$ — геометрическая прогрессия. Её знаменатель можно найти, например, из соотношения $q=frac{a^{a_2}}{a^{a_1}}=frac{a^{a_1+d}}{a^{a_1}}=a^d$ .

Следствие: если последовательность положительных чисел образует геометрическую прогрессию, то последовательность их логарифмов образует арифметическую прогрессию.

Арифметические прогрессии высших порядков[править | править код]

Арифметической прогрессией второго порядка называется такая последовательность чисел, что последовательность их разностей сама образует простую арифметическую прогрессию. Примером может служить последовательность квадратов натуральных чисел:

1, 4, 9, 16, 25, 36, …

разности которых образуют простую арифметическую прогрессию с разностью 2:

3, 5, 7, 9, 11, …

Треугольные числа также образуют арифметическую прогрессию второго порядка, их разности образуют простую арифметическую прогрессию

Тетраэдральные числа образуют арифметическую прогрессию третьего порядка, их разности являются треугольными числами.

Аналогично определяются и прогрессии более высоких порядков. В частности, последовательность n-ных степеней образует арифметическую прогрессию n-го порядка.

Если $left[a_{{i}}right]_{{1}}^{{n}}$ — арифметическая прогрессия порядка , то существует многочлен $P_{{m}}(i)=c_{{m}}i^{{m}}+...+c_{{1}}i+c_{{0}}$ , такой, что для всех выполняется равенство $a_{{i}}=P_{{m}}(i)$ ^[11]

Примеры[править | править код]

${displaystyle T_{n}=sum _{i=1}^{n}i=1+2+3+ldots +n={frac {n(n+1)}{2}}}$

Формула для разности[править | править код]

Если известны два члена арифметической прогрессии, а также их номера в ней, то можно найти разность как

${displaystyle {mathit {d={frac {a_{m}-a_{n}}{m-n}}}}}$

Сумма чисел от 1 до 100[править | править код]

Согласно легенде, школьный учитель математики юного Гаусса, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 5050.
Действительно, легко видеть, что решение сводится к формуле

$frac{n(n+1)}2$

то есть к формуле суммы первых чисел натурального ряда.

См. также[править | править код]

Геометрическая прогрессия
Арифметико-геометрическая прогрессия

Примечания[править | править код]

↑ Такое соотношение называют рекуррентным соотношением первого порядка. Поэтому арифметическая прогрессия есть множество последовательностей, задающихся именно таким образом.
↑ Фильчаков П. Ф. Глава II. Алгебра и элементарные функции. Функции натурального аргумента (§ 75. Арифметическая прогрессия) // Справочник по элементарной математике: для поступающих в вузы : книга / под ред. чл.-кор. АН УССР П. Ф. Фильчакова. — Киев : «Наукова думка», 1972. — С. 303. — 528 с. — 400 000 экз. — УДК 51 (08)^(G).
↑ Шахмейстер А. Х. Прогрессии. Арифметическая прогрессия // Множества. Функции. Последовательности. Прогрессии : книга / А. Х. Шахмейстер, под общ. ред. Б. Г. Зива. — 2-е изд., испр. и доп. — СПб. : «Петроглиф» : «Виктория плюс» ; М. : Издательство МЦНМО, 2008. — С. 135. — 296 с. : илл. — (Математика. Элективные курсы). — 3000 экз. — ББК 22.141я71.6. — УДК 373.167.1:512^(G). — ISBN 978-5-94057-423-1. — ISBN 978-5-98712-027-9. — ISBN 978-5-91673-006-7.
↑ Соотношение между любыми тремя членами арифметической прогрессии и их номерами (Мусинов В. А.) // Материалы студенческой научной сессии Института математики и информатики МПГУ. 2021–2022 учебный год : сборник статей / под общ. ред. Е. С. Крупицына. — М.: МПГУ, 2022. — С. 91—93. — 156 с. — ISBN 978-5-4263-1109-1, ББК 22.1я431+32.81я431+22.1р30я431+74.262.21я431+74.263.2я431.
↑ Это означает, что выражаемый член есть комбинация любых двух других членов данной последовательности, причём эта комбинация составлена с помощью арифметических операций и конечного набора символов. Для арифметической последовательности такая комбинация будет линейной.
↑ Шахмейстер А. Х. Прогрессии. Арифметическая прогрессия // Множества. Функции. Последовательности. Прогрессии : книга / А. Х. Шахмейстер, под общ. ред. Б. Г. Зива. — 2-е изд., испр. и доп. — СПб. : «Петроглиф» : «Виктория плюс» ; М. : Издательство МЦНМО, 2008. — С. 141. — 296 с. : илл. — (Математика. Элективные курсы). — 3000 экз. — ББК 22.141я71.6. — УДК 373.167.1:512^(G). — ISBN 978-5-94057-423-1. — ISBN 978-5-98712-027-9. — ISBN 978-5-91673-006-7.
↑ Из доказательства необходимости следует, что ${displaystyle S_{n}=an^{2}+bn}$ , поэтому, если ${displaystyle S_{n}=an^{2}+bn+c}$ , то необходимо сделать проверку. Например, если ${displaystyle S_{n}=2n^{2}-n-6}$ — сумма первых членов последовательности, то такая последовательность НЕ является арифметической прогрессией. А последовательность, заданная суммой ${displaystyle S_{n}=2n^{2}-n}$ первых членов, будет арифметической прогрессией.
↑ При произведение $P_{n}$ равно ${displaystyle a_{frac {1+1}{2}}=a_{1}}$ , что безусловно верно.
↑ Эту формулу удобно использовать для выполнения итераций в программном коде, так как результат зависит от значения только двух величин: постоянного числа — разности, и члена, стоящего ровно по середине между первым и -м членом.
↑ Пример применения формулы.
Пусть ${displaystyle div left{a_{n}right}:quad underbrace {27} _{a_{1}},;underbrace {20} _{a_{2}},;underbrace {13} _{a_{3}},;underbrace {6} _{a_{4}},;underbrace {-1} _{a_{5}}}$ , где .

По формуле ${displaystyle P_{n}=a_{frac {n+1}{2}}cdot prod limits _{i=1}^{frac {n-1}{2}}{left(a_{frac {n+1}{2}}^{2}-{left[idright]}^{2}right)}}$ найдём произведение пяти первых членов. Количество сомножителей должно равняться ${displaystyle {dfrac {5+1}{2}}=3}$ . Причём первым сомножителем будет ${displaystyle a_{frac {5+1}{2}}=a_{3}=13}$ .

Далее ${displaystyle prod limits _{i=1}^{frac {5-1}{2}}{left(a_{frac {5+1}{2}}^{2}-{left[idright]}^{2}right)}=prod limits _{i=1}^{2}{left(a_{3}^{2}-{left[idright]}^{2}right)}=}$ ${displaystyle ={left(a_{3}^{2}-{left[dright]}^{2}right)}cdot {left(a_{3}^{2}-{left[2dright]}^{2}right)}={left(169-49right)}cdot {left(169-4cdot 49right)}=}$ .

Наконец, ${displaystyle P_{n}=13cdot 120cdot {left(-27right)}=-42120}$ .
↑ Бронштейн, 1986, с. 139.

Литература[править | править код]

Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. — М.: Наука, 1986. — 544 с.

Ссылки[править | править код]

Арифметическая прогрессия // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890. — Т. II. — С. 98.

Источник

Многие слышали об арифметической прогрессии, но не все хорошо представляют, что это такое. В данной статье дадим соответствующее определение, а также рассмотрим вопрос, как найти разность прогрессии арифметической, и приведем ряд примеров.

Математическое определение

Итак, если речь идет о прогрессии арифметической или алгебраической (эти понятия определяют одно и то же), то это означает, что имеется некоторый числовой ряд, удовлетворяющий следующему закону: каждые два соседних числа в ряду отличаются на одно и то же значение. Математически это записывается так:

a_{n + 1}-a_n = d

Здесь n означает номер элемента a_n в последовательности, а число d – это разность прогрессии (ее название следует из представленной формулы).

О чем говорит знание разности d? О том, как “далеко” друг от друга отстоят соседние числа. Однако знание d является необходимым, но не достаточным условием для определения (восстановления) всей прогрессии. Необходимо знать еще одно число, которым может быть совершенно любой элемент рассматриваемого ряда, например, a₄, a10, но, как правило, используют первое число, то есть a₁.

Формулы для определения элементов прогрессии

В общем, информации выше уже достаточно, чтобы переходить к решению конкретных задач. Тем не менее до того, как будет дана прогрессия арифметическая, и найти разность ее будет необходимо, приведем пару полезных формул, облегчив тем самым последующий процесс решения задач.

Несложно показать, что любой элемент последовательности с номером n может быть найден следующим образом:

a_n = a₁ + (n – 1) * d

Действительно, проверить эту формулу может каждый простым перебором: если подставить n = 1, то получится первый элемент, если подставить n = 2, тогда выражение выдает сумму первого числа и разности, и так далее.

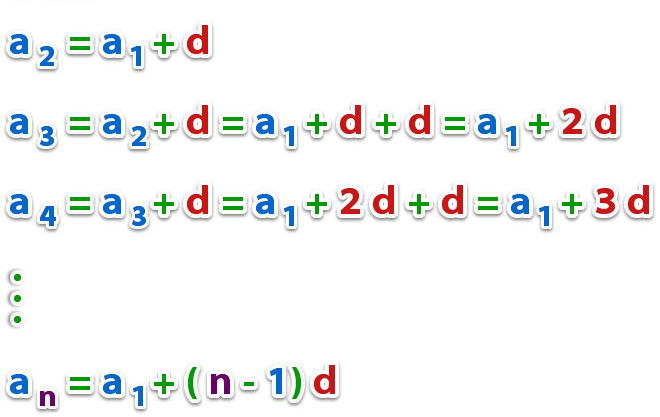
Условия многих задач составляются таким образом, что по известной паре чисел, номера которых в последовательности также даны, необходимо восстановить весь числовой ряд (найти разность и первый элемент). Сейчас мы решим эту задачу в общем виде.

Итак, пусть даны два элемента с номерами n и m. Пользуясь полученной выше формулой, можно составить систему из двух уравнений:

a_n = a₁ + (n – 1) * d;

a_m = a₁ + (m – 1) * d

Для нахождения неизвестных величин воспользуемся известным простым приемом решения такой системы: вычтем попарно левую и правую части, равенство при этом останется справедливым. Имеем:

a_n = a₁ + (n – 1) * d;

a_n– a_m = (n – 1) * d – (m – 1) * d = d * (n – m)

Таким образом, мы исключили одну неизвестную (a₁). Теперь можно записать окончательное выражение для определения d:

d = (a_n– a_m) / (n – m), где n > m

Мы получили очень простую формулу: чтобы вычислить разность d в соответствии с условиями задачи, необходимо лишь взять отношение разностей самих элементов и их порядковых номеров. Следует обратить на один важный момент внимание: разности берутся между “старшим” и “младшим” членами, то есть n > m (“старший” – имеется в виду стоящий дальше от начала последовательности, его абсолютное значение может быть как больше, так и меньше более “младшего” элемента).

Выражение для разности d прогрессии следует подставить в любое из уравнений в начале решения задачи, чтобы получить значение первого члена.

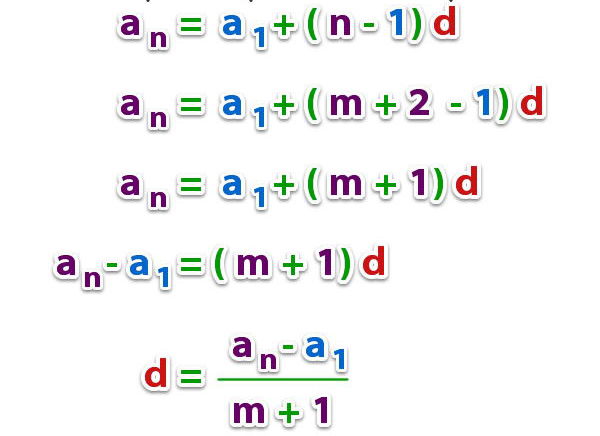
Далее в статье приведем примеры решения задач на вычисления d и на восстановление числового ряда алгебраической прогрессии. Здесь же хотелось бы отметить один важный момент.

В наш век развития компьютерных технологий многие школьники стараются найти решения для своих заданий в Интернете, поэтому часто возникают вопросы такого типа: найти разность арифметической прогрессии онлайн. По подобному запросу поисковик выдаст ряд web-страниц, перейдя на которые, нужно будет ввести известные из условия данные (это могут быть как два члена прогрессии, так и сумма некоторого их числа) и моментально получить ответ. Тем не менее такой подход к решению задачи является непродуктивным в плане развития школьника и понимания сути поставленной перед ним задачи.

Рекомендуется по указанным причинам самостоятельно решать подобные задачи. Кроме того, они не являются сложными.

Решение без использования формул

Решим первую задачу, при этом не будем использовать никакие из приведенных формул. Пусть даны элементы ряда: а6 = 3, а9 = 18. Найти разность прогрессии арифметической.

Известные элементы стоят близко друг к другу в ряду. Сколько раз нужно добавить разность d к наименьшему, чтобы получить наибольшее из них? Три раза (первый раз добавив d, мы получим 7-й элемент, второй раз – восьмой, наконец, третий раз – девятый). Какое число нужно добавить к трем три раза, чтобы получить 18? Это число пять. Действительно:

3 + 5 + 5 + 5 = 18

Таким образом, неизвестная разность d = 5.

Конечно же, решение можно было выполнить с применением соответствующей формулы, но этого не было сделано намеренно. Подробное объяснение решения задачи должно стать понятным и ярким примером, что такое арифметическая прогрессия.

Задача, подобная предыдущей

Теперь решим похожую задачу, но изменим входные данные. Итак, следует найти разность прогрессии арифметической, если а3 = 2, а9 = 19.

Конечно, можно прибегнуть снова к методу решения “в лоб”. Но поскольку даны элементы ряда, которые стоят относительно далеко друг от друга, такой метод станет не совсем удобным. А вот использование полученной формулы быстро приведет нас к ответу:

d = (а₉ – а₃) / (9 – 3) = (19 – 2) / (6) = 17 / 6 ≈ 2,83

Здесь мы округлили конечное число. Насколько это округление привело к ошибке, можно судить, проверив полученный результат:

a₉ = a₃+ 2,83 + 2,83 + 2,83 + 2,83 + 2,83 + 2,83 = 18,98

Этот результат отличается всего на 0,1 % от значения, данного в условии. Поэтому использованное округление до сотых можно считать успешным выбором.

Задачи на применение формулы для an члена

Рассмотрим классический пример задачи на определение неизвестной d: найти разность прогрессии арифметической, если а1 = 12, а5 = 40.

Когда даны два числа неизвестной алгебраической последовательности, причем одним из них является элемент a₁, тогда не нужно долго думать, а следует сразу же применить формулу для a_n члена. В данном случае имеем:

a₅ = a₁ + d * (5 – 1) => d = (a₅ – a₁) / 4 = (40 – 12) / 4 = 7

Мы получили точное число при делении, поэтому нет смысла проверять точность рассчитанного результата, как это было сделано в предыдущем пункте.

Решим еще одну аналогичную задачу: следует найти разность арифметической прогрессии, если а1 = 16, а8 = 37.

Используем аналогичный предыдущему подход и получаем:

a₈ = a₁ + d * (8 – 1) => d = (a₈ – a₁) / 7 = (37 – 16) / 7 = 3

Что еще следует знать о прогрессии арифметической

Помимо задач на нахождение неизвестной разности или отдельных элементов, часто необходимо решать проблемы суммы первых членов последовательности. Рассмотрение этих задач выходит за рамки темы статьи, тем не менее для полноты информации приведем общую формулу для суммы n чисел ряда:

∑ⁿ_{i = 1}(a_i) = n * (a₁+ a_n) / 2

Источник

Арифметическая прогрессия

Понятие арифметической прогрессии
Формула n-го члена арифметической прогрессии
Свойства арифметической прогрессии
Сумма первых n членов арифметической прогрессии
Примеры

п.1. Понятие арифметической прогрессии

Арифметической прогрессией называют числовую последовательность, каждый член которой a_n, начиная со второго, равен сумме предыдущего члена a_n-1 и некоторого постоянного числа d: $$ mathrm{ a_n=a_{n-1}+d, ninmathbb{N}, nleq 2 } $$ Число d называют разностью арифметической прогрессии.

Например:
1. Последовательность 2, 5, 8, 11, 14, … является арифметической прогрессией с разностью d = 3.

2. Последовательность 12, 9, 6, 3, 0, –3, –6, … является арифметической прогрессией с разностью d = –3.

п.2. Формула n-го члена арифметической прогрессии

По определению арифметической прогрессии мы получаем рекуррентную формулу для n-го члена: a_n = a_n-1 + d. Из неё можно вывести аналитическую формулу:

a₂ = a₁ + d, $qquad$ a₃ = a₂ + d = (a₁ + d) + d = a₁ + 2d
a₄ = a₃ + d = (a₁ + 2d) + d = a₁ + 3d,…

Получаем:

a_n = a₁ + (n – 1)d

Например:
Найдём a₇, если известно, что a₁ = 5, d = 3.
По формуле n-го члена получаем: a₇ = a₁ + 6d = 5 + 6 · 3 = 23

п.3. Свойства арифметической прогрессии

Свойство 1. Линейность

Арифметическая прогрессия является линейной функцией f(n) = kn + b:

a_n = dn + (a₁ – d)

с угловым коэффициентом k = d и свободным членом b = a₁ – d.

При d > 0 прогрессия линейно возрастает

При d < 0 прогрессия линейно убывает

Следствие: любую арифметическую прогрессию можно задать формулой: $$ mathrm{ a_n=dn+b, ninmathbb{N}, binmathbb{R}, dinmathbb{R}} $$ где d, b – некоторые числа.

Свойство 2. Признак арифметической прогрессии

Для того чтобы числовая последовательность была арифметической прогрессией необходимо и достаточно, чтобы каждый её член, начиная со второго, был средним арифметическим предыдущего и последующего членов: $$ mathrm{ left{a_nright} – text{арифметическая прогрессия} Leftrightarrow a_n=frac{a_{n-1}+a_{n+1}}{2}, ninmathbb{N}, n geq 2 } $$ Следствие: каждый член прогрессии является средним арифметическим двух равноудалённых от него членов: $$ mathrm{ a_n=frac{a_{n-k}+a_{n+k}}{2}, ninmathbb{N}, ninmathbb{N}, n geq k+1 } $$

Например:
Найдём a₉, если известно, что a₇ = 10, a₁₁ = 15
По следствию из признака арифметической прогрессии: (mathrm{a_9=frac{a_7+a_{11}}{2}=frac{10+15}{2}=12,5})

Свойство 3. Равенство сумм индексов

Если {a_n} – арифметическая прогрессия, то из равенства сумм индексов следует равенство сумм членов: $$ mathrm{ m+k=p+q Rightarrow a_m+a_k=a_p+a_q } $$ Следствие: сумма членов, равноудалённых от концов прогрессии, является постоянной величиной: $$ mathrm{ a_1 + a_n=a_2+a_{n-1}=a_3+a_{n-2}=… } $$

Например:
Найдём a₆, если известно, что a₂ = 5, a₄ = 10, a₈ = 20
По равенству сумм индексов a₂ + a₈ = a₄ + a₆
Откуда a₆ = a₂ + a₈ – a₄ = 5 + 20 – 10 = 15

п.4. Сумма первых n членов арифметической прогрессии

Сумма первых n членов арифметической прогрессии равна произведению среднего арифметического её крайних членов и количества членов: $$mathrm{ S_n=frac{a_1+a_n}{2}n} $$

Если учесть, что a_n = a₁ + d(n – 1), получаем ещё одну формулу для суммы: $$mathrm{ S_n=frac{2a_1+d(n-1)}{2}n} $$

Например:
Найдём сумму первых 100 натуральных чисел: 1 + 2 +…+ 100
В этом случае a₁ = 1, a₁₀₀ = 100, n = 100
(mathrm{ S_{100}=frac{1+100}{2}cdot 100=5050})

п.5. Примеры

Пример 1. Найдите первый член и разность арифметической прогрессии, если:
а) a₇ = 10, a₁₅ = 42
Найдем разность данных членов: a₁₅ – a₇ = (a₁ + 14d) – (a₁ + 6d) = 8d
Получаем разность прогрессии: 42 – 10 = 8d ⇒ d = 32 : 8 = 4
7-й член: a₇ = a₁ + 6d = a₁ + 6 · 4 = 10 ⇒ a₁ = 10 – 24 = –14
Ответ: a₁ = –14, d = 4

б) a₁₀ = 95, S₁₀ = 500
Сумма прогрессии: (mathrm{S_{10}=frac{a_1+a_{10}}{2}cdot 10Rightarrow 500=(a_1+95)cdot 5Rightarrow a_1+95=100Rightarrow a_1=5})
10-й член: (mathrm{a_{10}=a_1+9dRightarrow95=5+9dRightarrow 9d=90Rightarrow d=10})
Ответ: a₁ = 5, d = 10

Пример 2. Найдите сумму первых 100 нечётных натуральных чисел.
Чему равно последнее слагаемое этой суммы?
Ищем сумму (mathrm{underbrace{1+3+5+…}_{100 text{слагаемых}}})
По условию a₁ = 1, d = 2, n = 100. Получаем:
(mathrm{S_{100}=frac{2a_1+d(n-1)}{2}n=frac{2cdot 1+2cdot 99}{2}cdot 100=10000})
Формула n-го члена данной прогрессии: (mathrm{a_n=a_1+d(n-1)=dn+(a_1-d)=2n-1})
100-й член (mathrm{a_{100}=2cdot 100-1=199})
Ответ: S₁₀₀ = 10000, a₁₀₀ = 199

Пример 3*. Сколько членов арифметической прогрессии 10, 16, 22, … находится между числами 110 и 345?
По условию a₁ = 10, d = 16 – 10 = 6
Формула n-го члена данной прогрессии a_n = a₁ + d(n – 1) = dn + (a₁ – d) = 6n + 4
Заданные числа могут быть членами данной прогрессии или находиться по «соседству» с ними. Подставим их в формулу для n-го члена: begin{gather*} mathrm{ 6k+4=110Rightarrow 6k=106Rightarrow k=17frac23Rightarrow 17lt klt 18 }\ mathrm{ 6m+4=345Rightarrow 6m=341Rightarrow m=56frac56Rightarrow 56lt mlt 57 } end{gather*} Ближайший сосед справа к 100 – это a₁₈ = 6 · 18 + 4 = 112, k = 18
Ближайший сосед слева к 345 – это a₅₆ = 6 · 56 + 4 = 340, m = 56

Количество членов прогрессии в заданном интервале:

n = m – k + 1 = 56 – 18 + 1 = 39

Ответ: 39

Пример 4. Одиннадцатый член арифметической прогрессии равен 7.
Найдите сумму её первых 21 членов.
По свойству суммы индексов: a₁₁ + a₁₁ = a₁ + a₂₁
Откуда a₁ + a₂₁ = 2a₁₁ = 14
Искомая сумма: (mathrm{S_{21}=frac{a_1+a_{21}}{2}cdot 21=frac{14}{2}cdot 21=147})
Ответ: 147

Пример 5. Величины углов выпуклого пятиугольника образуют арифметическую прогрессию. Найдите третий член этой прогрессии.
Сумма углов выпуклого пятиугольника S₅ = 180° · (5 – 2) = 540°
Если углы образуют арифметическую прогрессию, то: $$ mathrm{ S_5=frac{a_1+a_5}{2}cdot 5=540^circRightarrow a_1+a_5=216^circ } $$ По свойству суммы индексов: a₃ + a₃ = a₁ + a₅
Откуда: (mathrm{a_3=frac{a_1+a_5}{2}=108^circ})
Ответ: 108°

Пример 6. При каких значениях x числа x² – 11, 2x² + 29, x⁴ – 139 в заданной последовательности являются членами арифметической прогрессии?
Для последовательных членов получаем уравнение:

a₂ – a₁ = a₃ – a₂
(2x² + 29) – (x² – 11) = (x⁴ – 139) – (2x² + 29)
x⁴ – 3x² – 208 = 0 ⇒ (x² + 13)(x² – 16) = 0 ⇒ x² = 16 ⇒ x = ±4

Ответ: x = ±4

Пример 7. Сумма первых трёх членов убывающей арифметической прогрессии равна 9, а сумма их квадратов равна 99. Найдите седьмой член прогрессии.
По условию d < 0 и: $$ left{ begin{array}{ l } mathrm{a_1+a_2+a_3=9} & \ mathrm{a_1^2+a_2^2+a_3^2=99} & end{array}right. $$ Используем свойство прогрессии: (mathrm{a_2=frac{a_1+a_3}{2}}). Получаем из первого уравнения:

3a₂ = 9 ⇒ a_2 = 3

Тогда a₁ = a₂ – d = 3 – d, a₃ = a₂ + d = 3 + d. Подставляем во второе уравнение:

(3 – d)² + 3² + (3 + d)² = 99
9 – 6d + d² + 9 + 9 + 6d + d² = 99
2d² = 72 ⇒ d² = 36 ⇒ d = ±6

Выбираем отрицательное значение d = –6
1-й член прогрессии: a₁ = a₂ – d = 3 + 6 = 9
7-й член прогрессии: a₇ = a₁ + 6d = 9 + 6(–6) = –27
Ответ: x = –27

Источник

Определение

Арифметическая прогрессия — последовательность чисел, в которой каждое число, начиная со второго, получается из первого добавлением к нему постоянного числа. Данное постоянное число называют разностью арифметической прогрессии.

-ый элемент арифметической прогрессии

Чтобы найти -ый элемент, нужно к элементу прибавить разность арифметической прогрессии.

$[a_n=a_{n-1}+d,]$

где — разность арифметической прогрессии, — -ый элемент арифметической прогрессии.

Выразим -ый элемент арифметической прогрессии через первый член и разность прогрессии.

$[a_{2}=a_{1}+d]$

$[a_{3}=a_{2}+d=a_1+d+d=a_1+2d]$

$[a_{4}=a_{3}+d=a_1+2d+d=a_1+3d]$

Получаем, что

Пример 1. Найти -ый элемент арифметической прогрессии, если её первый элемент равен , а разность .

Решение.

$a_{10}=a_1+d(10-1)=2+0,5(10-1)=2+4,5=6,5.$

Ответ: .

Пример 2. Найти разность арифметической прогрессии, если пятый элемент прогрессии равен , а -ый — -ти.

Решение.

$[a_{10}=a_1+9d]$

Вычтем из второго уравнения первое: $a_{10}-a_5=a_1-a_1+9d-4d.$

$d=frac{a_{10}-a_5}{9-4}=frac{18-15}{5}=frac{3}{5}=0,6.$

Ответ: .

Сумма арифметической прогрессии

Чтобы найти сумму первых членов арифметической прогрессии можно воспользоваться следующими формулами:

$[S_n=frac{a_1+a_n}{2}cdot n;]$

$[S_n=frac{2a_1+d(n-1)}{2}cdot n.]$

Докажем первую формулу.

$[S_n=a_1+a_2+a_3+a_4+ldots+a_{n-3}+a_{n-2}+a_{n-1}+a_{n}]$

$[S_n=a_{n}+a_{n-1}+a_{n-2}+a_{n-3}+ldots+a_{4}+a_{3}+a_{2}+a_{1}]$

Сложим почленно два последних равенства.

Получаем,

$[S_n+S_n=a_1+a_{n}+a_{2}+a_{n-1}+ldots +a_2+a_{n-1}+a_1+a_n]$

Так как, $a_k+a_{n-(k-1)}=a_1+d(k-1)+a_n-d(k-1)=a_1+a_n,$ то

Следовательно,

$[S_n=frac{a_1+a_n}{2}cdot n.]$

Пример 3. Найдите сумму натуральных чисел от 1 до 100.

Решение.

Ответ: .

Пример 4. Первый элемент арифметической прогрессии равен , а разность арифметической прогрессии равна . Найдите сумму первых элементов данной арифметической прогрессии.

Решение.

$S_10=frac{2 cdot 15+2(10-1)}{2}cdot 10 =(30+18)cdot 5=48cdot 5=240.$

Ответ: .

Пример 5. Арине надо решить задач по геометрии. Ежедневно она решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что в первый день она решила задач, а в последний она запланировала решить задач. Определите за сколько дней она решит все задачи.