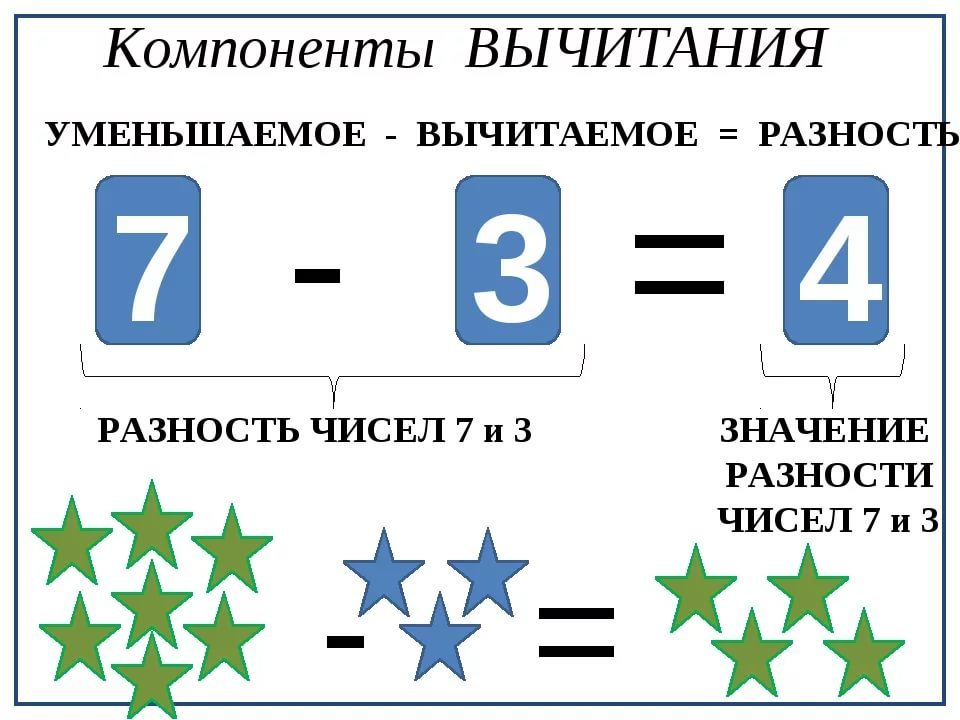
Разность чисел как определить?
Ирина Эргашева
17 октября 2018 · 87,3 K
Разность – это число, составляющее остаток в вычитании.
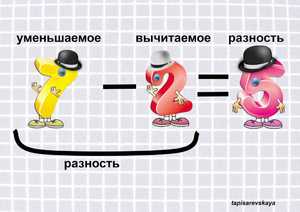
То есть, разность чисел определяется вычитанием одного числа из другого. Например: 10-7=3. В этом примере “10” – уменьшаемое, “7” – вычитаемое, а “3” – разность.
23,0 K
Разность – это число, обладающее свойством: в сумме с вычитаемым давать уменьшаемое.
Странно, но в учебнике этого… Читать дальше
Комментировать ответ…Комментировать…
Любитель книг, кошек, увлекаюсь написанием рецензий · 21 нояб 2018
Разность получается путем вычитания одного числа (вычитаемого) из другого (уменьшаемого). То есть, чтобы определить разность, нужно просто вычесть из большего числа меньшее. Например, числа 15 и 10.
15-10=5
5 и будет разность этих чисел
61,3 K
Комментировать ответ…Комментировать…

…
Оглавление:
- Арифметические действия с числами
- Разность в математике
- Видео: Математика 6 Делимость суммы и разности чисел
- Как найти разницу величин
- Математические действия с разностью чисел
- Видео: Математика 2 класс. Разность двухзначных чисел
- Простые примеры
- Более сложные примеры
- Математика для блондинок
- Видео: Разность двух отрицательных целых чисел. Математика 6 класс.
Арифметические действия с числами
Основными арифметическими действиями в математике являются:
- сложение;
- вычитание;
- умножение;
- деление.
Каждый результат этих действий также имеет своё название:
- сумма — результат, получившийся при сложении чисел;
- разность — результат, получившийся при вычитании чисел;
- произведение — результат умножения чисел;
- частное — результат деления.
Это интересно: что такое модуль числа?
Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:
- сумма — прибавить;
- разность — отнять;
- произведение — умножить;
- частное — разделить.
Разность в математике
Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:
Разность чисел означает, насколько одно из них больше другого.
- Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.
- Это вычитание одного числа из другого.
- Это цифра, составляющая остаток при минусовании двух величин.
- Это величина, являющаяся результатом вычитания двух значений.
- Разность показывает количественное различие между двумя цифрами.
- Это результат одного из четырёх арифметических действий, которым является вычитание.
- Это то, что получится, если из уменьшаемого отнять вычитаемое.
Видео: Математика 6 Делимость суммы и разности чисел
И все эти определения являются верными.
Как найти разницу величин
Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:
- Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.
Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:
- Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.
Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?
- Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
- Вычитаемое — это математическое число, которое вычитают из уменьшаемого.
Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:
- Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
- Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
Математические действия с разностью чисел
Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.
Видео: Математика 2 класс. Разность двухзначных чисел
Простые примеры
- Пример 1. Найти разницу двух величин.
Дано:
20 — уменьшаемое значение,
15 — вычитаемое.
Решение: 20 — 15 = 5
Ответ: 5 — разница величин.
- Пример 2. Найти уменьшаемое.
Дано:
48 — разность,
32 — вычитаемое значение.
Решение: 32 + 48 = 80
Ответ: 80.
- Пример 3. Найти вычитаемое значение.
Дано:
7 — разность,
17 — уменьшаемая величина.
Решение: 17 — 7 = 10
Ответ: вычитаемое значение 10.
Более сложные примеры
На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.
- Пример 4. Найти разницу трёх значений.
56 — уменьшаемое значение,
12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);
2) 44 — 4 = 40.
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);
2) 56 — 16 = 40.
Ответ: 40 — разница трёх значений.
- Пример 5. Найти разницу рациональных дробных чисел.
Даны дроби с одинаковыми знаменателями, где
4/5 — уменьшаемая дробь,
3/5 — вычитаемая.
Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.
Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5
Ответ: 1/5.
- Пример 6. Утроить разницу чисел.
А как выполнить такой пример, когда требуется удвоить или утроить разницу?
Вновь прибегнем к правилам:
- Удвоенное число — это величина, умноженная на два.
- Утроенное число — это величина, умноженная на три.
- Удвоенная разность — это разница величин, умноженная на два.
- Утроенная разность — это разница величин, умноженная на три.
Дано:
7 — уменьшаемая величина,
5 — вычитаемая величина.
Решение:
1) 7 — 5 = 2;
2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.
- Пример 7. Найти разницу величин 7 и 18.
Дано:
7 — уменьшаемая величина;
18 — вычитаемая.
Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?
И опять есть применяемое для конкретного случая правило:
- Если вычитаемое больше уменьшаемого, разница окажется отрицательной.
Решение:
7 — 18 = — 11
Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.
Математика для блондинок
В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.
И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:
- сумму — сложением слагаемых;
- произведение — умножением множителей;
- частное — делением делимого на делитель.
Вот такая интересная арифметика.
Видео: Разность двух отрицательных целых чисел. Математика 6 класс.
Разность чисел
Содержание:
- Что такое разность чисел в математике
- Математические действия с разностью чисел
- Зависимость между данными и искомыми вычитания
Что такое разность чисел в математике
Определение
Разность чисел в математике — это результат вычитания одного числа из другого.
Формула РЧ выглядит так:
a – b = c
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Здесь a — уменьшаемое, b — вычитаемое, c — разность.
Математические действия с разностью чисел
Чтобы узнать разность чисел, нужно совершить такое арифметическое действие как вычитание, в результате которого по одному данному слагаемому и данной сумме можно найти другое слагаемое.
Вычитание принято обозначать знаком «–» (минус).
Примечание
Обычно вычитание натуральных чисел возможно только в том случае, если уменьшаемое больше вычитаемого. Однако если уменьшаемое меньше вычитаемого, то значение разности получается отрицательным.
Следует привести некоторые особенности действий с нулем:
- Прибавление к числу нуля не изменяет этого числа.
- Если первое слагаемое равно второму, то их разность равна нулю.
Необходимо также обозначить свойства вычитания:
- x-(y+z)=x-y-z: 26-(14+4)=26-4-14=22-14=8.
- (x+y)-z=(x-z)+y=x+(y-z): (37+28)-5=(37-5)+28=60.
- x+(y-z)=x+y-z: 51+(34-7)=51+32=19.
- x-(y-z)=x-y+z: 66-(34-7)=(66-34)+7=39.
- если x-y=z, то x=y+z: х-7=6, х=7+6, х=13.
- если x-y=z, то y=x-z: 46-у=16, у=46-16, у=30.
- если x-y=z, то (x+n)-y=z+n и (x-n)-y=z-n: 19-11=8, (19+6)-11=8+6, (19-1)+11=8-1.
- если x-y=z, то x-(y+n)=z-n и x-(y-n)=z+n: 46-11=35, 46-(11+4)=35+4, 46-(11-9)=35-9.
- если x-y=z, то (x+n)+(y-n)=z: 100-50=50, (100+10)+(50-10)=50.
- если x-y=z, то (x+n)-(y+n)=z и (x-n)-(y-n)=z: 300-150=150, (300+25)-(150+25)=150, (300-25)-(150-25)=150.
Определение
Однозначное число — это число, состоящее из одной цифры.
Определение
Многозначное число — включающее две и более цифры.
Чтобы найти разницу между однозначными числами, стоит вычесть из первого слагаемого второе. В этом поможет таблица вычитания, которую заучивают наизусть.
Чтобы посчитать результат вычитания многозначных чисел, можно воспользоваться счетом «в столбик». Этот способ подразумевает, что вычитаемое записывают под уменьшаемым в соответствии с десятками, сотнями, тысячами и так далее. После этого, начиная с конца, то есть с десятков, производят вычисление.
Пример
653-132
Сначала находим разность единиц, то есть от 3 отнимаем 2. Получаем 1.
Затем вычисляем десятки, то есть от 5 отнимаем 3. Результат равен 2.
И, наконец, считаем сотни, то есть от 6 отнимаем 1 и получаем 5.
Ответ: 521.
Если одно и то же число вычитается из другого множество раз, то можно умножить данное значение на столько раз, сколько представлено в примере, и таким образом получить одно вычитаемое число.
Пример
440-10-10-10=440-(10*3)=440-30=410.
Зависимость между данными и искомыми вычитания
Данные вычитания представляют уменьшаемое и вычитаемое. Искомое вычитания — это разность. Зависимость между ДВ и ИВ состоит в том, что второе чаще всего меньше первого.
Однако бывают случаи, когда ИВ может оказаться больше, чем ДВ. Это происходит, когда от первого слагаемого вычитают отрицательное число. Тогда, согласно правилам арифметики, два минуса дают общий знак плюс.
Пример
140-(-38)=140+38=178.
Что такое разность чисел и как ее найти
Добавлено: 22 марта 2022 в 10:52

К слову «разность» можно подобрать однокоренные слова, такие как, различный, разный.
То есть, разность имеет значение того, что между объектами имеются какие-либо отличия, что они не одинаковые. В математике данный термин является часто используемым. Изучение отличия чисел начинается с первого класса. Это основной, базовый процесс, который должен знать каждый.
По мимо математики, без определения разницы не обходится ни одна точная наука. Разность определяется и в быту, ежедневно. Например, при походе в магазин, необходимо из числа, которое является номиналом купюры, вычесть стоимость продукта. То, что останется (сдача), будет называться разностью.
Таким образом, отличия чисел — это результат математического действия, вычитания.
Виды математических действий и их результаты
- Вычитание (результат — разность).
- Сложение (результат — сумма).
- Деление (частное).
- Умножение (произведение).
Данные действия являются основополагающими в вычислительных процессах. Они не взаимозаменяемы. Это индивидуальные виды вычислений, которые не следует путать.
Как найти разность чисел
Чтобы найти разность чисел, необходимо выполнить процесс вычитания. А именно, из уменьшаемого вычесть (или отнять) вычитаемое. В результате получится разница.
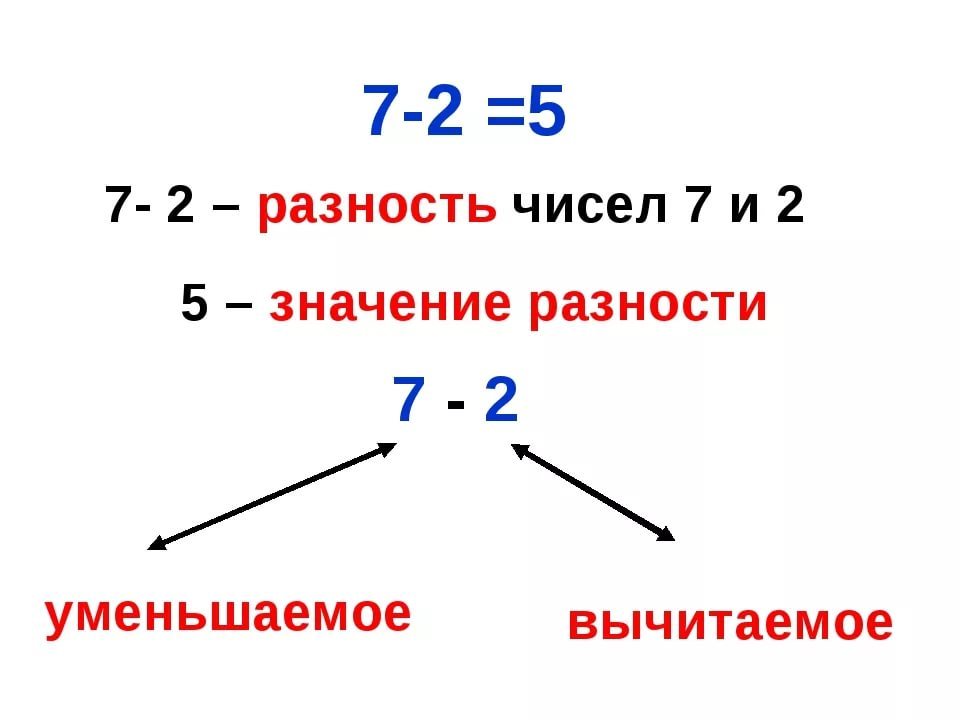
Пример: 7 — 2 = 5,
В данном случае, разность равна 5. Уменьшаемое 7, его мы уменьшаем, делаем меньше. Вычитаемое 2, это число мы вычитаем (отнимаем).
Данную процедуру можно записать и в буквенном выражении.
Пример: С — А = В,
В — разность; С — уменьшаемое; А — вычитаемое.
В младших классах ученикам объясняют то, чтобы найти разность чисел, нужно из большего числа вычесть меньшее. Это наиболее часто встречающееся правило. Но, при более глубоком изучении математики становится ясно, что и из меньшего числа можно вычесть большее. Тогда получится результат со знаком «-«.
Пример: 5 — 7 = — 2,
Но дело в том, что разность показывает:
— чем отличаются числа,
— на сколько они отличаются,
— на сколько одно число больше другого,
— на сколько одно число меньше другого,
— отличаются ли числа, или они равны.
Следовательно, разность не может выражаться со знаком «-«. Иначе, она не будет иметь логического смысла. Поэтому, в ситуациях, когда из меньшего вычитается большее, берется модуль разницы, то есть число без минуса «-«.
Знак «модуля» в математике обозначается двумя вертикальными линиями, между которыми пишется число. Модуль всегда положительный.
Математика включает себя бесконечное количество различных чисел, не только целых, но и дробных. Разность дробей находится аналогичным способом.
Пример: 1 — 1/4 = 3/4,
Разность 3/4, уменьшаемое 1, вычитаемое 1/4.
То же самое можно проводить с процентами, буквенными и числовыми выражениями в скобках.
Как проверить, верно ли найдена разность
В математических вычислениях большую роль играет проверка. Когда решен пример по поиску избытка, чтобы проверить его правильность, нужно совершить обратное действие.
Пример: 8 — 5 = 3, (разность 3),
Чтобы совершить проверку, сделаем известное уменьшаемое неизвестным. Чтобы найти уменьшаемое, нужно к разнице прибавить вычитаемое.
Тогда получим: 5 + 3 = 8 (получилось 8, как и было, следовательно, пример решен верно).
Второй способ проверки: 8 — 3 = 5 (тоже верно). Чтобы найти вычитаемое, из уменьшаемого отнимают разницу.
То есть, чтобы уметь проверять правильность решения, важно знать не только, как найти разность, но и как вычисляются уменьшаемое и вычитаемое.
А — С = В,
А — В = С,
С + В = А.
Бывают примеры, когда разность равна нулю (0). Это означает, что уменьшаемое и вычитаемое равны между собой. Нет между ними различия.
Сложные примеры с разностью
В математике помимо стандартного нахождения отличий существует множество усложненных вычислений, которые можно решать не в одно действие.
Пример: Из уменьшаемого 40 нужно отнять два вычитаемых 10 и 15.
Данный пример можно вычислить одним действием или двумя.
Решение в одно действие: 40 — 10 — 15 = 15,
Решение в два действия:
Сначала находим сумму: 10 + 15 = 25,
40 — 25 = 15.
Главное, чтобы ответы совпали в обоих способах.
Также, может вызвать затруднение пример: Утройте разность. В данном случае нужно будет найти отличия чисел и умножить ее на 3.
Навык нахождения разности бесспорно важен. Но не более и не менее, чем навыки нахождения суммы, произведения, частного. В математике все взаимосвязано и без одних знаний невозможно получить другие. Не зря говорят, что математика является «царицей наук», и ее азы используются повсеместно.
Поэтому, для достижения успеха в математике одной лишь школьной программы будет не достаточно.
Для достижения максимальных результатов в изучении этого предмета мы рекомендуем начать посещать курсы по математике для школьников в Москве. Обучение на этих курсах проходит по запатентованной методологии в малых группах. Это увеличивает эффективность занятий в несколько раз.
Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:

Эксперт по подготовке к ЕГЭ, ОГЭ и ВПР
Задать вопрос
Закончил Московский физико-технический институт (Физтех) по специальности прикладная физика и математика. Магистр физико-математических наук. Преподавательский стаж более 13 лет. Соучредитель курсов ЕГЭ и ОГЭ в паре TwoStu.
Читайте также:
Статья познакомит читателя с понятиями «разность чисел», «вычитаемое» и «уменьшаемое».
Содержание
- Что значит число уменьшаемое, число вычитаемое и разность чисел?
- Как найти уменьшаемое и вычитаемое число?
- Видео: Уменьшаемое, вычитаемое, разность
В арифметике существует всего четыре основных действия, которые мы называем сложением, умножением, вычитанием и делением. Такие действия являются основой всей математики – они позволяют нам осуществлять все вычисления: как простые, так и самые сложные. Самыми простыми действиями считаются сложение и вычитание, которые противоположны друг другу. Правда, слово «сложение» мы также используем и в обычной жизни.
Мы можем встретить фразу «сложить усилия, например, когда нам нужно сделать какую-нибудь работу всем вместе. Но вот с термином «вычитание» дело обстоит немного сложнее, и в разговоре оно встречается реже. Мы редко услышим такие выражения, как «уменьшаемое», «вычитаемое», «разность». Но в сегодняшней статье мы подробно поговорим о них с точки зрения математики.
Что значит число уменьшаемое, число вычитаемое и разность чисел?
Что значит число уменьшаемое, число вычитаемое и разность чисел? Как известно, многие научные термины и выражения взяты из других языков, чаще греческого и латинского. Но те слова, которые будут рассмотрены ниже, имеют русское происхождение, потому нам будет проще их разобрать.
Например, что можно сказать о разности чисел? Если мы обратим внимание на корень слова «разность», то нам представится, например, его однокоренное слово «разница». А если речь идет о математике, то тут и думать нечего – слово «разность» означает разницу между какими-то цифрами, а точнее, двумя числами. Разница нам показывает, насколько одна величина больше другой или, наоборот, вторая меньше первой. Строго в математике это выглядит как результат вычитания.
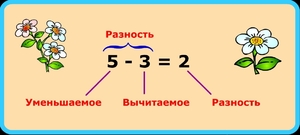
Сразу же приведем пример. Допустим, буфетчица несет на подносе восемь пирожков. Пять из них она раздала посетителям. Сколько пирожков останется у буфетчицы на подносе? Если из 8 вычесть 5, то получится — 3. Теперь запишем это математически:
- 8 – 5 = 3
То есть разница между восемью и пятью – это три. Теперь нам понятно, что такое термин «разница».
Внимание: Если два числа равны друг другу, то разницы между ними не существует, она равна нулю (8 – 8 = 0).
Теперь нам следует выяснить, что такое вычитаемое и уменьшаемое. Снова представим значение слов по их смыслу. Чем может являться число уменьшаемое? Уменьшаемое – это то число, которое уменьшается при вычитании. От этого числа отнимают другое число. А что такое вычитаемое? Вычитаемым как раз и является том числом, которые мы отнимаем от уменьшаемого.
Вернемся к примеру с буфетчицей. Мы помним, как от восьми отнимали пять, и у нас получилось три. Мы выяснили, что тройка является разницей между двумя этими числами. Теперь нам уже не сложно понять, что 8 – это число уменьшаемое, а 5 – это число вычитаемое.
Как найти уменьшаемое и вычитаемое число?
Как в математике найти разницу чисел мы уже разобрались. Это довольно просто. Но сможем ли мы найти уменьшаемое и вычитаемое число, если одно число неизвестно? Конечно можем, так как нам будут известны два других числа. Например, как мы можем найти уменьшаемое число? Если мы знаем значение разницы и вычитаемого, то сумма этих двух чисел равняется уменьшаемому:
- Y – 10 = 18, где Y – число уменьшаемое
- Значит, Y = 18 + 10
- 18 + 10 = 28
- Y = 28
Вычитаемое находится так же просто. Если мы знаем разницу и уменьшаемое, значит вычитаемое мы получим, отняв от уменьшаемого числа разность:
- 28 – B = 10, где B – число вычитаемое
- Значит, B = 28 – 10
- 28 – 10 = 18
- B = 18
 Разность чисел означает, насколько одно из них больше другого.
Разность чисел означает, насколько одно из них больше другого.