Вычисление разности двух дат
Используйте функцию РАЗНДАТ, если нужно вычислить разницу двух дат. Сначала поместите дату начала в одну ячейку, а дату окончания — в другую. Затем введите формулу, например одну из следующих.
Предупреждение: Если значение нач_дата больше значения кон_дата, возникнет ошибка #ЧИСЛО!
Разница в днях
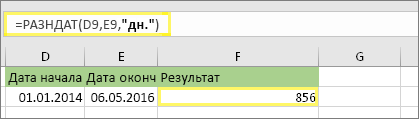
В этом примере дата начала находится в ячейке D9, а дата окончания — в ячейке E9. Формула находится в ячейке F9. Параметр “д” возвращает количество полных дней между двумя датами.
Разница в неделях
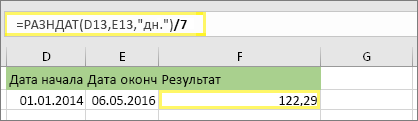
В этом примере дата начала находится в ячейке D13, а дата окончания — в ячейке E13. Параметр “д” возвращает количество дней. Но обратите внимание на /7 в конце. Это делит количество дней на 7, так как в неделе содержится 7 дней. Обратите внимание, что этот результат также должен быть представлен в числовом формате. Нажмите клавиши CTRL+1. Затем щелкните Числовой > Число десятичных знаков: 2.
Разница в месяцах
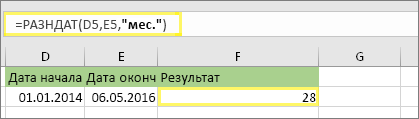
В этом примере дата начала находится в ячейке D5, а дата окончания — в ячейке E5. В формуле “м” возвращает количество полных месяцев между двумя днями.
Разница в годах
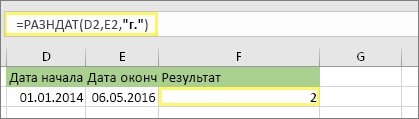
В этом примере дата начала находится в ячейке D2, а дата окончания — в ячейке E2. Параметр “г” возвращает количество полных лет между двумя днями.
Расчет возраста в накопленных годах, месяцах и днях
Вы также можете вычислить возраст или время работы другого человека. Результат может выглядеть так: “2 года, 4 месяца, 5 дней”.
1. Используйте функцию РАЗНДАТ, чтобы найти общее количество лет.

В этом примере дата начала находится в ячейке D17, а дата окончания — в ячейке E17. В формуле параметр “г” возвращает количество полных лет между двумя днями.
2. Снова используйте функцию РАЗНДАТ с “гм”, чтобы найти месяцы.
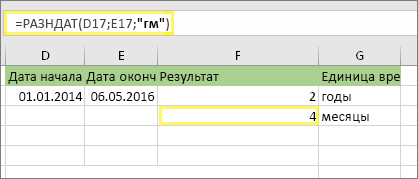
В другой ячейке используйте функцию РАЗНДАТ с параметром “гм”. Параметр “гм” возвращает количество оставшихся месяцев с последнего полного года.
3. Используйте другую формулу для поиска дней.
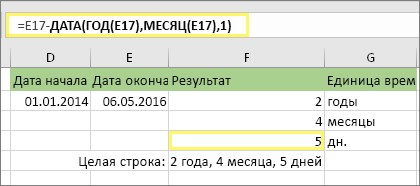
Теперь нужно найти количество оставшихся дней. Для этого мы напишем формулу другого типа, показанную выше. Эта формула вычитает первый день окончания месяца (01.05.2016) из исходной даты окончания в ячейке E17 (06.05.2016). Вот как это делается: сначала функция ДАТА создает дату 01.05.2016. Она создается с помощью года в ячейке E17 и месяца в ячейке E17. 1 обозначает первый день месяца. Результатом функции ДАТА будет 01.05.2016. Затем мы вычитаем эту дату из исходной даты окончания в ячейке E17 (06.05.2016), в результате чего получается 5 дней.
Предупреждение: Не рекомендуется использовать аргумент “мд” функции РАЗНДАТ, так как он может вычислять неточные результаты.
4. Необязательно: объединение трех формул в одну.
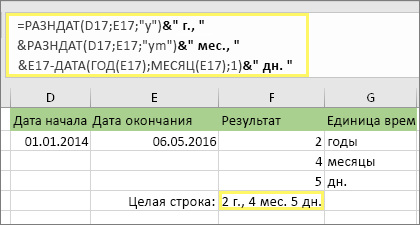
Все три вычисления можно поместить в одну ячейку, как в этом примере. Используйте амперсанды, кавычки и текст. Эту формулу дольше вводить, но она содержит в себе все вычисления. Совет. Нажмите клавиши ALT+ВВОД, чтобы ввести разрывы строк в формулу. Это упрощает чтение. Кроме того, если вы не видите всю формулу, нажмите клавиши CTRL+SHIFT+U.
Скачивание примеров
Вы можете скачать образец книги со всеми примерами из этой статьи. Вы можете воспользоваться ими или создать собственные формулы.
Скачать примеры вычислений дат
Другие вычисления даты и времени
Как показано выше, функция РАЗНДАТ вычисляет разницу между датой начала и датой окончания. Однако вместо ввода определенных дат в формуле можно также использовать функцию СЕГОДНЯ(). При использовании функции СЕГОДНЯ() Excel в качестве даты использует текущую дату компьютера. Имейте в виду, что эта переменная будет меняться при повторном открыть файле в будущем.
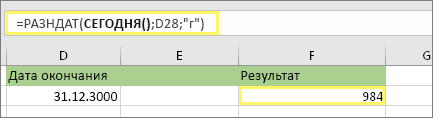
Обратите внимание, эта статья была написана 6 октября 2016 г.
Используйте функцию ЧИСТРАБДНИ.МЕЖД, если нужно вычислить количество рабочих дней между двумя датами. Вы также можете исключить выходные и праздники.
Прежде чем начать. Решите, нужно ли исключить даты праздников. При исключении введите список дат праздников в отдельной области или на отдельном листе. Поместите каждую дату праздника в собственную ячейку. Затем выделите эти ячейки и нажмите Формулы > Задать имя. Назовите диапазон МоиПраздники и нажмите ОК. Затем создайте формулу с помощью указанных ниже действий.
1. Введите дату начала и окончания.
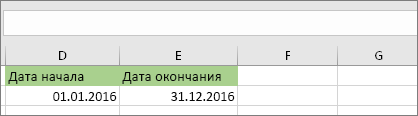
В этом примере дата начала находится в ячейке D53, а дата окончания — в ячейке E53.
2. В другой ячейке введите формулу следующего вида.
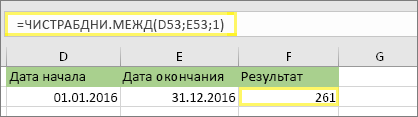
Введите формулу, как в примере выше. Цифра 1 в формуле устанавливает субботы и воскресенья в качестве выходных и исключает их из общего количества.
Примечание. В Excel 2007 нет функции ЧИСТРАБДНИ.МЕЖД. Однако там есть функция ЧИСТРАБДНИ. Указанный выше пример будет выглядеть в Excel 2007 следующим образом: =ЧИСТРАБДНИ(D53;E53). Не нужно указывать цифру 1, так как функция ЧИСТРАБДНИ предполагает, что выходными являются суббота и воскресенье.
3. При необходимости измените цифру 1.
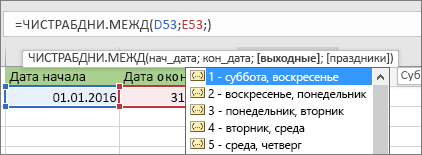
Если суббота и воскресенье не являются выходными днями, измените 1 на другое числовое значение из списка IntelliSense. Например, значение 2 устанавливает воскресенья и понедельники в качестве выходных дней.
Если вы используете Excel 2007, пропустите этот шаг. Функция ЧИСТРАБДНИ в Excel 2007 всегда предполагает, что выходными являются суббота и воскресенье.
4. Введите имя диапазона праздников.
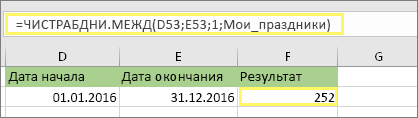
Если вы создали имя диапазона праздников в разделе “Прежде чем начать” выше, введите его в конце следующим образом. Если у вас нет праздников, вы можете не использовать точку с запятой и МоиПраздники. Если вы используете Excel 2007, указанный выше пример будет выглядеть так: =ЧИСТРАБДНИ(D53;E53;MyHolidays).
Совет. Если вы не хотите указывать имя диапазона праздников, вместо этого вы можете ввести диапазон, например D35:E39. Или можно ввести в формулу каждый праздник. Например, если ваши праздники приходились на 1 и 2 января 2016 г., введите их следующим образом: =ЧИСТРАБДНИ.МЕЖД(D53;E53;1;{“01.01.2016″;”02.01.2016”}). В Excel 2007 это будет выглядеть так: =ЧИСТРАБДНИ(D53;E53;{“01.01.2016″;”02.01.2016”})
Вы можете вычислить затраченное время, вычитая одно время из другого. Сначала поместите время начала в одну ячейку, а время окончания — в другую. Вводите время полностью, включая час, минуты и пробел перед AM или PM. Ниже рассказывается, как это сделать.
1. Введите время начала и время окончания.
В этом примере время начала находится в ячейке D80, а время окончания — в ячейке E80. Введите час, минуты и пробел перед AM или PM.
2. Установите формат “ч:мм AM/PM”.
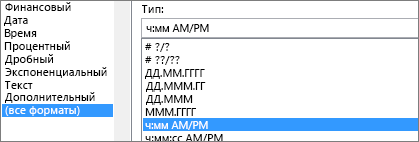
Выберите обе даты и нажмите клавиши CTRL+1 (или  +1 на компьютере Mac). Выберите вариант (все форматы) > ч:мм AM/PM, если он еще не установлен.
+1 на компьютере Mac). Выберите вариант (все форматы) > ч:мм AM/PM, если он еще не установлен.
3. Вычтите два времени.
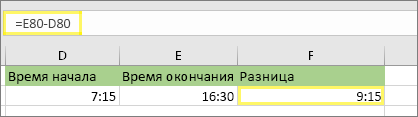
В другой ячейке вычтите ячейку времени начала из ячейки времени окончания.
4. Установите формат “ч:мм”.
Нажмите клавиши CTRL+1 (или  +1 на Mac). Выберите (все форматы) > ч:мм, чтобы результат не содержал AM и PM.
+1 на Mac). Выберите (все форматы) > ч:мм, чтобы результат не содержал AM и PM.
Чтобы вычислить время между двумя датами со временем, можно просто вычесть одно значение из другого. Однако необходимо применить форматирование к каждой ячейке, чтобы Excel возвращал нужный результат.
1. Введите две полные даты со временем.
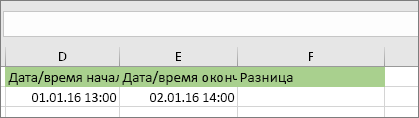
В одной ячейке введите полную дату и время начала. А в другой ячейке введите полную дату и время окончания. Каждая ячейка должна содержать месяц, день, год, час, минуты, и пробел перед AM или PM.
2. Установите формат “14.03.12 1:30 PM”.
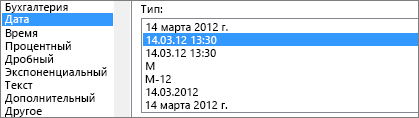
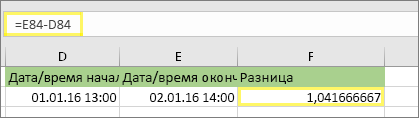
Выберите обе ячейки и нажмите клавиши CTRL+1 (или 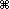 +1 на компьютере Mac). Затем выберите Дата > 14.03.12 1:30 PM. Это не дата, которую вы установили, а просто пример того, как будет выглядеть формат. Обратите внимание, что в версиях до Excel 2016 этот формат может использовать другой пример даты, например 14.03.01 1:30 PM.
+1 на компьютере Mac). Затем выберите Дата > 14.03.12 1:30 PM. Это не дата, которую вы установили, а просто пример того, как будет выглядеть формат. Обратите внимание, что в версиях до Excel 2016 этот формат может использовать другой пример даты, например 14.03.01 1:30 PM.
3. Вычтите два значения.
В другой ячейке вычтите ячейку даты и времени начала из даты и времени окончания. Скорее всего, результат будет выглядеть как число с десятичным знаком. Вы исправите это на следующем шаге.
4. Установите формат “[ч]:мм”.
![Диалоговое окно "Формат ячеек", настраиваемая команда, тип [ч]:мм](https://support.content.office.net/ru-ru/media/2edbd461-d4c5-49a7-a5a2-b6d9329c0411.png)
Нажмите клавиши CTRL+1 (или 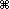 +1 на Mac). Выберите пункт (все форматы). В поле Тип введите [ч]:мм.
+1 на Mac). Выберите пункт (все форматы). В поле Тип введите [ч]:мм.
Статьи по теме
Функция РАЗНДАТ
Функция ЧИСТРАБДНИ.МЕЖД
ЧИСТРАБДНИ
Дополнительные функции даты и времени
Вычисление разницы во времени
Нужна дополнительная помощь?
Нужны дополнительные параметры?
Изучите преимущества подписки, просмотрите учебные курсы, узнайте, как защитить свое устройство и т. д.
В сообществах можно задавать вопросы и отвечать на них, отправлять отзывы и консультироваться с экспертами разных профилей.
Вычесть значит отнять одно число от другого. Вычитание есть такое действие, в котором отнимают меньшее число от большего. При вычитании целых чисел большее число уменьшается на столько единиц, сколько их содержится в меньшем.
Вычесть одно число из другого значит убавить одно число другим, поэтому вычитание есть действие обратное сложению.
Вычитание

В вычитании два данных числа называются уменьшаемым и вычитаемым, а искомое — разностью.
Уменьшаемым называют большее число, от которого отнимают другое. Оно уменьшается от вычитания.
Вычитаемым называют меньшее число, которое отнимают от большего.
Разностью называют вывод, полученный от вычитания. Разность определяет, чем одно число больше другого или показывает разницу между двумя числами.
Знак вычитания. Действие вычитания обозначается знаком — (минус).
Вычитание однозначных чисел
Чтобы обозначить, что из 9 нужно вычесть 6, пишут эти числа рядом, отделяя их знаком — (минус):
- 9 — 6.
Разность между этими числами будет 3, и ход вычисления выражают словесно:
девять без шести равно трем.
Письменно:
- 9 — 6 = 3.
Большее число 9 будет уменьшаемым, меньшее 6 вычитаемым, число 3 остатком.
Способы вычитания
Можно двумя способами вычесть одно число из другого:
- или можно отнять от большего числа столько единиц, сколько их содержится в меньшем. Так, из 9 вычесть 6 значит от 9 отнять 6. Число 3 будет искомый остаток;
- или можно к меньшему числу прибавлять по единице до тех пор, пока не получим большее число. Так, вычитая 6 из 9, мы к 6 прибавляем 3 единицы.
Число единиц, которое нужно прибавить к меньшему числу, чтобы уравнять его с большим, определяет разность.
Меньшее число с разностью должно равняться большему числу, следовательно, меньшее число и разность суть слагаемые, а большее — их сумма. На этом основано другое определение вычитания:
- Вычитание есть такое действие, в котором по данной сумме и одному слагаемому отыскивается другое слагаемое.
В этом случае данная сумма есть уменьшаемое, данное слагаемое — вычитаемое, а искомаяразность — другое слагаемое.
Вычитание многозначных чисел
Вычитание многозначных чисел основывается на том свойстве чисел, по которому вычесть число все-равно, что вычесть все его части. Из этого свойства видно, что вычесть какое-нибудь число все-равно, что вычесть последовательно все его единицы, десятки, сотни и т. д. Чтобы обозначить, что из числа 7228 нужно вычесть 3517, пишут:
- 7228 — 3517 и вычитают отдельно единицы из единиц, десятки из десятков и т. д.
Чтобы облегчить вычитание, подписывают меньшее число под большим так, чтобы единицы одинаковых порядков находились в одном вертикальном столбце, проводят черту, слева ставят знак вычитания — и под чертою подписывают разность.
Ход вычисления выражают словесно:
- Начинаем вычитание с простых единиц: 8 без 7 составляют 1; подписывают под единицами 1.
- Вычитаем десятки: 2 без 1 дают 1, подписываем под десятками 1.
- Вычитаем сотни. Пять нельзя вычесть из 2, поэтому занимаем у следующего высшего порядка (тысяч) единицу, что и обозначаем тем, что над 7 ставим точку. Единица каждого порядка содержит 10 единиц следующего меньшего порядка. Присоединяя эти 10 единиц к 2, получим 12; 12 без 5 составляют 7, подписываем под сотнями 7. Когда занимают единицу у высшего порядка, обозначают это тем, что ставят точку над порядком, у которого занимают.
- Вычитаем тысячи. Тысяч осталось вместо 7 только 6, ибо одна была взята. 6 без 3 составляют 3; подписываем под тысячами 3.
Ход вычисления выражают письменно:

Пример. Из 17004 вычесть 6025.

Из 4 нельзя вычесть 5. Занимаем единицу у десятков, следующего высшего порядка, но в этом порядке единиц нет; занимаем у сотен, — и сотен нет; занимаем у тысяч и обозначаем это точкой над цифрой 7.
Единица четвертого имеет 10 единиц третьего порядка. Взяв из них одну для десятков, оставляем их в сотнях только 9. Присоединив 10 к 4, имеем 14.
Производя вычитание, получим:
- для единиц 14 — 5 = 9
- для десятков 9 — 2 = 7
- для сотен 9 — 0 = 9
- для тысяч 6 — 6 = 0
Для десятков тысяч имеем 1, ибо эту цифру уменьшаемого переносим в разность без изменения.
Ход вычисления выразится письменно:

Из предыдущих примеров выводим правила вычитания:
- Чтобы сделать вычитание целых чисел, нужно вычитаемое подписать под уменьшаемым так, чтобы единицы одинаковых порядков стояли в одном вертикальном столбце, провести черту, под которою и подписать разность.
- Вычитание нужно начинать с простых единиц, то есть с первого столбца, и затем, переходя к следующим столбцам от правой руки к левой, вычитают десятки из десятков, сотни из сотен и т. д.
- Если цифра вычитаемого меньше цифры уменьшаемого, разность подписывают в том же столбце; если цифры равны, разность будет нуль.
- Если же цифра вычитаемого больше соответствующей цифры уменьшаемого, занимают единицу у следующего порядка уменьшаемого, отмечая это точкой, поставленной над цифрой, у которой занимают, прикладывают 10 к цифре уменьшаемого и производят вычитание. Цифру же с точкой считают на единицу меньше.
- Если при вычитании цифра уменьшаемого, у которого занимают, будет 0, за которым в уменьшаемом следуют тоже нули, то занимают у первой значащей цифры, ставя над нею и всеми промежуточными нулями точки. Цифру с точкой считают на единицу меньше, а нули с точкой считают за 9.
- Вычитание продолжают до тех пор, пока не получат полной разности.
- Лишние цифры уменьшаемого переносят в разность.
Зависимость между данными и искомыми вычитания
Из примера 9 — 6 = 3 видно, что
- Уменьшаемое равно вычитаемому, сложенному с разностью: 9 = 6 + 3.
- Вычитаемое равно уменьшаемому без разности: 6 = 9 — 3.
- Разность равна уменьшаемому без вычитаемого: 3 = 9 — 6.
Арифметическое дополнение. Разность между числом и ближайшей большей единицей называется арифметическим дополнением. Так, арифметическими дополнениями чисел 7, 79, 983 будут числа:
- 10 — 7 = 3
- 100 — 79 = 21
- 1000 — 983 = 17
Арифметическим дополнением иногда пользуются для облегчения арифметических вычислений.
Источник: https://maths-public.ru/arithmetic/subtraction
Вычитание чисел
Вычитание – это арифметическое действие обратное сложению, посредством которого из одного числа вычитают (отнимают) столько единиц, сколько их содержится в другом числе.
Число, из которого вычитают, называется уменьшаемым, число, которое указывает сколько единиц будет вычтено из первого числа, называется вычитаемым. Число, получаемое в результате вычитания, называется разностью (или остатком).
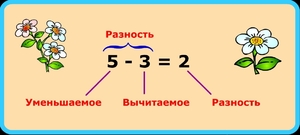
Рассмотрим вычитание на примере. На столе лежит 9 конфет, если съесть 5 конфет, то их останется 4. Число 9 является уменьшаемым, 5 – вычитаемым, а 4 – остатком (разностью):

Для записи вычитания используется знак — (минус). Он ставится между уменьшаемым и вычитаемым, при этом уменьшаемое записывается слева от знака минус, а вычитаемое – справа. Например, запись 9 — 5 означает, что из числа 9 вычитается число 5. Справа от записи вычитания ставят знак = (равно), после которого записывают результат вычитания. Таким образом, полная запись вычитания выглядит так:

Эта запись читается так: разность девяти и пяти равняется четырём или девять минус пять равно четыре.
Чтобы в результате вычитания получить натуральное число или 0, уменьшаемое должно быть больше вычитаемого или равно ему.
Рассмотрим, как, используя натуральный ряд, можно выполнить вычитание и найти разность двух натуральных чисел. Например, нам необходимо вычислить разность чисел 9 и 6, отметим в натуральном ряду число 9 и отсчитаем от него влево 6 чисел. Получим число 3:

9 — 6 = 3
Вычитание также можно использовать для сравнения двух чисел. Желая сравнить между собой два числа, мы задаёмся вопросом, на сколько единиц одно число больше или меньше другого.
Чтобы узнать это, надо из большего числа вычесть меньшее. Например, чтобы узнать, на сколько 10 меньше 25 (или на сколько 25 больше 10), надо из 25 вычесть 10.
Тогда найдём, что 10 меньше 25 (или 25 больше 10) на 15 единиц.
Проверка вычитания
Рассмотрим выражение
15 — 7 = 8
где 15 – это уменьшаемое, 7 – это вычитаемое, а 8 – разность. Чтобы узнать правильно ли было выполнено вычитание, можно:
- вычитаемое сложить с разностью, если получится уменьшаемое, то вычитание было выполнено верно:7 + 8 = 15
- от уменьшаемого отнять разность, если получится вычитаемое, то вычитание было выполнено верно:15 — 8 = 7
Источник: https://naobumium.info/arifmetika/vychitanie.php
Что такое разность чисел в математике?

Для многих точные науки, вроде математики, воспринимаются как нечто более простое, чем сферы, требующие рассуждений, предполагающие большую вариативность. Однако все предметы имеют свои сложности, в том числе и технические.
Вычитание
Для того, чтобы понять, чем является разность, необходимо разобраться в ряде математической терминологии. В первую очередь, нужно выяснить, чем является вычитание.
По-другому это понятие называют убавлением, и по такому названию понять смысл процесса несколько проще. По своей сути вычитание является одной из математических операций.
Что же это за операции? Как правило, под ними понимают определенные арифметические или логические действия. Встает логичный вопрос – в чем же суть арифметических действий?
Понятие арифметики появилось достаточно давно. Оно зародилось в древнегреческом языке, где переводилось как «число». Сегодня это раздел математики, который изучает числа, их отношения друг к другу, а также свойства.
Итак, вычитание – это операции с числами, относящиеся к бинарным. Суть бинарных операций в том, что в них используются два аргумента (параметра), и получается один результат.
Стоит рассмотреть, как найти разность какого-то числа. В первую очередь, необходимы два аргумента, то есть два числа. Затем необходимо уменьшить значение первого числа на значение второго.
Когда данная операция выражается письменно, используется знак «минус». Это выглядит так: а – б = с, где а является первым числовым значением, б – вторым, а с – разностью чисел.
Как правило, у учеников возникает гораздо больше проблем именно с вычитанием, нежели со сложением. Отчасти это связано со свойствами данных математических операций.
Всем известно, что от перемены мест слагаемых значение суммы не меняется. В вычитании же всё гораздо сложней. Если поменять числа местами, получится совершенно другой результат.
Схожим свойством в прибавлении и убавлении является то, что нулевой элемент не меняет исходное число.
В вычитании всё относительно просто, если первое число больше второго, однако в школе будут рассматриваться и противоположные примеры. В этом случае возникает понятие отрицательного числа.
Например, если нужно вычесть из 5 число 2, то всё несложно. 5-2=3, таким образом разность числа составит 3. Однако, что делать, если необходимо посчитать, сколько будет два минус пять?
В выражении 2-5 разность уйдет в минус, то есть в отрицательное значение. Из двойки легко можно вычесть двойку, получив таким образом ноль, однако от пятерки остается ещё три. Таким образом, результатом данного выражения будет отрицательное число три. То есть, 2-5=-3.
Источник: https://topkin.ru/voprosy/nauka-voprosy/chto-takoe-raznost-chisel-v-matematike/
Что такое разность чисел: уменьшаемое, вычитаемое, разность — правило
Статья познакомит читателя с понятиями «разность чисел», «вычитаемое» и «уменьшаемое».
В арифметике существует всего четыре основных действия, которые мы называем сложением, умножением, вычитанием и делением.
Такие действия являются основой всей математики – они позволяют нам осуществлять все вычисления: как простые, так и самые сложные.
Самыми простыми действиями считаются сложение и вычитание, которые противоположны друг другу. Правда, слово «сложение» мы также используем и в обычной жизни.
Мы можем встретить фразу «сложить усилия, например, когда нам нужно сделать какую-нибудь работу всем вместе. Но вот с термином «вычитание» дело обстоит немного сложнее, и в разговоре оно встречается реже.
Мы редко услышим такие выражения, как «уменьшаемое», «вычитаемое», «разность». Но в сегодняшней статье мы подробно поговорим о них с точки зрения математики.
Что значит число уменьшаемое, число вычитаемое и разность чисел?
Что значит число уменьшаемое, число вычитаемое и разность чисел? Как известно, многие научные термины и выражения взяты из других языков, чаще греческого и латинского. Но те слова, которые будут рассмотрены ниже, имеют русское происхождение, потому нам будет проще их разобрать.
Например, что можно сказать о разности чисел? Если мы обратим внимание на корень слова «разность», то нам представится, например, его однокоренное слово «разница».
А если речь идет о математике, то тут и думать нечего – слово «разность» означает разницу между какими-то цифрами, а точнее, двумя числами.
Разница нам показывает, насколько одна величина больше другой или, наоборот, вторая меньше первой. Строго в математике это выглядит как результат вычитания.
Сразу же приведем пример. Допустим, буфетчица несет на подносе восемь пирожков. Пять из них она раздала посетителям. Сколько пирожков останется у буфетчицы на подносе? Если из 8 вычесть 5, то получится — 3. Теперь запишем это математически:
То есть разница между восемью и пятью – это три. Теперь нам понятно, что такое термин «разница».
Внимание: Если два числа равны друг другу, то разницы между ними не существует, она равна нулю (8 – 8 = 0).
Теперь нам следует выяснить, что такое вычитаемое и уменьшаемое. Снова представим значение слов по их смыслу. Чем может являться число уменьшаемое? Уменьшаемое – это то число, которое уменьшается при вычитании. От этого числа отнимают другое число. А что такое вычитаемое? Вычитаемым как раз и является том числом, которые мы отнимаем от уменьшаемого.
Вернемся к примеру с буфетчицей. Мы помним, как от восьми отнимали пять, и у нас получилось три. Мы выяснили, что тройка является разницей между двумя этими числами. Теперь нам уже не сложно понять, что 8 – это число уменьшаемое, а 5 – это число вычитаемое.
Как найти уменьшаемое и вычитаемое число?
Как в математике найти разницу чисел мы уже разобрались. Это довольно просто. Но сможем ли мы найти уменьшаемое и вычитаемое число, если одно число неизвестно? Конечно можем, так как нам будут известны два других числа. Например, как мы можем найти уменьшаемое число? Если мы знаем значение разницы и вычитаемого, то сумма этих двух чисел равняется уменьшаемому:
- Y – 10 = 18, где Y – число уменьшаемое
- Значит, Y = 18 + 10
- 18 + 10 = 28
- Y = 28
Вычитаемое находится так же просто. Если мы знаем разницу и уменьшаемое, значит вычитаемое мы получим, отняв от уменьшаемого числа разность:
- 28 – B = 10, где B – число вычитаемое
- Значит, B = 28 – 10
- 28 – 10 = 18
- B = 18
Источник: https://heaclub.ru/chto-takoe-raznost-chisel-umenshaemoe-vychitaemoe-raznost-pravilo
Что такое разность чисел в математике и как найти разность чисел
В этой статье мы рассмотрим, что такое разность чисел в математике, и как человеку, интересующемуся этой наукой, найти разность чисел.
Что такое разность чисел в математике
Вычитание является одной из 4 арифметических операций. Для его обозначения служит математический знак «−» (минус). Вычитание противоположно по смыслу операции сложения.
Операция вычитания в общем случае записывается следующим образом:
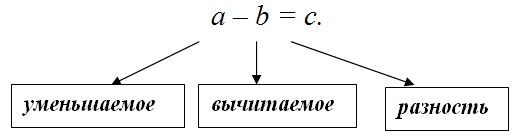
A − B = C
Число Математическое название
| A | Уменьшаемое |
| B | Вычитаемое |
| C | Разность чисел |
Пример: 6 − 2 =4
Здесь разностью чисел будет являться число 4. Следовательно, разность между любыми числами A и B это такое число C, которое при прибавлении к B даст в сумме A (4 при прибавлении к 2 дает 6 — значит, 4 это разность 6 и 2).
Как найти разность чисел
Уже из самого определения следует, как вычислить разность между двумя числами. При небольших числах можно делать это в уме. Детей в начальной школе учат следующим образом. Представьте, что у Вас есть 5 яблок, и 3 из них забрали. Сколько у Вас осталось? Правильно — 2 яблока. Постепенно Вы доведете вычисления до автоматизма и будете сразу выдавать ответ.
Однако для чисел выше 50 такое наглядное представление перестает работать. Большое количество предметов тяжело представить в уме, поэтому здесь на помощь приходит другой способ:
Вычисление разности в столбик
Школьники изучают этот способ в рамках курса математики, обычно во втором или третьем классе. Взрослые люди, пользующиеся калькулятором, зачастую забывают, как считать в столбик. Однако калькулятор не всегда бывает под рукой. Освежите в памяти школьные знания, посмотрев это видео.
Вычисление разности в столбик – видео
Этот способ применим и тогда, когда Вам нужно вычесть большее число из меньшего. В реальной жизни такое обычно не требуется, но может пригодиться при решении математических задач.
Допустим, в примере «A − B = C» B больше, чем A. Тогда C будет отрицательным. Чтобы вычислить разность, «разверните» пример: посчитайте значение B − A.
Когда Вы закончите считать эту разность, у вас получится число C, только с противоположным знаком: оно будет больше нуля. Чтобы завершить вычисления, припишите к нему спереди знак минус.
Источник: https://www.chto-kak-skolko.ru/index.php/nauki/matematika/chto-takoe-raznost-chisel-v-matematike-i-kak-najti-raznost-chisel
Содержание
- Сумма и разность чисел
- Что такое сумма, и как ее найти
- Как найти разность чисел
- Как найти разность чисел в математике
- Арифметические действия с числами
- Разность в математике
- Видео: Математика 6 Делимость суммы и разности чисел
- Как найти разницу величин
- Математические действия с разностью чисел
- Видео: Математика 2 класс. Разность двухзначных чисел
- Простые примеры
- Более сложные примеры
- Математика для блондинок
- Свойства сложения и вычитания
- Свойства сложения
- Свойства вычитания
- Примеры использования свойств сложения и вычитания
Сумма и разность чисел
Что такое сумма, и как ее найти
Сумма – это результат складывания двух чисел (слагаемых), между которыми стоит знак +. Чтобы получить сумму, нужно к одному слагаемому прибавить второе слагаемое. В общем виде пример можно показать так: a + b = s, где а – первое слагаемое, b – второе слагаемое, а s – результат сложения этих двух слагаемых. При этом нужно знать, что от перестановки слагаемых сумма не меняется, — это одно из самых первых правил в математике, которое проходят в начальной школе.
Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.
Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.
Как найти разность чисел
 Разность – результат вычитания одного числа из другого. В отличие от суммы, здесь мы не можем воспользоваться правилом «от перестановки слагаемых разность не меняется», так как в вычитании всегда есть уменьшаемое и вычитаемое. Чтобы найти вычитаемое и разность, для начала нужно разобраться с этими понятиями. Уменьшаемое – это то, из чего мы «вычитаем», то есть убираем, а вычитаемое – количество того, что мы у этого уменьшаемого вернем.
Разность – результат вычитания одного числа из другого. В отличие от суммы, здесь мы не можем воспользоваться правилом «от перестановки слагаемых разность не меняется», так как в вычитании всегда есть уменьшаемое и вычитаемое. Чтобы найти вычитаемое и разность, для начала нужно разобраться с этими понятиями. Уменьшаемое – это то, из чего мы «вычитаем», то есть убираем, а вычитаемое – количество того, что мы у этого уменьшаемого вернем.
В общем виде вычитание можно записать так: a — b = r.
Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел, возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.
А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.
Источник
Как найти разность чисел в математике
 Слово «разность» может употребляться во многих значениях. Это может означать и разницу чего-либо, например, мнений, взглядов, интересов. В некоторых научных, медицинских и других профессиональных сферах этим термином обозначают разные показатели, к примеру, уровня сахара в крови, атмосферного давления, погодных условий. Понятие «разность», как математический термин тоже существует.
Слово «разность» может употребляться во многих значениях. Это может означать и разницу чего-либо, например, мнений, взглядов, интересов. В некоторых научных, медицинских и других профессиональных сферах этим термином обозначают разные показатели, к примеру, уровня сахара в крови, атмосферного давления, погодных условий. Понятие «разность», как математический термин тоже существует.
Арифметические действия с числами
Основными арифметическими действиями в математике являются:
Каждый результат этих действий также имеет своё название:
- сумма — результат, получившийся при сложении чисел;
- разность — результат, получившийся при вычитании чисел;
- произведение — результат умножения чисел;
- частное — результат деления.
Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:
- сумма — прибавить;
- разность — отнять;
- произведение — умножить;
- частное — разделить.
Разность в математике
Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:
 Разность чисел означает, насколько одно из них больше другого.
Разность чисел означает, насколько одно из них больше другого.- Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.
- Это вычитание одного числа из другого.
- Это цифра, составляющая остаток при минусовании двух величин.
- Это величина, являющаяся результатом вычитания двух значений.
- Разность показывает количественное различие между двумя цифрами.
- Это результат одного из четырёх арифметических действий, которым является вычитание.
- Это то, что получится, если из уменьшаемого отнять вычитаемое.
Видео: Математика 6 Делимость суммы и разности чисел
И все эти определения являются верными.
Как найти разницу величин
Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:
- Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.
Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:
- Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.
Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?
- Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
- Вычитаемое — это математическое число, которое вычитают из уменьшаемого.
Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:
- Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
- Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
Математические действия с разностью чисел
Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.
Видео: Математика 2 класс. Разность двухзначных чисел
Простые примеры
- Пример 1. Найти разницу двух величин.
20 — уменьшаемое значение,
Решение: 20 — 15 = 5
Ответ: 5 — разница величин.
- Пример 2. Найти уменьшаемое.
32 — вычитаемое значение.
Решение: 32 + 48 = 80
- Пример 3. Найти вычитаемое значение.
17 — уменьшаемая величина.
Решение: 17 — 7 = 10
Ответ: вычитаемое значение 10.
Более сложные примеры
На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.
- Пример 4. Найти разницу трёх значений.
 Даны целые значения: 56, 12, 4.
Даны целые значения: 56, 12, 4.
56 — уменьшаемое значение,
12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);
Ответ: 40 — разница трёх значений.
- Пример 5. Найти разницу рациональных дробных чисел.
Даны дроби с одинаковыми знаменателями, где
4/5 — уменьшаемая дробь,
Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.
Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5
- Пример 6. Утроить разницу чисел.
А как выполнить такой пример, когда требуется удвоить или утроить разницу?
Вновь прибегнем к правилам:
- Удвоенное число — это величина, умноженная на два.
- Утроенное число — это величина, умноженная на три.
- Удвоенная разность — это разница величин, умноженная на два.
- Утроенная разность — это разница величин, умноженная на три.
7 — уменьшаемая величина,
5 — вычитаемая величина.
2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.
- Пример 7. Найти разницу величин 7 и 18.
7 — уменьшаемая величина;
Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?
И опять есть применяемое для конкретного случая правило:
- Если вычитаемое больше уменьшаемого, разница окажется отрицательной.
Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.
Математика для блондинок
 Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.
Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.
В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.
И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:
- сумму — сложением слагаемых;
- произведение — умножением множителей;
- частное — делением делимого на делитель.
Источник
Свойства сложения и вычитания

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
- 2 — это первое слагаемое,
- 5 — второе слагаемое,
- 7 — это сумма.
При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
- Переместительное свойство сложения
От перестановки мест слагаемых сумма не меняется.
a + b = b + a - Сочетательное свойство сложения
Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.
(a + b) + c = a + (b + c) - Свойство нуля при сложении
Если к числу прибавить нуль, получится само число.
a + 0 = 0 + a = a
Свойства вычитания
Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.
Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.
Уменьшаемое — это число, из которого вычитают.
Вычитаемое — это число, которое вычитают.
Разность — это число, которое получается в результате вычитания.
Рассмотрим пример 9 — 4 = 5, в котором:
При этом саму запись (9 — 4) тоже можно назвать разностью.

- Свойство нуля при вычитании
Если из числа вычесть нуль, получится само число.
a — 0 = a
Если из числа вычесть само число, то получится нуль.
a — a = 0 - Свойство вычитания суммы из числа
Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое.
a — (b + c) = a — b — c - Свойство вычитания числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
(a + b) — c = (a — c) + b (если a > c или а = с)
(a + b) — c = (b — c) + a (если b > c или b = с)
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Примеры использования свойств сложения и вычитания
Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:

Пример 1
Вычислить сумму слагаемых с использованием разных свойств:
а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15
б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22
в) 30 + 0 + 13 = 30 + 13 = 43
Пример 2
Применить разные свойства при вычислении разности:
а) 25 — 0 — 2 = 25 — 2 = 23
б) 18 — (1 + 4) = 18 — 1 — 4 = 17 — 4 = 13
Пример 3
Найти значение выражения удобным способом:
а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32
б) 16 — (4 + 3) + 7 = 16 — 4 — 3 + 7 = (16 — 4) — 3 + 7 = 12 — 3 + 7 = 9 + 7 = 16
Источник
Содержание:
- Определение разности чисел
Определение разности чисел
Разность $r$ чисел $a$ и $b$ – это результат вычитания числа $b$ из числа $a$ .
Пример
Задание. Найти разность чисел:
1) $17-5$ ; 2) $13-27$ ; 3) $2,34-1,24$
Ответ.
$17-5=12$
$13-27=-14$
$2,34-1,24=1,1$
В случае если вычитаются большие числа или
десятичные дроби, то используют способ вычитания в столбик.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти разность чисел:
1) $5637-172$ ; 2) $43,56-23,94$
Решение. Найдем разность этих чисел, используя метод вычитания в столбик. В первом примере запишем числа
друг под другом так, чтобы единицы были под единицами, десятки под десятками и т.д. Вычитание будем производить справа налево,
вычитая из верхнего числа меньшее. В случае, если верхнее число меньше нижнего занимаем десяток у верхнего числа стоящего
левее данного, при этом число стоящее левее уменьшится на единицу, а данное число увеличится на 10.
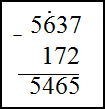
Для нахождения второй разности запишем заданные десятичные дроби в столбик так, чтобы запятая верхнего числа совпадала
с запятой нижнего. После чего вычтем их в столбик как числа в первом примере.
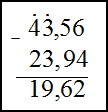
Ответ.
$5637-172=5465$
$43,56-23,94=19,62$
Разность рациональных дробей находится по правилу
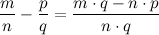
Пример
Задание. Найти разность рациональных дробей:
1) $frac{5}{13}-frac{2}{11}$ ; 2) $1 frac{1}{7}-frac{2}{5}$
Решение. По правилу вычитания рациональных дробей имеем
$$frac{5}{13}-frac{2}{11}=frac{5 cdot 11-2 cdot 13}{13 cdot 11}=frac{55-26}{143}=frac{29}{143}$$
Во втором примере, перед тем как производить вычитание дробей запишем первую дробь в виде
неправильной. Для этого целую
часть умножим на знаменатель и прибавим к числителю:
$$1 frac{1}{7}-frac{2}{5}=frac{8}{7}-frac{2}{5}=frac{8 cdot 5-2 cdot 7}{7 cdot 5}=frac{40-14}{35}=frac{26}{35}$$
Ответ.
$$frac{5}{13}-frac{2}{11}=frac{29}{143}$$
$$1 frac{1}{7}-frac{2}{5}=frac{26}{35}$$
Читать дальше: что такое целое число.
Определение пересечения периодов (числовых множеств)
Супер-пупер быстрая конкатенация(сложение) строк
Я думаю, каждый разработчик сталкивался с вычислением разности дат в днях, минутах или секундах. На платформе 1С существует два способа вычисления разности дат:
- С помощью языка запросов;
- С помощью арифметических операций.
Разберем первый способ. Для вычисления разности дат используется стандартная функция языка запросов РАЗНОСТЬДАТ, она имеет три параметра: первый параметр – вычитаемая дата; второй параметр – исходная дата; третий параметр – тип разности, одно из: СЕКУНДА, МИНУТА, ЧАС, ДЕНЬ, МЕСЯЦ, КВАРТАЛ, ГОД. Но помним, что функция рассчитывает календарную разницу между двумя датами, поэтому ее нельзя
использовать в местах, где необходимо рассчитать количество банковских или
рабочих дней между двумя датами.
Напишем функцию:
Функция ПолучитьРазностьДатВДняхЗапрос(НачалоПериода, КонецПериода)
Запрос = Новый Запрос;
Запрос.Текст =
"ВЫБРАТЬ
| РАЗНОСТЬДАТ(&ДатаНачалаПериода, &ДатаОкончанияПериода, ДЕНЬ) КАК Результат";
Запрос.УстановитьПараметр("ДатаНачалаПериода", НачалоДня(НачалоПериода));
Запрос.УстановитьПараметр("ДатаОкончанияПериода", НачалоДня(КонецПериода));
РезультатЗапроса = Запрос.Выполнить();
ВыборкаДетальныеЗаписи = РезультатЗапроса.Выбрать();
КоличествоДней = 0;
Пока ВыборкаДетальныеЗаписи.Следующий() Цикл
КоличествоДней = ВыборкаДетальныеЗаписи.Результат;
КонецЦикла;
Возврат КоличествоДней;
КонецФункции
Из плюсов данного способа можно отметить: простота реализации, не надо ничего делить и вычитать; третий параметр функции языка запросов, отвечающий за тип разности, можно параметризировать, то есть можно легко получить разность дат не только в днях, но и в минутах, часах и так далее.
Из минусов стоит отметить исполнение функции только на стороне сервера, так как используется объект Запрос.
Во втором способе нужно уметь делить и знать сколько секунд в минуте, минут в часах и так далее. Если на платформе 1С произвести вычитание над датами, то получим целое число – это разница между датами в секундах. Если исходная дата больше чем вычитаемая, то получим положительное количество секунд, если исходная дата меньше чем вычитаемая, то отрицательное количество секунд.
Напишем функцию, которая будет вычислять разность между двумя датами в днях:
Функция ПолучитьРазностьДатВДнях(НачалоПериода, КонецПериода)
РазностьВСекундах = НачалоДня(КонецПериода) - НачалоДня(НачалоПериода);
КоличествоДней = Окр(РазностьВСекундах / 60 / 60 / 24);
Возврат КоличествоДней;
КонецФункции
Хочу заметить, что как и в первом способе, рассчитывается календарная разница между датами. Из плюсов хочу отметить исполнение функции в любом контексте, из минусов – для параметризации типа разности придется написать сочинение из условий или как-то так.
На практике мне встретился тот факт, что программисты предпочитают пользоваться первым способом, и я так же последовал этому мейнстриму и применил первый способ в одном из тяжелых алгоритмов, где вычисление разницы между двумя датами в днях выполнялось тысячи раз.
После запуска алгоритма огорчила скорость его выполнения, решил замерить производительность и выяснить где проседает алгоритм, и был бурно (бл#, пзд#ц) удивлен. Не малую часть времени уходит на вычисление разницы дат. После перехода на второй способ ситуация улучшилась.
Привожу демонстрацию замера производительности системы при вычислении разница дат обоими способами, выполнив 10000 раз (см. рисунок 1).
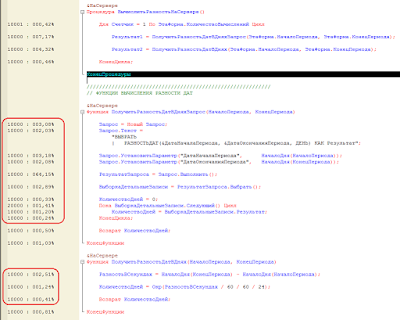 |
| Рисунок 1. Замер производительности вычисления разности дат |
Как видите, почти 70% от общего времени уходит на первый способ, и 30% на второй. Будьте внимательны, и проверяйте то, что советуют на просторах интернета.
