При вычитании дробей, как и при сложении, могут встретиться несколько случаев.
Вычитание дробей с одинаковыми знаменателями
При вычитании дробей с одинаковыми знаменателями от числителя уменьшаемого (первой дроби) отнимают
числитель вычитаемого (второй дроби), а знаменатель оставляют прежним.
Пример.
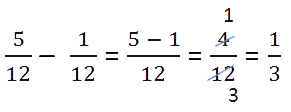
Запомните!
![]()
Прежде чем записать конечный ответ, проверьте, нельзя ли сократить полученную дробь.
В буквенном виде правило вычитания дробей с одинаковыми знаменателями
записывают так:
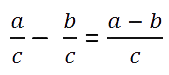
Вычитание правильной дроби из единицы
Когда нужно вычесть из единицы правильную дробь, единицу представляют в виде
неправильной дроби, знаменатель которой, равен знаменателю вычитаемой дроби.
Пример.
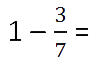
Знаменатель вычитаемой дроби равен 7, значит, единицу представляют как неправильную
дробь
и вычитают по правилу вычитания дробей с одинаковыми знаменателями.
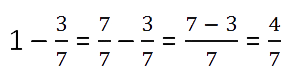
Вычитание правильной дроби из целого числа
Чтобы из целого числа вычесть правильную дробь нужно представить это натуральное число
в виде смешанного числа.
Для этого занимаем единицу в натуральном числе и представляем её в виде неправильной дроби,
знаменатель которой равен знаменателю вычитаемой дроби.
Пример.
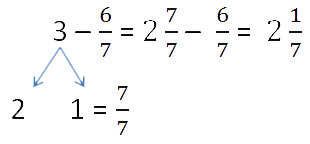
В примере единицу мы заменили неправильной дробью
и вместо 3 записали смешанное
число и от дробной части отняли дробь.
Вычитание смешанных чисел
При вычитании смешанных чисел отдельно из целой части вычитают целую часть, а из дробной части
вычитают дробную часть.
При подобных расчётах могут встретиться разные случаи.
Первый случай вычитания смешанных чисел
У дробных частей одинаковые знаменатели и числитель дробной части
уменьшаемого (из чего вычитаем) больше или равен числителю дробной части вычитаемого
(что вычитаем).
Пример.
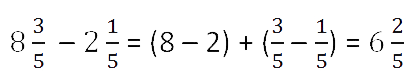
Второй случай вычитания смешанных чисел
У дробных частей разные знаменатели.
В этом случае вначале нужно
привести к общему знаменателю
дробные части, а затем
выполнить вычитание целой части из целой, а дробной из дробной.
Пример.
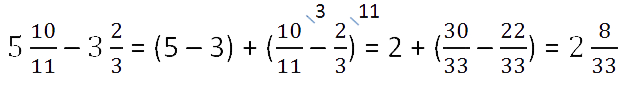
Третий случай вычитания смешанных чисел
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример.
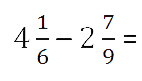
Так как у дробных частей разные знаменатели, то как и
во втором случае, вначале приведём обыкновенные дроби к общему знаменателю.
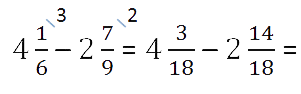
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого.
3 < 14
Поэтому, вспомнив
вычитание правильной дроби из целого числа, займём единицу из целой части и представим
эту единицу в виде неправильной дроби с одинаковым знаменателем и числителем равным 18.
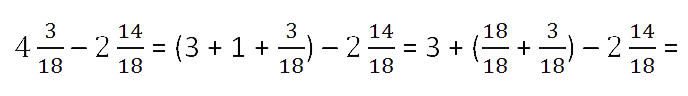
Сложим полученную неправильную дробь
и дробную часть
уменьшаемого и получим:
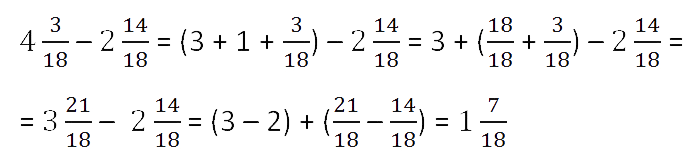
Все рассмотренные случаи можно описать с помощью правил вычитания
смешанных чисел.
- Привести дробные части уменьшаемого и вычитаемого к наименьшему общему знаменателю.
- Если дробная часть уменьшаемого меньше дробной части
вычитаемого, то занимаем у целой части уменьшаемого единицу. Эту единицу
превращаем в неправильную дробь с одинаковым числителем и знаменателем равными наименьшему общему знаменателю. - Прибавляем полученную неправильную дробь к дробной части уменьшаемого.
- Вычитаем из целой части целую, а из дробной — дробную.
- Проверяем, нельзя ли сократить и выделить целую часть в конечной дроби.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
13 ноября 2019 в 6:24
Валя Гутник

Профиль
Благодарили: 0
Сообщений: 7

Валя Гутник
Профиль
Благодарили: 0
Сообщений: 7
как вычитать дроби с разным знаменателем
−
0
Спасибо
Ответить
15 апреля 2020 в 13:34
Ответ для Валя Гутник
Саша Алекс

Профиль
Благодарили: 0
Сообщений: 1

Саша Алекс
Профиль
Благодарили: 0
Сообщений: 1
Хз
0
Спасибо
Ответить
18 марта 2019 в 18:37
Никита Рулькевич

Профиль
Благодарили: 0
Сообщений: 2

Никита Рулькевич
Профиль
Благодарили: 0
Сообщений: 2
0
Спасибо
Ответить
18 марта 2019 в 18:51
Ответ для Никита Рулькевич
Никита Рулькевич

Профиль
Благодарили: 0
Сообщений: 2

Никита Рулькевич
Профиль
Благодарили: 0
Сообщений: 2
11 ![]()
0
Спасибо
Ответить
4 сентября 2015 в 12:08
Зарина-И-Владимир Вебер

Профиль
Благодарили: 0
Сообщений: 1

Зарина-И-Владимир Вебер
Профиль
Благодарили: 0
Сообщений: 1
?12
? 7
? ?
?я незнаю ответ помогите пожалуста
0
Спасибо
Ответить
2 сентября 2016 в 14:33
Ответ для Зарина-И-Владимир Вебер
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Сначала — действие в скобках. Переводим в дробь целую часть, приводим к общему знаменателю, производим действие, далее производим умножение.
= (
?) · = · = = == 2=2,5
0
Спасибо
Ответить
7 апреля 2015 в 13:14
Женечка Беляевская

Профиль
Благодарили: 0
Сообщений: 1

Женечка Беляевская
Профиль
Благодарили: 0
Сообщений: 1
вычитание дроби из целого числа 9-
0
Спасибо
Ответить
8 апреля 2015 в 0:39
Ответ для Женечка Беляевская
Алёна Гермес

Профиль
Благодарили: 0
Сообщений: 2

Алёна Гермес
Профиль
Благодарили: 0
Сообщений: 2
9-3/4 = 9/1-3/4 = 36/4-3/4 = 33/4 = 8
Целое число представляем в виде дроби, затем приводим к общему знаменателю, путем умножения первой дроби на знаменаетль второй и знаменателя первой на вторую дробь. Получаем неправельную дробь, и превращаем её в правильную, делим 33 на 4 и получаем 8 и остаток от деления 1.
0
Спасибо
Ответить
14 апреля 2015 в 17:00
Ответ для Женечка Беляевская
Asel Talantbekovna

Профиль
Благодарили: 0
Сообщений: 8

Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
9- = 8 — =8 =8
0
Спасибо
Ответить
6 апреля 2015 в 14:02
Алексей Старков

Профиль
Благодарили: 0
Сообщений: 1

Алексей Старков
Профиль
Благодарили: 0
Сообщений: 1
(1 — 1/2): (1/2 — 1/3) =
0
Спасибо
Ответить
7 апреля 2015 в 3:34
Ответ для Алексей Старков
Алёна Гермес

Профиль
Благодарили: 0
Сообщений: 2

Алёна Гермес
Профиль
Благодарили: 0
Сообщений: 2
1) (1 — 1/2) = 1/1 — 1/2 = 2/2 — 1/2 = 1/2
Находим общий заменатель, перемножая первую дробь на знаменатель второй, и вторую на знаменатель первой.
2) (1/2 — 1/3) = 3/6 — 2/6 = 1/6
Находим общий знаменатель.
3) 1/2: 1/6 = 1/2 · 6/1 = 6/2 =3/1 = 3
Что бы разделить одну дробь на другую, нужно перевернуть вторую дробь и разделить её на первую. Затем следует сократить дробь.
0
Спасибо
Ответить
14 апреля 2015 в 17:08
Ответ для Алексей Старков
Asel Talantbekovna

Профиль
Благодарили: 0
Сообщений: 8

Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
(1- ): ( — )
1)
— =
2)
=
3)
– = =
0
Спасибо
Ответить
14 апреля 2015 в 17:10
Ответ для Алексей Старков
Asel Talantbekovna

Профиль
Благодарили: 0
Сообщений: 8

Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
последнее дествие исправлю!
: =
0
Спасибо
Ответить
9 апреля 2019 в 17:24
Ответ для Алексей Старков
Настя Бородина

Профиль
Благодарили: 0
Сообщений: 1

Настя Бородина
Профиль
Благодарили: 0
Сообщений: 1
самый понятный овет
0
Спасибо
Ответить
В предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.
Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.
Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.
Сложение целого числа и правильной дроби
Встречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь ![]() . Чтобы решить этот пример, нужно число 2 представить в виде дроби
. Чтобы решить этот пример, нужно число 2 представить в виде дроби ![]() . Затем сложить дроби с разными знаменателями:
. Затем сложить дроби с разными знаменателями:
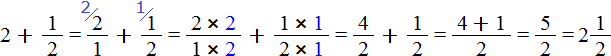
А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: ![]() , а конец так:
, а конец так: ![]() . Различие в том, что в первом случае число 2 и дробь
. Различие в том, что в первом случае число 2 и дробь ![]() соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что
соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что ![]() это свёрнутая форма записи смешанного числа, а
это свёрнутая форма записи смешанного числа, а ![]() — развёрнутая.
— развёрнутая.
Когда перед нами смешанное число вида ![]() , мы должны понимать, что знак сложения опущен.
, мы должны понимать, что знак сложения опущен.
Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.
Значит значение выражения ![]() равно
равно ![]()
![]()
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:
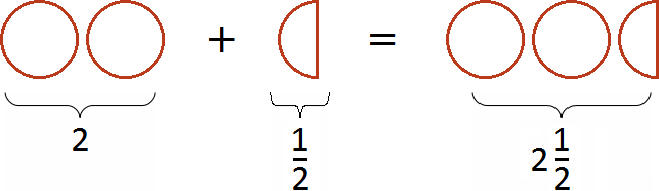
Пример 2. Найти значение выражения ![]()
Представим число 3 в виде дроби ![]() . Затем сложим дроби с разными знаменателями:
. Затем сложим дроби с разными знаменателями:
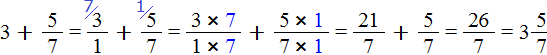
Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:
![]()
Пример 3. Найти значение выражения ![]()
Можно записать вместе число 2 и дробь ![]() , но этот ответ не будет окончательным, поскольку в дроби
, но этот ответ не будет окончательным, поскольку в дроби ![]() можно выделить целую часть.
можно выделить целую часть.
Поэтому в данном примере сначала нужно выделить целую часть в дроби ![]() . Пять вторых это две целых и одна вторая:
. Пять вторых это две целых и одна вторая:
![]()
Теперь в главном выражении ![]() вместо дроби
вместо дроби ![]() запишем смешанное число
запишем смешанное число ![]()
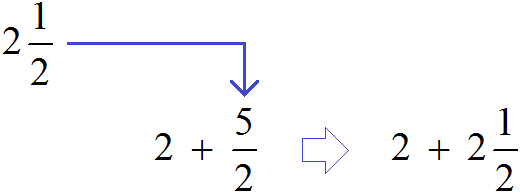
Получили новое выражение ![]() . В этом выражении смешанное число
. В этом выражении смешанное число ![]() запишем в развёрнутом виде:
запишем в развёрнутом виде:
![]()
Применим сочетательный закон сложения. Сложим две двойки, получим 4:
![]()
Теперь свернём полученное смешанное число:
![]()
Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:
![]()
Сложение смешанных чисел
Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения ![]() . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
. Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
![]()
Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:
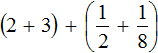
Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:
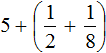
Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:
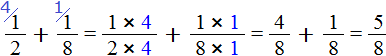
Получили ![]() . Теперь в главном выражении
. Теперь в главном выражении 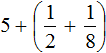 заменяем дробные части на полученную дробь
заменяем дробные части на полученную дробь ![]()
![]()
Теперь свернем полученное смешанное число:
![]()
Таким образом, значение выражения ![]() равно
равно ![]() . Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
. Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
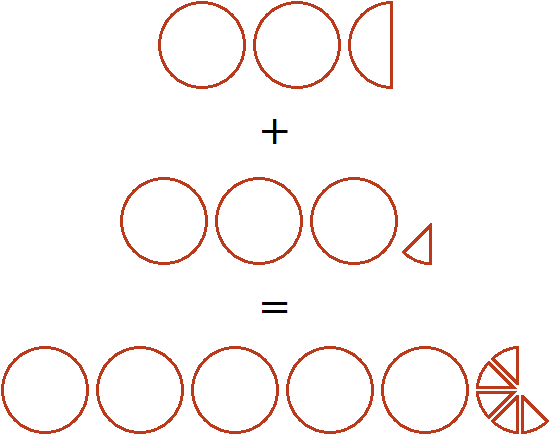
Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:
![]()
Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.
Пример 2. Найти значение выражения
Запишем смешанные числа в развёрнутом виде:
![]()
Сгруппируем целые и дробные части по отдельности:
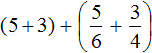
Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8
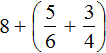
Теперь вычислим дробные части:
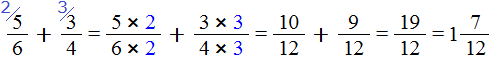
Получили смешанное число ![]() . Теперь в главном выражении
. Теперь в главном выражении 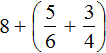 заменяем выражение в скобках на полученное смешанное число
заменяем выражение в скобках на полученное смешанное число ![]()
![]()
Получили выражение ![]() . В данном случае число 8 надо прибавить к целой части смешанного числа
. В данном случае число 8 надо прибавить к целой части смешанного числа ![]() . Для этого смешанное число
. Для этого смешанное число ![]() можно временно развернуть, чтобы было понятнее, что с чем складывать:
можно временно развернуть, чтобы было понятнее, что с чем складывать:
![]()
Сложим целые части. Получаем 9
![]()
Сворачиваем готовый ответ:
![]()
Таким образом, значение выражения равно
![]() .
.
Полное решение этого примера выглядит следующим образом:
![]()
Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:
Чтобы сложить смешанные числа, надо:
- привести дробные части этих чисел к общему знаменателю;
- отдельно выполнить сложение целых и дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.
Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Пример 3. Найти значение выражения ![]()
Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:
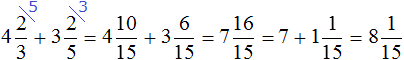
Сложение целого и смешанного числа
Встречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число ![]() . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
. В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
![]()
Здесь смешанная дробь ![]() была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ
была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ ![]() .
.
Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
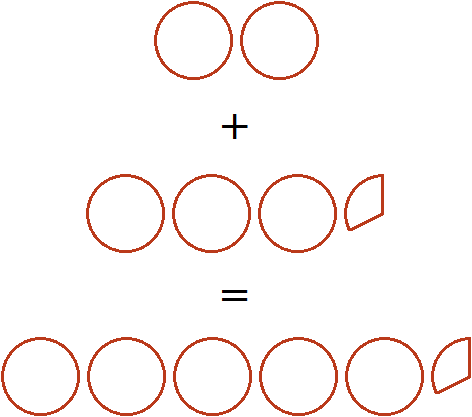
Пример 2. Найти значение выражения ![]()
В этом примере, как и в предыдущем, нужно сложить целые части:
![]()
Осталось свернуть целую и дробную части, но дело в том, что дробная часть ![]() представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
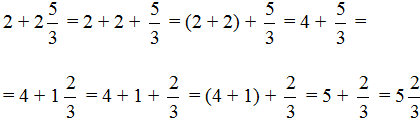
Вычитание дроби из целого числа
Встречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь ![]() . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби
. Чтобы решить такой пример, нужно целое число 1 представить в виде дроби ![]() , и выполнить вычитание дробей с разными знаменателями:
, и выполнить вычитание дробей с разными знаменателями:
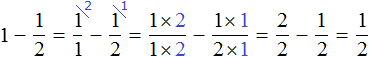
Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:
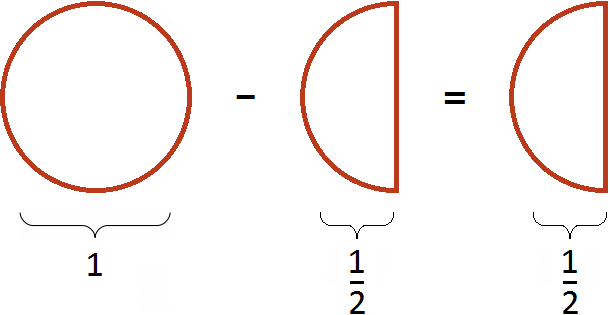
Пример 2. Найти значение выражения ![]() .
.
Представим число 2 в виде дроби ![]() , и выполним вычитание дробей с разными знаменателями:
, и выполним вычитание дробей с разными знаменателями:
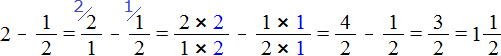
Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:
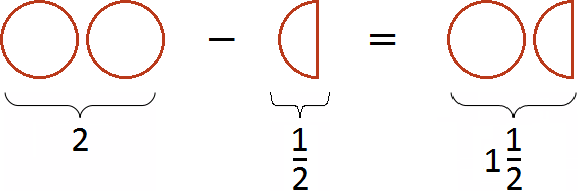
Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения ![]() , не приводя на бумаге никаких вычислений.
, не приводя на бумаге никаких вычислений.
Представим, что число 3 это три пиццы:

Нужно вычесть из них ![]() . Мы помним, что треть выглядит следующим образом:
. Мы помним, что треть выглядит следующим образом:

Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть

Получилось ![]() (две целых и две трети пиццы).
(две целых и две трети пиццы).
Чтобы убедиться в правильности решения, можно найти значение выражения ![]() обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
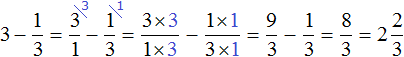
Пример 3. Найти значение выражения ![]()
Представим число 3 в виде дроби ![]() . Затем выполним вычитание дробей с разными знаменателями:
. Затем выполним вычитание дробей с разными знаменателями:
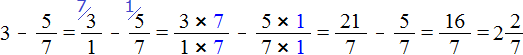
Вычитание смешанного числа из целого числа
Теперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения .
Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число перевести в неправильную дробь. После перевода смешанного числа
в неправильную дробь, получим дробь
![]() . Теперь выполним вычитание дробей с разными знаменателями:
. Теперь выполним вычитание дробей с разными знаменателями:
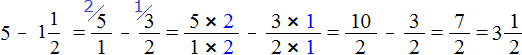
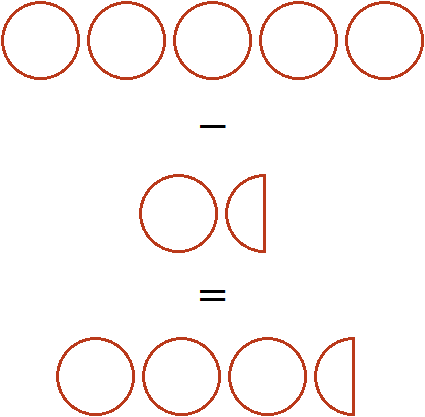
Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:
Пример 2. Найти значение выражения ![]()
Представим 6 в виде дроби ![]() , а смешанное число
, а смешанное число ![]() , в виде неправильной дроби. После перевода смешанного числа
, в виде неправильной дроби. После перевода смешанного числа ![]() в неправильную дробь, получим дробь
в неправильную дробь, получим дробь ![]() . Теперь выполним вычитание дробей с разными знаменателями:
. Теперь выполним вычитание дробей с разными знаменателями:
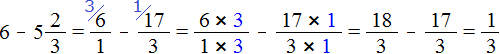
Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.
К примеру, если нужно быстро найти значение выражения ![]() , то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)
, то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)

Тогда от той пиццы, от которой отрезали останется
![]() пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
![]()
Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.
Вычитание смешанных чисел
Встречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения: ![]()
Чтобы решить этот пример, нужно смешанные числа ![]() и
и ![]() перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
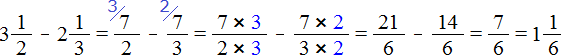
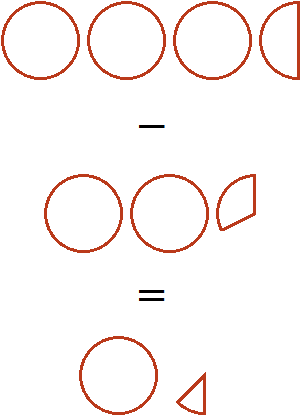
Если от трёх целых и половины пиццы вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:
Пример 2. Найти значение выражения ![]()
Переводим смешанные числа ![]() и
и ![]() в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
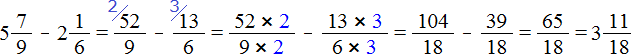
К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.
Умножение целого числа на дробь
Чтобы целое число умножить на дробь, достаточно умножить это целое число на числитель дроби, а знаменатель оставить без изменения.
Например, умножим число 5 на дробь ![]() . Чтобы решить этот пример, нужно число 5 умножить на числитель дроби
. Чтобы решить этот пример, нужно число 5 умножить на числитель дроби ![]() , а знаменатель оставить без изменения:
, а знаменатель оставить без изменения:
![]()
В ответе получилась неправильная дробь. Выделим в ней целую часть:
![]()
Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:
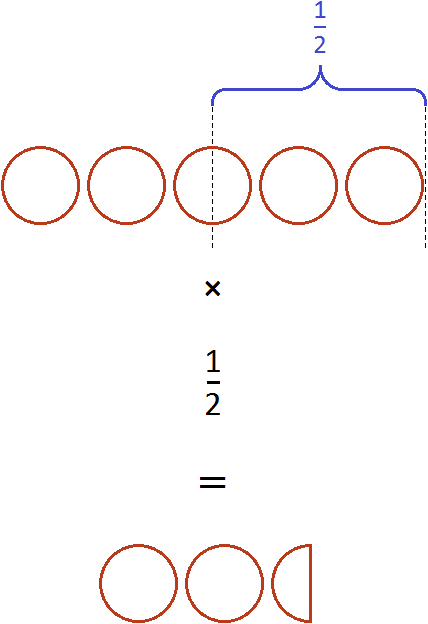
Пример 2. Найти значение выражения ![]()
Умножим число 3 на числитель дроби ![]()
![]()
В ответе получилась неправильная дробь ![]() , но мы выделили её целую часть и получили 2.
, но мы выделили её целую часть и получили 2.
Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:
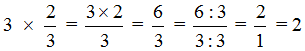
Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:
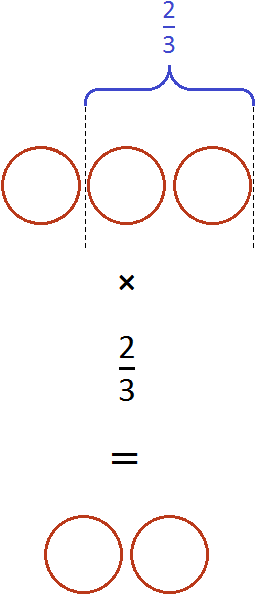
Пример 3. Найти значение выражения ![]()
Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:
![]()
Пример 4. Найти значение выражения ![]()
Умножим число 3 на числитель дроби ![]()
![]()
Умножение смешанного числа на дробь
Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.
Пример 1. Найти значение выражения ![]()
Переведём смешанное число ![]() в неправильную дробь. После перевода это число превратится в дробь
в неправильную дробь. После перевода это число превратится в дробь ![]() . Затем можно будет умножить эту дробь на
. Затем можно будет умножить эту дробь на
![]()
Допустим, имеются одна целая и половина пиццы:

Умножить эти куски на означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:
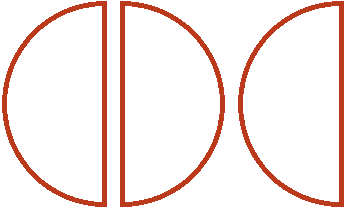
Теперь если мы возьмем (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:
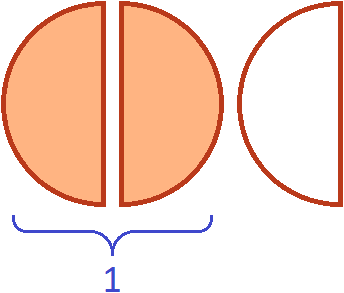
Поэтому значение выражения ![]() было равно 1
было равно 1
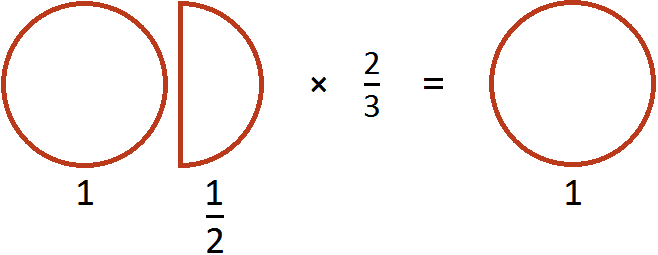
Умножение смешанных чисел
Встречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить ![]() и
и ![]() . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
. Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
![]()
Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:
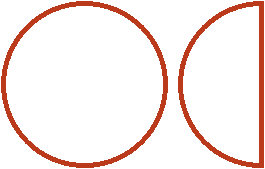
Теперь разберемся со смешанным множителем ![]() . Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще
. Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще ![]() раза.
раза.
С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:
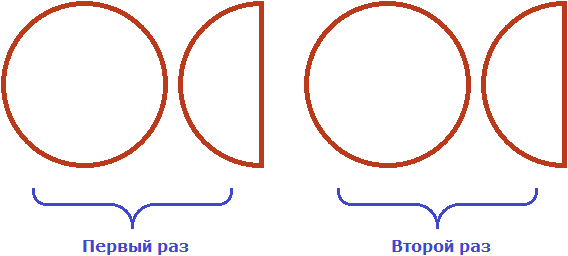
Но ещё осталось взять ![]() от изначальной целой пиццы и половины, ведь множителем было смешанное число
от изначальной целой пиццы и половины, ведь множителем было смешанное число ![]() . Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
. Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
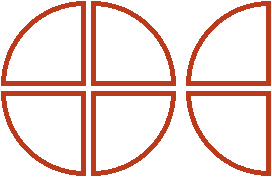
Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:
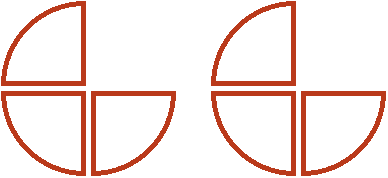
А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является пиццы.
Поэтому значение выражения ![]() равно
равно ![]()
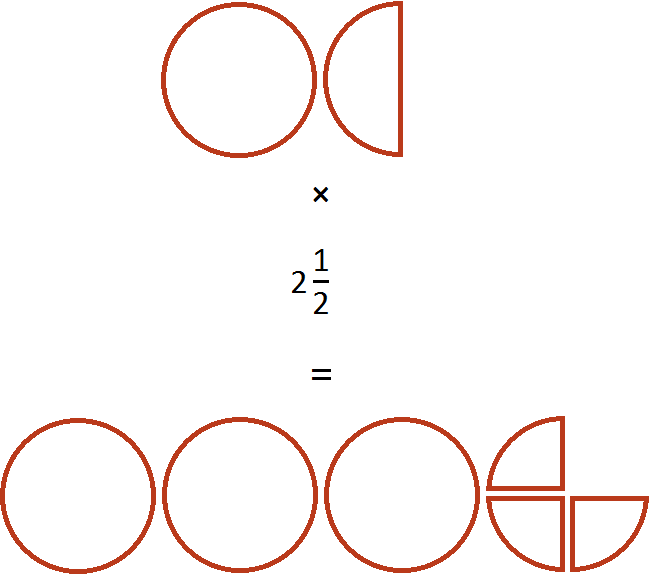
Пример 2. Найти значение выражения ![]()
Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:
![]()
Деление целого числа на дробь
Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.
Например, разделим число 3 на дробь ![]() . Здесь число 3 — это делимое, а дробь
. Здесь число 3 — это делимое, а дробь ![]() — делитель.
— делитель.
Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь ![]() . Поэтому умножаем число 3 на дробь
. Поэтому умножаем число 3 на дробь ![]()
![]()
Допустим, имеются три целые пиццы:

Если мы зададим вопрос «cколько раз ![]() (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
(половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:
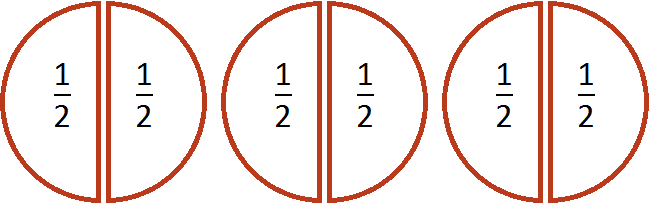
Поэтому значение выражения ![]() равно 6.
равно 6.
Пример 2. Найти значение выражения ![]()
Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь
![]()
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз ![]() пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби
пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби ![]() . После выделения целой части в этой дроби получим
. После выделения целой части в этой дроби получим ![]()
Теперь поставим вопрос так: «Сколько раз ![]() (одна целая и половина пиццы) содержится в двух пиццах?».
(одна целая и половина пиццы) содержится в двух пиццах?».
Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:

В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
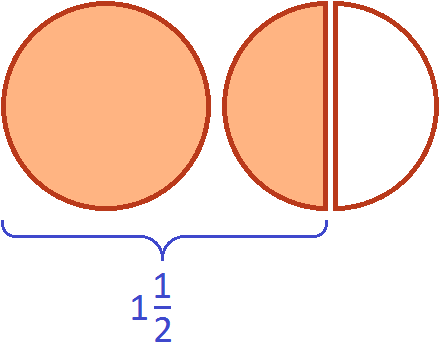
А оставшаяся половина это треть от ![]() , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
, которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
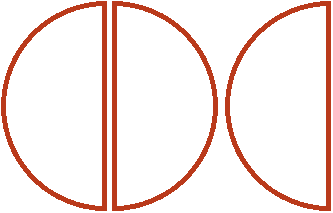
Поэтому значение выражения ![]() равно
равно ![]()
Пример 3. Найти значение выражения ![]()
Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь ![]() . Поэтому умножаем число 5 на
. Поэтому умножаем число 5 на ![]()
![]()
Дробь ![]() это 2 целых и
это 2 целых и ![]() . Проще говоря, две целые и четверть пиццы:
. Проще говоря, две целые и четверть пиццы:

А выражение ![]() определяет сколько раз
определяет сколько раз ![]() содержится в пяти целых пиццах. Ответом было смешанное число
содержится в пяти целых пиццах. Ответом было смешанное число ![]() .
.
То есть ![]() пиццы содержится в пяти целых пиццах
пиццы содержится в пяти целых пиццах ![]() раза.
раза.
Давайте нащупаем в пяти пиццах два раза по ![]()
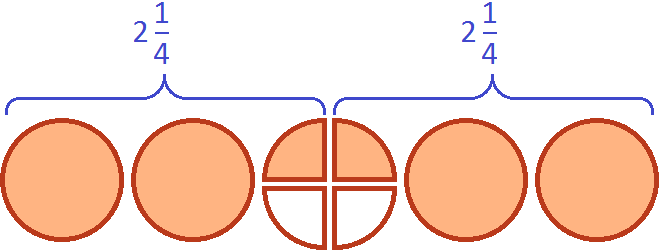
Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой ![]() от
от ![]() , которые не вместились. Двумя девятыми они являются по той причине, что в
, которые не вместились. Двумя девятыми они являются по той причине, что в ![]() пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
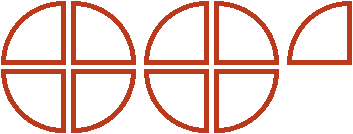
Поэтому значение выражения ![]() равно
равно ![]()
Деление дроби на целое число
Чтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Пример 1. Разделим дробь ![]() на число 2
на число 2
Чтобы разделить дробь ![]() на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь
на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь ![]()
![]()
Пусть имеется половина пиццы:

Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:
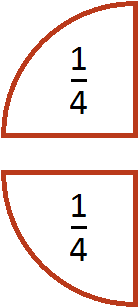
Поэтому значение выражения ![]() равно
равно ![]()
Пример 2. Найти значение выражения ![]()
Чтобы решить этот пример, нужно дробь ![]() умножить на число, обратное числу 2. Обратное числу 2 это дробь
умножить на число, обратное числу 2. Обратное числу 2 это дробь ![]()
![]()
Пример 3. Найти значение выражения ![]()
Умножаем первую дробь ![]() на число, обратное числу 3. Обратное числу 3 это дробь
на число, обратное числу 3. Обратное числу 3 это дробь ![]()
![]()
Деление целого числа на смешанное число
Встречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на ![]() .
.
Чтобы решить этот пример, нужно делитель ![]() перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
Переведём делитель ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() . Затем умножим 2 на дробь, обратную дроби
. Затем умножим 2 на дробь, обратную дроби ![]() . Обратная для дроби
. Обратная для дроби ![]() это дробь
это дробь
![]()
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз ![]() (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
(одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:

А оставшаяся половина это треть от ![]() , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
, которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:

Поэтому значение выражения ![]() равно
равно ![]()
Пример 2. Найти значение выражения ![]()
Переводим делитель ![]() в неправильную дробь, получаем
в неправильную дробь, получаем ![]() . Теперь умножаем число 5 на дробь, обратную дроби
. Теперь умножаем число 5 на дробь, обратную дроби ![]() . Обратная для дроби
. Обратная для дроби ![]() это дробь
это дробь ![]()
![]()
Сначала мы получили ответ ![]() , затем сократили эту дробь на 5, и получили
, затем сократили эту дробь на 5, и получили ![]() , но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ
, но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ ![]()
Деление смешанного числа на целое число
Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Например, разделим ![]() на 2. Чтобы решить этот пример, нужно делимое
на 2. Чтобы решить этот пример, нужно делимое ![]() перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
Переведём смешанное число ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() .
.
Теперь умножаем ![]() на число, обратное числу 2. Обратное числу 2 это дробь
на число, обратное числу 2. Обратное числу 2 это дробь ![]()
![]()
Допустим, имеется одна целая и половина пиццы:

Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:

Затем разделим поровну на две части и половину:

Теперь если мы сгруппируем эти кусочки на две группы, то получим по пиццы в каждой группе:
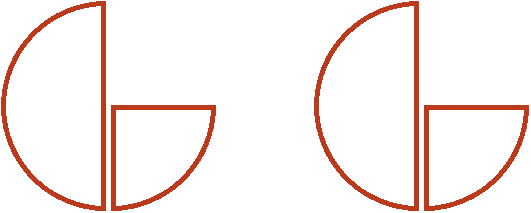
Поэтому значение выражения ![]() равно
равно
Пример 2. Найти значение выражения ![]()
Переведём делимое ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() . Теперь умножаем
. Теперь умножаем ![]() на число, обратное числу 4. Обратное числу 4 это дробь
на число, обратное числу 4. Обратное числу 4 это дробь ![]() .
.
![]()
Деление смешанных чисел
Чтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.
Пример 1. Найти значение выражения ![]()
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
![]()
Как решать дальше мы уже знаем. Первую дробь ![]() нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь
нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь ![]() .
.
Дорешаем данный пример до конца:
![]()
Допустим, имеются две целые и половина пиццы:
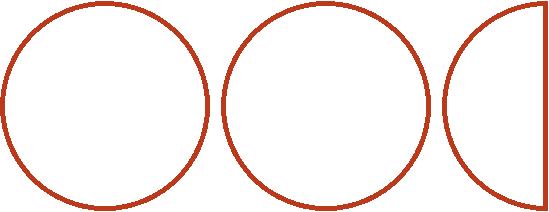
Если зададим вопрос «Сколько раз ![]() (одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
(одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
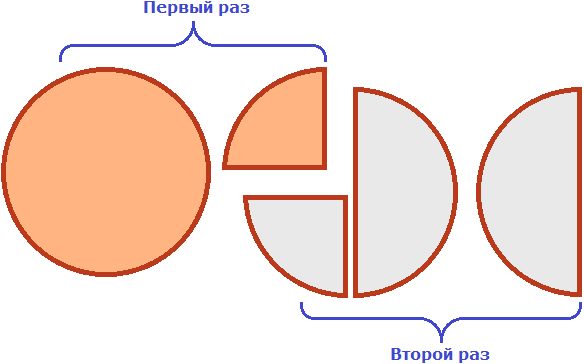
Пример 2. Найти значение выражения ![]()
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
![]()
Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь ![]()
![]()
Сначала мы получили дробь![]() . Эту дробь мы сократили на 9. В результате получили дробь
. Эту дробь мы сократили на 9. В результате получили дробь ![]() , но такой ответ нас тоже не устроил и мы выделили в дроби
, но такой ответ нас тоже не устроил и мы выделили в дроби ![]() целую часть. В результате получили окончательный ответ
целую часть. В результате получили окончательный ответ ![]() .
.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:

Решение:
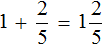
Задание 2. Найдите значение выражения:
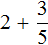
Решение:

Задание 3. Найдите значение выражения:

Решение:

Задание 4. Найдите значение выражения:

Решение:
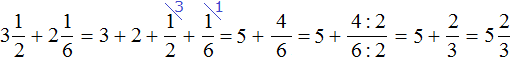
Задание 5. Найдите значение выражения:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Перед тем как перейти к сложению дробей, вспомним теоретические основы. Итак, дробь — это форма записи числа:
где a — числитель, b — знаменатель.
Дробь называется правильной — если числитель меньше знаменателя (к примеру, 1/3), неправильной — если числитель больше знаменателя (например, 5/2).
Вычитание обыкновенных дробей
Вычитание дробей — это арифметическое действие, в результате которого получается новое число, содержащее разность заданных чисел.
Разберем на конкретных примерах: как находить разность дробей с одинаковыми и разными знаменателями, как из натурального числа вычесть дробь и наоборот, познакомимся с вычитанием смешанных дробей.
Вычитание дробей с одинаковыми знаменателями
Чтобы вычесть дроби с одинаковыми знаменателями нужно из числителя первой дроби вычесть числитель второй, а знаменатели оставить без изменения. В общем виде это будет выглядеть следующим образом:
Пример 1:
7 8
—
2 8
Решение:
7 8
—
2 8
=
7 — 2 8
=
5 8
Таким образом, чтобы вычесть дроби с одинаковыми знаменателями нужно найти разность их числителей, а знаменатель оставить без изменения.
Как вычитать дроби с разными знаменателями
В общем виде, вычитание дробей с разными знаменателями, выглядит следующим образом:
a b
—
c d
=
a ∙ m1 — c ∙ m2 e
где e — наименьший общий знаменатель (НОЗ — наименьшее число, которое делится без остатка и на b и на d), m1 и m2 — дополнительные множители (m1 = e : b, m2 = e : d).
Пример 3:
5 3
—
2 7
Решение:
5 3
—
2 7
=
5 ∙ 7 21
—
2 ∙ 3 21
=
35 21
—
6 21
=
35 — 6 21
=
29 21
=
1
8 21
Подробнее про нахождение НОЗ — смотрите тут.
Как из целого числа вычесть дробь?
Вычитание обыкновенной дроби из целого числа, сводится к представлению целого числа в виде дроби, в которой знаменатель будет единицей, а числитель самим числом, к примеру:
Дальнейшее вычисление происходит по стандартному алгоритму.
Как из обыкновенной дроби вычесть целое число?
Порядок действий, при вычитании целого числа из дробного, аналогичен, т.е. представляем целое число в виде дроби со знаменателем — 1 и находим разность, согласно представленным выше алгоритмам вычитания.
Как вычитать смешанные дроби?
Вычитание смешанных дробей сводится к переводу их к неправильному виду и дальнейшим действиям согласно вышеописанным алгоритмам. Перевод смешанного числа в неправильную дробь, в общем виде, выглядит следующим образом:
Пример 4:
3
2 4
—
3 5
Решение:
3
2 4
—
3 5
=
3 ∙ 4 + 2 4
—
3 5
=
14 4
—
3 5
=
14 ∙ 5 20
—
3 ∙ 4 20
=
70 20
—
12 20
=
70 — 12 20
=
58 20
=
29 10
=
2
9 10
Правила вычитания дробей
Резюмируя вышесказанное, выведем общий алгоритм вычитания дробей:
- Если дробь смешанная — приводим её к неправильному виду;
- Если дроби имеют одинаковые знаменатели — из числителя первой дроби вычитаем числитель второй;
- Если дроби имеют разные знаменатели — находим НОЗ и дополнительные множители, находим разность числителей;
- При необходимости сокращаем и приводим к неправильному виду.
Смотрите также:
- Смотрите также
- Калькуляторы
- Последние примеры
Калькулятор вычитания дробей
Оцените материал:
![]() Загрузка…
Загрузка…
В данной статье рассмотрим правила, согласно которым выполняется действие вычитания смешанных чисел. Разберем конкретные примеры и некоторые нюансы при их решении. Изучим вычитание обыкновенной дроби и натурального числа из смешанного числа, а также – вычитание смешанного числа из дроби и натурального числа. Рассматривать вычитание мы будем при условии вычитания из большего числа меньшее.
Вычитание смешанных чисел
Пусть в качестве исходных данных даны два смешанных числа: abc и def , необходимо выполнить вычитание данных смешанных чисел.
Нам известно, что любое смешанное число возможно представить, как сумму его целой и дробной части, тогда получим:
abc-def=a+bc-d+ef
Свойства действий сложения и вычитания дают возможность выполнить вычисление полученного выражения различными способами. Опираясь на значения дробных частей смешанных чисел
abc и def , необходимо придерживаться следующих схем вычисления:
- если дробная часть уменьшаемого больше, чем дробная часть вычитаемого:
bc>ef, то вычитание оптимально будет произвести так:
abc-def=(a-d)+bc-ef
Произвести вычитание смешанных чисел: 356-249 .
Решение
Сравним дробные части смешанных чисел, т.е. 56 и 49 . Чтобы определить, какая из дробей больше, приведем их к общему наименьшем знаменателю или наименьшему общему кратному: НОК (6, 9) = 18. При этом дополнительным множителем для дроби 56 станет 18 : 6 = 3; а для дроби 49 – 18 : 9 = 2, поэтому : 56=5·36·3=1518 и 49=4·29·2=818 .
Оценим полученный результат: 1518>818, что означает 56>49. Т.е. дробная часть уменьшаемого больше дробной части вычитаемого, и тогда действие вычитания производится путем раздельного вычитания целых и дробных частей заданных смешанных чисел:
3-2=156-49=1518-818=15-818=718
Т.е.: (3-2)+56-49=1+718=1718
Ответ: 356-249=1718
- если дробные части заданных смешанных чисел равны: bc=ef , а, соответственно разность их равна нулю, то результатом вычитания таких смешанных чисел будет разность их целых частей:
abc-def=(a-d)+bc-ef=a-d+0=a-d
Произвести вычитание смешанных чисел 15710 и 2710 .
Решение
Мы видим, что дробные части заданных чисел равны, т.е. их разность есть нуль. Таким образом, действие вычитания заданных чисел сводится к нахождению разности их целых частей: 15710-2710=15+710-2+710=15-2+710-710=15-2+0=13
Ответ: 15710-2710=13
- если дробная часть уменьшаемого меньше дробной части вычитаемого: bc<ef , то действие вычитания оптимально произвести так:
abc-def=a-d-ef+bc
Произвести вычитание смешанных чисел: 2625-81415 .
Решение
Проведем сравнение дробных частей заданных чисел, определив для начала наименьший общий знаменатель: НОК (5, 15) = 15, тогда 25=2·35·3=615 .
Следовательно: 615<1415, т.е. дробная часть уменьшаемого меньше дробной части вычитаемого. Таким образом, находить разность заданных смешанных чисел будем так: 2625-81415=26615-81415=26+615-8+1415==26-8-1415+615=18-1415+615
Для начала вычтем дробь из натурального числа (в скобках): 18-1415=(17+1)-1415=17+1+1415=17+11+1415==17+1515-1415=17+115
Тогда 18-1415+615=17+115+615=17+115+615==17+715=17715
Ответ: 2625-81415=17715 .
Вычитание обыкновенной дроби из смешанного числа
Схема вычитания правильной дроби из смешанного числа такая же, как при действии вычитания смешанных чисел.
Найти разницу: 356-415
Решение:
Приведем дробные части заданных чисел к единому наименьшему общему кратному: НОК (6, 15) = 30, тогда 65=5·56·5=2530 и 415=4·215·2=830 .
Таким образом, 56>415 .
В итоге вычитание возможно произвести так: 356-415=3+56-415=3+56-415=3+2530-830=3+1730=31730
Ответ: 356-415=31730
Произвести действие вычитания: 127-37
Решение
Дробные части исходных чисел имеют одинаковый знаменатель, что дает возможность их легко сравнить. Понятно, что 27 меньше, чем 37.
Тогда находить разницу будем так:
127-37=1+27-37=1-37+27=11-37+27==77-37+27=47+27=67
Ответ: 127-37=67.
Добавим еще одну, в общем очевидную деталь вычислений: если дробная часть смешанного числа равна вычитаемой дроби, то итогом вычисления будет число, равное целой части уменьшаемого смешанного числа. К примеру:
16311-311=16+311-311=16+311-311=16+0=16
Чтобы вычесть неправильную дробь из смешанного числа, необходимо выделить целую часть из неправильной дроби, а затем производить вычисление.
Вычислить значение разности: 7512-199 .
Решение: вычитаемая дробь является неправильной, выделим из нее целую часть и получим: 199=219
Приведем к общему знаменателю дробные части заданных чисел и согласно указанным выше схемам произведем вычитание смешанных чисел:
7512-219=7+512-2+19=7-2+512-19==5+1536-436=5+1136=51136
Ответ: 7512-199=51136 .
Вычитание натурального числа из смешанного
Для совершения действия вычитания натурального числа из смешанного, необходимо вычесть заданное натуральное число из целой части смешанного числа, а дробную часть оставить без изменений: abc-n=a-n+bc
Необходимо вычесть из смешанного числа 1511528 натуральное число 44.
Решение: 1511528-44=151+1528-44=151-44+1528=107+1528=1071528
Ответ: 1511528-44=1071528
Вычитание смешанного числа из обыкновенной дроби
Очевидно, что любое заданное смешанное число будет больше единицы. Уменьшаемая дробь должна быть больше вычитаемого, тогда эта дробь – неправильная. Необходимо выделить целую часть из неправильной дроби, и далее выполнение действия вычитания смешанного числа из обыкновенной дроби сведется к вычитанию смешанных чисел.
Необходимо выполнить вычитание: 749-612
Решение
В первую очередь выделим целую часть неправильной уменьшаемой дроби: 749=829 , тогда заданный пример примет вид: 749-612=829-612
Найдем наименьший общий знаменатель: НОК (9, 2) = 18.
Получим: 29=2·29·2=418 и 12=1·92·9=918.
Тогда:
829-612=8418-6918=8+418-6+918=8-6-918+418==2-918+418=1+1-918+418=1+1-918+418==1+1-918+418=1+918+418=1+918+418==1+9+418=1+1318=11318
Ответ: 749-612=11318
Вычитание смешанного числа из натурального
Чтобы произвести действие вычитания смешанного числа из натурального, сначала от натурального числа отнимаем целую часть смешанного, после чего из полученного результата вычитаем дробную часть:
n-abc=n-a+bc=n-a-bc
Необходимо вычесть из натурального числа 18 смешанное число.
Решение
18-535=18-5+35=18-5-35=13-35=12+1-35==12+1-35=12+11-35=12+55-35=12+5-35==12+25=1225
Ответ: 18-535=1225
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Загрузить PDF
Загрузить PDF
Вычитать дроби из целых чисел проще, чем кажется. Для этого можно воспользоваться одним из двух способов: преобразовать целое число в дробь или вычесть 1 из целого числа и преобразовать 1 в дробь с тем же знаменателем, как у вычитаемой дроби. Помните, что вычитать можно только дроби с общим знаменателем.
-

1
Преобразуйте целое число в дробь. Для этого под целым число запишите цифру 1 — это будет знаменатель новой дроби.[1]
- Пример:
- Пример:
-

2
-

3
-

4
Реклама
-

1
Воспользуйтесь этим методом, если дано большое целое число. В предыдущем разделе мы рассказали вам, как преобразовать целое число в дробь и неправильную дробь в смешанное число. В этом методе мы будем работать с небольшими дробями.
-

2
-

3
Разложите целое число на сумму 1 и другого целого числа. Например, 5 = 4 + 1 или 22 = 21 + 1.
-

4
Преобразуйте 1 в дробь. Для этого воспользуйтесь действиями, описанными в предыдущем разделе. Сейчас мы покажем, как решить часть выражения «1 – дробь». Другое целое число останется неизменным.
-

5
Приведите обе дроби к общему знаменателю. Для этого воспользуйтесь действиями, которые описаны в предыдущем разделе, а именно умножьте числитель и знаменатель новой дроби на знаменатель исходной дроби.
-

6
Реклама
Что вам понадобится
- Карандаш
- Лист бумаги
Об этой статье
Эту страницу просматривали 238 849 раз.







