Следующее действие, которое можно выполнять с обыкновенными дробями, – вычитание. В рамках этого материала мы рассмотрим, как правильно вычислить разность дробей с одинаковыми и разными знаменателями, как вычесть дробь из натурального числа и наоборот. Все примеры будут проиллюстрированы задачами. Заранее уточним, что мы будем разбирать лишь случаи, когда разность дробей дает в итоге положительное число.
Как найти разность дробей с одинаковыми знаменателями
Начнем сразу с наглядного примера: допустим, у нас есть яблоко, которое разделили на восемь частей. Оставим пять частей на тарелке и заберем две из них. Это действие можно записать так:
58-28
В итоге у нас осталось 3 восьмых доли, поскольку 5−2=3. Получается, что 58-28=38.
Благодаря этому простому примеру мы увидели, как именно работает правило вычитания для дробей, знаменатели которых одинаковы. Сформулируем его.
Чтобы найти разность дробей с одинаковыми знаменателями, нужно из числителя одной вычесть числитель другой, а знаменатель оставить прежним. Это правило можно записать в виде ab-cb=a-cb.
Такую формулу мы будем использовать и в дальнейшем.
Возьмем конкретные примеры.
Вычтите из дроби 2415 обыкновенную дробь 1715.
Решение
Мы видим, что эти дроби имеют одинаковые знаменатели. Поэтому все, что нам нужно сделать, – это вычесть 17 из 24. Мы получаем 7 и дописываем к ней знаменатель, получаем 715.
Наши подсчеты можно записать так: 2415-1715=24-1715=715
Если необходимо, можно сократить сложную дробь или выделить целую часть из неправильной, чтобы считать было удобнее.
Найдите разность 3712-1512.
Решение
Воспользуемся описанной выше формулой и подсчитаем: 3712-1512=37-1512=2212
Легко заметить, что числитель и знаменатель можно разделить на 2 (об этом мы уже говорили ранее, когда разбирали признаки делимости). Сократив ответ, получим 116. Это неправильная дробь, из которой мы выделим целую часть: 116=156.
Как найти разность дробей с разными знаменателями
Такое математическое действие можно свести к тому, что мы уже описывали выше. Для этого просто приведем нужные дроби к одному знаменателю. Сформулируем определение:
Чтобы найти разность дробей, у которых разные знаменатели, необходимо привести их к одному знаменателю и найти разность числителей.
Рассмотрим на примере, как это делается.
Вычтите из 29 дробь 115.
Решение
Знаменатели разные, и нужно привести их к наименьшему общему значению. В данном случае НОК равно 45. Для первой дроби необходим дополнительный множитель 5, а для второй – 3.
Подсчитаем: 29=2·59·5=1045115=1·315·3=345
У нас получились две дроби с одинаковым знаменателем, и теперь мы легко можем найти их разность по описанному ранее алгоритму: 1045-345=10-345=745
Краткая запись решения выглядит так: 29-115=1045-345=10-345=745.
Не стоит пренебрегать сокращением результата или выделением из него целой части, если это необходимо. В данном примере нам этого не нужно делать.
Найдите разность 199 – 736.
Решение
Приведем указанные в условии дроби к наименьшему общему знаменателю 36 и получим соответственно 769 и 736.
Считаем ответ: 7636-736=76-736=6936
Результат можно сократить на 3 и получить 2312. Числитель больше знаменателя, а значит, мы можем выделить целую часть. Итоговый ответ – 11112.
Краткая запись всего решения – 199-736=11112.
Как вычесть из обыкновенной дроби натуральное число
Такое действие также легко свести к простому вычитанию обыкновенных дробей. Это можно сделать, представив натуральное число в виде дроби. Покажем на примере.
Найдите разность 8321 – 3.
Решение
3 – то же самое, что и 31. Тогда можно подсчитать так: 8321-3=2021.
Если в условии необходимо вычесть целое число из неправильной дроби, удобнее сначала выделить из нее целое, записав ее в виде смешанного числа. Тогда предыдущий пример можно решить иначе.
Из дроби 8321 при выделении целой части получится 8321=32021.
Теперь просто вычтем 3 из него: 32021-3=2021.
Как вычесть обыкновенную дробь из натурального числа
Это действие делается аналогично предыдущему: мы переписываем натуральное число в виде дроби, приводим обе к единому знаменателю и находим разность. Проиллюстрируем это примером.
Найдите разность: 7-53.
Решение
Сделаем 7 дробью 71. Делаем вычитание и преобразуем конечный результат, выделяя из него целую часть: 7-53=513.
Есть и другой способ произвести расчеты. Он обладает некоторыми преимуществами, которыми можно воспользоваться в тех случаях, если числители и знаменатели дробей в задаче – большие числа.
Если та дробь, которую нужно вычесть, является правильной, то натуральное число, из которого мы вычитаем, нужно представить в виде суммы двух чисел, одно из которых равно 1. После этого нужно вычесть нужную дробь из единицы и получить ответ.
Вычислите разность 1 065 -1362.
Решение
Дробь, которую нужно вычесть – правильная, ведь ее числитель меньше знаменателя. Поэтому нам нужно отнять единицу от 1065 и вычесть из нее нужную дробь: 1065-1362=(1064+1)-1362
Теперь нам нужно найти ответ. Используя свойства вычитания, полученное выражение можно записать как 1064+1-1362. Подсчитаем разность в скобках. Для этого единицу представим как дробь 11.
Получается, что 1-1362=11-1362=6262-1362=4962.
Теперь вспомним про 1064 и сформулируем ответ: 10644962.
Используем старый способ, чтобы доказать, что он менее удобен. Вот такие вычисления вышли бы у нас:
1065-1362=10651-1362=1065·621·62-1362=6603062-1362==66030-1362=6601762=106446
Ответ тот же, но подсчеты, очевидно, более громоздкие.
Мы рассмотрели случай, когда нужно вычесть правильную дробь. Если она неправильная, мы заменяем ее смешанным числом и производим вычитание по знакомым правилам.
Вычислите разность 644 – 735.
Решение
Вторая дробь – неправильная, и от нее надо отделить целую часть.
735=1435
Теперь вычисляем аналогично предыдущему примеру: 630-35=(629+1)-35=629+1-35=629+25=62925
Свойства вычитания при работе с дробями
Те свойства, которыми обладает вычитание натуральных чисел, распространяются и на случаи вычитания обыкновенных дробей. Рассмотрим, как использовать их при решении примеров.
Найдите разность 244-32-56.
Решение
Схожие примеры мы уже решали, когда разбирали вычитание суммы из числа, поэтому действуем по уже известному алгоритму. Сначала подсчитаем разность 254-32, а потом отнимем от нее последнюю дробь:
254-32=244-64=194194-56=5712-1012=4712
Преобразуем ответ, выделив из него целую часть. Итог – 31112.
Краткая запись всего решения:
254-32-56=254-32-56=254-64-56==194-56=5712-1012=4712=31112
Если в выражении присутствуют и дроби, и натуральные числа, то рекомендуется при подсчетах сгруппировать их по типам.
Н айдите разность 98+1720-5+35.
Решение
Зная основные свойства вычитания и сложения, мы можем сгруппировать числа следующим образом: 98+1720-5+35=98+1720-5-35=98-5+1720-35
Завершим расчеты: 98-5+1720-35=93+1720-1220=93+520=93+14=9314
Перед тем как перейти к сложению дробей, вспомним теоретические основы. Итак, дробь — это форма записи числа:
где a — числитель, b — знаменатель.
Дробь называется правильной — если числитель меньше знаменателя (к примеру, 1/3), неправильной — если числитель больше знаменателя (например, 5/2).
Вычитание обыкновенных дробей
Вычитание дробей — это арифметическое действие, в результате которого получается новое число, содержащее разность заданных чисел.
Разберем на конкретных примерах: как находить разность дробей с одинаковыми и разными знаменателями, как из натурального числа вычесть дробь и наоборот, познакомимся с вычитанием смешанных дробей.
Вычитание дробей с одинаковыми знаменателями
Чтобы вычесть дроби с одинаковыми знаменателями нужно из числителя первой дроби вычесть числитель второй, а знаменатели оставить без изменения. В общем виде это будет выглядеть следующим образом:
Пример 1:
7 8
—
2 8
Решение:
7 8
—
2 8
=
7 — 2 8
=
5 8
Таким образом, чтобы вычесть дроби с одинаковыми знаменателями нужно найти разность их числителей, а знаменатель оставить без изменения.
Как вычитать дроби с разными знаменателями
В общем виде, вычитание дробей с разными знаменателями, выглядит следующим образом:
a b
—
c d
=
a ∙ m1 — c ∙ m2 e
где e — наименьший общий знаменатель (НОЗ — наименьшее число, которое делится без остатка и на b и на d), m1 и m2 — дополнительные множители (m1 = e : b, m2 = e : d).
Пример 3:
5 3
—
2 7
Решение:
5 3
—
2 7
=
5 ∙ 7 21
—
2 ∙ 3 21
=
35 21
—
6 21
=
35 — 6 21
=
29 21
=
1
8 21
Подробнее про нахождение НОЗ — смотрите тут.
Как из целого числа вычесть дробь?
Вычитание обыкновенной дроби из целого числа, сводится к представлению целого числа в виде дроби, в которой знаменатель будет единицей, а числитель самим числом, к примеру:
Дальнейшее вычисление происходит по стандартному алгоритму.
Как из обыкновенной дроби вычесть целое число?
Порядок действий, при вычитании целого числа из дробного, аналогичен, т.е. представляем целое число в виде дроби со знаменателем — 1 и находим разность, согласно представленным выше алгоритмам вычитания.
Как вычитать смешанные дроби?
Вычитание смешанных дробей сводится к переводу их к неправильному виду и дальнейшим действиям согласно вышеописанным алгоритмам. Перевод смешанного числа в неправильную дробь, в общем виде, выглядит следующим образом:
Пример 4:
3
2 4
—
3 5
Решение:
3
2 4
—
3 5
=
3 ∙ 4 + 2 4
—
3 5
=
14 4
—
3 5
=
14 ∙ 5 20
—
3 ∙ 4 20
=
70 20
—
12 20
=
70 — 12 20
=
58 20
=
29 10
=
2
9 10
Правила вычитания дробей
Резюмируя вышесказанное, выведем общий алгоритм вычитания дробей:
- Если дробь смешанная — приводим её к неправильному виду;
- Если дроби имеют одинаковые знаменатели — из числителя первой дроби вычитаем числитель второй;
- Если дроби имеют разные знаменатели — находим НОЗ и дополнительные множители, находим разность числителей;
- При необходимости сокращаем и приводим к неправильному виду.
Смотрите также:
- Смотрите также
- Калькуляторы
- Последние примеры
Калькулятор вычитания дробей
Оцените материал:
![]() Загрузка…
Загрузка…
Вычитание обыкновенных дробей
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
- Онлайн калькулятор вычитания дробей
Вычитание дробей с одинаковыми знаменателями
Чтобы найти разность двух обыкновенных дробей, у которых одинаковые знаменатели, надо из числителя первой дроби вычесть числитель второй дроби и под полученной разностью подписать их общий знаменатель.
Используя буквы, запишем правило вычитания обыкновенных дробей с одинаковыми знаменателями в виде формулы:

Пример. Выполнить вычитание дробей с одинаковыми знаменателями:

Если уменьшаемое равно вычитаемому, то разность равна нулю:

Вычитание дробей с разными знаменателями
Чтобы найти разность двух дробей , у которых разные знаменатели, нужно:
- найти общий знаменатель;
- привести дроби к общему знаменателю (желательно к наименьшему общему знаменателю);
- выполнить вычитание дробей: из числителя первой дроби вычесть числитель второй дроби и под полученной разностью подписать общий знаменатель;
- сократить полученную дробь, если это возможно.
Пример. Выполнить вычитание дробей с разными знаменателями:

Онлайн калькулятор вычитания дробей
Данный калькулятор поможет вам найти разность двух обыкновенных дробей с одинаковыми или разными знаменателями. Просто введите две дроби и нажмите кнопку Вычислить
.
Математика
5 класс
Урок № 59
Вычитание дробей
Перечень рассматриваемых вопросов:
– вычитание дробей с одинаковыми знаменателями;
– вычитание дробей с разными знаменателями;
– проверка вычитания сложением.
Тезаурус
Разность двух дробей – это дробь, которая в сумме с вычитаемым даёт уменьшаемое.
Разность двух дробей с общим знаменателем – это дробь с тем же знаменателем, числитель которой равен разности числителей уменьшаемого и вычитаемого.
Обязательная литература:
- Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. ФГОС. / С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 272.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты. 5 кл. / П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009, стр.142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. / И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Вспомним, что такое разность дробей. Разностью двух дробей называют дробь, которая в сумме с вычитаемым даёт уменьшаемое.

Будем пока рассматривать случаи, когда уменьшаемое больше вычитаемого.
Разность двух дробей с общим знаменателем есть дробь с тем же знаменателем, числитель которой равен разности числителей уменьшаемого и вычитаемого.


Какую часть корзинки осталось набрать?
Давайте подумаем, как построить ход решения и какими арифметическими действиями его сопроводить?
Так как Таня ходила за ягодами два раза, то найти, сколько всего ягод она набрала, нам поможет арифметическое действие – сложение:

Вопрос в задаче – какую часть корзинки осталось набрать?
Значит, нам нужно из объёма всей корзинки, вычесть ту часть, которую Таня уже набрала.

Сделаем проверку:

Сумма разности и вычитаемого действительно равна уменьшаемому.
Чтобы найти разность двух дробей с разными знаменателями, надо привести их к общему знаменателю, а затем применить правило вычитания дробей с общим знаменателем.

Например, найдём разность семи восьмых и трёх пятых. Знаменатели дробей взаимно простые числа, поэтому общий знаменатель равен их произведению, т. е. сорока.
Не забываем умножить дополнительные множители и на числители. В итоге получаем дробь одиннадцать сороковых.

Решим задачу. Две сестры помогли маме помыть посуду.

Младшая – ?
Найдём разность всей вымытой посуды и той части, которую вымыла старшая дочь.

Итак, чтобы найти разность двух дробей, нужно определить равные или разные у них знаменатели, а затем использовать то правило вычитания дробей, которое подходит в конкретном случае.
Вычитание обыкновенных дробей

Разбор решения заданий тренировочного модуля
№1. На ветке сидели воробьи. Когда четверть воробьёв улетела, их осталось 9. Сколько воробьёв было на ветке?


По рисунку видно, что в трёх равных оставшихся частях 9 воробьёв, значит в одной части:
- 9 : 3 = 3 – воробья в одной части.
Одна часть воробьёв улетела, значит, улетело 3.
Тогда:
- 3 + 9 = 12 – воробьёв было всего на ветке.
Или можно ответить на вопрос так: в одной части 3 воробья, а всего таких частей 4, значит:
- 3 ∙ 4 = 12 – воробьёв было всего на ветке.
Ответ: 12 воробьёв сидело на ветке.
№2. Выберите выражения, в которых в результате вычитания получается единица.

Решение: найдём результаты каждого выражения.

Мы видим, что только в двух выражениях в результате получилась единица. Это и есть верные ответы.

При вычитании дробей, как и при сложении, могут встретиться несколько случаев.
Вычитание дробей с одинаковыми знаменателями
При вычитании дробей с одинаковыми знаменателями от числителя уменьшаемого (первой дроби) отнимают
числитель вычитаемого (второй дроби), а знаменатель оставляют прежним.
Пример.
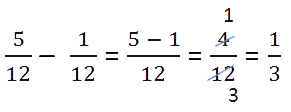
Запомните!
![]()
Прежде чем записать конечный ответ, проверьте, нельзя ли сократить полученную дробь.
В буквенном виде правило вычитания дробей с одинаковыми знаменателями
записывают так:
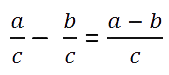
Вычитание правильной дроби из единицы
Когда нужно вычесть из единицы правильную дробь, единицу представляют в виде
неправильной дроби, знаменатель которой, равен знаменателю вычитаемой дроби.
Пример.
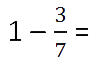
Знаменатель вычитаемой дроби равен 7, значит, единицу представляют как неправильную
дробь
и вычитают по правилу вычитания дробей с одинаковыми знаменателями.
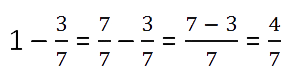
Вычитание правильной дроби из целого числа
Чтобы из целого числа вычесть правильную дробь нужно представить это натуральное число
в виде смешанного числа.
Для этого занимаем единицу в натуральном числе и представляем её в виде неправильной дроби,
знаменатель которой равен знаменателю вычитаемой дроби.
Пример.
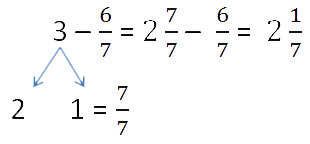
В примере единицу мы заменили неправильной дробью
и вместо 3 записали смешанное
число и от дробной части отняли дробь.
Вычитание смешанных чисел
При вычитании смешанных чисел отдельно из целой части вычитают целую часть, а из дробной части
вычитают дробную часть.
При подобных расчётах могут встретиться разные случаи.
Первый случай вычитания смешанных чисел
У дробных частей одинаковые знаменатели и числитель дробной части
уменьшаемого (из чего вычитаем) больше или равен числителю дробной части вычитаемого
(что вычитаем).
Пример.
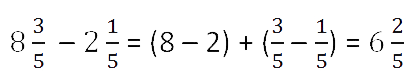
Второй случай вычитания смешанных чисел
У дробных частей разные знаменатели.
В этом случае вначале нужно
привести к общему знаменателю
дробные части, а затем
выполнить вычитание целой части из целой, а дробной из дробной.
Пример.
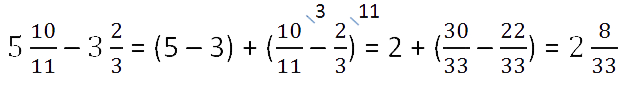
Третий случай вычитания смешанных чисел
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример.
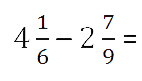
Так как у дробных частей разные знаменатели, то как и
во втором случае, вначале приведём обыкновенные дроби к общему знаменателю.
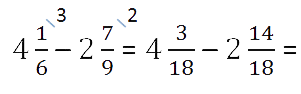
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого.
3 < 14
Поэтому, вспомнив
вычитание правильной дроби из целого числа, займём единицу из целой части и представим
эту единицу в виде неправильной дроби с одинаковым знаменателем и числителем равным 18.
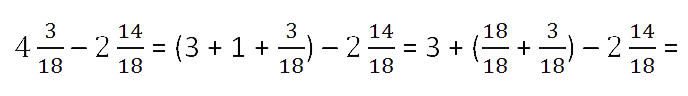
Сложим полученную неправильную дробь
и дробную часть
уменьшаемого и получим:
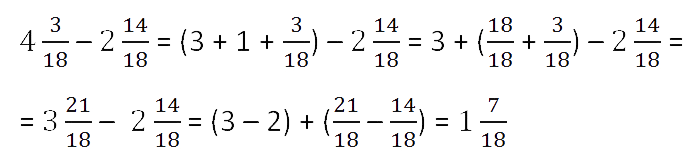
Все рассмотренные случаи можно описать с помощью правил вычитания
смешанных чисел.
- Привести дробные части уменьшаемого и вычитаемого к наименьшему общему знаменателю.
- Если дробная часть уменьшаемого меньше дробной части
вычитаемого, то занимаем у целой части уменьшаемого единицу. Эту единицу
превращаем в неправильную дробь с одинаковым числителем и знаменателем равными наименьшему общему знаменателю. - Прибавляем полученную неправильную дробь к дробной части уменьшаемого.
- Вычитаем из целой части целую, а из дробной — дробную.
- Проверяем, нельзя ли сократить и выделить целую часть в конечной дроби.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
13 ноября 2019 в 6:24
Валя Гутник

Профиль
Благодарили: 0
Сообщений: 7

Валя Гутник
Профиль
Благодарили: 0
Сообщений: 7
как вычитать дроби с разным знаменателем
−
0
Спасибо
Ответить
15 апреля 2020 в 13:34
Ответ для Валя Гутник
Саша Алекс

Профиль
Благодарили: 0
Сообщений: 1

Саша Алекс
Профиль
Благодарили: 0
Сообщений: 1
Хз
0
Спасибо
Ответить
18 марта 2019 в 18:37
Никита Рулькевич

Профиль
Благодарили: 0
Сообщений: 2

Никита Рулькевич
Профиль
Благодарили: 0
Сообщений: 2
0
Спасибо
Ответить
18 марта 2019 в 18:51
Ответ для Никита Рулькевич
Никита Рулькевич

Профиль
Благодарили: 0
Сообщений: 2

Никита Рулькевич
Профиль
Благодарили: 0
Сообщений: 2
11 ![]()
0
Спасибо
Ответить
4 сентября 2015 в 12:08
Зарина-И-Владимир Вебер

Профиль
Благодарили: 0
Сообщений: 1

Зарина-И-Владимир Вебер
Профиль
Благодарили: 0
Сообщений: 1
?12
? 7
? ?
?я незнаю ответ помогите пожалуста
0
Спасибо
Ответить
2 сентября 2016 в 14:33
Ответ для Зарина-И-Владимир Вебер
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Сначала — действие в скобках. Переводим в дробь целую часть, приводим к общему знаменателю, производим действие, далее производим умножение.
= (
?) · = · = = == 2=2,5
0
Спасибо
Ответить
7 апреля 2015 в 13:14
Женечка Беляевская

Профиль
Благодарили: 0
Сообщений: 1

Женечка Беляевская
Профиль
Благодарили: 0
Сообщений: 1
вычитание дроби из целого числа 9-
0
Спасибо
Ответить
8 апреля 2015 в 0:39
Ответ для Женечка Беляевская
Алёна Гермес

Профиль
Благодарили: 0
Сообщений: 2

Алёна Гермес
Профиль
Благодарили: 0
Сообщений: 2
9-3/4 = 9/1-3/4 = 36/4-3/4 = 33/4 = 8
Целое число представляем в виде дроби, затем приводим к общему знаменателю, путем умножения первой дроби на знаменаетль второй и знаменателя первой на вторую дробь. Получаем неправельную дробь, и превращаем её в правильную, делим 33 на 4 и получаем 8 и остаток от деления 1.
0
Спасибо
Ответить
14 апреля 2015 в 17:00
Ответ для Женечка Беляевская
Asel Talantbekovna

Профиль
Благодарили: 0
Сообщений: 8

Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
9- = 8 — =8 =8
0
Спасибо
Ответить
6 апреля 2015 в 14:02
Алексей Старков

Профиль
Благодарили: 0
Сообщений: 1

Алексей Старков
Профиль
Благодарили: 0
Сообщений: 1
(1 — 1/2): (1/2 — 1/3) =
0
Спасибо
Ответить
7 апреля 2015 в 3:34
Ответ для Алексей Старков
Алёна Гермес

Профиль
Благодарили: 0
Сообщений: 2

Алёна Гермес
Профиль
Благодарили: 0
Сообщений: 2
1) (1 — 1/2) = 1/1 — 1/2 = 2/2 — 1/2 = 1/2
Находим общий заменатель, перемножая первую дробь на знаменатель второй, и вторую на знаменатель первой.
2) (1/2 — 1/3) = 3/6 — 2/6 = 1/6
Находим общий знаменатель.
3) 1/2: 1/6 = 1/2 · 6/1 = 6/2 =3/1 = 3
Что бы разделить одну дробь на другую, нужно перевернуть вторую дробь и разделить её на первую. Затем следует сократить дробь.
0
Спасибо
Ответить
14 апреля 2015 в 17:08
Ответ для Алексей Старков
Asel Talantbekovna

Профиль
Благодарили: 0
Сообщений: 8

Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
(1- ): ( — )
1)
— =
2)
=
3)
– = =
0
Спасибо
Ответить
14 апреля 2015 в 17:10
Ответ для Алексей Старков
Asel Talantbekovna

Профиль
Благодарили: 0
Сообщений: 8

Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
последнее дествие исправлю!
: =
0
Спасибо
Ответить
9 апреля 2019 в 17:24
Ответ для Алексей Старков
Настя Бородина

Профиль
Благодарили: 0
Сообщений: 1

Настя Бородина
Профиль
Благодарили: 0
Сообщений: 1
самый понятный овет
0
Спасибо
Ответить
